stat341 / CM 361

Computational Statistics and Data Analysis is a course offered at the University of Waterloo
Spring 2009
Instructor: Ali Ghodsi

Sampling (Generating random numbers)

Generating Random Numbers - May 12, 2009

Generating random numbers in a computational setting presents challenges. A good way to generate random numbers in computational statistics involves analyzing various distributions using computational methods. As a result, the probability distribution of each possible number appears to be uniform (pseudo-random). Outside a computational setting, presenting a uniform distribution is fairly easy (for example, rolling a fair die repetitively to produce a series of random numbers from 1 to 6).

We begin by considering the simplest case: the uniform distribution.

Multiplicative Congruential Method

One way to generate pseudo random numbers from the uniform distribution is using the Multiplicative Congruential Method. This involves three integer parameters a, b, and m, and a seed variable x₀. This method deterministically generates a sequence of numbers (based on the seed) with a seemingly random distribution (with some caveats). It proceeds as follows:

[math]\displaystyle{ x_{i+1} = (ax_{i} + b) \mod{m} }[/math]

For example, with a = 13, b = 0, m = 31, x₀ = 1, we have:

[math]\displaystyle{ x_{i+1} = 13x_{i} \mod{31} }[/math]

So,

[math]\displaystyle{ \begin{align} x_{0} &{}= 1 \end{align} }[/math]

[math]\displaystyle{ \begin{align} x_{1} &{}= 13 \times 1 + 0 \mod{31} = 13 \\ \end{align} }[/math]

[math]\displaystyle{ \begin{align} x_{2} &{}= 13 \times 13 + 0 \mod{31} = 14 \\ \end{align} }[/math]

[math]\displaystyle{ \begin{align} x_{3} &{}= 13 \times 14 + 0 \mod{31} =27 \\ \end{align} }[/math]

etc.

The above generator of pseudorandom numbers is called a Mixed Congruential Generator or Linear Congruential Generator, as they involve both an additive and a muliplicative term. For correctly chosen values of a, b, and m, this method will generate a sequence of integers including all integers between 0 and m - 1. Scaling the output by dividing the terms of the resulting sequence by m - 1, we create a sequence of numbers between 0 and 1, which is similar to sampling from a uniform distribution.

Of course, not all values of a, b, and m will behave in this way, and will not be suitable for use in generating pseudo random numbers.

For example, with a = 3, b = 2, m = 4, x₀ = 1, we have:

[math]\displaystyle{ x_{i+1} = (3x_{i} + 2) \mod{4} }[/math]

So,

[math]\displaystyle{ \begin{align} x_{0} &{}= 1 \end{align} }[/math]

[math]\displaystyle{ \begin{align} x_{1} &{}= 3 \times 1 + 2 \mod{4} = 1 \\ \end{align} }[/math]

[math]\displaystyle{ \begin{align} x_{2} &{}= 3 \times 1 + 2 \mod{4} = 1 \\ \end{align} }[/math]

etc.

For an ideal situation, we want m to be a very large prime number, [math]\displaystyle{ x_{n}\not= 0 }[/math] for any n, and the period is equal to m-1. In practice, it has been found by a paper published in 1988 by Park and Miller, that a = 7⁵, b = 0, and m = 2³¹ - 1 = 2147483647 (the maximum size of a signed integer in a 32-bit system) are good values for the Multiplicative Congruential Method.

Java's Random class is based on a generator with a = 25214903917, b = 11, and m = 2⁴⁸<ref>http://java.sun.com/javase/6/docs/api/java/util/Random.html#next(int)</ref>. The class returns at most 32 leading bits from each x_i, so it is possible to get the same value twice in a row, (when x₀ = 18698324575379, for instance) without repeating it forever.

General Methods

Since the Multiplicative Congruential Method can only be used for the uniform distribution, other methods must be developed in order to generate pseudo random numbers from other distributions.

Inverse Transform Method

This method uses the fact that when a random sample from the uniform distribution is applied to the inverse of a cumulative density function (cdf) of some distribution, the result is a random sample of that distribution. This is shown by this theorem:

Theorem:

If [math]\displaystyle{ U \sim~ \mathrm{Unif}[0, 1] }[/math] is a random variable and [math]\displaystyle{ X = F^{-1}(U) }[/math], where F is continuous, monotonic, and is the cumulative density function (cdf) for some distribution, then the distribution of the random variable X is given by F(X).

Proof:

Recall that, if f is the pdf corresponding to F, then,

[math]\displaystyle{ F(x) = P(X \leq x) = \int_{-\infty}^x f(x) }[/math]

[math]\displaystyle{ \int_1^{\infty} \frac{x^k}{x^2} dx }[/math]

So F is monotonically increasing, since the probability that X is less than a greater number must be greater than the probability that X is less than a lesser number.

Note also that in the uniform distribution on [0, 1], we have for all a within [0, 1], [math]\displaystyle{ P(U \leq a) = a }[/math].

So,

[math]\displaystyle{ \begin{align} P(F^{-1}(U) \leq x) &{}= P(F(F^{-1}(U)) \leq F(x)) \\ &{}= P(U \leq F(x)) \\ &{}= F(x) \end{align} }[/math]

Completing the proof.

Procedure (Continuous Case)

This method then gives us the following procedure for finding pseudo random numbers from a continuous distribution:

• Step 1: Draw [math]\displaystyle{ U \sim~ Unif [0, 1] }[/math].
• Step 2: Compute [math]\displaystyle{ X = F^{-1}(U) }[/math].

Example:

Suppose we want to draw a sample from [math]\displaystyle{ f(x) = \lambda e^{-\lambda x} }[/math] where [math]\displaystyle{ x \gt 0 }[/math] (the exponential distribution).

We need to first find [math]\displaystyle{ F(x) }[/math] and then its inverse, [math]\displaystyle{ F^{-1} }[/math].

[math]\displaystyle{ F(x) = \int^x_0 \theta e^{-\theta u} du = 1 - e^{-\theta x} }[/math]

[math]\displaystyle{ F^{-1}(x) = \frac{-\log(1-y)}{\theta} = \frac{-\log(u)}{\theta} }[/math]

Now we can generate our random sample [math]\displaystyle{ i=1\dots n }[/math] from [math]\displaystyle{ f(x) }[/math] by:

[math]\displaystyle{ 1)\ u_i \sim Unif[0, 1] }[/math]

[math]\displaystyle{ 2)\ x_i = \frac{-\log(u_i)}{\theta} }[/math]

The [math]\displaystyle{ x_i }[/math] are now a random sample from [math]\displaystyle{ f(x) }[/math].

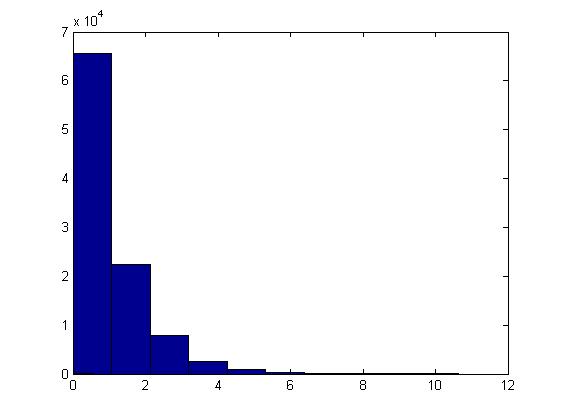
This example can be illustrated in Matlab using the code below. Generate [math]\displaystyle{ u_i }[/math], calculate [math]\displaystyle{ x_i }[/math] using the above formula and letting [math]\displaystyle{ \theta=1 }[/math], plot the histogram of [math]\displaystyle{ x_i }[/math]'s for [math]\displaystyle{ i=1,...,100,000 }[/math].

u=rand(1,100000);
x=-log(1-u)/1;
hist(x)

The histogram shows exponential pattern as expected.

The major problem with this approach is that we have to find [math]\displaystyle{ F^{-1} }[/math] and for many distributions it is too difficult (or impossible) to find the inverse of [math]\displaystyle{ F(x) }[/math]. Further, for some distributions it is not even possible to find [math]\displaystyle{ F(x) }[/math] (i.e. a closed form expression for the distribution function, or otherwise; even if the closed form expression exists, it's usually difficult to find [math]\displaystyle{ F^{-1} }[/math]).

Procedure (Discrete Case)

The above method can be easily adapted to work on discrete distributions as well.

In general in the discrete case, we have [math]\displaystyle{ x_0, \dots , x_n }[/math] where:

[math]\displaystyle{ \begin{align}P(X = x_i) &{}= p_i \end{align} }[/math]

[math]\displaystyle{ x_0 \leq x_1 \leq x_2 \dots \leq x_n }[/math]

[math]\displaystyle{ \sum p_i = 1 }[/math]

Thus we can define the following method to find pseudo random numbers in the discrete case (note that the less-than signs from class have been changed to less-than-or-equal-to signs by me, since otherwise the case of [math]\displaystyle{ U = 1 }[/math] is missed):

• Step 1: Draw [math]\displaystyle{ U~ \sim~ Unif [0,1] }[/math].
• Step 2:
  • If [math]\displaystyle{ U \lt p_0 }[/math], return [math]\displaystyle{ X = x_0 }[/math]
  • If [math]\displaystyle{ p_0 \leq U \lt p_0 + p_1 }[/math], return [math]\displaystyle{ X = x_1 }[/math]
  • ...
  • In general, if [math]\displaystyle{ p_0+ p_1 + \dots + p_{k-1} \leq U \lt p_0 + \dots + p_k }[/math], return [math]\displaystyle{ X = x_k }[/math]

Example (from class):

Suppose we have the following discrete distribution:

[math]\displaystyle{ \begin{align} P(X = 0) &{}= 0.3 \\ P(X = 1) &{}= 0.2 \\ P(X = 2) &{}= 0.5 \end{align} }[/math]

The cumulative density function (cdf) for this distribution is then:

[math]\displaystyle{ F(x) = \begin{cases} 0, & \text{if } x \lt 0 \\ 0.3, & \text{if } 0 \leq x \lt 1 \\ 0.5, & \text{if } 1 \leq x \lt 2 \\ 1, & \text{if } 2 \leq x \end{cases} }[/math]

Then we can generate numbers from this distribution like this, given [math]\displaystyle{ u_0, \dots, u_n }[/math] from [math]\displaystyle{ U \sim~ Unif[0, 1] }[/math]:

[math]\displaystyle{ x_i = \begin{cases} 0, & \text{if } u_i \leq 0.3 \\ 1, & \text{if } 0.3 \lt u_i \leq 0.5 \\ 2, & \text{if } 0.5 \lt u_i \leq 1 \end{cases} }[/math]

This example can be illustrated in Matlab using the code below:

p=[0.3,0.2,0.5];
for i=1:1000;
  u=rand;
  if u <= p(1)
    x(i)=0;
  elseif u < sum(p(1,2))
    x(i)=1;
  else
    x(i)=2;
  end
end

Acceptance-Rejection Sampling - May 14, 2009

Today, we continue the discussion on sampling (generating random numbers) from general distributions with the Acceptance/Rejection Method.

Acceptance/Rejection Method

Suppose we wish to sample from a target distribution [math]\displaystyle{ f(x) }[/math] that is difficult or impossible to sample from directly. Suppose also that we have a proposal distribution [math]\displaystyle{ g(x) }[/math] from which we have a reasonable method of sampling (e.g. the uniform distribution). Then, if there is a constant [math]\displaystyle{ c \ |\ c \cdot g(x) \geq f(x)\ \forall x }[/math], accepting samples drawn in successions from [math]\displaystyle{ c \cdot g(x) }[/math] with ratio [math]\displaystyle{ \frac {f(x)}{c \cdot g(x)} }[/math] close to 1 will yield a sample that follows the target distribution [math]\displaystyle{ f(x) }[/math]; on the other hand we would reject the samples if the ratio is not close to 1.

The following graph shows the pdf of [math]\displaystyle{ f(x) }[/math] (target distribution) and [math]\displaystyle{ c \cdot g(x) }[/math] (proposal distribution)

File:fxcgx.JPG

At x=7; sampling from [math]\displaystyle{ c \cdot g(x) }[/math] will yield a sample that follows the target distribution [math]\displaystyle{ f(x) }[/math]

At x=9; we will reject samples according to the ratio [math]\displaystyle{ \frac {f(x)}{c \cdot g(x)} }[/math] after sampling from [math]\displaystyle{ c \cdot g(x) }[/math]

Proof

Note the following:

• [math]\displaystyle{ Pr(X|accept) = \frac{Pr(accept|X) \times Pr(X)}{Pr(accept)} }[/math] (Bayes' theorem)
• [math]\displaystyle{ Pr(accept|X) = \frac{f(x)}{c \cdot g(x)} }[/math]
• [math]\displaystyle{ Pr(X) = g(x)\frac{}{} }[/math]

So, [math]\displaystyle{ Pr(accept) = \int^{}_x Pr(accept|X) \times Pr(X) dx }[/math] [math]\displaystyle{ = \int^{}_x \frac{f(x)}{c \cdot g(x)} g(x) dx }[/math] [math]\displaystyle{ = \frac{1}{c} \int^{}_x f(x) dx }[/math] [math]\displaystyle{ = \frac{1}{c} }[/math]

Therefore, [math]\displaystyle{ Pr(X|accept) = \frac{\frac{f(x)}{c\ \cdot g(x)} \times g(x)}{\frac{1}{c}} = f(x) }[/math] as required.

Procedure (Continuous Case)

• Choose [math]\displaystyle{ g(x) }[/math] (a density function that is simple to sample from)
• Find a constant c such that :[math]\displaystyle{ c \cdot g(x) \geq f(x) }[/math]

1. Let [math]\displaystyle{ Y \sim~ g(y) }[/math]
2. Let [math]\displaystyle{ U \sim~ Unif [0,1] }[/math]
3. If [math]\displaystyle{ U \leq \frac{f(x)}{c \cdot g(x)} }[/math] then X=Y; else reject and go to step 1

Example:

Suppose we want to sample from Beta(2,1), for [math]\displaystyle{ 0 \leq x \leq 1 }[/math]. Recall:

[math]\displaystyle{ Beta(2,1) = \frac{\Gamma (2+1)}{\Gamma (2) \Gamma(1)} \times x^1(1-x)^0 = \frac{2!}{1!0!} \times x = 2x }[/math]

• Choose [math]\displaystyle{ g(x) \sim~ Unif [0,1] }[/math]
• Find c: c = 2 (see notes below)

1. Let [math]\displaystyle{ Y \sim~ Unif [0,1] }[/math]
2. Let [math]\displaystyle{ U \sim~ Unif [0,1] }[/math]
3. If [math]\displaystyle{ U \leq \frac{2Y}{2} = Y }[/math], then X=Y; else go to step 1

[math]\displaystyle{ c }[/math] was chosen to be 2 in this example since [math]\displaystyle{ \max \left(\frac{f(x)}{g(x)}\right) }[/math] in this example is 2. This condition is important since it helps us in finding a suitable [math]\displaystyle{ c }[/math] to apply the Acceptance/Rejection Method.

In MATLAB, the code that demonstrates the result of this example is:

   j = 1;
       while i < 1000
           y = rand;
           u = rand;
           if u <= y
               x(j) = y;
               j = j + 1;
               i = i + 1;
           end
       end
       hist(x);
       

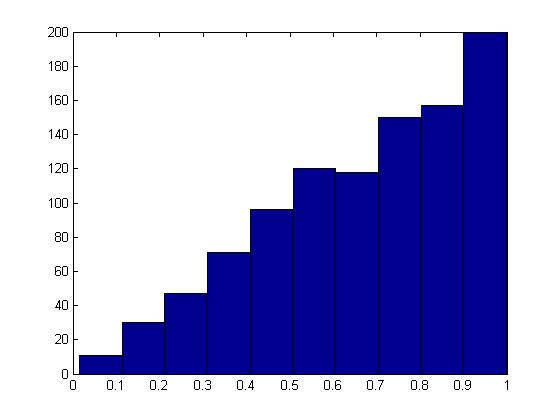
The histogram produced here should follow the target distribution, [math]\displaystyle{ f(x) = 2x }[/math], for the interval [math]\displaystyle{ 0 \leq x \leq 1 }[/math].

The histogram shows the PDF of a Beta(2,1) distribution as expected.

The Discrete Case

The Acceptance/Rejection Method can be extended for discrete target distributions. The difference compared to the continuous case is that the proposal distribution [math]\displaystyle{ g(x) }[/math] must also be discrete distribution. For our purposes, we can consider g(x) to be a discrete uniform distribution on the set of values that X may take on in the target distribution.

Example

Suppose we want to sample from a distribution with the following probability mass function (pmf):

P(X=1) = 0.15
P(X=2) = 0.55
P(X=3) = 0.20
P(X=4) = 0.10 

• Choose [math]\displaystyle{ g(x) }[/math] to be the discrete uniform distribution on the set [math]\displaystyle{ \{1,2,3,4\} }[/math]
• Find c: [math]\displaystyle{ c = \max \left(\frac{f(x)}{g(x)} \right)= 0.55/0.25 = 2.2 }[/math]

1. Generate [math]\displaystyle{ Y \sim~ Unif \{1,2,3,4\} }[/math]
2. Let [math]\displaystyle{ U \sim~ Unif [0,1] }[/math]
3. If [math]\displaystyle{ U \leq \frac{f(x)}{2.2 \times 0.25} }[/math], then X=Y; else go to step 1

Limitations

If the proposed distribution is very different from the target distribution, we may have to reject a large number of points before a good sample size of the target distribution can be established. It may also be difficult to find such [math]\displaystyle{ g(x) }[/math] that satisfies all the conditions of the procedure.

We will now begin to discuss sampling from specific distributions.

Special Technique for sampling from Gamma Distribution

Recall that the cdf of the Gamma distribution is:

[math]\displaystyle{ F(x) = \int_0^{\lambda x} \frac{e^{-y}y^{t-1}}{(t-1)!} dy }[/math]

If we wish to sample from this distribution, it will be difficult for both the Inverse Method (difficulty in computing the inverse function) and the Acceptance/Rejection Method.

Additive Property of Gamma Distribution

Recall that if [math]\displaystyle{ X_1, \dots, X_t }[/math] are independent exponential distributions with mean [math]\displaystyle{ \lambda }[/math] (in other words, [math]\displaystyle{ X_i\sim~ Exp (\lambda) }[/math]), then [math]\displaystyle{ \Sigma_{i=1}^t X_i \sim~ Gamma (t, \lambda) }[/math]

It appears that if we want to sample from the Gamma distribution, we can consider sampling from t independent exponential distributions with mean [math]\displaystyle{ \lambda }[/math] (using the Inverse Method) and add them up. Details will be discussed in the next lecture.

Techniques for Normal and Gamma Sampling - May 19, 2009

We have examined two general techniques for sampling from distributions. However, for certain distributions more practical methods exist. We will now look at two cases,
Gamma distributions and Normal distributions, where such practical methods exist.

Gamma Distribution

Given the additive property of the gamma distribution,

If [math]\displaystyle{ X_1, \dots, X_t }[/math] are independent random variables with [math]\displaystyle{ X_i\sim~ Exp (\lambda) }[/math] then,

[math]\displaystyle{ \Sigma_{i=1}^t X_i \sim~ Gamma (t, \lambda) }[/math]

We can use the Inverse Transform Method and sample from independent uniform distributions seen before to generate a sample following a Gamma distribution.

Procedure

1. Sample independently from a uniform distribution [math]\displaystyle{ t }[/math] times, giving [math]\displaystyle{ u_1,\dots,u_t }[/math]
2. Sample independently from an exponential distribution [math]\displaystyle{ t }[/math] times, giving [math]\displaystyle{ x_1,\dots,x_t }[/math] such that,
   [math]\displaystyle{ \begin{align} x_1 \sim~ Exp(\lambda)\\ \vdots \\ x_t \sim~ Exp(\lambda) \end{align} }[/math]
   
   Using the Inverse Transform Method,
   [math]\displaystyle{ \begin{align} x_i = -\frac {1}{\lambda}\log(u_i) \end{align} }[/math]
3. Using the additive property,
   [math]\displaystyle{ \begin{align} X &{}= x_1 + x_2 + \dots + x_t \\ X &{}= -\frac {1}{\lambda}\log(u_1) - \frac {1}{\lambda}\log(u_2) \dots - \frac {1}{\lambda}\log(u_t) \\ X &{}= -\frac {1}{\lambda}\log(\prod_{i=1}^{t}u_i) \sim~ Gamma (t, \lambda) \end{align} }[/math]

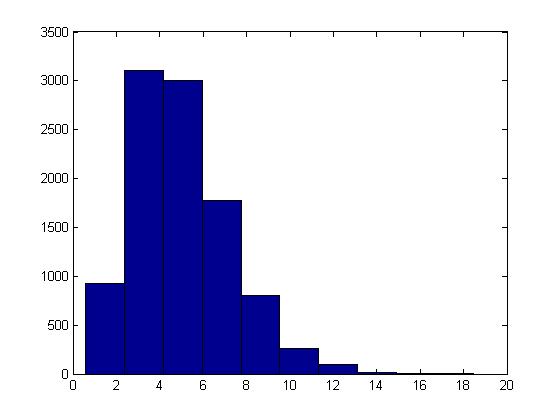
This procedure can be illustrated in Matlab using the code below with [math]\displaystyle{ t = 5, \lambda = 1 }[/math] :

U = rand(10000,5);
X = sum( -log(U), 2);
hist(X)

Normal Distribution

The cdf for the Standard Normal distribution is:

[math]\displaystyle{ F(Z) = \int_{-\infty}^{Z}\frac{1}{\sqrt{2\pi}}e^{-x^2/2}dx }[/math]

We can see that the normal distribution is difficult to sample from using the general methods seen so far, eg. the inverse is not easy to obtain from F(Z); we may be able to use the Acceptance-Rejection method, but there are still better ways to sample from a Standard Normal Distribution.

=====Box-Muller Method===== [Add a picture WikiSysop 19:25, 1 June 2009 (UTC)]

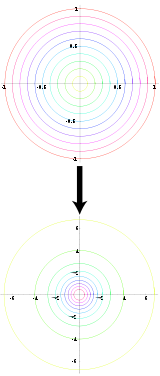"Diagram of the Box Muller transform, which transforms uniformly distributed value pairs to normally distributed value pairs." [Box-Muller Transform, Wikipedia]

The Box-Muller or Polar method uses an approach where we have one space that is easy to sample in, and another with the desired distribution under a transformation. If we know such a transformation for the Standard Normal, then all we have to do is transform our easy sample and obtain a sample from the Standard Normal distribution.

Properties of Polar and Cartesian Coordinates

If x and y are points on the Cartesian plane, r is the length of the radius from a point in the polar plane to the pole, and θ is the angle formed with the polar axis then,

• [math]\displaystyle{ \begin{align} r^2 = x^2 + y^2 \end{align} }[/math]
• [math]\displaystyle{ \tan(\theta) = \frac{y}{x} }[/math]

• [math]\displaystyle{ \begin{align} x = r \cos(\theta) \end{align} }[/math]
• [math]\displaystyle{ \begin{align} y = r \sin(\theta) \end{align} }[/math]

Let X and Y be independent random variables with a standard normal distribution,

[math]\displaystyle{ X \sim~ N(0,1) }[/math]

[math]\displaystyle{ Y \sim~ N(0,1) }[/math]

also, let [math]\displaystyle{ r }[/math] and [math]\displaystyle{ \theta }[/math] be the polar coordinates of (x,y). Then the joint distribution of independent x and y is given by,

[math]\displaystyle{ \begin{align} f(x,y) = f(x)f(y) &{}= \frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}\frac{1}{\sqrt{2\pi}}e^{-\frac{y^2}{2}} \\ &{}=\frac{1}{2\pi}e^{-\frac{x^2+y^2}{2}} \end{align} }[/math]

It can also be shown that the joint distribution of r and θ is given by,

[math]\displaystyle{ \begin{matrix} f(r,\theta) = \frac{1}{2}e^{-\frac{d}{2}}*\frac{1}{2\pi},\quad d = r^2 \end{matrix} }[/math]

Note that [math]\displaystyle{ \begin{matrix}f(r,\theta)\end{matrix} }[/math] consists of two density functions, Exponential and Uniform, so assuming that r and [math]\displaystyle{ \theta }[/math] are independent [math]\displaystyle{ \begin{matrix} \Rightarrow d \sim~ Exp(1/2), \theta \sim~ Unif[0,2\pi] \end{matrix} }[/math]

Procedure for using Box-Muller Method

1. Sample independently from a uniform distribution twice, giving [math]\displaystyle{ \begin{align} u_1,u_2 \sim~ \mathrm{Unif}(0, 1) \end{align} }[/math]
2. Generate polar coordinates using the exponential distribution of d and uniform distribution of θ,
   [math]\displaystyle{ \begin{align} d = -2\log(u_1),& \quad r = \sqrt{d} \\ & \quad \theta = 2\pi u_2 \end{align} }[/math]
3. Transform r and θ back to x and y,
   [math]\displaystyle{ \begin{align} x = r\cos(\theta) \\ y = r\sin(\theta) \end{align} }[/math]

Notice that the Box-Muller Method generates a pair of independent Standard Normal distributions, x and y.

This procedure can be illustrated in Matlab using the code below:

u1 = rand(5000,1);
u2 = rand(5000,1);

d = -2*log(u1);
theta = 2*pi*u2;

x = d.^(1/2).*cos(theta);
y = d.^(1/2).*sin(theta);

figure(1);

subplot(2,1,1);
hist(x);
title('X');
subplot(2,1,2);
hist(y);
title('Y');

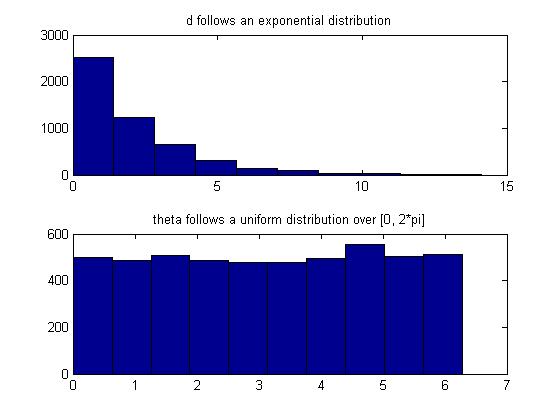
Also, we can confirm that d and theta are indeed exponential and uniform random variables, respectively, in Matlab by:

subplot(2,1,1);
hist(d);
title('d follows an exponential distribution');
subplot(2,1,2);
hist(theta);
title('theta follows a uniform distribution over [0, 2*pi]');

Useful Properties (Single and Multivariate)

Box-Muller can be used to sample a standard normal distribution. However, there are many properties of Normal distributions that allow us to use the samples from Box-Muller method to sample any Normal distribution in general.

Properties of Normal distributions

• [math]\displaystyle{ \begin{align} \text{If } & X = \mu + \sigma Z, & Z \sim~ N(0,1) \\ &\text{then } X \sim~ N(\mu,\sigma ^2) \end{align} }[/math]

• [math]\displaystyle{ \begin{align} \text{If } & \vec{Z} = (Z_1,\dots,Z_d)^T, & Z_1,\dots,Z_d \sim~ N(0,1) \\ &\text{then } \vec{Z} \sim~ N(\vec{0},I) \end{align} }[/math]

• [math]\displaystyle{ \begin{align} \text{If } & \vec{X} = \vec{\mu} + \Sigma^{1/2} \vec{Z}, & \vec{Z} \sim~ N(\vec{0},I) \\ &\text{then } \vec{X} \sim~ N(\vec{\mu},\Sigma) \end{align} }[/math]

These properties can be illustrated through the following example in Matlab using the code below:

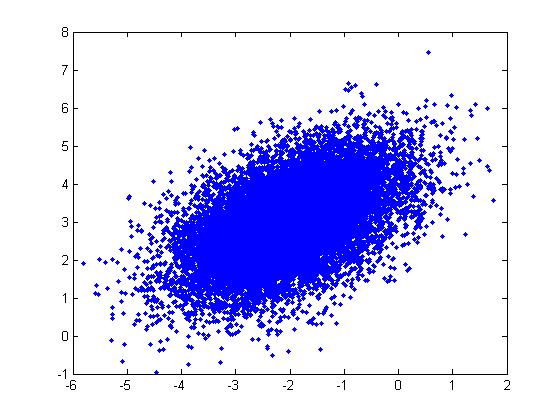
Example: For a Multivariate Normal distribution [math]\displaystyle{ u=\begin{bmatrix} -2 \\ 3 \end{bmatrix} }[/math] and [math]\displaystyle{ \Sigma=\begin{bmatrix} 1&0.5\\ 0.5&1\end{bmatrix} }[/math]

u = [-2; 3];
sigma = [ 1 1/2; 1/2 1];

r = randn(15000,2);
ss = chol(sigma);

X = ones(15000,1)*u' + r*ss;
plot(X(:,1),X(:,2), '.');

Note: In the example above, we had to generate the square root of [math]\displaystyle{ \Sigma }[/math] using the Cholesky decomposition,

ss = chol(sigma);

which gives [math]\displaystyle{ ss=\begin{bmatrix} 1&0.5\\ 0&0.8660\end{bmatrix} }[/math]. Matlab also has the sqrtm function:

ss = sqrtm(sigma);

which gives a different matrix, [math]\displaystyle{ ss=\begin{bmatrix} 0.9659&0.2588\\ 0.2588&0.9659\end{bmatrix} }[/math], but the plot looks about the same (X has the same distribution).

Monte Carlo Integration - May 26, 2009

Today's lecture completes the discussion on the Frequentists and Bayesian schools of thought and introduces Basic Monte Carlo Integration.

Frequentist vs Bayesian Example - Estimating Parameters

Estimating parameters of a univariate Gaussian:

Frequentist: [math]\displaystyle{ f(x|\theta)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{1}{2}*(\frac{x-\mu}{\sigma})^2} }[/math]
Bayesian: [math]\displaystyle{ f(\theta|x)=\frac{f(x|\theta)f(\theta)}{f(x)} }[/math]

Frequentist Approach

Let [math]\displaystyle{ X^N }[/math] denote [math]\displaystyle{ (x_1, x_2, ..., x_n) }[/math]. Using the Maximum Likelihood Estimation approach for estimating parameters we get:

[math]\displaystyle{ L(X^N; \theta) = \prod_{i=1}^N \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{1}{2}(\frac{x_i- \mu} {\sigma})^2} }[/math]

[math]\displaystyle{ l(X^N; \theta) = \sum_{i=1}^N -\frac{1}{2}log (2\pi) - log(\sigma) - \frac{1}{2} \left(\frac{x_i- \mu}{\sigma}\right)^2 }[/math]

[math]\displaystyle{ \frac{dl}{d\mu} = \displaystyle\sum_{i=1}^N(x_i-\mu) }[/math]

Setting [math]\displaystyle{ \frac{dl}{d\mu} = 0 }[/math] we get

[math]\displaystyle{ \displaystyle\sum_{i=1}^Nx_i = \displaystyle\sum_{i=1}^N\mu }[/math]

[math]\displaystyle{ \displaystyle\sum_{i=1}^Nx_i = N\mu \rightarrow \mu = \frac{1}{N}\displaystyle\sum_{i=1}^Nx_i }[/math]

Bayesian Approach

Assuming the prior is Gaussian:

[math]\displaystyle{ P(\theta) = \frac{1}{\sqrt{2\pi}\tau}e^{-\frac{1}{2}(\frac{x-\mu_0}{\tau})^2} }[/math]

[math]\displaystyle{ f(\theta|x) \propto \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{1}{2}(\frac{x_i-\mu}{\sigma})^2} * \frac{1}{\sqrt{2\pi}\tau}e^{-\frac{1}{2}(\frac{x-\mu_0}{\tau})^2} }[/math]

By completing the square we conclude that the posterior is Gaussian as well:

[math]\displaystyle{ f(\theta|x)=\frac{1}{\sqrt{2\pi}\tilde{\sigma}}e^{-\frac{1}{2}(\frac{x-\tilde{\mu}}{\tilde{\sigma}})^2} }[/math]

Where

[math]\displaystyle{ \tilde{\mu} = \frac{\frac{N}{\sigma^2}}{{\frac{N}{\sigma^2}}+\frac{1}{\tau^2}}\bar{x} + \frac{\frac{1}{\tau^2}}{{\frac{N}{\sigma^2}}+\frac{1}{\tau^2}}\mu_0 }[/math]

The expectation from the posterior is different from the MLE method. Note that [math]\displaystyle{ \displaystyle\lim_{N\to\infty}\tilde{\mu} = \bar{x} }[/math]. Also note that when [math]\displaystyle{ N = 0 }[/math] we get [math]\displaystyle{ \tilde{\mu} = \mu_0 }[/math].

Basic Monte Carlo Integration

Although it is almost impossible to find a precise definition of "Monte Carlo Method", the method is widely used and has numerous descriptions in articles and monographs. As an interesting fact, the term Monte Carlo is claimed to have been first used by Ulam and von Neumann as a Los Alamos code word for the stochastic simulations they applied to building better atomic bombs. Stochastic simulation refers to a random process in which its future evolution is described by probability distributions (counterpart to a deterministic process), and these simulation methods are known as Monte Carlo methods. [Stochastic process, Wikipedia]. The following example (external link) illustrates a Monte Carlo Calculation of Pi: [1]

We start with a simple example:

[math]\displaystyle{ I = \displaystyle\int_a^b h(x)\,dx }[/math]

[math]\displaystyle{ = \displaystyle\int_a^b w(x)f(x)\,dx }[/math]

where

[math]\displaystyle{ \displaystyle w(x) = h(x)(b-a) }[/math]

[math]\displaystyle{ f(x) = \frac{1}{b-a} \rightarrow }[/math] the p.d.f. is Unif[math]\displaystyle{ (a,b) }[/math]

[math]\displaystyle{ \hat{I} = E_f[w(x)] = \frac{1}{N}\displaystyle\sum_{i=1}^Nw(x_i) }[/math]

If [math]\displaystyle{ x_i \sim~ Unif(a,b) }[/math] then by the Law of Large Numbers [math]\displaystyle{ \frac{1}{N}\displaystyle\sum_{i=1}^Nw(x_i) \rightarrow \displaystyle\int w(x)f(x)\,dx = E_f[w(x)] }[/math]

Process

Given [math]\displaystyle{ I = \displaystyle\int^b_ah(x)\,dx }[/math]

1. [math]\displaystyle{ \begin{matrix} w(x) = h(x)(b-a)\end{matrix} }[/math]
2. [math]\displaystyle{ \begin{matrix} x_1, x_2, ..., x_n \sim UNIF(a,b)\end{matrix} }[/math]
3. [math]\displaystyle{ \hat{I} = \frac{1}{N}\displaystyle\sum_{i=1}^Nw(x_i) }[/math]

From this we can compute other statistics, such as

1. [math]\displaystyle{ SE=\frac{s}{\sqrt{N}} }[/math] where [math]\displaystyle{ s^2=\frac{\sum_{i=1}^{N}(Y_i-\hat{I})^2 }{N-1} }[/math] with [math]\displaystyle{ \begin{matrix}Y_i=w(x_i)\end{matrix} }[/math]
2. [math]\displaystyle{ \begin{matrix} 1-\alpha \end{matrix} }[/math] CI's can be estimated as [math]\displaystyle{ \hat{I}\pm Z_\frac{\alpha}{2}*SE }[/math]

Example 1

Find [math]\displaystyle{ E[\sqrt{x}] }[/math] for [math]\displaystyle{ \begin{matrix} f(x) = e^{-x}\end{matrix} }[/math]

1. We need to draw from [math]\displaystyle{ \begin{matrix} f(x) = e^{-x}\end{matrix} }[/math]
2. [math]\displaystyle{ \hat{I} = \frac{1}{N}\displaystyle\sum_{i=1}^Nw(x_i) }[/math]

This example can be illustrated in Matlab using the code below:

u=rand(100,1)
x=-log(u)
h= x.* .5
mean(h)
%The value obtained using the Monte Carlo method
F = @ (x) sqrt (x). * exp(-x)
quad(F,0,50)
%The value of the real function using Matlab

Example 2 Find [math]\displaystyle{ I = \displaystyle\int^1_0h(x)\,dx, h(x) = x^3 }[/math]

1. [math]\displaystyle{ \displaystyle I = x^4/4 = 1/4 }[/math]
2. [math]\displaystyle{ \displaystyle W(x) = x^3*(1-0) }[/math]
3. [math]\displaystyle{ Xi \sim~Unif(0,1) }[/math]
4. [math]\displaystyle{ \hat{I} = \frac{1}{N}\displaystyle\sum_{i=1}^N(x_i^3) }[/math]

This example can be illustrated in Matlab using the code below:

x = rand (1000)
mean(x^3)

Example 3 To estimate an infinite integral such as [math]\displaystyle{ I = \displaystyle\int^\infty_5 h(x)\,dx, h(x) = 3e^{-x} }[/math]

1. Substitute in [math]\displaystyle{ y=\frac{1}{x-5+1} =\gt dy=-\frac{1}{(x-4)^2}dx =\gt dy=-y^2dx }[/math]
2. [math]\displaystyle{ I = \displaystyle\int^1_0 \frac{3e^{-(\frac{1}{y}+4)}}{-y^2}\,dy }[/math]
3. [math]\displaystyle{ w(y) = \frac{3e^{-(\frac{1}{y}+4)}}{-y^2}(1-0) }[/math]
4. [math]\displaystyle{ Y_i \sim~Unif(0,1) }[/math]
5. [math]\displaystyle{ \hat{I} = \frac{1}{N}\displaystyle\sum_{i=1}^N(\frac{3e^{-(\frac{1}{y_i}+4)}}{-y_i^2}) }[/math]

Importance Sampling and Monte Carlo Simulation - May 28, 2009

During this lecture we covered two more examples of Monte Carlo simulation, finishing that topic, and begun talking about Importance Sampling.

Binomial Probability Monte Carlo Simulations

Example 1:

You are given two independent Binomial distributions with probabilities [math]\displaystyle{ \displaystyle p_1\text{, }p_2 }[/math]. Using a Monte Carlo simulation, approximate the value of [math]\displaystyle{ \displaystyle \delta }[/math], where [math]\displaystyle{ \displaystyle \delta = p_1 - p_2 }[/math].

[math]\displaystyle{ \displaystyle X \sim BIN(n, p_1) }[/math]; [math]\displaystyle{ \displaystyle Y \sim BIN(n, p_2) }[/math]; [math]\displaystyle{ \displaystyle \delta = p_1 - p_2 }[/math]

So [math]\displaystyle{ \displaystyle f(p_1, p_2 | x,y) = \frac{f(x, y|p_1, p_2)*f(p_1,p_2)}{f(x,y)} }[/math] where [math]\displaystyle{ \displaystyle f(x,y) }[/math] is a flat distribution and the expected value of [math]\displaystyle{ \displaystyle \delta }[/math] is as follows:

[math]\displaystyle{ \displaystyle \hat{\delta} = \int\int\delta f(p_1,p_2|X,Y)\,dp_1dp_2 }[/math]

Since X, Y are independent, we can split the conditional probability distribution:

[math]\displaystyle{ \displaystyle f(p_1,p_2|X,Y) \propto f(p_1|X)f(p_2|Y) }[/math]

We need to find conditional distribution functions for [math]\displaystyle{ \displaystyle p_1, p_2 }[/math] to draw samples from. In order to get a distribution for the probability 'p' of a Binomial, we have to divide the Binomial distribution by n. This new distribution has the same shape as the original, but is scaled. A Beta distribution is a suitable approximation. Let

[math]\displaystyle{ \displaystyle f(p_1 | X) \sim \text{Beta}(x+1, n-x+1) }[/math] and [math]\displaystyle{ \displaystyle f(p_2 | Y) \sim \text{Beta}(y+1, n-y+1) }[/math], where

[math]\displaystyle{ \displaystyle \text{Beta}(\alpha,\beta) = \frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha)\Gamma(\beta)}p^{\alpha-1}(1-p)^{\beta-1} }[/math]

Process:

1. Draw samples for [math]\displaystyle{ \displaystyle p_1 }[/math] and [math]\displaystyle{ \displaystyle p_2 }[/math]: [math]\displaystyle{ \displaystyle (p_1,p_2)^{(1)} }[/math], [math]\displaystyle{ \displaystyle (p_1,p_2)^{(2)} }[/math], ..., [math]\displaystyle{ \displaystyle (p_1,p_2)^{(n)} }[/math];
2. Compute [math]\displaystyle{ \displaystyle \delta = p_1 - p_2 }[/math] in order to get n values for [math]\displaystyle{ \displaystyle \delta }[/math];
3. [math]\displaystyle{ \displaystyle \hat{\delta}=\frac{\displaystyle\sum_{\forall i}\delta^{(i)}}{N} }[/math].
   
   

Matlab Code:

The Matlab code for recreating the above example is as follows:

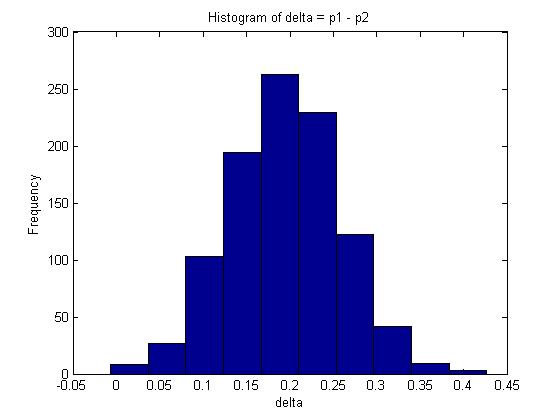
n=100; %number of trials for X
m=100; %number of trials for Y
x=80; %number of successes for X trials
y=60; %number of successes for y trials
p1=betarnd(x+1, n-x+1, 1, 1000);
p2=betarnd(y+1, m-y+1, 1, 1000);
delta=p1-p2;
mean(delta);

The mean in this example is given by 0.1938.

A 95% confidence interval for [math]\displaystyle{ \delta }[/math] is represented by the interval between the 2.5% and 97.5% quantiles which covers 95% of the probability distribution. In Matlab, this can be calculated as follows:

q1=quantile(delta,0.025);
q2=quantile(delta,0.975);

The interval is approximately [math]\displaystyle{ 95% CI \approx (0.06606, 0.32204) }[/math]

The histogram of delta is:

Note: In this case, we can also find [math]\displaystyle{ E(\delta) }[/math] analytically since [math]\displaystyle{ E(\delta) = E(p_1 - p_2) = E(p_1) - E(p_2) = \frac{x+1}{n+2} - \frac{y+1}{m+2} \approx 0.1961 }[/math]. Compare this with the maximum likelihood estimate for [math]\displaystyle{ \delta }[/math]: [math]\displaystyle{ \frac{x}{n} - \frac{y}{m} = 0.2 }[/math].

Example 2:

Bayesian Inference for Dose Response

We conduct an experiment by giving rats one of ten possible doses of a drug, where each subsequent dose is more lethal than the previous one:

[math]\displaystyle{ \displaystyle x_1\lt x_2\lt ...\lt x_{10} }[/math]

For each dose [math]\displaystyle{ \displaystyle x_i }[/math] we test n rats and observe [math]\displaystyle{ \displaystyle Y_i }[/math], the number of rats that survive. Therefore,

[math]\displaystyle{ \displaystyle Y_i \sim~ BIN(n, p_i) }[/math]
.

We can assume that the probability of death grows with the concentration of drug given, i.e. [math]\displaystyle{ \displaystyle p_1\lt p_2\lt ...\lt p_{10} }[/math]. Estimate the dose at which the animals have at least 50% chance of dying.

Let [math]\displaystyle{ \displaystyle \delta=x_j }[/math] where [math]\displaystyle{ \displaystyle j=min\{i|p_i\geq0.5\} }[/math]

We are interested in [math]\displaystyle{ \displaystyle \delta }[/math] since any higher concentrations are known to have a higher death rate.

Solving this analytically is difficult:

[math]\displaystyle{ \displaystyle \delta = g(p_1, p_2, ..., p_{10}) }[/math] where g is an unknown function

[math]\displaystyle{ \displaystyle \hat{\delta} = \int \int..\int_A \delta f(p_1,p_2,...,p_{10}|Y_1,Y_2,...,Y_{10})\,dp_1dp_2...dp_{10} }[/math]

where [math]\displaystyle{ \displaystyle A=\{(p_1,p_2,...,p_{10})|p_1\leq p_2\leq ...\leq p_{10} \} }[/math]

Process: Monte Carlo
We assume that

1. Draw [math]\displaystyle{ \displaystyle p_i \sim~ BETA(y_i+1, n-y_i+1) }[/math]
2. Keep sample only if it satisfies [math]\displaystyle{ \displaystyle p_1\leq p_2\leq ...\leq p_{10} }[/math], otherwise discard and try again.
3. Compute [math]\displaystyle{ \displaystyle \delta }[/math] by finding the first [math]\displaystyle{ \displaystyle p_i }[/math] sample with over 50% deaths.
4. Repeat process n times to get n estimates for [math]\displaystyle{ \displaystyle \delta_1, \delta_2, ..., \delta_N }[/math].
5. [math]\displaystyle{ \displaystyle \bar{\delta} = \frac{\displaystyle\sum_{\forall i} \delta_i}{N} }[/math].

For instance, for each dose level [math]\displaystyle{ X_i }[/math], for [math]\displaystyle{ 1\lt =i\lt =10 }[/math], 10 rats are used and it is observed that the numbers that are dying is [math]\displaystyle{ Y_i }[/math], where [math]\displaystyle{ Y_1 = 4, Y_2 = 3, }[/math]etc.

Importance Sampling

In statistics, Importance Sampling helps estimating the properties of a particular distribution. As in the case with the Acceptance/Rejection method, we choose a good distribution from which to simulate the given random variables. The main difference in importance sampling however, is that certain values of the input random variables in a simulation have more impact on the parameter being estimated than others. [Importance Sampling, Wikipedia] The following diagram illustrates a Monte Carlo approximation for g(x):

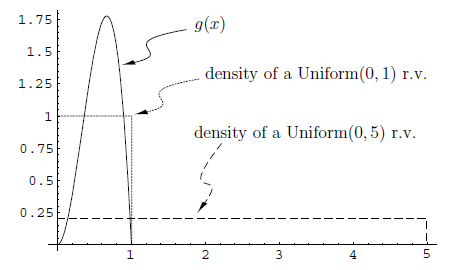
As the figure above shows, the uniform distribution [math]\displaystyle{ U\sim~Unif[0,1] }[/math] is a proposal distribution to sample from and g(x) is the target distribution. Here we cast the integral [math]\displaystyle{ \int_{0}^1 g(x)dx }[/math], as the expectation with respect to U such that [math]\displaystyle{ \int_{0}^1 g(x)= E(g(U)) }[/math]. Hence we can approximate by [math]\displaystyle{ \frac{1}{n}\displaystyle\sum_{i=1}^{n} g(u_i) }[/math].
[Source: Monte Carlo Methods and Importance Sampling, Eric C. Anderson (1999). Retrieved June 9th from URL: http://ib.berkeley.edu/labs/slatkin/eriq/classes/guest_lect/mc_lecture_notes.pdf]

In [math]\displaystyle{ I = \displaystyle\int h(x)f(x)\,dx }[/math], Monte Carlo simulation can be used only if it easy to sample from f(x). Otherwise, another method must be applied. If sampling from f(x) is difficult but there exists a probability distribution function g(x) which is easy to sample from, then [math]\displaystyle{ I }[/math] can be written as

[math]\displaystyle{ I = \displaystyle\int h(x)f(x)\,dx }[/math]

[math]\displaystyle{ = \displaystyle\int \frac{h(x)f(x)}{g(x)}g(x)\,dx }[/math]

[math]\displaystyle{ = \displaystyle E_g(w(x)) \rightarrow }[/math]the expectation of w(x) with respect to g(x) and therefore [math]\displaystyle{ \displaystyle x_1,x_2,...,x_N \sim~ g }[/math]

[math]\displaystyle{ = \frac{\displaystyle\sum_{i=1}^{N} w(x_i)}{N} }[/math] where [math]\displaystyle{ \displaystyle w(x) = \frac{h(x)f(x)}{g(x)} }[/math]

Process

1. Choose [math]\displaystyle{ \displaystyle g(x) }[/math] such that it's easy to sample from.
2. Compute [math]\displaystyle{ \displaystyle w(x)=\frac{h(x)f(x)}{g(x)} }[/math]
3. [math]\displaystyle{ \displaystyle \hat{I} = \frac{\displaystyle\sum_{i=1}^{N} w(x_i)}{N} }[/math]
   
   

Note: By the law of large number, we can say that [math]\displaystyle{ \hat{I} }[/math] converges in probability to [math]\displaystyle{ I }[/math].

"Weighted" average

The term "importance sampling" is used to describe this method because a higher 'importance' or 'weighting' is given to the values sampled from [math]\displaystyle{ \displaystyle g(x) }[/math] that are closer to the original distribution [math]\displaystyle{ \displaystyle f(x) }[/math], which we would ideally like to sample from (but cannot because it is too difficult).

[math]\displaystyle{ \displaystyle I = \int\frac{h(x)f(x)}{g(x)}g(x)\,dx }[/math]

[math]\displaystyle{ =\displaystyle \int \frac{f(x)}{g(x)}h(x)g(x)\,dx }[/math]

[math]\displaystyle{ =\displaystyle \int \frac{f(x)}{g(x)}E_g(h(x))\,dx }[/math] which is the same thing as saying that we are applying a regular Monte Carlo Simulation method to [math]\displaystyle{ \displaystyle\int h(x)g(x)\,dx }[/math], taking each result from this process and weighting the more accurate ones (i.e. the ones for which [math]\displaystyle{ \displaystyle \frac{f(x)}{g(x)} }[/math] is high) higher.

One can view [math]\displaystyle{ \frac{f(x)}{g(x)}\ = B(x) }[/math] as a weight.

Then [math]\displaystyle{ \displaystyle \hat{I} = \frac{\displaystyle\sum_{i=1}^{N} w(x_i)}{N} = \frac{\displaystyle\sum_{i=1}^{N} B(x_i)*h(x_i)}{N} }[/math]

i.e. we are computing a weighted sum of [math]\displaystyle{ h(x_i) }[/math] instead of a sum

A Deeper Look into Importance Sampling - June 2, 2009

From last class, we have determined that an integral can be written in the form [math]\displaystyle{ I = \displaystyle\int h(x)f(x)\,dx }[/math] [math]\displaystyle{ = \displaystyle\int \frac{h(x)f(x)}{g(x)}g(x)\,dx }[/math] We continue our discussion of Importance Sampling here.

Importance Sampling

We can see that the integral [math]\displaystyle{ \displaystyle\int \frac{h(x)f(x)}{g(x)}g(x)\,dx = \int \frac{f(x)}{g(x)}h(x) g(x)\,dx }[/math] is just [math]\displaystyle{ \displaystyle E_g(h(x)) \rightarrow }[/math]the expectation of h(x) with respect to g(x), where [math]\displaystyle{ \displaystyle \frac{f(x)}{g(x)} }[/math] is a weight [math]\displaystyle{ \displaystyle\beta(x) }[/math]. In the case where [math]\displaystyle{ \displaystyle f \gt g }[/math], a greater weight for [math]\displaystyle{ \displaystyle\beta(x) }[/math] will be assigned. Thus, the points with more weight are deemed more important, hence "importance sampling". This can be seen as a variance reduction technique.

Problem

The method of Importance Sampling is simple but can lead to some problems. The [math]\displaystyle{ \displaystyle \hat I }[/math] estimated by Importance Sampling could have infinite standard error.

Given [math]\displaystyle{ \displaystyle I= \int w(x) g(x) dx }[/math] [math]\displaystyle{ = \displaystyle E_g(w(x)) }[/math] [math]\displaystyle{ = \displaystyle \frac{1}{N}\sum_{i=1}^{N} w(x_i) }[/math] where [math]\displaystyle{ \displaystyle w(x)=\frac{f(x)h(x)}{g(x)} }[/math].

Obtaining the second moment,

[math]\displaystyle{ \displaystyle E[(w(x))^2] }[/math]

[math]\displaystyle{ \displaystyle = \int (\frac{h(x)f(x)}{g(x)})^2 g(x) dx }[/math]

[math]\displaystyle{ \displaystyle = \int \frac{h^2(x) f^2(x)}{g^2(x)} g(x) dx }[/math]

[math]\displaystyle{ \displaystyle = \int \frac{h^2(x)f^2(x)}{g(x)} dx }[/math]

We can see that if [math]\displaystyle{ \displaystyle g(x) \rightarrow 0 }[/math], then [math]\displaystyle{ \displaystyle E[(w(x))^2] \rightarrow \infty }[/math]. This occurs if [math]\displaystyle{ \displaystyle g }[/math] has a thinner tail than [math]\displaystyle{ \displaystyle f }[/math] then [math]\displaystyle{ \frac{h^2(x)f^2(x)}{g(x)} }[/math] could be infinitely large. The general idea here is that [math]\displaystyle{ \frac{f(x)}{g(x)} }[/math] should not be large.

Remark 1

It is evident that [math]\displaystyle{ \displaystyle g(x) }[/math] should be chosen such that it has a thicker tail than [math]\displaystyle{ \displaystyle f(x) }[/math]. If [math]\displaystyle{ \displaystyle f }[/math] is large over set [math]\displaystyle{ \displaystyle A }[/math] but [math]\displaystyle{ \displaystyle g }[/math] is small, then [math]\displaystyle{ \displaystyle \frac{f}{g} }[/math] would be large and it would result in a large variance.

Remark 2

It is useful if we can choose [math]\displaystyle{ \displaystyle g }[/math] to be similar to [math]\displaystyle{ \displaystyle f }[/math] in terms of shape. Ideally, the optimal [math]\displaystyle{ \displaystyle g }[/math] should be similar to [math]\displaystyle{ \displaystyle \left| h(x) \right|f(x) }[/math], and have a thicker tail. It's important to take the absolute value of [math]\displaystyle{ \displaystyle h(x) }[/math], since a variance can't be negative. Analytically, we can show that the best [math]\displaystyle{ \displaystyle g }[/math] is the one that would result in a variance that is minimized.

Remark 3

Choose [math]\displaystyle{ \displaystyle g }[/math] such that it is similar to [math]\displaystyle{ \displaystyle \left| h(x) \right| f(x) }[/math] in terms of shape. That is, we want [math]\displaystyle{ \displaystyle g \propto \displaystyle \left| h(x) \right| f(x) }[/math]

Theorem (Minimum Variance Choice of [math]\displaystyle{ \displaystyle g }[/math])

The choice of [math]\displaystyle{ \displaystyle g }[/math] that minimizes variance of [math]\displaystyle{ \hat I }[/math] is [math]\displaystyle{ \displaystyle g^*(x)=\frac{\left| h(x) \right| f(x)}{\int \left| h(s) \right| f(s) ds} }[/math].

Proof:

We know that [math]\displaystyle{ \displaystyle w(x)=\frac{f(x)h(x)}{g(x)} }[/math]

The variance of [math]\displaystyle{ \displaystyle w(x) }[/math] is

[math]\displaystyle{ \displaystyle Var[w(x)] }[/math]

[math]\displaystyle{ \displaystyle = E[(w(x)^2)] - [E[w(x)]]^2 }[/math]

[math]\displaystyle{ \displaystyle = \int \left(\frac{f(x)h(x)}{g(x)} \right)^2 g(x) dx - \left[\int \frac{f(x)h(x)}{g(x)}g(x)dx \right]^2 }[/math]

[math]\displaystyle{ \displaystyle = \int \left(\frac{f(x)h(x)}{g(x)} \right)^2 g(x) dx - \left[\int f(x)h(x) \right]^2 }[/math]

As we can see, the second term does not depend on [math]\displaystyle{ \displaystyle g(x) }[/math]. Therefore to minimize [math]\displaystyle{ \displaystyle Var[w(x)] }[/math] we only need to minimize the first term. In doing so we will use Jensen's Inequality.

[math]\displaystyle{ \displaystyle ======Aside: Jensen's Inequality====== }[/math]

If [math]\displaystyle{ \displaystyle g }[/math] is a convex function ( twice differentiable and [math]\displaystyle{ \displaystyle g''(x) \geq 0 }[/math] ) then [math]\displaystyle{ \displaystyle g(\alpha x_1 + (1-\alpha)x_2) \leq \alpha g(x_1) + (1-\alpha) g(x_2) }[/math]
Essentially the definition of convexity implies that the line segment between two points on a curve lies above the curve, which can then be generalized to higher dimensions:

[math]\displaystyle{ \displaystyle g(\alpha_1 x_1 + \alpha_2 x_2 + ... + \alpha_n x_n) \leq \alpha_1 g(x_1) + \alpha_2 g(x_2) + ... + \alpha_n g(x_n) }[/math] where [math]\displaystyle{ \displaystyle \alpha_1 + \alpha_2 + ... + \alpha_n = 1 }[/math]

=======================================================

Proof (cont)

Using Jensen's Inequality,

[math]\displaystyle{ \displaystyle g(E[x]) \leq E[g(x)] }[/math] as [math]\displaystyle{ \displaystyle g(E[x]) = g(p_1 x_1 + ... p_n x_n) \leq p_1 g(x_1) + ... + p_n g(x_n) = E[g(x)] }[/math]

Therefore

[math]\displaystyle{ \displaystyle E[(w(x))^2] \geq (E[\left| w(x) \right|])^2 }[/math]

[math]\displaystyle{ \displaystyle E[(w(x))^2] \geq \left(\int \left| \frac{f(x)h(x)}{g(x)} \right| g(x) dx \right)^2 }[/math]

and

[math]\displaystyle{ \displaystyle \left(\int \left| \frac{f(x)h(x)}{g(x)} \right| g(x) dx \right)^2 }[/math]

[math]\displaystyle{ \displaystyle = \left(\int \frac{f(x)\left| h(x) \right|}{g(x)} g(x) dx \right)^2 }[/math]

[math]\displaystyle{ \displaystyle = \left(\int \left| h(x) \right| f(x) dx \right)^2 }[/math] since [math]\displaystyle{ \displaystyle f }[/math] and [math]\displaystyle{ \displaystyle g }[/math] are density functions, [math]\displaystyle{ \displaystyle f, g }[/math] cannot be negative.

Thus, this is a lower bound on [math]\displaystyle{ \displaystyle E[(w(x))^2] }[/math]. If we replace [math]\displaystyle{ \displaystyle g^*(x) }[/math] into [math]\displaystyle{ \displaystyle E[g^*(x)] }[/math], we can see that the result is as we require. Details omitted.

However, this is mostly of theoritical interest. In practice, it is impossible or very difficult to compute [math]\displaystyle{ \displaystyle g^* }[/math].

Note: Jensen's inequality is actually unnecessary here. We just use it to get [math]\displaystyle{ E[(w(x))^2] \geq (E[|w(x)|])^2 }[/math], which could be derived using variance properties: [math]\displaystyle{ 0 \leq Var[|w(x)|] = E[|w(x)|^2] - (E[|w(x)|])^2 = E[(w(x))^2] - (E[|w(x)|])^2 }[/math].

Importance Sampling and Markov Chain Monte Carlo (MCMC) - June 4, 2009

Remark 4: [math]\displaystyle{ I = \displaystyle\int^\ h(x)f(x)\,dx }[/math]

[math]\displaystyle{ = \displaystyle\int \ h(x)\frac{f(x)}{g(x)}g(x)\,dx }[/math]

[math]\displaystyle{ = \displaystyle\sum_{i=1}^{N} h(x_i)b(x_i) }[/math] where [math]\displaystyle{ \displaystyle b(x_i) = \frac{f(x_i)}{g(x_i)} }[/math]

[math]\displaystyle{ =\displaystyle \frac{\int\ h(x)f(x)\,dx}{\int f(x) dx} }[/math]

Apply the idea of importance sampling to both the numerator and denominator:

[math]\displaystyle{ =\displaystyle \frac{\int\ h(x)\frac{f(x)}{g(x)}g(x)\,dx}{\int\frac{f(x)}{g(x)}g(x) dx} }[/math]

[math]\displaystyle{ = \displaystyle\frac{\sum_{i=1}^{N} h(x_i)b(x_i)}{\sum_{1=1}^{N} b(x_i)} }[/math]

[math]\displaystyle{ = \displaystyle\sum_{i=1}^{N} h(x_i)b'(x_i) }[/math] where [math]\displaystyle{ \displaystyle b'(x_i) = \frac{b(x_i)}{\sum_{i=1}^{N} b(x_i)} }[/math]

The above results in the following form of Importance Sampling:

[math]\displaystyle{ \hat{I} = \displaystyle\sum_{i=1}^{N} b'(x_i)h(x_i) }[/math] where [math]\displaystyle{ \displaystyle b'(x_i) = \frac{b(x_i)}{\sum_{i=1}^{N} b(x_i)} }[/math]

This is very important and useful especially when f is known only up to a proportionality constant. Often, this is the case in the Bayesian approach when f is a posterior density function.

Example of Importance Sampling

Estimate [math]\displaystyle{ I = \displaystyle\ Pr (Z\gt 3) }[/math] when [math]\displaystyle{ Z \sim~ N(0,1) }[/math]

[math]\displaystyle{ I = \displaystyle\int^\infty_3 f(x)\,dx \approx 0.0013 }[/math]

[math]\displaystyle{ = \displaystyle\int^\infty_3 h(x)f(x)\,dx }[/math]

Define [math]\displaystyle{ h(x) = \begin{cases} 0, & \text{if } x \lt 3 \\ 1, & \text{if } 3 \leq x \end{cases} }[/math]

Approach I: Monte Carlo

[math]\displaystyle{ \hat{I} = \frac{1}{N}\displaystyle\sum_{i=1}^Nh(x_i) }[/math] where [math]\displaystyle{ X \sim~ N(0,1) }[/math]

The idea here is to sample from normal distribution and to count number of observations that is greater than 3.

The variability will be high in this case if using Monte Carlo since this is considered a low probability event (a tail event), and different runs may give significantly different values. For example: the first run may give only 3 occurences (i.e if we generate 1000 samples, thus the probability will be .003), the second run may give 5 occurences (probability .005), etc.

This example can be illustrated in Matlab using the code below (we will be generating 100 samples in this case):

format long
for i = 1:100
   a(i) = sum(randn(100,1)>=3)/100;
end
meanMC  = mean(a)
varMC   = var(a)

On running this, we get [math]\displaystyle{ meanMC = 0.0005 }[/math] and [math]\displaystyle{ varMC \approx 1.31313 * 10^{-5} }[/math]

Approach II: Importance Sampling

[math]\displaystyle{ \hat{I} = \frac{1}{N}\displaystyle\sum_{i=1}^Nh(x_i)\frac{f(x_i)}{g(x_i)} }[/math] where [math]\displaystyle{ f(x) }[/math] is standard normal and [math]\displaystyle{ g(x) }[/math] needs to be chosen wisely so that it is similar to the target distribution.

Let [math]\displaystyle{ g(x) \sim~ N(4,1) }[/math]

[math]\displaystyle{ b(x) = \frac{f(x)}{g(x)} = e^{(8-4x)} }[/math]

[math]\displaystyle{ \hat{I} = \frac{1}{N}\displaystyle\sum_{i=1}^Nb(x_i)h(x_i) }[/math]

This example can be illustrated in Matlab using the code below:

for j = 1:100
   N = 100;
   x = randn (N,1) + 4;
     for ii = 1:N
         h = x(ii)>=3;
         b = exp(8-4*x(ii));
         w(ii) = h*b;
     end
  I(j) = sum(w)/N;
end
MEAN = mean(I)
VAR = var(I)

Running the above code gave us [math]\displaystyle{ MEAN \approx 0.001353 }[/math] and [math]\displaystyle{ VAR \approx 9.666 * 10^{-8} }[/math] which is very close to 0, and is much less than the variability observed when using Monte Carlo

Markov Chain Monte Carlo (MCMC)

Before we tackle Markov chain Monte Carlo methods, which essentially are a 'class of algorithms for sampling from probability distributions based on constructing a Markov chain' [MCMC, Wikipedia], we will first give a formal definition of Markov Chain.

Consider the same integral: [math]\displaystyle{ I = \displaystyle\int^\ h(x)f(x)\,dx }[/math]

Idea: If [math]\displaystyle{ \displaystyle X_1, X_2,...X_N }[/math] is a Markov Chain with stationary distribution f(x), then under some conditions

[math]\displaystyle{ \hat{I} = \frac{1}{N}\displaystyle\sum_{i=1}^Nh(x_i)\xrightarrow{P}\int^\ h(x)f(x)\,dx = I }[/math]

Stochastic Process:
A Stochastic Process is a collection of random variables [math]\displaystyle{ \displaystyle \{ X_t : t \in T \} }[/math]

• State Space Set:[math]\displaystyle{ \displaystyle X }[/math]is the set that random variables [math]\displaystyle{ \displaystyle X_t }[/math] takes values from.
• Indexed Set:[math]\displaystyle{ \displaystyle T }[/math]is the set that t takes values from, which could be discrete or continuous in general, but we are only interested in discrete case in this course.

Example 1
i.i.d random variables

[math]\displaystyle{ \{ X_t : t \in T \}, X_t \in X }[/math]

[math]\displaystyle{ X = \{0, 1, 2, 3, 4, 5, 6, 7, 8\} \rightarrow }[/math]State Space

[math]\displaystyle{ T = \{1, 2, 3, 4, 5\} \rightarrow }[/math]Indexed Set

Example 2

[math]\displaystyle{ \displaystyle X_t }[/math]: price of a stock

[math]\displaystyle{ \displaystyle t }[/math]: opening date of the market

Basic Fact: In general, if we have random variables [math]\displaystyle{ \displaystyle X_1,...X_n }[/math]

[math]\displaystyle{ \displaystyle f(X_1,...X_n)= f(X_1)f(X_2|X_1)f(X_3|X_2,X_1)...f(X_n|X_n-1,...,X_1) }[/math]

[math]\displaystyle{ \displaystyle f(X_1,...X_n)= \prod_{i = 1}^n f(X_i|Past_i) }[/math] where [math]\displaystyle{ \displaystyle Past_i = (X_i-1, X_i-2,...,X_1) }[/math]

Markov Chain:
A Markov Chain is a special form of stochastic process in which [math]\displaystyle{ \displaystyle X_t }[/math] depends only on [math]\displaystyle{ X_t-1 }[/math].

For example,

[math]\displaystyle{ \displaystyle f(X_1,...X_n)= f(X_1)f(X_2|X_1)f(X_3|X_2)...f(X_n|X_n-1) }[/math]

Transition Probability:
The probability of going from one state to another state.

[math]\displaystyle{ p_{ij} = \Pr(X=X_j\mid X= X_i). \, }[/math]

Transition Matrix:
For n states, transition matrix P is an [math]\displaystyle{ N \times N }[/math] matrix with entries [math]\displaystyle{ \displaystyle P_{ij} }[/math] as below:

[math]\displaystyle{ P=\left(\begin{matrix}p_{1,1}&p_{1,2}&\dots&p_{1,j}&\dots\\ p_{2,1}&p_{2,2}&\dots&p_{2,j}&\dots\\ \vdots&\vdots&\ddots&\vdots&\ddots\\ p_{i,1}&p_{i,2}&\dots&p_{i,j}&\dots\\ \vdots&\vdots&\ddots&\vdots&\ddots \end{matrix}\right) }[/math]

Example:
A "Random Walk" is an example of a Markov Chain. Let's suppose that the direction of our next step is decided in a probabilistic way. The probability of moving to the right is [math]\displaystyle{ \displaystyle Pr(heads) = p }[/math]. And the probability of moving to the left is [math]\displaystyle{ \displaystyle Pr(tails) = q = 1-p }[/math]. Once the first or the last state is reached, then we stop. The transition matrix that express this process is shown as below:

[math]\displaystyle{ P=\left(\begin{matrix}1&0&\dots&0&\dots\\ p&0&q&0&\dots\\ 0&p&0&q&0\dots\\ \vdots&\vdots&\ddots&\vdots&\ddots\\ p_{i,1}&p_{i,2}&\dots&p_{i,j}&\dots\\ \vdots&\vdots&\ddots&\vdots&\ddots\\ 0&0&\dots&0&1 \end{matrix}\right) }[/math]

Markov Chain Definitions - June 9, 2009

Practical application for estimation: The general concept for the application of this lies within having a set of generated [math]\displaystyle{ x_i }[/math] which approach a distribution [math]\displaystyle{ f(x) }[/math] so that a variation of importance estimation can be used to estimate an integral in the form
[math]\displaystyle{ I = \displaystyle\int^\ h(x)f(x)\,dx }[/math] by [math]\displaystyle{ \hat{I} = \frac{1}{N}\displaystyle\sum_{i=1}^Nh(x_i) }[/math]
All that is required is a Markov chain which eventually converges to [math]\displaystyle{ f(x) }[/math].

In the previous example, the entries [math]\displaystyle{ p_{ij} }[/math] in the transition matrix [math]\displaystyle{ P }[/math] represent the probability of reaching state [math]\displaystyle{ j }[/math] from state [math]\displaystyle{ i }[/math] after one step. For this reason, the sum over all entries j in a particular column sum to 1, as this itself must be a pmf if a transition from [math]\displaystyle{ i }[/math] is to lead to a state still within the state set for [math]\displaystyle{ X_t }[/math].

Homogeneous Markov Chain
The probability matrix [math]\displaystyle{ P }[/math] is the same for all indicies [math]\displaystyle{ n\in T }[/math]. [math]\displaystyle{ Pr(X_n=j|X_{n-1}=i)= Pr(X_1=j|X_0=i) }[/math]

If we denote the pmf of X_n by a probability vector [math]\displaystyle{ \frac{}{}\mu_n = [P(X_n=x_1),P(X_n=x_2),..,P(X_n=x_i)] }[/math]
where [math]\displaystyle{ i }[/math] denotes an ordered index of all possible states of [math]\displaystyle{ X }[/math].
Then we have a definition for the
marginal probabilty [math]\displaystyle{ \frac{}{}\mu_n(i) = P(X_n=i) }[/math]
where we simplify [math]\displaystyle{ X_n }[/math] to represent the ordered index of a state rather than the state itself.

From this definition it can be shown that, [math]\displaystyle{ \frac{}{}\mu_{n-1}P=\mu_0P^n }[/math]

Proof:

[math]\displaystyle{ \mu_{n-1}P=[\sum_{\forall i}(\mu_{n-1}(i))P_{i1},\sum_{\forall i}(\mu_{n-1}(i))P_{i2},..,\sum_{\forall i}(\mu_{n-1}(i))P_{ij}] }[/math] and since

[math]\displaystyle{ \sum_{\forall i}(\mu_{n-1}(i))P_{ij}=\sum_{\forall i}P(X_n=x_i)Pr(X_n=j|X_{n-1}=i)=\sum_{\forall i}P(X_n=x_i)\frac{Pr(X_n=j,X_{n-1}=i)}{P(X_n=x_i)} }[/math] [math]\displaystyle{ =\sum_{\forall i}Pr(X_n=j,X_{n-1}=i)=Pr(X_n=j)=\mu_{n}(j) }[/math]

Therefore,
[math]\displaystyle{ \frac{}{}\mu_{n-1}P=[\mu_{n}(1),\mu_{n}(2),...,\mu_{n}(i)]=\mu_{n} }[/math]

With this, it is possible to define [math]\displaystyle{ P(n) }[/math] as an n-step transition matrix where [math]\displaystyle{ \frac{}{}P_{ij}(n) = Pr(X_n=j|X_0=i) }[/math]
Theorem: [math]\displaystyle{ \frac{}{}\mu_n=\mu_0P^n }[/math]
Proof: [math]\displaystyle{ \frac{}{}\mu_n=\mu_{n-1}P }[/math] From the previous conclusion
[math]\displaystyle{ \frac{}{}=\mu_{n-2}PP=...=\mu_0\prod_{i = 1}^nP }[/math] And since this is a homogeneous Markov chain, [math]\displaystyle{ P }[/math] does not depend on [math]\displaystyle{ i }[/math] so
[math]\displaystyle{ \frac{}{}=\mu_0P^n }[/math]

From this it becomes easy to define the n-step transition matrix as [math]\displaystyle{ \frac{}{}P(n)=P^n }[/math]

Summary of definitions

• transition matrix is an NxN when [math]\displaystyle{ N=|X| }[/math] matrix with [math]\displaystyle{ P_{ij}=Pr(X_1=j|X_0=i) }[/math] where [math]\displaystyle{ i,j \in X }[/math]
  
• n-step transition matrix also NxN with [math]\displaystyle{ P_{ij}(n)=Pr(X_n=j|X_0=i) }[/math]
  
• marginal (probability of X)[math]\displaystyle{ \mu_n(i) = Pr(X_n=i) }[/math]
  
• Theorem: [math]\displaystyle{ P_n=P^n }[/math]
  
• Theorem: [math]\displaystyle{ \mu_n=\mu_0P^n }[/math]
  

---

Definitions of different types of state sets

Define [math]\displaystyle{ i,j \in }[/math] State Space
If [math]\displaystyle{ P_{ij}(n) \gt 0 }[/math] for some [math]\displaystyle{ n }[/math] , then we say [math]\displaystyle{ i }[/math] reaches [math]\displaystyle{ j }[/math] denoted by [math]\displaystyle{ i\longrightarrow j }[/math]
This also mean j is accessible by i [math]\displaystyle{ j\longleftarrow i }[/math]
If [math]\displaystyle{ i\longrightarrow j }[/math] and [math]\displaystyle{ j\longrightarrow i }[/math] then we say [math]\displaystyle{ i }[/math] and [math]\displaystyle{ j }[/math] communicate, denoted by [math]\displaystyle{ i\longleftrightarrow j }[/math]

Theorems
1) [math]\displaystyle{ i\longleftrightarrow i }[/math]
2) [math]\displaystyle{ i\longleftrightarrow j,j\longleftrightarrow k\Rightarrow i\longleftrightarrow k }[/math]
3) The set of states of [math]\displaystyle{ X }[/math] can be written as a unique disjoint union of subsets [math]\displaystyle{ X=X_1\bigcup X_2\bigcup ...\bigcup X_k,k\gt 0 }[/math] where two states [math]\displaystyle{ i }[/math] and [math]\displaystyle{ j }[/math] communicate [math]\displaystyle{ IFF }[/math] they belong to the same subset

More Definitions
A set is Irreducible if all states communicate with each other ([math]\displaystyle{ \Leftrightarrow k=1 }[/math])
A subset of states is Closed if once you enter it, you can never leave.
An Absorbing set is a closed set with only 1 element