hamming Distance Metric Learning
Introduction
This paper tries to propose a method to learn mappings from high dimensional data to binary codes. One of the main advantages of using binary space is that one can do exact KNN classification in sublinear time with respect to the number of samples. Like other metric learning methods this paper also tries to optimize some cost function which is based one a similarity measure between data points. One choice of similarity measure is Euclidean distance which often produces unsatisfactory results for binary data. Another choice is Hamming distance, which is the total number of positions at which the corresponding bits are different. In general, Hamming measure is more suitable for binary data than Euclidean measure.
The task is to learn a mapping from b(x) that project p-dimensional real valued input x onto a q dimensional binary code while preserving some notion of similarity. This mapping, which is called hash function is parameterized by a matrix w such that:
In a previous paper, the authors tried to used a loss function which bears some similarity to the hinge function used in SVM. It includes a hyper-parameter which is a threshold in Hamming space that differentiates neighbors from non-neighbors. such that similar points are mapped to binary codes that do differ in more than P bits and disimilar points should map to points closer no more than P bits. For two binary codes [math]\displaystyle{ h }[/math] and [math]\displaystyle{ g }[/math] with hamming distance [math]\displaystyle{ ||h-g||_H }[/math] and a similarity label [math]\displaystyle{ s \in {0,1} }[/math] the pairwise hinge loss function is defined as:
[math]\displaystyle{ l_{pair}(h,g,\rho)= \begin{cases} [\|h-g\|_H-\rho+1]_{+} & for s=1(similar) \\ {[}\rho-\|h-g\|_H+1]_+ & for s=0(dissimilar) \end{cases} }[/math]
where [math]\displaystyle{ {[}\alpha]_{+}=max(\alpha,0) }[/math] and [math]\displaystyle{ \rho }[/math] is a threshold value that separates similar from dissimilar codes.
In practice finding value of [math]\displaystyle{ \rho }[/math] is not easy. Moreover in some datasets the relative pairwise distance is important not the precise numerical value. As a result in this paper authors defined the loss function in terms of the relative similarity. To define relative similarity it is assumed that dataset include triplet of items [math]\displaystyle{ (x,x^+,x^-) }[/math] such that [math]\displaystyle{ x }[/math] is more similar to [math]\displaystyle{ x^+ }[/math] than [math]\displaystyle{ x^- }[/math]. With this assumption the ranking loss on triplet of binary codes [math]\displaystyle{ (h,h^+,h^-) }[/math] is:
Optimization
Given a training set of triplets, [math]\displaystyle{ D={(x_i,x_i^+,x_i^-)}_{i=1}^n }[/math], the objective is to minimize the sum of ranking loss for all training samples and a simple regularizer on the vector of unknown parameters [math]\displaystyle{ w }[/math]:
which is a discontinuous and non-convex function and optimization is not trivial. The discontinuity is because of the sign function and can be mitigated through construction of upper bound on the empirical loss. To do that one can rewrite function b as following
where [math]\displaystyle{ H=\{-1,+1\}^q }[/math].
Upper bound on empirical loss
The upper bound on loss has the following form:
This upper bound is continuous and piece wise smooth in w as long as f is continuous in w. In particular when [math]\displaystyle{ f }[/math] is linear in [math]\displaystyle{ w }[/math], the bound becomes piece-wise linear and convex. To prove that this is actually an upper bound, it suffices to substitute [math]\displaystyle{ (b,b^-,b^+) }[/math] in the first term of the bound.
To use the upper bound for optimization we should be able to find [math]\displaystyle{ (g,g^-,g^+) }[/math] that maximizes the first term of the above equation. There [math]\displaystyle{ 2^{3q} }[/math] possible combinations for codes which makes this optimization challenging. However this optimization can be solved efficiently for the class of triplet loss functions, such loss function do not depend on the specific binary codes, but rather the differences which can take only [math]\displaystyle{ 2q }[/math] values (because it is an integer between [math]\displaystyle{ -q }[/math] and [math]\displaystyle{ q }[/math]). Therefore, this optimization can be done in [math]\displaystyle{ O(q^3) }[/math] using dynamic programming.
Perceptron-like learning
Now to learn the efficient value for [math]\displaystyle{ w }[/math] the authors used a stochastic gradient descent approach in which they first initialize [math]\displaystyle{ w^0 }[/math] randomly and then at iteration this value is updated by following algorithm: 1.Select a random triplet [math]\displaystyle{ (x,x^+,x^-) }[/math] from dataset [math]\displaystyle{ D }[/math]
2.Compute [math]\displaystyle{ (\hat{h},\hat{h}^+,\hat{h}^-)=(b(x,w^t),b(x^+,w^t),b(x^-,w^t)) }[/math]
3.Compute [math]\displaystyle{ (\hat{g},\hat{g}^+,\hat{g}^-) }[/math]
4.Update the model parameters using
where [math]\displaystyle{ n }[/math] is the learning rate and [math]\displaystyle{ \frac{\partial f(x)}{\partial w} }[/math] is the transpose of the Jacobian Matrix.
It is noteworthy that the target optimization function is not smooth at some points (i.e., it is piece-wise smooth), therefore, the gradient may not exist in some points. However, the authors argue that they have not encountered this situation in the experiments.
Asymmetric Hamming distance
When Hamming distance is used to score and retrieve the nearest neighbors to a given query, there is a high probability of a tie, where multiple items are equidistant from the query in Hamming space. To break ties and improve the similarity measure, previous work suggests the use of an asymmetric Hamming (AH) distance.
In this work, the following asymmetric Hamming distance function is used
where [math]\displaystyle{ h }[/math] is a database binary code; [math]\displaystyle{ v\in \mathbb{R}^q }[/math] is a real-valued query vector; [math]\displaystyle{ s\in \mathbb{R}^q }[/math] is a vector of scaling parameters that control the slop of hyperbolic tangent applied to different bits; [math]\displaystyle{ Diag(s) }[/math] is a diagonal matrix with the elements of [math]\displaystyle{ s }[/math] on its diagonal.
It is noteworthy that this distance is used in the recall phase, not the training phase.
Implementation details
In practice, the basic Perceptron-like learning algorithm is implemented with several modifications. First, instead of using a single training triplet to estimate the gradients, they use mini-batches comprising 100 triplets and average the gradient.
Second, for each triplet [math]\displaystyle{ (x,x^+,x^-) }[/math], they replace [math]\displaystyle{ x^- }[/math] with a "hard" example by selecting an item among all negative examples in the mini-batch that is closest in the current Hamming distance to [math]\displaystyle{ b(x) }[/math].
Third, to find good binary codes, the authors encourage each bit, averaged over the training data, to be mean-zero before quantization. This is accomplished by adding the following penalty to the objective function:
They use a heuristic to adapt learning rates, know as bold driver. For each mini-batch they evaluate the learning objective before the parameters are updated. As long as the objective is decreasing, the learning rate [math]\displaystyle{ \eta }[/math] is increased.
Experiments
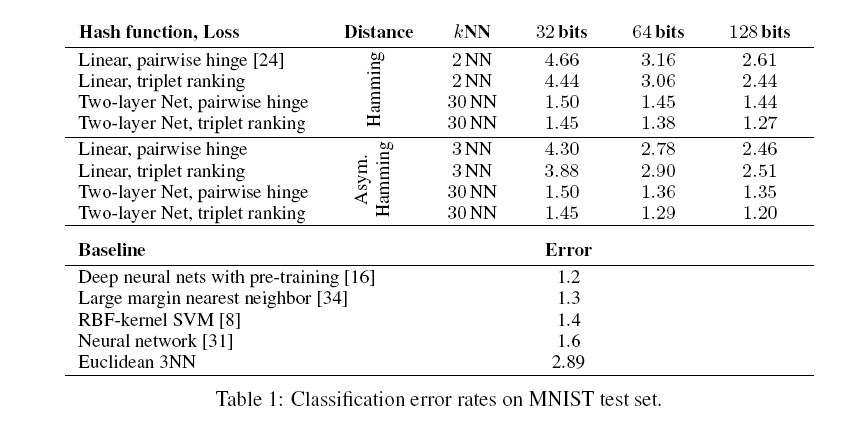
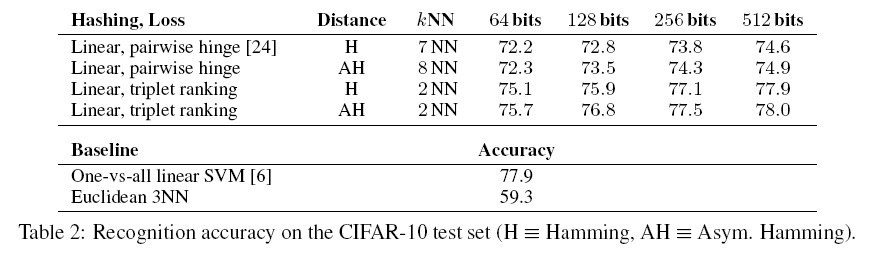
The paper conducts experiments on two image corpora: MNIST and CIFAR-10 (<ref> Krizhevsky A. Learning multiple layers of features from tiny images. MSc. thesis, Univ. Toronto, 2009 </ref>), to evalues the performance of Hamming distance metric learning.
Two families of hash functions are chosen: linear transforms and multilayer neural networks.
Two loss functions are chosen: the pairwise hinge loss and the triplet ranking loss.
In each test set, the precision@k, (i.e. the fraction of k closest items in Hamming distance that are same-class neighbors) are reported. The classification error rates for both Hamming (H) and asymmetric Hamming (AH) are also reported. The results are summarized in table 1 and table 2 (<ref> Norouziy, M and Fleety, D. J. and Salakhutdinov, R. Hamming Distance Metric Learning, Advances in Neural Information Processing Systems 25. 2012. </ref>).
Conclusion
The paper presents a framework for Hamming distance metric learning, which entails learning a discrete mapping from the input space onto binary codes. This framework accommodates different families of hash functions, including quantized linear transforms, and multilayer neural nets. By using a piecewise-smooth upper bound on a triplet ranking loss, they optimize hash functions that are shown to preserve semantic similarity on complex datasets. In particular, the experiments show that a simple kNN classifier on the learned binary codes is competitive with sophisticated discriminative classifiers. While other hashing papers have used CIFAR or MNIST, none report kNN classification performance, often because it has been thought that the bar established by state-of-the-art classifiers is too high. On the contrary the kNN classification performance in the paper suggests that Hamming space can be used to represent complex semantic structures with high fidelity. One appeal of this approach is the scalability of kNN search on binary codes to billions of data points, and of kNN classification to millions of class labels.
However, there are some pints that are not clear in the paper. First of all, the intuition behind the upper bound is missing and it is not clear how tight is the bound. The second issue is that the gradient that is computed does not exactly correspond to the optimization function (the maximization parts in the optimization target are simplified before taking the derivative). There is no evidence to show that this simplification is good, except that they have acquired acceptable experimental results. Furthermore, it was good if they managed to compare their method to the simplified Euclidean version of it (e.g., multilayer neural network with triplet constraints)
References
<references />