conditional neural process
Motivation
Deep neural networks are good at function approximations, yet they are typically trained from scratch for each new function. While Bayesian methods, such as Gaussian Processes (GPs), exploit prior knowledge to quickly infer the shape of a new function at test time. Yet GPs are computationally expensive, and it can be hard to design appropriate priors. Hence the authors propose a family of neural models called, Conditional Neural Processes (CNPs), that combine the benefits of both.
Introduction
To train a model effectively, deep neural networks typically require large datasets. To mitigate this data efficiency problem, learning in two phases is one approach: the first phase learns the statistics of a generic domain without committing to a specific learning task; the second phase learns a function for a specific task but does so using only a small number of data points by exploiting the domain-wide statistics already learned. Taking a probabilistic stance and specifying a distribution over functions (stochastic processes) is another approach -- Gaussian Processes being a commonly used example of this. Such Bayesian methods can be computationally expensive.
The authors of the paper propose a family of models that represent solutions to the supervised problem, and an end-to-end training approach to learning them that combines neural networks with features reminiscent of Gaussian Processes. They call this family of models Conditional Neural Processes (CNPs). CNPs can be trained on very few data points to make accurate predictions, while they also have the capacity to scale to complex functions and large datasets.
Model
Stochastic Processes
Consider a data set [math]\displaystyle{ \{x_i, y_i\} }[/math] with evaluations [math]\displaystyle{ y_i = f(x_i) }[/math] for some unknown function [math]\displaystyle{ f }[/math]. Assume [math]\displaystyle{ g }[/math] is an approximating function of [math]\displaystyle{ f }[/math]. The aim is to minimize the loss between [math]\displaystyle{ f }[/math] and [math]\displaystyle{ g }[/math] on the entire space [math]\displaystyle{ X }[/math]. In practice, the routine is evaluated on a finite set of observations.
Let training set be [math]\displaystyle{ O = \{x_i, y_i\}_{i = 0} ^{n-1} }[/math], and test set be [math]\displaystyle{ T = \{x_i, y_i\}_{i = n} ^ {n + m - 1} \subset X }[/math] of unlabelled points.
Let [math]\displaystyle{ P }[/math] be a probability distribution over functions [math]\displaystyle{ F : X \to Y }[/math], formally known as a stochastic process. Thus, [math]\displaystyle{ P }[/math] defines a joint distribution over the random variables [math]\displaystyle{ {f(x_i)}_{i = 0} ^{n + m - 1} }[/math]. Therefore, for [math]\displaystyle{ P(f(x)|O, T) }[/math], our task is to predict the output values [math]\displaystyle{ f(x_i) }[/math] for [math]\displaystyle{ x_i \in T }[/math], given [math]\displaystyle{ O }[/math].
A good example is given by the authors, consider a random 1-dimensional function [math]\displaystyle{ f ∼ P }[/math] defined on the real line (i.e., [math]\displaystyle{ X := R }[/math], [math]\displaystyle{ Y := R }[/math]). [math]\displaystyle{ O }[/math] would constitute [math]\displaystyle{ n }[/math] observations of [math]\displaystyle{ f }[/math]’s value [math]\displaystyle{ y_i }[/math] at different locations [math]\displaystyle{ x_i }[/math] on the real line. Given these observations, we are interested in predicting [math]\displaystyle{ f }[/math]’s value at new locations on the real line.
A common assumption made on [math]\displaystyle{ P }[/math] is that all function evaluations of [math]\displaystyle{ f }[/math] are Gaussian distributed. The random functions class is called Gaussian Processes (GPs). This framework of the stochastic process allows a model to be data efficient. However, it's hard to get appropriate priors and stochastic processes are expensive in computation, scaling poorly with [math]\displaystyle{ n }[/math] and [math]\displaystyle{ m }[/math]. One of the examples is GPs, which has running time [math]\displaystyle{ O(n+m)^3 }[/math].
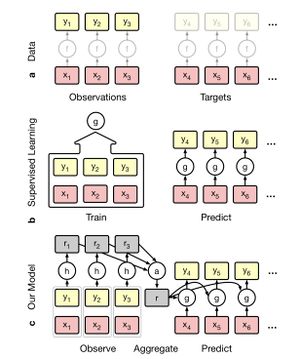
Conditional Neural Process
Conditional Neural Process models directly parametrize conditional stochastic processes without imposing consistency with respect to some prior process. CNP parametrize distributions over [math]\displaystyle{ f(T) }[/math] given a distributed representation of [math]\displaystyle{ O }[/math] of fixed dimensionality. Thus, the mathematical guarantees associated with stochastic processes is traded off for functional flexibility and scalability.
CNP is a conditional stochastic process [math]\displaystyle{ Q_\theta }[/math] defines distributions over [math]\displaystyle{ f(x_i) }[/math] for [math]\displaystyle{ x_i \in T }[/math], given a set of observations [math]\displaystyle{ O }[/math]. For stochastic processs, the authors assume that [math]\displaystyle{ Q_{\theta} }[/math] is invariant to permutations, and [math]\displaystyle{ Q_\theta(f(T) | O, T)= Q_\theta(f(T') | O, T')=Q_\theta(f(T) | O', T) }[/math] when [math]\displaystyle{ O', T' }[/math] are permutations of [math]\displaystyle{ O }[/math] and [math]\displaystyle{ T }[/math]. In this work, we generally enforce permutation invariance with respect to [math]\displaystyle{ T }[/math] be assuming a factored structure, which is the easiest way to ensure a valid stochastic process. That is, [math]\displaystyle{ Q_\theta(f(T) | O, T) = \prod _{x \in T} Q_\theta(f(x) | O, x) }[/math]. Moreover, this framework can be extended to non-factored distributions.
In detail, the following architecture is used.
[math]\displaystyle{ r_i = h_\theta(x_i, y_i) }[/math] ∀ [math]\displaystyle{ (x_i, y_i) \in O }[/math], where [math]\displaystyle{ h_\theta : X \times Y \to \mathbb{R} ^ d }[/math]
[math]\displaystyle{ r = r_i * r_2 * ... * r_n }[/math], where [math]\displaystyle{ * }[/math] is a commutative operation that takes elements in [math]\displaystyle{ \mathbb{R}^d }[/math] and maps them into a single element of [math]\displaystyle{ \mathbb{R} ^ d }[/math]
[math]\displaystyle{ \Phi_i = g_\theta }[/math] ∀ [math]\displaystyle{ x_i \in T }[/math], where [math]\displaystyle{ g_\theta : X \times \mathbb{R} ^ d \to \mathbb{R} ^ e }[/math] and [math]\displaystyle{ \Phi_i }[/math] are parameters for [math]\displaystyle{ Q_\theta }[/math]
Note that this architecture ensures permutation invariance and [math]\displaystyle{ O(n + m) }[/math] scaling for conditional prediction. Also, [math]\displaystyle{ r = r_i * r_2 * ... * r_n }[/math] can be computed in [math]\displaystyle{ O(n) }[/math], this architecture supports streaming observation with minimal overhead.
We train [math]\displaystyle{ Q_\theta }[/math] by asking it to predict [math]\displaystyle{ O }[/math] conditioned on a randomly chosen subset of [math]\displaystyle{ O }[/math]. This gives the model a signal of the uncertainty over the space X inherent in the distribution P given a set of observations. The authors let [math]\displaystyle{ f \sim P }[/math], [math]\displaystyle{ O = \{(x_i, y_i)\}_{i = 0} ^{n-1} }[/math], and N ~ uniform[0, 1, ..... ,n-1]. Subset [math]\displaystyle{ O = \{(x_i, y_i)\}_{i = 0} ^{N} }[/math] that is first N elements of [math]\displaystyle{ O }[/math] is regarded as condition. The negative conditional log probability is given by \[\mathcal{L}(\theta)=-\mathbb{E}_{f \sim p}[\mathbb{E}_{N}[\log Q_\theta(\{y_i\}_{i = 0} ^{n-1}|O_{N}, \{x_i\}_{i = 0} ^{n-1})]]\] Thus, the targets it scores [math]\displaystyle{ Q_\theta }[/math] on include both the observed and unobserved values. In practice, Monte Carlo estimates of the gradient of this loss is taken by sampling [math]\displaystyle{ f }[/math] and [math]\displaystyle{ N }[/math].
This approach shifts the burden of imposing prior knowledge from an analytic prior to empirical data. This has the advantage of liberating a practitioner from having to specify an analytic form for the prior, which is ultimately intended to summarize their empirical experience. Still, we emphasize that the [math]\displaystyle{ Q_\theta }[/math] are not necessarily a consistent set of conditionals for all observation sets, and the training routine does not guarantee that.
In summary,
1. A CNP is a conditional distribution over functions trained to model the empirical conditional distributions of functions [math]\displaystyle{ f \sim P }[/math].
2. A CNP is permutation invariant in [math]\displaystyle{ O }[/math] and [math]\displaystyle{ T }[/math].
3. A CNP is scalable, achieving a running time complexity of [math]\displaystyle{ O(n + m) }[/math] for making [math]\displaystyle{ m }[/math] predictions with [math]\displaystyle{ n }[/math] observations.
Related Work
Gaussian Process Framework
A Gaussian Process (GP) is a non-parametric method for regression, used extensively for regression and classification problems in the machine learning community. A GP is defined as a collection of random variables, any finite number of which have a joint Gaussian distribution. A standard approach is to model data as [math]\displaystyle{ y = m(X, φ) + \epsilon }[/math] where [math]\displaystyle{ m }[/math] is the mean function with parameter vector [math]\displaystyle{ φ }[/math], and [math]\displaystyle{ \epsilon }[/math] represents independent and identically distributed (i.i.d.) Gaussian noise: [math]\displaystyle{ N\sim (0,\sigma^2) }[/math]
For more info on Gaussian Process Framework: A Gaussian process framework for modeling instrumental systematics: application to transmission spectroscopy
Several papers attempt to address various issues with GPs. These include:
- Using sparse GPs to aid in scaling (Snelson & Ghahramani, 2006)
- Using Deep GPs to achieve more expressiveness (Damianou & Lawrence, 2013; Salimbeni & Deisenroth, 2017)
- Using neural networks to learn more expressive kernels (Wilson et al., 2016)
A Python resource for Gaussian Process Framework implementation: Gaussian Process Framework in Python
The goal of this paper is to incorporate ideas from standard neural networks with Gaussian processes in order to overcome drawbacks of both. Bayesian techniques work better with less data, but complex Bayesian networks become intractable on even moderate sized data sizes. NNs on the other hand, cannot make use of prior knowledge and often have to be retrained from scratch. Without sufficient data, they also perform poorly. Combining both frameworks, we get Conditional Neural Processes serves to learn the kernels of the Gaussian Process through neural networks and uses these learned kernels on a framework similar to GPs for prediction.
Meta Learning
Meta-Learning attempts to allow neural networks to learn more generalizable functions, as opposed to only approximating one function. This can be done by learning deep generative models which can do few-shot estimations of data. This can be implemented with attention mechanisms (Reed et al., 2017) or additional memory units in a VAE model (Bornschein et al., 2017). Another successful latent variable approach is to explicitly condition on some context during inference (J. Rezende et al., 2016). Given the generative nature of these models they are usually applied to image generation tasks, but models that include a conditioning class-variable can be used for classification as well. Recently meta-learning has also been applied to a wide range of tasks like RL (Wang et al., 2016; Finn et al., 2017) or program induction (Devlin et al., 2017).
Classification is another common task in meta-learning. Few-shot classification algorithms usually rely on some distance metric in feature space to compare target images and the observations (Koch et al., 2015), (Santoro et al., 2016).. Matching networks(Vinyals et al., 2016; Bartunov & Vetrov, 2016) are closely related to CNPs. In their case features of samples are compared with target features using an attention kernel. At a higher level one can interpret this model as a CNP where the aggregator is just the concatenation over all input samples and the decoder [math]\displaystyle{ g }[/math] contains an explicitly defined distance kernel. In this sense matching networks are closer to GPs than to CNPs, since they require the specification of a distance kernel that CNPs learn from the data instead. In addition, as MNs carry out all- to-all comparisons they scale with [math]\displaystyle{ O(n × m) }[/math], although they can be modified to have the same complexity of [math]\displaystyle{ O(n + m) }[/math] as CNPs (Snell et al., 2017).
Another field in the meta-learning field is Neural architecture search. It requires the search algorithm to define three things: the search space, search strategy, and performance evaluation strategy. It is one of the most popular trends in the meta-learning field now. The idea is we can define some search space, and let algorithms help us decide what architecture and hyperparameters would be best for a particular task. Also, since evaluating a neural network is expensive(needs train the neural network first), it needs a well designed performance evaluation strategy to lower down the computational cost. One recent example of the architecture search approach (Liu et al. 2017) involves the use of evolutionary algorithms that combines both random step selection of candidates and evaluation of the best-suited ones for growing an initial population.
A model that is conceptually very similar to CNPs (and in particular the latent variable version) is the “neural statistician” paper (Edwards & Storkey, 2016) and the related variational homoencoder (Hewitt et al., 2018). As with the other generative models the neural statistician learns to estimate the density of the observed data but does not allow for targeted sampling at what we have been referring to as input positions [math]\displaystyle{ x_i }[/math]. Instead, one can only generate i.i.d. samples from the estimated density. Finally, the latest variant of Conditional Neural Process can also be seen as an approximated amortized version of Bayesian DL(Gal & Ghahramani, 2016; Blundell et al., 2015; Louizos et al., 2017; Louizos & Welling, 2017). For example, Gal & Ghahramani 2016 develop a new theoretical framework casting dropout training in deep neural networks as approximate Bayesian inference in deep Gaussian processes. Their theory extracts information from existing models and gives us tools to model uncertainty.
Experimental Result I: Function Regression
Classical 1D regression task that used as a common baseline for GP is the first example. They generated two different datasets that consisted of functions generated from a GP with an exponential kernel. In the first dataset they used a kernel with fixed parameters, and in the second dataset, the function switched at some random point. on the real line between two functions, each sampled with different kernel parameters. At every training step, they sampled a curve from the GP, select a subset of n points as observations, and a subset of t points as target points. Using the model, the observed points are encoded using a three-layer MLP encoder h with a 128-dimensional output representation. The representations are aggregated into a single representation [math]\displaystyle{ r = \frac{1}{n} \sum r_i }[/math] , which is concatenated to [math]\displaystyle{ x_t }[/math] and passed to a decoder g consisting of a five layer MLP. The function outputs a Gaussian mean and variance for the target outputs. The model is trained to maximize the log-likelihood of the target points using the Adam optimizer.
Two examples of the regression results obtained for each of the datasets are shown in the following figure.
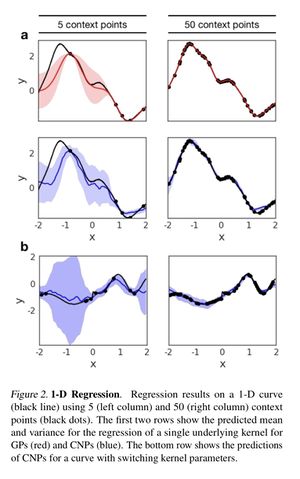
They compared the model to the predictions generated by a GP with the correct hyperparameters, which constitutes an upper bound on our performance. Although the prediction generated by the GP is smoother than the CNP's prediction both for the mean and variance, the model is able to learn to regress from a few context points for both the fixed kernels and switching kernels. As the number of context points grows, the accuracy of the model improves and the approximated uncertainty of the model decreases. Crucially, we see the model learns to estimate its own uncertainty given the observations very accurately. Nonetheless, it provides a good approximation that increases in accuracy as the number of context points increases. Furthermore, the model achieves similarly good performance on the switching kernel task. This type of regression task is not trivial for GPs whereas in our case we only have to change the dataset used for training
Experimental Result II: Image Completion for Digits
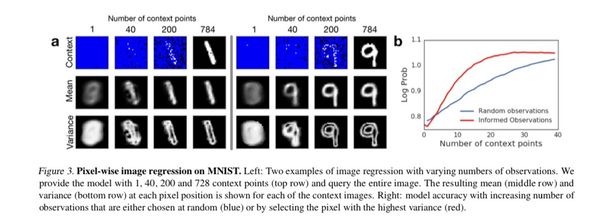
They also tested CNP on the MNIST dataset and use the test set to evaluate its performance. As shown in the above figure the model learns to make good predictions of the underlying digit even for a small number of context points. Crucially, when conditioned only on one non-informative context point the model’s prediction corresponds to the average overall MNIST digits. As the number of context points increases the predictions become more similar to the underlying ground truth. This demonstrates the model’s capacity to extract dataset specific prior knowledge. It is worth mentioning that even with a complete set of observations, the model does not achieve pixel-perfect reconstruction, as we have a bottleneck at the representation level.
To generate a coherent sample, the authors compute the representation r from the observations, which parametrizes a Gaussian distribution over the latents z. Then z sampled once and used to generate the predictions for all targets. To get a different coherent sample they draw a new sample from the latents z and run the decoder again for all targets.
Since this implementation of CNP returns factored outputs, the best prediction it can produce given limited context information is to average over all possible predictions that agree with the context. An alternative to this is to add latent variables in the model such that they can be sampled conditioned on the context to produce predictions with high probability in the data distribution.
In order to generate a coherent sample, we compute the representation r from the observations, which parametrizes a Gaussian distribution over the latents z. z is then sampled once and used to generate the predictions for all targets. To get a different coherent sample we draw a new sample from the latents z and run the decoder again for all targets.
An important aspect of the model is its ability to estimate
the uncertainty of the prediction. As shown in the bottom
row of the above figure, as they added more observations, the variance
shifts from being almost uniformly spread over the digit
positions to being localized around areas that are specific
to the underlying digit, specifically its edges. Being able to
model the uncertainty given some context can be helpful for
many tasks. One example is active exploration, where the
model has a choice over where to observe.
They tested this by
comparing the predictions of CNP when the observations
are chosen according to uncertainty, versus random pixels. This method is a very simple way of doing active
exploration, but it already produces better prediction results
then selecting the conditioning points at random.
Experimental Result III: Image Completion for Faces
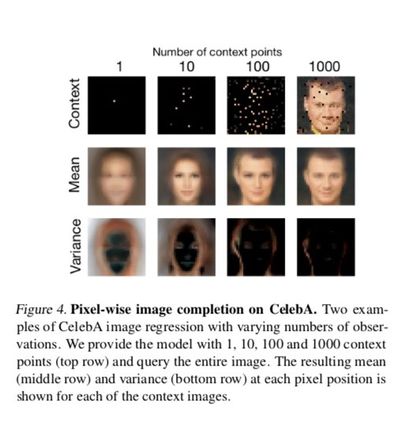
They also applied CNP to CelebA, a dataset of images of
celebrity faces and reported performance obtained on the
test set.
As shown in the above figure our model is able to capture the complex shapes and colors of this dataset with predictions conditioned on less than 10% of the pixels being already close to the ground truth. As before, given a few contexts points the model averages over all possible faces, but as the number of context pairs increases the predictions capture image-specific details like face orientation and facial expression. Furthermore, as the number of context points increases the variance is shifted towards the edges in the image.

An important aspect of CNPs demonstrated in the above figure is it's flexibility not only in the number of observations and targets it receives but also with regards to their input values. It is interesting to compare this property to GPs on one hand, and to trained generative models (van den Oord et al., 2016; Gregor et al., 2015) on the other hand. The first type of flexibility can be seen when conditioning on subsets that the model has not encountered during training. Consider conditioning the model on one half of the image, fox example. This forces the model to not only predict the pixel values according to some stationary smoothness property of the images, but also according to global spatial properties, e.g. symmetry and the relative location of different parts of faces. As seen in the first row of the figure, CNPs are able to capture those properties. A GP with a stationary kernel cannot capture this, and in the absence of observations would revert to its mean (the mean itself can be non-stationary but usually, this would not be enough to capture the interesting properties).
In addition, the model is flexible with regards to the target input values. This means, e.g., we can query the model at resolutions it has not seen during training. We take a model that has only been trained using pixel coordinates of a specific resolution and predict at test time subpixel values for targets between the original coordinates. As shown in Figure 5, with one forward pass we can query the model at different resolutions. While GPs also exhibit this type of flexibility, it is not the case for trained generative models, which can only predict values for the pixel coordinates on which they were trained. In this sense, CNPs capture the best of both worlds – it is flexible in regards to the conditioning and prediction task and has the capacity to extract domain knowledge from a training set.
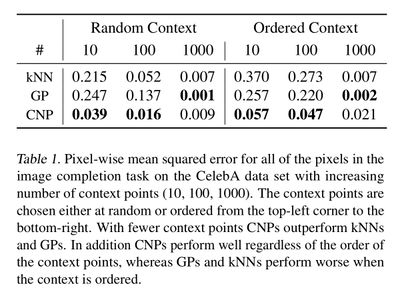
They compared CNPs quantitatively to two related models:
kNNs and GPs. As shown in the above table CNPs outperform
the latter when a number of context points are small (empirically
when half of the image or less is provided as context).
When the majority of the image is given as context exact
methods like GPs and kNN will perform better. From the table
we can also see that the order in which the context points
are provided is less important for CNPs, since providing the
context points in order from top to bottom still results in
good performance. Both insights point to the fact that CNPs
learn a data-specific ‘prior’ that will generate good samples
even when the number of context points is very small.
Experimental Result IV: Classification
Finally, they applied the model to one-shot classification using the Omniglot dataset. This dataset consists of 1,623 classes of characters from 50 different alphabets. Each class has only 20 examples and as such this dataset is particularly suitable for few-shot learning algorithms. The authors used 1,200 randomly selected classes as their training set and the remainder as the testing data set.
Additionally, to apply data augmentation the authors cropped the image from 32 × 32 to 28 × 28, applied small random translations and rotations to the inputs, and also increased the number of classes by rotating every character by 90 degrees and defining that to be a new class. They generated the labels for an N-way classification task by choosing N random classes at each training step and arbitrarily assigning the labels [math]\displaystyle{ 0, ..., N − 1 }[/math] to each.
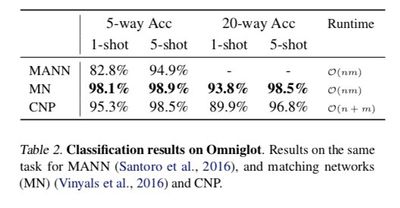
Given that the input points are images, they modified the architecture of the encoder h to include convolution layers as mentioned in section 2. In addition, they only aggregated over inputs of the same class by using the information provided by the input label. The aggregated class-specific representations are then concatenated to form the final representation. Given that both the size of the class-specific representations and the number of classes is constant, the size of the final representation is still constant and thus the [math]\displaystyle{ O(n + m) }[/math] runtime still holds. The results of the classification are summarized in the following table CNPs achieve higher accuracy than models that are significantly more complex (like MANN). While CNPs do not beat state of the art for one-shot classification our accuracy values are comparable. Crucially, they reached those values using a significantly simpler architecture (three convolutional layers for the encoder and a three-layer MLP for the decoder) and with a lower runtime of [math]\displaystyle{ O(n + m) }[/math] at test time as opposed to [math]\displaystyle{ O(nm) }[/math]
Conclusion
The paper introduced Conditional Neural Processes, a model that is both flexible at test time and has the capacity to extract prior knowledge from training data.
The authors had demonstrated its ability to perform a variety of tasks including regression, classification and image completion. The paper compared CNP's to Gaussian Processes on one hand, and deep learning methods on the other, and also discussed the relation to meta-learning and few-shot learning. It is important to note that the specific CNP implementations described here are just simple proofs-of-concept and can be substantially extended, e.g. by including more elaborate architectures in line with modern deep learning advances. To summarize, this work can be seen as a step towards learning high-level abstractions, one of the grand challenges of contemporary machine learning. Functions learned by most Conditional Neural Processes conventional deep learning models are tied to a specific, constrained statistical context at any stage of training. A trained CNP is more general, in that it encapsulates the high-level statistics of a family of functions. As such it constitutes a high-level abstraction that can be reused for multiple tasks. In future work, they are going to explore how far these models can help in tackling the many key machine learning problems that seem to hinge on abstraction, such as transfer learning, meta-learning, and data efficiency.
Critiques
This paper introduces a method, for reducing the computational complexity of the more famous Gaussian Processes model, but they have mentioned a complexity of O(n + m) which is almost the same order of RBF kernel GP. With respect to performances in a sequence of tasks, the authors have not made metric comparisons to GP methods to prove the superiority of their approach.
It appears that the proposed model is effective in making accurate predictions using lower quality inputs. For example, a dataset with fewer data points or an image with fewer pixels. However, it is not clear whether the proposed algorithm can be trained with a smaller amount of input data.
Other Sources
- Code for this model and a simpler explanation can be found at [1]
- A newer version of the model is described in this paper [2]
- A good blog post on neural processes [3]
Reference
Bartunov, S. and Vetrov, D. P. Fast adaptation in generative models with generative matching networks. arXiv preprint arXiv:1612.02192, 2016.
Blundell, C., Cornebise, J., Kavukcuoglu, K., and Wierstra, D. Weight uncertainty in neural networks. arXiv preprint arXiv:1505.05424, 2015.
Bornschein, J., Mnih, A., Zoran, D., and J. Rezende, D. Variational memory addressing in generative models. In Advances in Neural Information Processing Systems, pp. 3923–3932, 2017.
Damianou, A. and Lawrence, N. Deep gaussian processes. In Artificial Intelligence and Statistics, pp. 207–215, 2013.
Devlin, J., Bunel, R. R., Singh, R., Hausknecht, M., and Kohli, P. Neural program meta-induction. In Advances in Neural Information Processing Systems, pp. 2077–2085, 2017.
Edwards, H. and Storkey, A. Towards a neural statistician. 2016.
Finn, C., Abbeel, P., and Levine, S. Model-agnostic metalearning for fast adaptation of deep networks. arXiv preprint arXiv:1703.03400, 2017.
Gal, Y. and Ghahramani, Z. Dropout as a bayesian approximation: Representing model uncertainty in deep learning. In international conference on machine learning, pp. 1050–1059, 2016.
Garnelo, M., Arulkumaran, K., and Shanahan, M. Towards deep symbolic reinforcement learning. arXiv preprint arXiv:1609.05518, 2016.
Gregor, K., Danihelka, I., Graves, A., Rezende, D. J., and Wierstra, D. Draw: A recurrent neural network for image generation. arXiv preprint arXiv:1502.04623, 2015.
Hewitt, L., Gane, A., Jaakkola, T., and Tenenbaum, J. B. The variational homoencoder: Learning to infer high-capacity generative models from few examples. 2018.
J. Rezende, D., Danihelka, I., Gregor, K., Wierstra, D., et al. One-shot generalization in deep generative models. In International Conference on Machine Learning, pp. 1521–1529, 2016.
Kingma, D. P. and Ba, J. Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980, 2014.
Kingma, D. P. and Welling, M. Auto-encoding variational bayes. arXiv preprint arXiv:1312.6114, 2013.
Koch, G., Zemel, R., and Salakhutdinov, R. Siamese neural networks for one-shot image recognition. In ICML Deep Learning Workshop, volume 2, 2015.
Lake, B. M., Salakhutdinov, R., and Tenenbaum, J. B. Human-level concept learning through probabilistic program induction. Science, 350(6266):1332–1338, 2015.
Lake, B. M., Ullman, T. D., Tenenbaum, J. B., and Gershman, S. J. Building machines that learn and think like people. Behavioral and Brain Sciences, 40, 2017.
LeCun, Y., Bottou, L., Bengio, Y., and Haffner, P. Gradientbased learning applied to document recognition. Proceedings of the IEEE, 86(11):2278–2324, 1998.
Liu, Z., Luo, P., Wang, X., and Tang, X. Deep learning face attributes in the wild. In Proceedings of International Conference on Computer Vision (ICCV), December 2015.
Louizos, C. and Welling, M. Multiplicative normalizing flows for variational bayesian neural networks. arXiv preprint arXiv:1703.01961, 2017.
Louizos, C., Ullrich, K., and Welling, M. Bayesian compression for deep learning. In Advances in Neural Information Processing Systems, pp. 3290–3300, 2017.
Rasmussen, C. E. and Williams, C. K. Gaussian processes in machine learning. In Advanced lectures on machine learning, pp. 63–71. Springer, 2004.
Reed, S., Chen, Y., Paine, T., Oord, A. v. d., Eslami, S., J. Rezende, D., Vinyals, O., and de Freitas, N. Few-shot autoregressive density estimation: Towards learning to learn distributions. 2017.
Rezende, D. J., Mohamed, S., and Wierstra, D. Stochastic backpropagation and approximate inference in deep generative models. arXiv preprint arXiv:1401.4082, 2014.
Salimbeni, H. and Deisenroth, M. Doubly stochastic variational inference for deep gaussian processes. In Advances in Neural Information Processing Systems, pp. 4591–4602, 2017.
Santoro, A., Bartunov, S., Botvinick, M., Wierstra, D., and Lillicrap, T. One-shot learning with memory-augmented neural networks. arXiv preprint arXiv:1605.06065, 2016.
Snell, J., Swersky, K., and Zemel, R. Prototypical networks for few-shot learning. In Advances in Neural Information Processing Systems, pp. 4080–4090, 2017.
Snelson, E. and Ghahramani, Z. Sparse gaussian processes using pseudo-inputs. In Advances in neural information processing systems, pp. 1257–1264, 2006.
van den Oord, A., Kalchbrenner, N., Espeholt, L., Vinyals, O., Graves, A., et al. Conditional image generation with pixelcnn decoders. In Advances in Neural Information Processing Systems, pp. 4790–4798, 2016.
Vinyals, O., Blundell, C., Lillicrap, T., Wierstra, D., et al. Matching networks for one shot learning. In Advances in Neural Information Processing Systems, pp. 3630–3638, 2016.
Wang, J. X., Kurth-Nelson, Z., Tirumala, D., Soyer, H., Leibo, J. Z., Munos, R., Blundell, C., Kumaran, D., and Botvinick, M. Learning to reinforcement learn. arXiv preprint arXiv:1611.05763, 2016.
Wilson, A. G., Hu, Z., Salakhutdinov, R., and Xing, E. P. Deep kernel learning. In Artificial Intelligence and Statistics, pp. 370–378, 2016.
Damianou, A. and Lawrence, N. Deep gaussian processes. In Artificial Intelligence and Statistics, pp. 207–215, 2013.