Understanding the Effective Receptive Field in Deep Convolutional Neural Networks
Introduction
What is the Receptive Field (RF) of a unit?
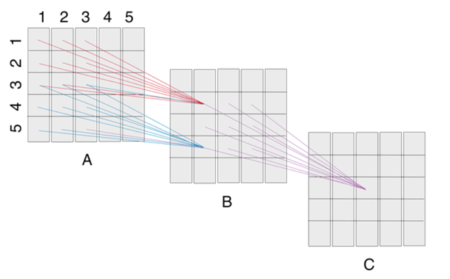
The receptive field of a unit is the region of input that is seen and responded to by the unit. When dealing with high-dimensional inputs such as images, it is impractical to connect neurons to all neurons in the previous volume. Instead, we connect each neuron to only a local region of the input volume. The spatial extent of this connectivity is a hyper-parameter called the receptive field of the neuron (equivalently this is the filter size). Hence, the dept of the input is the extent of the connectivity along the depth axis [4]. For instance, if we take an RGB CIFAR-10 image which has the input size of 32x32x3 (height, width, channels), wherein we have a receptive field (or the filter size) of 5x5 - then each neuron in the convolutional layer will have weights to a 5x5x3 region for every input image giving a total of 5*5*3 = 75 weights. It is important to note that the extent of the connectivity along the depth axis is 3 as the depth of the input is 3 (i.e. the channels).
An effective introduction to Receptive field arithmetic, including ways to calculate the receptive field of CNNs can be found here
Why is RF important?
The concept of receptive field is important for understanding and diagnosing how deep Convolutional neural networks (CNNs) work. Unlike in fully connected networks, where the value of each unit depends on the entire input to the network, in CNNs, anywhere in an input image outside the receptive field of a unit does not affect the value of that unit. Hence, it is necessary to carefully control the receptive field, to ensure that it covers the entire relevant image region. The property of receptive field allows for the response to be most sensitive to a local region in the image and to specific stimuli; similar stimuli trigger activations of similar magnitudes [2]. The initialization of each receptive field depends on the neuron's degrees of freedom [2]. One example outlined in this paper is that "the weights can be either of the same sign or centered with zero mean. This latter case favors a response to the contrast between the central and peripheral region of the receptive field." [2]. In many tasks, especially dense prediction tasks like semantic image segmentation, stereo and optical flow estimation, where we make a prediction for every single pixel in the input image, it is critical for each output pixel to have a big receptive field, such that no important information is left out when making the prediction.
How to increase RF size?
Make the network deeper by stacking more layers, which increases the receptive field size linearly by theory, as each extra layer increases the receptive field size by the kernel size (more accurate to say kernel size-1).
Add sub-sampling layers to increase the receptive field size multiplicatively. Actually, sub-sampling is simply AveragePooling with learnable weights per feature map. It acts like low pass filtering and then downsampling。
Modern deep CNN architectures like the VGG networks and Residual Networks use a combination of these techniques.
Intuition behind Effective Receptive Fields
The pixels at the center of an RF have a much larger impact on an output:
- In the forward pass, central pixels can propagate information to the output through many different paths, while the pixels in the outer area of the receptive field have very few paths to propagate its impact.
- In the backward pass, gradients from an output unit are propagated across all the paths, and therefore the central pixels have a much larger magnitude for the gradient from that output [More paths always mean larger gradient?].
- Not all pixels in a receptive field contribute equally to an output unit's response.
The authors prove that in many cases the distribution of impact in a receptive field distributes as a Gaussian. Since Gaussian distributions generally decay quickly from the center, the effective receptive field, only occupies a fraction of the theoretical receptive field.
The authors have correlated the theory of effective receptive field with some empirical observations. One such observation is that the random initializations lead some deep CNNs to start with a small effective receptive field, which then grows on training, which indicates a bad initialization bias.
Theoretical Results
The authors wanted to mathematically characterize how much each input pixel in a receptive field can impact the output of a unit $n$ layers up the network, i.e. when $n \rightarrow \infty$. More specifically, assume that pixels on each layer are indexed by $(i,j)$ with their centre at $(0,0)$. If we denote the pixel on the $p$th layer as $x_{i,j}^p$ , with $x_{i,j}^0$ as the input to the network, and $y_{i,j}=x_{i,j}^n$ as the output on the $n$th layer, we want to know how much each $x_{i,j}^0$ contributes to $y_{0,0}$. The effective receptive field (ERF) of this central output unit can be defined as the region containing input pixels with a non-negligible impact on it.
They used the partial derivative $\frac{\partial y_{0,0}}{\partial x_{i,j}^0}$ as the measure of such impact, which can be computed using backpropagation. Assuming $l$ as an arbitrary loss by the chain rule we can write $\frac{\partial l}{\partial x_{i,j}^0} = \sum_{i',j'}\frac{\partial l}{\partial y_{i',j'}}\frac{\partial y_{i',j'}}{\partial x_{i,j}^0}$. Now if $\frac{\partial l}{\partial y_{0,0}} =1$ and $\frac{\partial l}{\partial y_{i,j}}=0$ for all $i \neq 0$ and $j \neq 0$, then $\frac{\partial l}{\partial x_{i,j}^0} =\frac{\partial y_{0,0}}{\partial x_{i,j}^0}$.
For networks without nonlinearity (i.e., linear networks), this measure is independent of the input and depends only on the weights of the network and (i, j), which clearly shows how the impact of the pixels in the receptive field distributes.
Simplest case: Stack of convolutional layers of weights equal to 1
The authors first considered the case of $n$ convolutional layers using $k \times k$ kernels of stride 1 and a single channel on each layer and no nonlinearity, and bias.
For this special sub-case, the kernel was a $k \times k$ matrix of 1's. Since this kernel is separable to $k \times 1$ and $1 \times k$ matrices, the $2D$ convolution could be replaced by two $1D$ convolutions. This allowed the authors to focus their analysis on the $1D$ convolutions.
For this case, if we denote the gradient signal $\frac{\partial l}{\partial y_{i,j}}$ by $u(t)$ and the kernel by $v(t)$, we have
\begin{equation*} u(t)=\delta(t),\\ \quad v(t) = \sum_{m=0}^{k-1} \delta(t-m), \quad \text{where} \begin{cases} \delta(t)= 1\ \text{if}\ t=0, \\ \delta(t)= 0\ \text{if}\ t\neq 0, \end{cases} \end{equation*} and $t =0,1,-1,2,-2,...$ indexes the pixels.
The gradient signal $o(t)$ on the input pixels can now be computed by convolving $u(t)$ with $n$ such $v(t)$'s so that $o(t) = u *v* ...*v$.
Since convolution in time domain is equivalent to multiplication in Fourier domain, we can write
\begin{equation*} U(w) = \sum_{t=-\infty}^{\infty} u(t) e^{-jwt}=1,\\ V(w) = \sum_{t=-\infty}^{\infty} v(t) e^{-jwt}=\sum_{m=0}^{k-1} e^{-jwm},\\ O(w) = F(o(t))=F(u(t)*v(t)*...*v(t)) = U(w).V(w)^n = \Big ( \sum_{m=0}^{k-1} e^{-jwm} \Big )^n, \end{equation*}
where $O(w)$, $U(w)$, and $V(w)$ are discrete Fourier transformations of $o(t)$, $u(t)$, and $v(t)$. Next, we need to apply the inverse Fourier transform: \begin{equation*} o(t) = \frac{1}{2\pi} \int_{-\pi}^{\pi} (\sum_{m=0}^{k-1}e^{-j\omega m})^n e^{j \omega t} \ d\omega \end{equation*}
Now let us consider two non-trivial cases.
Case K=2: In this case $( \sum_{m=0}^{k-1} e^{-jwm} )^n = (1 + e^{-jw})^n$. Because $O(w)= \sum_{t=-\infty}^{\infty} o(t) e^{-jwt}= (1 + e^{-jw})^n$, we can think of $o(t)$ as coefficients of $e^{-jwt})$. Therefore, $o(t)= \begin{pmatrix} n\\t\end{pmatrix}$ is the standard binomial coefficients. As $n$ becomes large binomial coefficients distribute with respect to $t$ like a Gaussian distribution. More specifically, when $n \to \infty$ we can write
\begin{equation*}
\begin{pmatrix} n\\t \end{pmatrix} \sim \frac{2^n}{\sqrt{\frac{n\pi}{2}}}e^{-d^{2}/2n},
\end{equation*}
where $d = n-2t$ (see Binomial coefficient).
Case K>2: In this case the coefficients are known as "extended binomial coefficients" or "polynomial coefficients", and they too distribute like Gaussian [5].
Random Weights
Denote $g(i, j, p) = \frac{\partial l}{\partial x_{i,j}^p}$ as the gradient on the $p$th layer, and $g(i, j, n) = \frac{\partial l}{\partial y_{i,j}}$ . Then $g(, , 0)$ is the desired gradient image of the input. The backpropagation convolves $g(, , p)$ with the $k \times k$ kernel to get $g(, , p-1)$ for each p. So we can write
\begin{equation*} g(i,j,p-1) = \sum_{a=0}^{k-1} \sum_{b=0}^{k-1} w_{a,b}^p g(i+a,i+b,p), \end{equation*}
where $w_{a,b}^p$ is the convolution weight at $(a, b)$ in the convolution kernel on layer p. In this case, the initial weights are independently drawn from a fixed distribution with zero mean and variance $C$. By assuming that the gradients g are independent of the weights (linear networks only) and given that $\mathbb{E}_w[w_{a,b}^p] =0$
\begin{equation*} \mathbb{E}_{w,input}[g(i,j,p-1)] = \sum_{a=0}^{k-1} \sum_{b=0}^{k-1} \mathbb{E}_w[w_{a,b}^p] \mathbb{E}_{input}[g(i+a,i+b,p)]=0,\\ Var[g(i,j,p-1)] = \sum_{a=0}^{k-1} \sum_{b=0}^{k-1} Var[w_{a,b}^p] Var[g(i+a,i+b,p)]= C\sum_{a=0}^{k-1} \sum_{b=0}^{k-1} Var[g(i+a,i+b,p)]. \end{equation*}
Therefore, to get $Var[g(, , p-1)]$ we can convolve the gradient variance image $Var[g(, , p)]$ with a $k \times k$ kernel of 1’s, and then multiply it by $C$. Comparing this to the simplest case of all weights equal to one, we can see that the $g(, , 0)$ has a Gaussian shape, with only a slight change of having an extra $C^n$ constant factor multiplier on the variance gradient images, which does not affect the relative distribution within a receptive field.
Non-uniform Kernels
In the case of non-uniform weighting, when w(m)'s are normalized, we can simply use characteristic function to prove the Central Limit Theorem in this case. For $S_n = \sum_{i=1}^n$ $X_i$ and $X_i$’s are i.i.d.
As n → ∞, the distribution of $\sqrt{n}(\frac{1}{n}S_n - E[X])$ converges to Gaussian $N(0,Var[X])$ in distribution.
multinomial variables distributed according to $w(m)$’s, i.e. $p(X_i = m) = w(m)$, we have:
\begin{equation*} E[S_n] = n\sum_{m=0}^{k-1} mw(m),\\ Var[S_n] = n \left (\sum_{m=0}^{k-1} m^2w(m) - \left (\sum_{m=0}^{k-1} mw(m) \right )^2 \right ), \end{equation*}
If we take one standard deviation as the effective receptive field (ERF) size which is roughly the radius of the ERF, then this size is $\sqrt{Var[S_n]} = \sqrt{nVar[X_i]} = \mathcal{O}(\sqrt{n})$.
On the other hand, stacking more convolutional layers implies that the theoretical receptive field grows linearly, therefore relative to the theoretical receptive field, the ERF actually shrinks at a rate of $\mathcal{O}(1/\sqrt{n})$.
With uniform weighting, we can see that ERF size grows linearly as a function of the kernel size $k$. Using $w(m) = \frac{1}{k}$
\begin{equation*} \sqrt{Var[S_n]} = \sqrt{n}\sqrt{\sum_{m=0}^{k-1}\frac{m^2}{k} - \bigg(\sum_{m=0}^{k-1}\frac{m}{k}\bigg)^2} = \sqrt{\frac{n(k^2-1)}{12}} = \mathcal{O}(k\sqrt{n}) \end{equation*}
Non-linear Activation Functions
The math in this section is a bit "hand-wavy", as one of their reviewers wrote, and their conclusion (Gaussian-shape ERF) is not really well backed up by their experiments. The most important point take away here is that by the introduction of a nonlinear activation function, the gradients depends on the network's input as well.
Dropout
Dropout is a technique that sets each unit in a neural network randomly to zero during training, which has found great success as a regularizer to prevent deep networks from over-fitting. The authors show that dropout does not change the Gaussian ERF shape.
Subsampling and Dilated Convolutions
Subsampling reduces the resolution of the convolutional feature maps, and makes each of the following convolutional layers operate on a larger scale. It is therefore a great way to increase the receptive field. Subsampling followed by convolutional layers can be equivalently implemented as changing all the convolutional layers after subsampling from dense convolutions to dilated convolutions. Thus we can apply the same theory we developed above to understand networks with subsampling layers. However, with exponentially growing receptive field introduced by the subsampling or exponentially dilated convolutions, many more layers are needed to see the Gaussian shape clearly.
Skip Connections
Skip connections are another type of popular architecture designs for deep neural networks in general. Recent state-of-the-art models for image recognition, in particular the Residual Networks (ResNets) make extensive use of skip connections. The ResNet architecture is composed of residual blocks, each residual block has two pathways, one is a path of q (usually 2) convolutional layers plus nonlinearity and batch-normalization, the other one is a path of a skip connection that goes directly from the input to the output. The output is simply a sum of the results of the two pathways. Authors don't have explicit expression for the ERF size for skip connection, but it is smaller than the biggest receptive field possible, which is achieved when the pathway that goes through the convolutional layers are chosen in all residual block.
Remarks
The authors notice us about three critical assumptions in the analyses above: (1) all layers in the CNN use the same set of convolution weights. This is in general not true, however, when we apply the analysis of variance, the weight variance on all layers are usually the same up to a constant factor. (2) The convergence derived is convergence “in distribution”, as implied by the central limit theorem. So this is neither converging almost surely nor in probability, or rather, we are not able to guarantee convergence on any single model. (3) Although CLT gives the limit distribution of $\frac{1}{\sqrt{n}} S_n$, the distribution of $S_n$ does not have a limit, and its "deviation" from a corresponding normal distribution can be large on some finite set, but it still is Gaussian in terms of overall shape.
Verifying Theoretical Results
In all of the following experiments, a gradient signal of 1 was placed at the center of the output plane and 0 everywhere else, and then this gradient was backpropagated through the network to get input gradients. Also, random inputs, as well as proper random initialization of the kernels, were employed.
ERFs are Gaussian distributed: By looking at the figure,

we can observe Gaussian shapes for uniformly and randomly weighted convolution kernels without nonlinear activations, and near-Gaussian shapes for randomly weighted kernels with nonlinearity. Adding the ReLU nonlinearity makes the distribution a bit less Gaussian, as the ERF distribution depends on the input as well. Another reason is that ReLU units output exactly zero for half of its inputs and it is very easy to get a zero output for the center pixel on the output plane, which means no path from the receptive field can reach the output, hence the gradient is all zero. Here the ERFs are averaged over 20 runs with different random seed.
Figures below show the ERF for networks with 20 layers of random weights, with different nonlinearities. Here the results are averaged both across 100 runs with different random weights as well as different random inputs. In this setting, the receptive fields are a lot more Gaussian-like.

[math]\displaystyle{ \sqrt{n} }[/math] absolute growth and [math]\displaystyle{ 1/\sqrt{n} }[/math] relative shrinkage: The figure
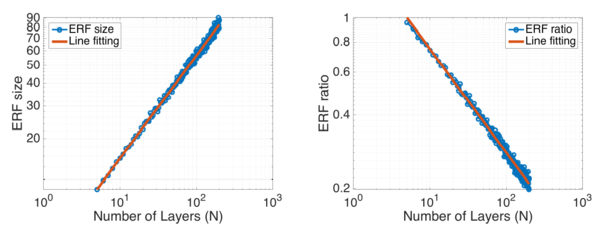
shows the change of ERF size and the relative ratio of ERF over theoretical RF wrt number of convolution layers. The fitted line for ERF size has the slope of 0.56 in log domain, while the line for ERF ratio has the slope of -0.43. This indicates ERF size is growing linearly wrt [math]\displaystyle{ \sqrt{n} }[/math] and ERF ratio is shrinking linearly wrt [math]\displaystyle{ 1/\sqrt{n} }[/math].
They used 2 standard deviations as the measurement for ERF size, i.e. any pixel with a value greater than 1 - 95.45% of the center point is considered in ERF. The ERF size is represented by the square root of the number of pixels within ERF, while the theoretical RF size is the side length of the square in which all pixel has a non-zero impact on the output pixel, no matter how small. All experiments here are averaged over 20 runs.
Subsampling & dilated convolution increases receptive field: The figure shows that the effect of subsampling and dilated convolution. The reference baseline is a CNN with 15 dense convolution layers. Its ERF is shown in the left-most figure. Replacing 3 of the 15 convolutional layers with stride-2 convolution results in the ERF for the ‘Subsample’ figure. Finally, replacing those 3 convolutional layers with dilated convolution with factor 2,4 and 8 gives the ‘Dilation’ figure. Both of them are able to increase the effect receptive field significantly. Note the ‘Dilation’ figure shows a rectangular ERF shape typical for dilated convolutions (why?).

How the ERF evolves during training
The authors looked at how the ERF of units in the top-most convolutional layers of a classification CNN and a semantic segmentation CNN evolve during training. For both tasks, they adopted the ResNet architecture which makes extensive use of skip-connections. As expected their analysis showed the ERF of these networks is significantly smaller than the theoretical receptive field. Also, as the networks learn, the ERF got bigger so that at the end of training was significantly larger than the initial ERF.
The classification network was a ResNet with 17 residual blocks trained on the CIFAR-10 dataset. Figure shows the ERF on the 32x32 image space at the beginning of training (with randomly initialized weights) and at the end of training when it reaches best validation accuracy. Note that the theoretical receptive field of the network is actually 74x74, bigger than the image size, but the ERF is not filling the image completely. Comparing the results before and after training demonstrates that ERF has grown significantly.

The semantic segmentation network was trained on the CamVid dataset for urban scene segmentation. The 'front-end' of the model was a purely convolutional network that predicted the output at a slightly lower resolution. And then, a ResNet with 16 residual blocks interleaved with 4 subsampling operations each with a factor of 2 was implemented. Due to subsampling operations, the output was 1/16 of the input size. For this model, the theoretical RF of the top convolutional layer units was 505x505. However, as Figure shows the ERF only got a fraction of that with a diameter of 100 at the beginning of training, and at the end of training reached almost a diameter around 150.
Reduce Gaussian Damage
The Effective Receptive Field (ERF) usually decays quickly from the centre (like 2D Gaussian) and only takes a small portion of the theoretical Receptive Field (RF). This "Gaussian damage" is undesirable for tasks that require a large RF and to reduce it, the authors suggested two solutions:
- New Initialization scheme to make the weights at the center of the convolution kernel to be smaller and the weights on the outside larger, which diffuses the concentration on the center out to the periphery. One way to implement this is to initialize the network with any initialization method, and then scale the weights according to a distribution that has a lower scale at the center and higher scale on the outside. They tested this solution for the CIFAR-10 classification task, with several random seeds. In a few cases, they get a 30% speed-up of training compared to the more standard initializations. But overall the benefit of this method is not always significant. This is only a partial solution as, no matter what is done to change the initial weights the ERF maintains a Gaussian distribution. Weight initialization is of importance for the deep learning model. Initial weights that are too large may result in exploding values during forward propagation or back propagation. One of the popular methods of weights initialization are the Batch normalization, proposed by Xavier et al.
- Architectural changes of CNNs is the 'better' approach that may change the ERF in more fundamental ways. For example, instead of connecting each unit in a CNN to a local rectangular convolution window, we can sparsely connect each unit to a larger area in the lower layer using the same number of connections. Dilated convolution belongs to this category, but we may push even further and use sparse connections that are not grid-like.
Discussion
Connection to biological neural networks: The authors established through their analysis that the ERF grows a lot slower than what was previously thought, which indicates that a lot of local information is still preserved even after many convolutional layers. This also contradicts some age-old relevant notions in deep biological networks. Another relevant observation from their analysis is that convolutional networks may automatically create a form of foveal representation.
Connection to previous work on CNNs: Though receptive fields in CNNs have not been studied extensively, some previous works on the topic explore how the variance does not change much when going through the network; utilizing which a good initialization scheme was developed for convolution layers. Researchers have also used visualization to show the importance of using natural-image priors and also what an activation of the convolutional layer would represent. Deconvolutional nets have been used to show the relation of pixels in the image and the neurons that are firing.
Summary & Conclusion
The authors showed, theoretically and experimentally, that the distribution of impact within the receptive field (the effective receptive field) is asymptotically Gaussian, and the ERF only takes up a fraction of the full theoretical receptive field. They also studied the effects of some standard CNN approaches on the effective receptive field. They found that dropout does not change the Gaussian ERF shape. Subsampling and dilated convolutions are effective ways to increase receptive field size quickly but skip-connections make ERFs smaller.
They argued that since larger ERFs are required for higher performance, new methods to achieve larger ERF will not only help the network to train faster but may also improve performance.
Critique
The authors' finding on $\sqrt{n}$ absolute growth of Effective Receptive Field (ERF) suffers from a discrepancy in ERF definition between their theoretical analysis and their experiments. Namely, in the theoretical analysis for the non-uniform-kernel case, they considered one standard deviation as the ERF size. However, they used two standard deviations as the measure for ERF size in the experiments.
It would be more practical if the paper also investigated the ERF for natural images (as opposed to random) as network input at least in the two cases where they examined trained networks.
The authors claim that the ERF results in the experimental section have Gaussian shapes but they never prove this claim. For example, they could fit different 2D-functions, including 2D-Gaussian, to the kernels and show that 2D-Gaussian gives the best fit. Furthermore, the pictures are given as proof of the claim that the ERF has a Gaussian distribution only show the ERF of the center pixel of the output [math]\displaystyle{ y_{0,0} }[/math]. Intuitively, the ERF of a node near the boundary of the output layer may have a significantly different shape. This was not addressed in the paper.
Another weakness is in the discussion section, where they make a connection to the biological networks. They jumped to disprove a well-observed phenomenon in the brain. The fact that the neurons in the higher areas of the visual hierarchy gradually lose their retinotopic property has been shown in a countless number of neuroscience studies. For example, grandmother cells do not care about the position of grandmother's face in the visual field. In general, the similarity between deep CNNs and biological visual systems is not as strong, hence we should take any generalization from CNNs to biological networks with a grain of salt.
Spectrograms are visual representations of audio where the axes represent time, frequency and amplitude of the frequency. The ERF of a CNN, when applied to a spectrogram, doesn't necessarily have to be from a Gaussian towards the center. In fact, many receptive fields are trained to look for the peaks of troughs and cliffs, which essentially imply that the ERF will have more weightage towards the outside rather than the center.
The paper talks about what ERF represents and how it can be increased but doesn't say how ERF can be used for improving the model accuracies by changing the configuration of the network, say the depth of the network, or kernel size etc. In addition, as an important part in Region-CNN, ERF can provide some useful information during object detection, it would be better if the authors could add analysis on with different ERF properties, how would the influence be over the mAP in object detection.
References
[1] Wenjie Luo, Yujia Li, Raquel Urtasun, and Richard Zemel. "Understanding the effective receptive field in deep convolutional neural networks." In Advances in Neural Information Processing Systems, pp. 4898-4906. 2016.
[2] Buessler, J.-L., Smagghe, P., & Urban, J.-P. (2014). Image receptive fields for artificial neural networks. Neurocomputing, 144(Supplement C), 258–270. https://doi.org/10.1016/j.neucom.2014.04.045
[3] Dilated Convolutions in Neural Network - [1]
[4] http://cs231n.github.io/convolutional-networks/
[5] Thorsten Neuschel. "A note on extended binomial coefficients." Journal of Integer Sequences, 17(2):3, 2014.
[6] Glorot, Xavier, and Yoshua Bengio. "Understanding the difficulty of training deep feedforward neural networks." Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics. 2010.