Patch Based Convolutional Neural Network for Whole Slide Tissue Image Classification
Presented by
Cassandra Wong, Anastasiia Livochka, Maryam Yalsavar, David Evans
Introduction
Despite the fact that CNN are well-known for their success in image classification, it is computationally impossible to use them for cancer classification. This problem is due to high-resolution images that cancer classification is dealing with. As a result, this paper argues that using a patch level CNN can outperform an image level based one and considers two main challenges in patch level classification – aggregation of patch-level classification results and existence of non-discriminative patches. For dealing with these challenges, training a decision fusion model and an Expectation-Maximization (EM) based method for locating the discriminative patches are suggested respectively. At the end the authors proved their claims and findings by testing their model to the classification of glioma and non-small-cell lung carcinoma cases.
Previous Work
The proposed patch-level CNN and training a decision fusion model as a two-level model was made apparent by the various breakthroughs and results noted below:
- Majority of Whole Slide Tissue Images classification methods fixate on classifying or obtaining features on patches [17, 35, 50, 56, 11, 4, 48, 14, 50]. These methods excel when an abundance of patch labels are provided [17, 35], allowing Patch-level supervised classifiers to learn the assortment of cancer subtypes. However, labeling patches requires specialized annotators; an excessive task at a large scale.
- Multiple Instance Learning (MIL) based classification [16, 51, 52] utilizes unlabeled patches to predict a label of a new bag and/or the label of each instance in said bag. Combining MIL with Neural Networks [43, 57, 31, 13], the Standard Multi-Instance assumption [18] is modeled by max-pooling. This approach is inefficient due to only one instance per bag being trained in one training iteration on the entire bag.
- MIL-based CNNs have been applied to object recognition [38] and semantic segmentation [40], following the Standard Multi-Instance assumption. Unfortunately, issues with misclassification errors due to the lack of robustness result in smooth output probability (feature) maps of the CNNS [12, 41, 39].
- Finally, to predict the image-level label, max-pooling and voting (average-pooling) were applied in [36, 30, 17]. However, learning decision fusion models can significantly improve performance in comparison to voting [42, 45, 24, 47, 26, 46].
EM-based method with CNN
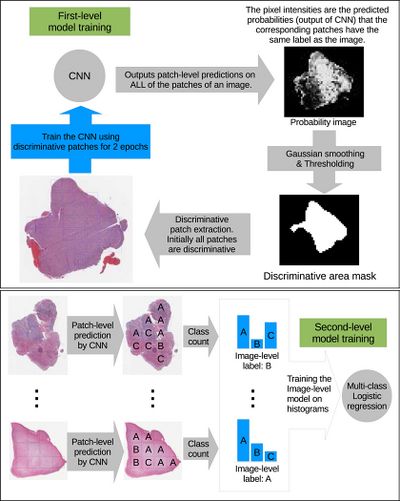
The high-resolution image is modelled as a bag, and patches extracted from it are instances that form a specific bag. The ground truth labels are provided for the bag only, so we model the labels of an instance (discriminative or not) as a hidden binary variable. Hidden binary variables are estimated by the Expectation-Maximization algorithm. A summary of the proposed approach can be found in Fig.2. Please note that this approach will work for any discriminative model.
In this paper [math]\displaystyle{ X = \{X_1, \dots, X_N\} }[/math] denotes dataset containing [math]\displaystyle{ N }[/math] bags. A bag [math]\displaystyle{ X_i= \{X_{i,1}, X_{i,2}, \dots, X_{i, N_i}\} }[/math] consists of [math]\displaystyle{ N_i }[/math] pathes (instances) and [math]\displaystyle{ X_{i,j} = \lt x_{i,j}, y_j\gt }[/math] denotes j-th instance and it’s label in i-th bag. We assume bags are i.i.d. (independent identically distributed), [math]\displaystyle{ X }[/math] and associated hidden labels [math]\displaystyle{ H }[/math] are generated by the following model: $$P(X, H) = \prod_{i = 1}^N P(X_{i,1}, \dots , X_{i,N_i}| H_i)P(H_i) \quad \quad \quad \quad (1) $$ [math]\displaystyle{ Hi = {H_{i, 1}, \dots, H_{i, Ni}} }[/math] denotes the set of hidden variables for instances in the bag [math]\displaystyle{ X_i }[/math] and [math]\displaystyle{ H_{i, j} }[/math] indicates whether the patch [math]\displaystyle{ X_{i,j} }[/math] is discriminative for [math]\displaystyle{ y_i }[/math] (it is discriminative if estimated label of the instance coincides with the label of the whole bag). Authors assume that [math]\displaystyle{ X_{i, j} }[/math] is independent from hidden labels of all other instances in the i-th bag, therefore [math]\displaystyle{ (1) }[/math] can be simplified as: $$P(X, H) = \prod_{i = 1}^{N} \prod_{j=1}^{N_i} P(X_{i, j}| H_{i, j})P(H_{i, j}) \quad \quad (2)$$ Authors propose to estimate the hidden labels of the individual patches [math]\displaystyle{ H }[/math] by maximizing the data likelihood [math]\displaystyle{ P(X) }[/math] using Expectation Maximization. In one iteration of EM we alternate between performing E step (Expectation) where we estimate hidden variables [math]\displaystyle{ H_{i, j} }[/math] and M step (Maximization) where we update the parameters of the model [math]\displaystyle{ (2) }[/math] such that data likelihood [math]\displaystyle{ P(X) }[/math] is maximized. Let's denote [math]\displaystyle{ D }[/math] the set of discriminative instances. We start by assuming all instances are in [math]\displaystyle{ D }[/math] (all [math]\displaystyle{ H_{i, j}=1 }[/math]).