Hierarchical Representations for Efficient Architecture Search: Difference between revisions
No edit summary |
No edit summary |
||
| Line 15: | Line 15: | ||
All the evaluated network architectures are directed acyclic graphs with only one source and one sink. Each node in the network represents a feature map and consequently each directed edge represents an operation that takes the feature map in the departing node as input and outputs a feature map on the arriving node. Under the previous assumption, any given architecture in the narrowed search space is formally expressed as a graph assembled by a series of operations (edges) among a defined set of adjacent feature maps (nodes). | All the evaluated network architectures are directed acyclic graphs with only one source and one sink. Each node in the network represents a feature map and consequently each directed edge represents an operation that takes the feature map in the departing node as input and outputs a feature map on the arriving node. Under the previous assumption, any given architecture in the narrowed search space is formally expressed as a graph assembled by a series of operations (edges) among a defined set of adjacent feature maps (nodes). | ||
[[File: | [[File:flatarch.PNG | 650px|thumb|center|Flat architecture representation]] | ||
Multiple primitive operations defined in section 2.3 are used to form small networks called “motifs” by the authors. To combine the outputs of multiple primitive operations and guarantee a unique output per motif the authors introduce a merge operation which in practice works as a depthwise concatenation who does not require inputs with the same number of channels. | |||
Accordingly, these motifs can also be combined to form more complex motifs on a higher level in the hierarchy until the network is complex enough to perform competitively in challenging classification tasks. | |||
==Hierarchical architecture representation== | |||
The composition of more complex motifs based on simpler motifs at lower levels allows the authors to create a hierarchy-like representation of very complex DNN starting with only few primitive operations. In other words, an architecture with L levels has only primitive operations at its bottom and only one (very complex) motif at its top. Any motif in between the bottom and top levels can be defined as the composition of motifs in lower levels of the hierarchy. | |||
[[File:hierarchicalrep.PNG | 700px|thumb|center|Hierarchical architecture representation]] | |||
==Primitive operations== | |||
The six primitive operations used as building blocks are: | |||
* 1 × 1 convolution of C channels | |||
* 3 × 3 depthwise convolution | |||
* 3 × 3 separable convolution of C channels | |||
* 3 × 3 max-pooling | |||
* 3 × 3 average-pooling | |||
* Identity | |||
The authors argue that convolution operations involving larger receptive fields can be obtained by the composition of lower-level motifs with smaller receptive fields. Accordingly, convolution operations considering a large number of channels can be generated by the depthwise concatenation of lower-level motifs. Batch normalization and ReLU activation function are applied after each convolution in the network. | |||
=Evolutionary architecture search= | |||
Before moving forward we introduce the concept of genotypes in the context of the article. In this article a genotype is a particular neural network architecture defined according to the components described in section 2. In order to make the NN architectures “evolve” the authors implemented a three stages process that includes establishing the permitted “mutations”, creating an initial population and make them “compete” in a tournament where only the best candidates will survive. | |||
==Mutation== | |||
One mutation over a specific architecture is a sequence of five changes in the following order: | |||
* Sample a level in the hierarchy, different than the basic level. | |||
* Sample a motif in that level. | |||
* Sample a successor node (i) in the motif. | |||
* Sample a predecessor node (j) in the motif. | |||
* Replace the current operation between nodes i and j from one of the available operations. | |||
The original operation between the nodes i and j in the graph is defined as <math> [G_{m}^{\left ( l \right )}] _{ij} = k </math>; therefore, a mutation between the same pair of nodes is defined as <math> [G_{m}^{\left ( l \right )}] _{ij} = {k}' </math>. | |||
==Initialization== | |||
An initial population is required to start the evolutionary algorithm; therefore, the authors introduced a trivial genotype composed only of identity mapping operations. Then a large number of random mutations was run over the “trivial genotype” to simulate a diversification process. The authors argue that this diversification process generates a representative population in the search space and at the same time prevents the use of any handcrafted NN structures. Surprisingly, some of these random architectures show a performance comparable to the performance achieved by the architectures found later during the evolutionary search algorithm. | |||
==Search algorithms== | |||
Tournament selection and random search are the two search algorithms used by the authors. In one iteration of the tournament selection algorithm 5% of the entire population is randomly selected, trained, and evaluated against a validation set. Then the best performing genotype is picked to go through the mutation process and put back into the population. No genotype is ever removed from the population, but the selection criteria guarantees that only the best performing models will be selected to “evolve” through the mutation process. In the random search algorithm every genotype from the initial population is trained and evaluated, then the best performing model is selected. In contrast to the tournament selection algorithm, the random search algorithm is much simpler and the training and evaluation process for every genotype can be run in parallel to reduce search time. | |||
==Implementation== | |||
To implement the tournament selection algorithm two auxiliary algorithms are introduced. The first is called the controller and directs the evolution process over the population, in other words, the controller repeatedly picks 5% of the population, send them to the tournament and then apply a random mutation over the best performing genotype from each group. | |||
[[File:asyncevoalgorithm1.PNG | 700px|thumb|center|Controller]] | |||
The second auxiliary algorithm is called the worker and is in charge of training and evaluating each genotype. | |||
[[File:asyncevoalgorithm2.PNG | 700px|thumb|center|Worker]] | |||
Both auxiliary algorithms work together asynchronously and communicate each other through a shared tabular memory file where genotypes and corresponding fitness are recorded. | |||
Revision as of 10:19, 18 October 2018
Introduction
Deep Neural Networks (DNN) have shown remarkable performance in several areas such as computer vision, natural language processing, among others; however, improvements over previous benchmarks have required extensive research and experimentation by domain experts. In DNN the composition of linear and nonlinear functions produces internal representations of data who are in most cases better than handcrafted ones; consequently, researchers using Deep Learning techniques have lately shifted their focus from working on input features to designing optimal DNN architectures. However, the quest for finding an optimal DNN architecture by combining layers and modules requires frequent trial and error experiments, a task that resembles the previous work on looking for handcrafted optimal features. As researchers aim to solve more difficult challenges the complexity of the resulting DNN is also increasing; therefore, some studies are introducing the use of automated techniques focused on searching for optimal architectures.
Lately, the use of algorithms for finding optimal DNN architectures has attracted the attention of researchers who have tackled the problem through four main groups of techniques. The first operates over the random DNN candidate’s weights and involves the use of an auxiliary HyperNetwork which maps architectures to feasible sets of weights and consequently allows an early evaluation of random DNN candidates. The second technique is Monte Carlo Tree Search (MCTS) who repeatedly narrows the search space by focusing on the most promising architectures previously seen. The third group of techniques use evolutionary algorithms where a fitness criteria is applied to filter the initial population of DNN candidates, then new individuals are added to the population by selecting the best performing ones and modifying them with one or several random mutations [Real, 2017]. The fourth and last group of techniques implement Reinforcement Learning where a policy based controller seeks to optimize the expected accuracy of new architectures based on rewards (accuracy) gained from previous proposals in the architecture space. From these four groups of techniques, Reinforcement Learning has offered the best experimental results; however, the paper we are summarizing implements evolutionary algorithms as its main approach.
Despite the technique used to look for an optimal architecture, searching in the architecture space usually requires the training and evaluation of many DNN candidates; therefore, it demands huge computational resources and pose a significant limitation for practical applications. Consequently, most techniques narrow the search space with predefined heuristics, either at the beginning or dynamically during the searching process. In the paper we are summarizing, the authors reduce the number of feasible architectures by forcing a hierarchical structure between network components. In other words, each DNN suggested as a candidate is formed by combining basic building blocks to form small modules, then the same basic structures introduced on the building blocks are used to combine and stack networks on the upper levels of the hierarchy. This approach allows the searching algorithm to sample highly complex and modularized networks similar to Inception or ResNet.
Despite some weaknesses regarding the efficiency of evolutionary algorithms, this study reveals that in fact these techniques can generate architectures who show competitive performance when a narrowing strategy is imposed over the search space. Accordingly, the main contributions of this paper are a well defined set of hierarchical representations who acts as the filtering criteria to pick DNN candidates and a novel evolutionary algorithm who produces image classifiers that achieve state of the art performance among similar evolutionary-based techniques.
Architecture representations
Flat architecture representation
All the evaluated network architectures are directed acyclic graphs with only one source and one sink. Each node in the network represents a feature map and consequently each directed edge represents an operation that takes the feature map in the departing node as input and outputs a feature map on the arriving node. Under the previous assumption, any given architecture in the narrowed search space is formally expressed as a graph assembled by a series of operations (edges) among a defined set of adjacent feature maps (nodes).

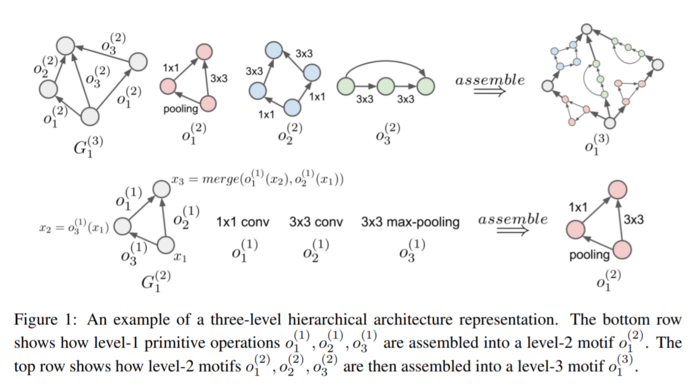
Multiple primitive operations defined in section 2.3 are used to form small networks called “motifs” by the authors. To combine the outputs of multiple primitive operations and guarantee a unique output per motif the authors introduce a merge operation which in practice works as a depthwise concatenation who does not require inputs with the same number of channels.
Accordingly, these motifs can also be combined to form more complex motifs on a higher level in the hierarchy until the network is complex enough to perform competitively in challenging classification tasks.
Hierarchical architecture representation
The composition of more complex motifs based on simpler motifs at lower levels allows the authors to create a hierarchy-like representation of very complex DNN starting with only few primitive operations. In other words, an architecture with L levels has only primitive operations at its bottom and only one (very complex) motif at its top. Any motif in between the bottom and top levels can be defined as the composition of motifs in lower levels of the hierarchy.
Primitive operations
The six primitive operations used as building blocks are:
- 1 × 1 convolution of C channels
- 3 × 3 depthwise convolution
- 3 × 3 separable convolution of C channels
- 3 × 3 max-pooling
- 3 × 3 average-pooling
- Identity
The authors argue that convolution operations involving larger receptive fields can be obtained by the composition of lower-level motifs with smaller receptive fields. Accordingly, convolution operations considering a large number of channels can be generated by the depthwise concatenation of lower-level motifs. Batch normalization and ReLU activation function are applied after each convolution in the network.
Evolutionary architecture search
Before moving forward we introduce the concept of genotypes in the context of the article. In this article a genotype is a particular neural network architecture defined according to the components described in section 2. In order to make the NN architectures “evolve” the authors implemented a three stages process that includes establishing the permitted “mutations”, creating an initial population and make them “compete” in a tournament where only the best candidates will survive.
Mutation
One mutation over a specific architecture is a sequence of five changes in the following order:
- Sample a level in the hierarchy, different than the basic level.
- Sample a motif in that level.
- Sample a successor node (i) in the motif.
- Sample a predecessor node (j) in the motif.
- Replace the current operation between nodes i and j from one of the available operations.
The original operation between the nodes i and j in the graph is defined as [math]\displaystyle{ [G_{m}^{\left ( l \right )}] _{ij} = k }[/math]; therefore, a mutation between the same pair of nodes is defined as [math]\displaystyle{ [G_{m}^{\left ( l \right )}] _{ij} = {k}' }[/math].
Initialization
An initial population is required to start the evolutionary algorithm; therefore, the authors introduced a trivial genotype composed only of identity mapping operations. Then a large number of random mutations was run over the “trivial genotype” to simulate a diversification process. The authors argue that this diversification process generates a representative population in the search space and at the same time prevents the use of any handcrafted NN structures. Surprisingly, some of these random architectures show a performance comparable to the performance achieved by the architectures found later during the evolutionary search algorithm.
Search algorithms
Tournament selection and random search are the two search algorithms used by the authors. In one iteration of the tournament selection algorithm 5% of the entire population is randomly selected, trained, and evaluated against a validation set. Then the best performing genotype is picked to go through the mutation process and put back into the population. No genotype is ever removed from the population, but the selection criteria guarantees that only the best performing models will be selected to “evolve” through the mutation process. In the random search algorithm every genotype from the initial population is trained and evaluated, then the best performing model is selected. In contrast to the tournament selection algorithm, the random search algorithm is much simpler and the training and evaluation process for every genotype can be run in parallel to reduce search time.
Implementation
To implement the tournament selection algorithm two auxiliary algorithms are introduced. The first is called the controller and directs the evolution process over the population, in other words, the controller repeatedly picks 5% of the population, send them to the tournament and then apply a random mutation over the best performing genotype from each group.

The second auxiliary algorithm is called the worker and is in charge of training and evaluating each genotype.

Both auxiliary algorithms work together asynchronously and communicate each other through a shared tabular memory file where genotypes and corresponding fitness are recorded.