Hash Embeddings for Efficient Word Representations
Introduction
ALmost all neural networks rely on loss function that is continuous in nature to compute the gradients for training hence because of this for whatever data we need to feed in the network has to be continuous in nature. Images can easily be represented as real-valued vectors in form of pixel values and colour intensities but this is not the same case with text input because if converted it would represent a discrete-valued distribution. There are different methods like Word2Vec or GloVe to get the specified word embeddings of a corpus. But the problem faced by these models is the number of parameters it needs to learn is quite high. There have been some solutions to it:
- Ignore infrequent words: if we calculate the frequency of each word and filter out the least frequent words the number of parameters can be reduced but the problem with this technique is we cannot arrive at a consensus what is the best threshold for filtering.
- Feature pruning: we can prune the feature from the embedding vector but this pruning is not possible for many models.
- Compression: The vectors can be compressed with the help of quantization or clustering them together with the help of previously determined centroids.
For some models constructing dictionaries also is a problem which is solved by feature hashing wherein each word [math]\displaystyle{ w ∈ \tau }[/math] ([math]\displaystyle{ \tau }[/math] is the token space of the corpus) is assigned to a fixed bucket. If the number of buckets is low it results in collisions hence it requires us to learn the best hash function for the problem.
In the paper, authors propose to use [math]\displaystyle{ \kappa }[/math] different hash functions and then train it with some parameters to find the best hash function for that particular word/token/phrase. This method has a lot of advantages and helps in reduction of parameters in the word embeddings.
Related Works
Argerich et al proposed an application of feature hashing for words called "Hash2Vec" in which they compare their results with GloVe and find that with word vectors obtained with simple feature hashing has performance equivalent to the GloVe if not better.
Hash Embeddings
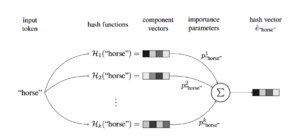
To generate the hash embeddings following procedure is followed.
- They use [math]\displaystyle{ k }[/math] different functions [math]\displaystyle{ H_1, . . . , H_k }[/math] to choose [math]\displaystyle{ k }[/math] component vectors for the token w from a predefined pool of B shared component vectors.
- Combine the chosen component vectors from step 1 as a weighted sum given by [math]\displaystyle{ \hat{e}_w = \sum_{i=1}^k p_w^i H_i(w) }[/math].
- Importance paramaters can be concatenated with the [math]\displaystyle{ \hat{e}_w }[/math] to get the final hash vector [math]\displaystyle{ e_w }[/math]
The same equation can be written in vector notations as:
[math]\displaystyle{ c_w = (H_1(w), H_2(w), . . . , H_k(w))^⊤ }[/math]
[math]\displaystyle{ p_w = (p_w^1, . . . , p_w^k)^⊤ }[/math]
[math]\displaystyle{ \hat{e}_w = p_w^⊤c_w }[/math]
[math]\displaystyle{ e_w^⊤ = \hat{e}_w^⊤⊕ p_w^⊤ }[/math]
( [math]\displaystyle{ ⊕ }[/math] is the concatenation operator)
The token to component vector functions [math]\displaystyle{ H_i(w) = E_{D_2 (D_1(w))} }[/math] is implemented as :
- [math]\displaystyle{ D_1 : \tau → {1, . . . K} }[/math] is a token to id function
- [math]\displaystyle{ D_2 : {1, . . . , K} → {1, . . . B} }[/math] is an id to bucket functions
- [math]\displaystyle{ E }[/math] is a [math]\displaystyle{ B × d }[/math] matrix
We can replace [math]\displaystyle{ D_1 }[/math] with normal enumeration if we choose to have a dictionary of the words for small values of [math]\displaystyle{ \tau }[/math]
The importance parameter vectors pw are represented as rows in a [math]\displaystyle{ K × k }[/math] matrix named [math]\displaystyle{ P }[/math], and the token to importance vector mapping is implemented by [math]\displaystyle{ w → P_{\hat{D}_(w)} }[/math] The authors decide use </math> D_1<math> as the function