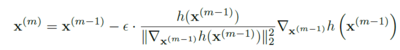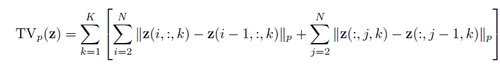Countering Adversarial Images Using Input Transformations
This is a summary of the paper titled: "Countering Adversarial Images using Input Transformations", authored by Chuan Guo, Mayank Rana, Moustapha Cisse, and Laurens van der Maaten. Available online at URL https://arxiv.org/abs/1711.00117
The code for this paper is available here[1]
Motivation
As the use of machine intelligence has increased, robustness has become a critical feature to guarantee the reliability of deployed machine-learning systems. However, recent research has shown that existing models are not robust to small, adversarially designed perturbations to the input. Adversarial examples are inputs to Machine Learning models so that an attacker has intentionally designed to cause the model to make a mistake. Adversarially perturbed examples have been deployed to attack image classification services (Liu et al., 2016)[11], speech recognition systems (Cisse et al., 2017a)[12], and robot vision (Melis et al., 2017)[13]. The existence of these adversarial examples has motivated proposals for approaches that increase the robustness of learning systems to such examples. In the example below (Goodfellow et. al) [17], a small perturbation is applied to the original image of a panda, changing the prediction to a gibbon.

Introduction
The paper studies strategies that defend against adversarial example attacks on image classification systems by transforming the images before feeding them to a Convolutional Network Classifier. Generally, defenses against adversarial examples fall into two main categories:
- Model-Specific – They enforce model properties such as smoothness and invariance via the learning algorithm.
- Model-Agnostic – They try to remove adversarial perturbations from the input.
Model-specific defense strategies make strong assumptions about expected adversarial attacks. As a result, they violate the Kerckhoffs principle, which states that adversaries can circumvent model-specific defenses by simply changing how an attack is executed. This paper focuses on increasing the effectiveness of model-agnostic defense strategies. Specifically, they investigated the following image transformations as a means for protecting against adversarial images:
- Image Cropping and Re-scaling (Graese et al, 2016).
- Bit Depth Reduction (Xu et al, 2017)
- JPEG Compression (Dziugaite et al, 2016)
- Total Variance Minimization (Rudin et al, 1992)
- Image Quilting (Efros & Freeman, 2001).
These image transformations have been studied against Adversarial attacks such as the fast gradient sign method (Goodfelow et. al., 2015), its iterative extension (Kurakin et al., 2016a), Deepfool (Moosavi-Dezfooli et al., 2016), and the Carlini & Wagner (2017) [math]\displaystyle{ L_2 }[/math]attack.
The authors in this paper try to focus on increasing the effectiveness of model-agnostic defense strategies through approaches that:
- remove the adversarial perturbations from input images,
- maintain sufficient information in input images to correctly classify them,
- and are still effective in situations where the adversary has information about the defense strategy being used.
From their experiments, the strongest defenses are based on Total Variance Minimization and Image Quilting. These defenses are non-differentiable and inherently random which makes it difficult for an adversary to get around them. The authors best defenses eliminate 60% of gray-box attacks and 90% of black-box attacks by four major attack methods that perturb pixel values by 8% on average.
Previous Work
Recently, a lot of research has focused on countering adversarial threats. Wang et al [4], proposed a new adversary resistant technique that obstructs attackers from constructing impactful adversarial images. This is done by randomly nullifying features within images. Tramer et al [2], showed the state-of-the-art Ensemble Adversarial Training Method, which augments the training process but not only included adversarial images constructed from their model but also including adversarial images generated from an ensemble of other models. Their method implemented on an Inception V2 classifier finished 1st among 70 submissions of NIPS 2017 competition on Defenses against Adversarial Attacks. Graese, et al. [3], showed how input transformation such as shifting, blurring and noise can render the majority of the adversarial examples as non-adversarial. Xu et al.[5] demonstrated, how feature squeezing methods, such as reducing the color bit depth of each pixel and spatial smoothing, defends against attacks. Dziugaite et al [6], studied the effect of JPG compression on adversarial images. Chen et al. [7] introduce an advanced denoising algorithm with GAN based noise modeling in order to improve the blind denoising performance in low-level vision processing. The GAN is trained to estimate the noise distribution over the input noisy images and to generate noise samples. Although meant for image processing, this method can be generalized to target adversarial examples where the unknown noise generating algorithm can be leveraged.
Terminology
Gray Box Attack : Model Architecture and parameters are public.
Black Box Attack: Consider a weak adversary with access to the DNN output only. The adversary has no knowledge of the architectural choices made to design the DNN, which include the number, type, and size of layers, nor of the training data used to learn the DNN’s parameters. Such attacks are referred to as black box, where adversaries need not know internal details of a system to compromise it [18].
An interesting and important observation of adversarial examples is that they generally are not model or architecture specific. Adversarial examples generated for one neural network architecture will transfer very well to another architecture. In other words, if you wanted to trick a model you could create your own model and adversarial examples based off of it. Then these same adversarial examples will most probably trick the other model as well. This has huge implications as it means that it is possible to create adversarial examples for a completely black box model where we have no prior knowledge of the internal mechanics. reference
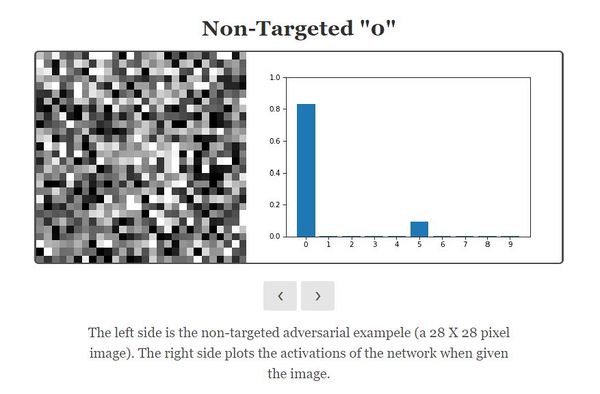
Non Targeted Adversarial Attack: The goal of the attack is to modify a source image in a way such that the image will be classified incorrectly by the network.
This is an example on non-targeted adversarial attacks to be more clear reference:
Targeted Adversarial Attack: The goal of the attack is to modify a source image in way such that image will be classified as a target class by the network.
This is an example on targeted adversarial attacks to be more clear reference:
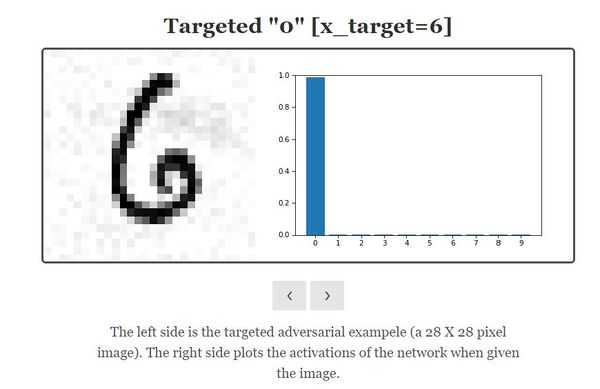
Defense: A defense is a strategy that aims to make the prediction on an adversarial example [math]\displaystyle{ h(x') }[/math] equal to the prediction on the corresponding clean example [math]\displaystyle{ h(x) }[/math].
Problem Definition
The paper discusses non-targeted adversarial attacks for image recognition systems. Given image space [math]\displaystyle{ \mathcal{X} = [0,1]^{H \times W \times C} }[/math], a source image [math]\displaystyle{ x \in \mathcal{X} }[/math], and a classifier [math]\displaystyle{ h(.) }[/math], a non-targeted adversarial example of [math]\displaystyle{ x }[/math] is a perturbed image [math]\displaystyle{ x' }[/math], such that [math]\displaystyle{ h(x) \neq h(x') }[/math] and [math]\displaystyle{ d(x, x') \leq \rho }[/math] for some dissimilarity function [math]\displaystyle{ d(·, ·) }[/math] and [math]\displaystyle{ \rho \geq 0 }[/math]. In the best case scenario, [math]\displaystyle{ d(·, ·) }[/math] measures the perceptual difference between the original image [math]\displaystyle{ x }[/math] and the perturbed image [math]\displaystyle{ x' }[/math], but usually, Euclidean distance ([math]\displaystyle{ ||x - x'||_2 }[/math]) or the Chebyshov distance ([math]\displaystyle{ ||x - x'||_{\infty} }[/math]) are used.
From a set of N clean images [math]\displaystyle{ [{x_{1}, …, x_{N}}] }[/math], an adversarial attack aims to generate [math]\displaystyle{ [{x'_{1}, …, x'_{N}}] }[/math] images, such that ([math]\displaystyle{ x'_{n} }[/math]) is an adversary of ([math]\displaystyle{ x_{n} }[/math]).
The success rate of an attack is given as:
which is the proportions of predictions that were altered by an attack.
The success rate is generally measured as a function of the magnitude of perturbations performed by the attack. In this paper, L2 perturbations are used and are quantified using the normalized L2-dissimilarity metric: [math]\displaystyle{ \frac{1}{N} \sum_{n=1}^N{\frac{\vert \vert x_n - x'_n \vert \vert_2}{\vert \vert x_n \vert \vert_2}} }[/math]
A strong adversarial attack has a high rate, while its normalized L2-dissimilarity given by the above equation is less.
In most practical settings, an adversary does not have direct access to the model [math]\displaystyle{ h(·) }[/math] and has to do a black-box attack.
However, prior work has shown successful attacks by transferring adversarial examples generated for a separately-trained model to an unknown target model (Liu et al., 2016), thus allowing efficient black-box attack.
As a result, the authors investigate both the black-box and a more difficult gray-box attack setting: the adversary has access to the model architecture and the model parameters, but is unaware of the defence strategy that is being used.
A defence is an approach that aims make the prediction on an adversarial example [math]\displaystyle{ h(x') }[/math] equal to the prediction on the corresponding clean example [math]\displaystyle{ h(x) }[/math]. In this study, the authors focus on image transformation defenses [math]\displaystyle{ g(x) }[/math] that perform prediction via [math]\displaystyle{ h(g(x')) }[/math]. Ideally, [math]\displaystyle{ g(·) }[/math] is a complex, non-differentiable, and potentially stochastic function: this makes it difficult for an adversary to attack the prediction model [math]\displaystyle{ h(g(x)) }[/math] even when the adversary knows both [math]\displaystyle{ h(·) }[/math] and [math]\displaystyle{ g(·) }[/math].
Adversarial Attacks
Although the exact effect that adversarial examples have on the network is unknown, Ian Goodfellow et. al's Deep Learning book states that adversarial examples exploit the linearity of neural networks to perturb the cost function to force incorrect classifications. Images are often high resolution, and thus have thousands of pixels (millions for HD images). An epsilon ball perturbation when dimensionality is in the magnitude of thousands/millions greatly effects the cost function (especially if it increases loss at every pixel). Hence, although the following methods such as FGSM and Iterative FGSM are very straightforward, they greatly influence the network under a white box attack.
For the experimental purposes, below 4 attacks have been studied in the paper:
1. Fast Gradient Sign Method (FGSM; Goodfellow et al. (2015)) [17]: Given a source input [math]\displaystyle{ x }[/math], and true label [math]\displaystyle{ y }[/math], and let [math]\displaystyle{ l(.,.) }[/math] be the differentiable loss function used to train the classifier [math]\displaystyle{ h(.) }[/math]. Then the corresponding adversarial example is given by:
[math]\displaystyle{ x' = x + \epsilon \cdot sign(\nabla_x l(x, y)) }[/math]
for some [math]\displaystyle{ \epsilon \gt 0 }[/math] which controls the perturbation magnitude.
2. Iterative FGSM ((I-FGSM; Kurakin et al. (2016b)) [14]: iteratively applies the FGSM update, where M is the number of iterations. It is given as:
[math]\displaystyle{ x^{(m)} = x^{(m-1)} + \epsilon \cdot sign(\nabla_{x^{m-1}} l(x^{m-1}, y)) }[/math]
where [math]\displaystyle{ m = 1,...,M; x^{(0)} = x; }[/math] and [math]\displaystyle{ x' = x^{(M)} }[/math]. M is set such that [math]\displaystyle{ h(x) \neq h(x') }[/math].
Both FGSM and I-FGSM work by minimizing the Chebyshev distance between the inputs and the generated adversarial examples.
3. DeepFool ((Moosavi-Dezfooliet al., 2016) [15]: projects x onto a linearization of the decision boundary defined by binary classifier h(.) for M iterations. This can be particularly effictive when a network uses ReLU activation functions. It is given as:
4. Carlini-Wagner's L2 attack (CW-L2; Carlini & Wagner (2017)) [16]: propose an optimization-based attack that combines a differentiable surrogate for the model’s classification accuracy with an L2-penalty term which encourages the adversary image to be close to the original image. Let [math]\displaystyle{ Z(x) }[/math] be the operation that computes the logit vector (i.e., the output before the softmax layer) for an input [math]\displaystyle{ x }[/math], and [math]\displaystyle{ Z(x)_k }[/math] be the logit value corresponding to class [math]\displaystyle{ k }[/math]. The untargeted variant of CW-L2 finds a solution to the unconstrained optimization problem. It is given as:
As mentioned earlier, the first two attacks minimize the Chebyshev distance whereas the last two attacks minimize the Euclidean distance between the inputs and the adversarial examples.
All the methods described above maintain [math]\displaystyle{ x' \in \mathcal{X} }[/math] by performing value clipping.
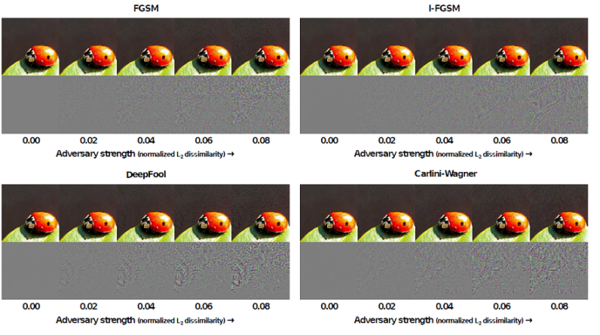
Below figure shows adversarial images and corresponding perturbations at five levels of normalized L2-dissimilarity for all four attacks, mentioned above.
Defenses
Defense is a strategy that aims to make the prediction on an adversarial example equal to the prediction on the corresponding clean example, and the particular structure of adversarial perturbations [math]\displaystyle{ x-x' }[/math] have been shown in Figure 1. Five image transformations that alter the structure of these perturbations have been studied:
- Image Cropping and Re-scaling,
- Bit Depth Reduction,
- JPEG Compression,
- Total Variance Minimization,
- Image Quilting.
Image cropping and Rescaling has the effect of altering the spatial positioning of the adversarial perturbation which is important in making attacks successful. In this study, images are cropped and re-scaled during training time as part of data-augmentation. At test time, the predictions of randomly cropped are averaged.
Bit Depth Reduction (Xu et. al) [5] performs a simple type of quantization that can remove small (adversarial) variations in pixel values from an image. During the bit reduction the input and output are in the same numerical scale. For reducing to -bit depth the input value is multiplied with [math]\displaystyle{ 2^{i}-1 }[/math] and then rounded to integers. The integers are then scaled back to the original range by dividing by [math]\displaystyle{ 2^{i}-1 }[/math]. The information capacity of the representation is reduced from 8-bit to i-bit with the integer rounding operation. Images are reduced to 3 bits in the experiment.
JPEG Compression and Decompression (Dziugaite etal., 2016) removes small perturbations by performing simple quantization. The authors use a quality level of 75/100 in their experiments
Total Variance Minimization (Rudin et. al) [9] : This combines pixel dropout with total variance minimization. This approach randomly selects a small set of pixels, and reconstructs the “simplest” image that is consistent with the selected pixels. The reconstructed image does not contain the adversarial perturbations because these perturbations tend to be small and localized.Specifically, we first select a random set of pixels by sampling a Bernoulli random variable [math]\displaystyle{ X(i; j; k) }[/math] for each pixel location [math]\displaystyle{ (i; j; k) }[/math];we maintain a pixel when [math]\displaystyle{ (i; j; k) }[/math]= 1. Next, we use total variation, minimization to constructs an image z that is similar to the (perturbed) input image x for the selected set of pixels, whilst also being “simple” in terms of total variation by solving:
where [math]\displaystyle{ TV_{p}(z) }[/math] represents [math]\displaystyle{ L_{p} }[/math] total variation of z :
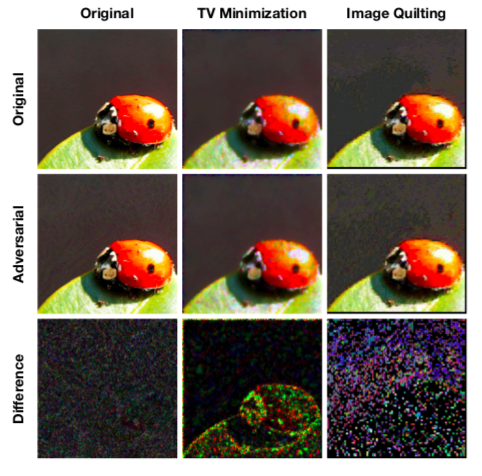
The total variation (TV) measures the amount of fine-scale variation in the image z, as a result of which TV minimization encourages removal of small (adversarial) perturbations in the image. The objective function is convex in [math]\displaystyle{ z }[/math], which makes solving for z straightforward. In the paper, p = 2 and a special-purpose solver based on the split Bregman method (Goldstein & Osher, 2009) to perform total variance minimization efficiently is employed. The effectiveness of TV minimization is illustrated by the images in the middle column of the figure below: in particular, note that the adversarial perturbations that were present in the background for the non- transformed image (see bottom-left image) have nearly completely disappeared in the TV-minimized adversarial image (bottom-center image). As expected, TV minimization also changes image structure in non-homogeneous regions of the image, but as these perturbations were not adversarially designed we expect the negative effect of these changes to be limited.
The figure above represents an illustration of total variance minimization and image quilting applied to an original and an adversarial image (produced using I-FGSM with ε = 0.03, corresponding to a normalized L2 - dissimilarity of 0.075). From left to right, the columns correspond to (1) no transformation, (2) total variance minimization, and (3) image quilting. From top to bottom, rows correspond to: (1) the original image, (2) the corresponding adversarial image produced by I-FGSM, and (3) the absolute difference between the two images above. Difference images were multiplied by a constant scaling factor to increase visibility.
Image Quilting (Efros & Freeman, 2001) [8]
Image Quilting is a non-parametric technique that synthesizes images by piecing together small patches that are taken from a database of image patches. The algorithm places appropriate patches in the database for a predefined set of grid points and computes minimum graph cuts in all overlapping boundary regions to remove edge artifacts. Image Quilting can be used to remove adversarial perturbations by constructing a patch database that only contains patches from "clean" images ( without adversarial perturbations); the patches used to create the synthesized image are selected by finding the K nearest neighbors ( in pixel space) of the corresponding patch from the adversarial image in the patch database, and picking one of these neighbors uniformly at random. The motivation for this defense is that resulting image only contains pixels that were not modified by the adversary - the database of real patches is unlikely to contain the structures that appear in adversarial images.
If we take a look at the effect of image quilting in the above figure, although interpretation of these images is more complicated due to the quantization errors that image quilting introduces, we can still observe that the absolute differences between quilted original and the quilted adversarial image appear to be smaller in non-homogeneous regions of the image. Based on this observation the authors suggest that TV minimization and image quilting lead to inherently different defenses.
Experiments
Five experiments were performed to test the efficacy of defenses. The first four experiments consider gray and black box attacks. The gray-box attack applies defenses on input adversarial images for the convolutional networks. The adversary is able to read model architecture and parameters but not the defense strategy. The black-box attack replaces convolutional network by a trained network with image-transformations. The final experiment compares the authors' defenses with prior work.
Set up: Experiments are performed on the ImageNet image classification dataset. The dataset comprises 1.2 million training images and 50,000 test images that correspond to one of 1000 classes. The adversarial images are produced by attacking a ResNet-50 model, with different kinds of attacks mentioned in Section5. The strength of an adversary is measured in terms of its normalized L2-dissimilarity. To produce the adversarial images, L2 dissimilarity for each of the attack was set as below:
- FGSM. Increasing the step size [math]\displaystyle{ \epsilon }[/math], increases the normalized L2-dissimilarity.
- I-FGSM. We fix M=10, and increase [math]\displaystyle{ \epsilon }[/math] to increase the normalized L2-dissimilarity.
- DeepFool. We fix M=5, and increase [math]\displaystyle{ \epsilon }[/math] to increase the normalized L2-dissimilarity.
- CW-L2. We fix [math]\displaystyle{ k }[/math]=0 and [math]\displaystyle{ \lambda_{f} }[/math] =10, and multiply the resulting perturbation
The hyperparameters of the defenses have been fixed in all the experiments. Specifically the pixel dropout probability was set to [math]\displaystyle{ p }[/math]=0.5 and regularization parameter of total variation minimizer [math]\displaystyle{ \lambda_{TV} }[/math]=0.03.
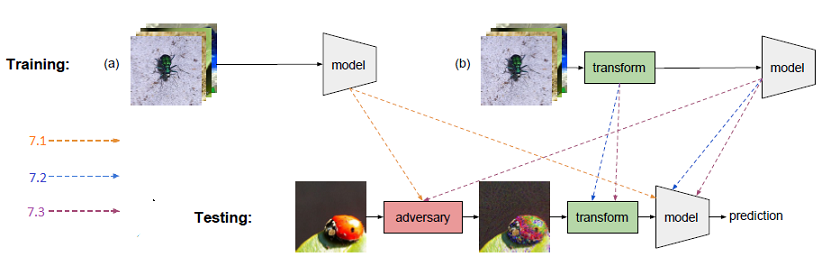
Below figure shows the difference between the set up in different experiments below. The network is either trained on a) regular images or b) transformed images. The different settings are marked by 8.1, 8.2 and 8.3
GrayBox - Image Transformation at Test Time
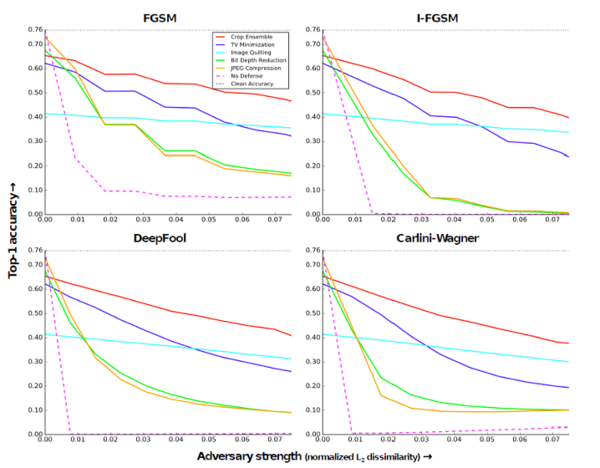
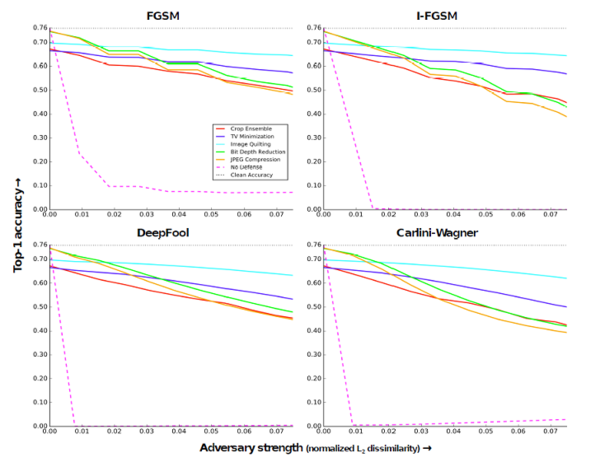
This experiment applies a transformation on adversarial images at test time before feeding them to a ResNet -50 which was trained to classify clean images. Below figure shows the results for five different transformations applied and their corresponding Top-1 accuracy. Few of the interesting observations from the plot are: All of the image transformations partly eliminate the effects of the attack, Crop ensemble gives the best accuracy around 40-60 percent, with an ensemble size of 30. The accuracy of Image Quilting Defense hardly deteriorates as the strength of the adversary increases. However, it does impact accuracy on non-adversarial examples.
BlackBox - Image Transformation at Training and Test Time
ResNet-50 model was trained on transformed ImageNet Training images. Before feeding the images to the network for training, standard data augmentation (from He et al) along with bit depth reduction, JPEG Compression, TV Minimization, or Image Quilting were applied on the images. The classification accuracy on the same adversarial images as in the previous case is shown Figure below. (Adversary cannot get this trained model to generate new images - Hence this is assumed as a Black Box setting!). Below figure concludes that training Convolutional Neural Networks on images that are transformed in the same way at test time, dramatically improves the effectiveness of all transformation defenses. Nearly 80 -90 % of the attacks are defended successfully, even when the L2- dissimilarity is high.
Blackbox - Ensembling
Four networks ResNet-50, ResNet-10, DenseNet-169, and Inception-v4 along with an ensemble of defenses were studied, as shown in Table 1. The adversarial images are produced by attacking a ResNet-50 model. The results in the table conclude that Inception-v4 performs best. This could be due to that network having a higher accuracy even in non-adversarial settings. The best ensemble of defenses achieves an accuracy of about 71% against all the other attacks. The attacks deteriorate the accuracy of the best defenses (a combination of cropping, TVM, image quilting, and model transfer) by at most 6%. Gains of 1-2% in classification accuracy could be found from ensembling different defenses, while gains of 2-3% were found from transferring attacks to different network architectures.

GrayBox - Image Transformation at Training and Test Time
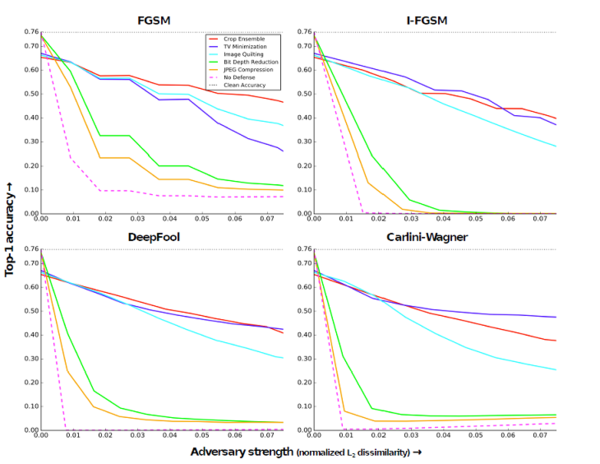
In this experiment, the adversary has access to the network and the related parameters (but does not have access to the input transformations applied at test time). From the network trained in-(BlackBox: Image Transformation at Training and Test Time), novel adversarial images were generated by the four attack methods. The results show that Bit-Depth Reduction and JPEG Compression are weak defenses in such a gray box setting. In contrast, image cropping, rescaling, variation minimization, and image quilting are more robust against adversarial images in this setting. The results for this experiment are shown in below figure. Networks using these defenses classify up to 50 % of images correctly.
Comparison With Ensemble Adversarial Training
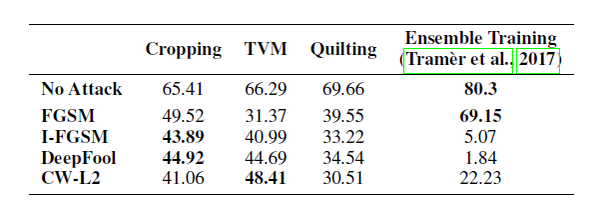
The results of the experiment are compared with the state of the art ensemble adversarial training approach proposed by Tramer et al. [2]. Ensemble Training fits the parameters of a Convolutional Neural Network on adversarial examples that were generated to attack an ensemble of pre-trained models. The model release by Tramer et al [2]: an Inception-Resnet-v2, trained on adversarial examples generated by FGSM against Inception-Resnet-v2 and Inception-v3 models. The authors compared their ResNet-50 models with image cropping, total variance minimization and image quilting defenses. Two assumption differences need to be noticed. Their defenses assume the input transformation is unknown to the adversary and no prior knowledge of the attacks is being used. The results of ensemble training and the pre-processing techniques mentioned in this paper are shown in Table 2. The results show that ensemble adversarial training works better on FGSM attacks (which it uses at training time), but is outperformed by each of the transformation-based defenses all other attacks.
Discussion/Conclusions
The paper proposed reasonable approaches to countering adversarial images. The authors evaluated Total Variance Minimization and Image Quilting and compared it with already proposed ideas like Image Cropping - Rescaling, Bit Depth Reduction, JPEG Compression, and Decompression on the challenging ImageNet dataset. Previous work by Wang et al. [10] shows that a strong input defense should be nondifferentiable and randomized. Two of the defenses - namely Total Variation Minimization and Image Quilting, both possess this property. However, it may still be possible to train a network to perhaps act as an approximation to the non-differentiable transformation.
Image quilting involves a discrete variable that conducts the selection of a patch from the database, which is a non-differentiable operation. Additionally, total variation minimization randomly conducts pixels selection from the pixels it uses to measure reconstruction error during creation of the de-noised image. Image quilting conducts a random selection of a particular K nearest neighbor uniformly but in a random manner. This inherent randomness makes it difficult to attack the model.
Future work suggests applying the same techniques to other domains such as speech recognition and image segmentation. For example, in speech recognition, total variance minimization can be used to remove perturbations from waveforms and "spectrogram quilting" techniques that reconstruct a spectrogram could be developed. The proposed input-transformation defenses can also be combined with ensemble adversarial training by Tramèr et al.[2] to study new attack methods.
Critiques
1. The terminology of Black Box, White Box, and Grey Box attack is not exactly given and clear.
2. White Box attacks could have been considered where the adversary has a full access to the model as well as the pre-processing techniques.
3. Though the authors did a considerable work in showing the effect of four attacks on ImageNet database, much stronger attacks (Madry et al) [7], could have been evaluated.
4. Authors claim that the success rate is generally measured as a function of the magnitude of perturbations, performed by the attack using the L2- dissimilarity, but the claim is not supported by any references. None of the previous work has used these metrics.
5. ([2])In the new draft of the paper, the authors add the sentence "our defenses assume that part of the defense strategy (viz., the input transformation) is unknown to the adversary".
This is a completely unreasonable assumption. Any algorithm which hopes to be secure must allow the adversary to, at the very least, understand what the defense is that's being used. Consider a world where the defense here is implemented in practice: any attacker in the world could just go look up the paper, read the description of the algorithm, and know how it works.
References
1. Chuan Guo , Mayank Rana & Moustapha Ciss´e & Laurens van der Maaten , Countering Adversarial Images Using Input Transformations
2. Florian Tramèr, Alexey Kurakin, Nicolas Papernot, Ian Goodfellow, Dan Boneh, Patrick McDaniel, Ensemble Adversarial Training: Attacks and defenses.
3. Abigail Graese, Andras Rozsa, and Terrance E. Boult. Assessing threat of adversarial examples of deep neural networks. CoRR, abs/1610.04256, 2016.
4. Qinglong Wang, Wenbo Guo, Kaixuan Zhang, Alexander G. Ororbia II, Xinyu Xing, C. Lee Giles, and Xue Liu. Adversary resistant deep neural networks with an application to malware detection. CoRR, abs/1610.01239, 2016a.
5. Weilin Xu, David Evans, and Yanjun Qi. Feature squeezing: Detecting adversarial examples in deep neural networks. CoRR, abs/1704.01155, 2017.
6. Gintare Karolina Dziugaite, Zoubin Ghahramani, and Daniel Roy. A study of the effect of JPG compression on adversarial images. CoRR, abs/1608.00853, 2016.
7. Aleksander Madry, Aleksandar Makelov, Ludwig Schmidt, Dimitris Tsipras, Adrian Vladu .Towards Deep Learning Models Resistant to Adversarial Attacks, arXiv:1706.06083v3
8. Alexei Efros and William Freeman. Image quilting for texture synthesis and transfer. In Proc. SIGGRAPH, pp. 341–346, 2001.
9. Leonid Rudin, Stanley Osher, and Emad Fatemi. Nonlinear total variation based noise removal algorithms. Physica D, 60:259–268, 1992.
10. Qinglong Wang, Wenbo Guo, Kaixuan Zhang, Alexander G. Ororbia II, Xinyu Xing, C. Lee Giles, and Xue Liu. Learning adversary-resistant deep neural networks. CoRR, abs/1612.01401, 2016b.
11. Yanpei Liu, Xinyun Chen, Chang Liu, and Dawn Song. Delving into transferable adversarial examples and black-box attacks. CoRR, abs/1611.02770, 2016.
12. Moustapha Cisse, Yossi Adi, Natalia Neverova, and Joseph Keshet. Houdini: Fooling deep structured prediction models. CoRR, abs/1707.05373, 2017
13. Marco Melis, Ambra Demontis, Battista Biggio, Gavin Brown, Giorgio Fumera, and Fabio Roli. Is deep learning safe for robot vision? adversarial examples against the icub humanoid. CoRR,abs/1708.06939, 2017.
14. Alexey Kurakin, Ian J. Goodfellow, and Samy Bengio. Adversarial examples in the physical world. CoRR, abs/1607.02533, 2016b.
15. Seyed-Mohsen Moosavi-Dezfooli, Alhussein Fawzi, and Pascal Frossard. Deepfool: A simple and accurate method to fool deep neural networks. In Proc. CVPR, pp. 2574–2582, 2016.
16. Nicholas Carlini and David A. Wagner. Towards evaluating the robustness of neural networks. In IEEE Symposium on Security and Privacy, pp. 39–57, 2017.
17. Ian Goodfellow, Jonathon Shlens, and Christian Szegedy. Explaining and harnessing adversarial examples. In Proc. ICLR, 2015.
18. Nicolas Papernot, Patrick McDaniel, Ian Goodfellow, Somesh Jha, Z Berkay Celik, and Ananthram Swami. Practical black-box attacks against machine learning. In ACM Asia Conference on Computer and Communications Security, 2017.