Continuous Adaptation via Meta-Learning in Nonstationary and Competitive Environments: Difference between revisions
No edit summary |
|||
| Line 12: | Line 12: | ||
In this paper, a probabilistic framework for meta learning is derived, then applied to tasks involving simulated robotic spiders. This framework generalizes the typical machine learning set up using Markov Decision Processes. This paper focuses on a multi-agent Non-stationary environment which requires Reinforcement Learning(RL) agents to do continuous adaptation in such an environment. Nonstationarity breaks the standard assumptions and requires agents to continuously adapt, both at training and execution time, in order to earn more rewards hence the approach is to break this into a sequence of stationary tasks and present it as a multi-task learning problem. | In this paper, a probabilistic framework for meta learning is derived, then applied to tasks involving simulated robotic spiders. This framework generalizes the typical machine learning set up using Markov Decision Processes. This paper focuses on a multi-agent Non-stationary environment which requires Reinforcement Learning(RL) agents to do continuous adaptation in such an environment. Nonstationarity breaks the standard assumptions and requires agents to continuously adapt, both at training and execution time, in order to earn more rewards hence the approach is to break this into a sequence of stationary tasks and present it as a multi-task learning problem. | ||
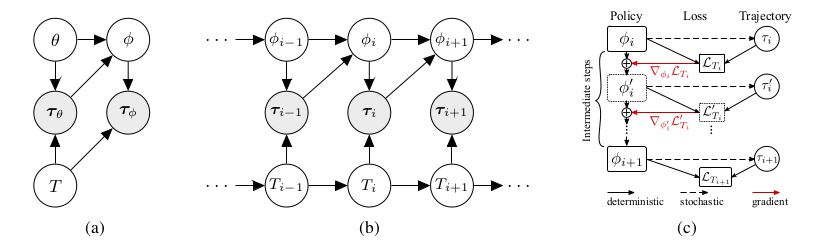
[[File:paper19_fig1.png|600px|frame|none|alt=Alt text| '''Figure 1'''. a) illustrates a probablistic model for Model Agnostic Meta-Learning(MAML) in a multi-task RL setting, where the taskes <math>T</math>, policies <math>\pi</math>, and trajectories <math>\tau</math> are all random variables with dependencies encoded in the edges of a given graph. b) The proposed extension to MAML by the author suitable for continuous adaptation to a task changing dynamically due to non-stationarity of the enviroment. The distribution of taskes is represented by a Markov chain, policies from a previous step and used to construct a new policy for the current step. c) The computation graph for the meta-update from <math>\phi_i</math> to <math>\phi_{i+1}</math>. Boxes represent replicas of the policy graphs with the specified parameters. The model is optimized using trancated backprogation through time starting from <math>L_{T_{i+1}}</math>]] | |||
= Model Agnostic Meta-Learning = | = Model Agnostic Meta-Learning = | ||
| Line 31: | Line 33: | ||
= Probabilistic Framework for Meta-Learning = | = Probabilistic Framework for Meta-Learning = | ||
This paper puts the meta-learning problem into a Markov Decision Process (MDP) framework common to RL. Instead of training examples <math>\{(x, y)\}</math>, we have trajectories <math>\tau = (x_0, a_1, x_1, R_1, x_2, ... a_H, x_H, R_H)</math>. A trajectory is sequence of states/observations <math>x_t</math>, actions <math>a_t</math> and rewards <math>R_t</math> that is sampled from a task <math> T </math> according to a policy <math>\pi_{\theta}</math>. Included with said task is a method for assigning loss values to trajectories <math>L_T(\tau)</math> which is typically the negative cumulative reward. A policy is a deterministic function that takes in a state and returns an action. Our goal here is to train a policy <math>\pi_{\theta}</math> with parameter vector <math>\theta</math>. This is analougous to training a function <math>f_{\theta}</math> that assigns labels <math>y</math> to feature vectors <math>x</math>. More precisely we have the following definitions: | This paper puts the meta-learning problem into a Markov Decision Process (MDP) framework common to RL, see Figure 1a. Instead of training examples <math>\{(x, y)\}</math>, we have trajectories <math>\tau = (x_0, a_1, x_1, R_1, x_2, ... a_H, x_H, R_H)</math>. A trajectory is sequence of states/observations <math>x_t</math>, actions <math>a_t</math> and rewards <math>R_t</math> that is sampled from a task <math> T </math> according to a policy <math>\pi_{\theta}</math>. Included with said task is a method for assigning loss values to trajectories <math>L_T(\tau)</math> which is typically the negative cumulative reward. A policy is a deterministic function that takes in a state and returns an action. Our goal here is to train a policy <math>\pi_{\theta}</math> with parameter vector <math>\theta</math>. This is analougous to training a function <math>f_{\theta}</math> that assigns labels <math>y</math> to feature vectors <math>x</math>. More precisely we have the following definitions: | ||
* <math>T :=(L_T, P_T(x), P_T(x_t | x_{t-1}, a_{t-1}), H )</math> (A Task) | * <math>T :=(L_T, P_T(x), P_T(x_t | x_{t-1}, a_{t-1}), H )</math> (A Task) | ||
| Line 39: | Line 41: | ||
* <math>H</math>: The horizon of the MDP. This is a fixed natural number specifying the lengths of the tasks trajectories. | * <math>H</math>: The horizon of the MDP. This is a fixed natural number specifying the lengths of the tasks trajectories. | ||
The papers goes further to define a Markov dynamic for sequences of tasks. Thus the policy that we would like to meta learn <math>\pi_{\theta}</math>, after being exposed to a sample of K trajectories <math>\tau_\theta^{1:K}</math> from the task <math>T_i</math>, should produce a new policy <math>\pi_{\phi}</math> that will perform well on the next task <math>T_{i+1}</math>. Thus we seek to minimize the following expectation: | The papers goes further to define a Markov dynamic for sequences of tasks as shown in Figure 1b. Thus the policy that we would like to meta learn <math>\pi_{\theta}</math>, after being exposed to a sample of K trajectories <math>\tau_\theta^{1:K}</math> from the task <math>T_i</math>, should produce a new policy <math>\pi_{\phi}</math> that will perform well on the next task <math>T_{i+1}</math>. Thus we seek to minimize the following expectation: | ||
<math>\mathrm{E}_{P(T_0), P(T_{i+1} | T_i)}\bigg(\sum_{i=1}^{l} \mathcal{L}_{T_i, T_{i+1}}(\theta)\bigg)</math>, | <math>\mathrm{E}_{P(T_0), P(T_{i+1} | T_i)}\bigg(\sum_{i=1}^{l} \mathcal{L}_{T_i, T_{i+1}}(\theta)\bigg)</math>, | ||
| Line 45: | Line 47: | ||
where <math>\mathcal{L}_{T_i, T_{i + 1}}(\theta) := \mathrm{E}_{\tau_{i, \theta}^{1:K} } \bigg( \mathrm{E}_{\tau_{i+1, \phi}}\Big( L_{T_{i+1}}(\tau_{i+1, \phi} | \tau_{i, \theta}^{1:K}, \theta) \Big) \bigg) </math> and <math>l</math> is the number of tasks. | where <math>\mathcal{L}_{T_i, T_{i + 1}}(\theta) := \mathrm{E}_{\tau_{i, \theta}^{1:K} } \bigg( \mathrm{E}_{\tau_{i+1, \phi}}\Big( L_{T_{i+1}}(\tau_{i+1, \phi} | \tau_{i, \theta}^{1:K}, \theta) \Big) \bigg) </math> and <math>l</math> is the number of tasks. | ||
The meta-policy <math>\pi_{\theta}</math> is trained and then adapted at test time using the following procedures. | The meta-policy <math>\pi_{\theta}</math> is trained and then adapted at test time using the following procedures. The computational graph is given in Figure 1c. | ||
[[File:MAML2.png | 800px]] | [[File:MAML2.png | 800px]] | ||
Revision as of 22:19, 17 March 2018
Introduction
Typically, the basic goal of machine learning is to train a model to perform a task. In Meta-learning, the goal is to train a model to perform the task of training a model to perform a task. Hence in this case the term "Meta-Learning" has the exact meaning you would expect; the word "Meta" has the precise function of introducing a layer of abstraction.
The meta-learning task can be made more concrete by a simple example. Consider the CIFAR-100 classification task that we used for our data competition. We can alter this task from being a 100-class classification problem to a collection of 100 binary classification problems. The goal of Meta-Learning here is to design and train and single binary classifier that will perform well on a randomly sampled task given a limited amount of training data for that specific task. In other words, we would like to train a model to perform the following procedure:
- A task is sampled. The task is "Is X a dog?"
- A small set of labeled training data is provided to the model. The labels represent whether or not the image is a picture of a dog.
- The model uses the training data to adjust itself to the specific task of checking whether or not an image is a picture of a dog.
This example also highlights the intuition that the skill of sight is distinct and separable from the skill of knowing what a dog looks like.
In this paper, a probabilistic framework for meta learning is derived, then applied to tasks involving simulated robotic spiders. This framework generalizes the typical machine learning set up using Markov Decision Processes. This paper focuses on a multi-agent Non-stationary environment which requires Reinforcement Learning(RL) agents to do continuous adaptation in such an environment. Nonstationarity breaks the standard assumptions and requires agents to continuously adapt, both at training and execution time, in order to earn more rewards hence the approach is to break this into a sequence of stationary tasks and present it as a multi-task learning problem.
Model Agnostic Meta-Learning
An initial framework for meta-learning is given in "Model-Agnostic Meta-Learning for Fast Adaptation of Deep Networks" (Finn et al, 2017):
"In our approach, the parameters of the model are explicitly trained such that a small number of gradient steps with a small amount of training data from a new task will produce good generalization performance on that task" (Finn et al, 2017).
In this training algorithm, the parameter vector [math]\displaystyle{ \theta }[/math] belonging to the model [math]\displaystyle{ f_{\theta} }[/math] is trained such that the meta-objective function [math]\displaystyle{ \mathcal{L} (\theta) = \sum_{\tau_i \sim P(\tau)} \mathcal{L}_{\tau_i} (f_{\theta_i' }) }[/math] is minimized. The sum in the objective function is over a sampled batch of training tasks. [math]\displaystyle{ \mathcal{L}_{\tau_i} (f_{\theta_i'}) }[/math] is the training loss function corresponding to the [math]\displaystyle{ i^{th} }[/math] task in the batch evaluated at the model [math]\displaystyle{ f_{\theta_i'} }[/math]. The parameter vector [math]\displaystyle{ \theta_i' }[/math] is obtained by updating the general parameter [math]\displaystyle{ \theta }[/math] using the loss function [math]\displaystyle{ \mathcal{L}_{\tau_i} }[/math] and set of K training examples specific to the [math]\displaystyle{ i^{th} }[/math] task. Note that in alternate versions of this algorithm, additional testing sets are sampled from [math]\displaystyle{ \tau_i }[/math] and used to update [math]\displaystyle{ \theta }[/math] using testing loss functions instead of training loss functions.
One of the important difference between this algorithm and more typical fine-tuning methods is that [math]\displaystyle{ \theta }[/math] is explicitly trained to be easily adjusted to perform well on different tasks rather than perform well on any specific tasks then fine tuned as the environment changes. (Sutton et al., 2007)
Probabilistic Framework for Meta-Learning
This paper puts the meta-learning problem into a Markov Decision Process (MDP) framework common to RL, see Figure 1a. Instead of training examples [math]\displaystyle{ \{(x, y)\} }[/math], we have trajectories [math]\displaystyle{ \tau = (x_0, a_1, x_1, R_1, x_2, ... a_H, x_H, R_H) }[/math]. A trajectory is sequence of states/observations [math]\displaystyle{ x_t }[/math], actions [math]\displaystyle{ a_t }[/math] and rewards [math]\displaystyle{ R_t }[/math] that is sampled from a task [math]\displaystyle{ T }[/math] according to a policy [math]\displaystyle{ \pi_{\theta} }[/math]. Included with said task is a method for assigning loss values to trajectories [math]\displaystyle{ L_T(\tau) }[/math] which is typically the negative cumulative reward. A policy is a deterministic function that takes in a state and returns an action. Our goal here is to train a policy [math]\displaystyle{ \pi_{\theta} }[/math] with parameter vector [math]\displaystyle{ \theta }[/math]. This is analougous to training a function [math]\displaystyle{ f_{\theta} }[/math] that assigns labels [math]\displaystyle{ y }[/math] to feature vectors [math]\displaystyle{ x }[/math]. More precisely we have the following definitions:
- [math]\displaystyle{ T :=(L_T, P_T(x), P_T(x_t | x_{t-1}, a_{t-1}), H ) }[/math] (A Task)
- [math]\displaystyle{ D(T) }[/math] : A distribution over tasks.
- [math]\displaystyle{ L_T }[/math]: A loss function for the task T that assigns numeric loss values to trajectories.
- [math]\displaystyle{ P_T(x), P_T(x_t | x_{t-1}, a_{t-1}) }[/math]: Probability measures specifying the markovian dynamics of the observations [math]\displaystyle{ x_t }[/math]
- [math]\displaystyle{ H }[/math]: The horizon of the MDP. This is a fixed natural number specifying the lengths of the tasks trajectories.
The papers goes further to define a Markov dynamic for sequences of tasks as shown in Figure 1b. Thus the policy that we would like to meta learn [math]\displaystyle{ \pi_{\theta} }[/math], after being exposed to a sample of K trajectories [math]\displaystyle{ \tau_\theta^{1:K} }[/math] from the task [math]\displaystyle{ T_i }[/math], should produce a new policy [math]\displaystyle{ \pi_{\phi} }[/math] that will perform well on the next task [math]\displaystyle{ T_{i+1} }[/math]. Thus we seek to minimize the following expectation:
[math]\displaystyle{ \mathrm{E}_{P(T_0), P(T_{i+1} | T_i)}\bigg(\sum_{i=1}^{l} \mathcal{L}_{T_i, T_{i+1}}(\theta)\bigg) }[/math],
where [math]\displaystyle{ \mathcal{L}_{T_i, T_{i + 1}}(\theta) := \mathrm{E}_{\tau_{i, \theta}^{1:K} } \bigg( \mathrm{E}_{\tau_{i+1, \phi}}\Big( L_{T_{i+1}}(\tau_{i+1, \phi} | \tau_{i, \theta}^{1:K}, \theta) \Big) \bigg) }[/math] and [math]\displaystyle{ l }[/math] is the number of tasks.
The meta-policy [math]\displaystyle{ \pi_{\theta} }[/math] is trained and then adapted at test time using the following procedures. The computational graph is given in Figure 1c.
The mathematics of calculating loss gradients is omitted.
Training Spiders to Run with Dynamic Handicaps (Robotic Locomotion in Non-Stationary Environments)
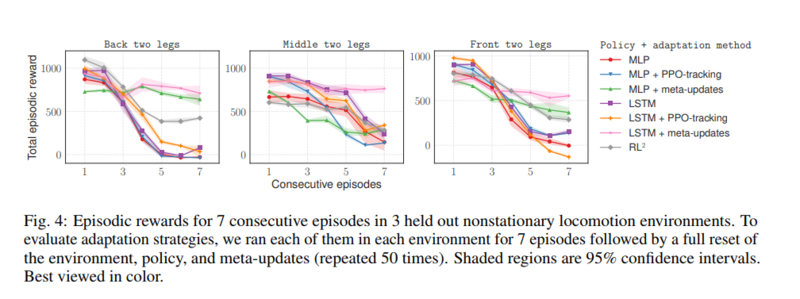
The authors used the MuJoCo physics simulator to create a simulated environment where robotic spiders with 6 legs are faced with the task of running due east as quickly as possible. The robotic spider observes the location and velocity of it's body, and the angles and velocities of its legs. It interacts with the environment by exerting torque on the joints of its legs. Each leg has two joints, the joint closer to the body rotates horizontally while the joint farther from the body rotates vertically. The environment is made non-stationary by gradually paralyzing two legs of the spider across training and testing episodes. Putting this example into the above probabilistic framework yields:
- [math]\displaystyle{ T_i }[/math]: The task of walking east with the torques of two legs scaled by [math]\displaystyle{ (i-1)/6 }[/math]
- [math]\displaystyle{ \{T_i\}_{i=1}^{7} }[/math]: A sequence of tasks with the same two legs handicapped in each task. Note there are 15 different ways to choose such legs resulting in 15 sequences of tasks. 12 are used for training and 3 for testing.
- A Markov Descision process composed of
- Observations [math]\displaystyle{ x_t }[/math] containing information about the state of the spider.
- Actions [math]\displaystyle{ a_t }[/math] containing information about the torques to apply to the spiders legs.
- Rewards [math]\displaystyle{ R_t }[/math] corresponding to the speed at which the spider is moving east.
Three differently structured policy neural networks are trained in this set up using both meta-learning and three different previously developed adaption methods.
At testing time, the spiders following meta learned policies initially perform worse than the spiders using non-adaptive policies. However, by the third episode [math]\displaystyle{ i=3 }[/math] the meta learners perform on par. And by the sixth episode, when the selected legs are mostly immobile, the meta learners significantly out perform. These results can be seen in the graphs below.
Training Spiders to Fight Each Other (Adversarial Meta-Learning)
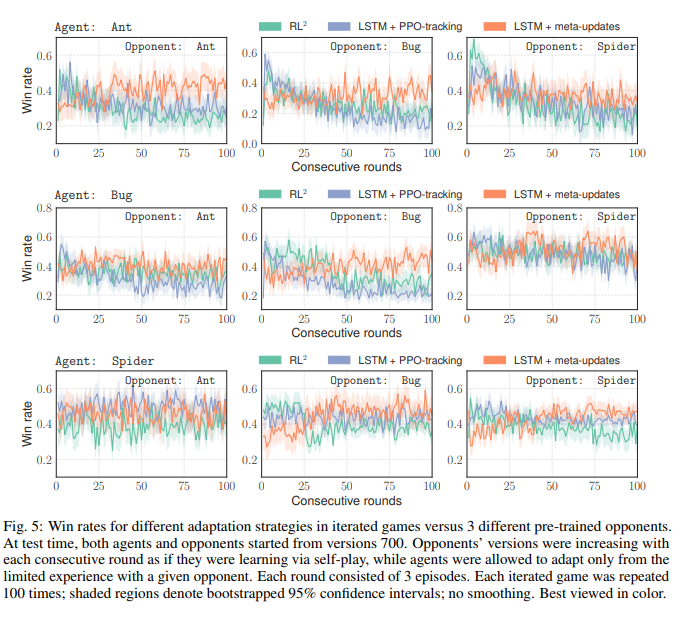
The authors created an adversarial environment called RoboSumo where pairs of agents with 4 (named Ants), 6 (named Bugs),or 8 legs (named spiders) sumo wrestle. The agents observe the location and velocity of their bodies and the bodies of their opponent, the angles and velocities of their legs, and the forces being exerted on them by their opponent (equivalent of tactile sense). The game is organized into episodes and rounds. Episodes are single wrestling matches with 500 time steps and win/lose/draw outcomes. Agents win by pushing their opponent out of the ring or making their opponent's body touch the ground. Rounds are batches of episodes. An episode results in a draw when neither of these things happen after 500 time steps. Rounds have possible outcomes win, lose, and draw that are decided based on majority of episodes won. K rounds will be fought. Both agents may update their policies between rounds. The agent that wins the majority of rounds is deemed the winner of the game.
Setup
Similar to the Robotic locomotion example, this game can be phrased in terms of the RL MDP framework.
- [math]\displaystyle{ T_i }[/math]: The task of fighting a round.
- [math]\displaystyle{ \{T_i\}_{i=1}^{K} }[/math]: A sequence of rounds against the same opponent. Note that the opponent may update their policy between rounds but the anatomy of both wrestlers will be constant across rounds.
- A Markov Descision process composed of
- A horizon [math]\displaystyle{ H = 500*n }[/math] where [math]\displaystyle{ n }[/math] is the number of episodes per round.
- Observations [math]\displaystyle{ x_t }[/math] containing information about the state of the agent and its opponent.
- Actions [math]\displaystyle{ a_t }[/math] containing information about the torques to apply to the agents legs.
- Rewards [math]\displaystyle{ R_t }[/math] rewards given to the agent based on its wrestling performance. [math]\displaystyle{ R_{500*n} = }[/math] +2000 if win episode, -2000 if lose, and -1000 if draw.
Note that the above reward set up is quite sparse, therefore in order to encourage fast training, rewards are introduced at every time step for the following.
- For staying close to the center of the ring.
- For exerting force on the opponents body.
- For moving towards the opponent.
- For the distance of the opponent to the center of the ring.
This makes sense intuitively as these are reasonable goals for agents to explore when they are learning to wrestle.
Training
The same combinations of policy networks and adaptation methods that were used in the locomotion example are trained and tested here. A family of non-adaptive policies are first trained via self-play and saved at all stages. Self-play simply means the two agents in the training environment use the same policy. All policy versions are saved so that agents of various skill levels can be sampled when training meta-learners. The weights of the different insects were calibrated such that the test win rate between two insects of differing anatomy, who have been trained for the same number of epochs via self-play, is close to 50%.
We can see in the above figure that the weight of the spider had to be increased by almost four times in order for the agents to be evenly matched.
The above figure shows testing results for various adaptation strategies. The agent and opponent both start with the self-trained policies. The opponent uses all of its testing experience to continue training. The agent uses only the last 75 episodes to adapt its policy network. This shows that metal learners need only a limited amount of experience in order to hold their own against a constantly improving opponent.
Future Work
The authors mention that their approach will likely not work well with sparse rewards. This is because the meta-updates, which use policy gradients, are very dependent on the reward signal. They mention that this is an issue they would like to address in the future. A potential solution they have outlined for this is to introduce auxiliary dense rewards which could enable meta-learning.
Sources
- Chelsea Finn, Pieter Abbeel, Sergey Levine. "Model-Agnostic Meta-Learning for Fast Adaptation of Deep Networks." arXiv preprint arXiv:1703.03400v3 (2017).
- Richard S Sutton, Anna Koop, and David Silver. On the role of tracking in stationary environments. In Proceedings of the 24th international conference on Machine learning, pp. 871–878. ACM, 2007.