ALBERT: A Lite BERT for Self-supervised Learning of Language Representations: Difference between revisions
No edit summary |
No edit summary |
||
| Line 33: | Line 33: | ||
===Inter-sentence coherence loss=== | ===Inter-sentence coherence loss=== | ||
The BERT uses two loss functions namely Masked language modeling (MLM) loss and Next-sentence prediction (NSP) loss. The NSP is a binary classification loss were positive examples are two consecutive segments from the training corpus and negative examples are pairing segments from different documents. The negative and positive examples are sampled with equal probability. However experiments show that NSP is not effective. The authors explained the reason as follows: | |||
A negative example in NSP is misaligned from both topic and coherence perspective. However, topic prediction is easier to learn compered to coherence prediction. Hence, the model ends up learning just the easier topic-prediction signal. | |||
They tried to solve this problem by introducing a new loss namely sentence order prediction (SOP) which is again A binary classification loss. Positive examples are the same as in NSP (two consecutive segments). But the negative examples are the same two consecutive segments with their order swapped. The SOP forces the model to learn the harder coherence prediction task. The following table compare NSP with SOP. AS we can see the NSP cannot solve the SOP task (it performs at random) but the SOP can solve the NSP task to a acceptable degree. We also see that on average the SOP improves results on downstream tasks by almost 1%. | |||
[[File:SOPvsNSP.png]] | [[File:SOPvsNSP.png]] | ||
===Removing dropout=== | ===Removing dropout=== | ||
Revision as of 20:45, 2 November 2020
Presented by
Maziar Dadbin
Introduction
In this paper, the authors have made some changes to the BERT model and the result is ALBERT, a model that out-performs BERT on GLUE, SQuAD, and RACE benchmarks. The important point is that ALBERT has fewer number of parameters than BERT-large, but still it gets better results. The above mentioned changes are Factorized embedding parameterization and Cross-layer parameter sharing which are two methods of parameter reduction. They also introduced a new loss function and replaced it with one of the loss functions being used in BERT (i.e. NSP). The last change is removing dropout from the model.
Motivation
In natural language representations, larger models often result in improved performance. However, at some point GPU/TPU memory and training time constraints limit our ability to increase the model size any further. There exist some attempts to reduce the memory consumption but at the cost of speed (look at Chen et al. (2016), Gomez et al. (2017), and also Raffel et al. (2019)). The authors of this paper claim that there parameter reduction techniques reduce memory consumption and increase training speed.
Model details
The fundamental structure of ALBERT is the same as BERT i.e. it uses transformer encoder with GELU nonlinearities. The authors set the feed-forward/filter size to be 4*H and the number of attention heads to be H/64 where H is the size of the hidden layer. Next we explain the changes the have been applied to the BERT.
Factorized embedding parameterization
In BERT (as well as subsequent models like XLNet and RoBERTa) we have E=H i.e. the size of the vocabulary embedding (E) and the size of the hidden layer (H) are tied together. This is not an efficient choice because we may need to have a large hidden layer but not a large vocabulary embedding layer. This is actually the case in many applications because the vocabulary embedding ‘E’ is meant to learn context-independent representations while the hidden-layer embedding ‘H’ is meant to learn context-dependent representation which usually is harder. However if we increase H and E together, it will result in a huge increase in the number of parameters because the size of the vocabulary embedding matrix is V×E where V is usually quite large (V is the size of the vocabulary and equals 30000 in both BERT and ALBERT). The authors proposed the following solution to the problem: Do not project one-hot vectors directly into hidden space, instead first project one-hot vectors into a lower dimensional space of size E and then project it to the hidden layer. This reduces embedding parameters from O(V×H) to O(V×E+E×H) which is significant when H is much larger than E.
Cross-layer parameter sharing
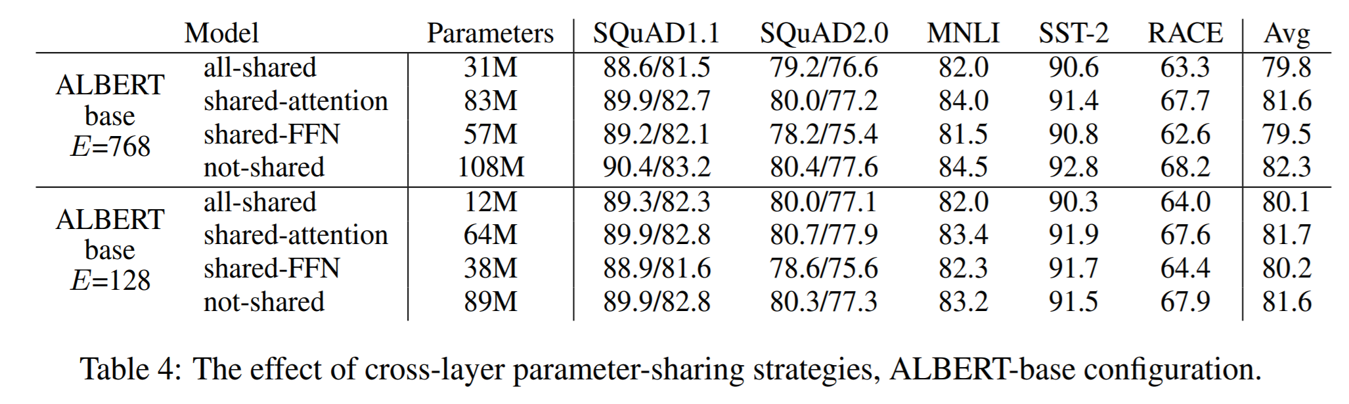
Another method the authors used for reducing the number of parameters is to share the parameters across layers. There are different strategies for parameter sharing for example one may only share feed-forward network parameters or only sharing attention parameters. However, the default choice for ALBERT is to simply share all parameters across layers. The following table shows the effect of different parameter sharing strategies in two setting for the vocabulary embedding size. As we can see in both cases, sharing all the parameters have a negative effect on the accuracy where most of this effect comes from sharing the FFN parameters not from sharing attention parameters. Given this, the authors have decided to share all the parameters across the layers which result in much smaller number of parameters which in turn enable them to have larger hidden layers and this is how they compensate what they have lost from parameter sharing.
Inter-sentence coherence loss
The BERT uses two loss functions namely Masked language modeling (MLM) loss and Next-sentence prediction (NSP) loss. The NSP is a binary classification loss were positive examples are two consecutive segments from the training corpus and negative examples are pairing segments from different documents. The negative and positive examples are sampled with equal probability. However experiments show that NSP is not effective. The authors explained the reason as follows: A negative example in NSP is misaligned from both topic and coherence perspective. However, topic prediction is easier to learn compered to coherence prediction. Hence, the model ends up learning just the easier topic-prediction signal. They tried to solve this problem by introducing a new loss namely sentence order prediction (SOP) which is again A binary classification loss. Positive examples are the same as in NSP (two consecutive segments). But the negative examples are the same two consecutive segments with their order swapped. The SOP forces the model to learn the harder coherence prediction task. The following table compare NSP with SOP. AS we can see the NSP cannot solve the SOP task (it performs at random) but the SOP can solve the NSP task to a acceptable degree. We also see that on average the SOP improves results on downstream tasks by almost 1%.