stat946f10
Proposal for STAT946 projects
Maximum Variance Unfolding (Semidefinite Embedding)
Maximum Variance Unfolding (MVU) is a variation of Kernel PCA in which the kernel matrix is also obtained from the data. The main proposal of this technique is not to choose a kernel function a priori like classical kernel PCA or construct a kernel matrix by algorithm like LLE and ISOMAP, but instead learn a kernel [math]\displaystyle{ K }[/math] optimizing an objective function with several constraints when the data set is given.
First, we give the constraints for the kernel.
Constraints
1. Semipositive definiteness
Kernel PCA is a kind of spectral decomposition in Hilbert space. The kernel matrix stores the inner products of vectors in a Hilbert space, hence it must be positive semidefinite. The semipositive definiteness means all eigenvalues are non-negative, i.e. [math]\displaystyle{ K\gt =0 }[/math].
2. Centering
Considering the centering process in Kernel PCA, it is also required here. The condition is given by
[math]\displaystyle{ \sum_i \Phi\left(x_i\right) =0 . }[/math]
Equivalently,
[math]\displaystyle{ 0 = \left|\sum_i \Phi(x_i)\right|^2 = \sum_{ij}\Phi(x_i)\Phi(x_j)=\sum_{ij}K_{ij}. }[/math]
3. Isometry
The local distance between a pairwise of data [math]\displaystyle{ x_i, x_j }[/math], under neighbourhood relation [math]\displaystyle{ \eta }[/math] (i.e. [math]\displaystyle{ \eta_{ij}=1 }[/math] indicates data [math]\displaystyle{ x_i, x_j }[/math] are neighbours), should be preserved in new space after mapping [math]\displaystyle{ \Phi(\cdot) }[/math]. In other words, for all [math]\displaystyle{ \eta_{ij}\gt 0 }[/math],
[math]\displaystyle{ \left|\Phi(x_i) - \Phi(x_j)\right|^2 = \left|x_i - x_j\right|^2. }[/math]
Additonally, for the consider of conformal map, the pairwise distance between two points having a common neighbour point should also be preserved. Two data points having a common neighbour can be identified as [math]\displaystyle{ [\eta^T\eta]_{ij}\gt 0. }[/math] This ensures that if two points have a common neighbour, we preserve their pairwise distances and angles.
[math]\displaystyle{ \left|\Phi(x_i) - \Phi(x_j)\right|^2 = \left(\Phi(x_i) - \Phi(x_j)\right)^{T}\left(\Phi(x_i) - \Phi(x_j)\right) }[/math]
[math]\displaystyle{ \left|\Phi(x_i) - \Phi(x_j)\right|^2 = \Phi(x_i)^{T}\Phi(x_i) - \Phi(x_j)^{T}\Phi(x_j) - 2 \Phi(x_i)^{T}\Phi(x_j) }[/math]
Thus, [math]\displaystyle{ K_{ii}+K_{jj}-2K_{ij}=\left|x_i - x_j\right|^2 }[/math] for all ij [math]\displaystyle{ \eta_{ij}\gt 0 }[/math] or [math]\displaystyle{ [\eta^T\eta]_{ij}\gt 0. }[/math]
Objective Functions
Given the conditions, the objective functions should be considered. The aim of dimensional reduction is to map high dimension data into a low dimension space with the minimum information losing cost. Recall the fact that the dimension of new space depends on the rank of the kernel. Hence, the best ideal kernel is the one which has minimum rank. So the ideal objective function should be
[math]\displaystyle{ \min\quad rank(K). }[/math]
However, minimizing the rank of a matrix is a hard problem. So we look at the question in another way. When doing dimensional reduction, we try to maximize the distance between non-neighbour data. In other words, we want to maximize the variance between non-neighbour datas, and it is the same as maximizing the sum of the eigenvalues. In such sense, we can change the objective function to
[math]\displaystyle{ \max \quad Trace(K) }[/math] .
Note that it is an interesting question that whether these two objective functions can be equivalent to each other. Although they are not totally equivallent, it can be shown that they usually converge to each other.
Algorithm for Optimization Problem
The objective function with linear constraints form a typical semidefinite programming problem. The optimization is convex and globally. We already have methods to slove such kind of optimization problem.
Colored Maximum Variance Unfolding .<ref>Song, L. and colleagues; Proceedings of the 2007 Conference, 1385-1392.</ref>
MVU is based on maximizing the overall variance while the local distances between neighbor points are preserved and it uses only one source of information. Colored MVU uses more than one source of information, i.e it reduces the dimension satisfying a combination of two goals
1- preserving the local distance (as first information)
2- optimum alignment with second information (side information)
Examples of how Colored MVU can leverage the side information
- Given text data from a newsgroup as first information, a hierarchy of topics can be used as side information to guide the embedding.
- Given term-frequency and inverse-document-frequency representation of academic papers as first information, co-author relationship can be used as side information to guide the embedding.
Rationale of separating the side information from the data
- We cannot merge all kind of information in one distance metric because the data(first information) and the side information may be heterogeneous
- The side information may be a feature of similarity(papers with the same co-authors tend to be more similar) rather than difference(papers with different co-authors are not necessarily far apart).
- When inserting new information, usually only new data but not new side information is added.
Algorithmic Modification
In Colored MVU, [math]\displaystyle{ Trace(KL) }[/math] is maximized instead of [math]\displaystyle{ Trace(K) }[/math], where [math]\displaystyle{ L }[/math] is the matrix of covariance of first and side information.
Application
One of the drawback of MVU is that its statistical interpretation is not always clear. However one of the application of Colored MVU, which has great statistical interpretation is to be used as a criterion to measure the Hilbert-Schmidt Independence.
Steps for SDE algorithm
- Generate a K nearest neighbor graph. It should be a connected graph and so if K is too small it would be an unbounded problem, having no solution.
- Semidefinite programming: Maximize [math]\displaystyle{ Tr(K) }[/math] subject to the above mentioned constraints.
- Do kernel PCA with this learned kernel.
Advantages
- The kernel that is learned from the data can actually reflect the intrinsic dimensionality of the data. More specifically, the eigen-spectrum of the kernel matrix K provides an estimation.
The dimension needed to preserve local distance while maximizing variance is dependent on the number of dominant eigenvalues of K. That is, if top r eigenvalues of K account for 90% of the trace then an r dimensional representation can reveal about 90% of the unfolded data's variance. - MVU is a convex problem which guarantees a unique solution.
- Distance-preserving constraints can be easily expressed and enforced in the semi-definite programming framework. This flexibility allows tailor-made constraints to be imposed on particular applications, for example analyzing robot motions(ARE).
Disadvantages
- SDE can be solved efficiently in polynomial time but still has a high computational complexity. (O(matrix_size ^ 3 + number_of_constraints ^ 3))
- SDE is limited to a isometric map
Application in SVM classification
The optimized kernel replaces the popular kernels using in SVM (i.e. linear kernel) for classification. It actually performs worse than other kernel functions chose in priori.
June 4th
Action Respecting Embedding (ARE)
It is a variation of Maximum Variance Unfolding.
The data here is temporal or ordered, i.e we move from one point to another by taking an action. In other words action [math]\displaystyle{ a_i }[/math] is taken between data points [math]\displaystyle{ x_i }[/math] and [math]\displaystyle{ x_{i+1} }[/math].
Action labels,even with no interpretation or implied meaning,provide more information about the underlying generation of the data.It is natural to expect that the actions correspond to some simple operator on the generator's own degrees of freedom.For example,a camera that is being panned left and then right,has actions that correspond to a simple translation in the camera's actuator space.We therefore want to constrain the learned representation so that the labeled actions correspond to simple transformations in that space.In particular,we can require all actions to be a simple rotation plus translation in the resulting low-dimensional representation.<ref>
M.Bowling, A.Ghodsi, and D.Wilkinson. Action respecting embedding. In International Conferenceon Machine Learning,2005.
</ref>
Consider action [math]\displaystyle{ a }[/math] taken between the points [math]\displaystyle{ x_i , x_{i+1} }[/math], and the points [math]\displaystyle{ x_j , x_{j+1} }[/math], in the original data space, it may not be a simple transformation (Rotation, Translation or combination of both).
A transformation [math]\displaystyle{ T }[/math] is called simple or distance preserving if and only if
[math]\displaystyle{ \forall x, x' }[/math] [math]\displaystyle{ \left \Vert T(x)-T(x') \right \|=\left \Vert x - x' \right \| }[/math]
Notice that [math]\displaystyle{ T_a(x_i)=x_{i+1} }[/math] and [math]\displaystyle{ T_a(x_j)=x_{j+1} }[/math]
In the low dimension space, as in the camera case where actions corresponds to a simple translation in the camera's actuator space, the action can become a simple transformation. Therefore constraining the action to be a simple transformation in dimension reduction would help us to find a low dimension representation close to the true one, if the action indeed corresponds to a simple transformation in the intrinsic dimension space.
The goal here is not only to reduce the dimensionality of the data but also reducing the complexity of actions in the sense that actions in this low dimension representation is a simple transformation. Therefore to obtain a low dimensional embedding of the high dimensional temporal data, the action in low dimension must be represented by a constraint that preserves the distance. This constraint is called action respecting constraint.
Constraint
For any two data points [math]\displaystyle{ x_i }[/math],[math]\displaystyle{ x_j }[/math] if the same action a [math]\displaystyle{ \left(a_{i}=a_{j}\right) }[/math] is carried out, transforming them into [math]\displaystyle{ x_{i+1} }[/math] and [math]\displaystyle{ x_{j+1} }[/math] respectively, then the distance between [math]\displaystyle{ y_i }[/math] and [math]\displaystyle{ y_j }[/math] must be equal to the distance between [math]\displaystyle{ y_{i+1} }[/math] and [math]\displaystyle{ y_{j+1} }[/math] where [math]\displaystyle{ y_i }[/math] , [math]\displaystyle{ y_j }[/math] , [math]\displaystyle{ y_{i+1} }[/math] , [math]\displaystyle{ y_{j+1} }[/math] are the corresponding points in the low dimension. This constraint is given as:
[math]\displaystyle{ \left|y_i - y_j\right|^2=\left|y_{i+1} - y_{j+1}\right|^2 \rightarrow \left|\Phi(x_i) - \Phi(x_j)\right|^2=\left|\Phi(x_{i+1}) - \Phi(x_{j+1})\right|^2 }[/math]
The kernel form of the above constarint is:
[math]\displaystyle{ \forall i, j a_{i}=a_{j} \Rightarrow K_{ii}+K_{jj}-2K_{ij}=K_{(i+1)(i+1)}+K_{(j+1)(j+1)}-2K_{(i+1)(j+1)} }[/math]
The above, action respecting constraint is added to the constraints of MVU and the algorithm of MVU is run to obtain a low dimension embedding for the temporal data.
Example
This example is extracted from the "Action Respecting Embedding" paper listed in the references.
Consider a virtual robot that observe a 100 by 100 patch of a 2048 by 1536 image. The actions of the robot consists of four translations(rightward/leftward/upward/downward). In this example, we consider two action sequences and compare their representations by SDE and ARE.
It is obvious that the first sequence of actions lie in a one-dimensional subspace and the second sequence lies in a two-dimensional subspace. Although both SDE and ARE succeed in capturing this low dimensionality, the embedding achieved by ARE is much smoother and corresponds much better(almost exactly) to the actual actions.
June 9th
Applications of ARE
- Planning: To find a sequence of events to achieve a desired goal i.e. we want to find a path that leads us to the desired goal given the initial point and the set of all possible actions.
In ARE, the action is constrained to be a simple transformation in the low dimension space. After obtaining the low dimension representation through ARE, we have a set a points [math]\displaystyle{ \lbrace y_t \rbrace }[/math].
Consider a collection of data point pairs [math]\displaystyle{ \lbrace (y_t }[/math], [math]\displaystyle{ y_{t+1}) \rbrace }[/math] such that [math]\displaystyle{ y_t \xrightarrow{a} y_{t+1} }[/math], We can learn the action a as a simple transformation [math]\displaystyle{ f_a }[/math] such that
[math]\displaystyle{ f_a(y_t)=A_ay_t+b_a }[/math] subject to [math]\displaystyle{ A_a^TA_a=I }[/math]
we can do breath-first expansion for a tree starting from root (represents the intial point)by considering all possible actions(simple transformation) until the desired goal is reached.
- Robot loaization: It is accomplished by using the motion and sensor probabilistic model. But using ARE, we can do robot localization in the low dimensional map rather than in the original space. This has the advantage that it becomes independent of the environmental constraints.
Metric Learning
Metric Learning is a supervised algorithm used for dimensionality reduction, in which class related side information are used. Two types of class-related information are brought in consideration, given a set of points [math]\displaystyle{ \{x_i, i=1, \cdots, m\} }[/math]. The first one is the similar set or class-equivalent set.
Similar Set
a set of pairs of similar points, denoted by [math]\displaystyle{ S }[/math]
[math]\displaystyle{ S : (x_i, x_j) \in S }[/math] if [math]\displaystyle{ x_i }[/math] and [math]\displaystyle{ x_j }[/math] are similar;
The second one is the dissimilar set or class-inequivalent set
Dissimilar Set
a set of pairs of dissimilar points, denoted by [math]\displaystyle{ D }[/math]
[math]\displaystyle{ D : (x_i, x_j) \in D }[/math] if [math]\displaystyle{ x_i }[/math] and [math]\displaystyle{ x_j }[/math] are dissimilar.
Note that pairs of points, which may not be known to be similar or dissimilar, will not be placed in either set. These two sets can come from knowing the class label or just the similarity or dissimilarity of some data. Some algorithms like Maximally Collapsing Metric Learning may require knowing the class label of data.
We want to learn a distance metric
[math]\displaystyle{ d_A(x_i, x_j) = \|x_i - x_j\|_A = \sqrt{(x_i-x_j)^T A(x_i-x_j)} }[/math], where [math]\displaystyle{ \|x_i - x_j\|_A }[/math] is not the euclidean distance but the mahalanobis distance determined by semi-definite matrix [math]\displaystyle{ A }[/math].
Equivalently, we want to learn semi-definite matrix [math]\displaystyle{ A }[/math] from the given data such that similiar points are close but dissimilar points are far apart.
[math]\displaystyle{ A= WW^T }[/math] where [math]\displaystyle{ W }[/math] is the transformation that maps data to the other space. The euclidean distance between the points in the transformed space is represented by mahalanobis distance in the oringinal space.
Such idea comes from firstly in 2004. After that, several different approaches are given to find the metric.
1. Original Optimization Problem
It is given by Eric P. Xing, Andrew Y. Ng, Michael I. Jordan and Stuart Russell in 2004 .<ref name="Xing">Eric P. Xing, Andrew Y. Ng, Michael I. Jordan and Stuart Russell, Distance metric learning, with application to clustering with side-information, </ref> .
The authors give the optimization problem in following form:
[math]\displaystyle{ \min_A \sum_{(x_i , x_j) \in S} \|x_i - x_j\|^2_A }[/math]
[math]\displaystyle{ s.t. \sum_{(x_i , x_j) \in D} \|x_i - x_j\|_A \ge 1 ,(*) }[/math]
[math]\displaystyle{ A \ge 0 . }[/math]
The constraint is given to keep the distance between dissimilar points. If the constraint is ignored, [math]\displaystyle{ A = 0 }[/math] will be a trivial but not useful solution, which means all points collapse to a single point. The choice of constant [math]\displaystyle{ 1 }[/math] is not important, and can be changed to any other positive number. In the paper, it is also shown that it is a convex optimization problem. Hence, we can solve it by some efficient algoritms without getting stuck at local minimas. In this paper, the author also notes that some possible alternatives to (*) would not be a good choice. For example, if this constraint is changed to [math]\displaystyle{ \sum_{(x_i , x_j) \in D} \|x_i - x_j\|^2_A \ge 1 }[/math], though it maintains a linear constraint, it would result in A always being rank 1 (i.e., the data are always projected onto a line).
Algorithms to Find A
Since no analytical formula is known for solving [math]\displaystyle{ A }[/math] in the above formulation, iterative algorithms are developed to approximate [math]\displaystyle{ A }[/math]. During the iterative process, the algorithms have to ensure that [math]\displaystyle{ A \ge 0 }[/math].
Algorithm to find a full matrix diagonal A
In the general case where we seek a full matrix [math]\displaystyle{ A }[/math], the constraint [math]\displaystyle{ A \ge 0 }[/math] is tricky to enforce and brute-force Newton method's is prohibitively expensive. An algorithm which uses the ideas of gradient descent and iterative projections is given in the aforementioned paper as follows:
Iterate
Iterate
[math]\displaystyle{ A := \arg \min_{A'} \{ \| A' - A \|_F : A' \in C_1 \} }[/math](first projection)
[math]\displaystyle{ A := \arg \min_{A'} \{ \| A' - A \|_F : A' \in C_2 \} }[/math](second projection)
until [math]\displaystyle{ A }[/math] converges
[math]\displaystyle{ A := A + \alpha \nabla_A(g(A))_{\perp \nabla_A f} }[/math](gradient ascent)
until convergence
where
[math]\displaystyle{ \| \cdot \|_F }[/math] is the Frobenium norm,
[math]\displaystyle{ C_1 = \{A:\sum_{(x_i, x_j) \in S}\| x_i - x_j \|^2_A \le 1\} }[/math] and [math]\displaystyle{ C_2 = \{A:A \ge 0 \} }[/math]
Efficient Algorithm to find a diagonal A
In the special case where we seek a diagonal matrix [math]\displaystyle{ A }[/math], the authors have derived a much more efficient algorithm, as explained below.
Obviously, letting A = I gives Euclidean distance. Now, let us suppose we want to learn a diagonal, that is [math]\displaystyle{ A=diag(A_{11},A_{22},...,A_{nn}) }[/math]
Define [math]\displaystyle{ g(A)=g(A_{11},A_{22},...,A_{nn})=\sum_{(x_i , x_j) \in S} \|x_i - x_j\|^2_A-log(\sum_{(x_i , x_j) \in D} \|x_i - x_j\|_A) }[/math]
We can use Newton-Raphson algorithm to optimize [math]\displaystyle{ g(A) }[/math].
2. Maximally Collapsing Metric Learning
Globerson & Roweis <ref> Globerson, A., and Roweis, S. 2006. Metric learning by
collapsing classes. In Weiss, Y.; Sch¨olkopf, B.; and Platt,
J., eds., Advances in Neural Information Processing Systems
18, 451–458. Cambridge, MA: MIT Press.</ref> proposed another metric learning method
which considerably overperforms the original technique suggested by Xing, et. al. Based on a distance metric matrix [math]\displaystyle{ A }[/math], they define a conditional probability distribution function as
[math]\displaystyle{ P^A(j|i)=\frac{e^{-({d_{ij}^A})^2}}{\sum_{k\neq i} e^{-({d_{ik}^A})^2}} }[/math]
Ideally, we expect all the points in the same class collapse to one point and all the points in different classes get infinitely far apart from each other. In this ideal situation the conditional probabilty distributions would be
[math]\displaystyle{ p_0(j|i)\propto \left\{\begin{matrix}
1 & y_i=y_j \\
0 & yi \neq y_j \end{matrix}\right. }[/math]
To learn a distance metric, Globerson & Roweis find the value of the matrix [math]\displaystyle{ A }[/math] such that the conditional probability distribution introduced above gets as close as possible to the ideal conditional distribution. To this end, they minimize the KL divergence between the two distributions (As known, KL divergence is a measure of difference between two probability distributions):
[math]\displaystyle{ \min_A \sum_{i} \textbf{KL}\left[ p_0(j|i)p^A(j|i)\right] }[/math]
subject to [math]\displaystyle{ A\succeq 0 }[/math]. This is a convex optimization problem and may be solved by a projected
gradient approach similar to the one used in Xing, et. al. <ref name="Xing"/>.
3. PSD formulation
Another approach is given in <ref name="Ali Ghodsi"> Ali Ghodsi, Dana Wilkinson, Finnegan Southey, Improving Embeddings by Flexible Exploitation of Side Information</ref>, in which the loss function is given by
[math]\displaystyle{ L(A) = \sum_{(x_i, x_j) \in S } \|x_i - x_j\|^2_A - \sum_{(x_i, x_j)\in D} \|x_i - x_j\|_A^2. }[/math]
This loss function is minimized if its first component (sum of the differences between points in similarity class) is minimized while, its second component (sum of the differences between points in dissimilarity class) is maximized. Unlike the original optimization problem proposed by Xing et al. minimizing the distance between similar points while keeping a certain distance between dissimilar points, here we want similar points to stay close but dissimilar points to be far apart
The optimization problem is
[math]\displaystyle{ \min_A L(A); s.t. A \ge 0, Tr(A) = 1 }[/math].
The Positive semi-definiteness ([math]\displaystyle{ A \ge 0 }[/math]) constrain guarantees a valid Euclidean metric and the trace constraints is to prevent the solution [math]\displaystyle{ A =0 }[/math].
In order to be able to use standard semidefinite programing software [math]\displaystyle{ L(A) }[/math] must be linearized. To do so function [math]\displaystyle{ vec() }[/math] (which rearranges a matrix by concatenating its columns) gives quite useful results
[math]\displaystyle{ vec(ABC)=(C^{T}\otimes A)vec(B) }[/math], in which [math]\displaystyle{ \otimes }[/math] is the Kroneker product.
since [math]\displaystyle{ (x_{i}-x_{j})^{T}A(x_{i}-x_{j}) }[/math] is a scalar, it can be written as
[math]\displaystyle{ (x_{i}-x_{j})^{T}A(x_{i}-x_{j})=vec((x_{i}-x_{j})^{T}A(x_{i}-x_{j}))=((x_{i}-x_{j})^{T}\otimes (x_{i}-x_{j})^{T})\cdot vec(A) }[/math]
[math]\displaystyle{ =((x_{i}-x_{j})\otimes (x_{i}-x_{j}))^{T}\cdot vec(A)=(vec((x_i - x_j)(x_i - x_j)^T))^T \cdot vec(A)=(vec(A))^T\cdot vec((x_i - x_j)(x_i - x_j)^T) }[/math]
Therefore
[math]\displaystyle{ L(A) = \sum_{(x_i, x_j) \in S } (x_i - x_j)^T A (x_i - x_j) - \sum_{(x_i, x_j)\in D} (x_i - x_j)^T A (x_i - x_j) }[/math]
[math]\displaystyle{ = \sum_{(x_i, x_j) \in S } (vec(A))^T vec((x_i - x_j)(x_i - x_j)^T) - \sum_{(x_i, x_j)\in D} (vec(A))^T vec((x_i - x_j)(x_i - x_j)^T) }[/math]
[math]\displaystyle{ = (vec(A))^T \left[ \sum_{(x_i, x_j) \in S } vec((x_i - x_j)(x_i - x_j)^T) - \sum_{(x_i, x_j)\in D} vec((x_i - x_j)(x_i - x_j)^T) \right] }[/math]
"This form along with the two linear constraints given in (1), makes a semidefinite positive problem that can be easily solved by a SDP solver, called SeDumi in Matlab. Therefore, it is a more convenient form than that used by Xing et all. Furthermore, in the original form, at least one dissimilar pair is required, while it is not necessary in the form given by Ali Ghodsi et al., because of the trace constraint. There can be only similar pairs, only dissimilar pairs, or any combination of the two, and the method will still avoid the trivial solution. Furthermore, in the absence of specific information regarding dissimilarities, Xing et al. assume that all points not explicitly identified as similar are dissimilar. This information may be misleading, forcing the algorithm to separate points that should be in fact be similar. The formulation presented by Ali Ghodsi et al. allows one to specify only the side information one actually has, partitioning the pairing into similar, dissimilar, and unknown."<ref> Lecture notes by Ali Ghodsi </ref>
June 11th
Closed form Metric learning (CFML)
The PSD formulation later is found to have closed form solution.
Replacing [math]\displaystyle{ A }[/math] by [math]\displaystyle{ WW^T }[/math] removes the constrain of positive semidefinite [math]\displaystyle{ A \ge 0 }[/math].
So, [math]\displaystyle{ (x_i-x_j)^T A(x_i-x_j) }[/math] can be written as
[math]\displaystyle{ Trace((x_i-x_j)^T A(x_i-x_j))=Trace(x_i-x_j)^T WW^T(x_i-x_j))=Trace(W^T(x_i-x_j)(x_i-x_j)^T W) }[/math]
The optimization problem becomes:
[math]\displaystyle{ \min_A \sum_{(x_i , x_j) \in S} (x_i-x_j)^T A(x_i-x_j)-\sum_{(x_i , x_j) \in D} (x_i-x_j)^T A(x_i-x_j) }[/math]
[math]\displaystyle{ =\min_W \sum_{(x_i , x_j) \in S} Trace(W^T(x_i-x_j)(x_i-x_j)^T W)-\sum_{(x_i , x_j) \in D} Trace(W^T(x_i-x_j)(x_i-x_j)^T W) }[/math]
[math]\displaystyle{ =\min_W Trace(W^T\sum_{(x_i , x_j) \in S}(x_i-x_j)(x_i-x_j)^T W)-Trace(W^T\sum_{(x_i , x_j) \in D} (x_i-x_j)(x_i-x_j)^T W) }[/math]
[math]\displaystyle{ =\mathbf{\min_W Trace(W^T M_S W)-Trace(W^T M_D W)} }[/math]
S.T. [math]\displaystyle{ \mathbf{Trace(WW^T)=1} }[/math]
where [math]\displaystyle{ \mathbf {M_S=\sum_{(x_i , x_j) \in S} (x_i-x_j)(x_i-x_j)^T} }[/math] and [math]\displaystyle{ \mathbf {M_D=\sum_{(x_i , x_j) \in D} (x_i-x_j)(x_i-x_j)^T} }[/math]
using lagrange multiplier formulation, the lagrange function is obtained.
[math]\displaystyle{ \mathbf f(W,\lambda)= Trace(W^T M_S W)-Trace(W^T M_D W)-\lambda (Trace(WW^T)-1) }[/math]
Taking the derivative and setting it to zero, we have
[math]\displaystyle{ \mathbf {(M_S-M_D)} \mathbf W = \lambda \mathbf W }[/math]
The optimal solution for [math]\displaystyle{ \mathbf W }[/math] corresponds to a matrix which consists of eigenvectors (as its columns) having the smallest nonzero eigenvalue of [math]\displaystyle{ \mathbf {(M_S-M_D)} }[/math] and therefore [math]\displaystyle{ A = WW^T }[/math] is rank [math]\displaystyle{ 1 }[/math]. This close form solution also explains why in the original optimization problem proposed by Xing et al., changing the constraint to [math]\displaystyle{ \sum_{(x_i , x_j) \in D} \|x_i - x_j\|^2_A \ge 1 }[/math] always results a Rank 1 solution, which all the data points are projected on a line. However, we don't want to always project points to a line or reduce the original dimension to 1. Projection of the data points on a line is due to the constraint imposed on the cost function and therefore to avoid that we need to change our constarint.
There are two alternative constraints that can be imposed on the cost function:
- One is: [math]\displaystyle{ \mathbf W^T\mathbf W= \mathbf I_m }[/math].
So, the optimization problem becomes:
[math]\displaystyle{ \mathbf{ \min_W Trace( W^T( M_S- M_D) W)} }[/math]
s.t [math]\displaystyle{ \mathbf W^T\mathbf W=\mathbf I_m }[/math].
using the lagrange multiplier formulation, we have
[math]\displaystyle{ \mathbf{f(W,\Lambda)= Trace(W^T (M_S-M_D) W)- Trace(\Lambda_{m}(W^TW-I_m))} }[/math]
Taking the derivative and setting it to zero, we have
[math]\displaystyle{ \mathbf {(M_S-M_D)W = W \Lambda_m} }[/math]
[math]\displaystyle{ \mathbf W }[/math] is the eigenvectors of [math]\displaystyle{ (\mathbf M_S-\mathbf M_D) }[/math] associating with [math]\displaystyle{ m }[/math] least non-zero eigenvalues.
- The other is: [math]\displaystyle{ \mathbf W^T\mathbf M_S\mathbf W= \mathbf I_m }[/math].
So, the optimization problem becomes:
[math]\displaystyle{ \mathbf{\min_W Trace(W^T( M_S-M_D)W)} }[/math]
s.t. [math]\displaystyle{ \mathbf {W^T M_S W=I_m} }[/math]
this alternative algorithm is called CFML-II.
To solve this new form of optimization problem, let [math]\displaystyle{ \mathbf M_S=\mathbf {HH^T} }[/math] and [math]\displaystyle{ \mathbf {Q=H^TW} }[/math], we get:
[math]\displaystyle{ \mathbf{\min_W Trace(W^T( M_S-M_D)W)=\min_W Trace(I_m-W^T M_D W)} }[/math]
[math]\displaystyle{ \mathbf{=\min_W Trace(Q^T I_n Q-((H^T)^{-1}Q)^T M_D (H^T)^{-1}Q)=\min_W Trace(Q^T I_n Q-Q^TH^{-1} M_D (H^{-1})^T Q)} }[/math]
[math]\displaystyle{ \mathbf{=\min_W Trace(Q^T (I_n -H^{-1} M_D (H^{-1})^T) Q)} }[/math]
s.t. [math]\displaystyle{ \mathbf {Q^T Q= I_m} }[/math]
using the lagrange multiplier formulation, we have
[math]\displaystyle{ (\mathbf{ I_n-H^{-1} M_D (H^{-1})^T) Q=Q\Lambda_m} }[/math]
So, [math]\displaystyle{ \mathbf {Q} }[/math] is the eigenvectors of [math]\displaystyle{ \mathbf{(I_n -H^{-1} M_D (H^{-1})^T)} }[/math] associating with [math]\displaystyle{ \mathbf m }[/math] least non-zero eigenvalues.
Equivalently, [math]\displaystyle{ \mathbf {Q} }[/math] is the eigenvectors of [math]\displaystyle{ \mathbf{H^{-1} M_D (H^{-1})^T} }[/math] associating with [math]\displaystyle{ \mathbf m }[/math] largest non-zero eigenvalues. That is,
[math]\displaystyle{ (\mathbf{(H^{-1} M_D (H^{-1})^T) Q=Q\Lambda_m} }[/math]
Considering [math]\displaystyle{ \mathbf {Q=H^TW} }[/math], we have,
[math]\displaystyle{ (\mathbf{(H^{-1} M_D (H^{-1})^T) H^TW=H^TW\Lambda_m} }[/math]
So, [math]\displaystyle{ \mathbf{(HH^T)^{-1} M_D W=W\Lambda_m} }[/math], knowing that [math]\displaystyle{ \mathbf {M_S=HH^T} }[/math], we got
[math]\displaystyle{ \mathbf{(M_S)^{-1} M_D W=W\Lambda_m} }[/math]
[math]\displaystyle{ \mathbf {W} }[/math] consists of the eigenvectors of [math]\displaystyle{ \mathbf{(M_S)^{-1} M_D} }[/math] associating with [math]\displaystyle{ \mathbf m }[/math] largest non-zero eigenvalues.
- This optimization problem is related to an old technique called Fischer discriminant analysis(FDA)
Comparison
So far , we have discussed a number of algorithms in metric learning. Xing et al., MCML, CFML, CFML-II, and FDA. Compared to the others, Xing doesn't give a good result, CFML and MCML compete with each other, CFML has a closed form and runs pretty fast, and FDA has a restriction on the rank such that given the number of classes as k, the rank is always equal to k-1.
A very short introduction to Fisher Discriminant Analysis(FDA)
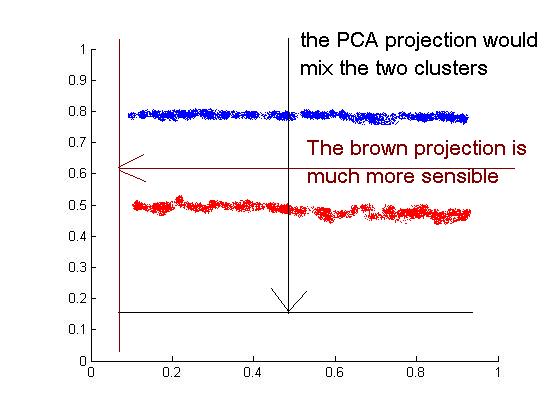
To motivate FDA, let us first consider why PCA, the most famous dimensionality reduction technique, can give terribly bad clustering results.
Consider the following data where we have two clusters of points and we KNOW the labels. Since PCA is an unsupervised algorithm , it makes no use of the labels and simply projects data to the direction with largest variance, which results in a complete mixing of the two clusters. As can be seen intuitively from the figure, a clustering algorithm should projection onto the brow line, which is the direction of least overall variance.
So the question is how to find a projection direction that achieves best clustering. By making use of the given label information, FDA aims to find such a direction by "maximizing between-class scatter" and "minimizing within-class scatter".<ref>Max Welling, Fisher Linear Discriminant Analysis</ref>
"For a general K-class problem, FDA maps the data into a K-1-dimensional space such that the distance between projected class means [math]\displaystyle{ \mathbf {W^T S_B W} }[/math] is maximized while the within class variance [math]\displaystyle{ \mathbf {W^T S_W W} }[/math] is minimized."<ref name="Babak">Babak Alipanahi, Michael Biggs and Ali Ghodsi; Proceedings of the Twenty-Third AAAI Conference on Artificial Intelligence (2008), pp598-603</ref>
Formally, Define the "between-class scatter matrix" [math]\displaystyle{ S_B }[/math] and "within-class scatter matrix" [math]\displaystyle{ S_W }[/math] as follows.
[math]\displaystyle{ \mathbf{S_B = \sum_c N_c(\mu_c - \mu)(\mu_c - \mu)^T, S_W = \sum_c \sum_{x_i \in c} (x_i - \mu_c)(x_i - \mu_c)^T} }[/math]
where the subscript [math]\displaystyle{ c }[/math] represents a class, [math]\displaystyle{ \mu_c }[/math] represents within-class mean, [math]\displaystyle{ \mu }[/math] represents overall mean and [math]\displaystyle{ x_i }[/math] represents a generic data point, [math]\displaystyle{ N_c }[/math] is the number of data points in class [math]\displaystyle{ c }[/math].
It is obvious from the formula that [math]\displaystyle{ S_B }[/math] is larger when the class means are more separated and [math]\displaystyle{ S_W }[/math] is larger when each class is more separated.
Now the FDA objective is to find the projection directions [math]\displaystyle{ \mathbf {W} }[/math] that maximizes
[math]\displaystyle{ \mathbf{J(W) = \frac{W^T S_B W}{W^T S_W W}} }[/math]
which is equivalently to maximize [math]\displaystyle{ \mathbf{Trace(\frac{W^T S_B W}{W^T S_W W})} }[/math].
The optimal solution for [math]\displaystyle{ \mathbf {W} }[/math] consists of the eigenvectors of [math]\displaystyle{ \mathbf {(S_W)^{-1}S_B} }[/math] associating with [math]\displaystyle{ \mathbf {m\lt K} }[/math] largest eigenvalues.
It is interesting that this result is closely related to what we have in CFML-II with [math]\displaystyle{ \mathbf {(M_S)^{-1}M_D} }[/math]
"It can be shown that these two methods yield identical results in the binary class problem when both classes have the same number of data
points" <ref name="Babak"/>
Using partial distance side information <ref name="Ali Ghodsi"/>
In this case, only partial distances are known i.e. we are given exact distances between some pairs of points.
Suppose a set of similarities is given: [math]\displaystyle{ S : (x_i, x_j) \in S }[/math] if the target distance [math]\displaystyle{ d_{ij} }[/math] is known, then the cost function that preserves the local distnces is:
[math]\displaystyle{ \min_{\mathbf A} \sum_S\|\|x_i-x_j\|_A^2-d_{ij}\|^2 }[/math] s.t [math]\displaystyle{ \mathbf A \succeq 0 }[/math]
The above function can be written as:
[math]\displaystyle{ L(A)=\min_{\mathbf A} \sum_S\|vec(A)^T vec(B_{ij})-d_{ij}\|^2 }[/math]
[math]\displaystyle{ L(A)=\min_{\mathbf A} \sum_S(vec(A)^T vec(B_{ij})vec(B_{ij})vec(A)+d_{ij}^2)-2d_{ij}vec(A)^Tvec(B_{ij}) }[/math]
where, [math]\displaystyle{ B_{ij}=(x_i-x_j)(x_i-x_j)^T }[/math] and as [math]\displaystyle{ d_{ij}^2 }[/math] is independent of A, it can be dropped.
Therefore, the loss function is:
[math]\displaystyle{ L(A)=vec(A)^T[Qvec(A)-2R] }[/math] where, [math]\displaystyle{ Q=\sum_S vec(B_{ij})vec(B_{ij})^T }[/math] and [math]\displaystyle{ R=\sum_S d_{ij}vec(B_{ij}) }[/math]
The above loss function being in the quadratic form, semi definite programming can not be applied. It can be converted to a linear function using 'Shur Complement.'
Shur Complement
[math]\displaystyle{ \begin{bmatrix} \mathbf X & \mathbf Y \\ \mathbf {Y^T} & \mathbf Z\end{bmatrix}\succeq 0 }[/math] if and only if [math]\displaystyle{ \mathbf {Z-Y^TX^{-1}Y}\succeq 0 }[/math]
By decomposing [math]\displaystyle{ \mathbf {Q = S^TS} }[/math], a matrix of the form
[math]\displaystyle{ J =\begin{bmatrix} I & Svec(A)\\(Svec(A))^T &2vec(A)^TR + t\end{bmatrix} }[/math] is constructed. By the Schur complement, if [math]\displaystyle{ J \succeq 0 }[/math], then the following relation holds
[math]\displaystyle{ \mathbf {2vec(A)^TR + t}- \mathbf {vec(A)^T S^T Svec(A)} \succeq 0 }[/math]
Scalar [math]\displaystyle{ \mathbf t }[/math] is an upper bound on the loss and therefore,
[math]\displaystyle{ \mathbf {vec(A)^T S^T Svec(A) }-\mathbf { 2vec(A)^TR} = \mathbf {vec(A)^TQvec(A)}-\mathbf{ 2vec(A)^TR} \lt = \mathbf t }[/math]
Therefore, minimizing t subject to [math]\displaystyle{ J \succeq 0 }[/math]also minimizes the objective. This optimization problem can be readily solved
by standard semidefinite programming software
[math]\displaystyle{ \min_A \mathbf t }[/math] s.t. [math]\displaystyle{ \mathbf A \succeq 0 }[/math]and [math]\displaystyle{ \mathbf J \succeq 0 }[/math]
June 16th
Nonnegative Matrix Factorization (NMF)
PCA can be seen as a way of matrix decomposition. Even if A is a nonnegative matrix, there is no guarantee that the 2 decompsed matrix (W, H) are non-negative. In other words, assume [math]\displaystyle{ A }[/math] is our data matrix with columns representing each data point. A matrix factorization of [math]\displaystyle{ A_{m\times n} \approx W_{m\times k}H_{k\times n} }[/math], in general, can be thought as a way of expressing columns of A as a weighted sum of [math]\displaystyle{ k }[/math] bases ([math]\displaystyle{ k \leq \min(m,n) }[/math]). The [math]\displaystyle{ k }[/math] bases are, in fact, columns of [math]\displaystyle{ W }[/math] and the weights corresponding to the [math]\displaystyle{ i }[/math]th data point are located in the [math]\displaystyle{ i }[/math]th column of matrix [math]\displaystyle{ H }[/math].
As known, PCA or equivalently SVD gives matrices [math]\displaystyle{ W }[/math] and [math]\displaystyle{ H }[/math] satisfying the following optimiztion constraint:
[math]\displaystyle{ \min_{W,H} \|A-WH\|^2 }[/math]
In the above factorization, matrix [math]\displaystyle{ A }[/math] and the output matrices [math]\displaystyle{ W }[/math] and [math]\displaystyle{ H }[/math] in general may have negative or non-negative entries.
However, there are many applications in which matrix [math]\displaystyle{ A }[/math] has only non-negative entries. Examples are images, word frequency vector of texts, DNA microarrays and music notes. In these applications, it would be helpful to impose non-negative constrains on the [math]\displaystyle{ W }[/math] and [math]\displaystyle{ H }[/math] matrices above. Summarily speaking, we want to factorize nonnegative matrix A into two non-negative matrices, [math]\displaystyle{ W }[/math] and [math]\displaystyle{ H }[/math], such that [math]\displaystyle{ A \approx WH }[/math]. Nonnegative means all entries in the matrix are non-negative. So NMF, in a sense, is similar to Singular Value Decomposition (SVD), but SVD does not guarantee non-negative entries.
The non-negativity of both [math]\displaystyle{ W }[/math] and [math]\displaystyle{ H }[/math] is meaningful here. For example, in the image example, non-negativity of [math]\displaystyle{ W }[/math] implies that the columns of [math]\displaystyle{ W }[/math] (the bases) may be interpreted as images. On the other, non-negativity of entries in matrix [math]\displaystyle{ H }[/math] implies the weights of reconstruction of each data point are non-negative. An important implication of this is that we may reconstruct the original data points using a (non-negative) summation of some non-negative bases, which means we will have a purely additive reconstruction. We may note that one way (not the only way) to have an additive reconstruction is to add parts of the objects under consideration to form the original points. Based on this, NMF induces the idea of learning parts or segments of the objects which is a pretty important concept<ref name="Lee Seung"/>.
As mentioned, for some applications we may require/prefer non-negative entries. e.g. in face/image data we may want our image intensities to be non-negative. It makes sense to interpret an image reconstruction as adding a set of images with non-negative intensities.
Nonnegative rank - Started from 1989 (Gregory and Pullman).
History
NMF became popular with the publication of the work of Lee and Seung in 1999 <ref name="Lee Seung">
D. Lee, and H. S. Seung, Learning the parts of objects by non-negative matrix factorization. Nature 401, 788-791 (21 October 1999). </ref>.
They presented an algorithm for NMF capable of learning parts of faces and semantic features of text, which is in contrast to other methods, such as PCA and vector quantization, that learn holistic, not parts-based, representations.This is because of the different constraints imposed upon the matrices W and H respectively.
In vector quantization (VQ), each column of H is constrained to be a unary vector, that is only elemant has a value equal to unity and all other elemants are zero. This results in a face being reconstructed from a single basis vector and also forces the algorithm to learn images that are basically the prototypical faces.
PCA overcomes this unary constraint of VQ. It gives a distributed representation in which a face is reconstructed as a linear combination of all the basis images, also called eigenfaces. PCA imposes the onstraints that W should be orthonormal,i.e. each column of W should be orthogonal to each other and should also be of unit length; whereas the matrix H is just orthogonal. Though these eigenfaces reflect the directions of variations, many of them do not have intutive interpretation. This is becuase the matrices W and H can have both positive and negative elements.
In NMF, W and H are imposed with the constraint of being non negative. This still results in a face being recontructed from multiple basis images instead of just one as in VQ, but it also has sparse distribution than PCA. Also, in contrast to PCA only additive operations occur (W and H being positive), no subtractions occur and this relates well to the notion of combining parts to form a whole.
The figure below shows the difference between the three kinds of factorization for images:
File:image.jpeg
Adapted from <ref name="Lee Seung">
D. Lee, and H. S. Seung, Learning the parts of objects by non-negative matrix factorization. Nature 401, 788-791 (21 October 1999). </ref>.
Applications
DNA microarray experiments (Ilmels and Barkai, 2003) using gene expression data.
Retrieve notes from an audio recording of polyphonic music (Smaragdis and Brown, 2003).
====Learn Semantic features of text<ref name="Lee Seung">
D. Lee, and H. S. Seung, Learning the parts of objects by non-negative matrix factorization. Nature 401, 788-791 (21 October 1999). </ref>.====
In this appication, a corpus of documents is represented y a term frequency matrix, where each column represents a document and each row is a term/word in the documents. An entry in this matrix is theconssists of frequency of the word in a document. The NMF of this data matrix gives two matrices, W and H. Each column of W is a set of similar words and each column of H is a set od similar documents. In a way, it results in bi-clustering. In addition to grouping semantically related words into semantic features, the algorithm can also differentiate between different meanings of the same word.
An example is shown below:
File:textcorpus.jpeg
Adapted from <ref name="Lee Seung">
D. Lee, and H. S. Seung, Learning the parts of objects by non-negative matrix factorization. Nature 401, 788-791 (21 October 1999). </ref>.
NMF For Polyphonic Music Transcription
To explain how NMF can be used to transcribe polyphonic music, we'll proceed as follows.
1. Explain the concept of magnitude spectrum.
2. Explain how to encode a musical time series into a matrix [math]\displaystyle{ X }[/math].
3. Explain the meaning of the NMF factor matrices [math]\displaystyle{ W }[/math] and [math]\displaystyle{ H }[/math], where [math]\displaystyle{ X \approx WH }[/math]
magnitude spectrum
A magnitude spectrum is just a plot of magnitude against spectrum at a particular moment.
encoding
Let's say we have a musical time series with a duration of 10 seconds. The first step of encoding is to sample the time series at equidistant points in time. For example, we can taken L=101 samples so that successive sample points are separated by 0.1 second. For each sample point in time, we obtain a magnitude spectrum which we can sample at particular frequency; let's say we sample at 500 frequencies. We can now encode the musical time series into a non-negative matrix [math]\displaystyle{ X }[/math] with 500 rows(different frequencies) and 101 columns(different time points) where each entry corresponds to the magnitude(which is non-negative) of the corresponding frequency at the corresponding moment.
Meanings of the NMF Factor
Please refer to <ref>Paris Smaragdis, Judith C. Brown: Non-Negative Matrix Factorization for Polyphonic Music Transcription</ref> for more details of this example and the above encoding process.
Consider the following musical scale which contains four different notes(pitches)
and its rank-4 NMF factors.
We see that each row of [math]\displaystyle{ H }[/math] corresponds to the temporal activity of the four notes.
(Row1: the 4th note; Row2: the 1st note; Row3: the 3rd note and the 5th note; Row4: the 2nd note)
Also, each column of [math]\displaystyle{ W }[/math] corresponds to the spectrum of each note. By looking at the lowest significant frequency from each of the columns of [math]\displaystyle{ W }[/math] which are 193.7Hz, 301.4Hz, 204.5Hz and 322.9 Hz, we can determine that they correspond to the notes [math]\displaystyle{ F^{\sharp}_3, D_4, G_3 }[/math] and [math]\displaystyle{ E^{\flat}_4 }[/math] respectively.
NMF Algorithms
Alternate updates to [math]\displaystyle{ W }[/math] and [math]\displaystyle{ H^T }[/math] using an ascent direction (Lee and Seung).
Want to minimise [math]\displaystyle{ ||A - WH^T||_F }[/math] - linear least squares for either [math]\displaystyle{ W }[/math] or [math]\displaystyle{ H }[/math] if the other is fixed.
Alternatively use an [math]\displaystyle{ L^1 }[/math] penalty term to enhance sparsity (Kim and Park).
NMF with sparseness constraint <ref>Hoyer O. Patrik; Non-negative Matrix Factorization with Sparseness Constraints, Journal of Machine Learning Research 5 (2004) 1457–1469</ref>
In this paper, they incorporate sparseness constraints into NMF, to overcome the problem that NMF sometimes does not give a parts based linear representation.
In the original algorithm the sparseness is a side effect and not a objective and there is no means by which the sparseness of the representation could be controlled. Therefore, a sparseness constraint was apllied to NMF.
Sparseness means that only a few units can be used to represent a typical data vectors. It follows that most of the units are zero and only some of them have non zero/positive values. Thus, a sparsest possible vector would be a vector containing only one non zero element and it should have a sparseness of one, whereas vectors in which most of the elements are non zero or equal should have a sparseness of zero.
A sparseness measure based on the relationship between the L1 norm and the L2 norm was used:
[math]\displaystyle{ sparseness(x) = \frac{\sqrt{n}-(\sum |x_i|)/\sqrt{\sum {x_i}^2}}{\sqrt{n}-1} }[/math],
where n is the dimensionality of x. x is a vector. This function evaluates to unity if and only if x contains only a
single non-zero component, and takes a value of zero if and only if all components are equal, interpolating smoothly between the two extremes.
The algorithm proposed is as follows:

Observations
Leading singular vectors of a nonnegative matrix are nonnegative. Used as the basis for R1D (rank-1 downdate).
Simple rank-1 NMF using SVD. Gives rank-1 approximation of [math]\displaystyle{ A }[/math].
Rows and columns of [math]\displaystyle{ A }[/math] can be clustered using singular vectors. If there are similar entries in [math]\displaystyle{ U }[/math], there will be corresponding similar rows in [math]\displaystyle{ A }[/math]. Likewise, similar entries in [math]\displaystyle{ V }[/math] correspond to similar columns of [math]\displaystyle{ A }[/math]. i.e. [math]\displaystyle{ U }[/math] and [math]\displaystyle{ V }[/math] can be though of as lower dimensional representations of the rows and columns, respectively, of [math]\displaystyle{ A }[/math].
Rank One Downdate(R1D)
As mentioned above, similar to any other factorization of the form [math]\displaystyle{ A\approx WH^T }[/math], NMF is a way to represent the original matrix [math]\displaystyle{ A }[/math] as a summation of [math]\displaystyle{ k }[/math] rank-1 matrices:
[math]\displaystyle{ A_{m\times n}=W_{m \times k}(H_{n\times k})^T=W(:,1)H(:,1)^T+...+W(:,k)H(:,k)^T \qquad \qquad (1) }[/math]
where [math]\displaystyle{ W(:,i) }[/math] and [math]\displaystyle{ H(:,i) }[/math] denote the [math]\displaystyle{ i }[/math]th column of [math]\displaystyle{ W }[/math] and [math]\displaystyle{ H }[/math], respectively. Note that here we have used [math]\displaystyle{ H^T }[/math] instead of [math]\displaystyle{ H }[/math] in our factorization. In many practical situation, it turns out that the above rank-1 components may not considerably overlap each other. Based on this, an idea to decompose matrix [math]\displaystyle{ A }[/math] would be trying to find rank-1 submatrices in [math]\displaystyle{ A }[/math] and use them to construct the [math]\displaystyle{ k }[/math] terms presented in the right-hand side of (1).
Let [math]\displaystyle{ M }[/math] be a subset of [math]\displaystyle{ \{1,...,m\} }[/math] and [math]\displaystyle{ N }[/math] be a subset of [math]\displaystyle{ \{1,...,n\} }[/math]. Following the methodology of Matlab software, we use [math]\displaystyle{ A(M,N) }[/math] to represent that submatrix of [math]\displaystyle{ A }[/math] which consists of columns [math]\displaystyle{ M }[/math] and rows [math]\displaystyle{ N }[/math] of [math]\displaystyle{ A }[/math]. We try to find the submatrix [math]\displaystyle{ A(M,N) }[/math] maximizing the following objective function:
[math]\displaystyle{ f(M,N,\mathbf{u},\sigma,\mathbf{v})=\| A(M,N)\|^2-\gamma \|A(M,N)-\mathbf{u}\sigma\mathbf{v}^T\|^2 }[/math]
where [math]\displaystyle{ \mathbf{u}\in \mathbf{R}^m }[/math] and [math]\displaystyle{ \mathbf{v}\in \mathbf{R}^n }[/math] are unit column vectors and [math]\displaystyle{ \sigma }[/math] is a scalar selected in away that [math]\displaystyle{ \mathbf{u} \sigma \mathbf{v}^T }[/math] best approximate submatrix [math]\displaystyle{ A(m,n) }[/math]. This selection indeed minimizes the second (Frobenius) norm in the objective function presented above. Based on this objective function, we favor large submatrices of [math]\displaystyle{ A }[/math] (term 1) which may be well approximated by a rank-1 matrix (term 2). (vectors [math]\displaystyle{ \mathbf{u} }[/math], [math]\displaystyle{ \mathbf{v} }[/math] and [math]\displaystyle{ \sigma }[/math], in fact, singular vectors and sigular value of the submatrix [math]\displaystyle{ A(m,n) }[/math]. However, as mentioned in the next section, it would be helpful to (more basically) think of them as the quantities minimizing the error [math]\displaystyle{ \|A(M,N)-\mathbf{u}\sigma\mathbf{v}^T\|^2 }[/math])
The method how to solve this optimization problem this will be described later. After finding such submatrix, we can use vectors [math]\displaystyle{ \mathbf{u} }[/math] and [math]\displaystyle{ \mathbf{v} }[/math] to obtain the first term in the right-hand side of equation (1), that is, to find [math]\displaystyle{ W(:,1) }[/math] and [math]\displaystyle{ H(:,1) }[/math]. After that, we vanish the entries corresponding to [math]\displaystyle{ A(m,n) }[/math] in the original matrix. We may perform the same process again and again to obtain other terms in the right-hand side of equation (1). A summary of this algorithm is presented in the following<ref name="R1D"/>:

Finding the solution to the objective function
Unfortunately, this optimization problem is conjectured to be an NP-hard one. However, the configuration of this objective function allows us to use a fast heuristic algorithm to solve it. To do so, we note that the objection function in (1) is separable in rows (and in columns). To explain this, assume at one point the subset [math]\displaystyle{ N }[/math] of columns and the vector [math]\displaystyle{ \mathbf{v} }[/math] are given. So we need to determine the optimum subset [math]\displaystyle{ M }[/math] of rows and the optimum vector [math]\displaystyle{ \mathbf{u} }[/math]. We note that this job can be done by examining each row of matrix in isolation and decide whether this row should be included in the desired submatrix [math]\displaystyle{ A(m,n) }[/math] or not. To do so, we note that the contribution of the [math]\displaystyle{ i }[/math]th row of [math]\displaystyle{ A }[/math], i.e., [math]\displaystyle{ A(i,N) }[/math], is given by:
[math]\displaystyle{ f_i=\|A(i,N)\|^2-\gamma\|A(i,N)-\beta_i\mathbf{v}^T\|^2 \qquad \qquad (2) }[/math]
where [math]\displaystyle{ \beta_i=u_i\sigma }[/math]. It can be easily shown that he value of [math]\displaystyle{ \beta_i }[/math] maximizing (2) is [math]\displaystyle{ A(i,N)\mathbf{v} }[/math], which can be obtained by solving a simple least square problem. So that maximum possible contribution of the [math]\displaystyle{ i }[/math]th row would be:
[math]\displaystyle{ f_i=\|A(i,N)\|^2-\gamma\|A(i,N)-A(i,N)\mathbf{v}\mathbf{v}^T\|^2 }[/math]
So to decide whether to include the [math]\displaystyle{ i }[/math]th row in the desired submatrix or not we may just check if [math]\displaystyle{ f_i\gt 0 }[/math] or not. If [math]\displaystyle{ f_i\gt 0 }[/math], we have to include the [math]\displaystyle{ i }[/math]th row as it can have a positive contribution to the objective function given in (1).
The form for [math]\displaystyle{ f_i }[/math] can be simplified as:
[math]\displaystyle{ =A(i, N)A(i, N)^T - \gamma|A(i, N)A(i, N)^T+A(i,N)vv^Tvv^TA(i, N)^T
- 2A(i,N)vv^TA(i, N)^T] }[/math]
[math]\displaystyle{ =A(i, N)A(i, N)^T - \gamma|A(i, N)A(i, N)^T - A(i,N)vv^TA(i, N)^T] }[/math]
[math]\displaystyle{ =-(\gamma - 1)A(i, N)A(i, N)^T + \gamma A(i,N)vv^TA(i, N)^T=-(\gamma-1)A(i,N)A(i,N)^T+\gamma(A(i,N)\mathbf{v})^2 }[/math]
Now, dividing by [math]\displaystyle{ (\gamma - 1) }[/math] we get:
[math]\displaystyle{ -A(i, N)A(i, N)^T + \frac{\gamma} {\gamma-1} (A(i,N)\mathbf{v})^2 }[/math]
[math]\displaystyle{ -A(i, N)A(i, N)^T + \bar{\gamma} (A(i,N)\mathbf{v})^2 }[/math]
if this is positive, row i will be put in set M. The same strategy can be applied when we know M and u instead of N and v. It can be easily seen that after taking each step of this process, the value of the objective function given in (1) does not decrease. Based on this, convergence to a local maximal state is guaranteed here.
A summary of this algorithms is given below<ref name="R1D">
M. Biggs, A. Ghodsi, and S. Vavasis. Nonnegative matrix factorization via rank-one
downdating. 2007.</ref>. In this algorithm, [math]\displaystyle{ \bar{\gamma} }[/math] is defined as [math]\displaystyle{ \gamma/(\gamma-1) }[/math].

Clustering Using NMF <ref>Tao Li and Colleagues:Solving consensus and semi-supervised clustering problems using NMF, 7th IEEE 2007</ref>
Tao Li and colleagues (2007) showed that NMF can be used to solve many of other kinds of optimization problems. for example; Kernel K-Means Clustering, Normalized Cut Spectral Clustering, and Semi-Supervised Clustering, as optimization problems, lead to the same optimization equations as NMF.
K-Means Clustering
Suppose [math]\displaystyle{ (p^{1},p^{2},...,p^{k}) }[/math] are different clustering of [math]\displaystyle{ X={x_{1},x_{2},...,x_{n}} }[/math] for which [math]\displaystyle{ p^{t}=(C_{1},C_{2},...,C_{k}) }[/math] where [math]\displaystyle{ C_{1}'s }[/math] are clusters and [math]\displaystyle{ X=\cup_{j=1}^{k}C_{j} }[/math].
If we define Connectivity Matrix for clustering [math]\displaystyle{ P^{t} }[/math] as follow;
[math]\displaystyle{ M_{ij}=1 }[/math] if [math]\displaystyle{ (i,j) }[/math] are both in [math]\displaystyle{ C_{k}(P^{t}) }[/math] and [math]\displaystyle{ M_{ij}=0 }[/math] otherwise
for any pair of nods, and let [math]\displaystyle{ {M}_{ij}^{*}=\frac{1}{T}\sum_{t=1}^{T} M{ij}(P^{t}) }[/math], then members of Connectivity matrix can be considered as similarity values (Kernel),because [math]\displaystyle{ M_{ij}=1 }[/math] means [math]\displaystyle{ i }[/math] and [math]\displaystyle{ j }[/math] are belong to the same cluster in clustering [math]\displaystyle{ p^{t} }[/math]
Now considering [math]\displaystyle{ W }[/math] as the matrix of pairwise similarities, equivalence of Symmetric NMF and K-Means Clustering will be clear.
Normalized Cut Spectral(NCS) Clustering
if we let [math]\displaystyle{ W^{*}=D^{-1/2}W D^{-1/2} }[/math] and [math]\displaystyle{ D=diag(d_{1},d_{2},...,d_{n}) }[/math] where [math]\displaystyle{ d_{i}=\sum W_{ij} }[/math] optimization problem for this NCS clustering will be equivalent to NMF optimization.
Semi-supervised Clustering
If we define A as our label matrix for nods those can be in a same cluster and B for nods those can not be in same cluster, then Tao Li and colleagues show that the optimization equation will be
[math]\displaystyle{ Max Tr(H^{T}WH + /alpha H^{T}AH)- /beta H^{T}BH) }[/math] ,[math]\displaystyle{ H^{T}H=I , H^{T}\geq0 }[/math]
where [math]\displaystyle{ H=(h_{1},h_{2},...,h_{k}) }[/math] and [math]\displaystyle{ h_{k}=\frac{1}{n_{k}}(0,...,0,1,1,...,1,0,0...,0) }[/math]
to find the NMF Based Algorithm They proposed [math]\displaystyle{ W^{+}=W+\alpha A }[/math] and [math]\displaystyle{ W^{-}=\beta B }[/math]
so the optimization equality is
[math]\displaystyle{ Max Tr(H^{T}(W^{+}-W^{-})H) }[/math] , ,[math]\displaystyle{ H^{T}H=I , H^{T}\geq0 }[/math]
from the mathematical relationship of Trace and Norm it is easy to show that optimization changes to
[math]\displaystyle{ ||(W^{+}-W^{-})-HH^{T}||^{2} }[/math]
June 18th
Applications
Page Rank
Google have used this in the search engine industry. Althought they haven't published the current algorithm they are using know, the first paper explainig their page rank algorithm can be brought as an applicationm of power method. This algorithm is based on the followings:
Have [math]\displaystyle{ n }[/math] webpages. Basic idea is that a page is important if it has been linked to by many webpages. However, different links have different weights. Some have higher importance, depending on the importance (or the rank) of the linking page. There is lower importance on the link if the linking page has many outgoing links (such as a 411 directory).
More formally, define the rank of the page [math]\displaystyle{ i }[/math] as [math]\displaystyle{ P_i }[/math].
[math]\displaystyle{ L_{i,j}= \left\{\begin{matrix} 1 & \text{if } j \text{ points to } i \\ 0 & \text{otherwise} \end{matrix}\right. }[/math]
[math]\displaystyle{ c_j }[/math] is the number of outgoing links. [math]\displaystyle{ c_j = \sum_{i=1}^n L_{ij} . }[/math]
Calculate page rank as [math]\displaystyle{ P_i = (1 - d) + d \sum_{j=1}^n \frac{L_{ij}}{c_j}P_j }[/math], where [math]\displaystyle{ d = 0.85 }[/math].
Alternatively, in matrix form [math]\displaystyle{ \mathbf{P} = (1 - d) \mathbf{e} + d \mathbf{LD}^{-1}\mathbf{P} }[/math]. Where [math]\displaystyle{ \mathbf{e} }[/math] is an [math]\displaystyle{ n \times 1 }[/math] vector of ones, [math]\displaystyle{ \mathbf{L} }[/math] is an [math]\displaystyle{ n \times n }[/math] matrix, and [math]\displaystyle{ \mathbf{D} }[/math] is a diagonal matrix of [math]\displaystyle{ c_1, \ldots, c_n }[/math].
Assume that [math]\displaystyle{ \mathbf{e}^{T}\mathbf{P} = n \rightarrow \frac{\mathbf{e}^{T}\mathbf{P}}{n} = 1 }[/math].
[math]\displaystyle{ \mathbf{P} = (1 - d) \mathbf{e} \frac{\mathbf{e}^{T}\mathbf{P}}{n} + d \mathbf{LD}^{-1}\mathbf{P} }[/math]
[math]\displaystyle{ \mathbf{P} = [(1 - d) \frac{\mathbf{e} \mathbf{e}^{T}}{n} + d \mathbf{LD}^{-1}]\mathbf{P} }[/math]
[math]\displaystyle{ \mathbf{P} = \mathbf{A}\mathbf{P} }[/math]
And so [math]\displaystyle{ \mathbf{P} }[/math] is an eigenvector of [math]\displaystyle{ \mathbf{A} }[/math] corresponding to an eigenvalue equal to [math]\displaystyle{ 1 }[/math]. The largest eigenvalue of [math]\displaystyle{ \mathbf{A} }[/math] will be the unique, real eigenvalue equal to [math]\displaystyle{ 1 }[/math]. Therefore, we can solve this problem by power method so that:
[math]\displaystyle{ \mathbf{P} = P_0 }[/math]
[math]\displaystyle{ \mathbf{P_{k+1}} = AP_k }[/math]
[math]\displaystyle{ \mathbf{P_{k}} = \frac{nP_k}{e^Tp} }[/math]
we can see this page rank as a model of user behaviuor in a way of
- Thinking of web-surifng as random-walk
- Thinking of the process as a Markov-Chain
- Page rank is stationary distribution of a Markov Chain. That's why the largest eigen value is one and it can be shown that this chain is :
- irreducible
- ergodic(recurrent, apreiodic, and non-null) which are the conditions of Markov-Chain convergence.
Interpreting as a Markov Chain, this eigenvector, and thus the page rank, is the stationary distribution of the Markov Chain.
The term [math]\displaystyle{ (1-d) }[/math] in the equation above can be seen as the probability of jumping to a page that does not have any links.
Definitions of some Markov chain terminologies
A Markov chain is said to be irreducible if it is possible to get to any state from any state. Formally, this means
[math]\displaystyle{ \forall i, j \, \exists n \in \mathbb{N} \, s.t. \, \Pr(X_n=j|X_0=i)\gt 0 }[/math].
A state i is aperiodic if returns to it can occur at irregular times. Formally, this means
[math]\displaystyle{ \operatorname{gcd}\{ n: \Pr(X_n = i | X_0 = i) \gt 0\} = 1 }[/math]
A Markov chain is aperiodic if all of its states are aperiodic.
A state i is positive recurrent if its expected first returning time is finite. Formally, this means
[math]\displaystyle{ E[\inf \{ n\ge1: X_n = i | X_0 = i\}] \lt \infty }[/math]
A Markov chain is positive recurrent if all of its states are positive recurrent.
A state i is ergodic if it is aperiodic and positive recurrent. A Markov chain is ergodic if all of its states are ergodic.
It can be shown that a finite state Markov chain(e.g. the Google matrix) is ergodic if it is both irreducible and aperiodic.
Example
Consider the 4 web pages below and the links between them represented by arrows.
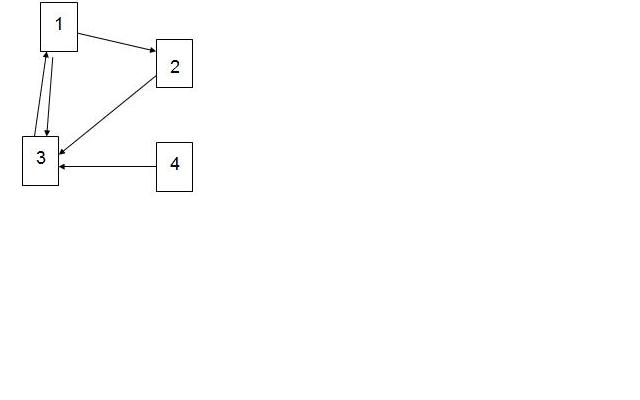
The L matrix is given as:
[math]\displaystyle{ \mathbf L= \begin{bmatrix} 0&0&0&1\\1&0&0&0\\1&1&0&1\\0&0&0&0 \end{bmatrix} }[/math]
The diagonal matrix D is:
[math]\displaystyle{ \mathbf D= \begin{bmatrix} 2&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1 \end{bmatrix} }[/math]
Then matrix A is computed using the formula:
[math]\displaystyle{ \mathbf A = [(1 - d) \frac{\mathbf{e} \mathbf{e}^{T}}{n} + d \mathbf{LD}^{-1}] }[/math] where, d=0.85
P is the eigenvector of A corresponding to the eigenvalue of 1.0
[math]\displaystyle{ \mathbf P= \begin{bmatrix} 0.6447\\0.3389\\0.6821\\0.0649 \end{bmatrix} }[/math]
Thus, page 3 has the highest rank, followed by page 1 and page 2, whereas page 4 has the lowest rank.
Sensor Localization
Suppose we have some sensors all over a certain are like a city or a country so that the sensors can identify the distance between them and their nearby neighbors. The problem is how localizing the sensors subject to the local distance constraints. In the word of dimensionality reduction, we should find a low-dimensional embedding (2,3 dimensions) subject to te local constraints.
This can be done using either:
- MVU
[math]\displaystyle{ \mathbf max Tr(k) }[/math]
[math]\displaystyle{ \mathbf |x_i - x_j|^2 = d_{ij} }[/math] if [math]\displaystyle{ \eta_{ij} \gt 0 }[/math]
- LLE
Random Projection
Dimensionality Reduction for Supervised Learning with Reproducing Kernel Hilbert Spaces
Dimensionality Reduction for Supervised Learning with Reproducing Kernel Hilbert Spaces
Measuring Statistical Dependence with Hilbert-Schmidt Norm
Measuring Statistical Dependence with Hilbert-Schmidt Norm
Sparse PCA
A direct formulation for sparse PCA using semidefinite programming
Neighbourhood Components Analysis
Neighbourhood Components Analysis
Learning Spectral Clustering, With Application To Speech Separation
Learning Spectral Clustering, With Application To Speech Separation
Learning a Nonlinear Embedding by Preserving Class Neighborhood Structure
Learning a Nonlinear Embedding by Preserving Class Neighborhood Structure
Independent Component Analysis: algorithms and applications
Independent Component Analysis: algorithms and applications
Visualizing Similarity Data with a Mixture of Maps
Visualizing Similarity Data with a Mixture of Maps
Convex and Semi Nonnegative Matrix Factorization
Convex and Semi Nonnegative Matrix Factorization
Graph Laplacian Regularization for Larg-Scale Semidefinite Programming
Graph Laplacian Regularization for Larg-Scale Semidefinite Programming
References
<references/>