convex and Semi Nonnegative Matrix Factorization
In the paper ‘Convex and semi non negative matrix factorization’, Jordan et al <ref name='Ding C'> Ding C, Li. T, and Jordan I. M; “Convex and semi nonnegative matrix factorization”. </ref> have proposed new NMF like algorithms on mixed sign data, called Semi NMF and Convex NMF. They also show that a kernel form of NMF can be obtained by ‘kernelizing’ convex NMF. They explore the connection between NMF algorithms and K means clustering to show that these NMF algorithms can be used for clustering in addition to matrix approximation. These new variants of algorithm thereby, broaden the application areas of NMF algorithm and also provide better interpretability to matrix factors.
Introduction
Nonnegative matrix factorization (NMF), factorizes a matrix X into two matrices F and G, with the constraints that all the three matrices are non negative i.e. they contain only positive values or zero but no negative values, such as: [math]\displaystyle{ X_+ \approx F_+{G_+}^T }[/math] where ,[math]\displaystyle{ X \in {\mathbb R}^{p \times n} }[/math] , [math]\displaystyle{ F \in {\mathbb R}^{p \times k} }[/math] , [math]\displaystyle{ G \in {\mathbb R}^{n \times k} }[/math]
The least square objective function of NMF is: [math]\displaystyle{ \mathbf {E(F,G) = \|X-FG^T\|^2} }[/math]
It has been shown that it is a NP hard problem and is convex in only F or only G but not convex in both F and G simultaneously <ref name='S. S Lee'> Lee S. S and Seung S. H; “Algorithms for Non-negative Matrix Factorization”. </ref> Also, the factors F and G are not always sparse and many different sparsification schemes have been applied to NMF.
Semi NMF
In semi NMF, the matrix G is constrained to be nonnegative whereas the data matrix X and the basis vectors of F are unconstrained, that is:
[math]\displaystyle{ X_{\pm} \approx F_{\pm}{G_+}^T }[/math]
They were motivated to this kind of factorization by K means clustering. The objective function of K means can be written in the form of matrix approximation as follows:
[math]\displaystyle{ J_{K-means} = \sum_{i=1}^n \sum_{k=1}^K g_{ik}||x_i-f_k||^2=||X-FG^T||^2 }[/math]
where, X is a mixed sign data matrix , F represents cluster centroids having both positive and negative entries and G represents cluster indicators having nonnegative entries.
K means clustering objective function can be viewed as Semi NMF matrix approximation with relaxed constraint on G. That is G is allowed to range over values (0, 1) or (0, infinity).
Convex NMF
While in Semi NMF, there is no constraint imposed upon the basis vector F, but in Convex NMF, the columns of F are restricted to be a convex combination of columns of data matrix X, such as:
[math]\displaystyle{ F=(f_1, \cdots , f_k) }[/math]
[math]\displaystyle{ f_l=w_{1l}x_1+ \cdots + w_{nl}x_n = Xw_l = XW }[/math] such that, [math]\displaystyle{ w_{ij}\gt 0 }[/math] [math]\displaystyle{ \forall i,j }[/math]
In this factorization each column of matrix F is a weighted sum of certain data points. This implies that we can think of F as weighted cluster centroids.
Convex NMF has the form: [math]\displaystyle{ X_{\pm} \approx X_{\pm}W_+{G_+}^T }[/math]
As F is considered to represent weighted cluster centroid, the constraint [math]\displaystyle{ \sum _{i=1}^n w_i = 1 }[/math] must be satisfied. But the authors do not actually state this.
SVD, Convex-NMF and Semi-NMF Comparison
Considering G and F as the result of matrix factorization through SVD, Convex-NMF, and semi-NMF factorizatrion, It can be shown that
Semi-NMF and Convex-NMF factorizations gives clustering results identical to the K-means clustering.
Sharper indicators of the clustering is given by Convex-NMF.
[math]\displaystyle{ \,F_{cnvx} }[/math] is close to [math]\displaystyle{ \,C_{Kmeans} }[/math], however, [math]\displaystyle{ \,F_{semi} }[/math]is not. The intuition behind this is that the restrictions on F can have large effects on subspace factorization
Getting larger residual values, [math]\displaystyle{ \,\|X-FG^T\| }[/math] for Convex-NMF intuitively says that the more highly constrained (Convex-NMF), the more degredation in accuracy.
Algorithms
The algorithms for these variants of NMF are based on iterative updating algorithms proposed for the original NMF, in which the factors are alternatively updated until convergence <ref name='S. S Lee'> Lee S. S and Seung S. H; “Algorithms for Non-negative Matrix Factorization”. </ref>. At each iteration of algorithm, the value for F or G is found by multiplying its current value by some factor. In <ref name='S. S Lee'> Lee S. S and Seung S. H; “Algorithms for Non-negative Matrix Factorization”. </ref>, they prove that by repeatedly applying these multiplicative update rules, the quality of approximation smoothly improves. That is, the update rule guarantees convergence to a locally optimal matrix factorization. In this paper, the same approach has been used by authors to present the algorithms for Semi NMF and Convex NMF.
Algorithm for Semi NMF
As already stated, the factors for semi NMF are computed by using an iterative updating algorithm that alternatively updates F and G till convergence is reached.
- Step 1: Initialize G
- Obtain cluster indicators by K means clustering.
- Step 2: Update F, fixing G using the rule:
[math]\displaystyle{ \mathbf{ F = XG(G^TG)^{-1}} }[/math]
- Step 3: Update G, fixing F using the rule:
[math]\displaystyle{ G_{ik} \leftarrow G_{ik} \sqrt{\frac {{(X^TF)^+}_{ik} + [G(F^TF)^-]_{ik}}{{(X^TF)^-}_{ik} + [G(F^TF)^+]_{ik}}} }[/math]
where, the positive and negative parts of a matrix are separated as: [math]\displaystyle{ {A_{ik}}^{+}=(|A_{ik}|+A_{ik})/2 }[/math] , [math]\displaystyle{ {A_{ik}}^{-}=(|A_{ik}|- A_{ik})/2 }[/math]
and, [math]\displaystyle{ A_{ik}= {A_{ik}}^{+} - {A_{ik}}^{-} }[/math]
Theorem 1: (A) The update rule for F gives the optimal solution to the [math]\displaystyle{ min_F \|X - FG^T\|^2 }[/math], while G is fixed. (B) When F is fixed, the residual [math]\displaystyle{ \|X - FG^T\|^2 }[/math] decreases monotonically under the update rule for G.
Proof:
(Not going to prove the entire theorem but discuss the main parts)
The objective function for semi NMF is: [math]\displaystyle{ J=\|X - FG^T\|^2= Tr(X^TX - 2X^TFG^T + GF^TFG^T) }[/math].
(A).The problem is unconstrained and the solution for F is trivial, given by:
[math]\displaystyle{ dJ/dF = -2XG + 2FG^TG = 0 }[/math]
Therefore, [math]\displaystyle{ F = XG(G^TG)^{-1} }[/math]
(B).This is a constraint problem having an inequality constraint. Because it is a constraint problem, solved by using Lagrange multipliers but the solution for the update rule must satisfy KKT condition at convergence. This implies the correctness of solution. Secondly, the update rule should cause the solution to converge. In the paper, correctness and convergence of update rule is proved as follows:
(i)Correctness of solution:
Lagrange function is: [math]\displaystyle{ L(G) = Tr (-2X^TFG^T + GF^TFG^T - \Beta G^T) }[/math]
where, [math]\displaystyle{ \Beta_{ij} }[/math] are the Lagrange multipliers enforcing the non negativity constraint on G.
Therefore, [math]\displaystyle{ \frac {\part L}{\part G}= -2X^TF + 2GF^TF - \Beta = 0 }[/math]
From complementary slackness condition, [math]\displaystyle{ (-2X^TF + 2GF^TF)_{ik}G_{ik} = \Beta_{ik}G_{ik} = 0. }[/math]
The above equation must be satisfied at convergence.
The update rule for G can be reduced to:
[math]\displaystyle{ (-2X^TF + 2GF^TF)_{ik}{G_{ik}}^2 = 0 }[/math] at convergence.
Both equations are identical and therefore the update rule satisfies the KKT fixed point condition.
(ii)Convergence of the solution given by update rule:
The authors used an auxiliary function approach to prove convergence, as done in <ref name='S. S Lee'> Lee S. S and Seung S. H; “Algorithms for Non-negative Matrix Factorization”. </ref>.
Definition of auxiliary function: A function G(h,h') is called an auxiliary function of F(h) if conditions; [math]\displaystyle{ G (h,h^') \ge F(h) }[/math] and [math]\displaystyle{ G (h,h) = F(h) }[/math] are satisfied.
The auxiliary function is a useful concept because of the following lemma:
Lemma: If G is an auxiliary function, then F is nonincreasing under the update [math]\displaystyle{ \mathbf{ h^{t+1} = \arg \min_h G(h,h^t)} }[/math]
Adapted from <ref name='S. S Lee'> Lee S. S and Seung S. H; “Algorithms for Non-negative Matrix Factorization”.</ref>.
That is, minimizing the auxiliary function [math]\displaystyle{ G(h,h^t) \ge F(h) }[/math] guarantees that [math]\displaystyle{ F(h^{t+1}) \le F(h^t) }[/math] for [math]\displaystyle{ \mathbf {h^{n+1} = \arg \min_h G(h, h^t) } }[/math] <ref name='S. S Lee'> Lee S. S and Seung S. H; “Algorithms for Non-negative Matrix Factorization”.</ref>.
Therefore the authors of the paper, found an auxiliary function and its global minimum for the cost function of Semi NMF.
The cost function for Semi NMF can be written as: [math]\displaystyle{ \mathbf {J(H) = Tr (-2H^TB^{+} + 2H^TB^{-} + HA^{+}H^T + HA^{-}H^T)} }[/math] where [math]\displaystyle{ A = F^TF , B = X^TF , H = G }[/math].
The auxiliary function of J (H) is:
[math]\displaystyle{ Z(H,H') = -\sum_{ik}2{B_{ik}}^{+}H'_{ik}(1+ \log \frac {H_{ik}}{H'_{ik}}) + \sum_{ik} {B^-}_{ik} \frac {{H^2}_{ik}+{{H'}^2}_{ik}}{{H'}_{ik}} + \sum_{ik} \frac {(H'A^{+})_{ik}{H^2}_{ik}}{{H'}_{ik}} - \sum_{ik} {A_{kl}}^{-}{H'}_{ik}{H'}_{il} (1+ \log \frac {H_{ik}H_{il}}{H'_{ik}H'_{il}}) }[/math]
Z (H, H') is convex in H and its global minimum is:
[math]\displaystyle{ H_{ik} = arg \min_H Z(H,H') = H'_{ik}\sqrt {\frac {{B_{ik}}^{+} + (H'A^{-})_{ik}}{{B_{ik}}^{-} + (H'A^{+})_{ik}}} }[/math]
(The derivation of auxiliary function and its minimum can be found in the paper <ref name='Ding C'> Ding C, Li. T, and Jordan I. M; “Convex and semi nonnegative matrix factorization” </ref>.)
Algorithm for Convex NMF
Here, again the factors G and W are computed iteratively by alternative updating until convergence.
- Step 1: Initialize G and W. There are two ways in which the initialization can be done.
- K means clustering: When K means clustering is done on the data set, cluster indicators [math]\displaystyle{ H = (h_1, \cdots , h_K) }[/math]are obtained. Then G is initialized to be equal to H. Then cluster centroids can be computed from H, as [math]\displaystyle{ \mathbf {f_k = Xh_k / n_k} }[/math] or [math]\displaystyle{ F=XH{D_n}^{-1} }[/math] where [math]\displaystyle{ D_n = diag (n_1, \cdots, n_K) }[/math]. And as, in convex NMF: [math]\displaystyle{ F = XW }[/math] , we get [math]\displaystyle{ W=H{D_n}^{-1} }[/math]
- Previous NMF or Semi NMF solution: The factor G is known in this case and a least square solution for W is obtained by solving [math]\displaystyle{ X=XWG^T }[/math]. Therefore, [math]\displaystyle{ W=G(G^TG)^{-1} }[/math]
- Step 2: Update G, while fixing W using the rule
[math]\displaystyle{ G_{ik} \leftarrow G_{ik} \sqrt{\frac {[(X^TX)^+W]_{ik} + [GW^T(X^TX)^-W]_{ik}} {[(X^TX)^-W]_{ik} + [GW^T(X^TX)^+W]_{ik}} } }[/math]
- Step 3: Update W, while fixing G using the rule
[math]\displaystyle{ W_{ik} \leftarrow W_{ik} \sqrt{\frac {[(X^TX)^+G]_{ik} + [(X^TX)^-WG^TG]_{ik}} {[(X^TX)^-G]_{ik} + [(X^TX)^+WG^TG]_{ik}} } }[/math]
The objective function to be minimized for convex NMF is:
[math]\displaystyle{ \mathbf {J=\|X-XWG^T\|^2= Tr(X^TX- 2G^TX^TXW + W^TX^TXWG^TG)} }[/math].
Theorem 2: Fixing W, under the update rule for G, (A) the residual [math]\displaystyle{ \|X - XWG^T \|^2 }[/math] decreases monotonically (non-increasing), and (B) the solution converges to a KKT fixed point.
The correctness and convergence of these rules is demonstrated in a manner similar to Semi NMF by replacing F=XW.
Theorem 3: Fixing G, under the update rule for W, (A) the residual [math]\displaystyle{ \|X - XWG^T \|^2 }[/math] decreases monotonically (non-increasing), and (B) the solution converges to a KKT fixed point.
The correctness is demonstrated by minimizing the objective function with respect to W and then obtaining KKT fixed point condition as:
[math]\displaystyle{ \mathbf {(-X^TXG + X^TXWG^TG)_{ik}W_{ik} = 0 } }[/math]
At convergence, the update rule for W can be shown to satisfy:
[math]\displaystyle{ \mathbf { (-X^TXG + X^TXWG^TG)_{ik}{W_{ik}}^2 = 0 } }[/math]
Therefore, the update rule for W satisfies KKT condition.
Convergence of these rules is demonstrated in a manner similar to Semi NMF by finding an auxiliary function and its global minimum.
Sparsity of Convex NMF
NMF is shown to learn parts based representation and therefore has sparse factors. But there is no means to control the degree of sparseness and many sparsification methods have been applied to NMF in order to obtain better parts based representation <ref name='Ding C'> Ding C, Li. T, and Jordan I. M; “Convex and semi nonnegative matrix factorization” </ref> , <ref name='Simon D. H' > Simon D. H, Ding C, and He X; “On the Equivalence of Nonnegative Matrix Factorization and Spectral Clustering” </ref>. However, in contrast the authors of this paper show that factors of Convex NMF are naturally sparse.
The convex NMF problem can be written as:
[math]\displaystyle{ \min_{W,G \ge 0}||X-XWG^T||^2 = ||X(I-WG^T)||^2= Tr (I-GW^T)X^TX(I-WG^T) }[/math]
by SVD of [math]\displaystyle{ X }[/math] we have [math]\displaystyle{ X = U \Sigma V^T }[/math] and thus, [math]\displaystyle{ X^TX = \sum_k {\sigma _k}^2v_k{v_k}^T. }[/math]
Therefore, [math]\displaystyle{ \min_{W,G \ge 0} Tr (I-GW^T)X^TX(I-WG^T) = \sum_k {\sigma_k}^2||{v_k}^T(I-WG^T)||^2 }[/math] s.t. [math]\displaystyle{ W \in {\mathbb R_+}^{n \times k} }[/math] , [math]\displaystyle{ G \in {\mathbb R_+}^{n \times k} }[/math]
They use the following Lemma to show that the above optimization problem gives sparse W and G.
Lemma: The solution of [math]\displaystyle{ \min_{W,G \ge 0}||I-WG^T||^2 }[/math] s.t. [math]\displaystyle{ W, G \in {\mathbb R_+}^{n \times K} }[/math] optimization problem is given by W = G = any K columns of (e1,…,eK), where ek is a basis vector. [math]\displaystyle{ (e_k)_{i \ne k} = 0 }[/math] , [math]\displaystyle{ (e_k)_{i = k} = 1 }[/math]
According to this Lemma, the solution to [math]\displaystyle{ \min_{W,G \ge 0}\|I - WG^T\|^2 }[/math] are the sparsest possible rank-K matrices W and G.
In the above equation, we can write: [math]\displaystyle{ \| I - WG^T \|^2 = \sum_k \|{e_k}^T (I - WG^T)\|^2 }[/math].
Therfore, projection of [math]\displaystyle{ ( I - WG^T ) }[/math] onto the principal components has more weight while its projection on non principal components has less weight. This implies that factors W and G are sparse in the principal component subspace and less sparse in the non principal component subspace.
Kernel NMF
Consider a mapping [math]\displaystyle{ \phi }[/math] that maps a point to a higher dimensional feature space, such that [math]\displaystyle{ \phi: x_i \rightarrow \phi(x_i) }[/math]. The factors for the kernel form of NMF or semi NMF : [math]\displaystyle{ \phi (X) = FG^T }[/math] would be difficult to compute as we need to know the mapping [math]\displaystyle{ \phi }[/math] explicitly.
This difficulty is overcome in the convex NMF, as it has the form: [math]\displaystyle{ \phi: (X) = \phi (X) WG^T }[/math] and therefore the objective to be minimized becomes,
[math]\displaystyle{ \|\phi (X)-\phi(X)WG^T\|^2 = Tr (K-2G^TKW+W^TKWG^TG) }[/math] where [math]\displaystyle{ K = \phi^T(X)\phi(X) }[/math] is the kernel.
Also, the update rules for the convex NMF algorithm (discussed above) depend only on [math]\displaystyle{ X^TX }[/math] and therefore convex NMF can be kernelized.
Cluster NMF
The factor G is considered to contain posterior cluster probabilities, then F, which represents cluster centroids is given as:
[math]\displaystyle{ \mathbf {f_k = Xg_k / n_k} }[/math] or [math]\displaystyle{ F = XG{D_n}^{-1} }[/math] where [math]\displaystyle{ D_n = diag (n_1, \cdots, n_K) }[/math].
Therefore, the factorization becomes, [math]\displaystyle{ X = XG{D_n}^{-1}G^T }[/math] or [math]\displaystyle{ X = X G G^T }[/math]. This is because NMF is invariant to diagonal rescaling.
This factorization is called Cluster NMF as it has the same degree of freedom as in any standard clustering problem, which is G (cluster indicator).
Relationship between NMF (its variants) and K means clustering
NMF and all its variants discussed above can be interpreted as K means clustering by imposing an additional constraint [math]\displaystyle{ G^TG=I }[/math], that is in each row of G there is only one nonzero element, which implies each data point can belong to only one cluster.
Theorem: G-orthogonal NMF, Semi NMF, Convex NMF, Cluster NMF and Kernel NMF are all relaxations of K means clustering.
Proof:
In all the above five cases of NMF, it can be shown that the objective function can be reduced to:
[math]\displaystyle{ \mathbf {J = Tr(X^TX -G^TKG)} }[/math] when [math]\displaystyle{ G^TG = I }[/math] and where [math]\displaystyle{ K = X^TX }[/math] or [math]\displaystyle{ K = \phi^T(X)\phi(X) }[/math]. As the first term is a constant, the minimization problem actually becomes:
[math]\displaystyle{ \max_{G^TG = I} Tr(G^TKG) }[/math]
The above objective function is the same as the objective function for kernel K means clustering <ref name='Simon D. H'> Simon D. H, Ding C, and He X; “On the Equivalence of Nonnegative Matrix Factorization and Spectral Clustering” </ref>.
Even without the orthogonality constraint, these NMF algorithms can be considered to be soft versions of K means clustering. That is each data point can be considered to fractionally belong to more than one cluster.
General properties of NMF algorithms
- Converge to local minimum and not global minimum.
- NMF factors are invariant to rescaling i.e. degree of freedom of diagonal rescaling is always present.
- Convergence rate of multiplicative algorithms is first order.
- Many different ways to initialize NMF. Here, the relationship between NMF and relaxed K means clustering is used.
Experimental Results
The authors have presented experimental results on synthetic data set to show that factors given by Convex NMF more closely resemble cluster centroids than those given by Semi NMF. However, semi NMF results are better in terms of accuracy than convex NMF. They have even compared the results of NMF, convex NMF and semi NMF with K means clustering on real dataset. They conclude that all of these matrix factorizations give better results than K means on all of the datasets they studied in terms of clustering accuracy.
A. Synthetic dataset
One of the main goals in here is to show that the Convex-NMF variants may provide subspace factorizations that have more interpretable factors than those obtained by other NMF variants (or PCA). Particularly we expect that in some cases the factor F will be interpretable as containing cluster representatives (centroids) and G will be interpretable as encoding cluster indicators.
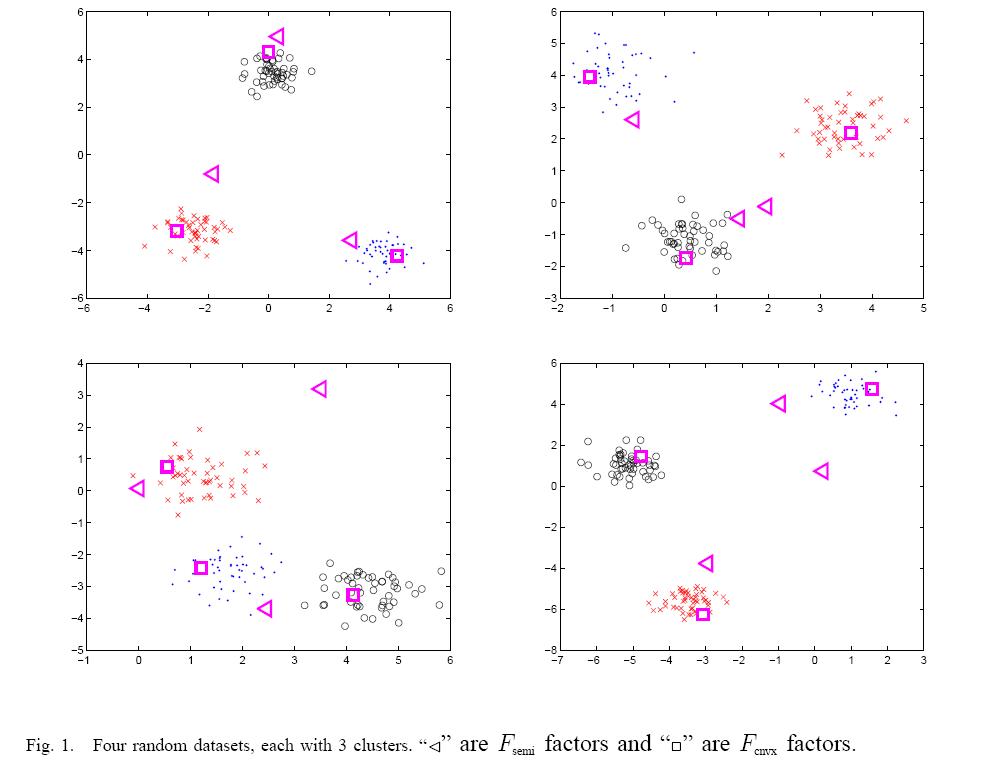
In Figure 1, we randomly generate four two-dimensional datasets with three clusters each. Computing both the Semi-NMF and Convex-NMF factorizations, we display the resulting F factors. We see that the Semi-NMF factors tend to lie distant from the cluster centroids. On the other hand, the Convex-NMF factors almost always lie within the clusters.
B. Real life datasets
The data sets which were used are: Ionosphere and Wave from the UCI repository, the document datasets URCS, WebkB4, Reuters (using a subset of the data collection which includes the 10 most frequent categories), WebAce and a dataset which contains 1367 log messages collected from several different machines with different operating systems at the School of Computer Science at Florida International University. The log messages are grouped into 9 categories: configuration, connection, create, dependency, other, report, request, start, and stop. Stop words were removed using a standard stop list. The top 1000 words were selected based on frequencies.
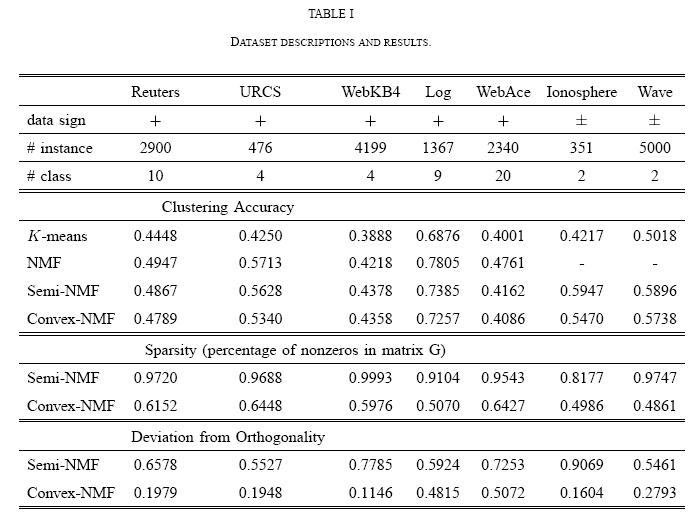
The results are shown in Table I. We derived these results by averaging over 10 runs for each dataset and algorithm. Clustering accuracy was computed using the known class labels in the following way: The confusion matrix is first computed. The columns and rows are then reordered so as to maximize the sum of the diagonal. This sum is taken as a measure of the accuracy: it represents the percentage of data points correctly clustered under the optimized permutation. To measure the sparsity of G in the experiments, the average of each column of G was computed and all elements below 0.001 times the average were set to zero. We report the number of the remaining nonzero elements as a percentage of the total number of elements. (Thus small values of this measure correspond to large sparsity). We can observe that:
1. Our main principal empirical result indicate that all of the matrix factorization models are better than K-means on all of the datasets. It states that the NMF family is competitive with K-means for the purposes of clustering.
2. On most of the nonnegative datasets, NMF gives somewhat better accuracy than Semi-NMF and Convex-NMF (with WebKb4 the exception). The differences are modest, however, suggesting that the more highly-constrained Semi-NMF and Convex-NMF may be worthwhile options if interpretability is viewed as a goal of a data analysis.
3. On the datasets containing both positive and negative values (where NMF is not applicable) the Semi-NMF results are better in terms of accuracy than the Convex-NMF results.
4. In general, Convex-NMF solutions are sparse, while Semi-NMF solutions are not.
5. Convex-NMF solutions are generally significantly more orthogonal than Semi-NMF solutions.
C. Shifting mixed-sign data to nonnegative
In this section we used only nonnegative by adding the smallest constant so all entries are nonnegative and performed experiments on data shifted in this way for the Wave and Ionosphere data. For Wave, the accuracy decreases to 0.503 from 0.590 for Semi-NMF and decreases to 0.5297 from 0.5738 for Convex-NMF. The sparsity increases to 0.586 from 0.498 for Convex-NMF. For Ionosphere, the accuracy decreases to 0.647 from 0.729 for Semi-NMF and decreases to 0.618 from 0.6877 for Convex-NMF. The sparsity increases to 0.829 from 0.498 for Convex-NMF.
In short, the shifting approach does not appear to provide a satisfactory alternative.
D. Flexibility of NMF
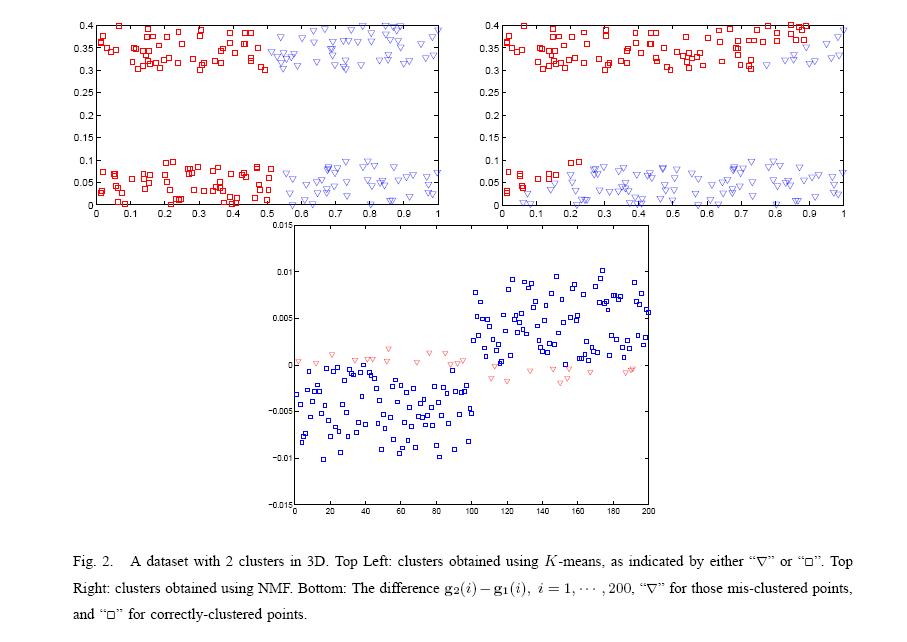
In general NMF almost always performs better than K-means in terms of clustering accuracy while providing a matrix approximation. This could be due to the flexibility of matrix factorization as compared to the rigid spherical clusters that the K-means clustering objective function attempts to capture. When the data distribution is far from a spherical clustering, NMF may have advantages. Figure 2 gives an example. The dataset consists of two parallel rods in 3D space containing 200 data points. The two central axes of the rods are 0.3 apart and they have diameter 0.1 and length 1. As seen in the figure, K-means gives a poor clustering, while NMF yields a good clustering. The bottom panel of Figure 2 shows the differences in the columns of G (each column is normalized to Pi gk(i) = 1). The mis-clustered points have small differences. Note that NMF is initialized randomly for the different runs. The stability of the solution over multiple runs was investigated; The results indicate that NMF converges to solutions F and G that are very similar across runs; moreover, the resulting discretized cluster indicators were identical.
Conclusion
In this paper:
- Number of new NMF algorithms has been proposed which tend to extend the applications of the NMF.
- They deal with mixed sign data.
- The connection between NMF (its variants) and K means clustering was analyzed.
- The matrix factors are shown to have convenient interpretation in terms of clustering.
References
<references/>