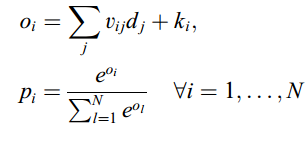continuous space language models

Model

The neural network language model has to perform two tasks: first, project all words of the context [math]\displaystyle{ \,h_j }[/math] = [math]\displaystyle{ \,w_{j-n+1}^{j-1} }[/math] onto a continuous space, and second, calculate the language model probability [math]\displaystyle{ P(w_{j}=i|h_{j}) }[/math]. The researchers for this paper sought to find a better model for this probability than the back-off n-grams model. Their approach was to map the n-1 words sequence onto a multi-dimension continuous space using a layer of neural network followed by another layer to estimate the probabilities of all possible next words. The formulas and model goes as follows:

For some sequence of n-1 words, encode each word using 1 of K encoding, i.e. 1 where the word is indexed and zero everywhere else. Label each 1 of K encoding by [math]\displaystyle{ (w_{j-n+1},\dots,w_j) }[/math] for some n-1 word sequence at the j'th word in some larger context.

Let P be a projection matrix common to all n-1 words and let

[math]\displaystyle{ \,a_i=Pw_{j-n+i},i=1,\dots,n-1 }[/math]

Let H be the weight matrix from the projection layer to the hidden layer and the state of H would be:

[math]\displaystyle{ \,h=tanh(Ha + b) }[/math] where A is the concatenation of all [math]\displaystyle{ \,a_i }[/math] and [math]\displaystyle{ \,b }[/math] is some bias vector

Finally, the output vector would be:

[math]\displaystyle{ \,o=Vh+k }[/math] where V is the weight matrix from hidden to output and k is another bias vector. [math]\displaystyle{ \,o }[/math] would be a vector with same dimensions as the total vocabulary size and the probabilities can be calculated from [math]\displaystyle{ \,o }[/math] by applying the softmax function.

The following figure shows the Architecture of the neural network language model. [math]\displaystyle{ \,h_j }[/math] denotes the context [math]\displaystyle{ \,w_{j-n+1}^{j-1} }[/math]. P is the size of one projection and H and N is the size of the second hidden and output layer, respectively. When short-lists are used the size of the output layer is much smaller than the size of the vocabulary.

In contrast to standard language modeling where we want to know the probability of a word i given its context, <math>P(w_{j} = i|h_{j}), the neural network simultaneously predicts the language model probability of all words in the word list: