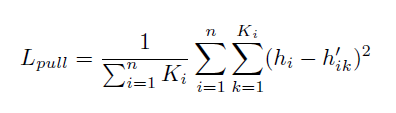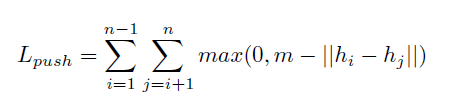Pixels to Graphs by Associative Embedding: Difference between revisions
No edit summary |
No edit summary |
||
| Line 7: | Line 7: | ||
Current state-of-the-art techniques break down the construction of scene graphs by first identifying objects, and then predicting the edges for any given pair of identified objects. This paper introduces an architecture that defines the entire graph directly from the image, enabling the network to reason across the entirety of the image to understand relationships, as opposed to only predicting relationships using object labels. | Current state-of-the-art techniques break down the construction of scene graphs by first identifying objects, and then predicting the edges for any given pair of identified objects. This paper introduces an architecture that defines the entire graph directly from the image, enabling the network to reason across the entirety of the image to understand relationships, as opposed to only predicting relationships using object labels. | ||
A key concern, given that the new architecture produces both vertices (objects) and edges (relationships) , is connecting the two. Specifically, the output of the network is some set of relationships E, and some set of Vertices V. The network needs to also output the “source” and “destination” of each relationship, so that the final graph can be formed. In the image above, for example, the network would also need to tell us that “holding” comes from “person” and goes to “Frisbee”. To do this, the paper uses associative embeddings. Specifically, the network outputs a particular “embedding vector” for each vertex, as well as a “source embedding” and “destination embedding” for each relationship. A final post-processing step finds the vertex embedding closest to each of the source / destination embeddings of each relationship and in this way assigns the edges to pairs of vertices. | A key concern, given that the new architecture produces both vertices (objects) and edges (relationships) , is connecting the two. Specifically, the output of the network is some set of relationships E, and some set of Vertices V. The network needs to also output the “source” and “destination” of each relationship, so that the final graph can be formed. In the image above, for example, the network would also need to tell us that “holding” comes from “person” and goes to “Frisbee”. To do this, the paper uses associative embeddings. Specifically, the network outputs a particular “embedding vector” for each vertex, as well as a “source embedding” and “destination embedding” for each relationship. A final post-processing step finds the vertex embedding closest to each of the source / destination embeddings of each relationship and in this way assigns the edges to pairs of vertices. | ||
| Line 13: | Line 14: | ||
Given an image of dimensions h x w, a stacked hourglass (Appendix 2) is used to generate a h x w x f representation of the image. It should be noted that the dimension of the output (which is non-trainable), to consider. Specifically, we need to have a resolution large enough to minimize the number of pixels with multiple detections while also being small enough to ensure that each 1 x 1 x f vector still contains the information needed for subsequent inference. | Given an image of dimensions h x w, a stacked hourglass (Appendix 2) is used to generate a h x w x f representation of the image. It should be noted that the dimension of the output (which is non-trainable), to consider. Specifically, we need to have a resolution large enough to minimize the number of pixels with multiple detections while also being small enough to ensure that each 1 x 1 x f vector still contains the information needed for subsequent inference. | ||
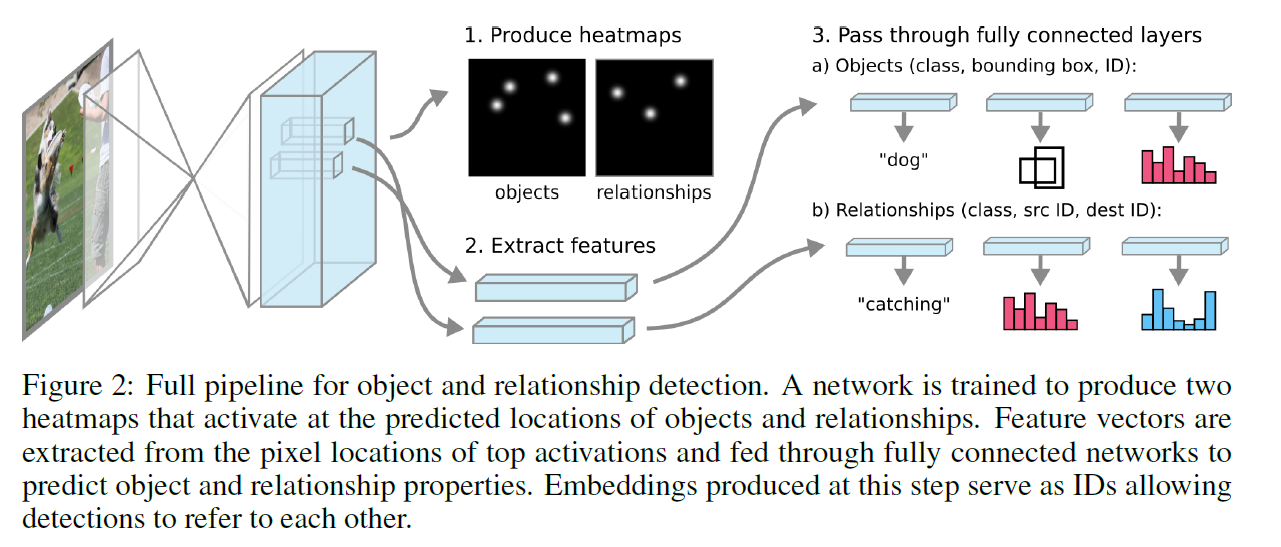
A 1x1 convolution and sigmoid activation is performed on this result to generate a heatmap (one for objects and one for relationships, using separately determined convolutions). The value at a given pixel can be interpreted as the likelihood of detection at that particular pixel in the original image. | A 1x1 convolution and sigmoid activation is performed on this result to generate a heatmap (one for objects and one for relationships, using separately determined convolutions). The value at a given pixel can be interpreted as the likelihood of detection at that particular pixel in the original image. | ||
In order to claim that there is an element at some pixel, we need to have some likelihood threshold. Then, if a given pixel in the map has a value >= the threshold, we claim that there is an element at that pixel. This threshold is calculated by using binary cross-entropy loss on the final values in the heatmap. Values with likelihoods greater than p-hat will be considered element detections. | In order to claim that there is an element at some pixel, we need to have some likelihood threshold. Then, if a given pixel in the map has a value >= the threshold, we claim that there is an element at that pixel. This threshold is calculated by using binary cross-entropy loss on the final values in the heatmap. Values with likelihoods greater than p-hat will be considered element detections. | ||
Finally, for each element that we detected, we extract the 1 x 1 x f feature vector. This is then used as an input to a set of FFNN, where we have a separate network for each characteristic of interest. The following image summarizes the process. | Finally, for each element that we detected, we extract the 1 x 1 x f feature vector. This is then used as an input to a set of FFNN, where we have a separate network for each characteristic of interest. The following image summarizes the process. | ||
| Line 22: | Line 26: | ||
:'''2. Connecting Elements with Associative Embeddings''' | :'''2. Connecting Elements with Associative Embeddings''' | ||
As explained earlier, to construct the scene graph, we need to know the source and destination of each edge. This is done through associative embeddings. | As explained earlier, to construct the scene graph, we need to know the source and destination of each edge. This is done through associative embeddings. | ||
First, let us define an embedding hi ϵ Rd produced for some vector i, and let us assume that we have n object detections in a particular image. Now, define hik, for k = 1 to Ki (where Ki is the number of edges in the graph with a vertex at vertex i) as the embedding associated with an edge that touches vertex i. We define two loss functions on these sets. | First, let us define an embedding hi ϵ Rd produced for some vector i, and let us assume that we have n object detections in a particular image. Now, define hik, for k = 1 to Ki (where Ki is the number of edges in the graph with a vertex at vertex i) as the embedding associated with an edge that touches vertex i. We define two loss functions on these sets. | ||
| Line 35: | Line 40: | ||
:'''3. Support for Overlapping Detections''' | :'''3. Support for Overlapping Detections''' | ||
An obvious concern is how the network would operate if there was more than one detection (be it object or relationship), in a given pixel. For example, detection of “shirt” and “person” may be centered at the exact same pixel. To account for this, the architecture is modified to allow for “slots” at each pixel. Specifically, so detections of objects are allowed at a particular pixel, while sr relationship detections are allowed at a given pixel. | An obvious concern is how the network would operate if there was more than one detection (be it object or relationship), in a given pixel. For example, detection of “shirt” and “person” may be centered at the exact same pixel. To account for this, the architecture is modified to allow for “slots” at each pixel. Specifically, so detections of objects are allowed at a particular pixel, while sr relationship detections are allowed at a given pixel. | ||
In order to allow for this, some changes are required after the feature extraction step. Specifically, we now use the 1x1xf vector as the input for so (or sr) different sets of 4 FFNNs, where the output is as shown in figure 2, but with the final FFNN outputting the probability of a detection existing in that particular slot, at that particular pixel. This new network is trained exclusively on whether or not a detection has been made in that slot, and, in prediction, is used to determine the number of slots to output at a given pixel. It is critical to note that this each of these so (or sr) sets of FFNNs share absolutely no weights. And each is trained for detection in its assigned slot. | In order to allow for this, some changes are required after the feature extraction step. Specifically, we now use the 1x1xf vector as the input for so (or sr) different sets of 4 FFNNs, where the output is as shown in figure 2, but with the final FFNN outputting the probability of a detection existing in that particular slot, at that particular pixel. This new network is trained exclusively on whether or not a detection has been made in that slot, and, in prediction, is used to determine the number of slots to output at a given pixel. It is critical to note that this each of these so (or sr) sets of FFNNs share absolutely no weights. And each is trained for detection in its assigned slot. | ||
It is important to note that that this implies a change in the training procedure. We now have so (or sr) different predictions (be it class, or class + bounding box), that we need to match with our set of ground truth detections at a given pixel. Without this step, we would not be able to assign a value to the error for that sample. To do this, we match a one-hot encoded vector of the ground-truth class and bounding box anchor (the reference vector), and then match them with the so (or sr) outputs provided at a given pixel. The Hungarian method is used to ensure maximum matching between the outputs and the reference method while ensuring we do not assign the same detection to multiple slots. | It is important to note that that this implies a change in the training procedure. We now have so (or sr) different predictions (be it class, or class + bounding box), that we need to match with our set of ground truth detections at a given pixel. Without this step, we would not be able to assign a value to the error for that sample. To do this, we match a one-hot encoded vector of the ground-truth class and bounding box anchor (the reference vector), and then match them with the so (or sr) outputs provided at a given pixel. The Hungarian method is used to ensure maximum matching between the outputs and the reference method while ensuring we do not assign the same detection to multiple slots. | ||
Revision as of 21:45, 23 October 2018
Introduction
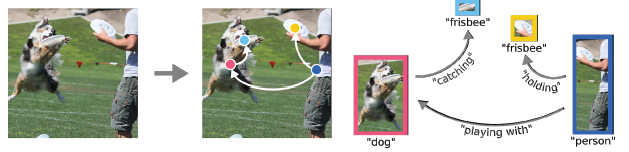
The paper presents a novel approach to proposing a scene graph. A scene graph, as it relates to an image, is a graph with a vertex that represents each object identified in the image and an edge that represents relationships between the objects.
An example of a scene graph:
Current state-of-the-art techniques break down the construction of scene graphs by first identifying objects, and then predicting the edges for any given pair of identified objects. This paper introduces an architecture that defines the entire graph directly from the image, enabling the network to reason across the entirety of the image to understand relationships, as opposed to only predicting relationships using object labels.
A key concern, given that the new architecture produces both vertices (objects) and edges (relationships) , is connecting the two. Specifically, the output of the network is some set of relationships E, and some set of Vertices V. The network needs to also output the “source” and “destination” of each relationship, so that the final graph can be formed. In the image above, for example, the network would also need to tell us that “holding” comes from “person” and goes to “Frisbee”. To do this, the paper uses associative embeddings. Specifically, the network outputs a particular “embedding vector” for each vertex, as well as a “source embedding” and “destination embedding” for each relationship. A final post-processing step finds the vertex embedding closest to each of the source / destination embeddings of each relationship and in this way assigns the edges to pairs of vertices.
The Architecture:
- 1. Detecting Graph Elements
Given an image of dimensions h x w, a stacked hourglass (Appendix 2) is used to generate a h x w x f representation of the image. It should be noted that the dimension of the output (which is non-trainable), to consider. Specifically, we need to have a resolution large enough to minimize the number of pixels with multiple detections while also being small enough to ensure that each 1 x 1 x f vector still contains the information needed for subsequent inference.
A 1x1 convolution and sigmoid activation is performed on this result to generate a heatmap (one for objects and one for relationships, using separately determined convolutions). The value at a given pixel can be interpreted as the likelihood of detection at that particular pixel in the original image.
In order to claim that there is an element at some pixel, we need to have some likelihood threshold. Then, if a given pixel in the map has a value >= the threshold, we claim that there is an element at that pixel. This threshold is calculated by using binary cross-entropy loss on the final values in the heatmap. Values with likelihoods greater than p-hat will be considered element detections.
Finally, for each element that we detected, we extract the 1 x 1 x f feature vector. This is then used as an input to a set of FFNN, where we have a separate network for each characteristic of interest. The following image summarizes the process.
- 2. Connecting Elements with Associative Embeddings
As explained earlier, to construct the scene graph, we need to know the source and destination of each edge. This is done through associative embeddings.
First, let us define an embedding hi ϵ Rd produced for some vector i, and let us assume that we have n object detections in a particular image. Now, define hik, for k = 1 to Ki (where Ki is the number of edges in the graph with a vertex at vertex i) as the embedding associated with an edge that touches vertex i. We define two loss functions on these sets.
The goal of Lpull is minimize the squared differences between the embedding of a given vertex and the embedding of an edge that references said vertex.
On the other hand, minimizing Lpush implies assigning embeddings to vertices that are as far apart as possible. The further apart they are, the lower the output of max becomes, until eventually it reaches 0. Here, m is just a constant. In the paper, the values used were m = 8 and d = 8 (that is, 8D embeddings). Combining these two loss functions (and weighing them equally), accomplishes the task of predicting embeddings such that vertices are differentiated, but the embedding of a vertex is most similar to the vertex it references.
- 3. Support for Overlapping Detections
An obvious concern is how the network would operate if there was more than one detection (be it object or relationship), in a given pixel. For example, detection of “shirt” and “person” may be centered at the exact same pixel. To account for this, the architecture is modified to allow for “slots” at each pixel. Specifically, so detections of objects are allowed at a particular pixel, while sr relationship detections are allowed at a given pixel.
In order to allow for this, some changes are required after the feature extraction step. Specifically, we now use the 1x1xf vector as the input for so (or sr) different sets of 4 FFNNs, where the output is as shown in figure 2, but with the final FFNN outputting the probability of a detection existing in that particular slot, at that particular pixel. This new network is trained exclusively on whether or not a detection has been made in that slot, and, in prediction, is used to determine the number of slots to output at a given pixel. It is critical to note that this each of these so (or sr) sets of FFNNs share absolutely no weights. And each is trained for detection in its assigned slot.
It is important to note that that this implies a change in the training procedure. We now have so (or sr) different predictions (be it class, or class + bounding box), that we need to match with our set of ground truth detections at a given pixel. Without this step, we would not be able to assign a value to the error for that sample. To do this, we match a one-hot encoded vector of the ground-truth class and bounding box anchor (the reference vector), and then match them with the so (or sr) outputs provided at a given pixel. The Hungarian method is used to ensure maximum matching between the outputs and the reference method while ensuring we do not assign the same detection to multiple slots.
Results
A quick note on notation: R@50 indicates what percentage of ground-truth subject-predicate-object tuples appeared in a proposal of 50 such tuples. Since R@100 offers more possibilities, it will necessarily be higher. The 6.7, for example, indicates that 6.7% of the ground truth tuples appeared in the proposals of the network.
The authors tested the network against two other architectures designed to develop semantic understanding of images. For this, they used the Visual Genome dataset, with so = 3 and sr = 6. Overall, the new architecture vastly outperformed past models. The results were as follows:
The table can be interpreted as follows:
- SGGen (no RPN): Given a particular image, without the use of Region Proposal networks, the accuracy of the proposed scene graph. No class predictions are provided.
- SGGen (with RPN): Same as above, except the output of the Region Proposal Network is used to enhance the input of a given image. No class predictions are provided.
- SGCIs: Ground-truth object bounding boxes are provided. The network is asked to classify them and determine relationships.
- PredCIs: As above, except the classes are also provided. The only goal is to predict relationships.
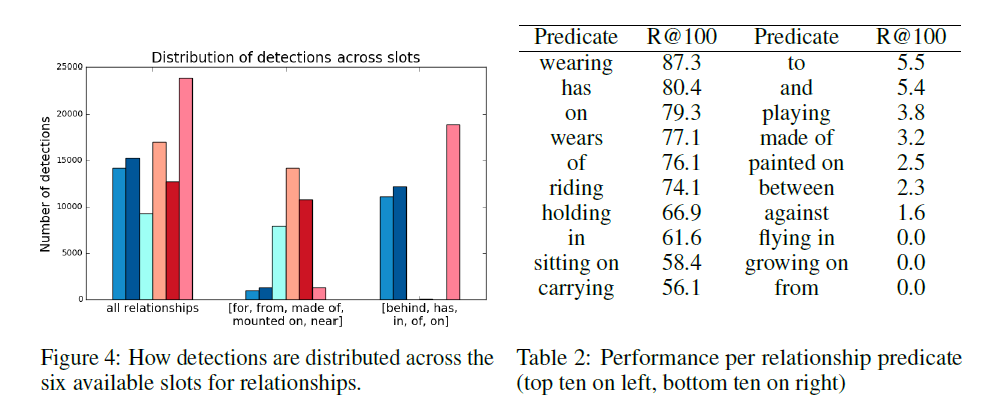
Further analysis into the accuracy, when looking at predicates individually, shows that the architecture is very sensitive to over-represented relationship predicates.
As shown in Figure 5, for many ground-truth predicates (those that do not appear often in the ground truth), the network does poorly. Even when allowed to propose 100 tuples, the network does not offer the predicate. Figure 4 simply observes the fact that certain sets of relationship predicates appear predominantly in a subset of slots. No general explanation has been offered for this behaviour.
Conclusion
In conclusion, the paper offers a novel approach to that enables the extraction of image semantics while perpetually reasoning over the entire context of the image. Associative embeddings are used to connect object and predicate relationships, and parallel “slots” allow for multiple detections in one pixel. While this approach offers noticeable improvements in accuracy, it is clear that work needs to be done to account for the non-uniform distributions of relationships in the dataset.
Appendices
Appendix 1: Sample Outputs
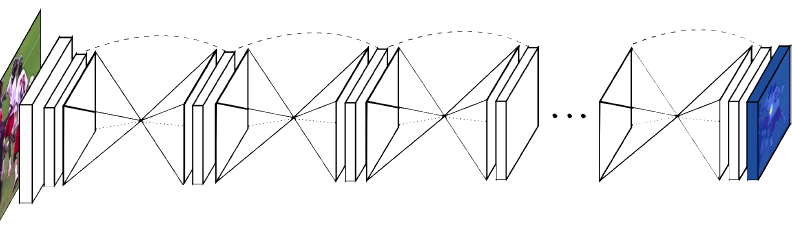
Appendix 2: Stacked Hourglass Architecture
Although this goes beyond the focus of the paper, I would like to add a brief overview of the stacked hourglass architecture used to generate the heatmap. This architecture is unique in that it allows cyclical top-down, bottom-up inference and recombination of features. While most architectures focus on optimizing the bottom-up portion (reducing dimensionality), the stacked-hourglass gives the network more flexibility in how it generates a representation by allowing it to learn a series of down-sampling / up-sampling steps.
References
1. Alejandro Newell and Jia Deng, “Pixels to Graphs by Associative Embedding,” in NIPS, 2017 2. Alejandro Newell, Kaiyu Yang, and Jia Deng. Stacked Hourglass Networks for Human Pose Estimation. ECCV, 2016