what game are we playing
Authors
Yuxin Wang, Evan Peters, Yifan Mou, Sangeeth Kalaichanthiran
Introduction
In recent times, there have been many different studies of methods for using AI to solve large-scale, zero-sum, extensive form problems. However, most of these works operate under the assumption that the parameters of the game are known, and the objective is just finding the optimal strategy to the game. This scenario proves to be unrealistic in real-world scenarios where there are often times when one must find the optimal strategy while the parameters of game are unknown. This paper proposes a framework for finding an optimal solution using a primal-dual Newton Method, and then using back-propagation to analytically compute the gradients of all the relevant game parameters.
The approach to solving this problem is to consider quantal response equilibrium (QRE), which is a generalization of Nash equilibrium (NE) where the agents can make suboptimal decisions. It is shown that the solution to the QRE is a differentiable function of the payoff matrix. Consequently, back-propagation can be used to analytically solve for the payoff matrix (or other game parameters). This strategy has many future application areas as it allows for game-solving (both extensive and normal form) to be integrated as a module in a deep neural network.
The effectiveness of this model is demonstrated using the games “Rock, Paper, Scissors”, one-card poker, and a security defence game.
Learning and Quantal Response in Normal Form Games
The game-solving module provides all elements required in differentiable learning, which maps contextual features to payoff matrices, and computes equilibrium strategies under a set of contextual features. This paper will learn zero-sum games and start with normal form games since they have game solver and learning approach capturing much of intuition and basic methodology.
Zero-Sum Normal Form Games
In two-player zero-sum games there is a payoff matrix P that describes the rewards for two players employing specific strategies u and v respectively. The optimal strategy mixture may be found with a classic min-max formulation: $$\min_u \max_v \ u^T P v \\ subject \ to \ 1^T u =1, u \ge 0 \\ 1^T v =1, v \ge 0. \ $$
The solution [math]\displaystyle{ (u^*, v_0) }[/math] to this optimization and the solution [math]\displaystyle{ (u_0,v^*) }[/math] to the corresponding problem with inverse player order form the Nash equilibrium. When the payoff matrix P is not known, we observe samples of actions [math]\displaystyle{ a^{(i)}, i =1,...,N }[/math] from one or both players, sampled from the equilibrium strategies [math]\displaystyle{ (u^*,v^*) }[/math], to recover the true underlying payoff matrix P or a function form P(x) depending on the current context.
Quantal Response Equilibria
However, NE is poorly suited because NEs are overly strict and discontinuous with respect to P, and NEs may not be unique. Thus, it is more common to model the players' actions with the quantal response equilibria (QRE) to address these issues. Specifically, consider the logit equilibrium for zero-sum games that obeys the fixed point: $$ u^* _i = \frac {exp(Pv)_i}{\sum_{q \in [n]} exp (-Pv)_q}, \ v^* _j= \frac {exp(P^T u)_j}{\sum_{q \in [m]} exp (P^T u)_q} .\qquad \ (1) $$ For a fixed opponent strategy, the logit equilibrium corresponding to a strategy is strictly convex, and thus the regularized best response is unique.
End-to-End Learning
Then to integrate zero-sum solver, [1] introduced a method to solve the QRE and to differentiate through its solution.
QRE solver: To find the fixed point in (1), it is equivalent to solve the regularized min-max game: $$ \min_{u \in \mathbb{R}^n} \max_{v \in \mathbb{R}^m} \ u^T P v -H(v) + H(u) \\ \text{subject to } 1^T u =1, \ 1^T v =1, $$ where H(y) is the Gibbs entropy [math]\displaystyle{ \sum_i y_i log y_i }[/math]. Entropy regularization guarantees the non-negative condition and makes the equilibrium continuous with respect to P, which means players are encouraged to play more randomly, and all actions have non-zero probability. Moreover, this problem has a unique saddle point corresponding to [math]\displaystyle{ (u^*, v^*) }[/math].
Using a primal-dual Newton Method to solve the QRE for two-player zero-sum games, the KKT conditions for the problem are: $$ Pv + \log(u) + 1 +\mu 1 = 0 \\ P^T v -\log(v) -1 +\nu 1 = 0 \\ 1^T u = 1, \ 1^T v = 1, $$ where [math]\displaystyle{ (\mu, \nu) }[/math] are Lagrange multipliers for the equality constraints on u, v respectively. Then applying Newton's method gives the the update rule: $$ Q \begin{bmatrix} \Delta u \\ \Delta v \\ \Delta \mu \\ \Delta \nu \\ \end{bmatrix} = - \begin{bmatrix} P v + \log u + 1 + \mu 1 \\ P^T u - \log v - 1 + \nu 1 \\ 1^T u - 1 \\ 1^T v - 1 \\ \end{bmatrix}, \qquad (2) $$ where Q is the Hessian of the Lagrangian, given by $$ Q = \begin{bmatrix} diag(\frac{1}{u}) & P & 1 & 0 \\ P^T & -diag(\frac{1}{v}) & 0 & 1\\ 1^T & 0 & 0 & 0 \\ 0 & 1^T & 0 & 0 \\ \end{bmatrix}. $$
Differentiating Through QRE Solutions: The QRE solver provides a method to compute the necessary Jacobian-vector products. Specifically, we compute the gradient of the loss given the solution [math]\displaystyle{ (u^*,v^*) }[/math] to the QRE, and some loss function [math]\displaystyle{ L(u^*,v^*) }[/math]:
1. Take differentials of the KKT conditions: [math]\displaystyle{ Q \begin{bmatrix} du & dv & d\mu & d\nu \\ \end{bmatrix} ^T = \begin{bmatrix} -dPv & -dP^Tu & 0 & 0 \\ \end{bmatrix}^T. \ }[/math]
2. For small changes du, dv, [math]\displaystyle{ dL = \begin{bmatrix} v^TdP^T & u^TdP & 0 & 0 \\ \end{bmatrix} Q^{-1} \begin{bmatrix} -\nabla_u L & -\nabla_v L & 0 & 0 \\ \end{bmatrix}^T. }[/math]
3. Apply this to P, and take limits as dP is small: [math]\displaystyle{ \nabla_P L = y_u v^T + u y_v^T, \qquad (3) }[/math] where [math]\displaystyle{ \begin{bmatrix} y_u & y_v & y_{\mu} & y_{\nu}\\ \end{bmatrix}=Q^{-1}\begin{bmatrix} -\nabla_u L & -\nabla_v L & 0 & 0 \\ \end{bmatrix}^T. }[/math]
Hence, the forward pass is given by using the expression in (2) to solve for the logit equilibrium given P, and the backward pass is given by using [math]\displaystyle{ \nabla_u L }[/math] and [math]\displaystyle{ \nabla_v L }[/math] to obtain [math]\displaystyle{ \nabla_P L }[/math] using (3). There does not always exist a unique P which generates [math]\displaystyle{ u^*, v^* }[/math] under the logit QRE, and we cannot expect to recover P when under-constrained.
Learning Extensive form games
The normal form representation for games where players have many choices quickly becomes intractable. For example, consider a chess game: One the first turn, player 1 has 20 possible moves and then player 2 has 20 possible responses. If in the following number of turns each player is estimated to have ~30 possible moves and if a typical game is 40 moves per player, the total number of strategies is roughly [math]\displaystyle{ 10^{120} }[/math] per player (this is known as the Shannon number for game-tree complexity of chess) and so the payoff matrix for a typical game of chess must therefore have [math]\displaystyle{ O(10^{240}) }[/math] entries.
Instead, it is much more useful to represent the game graphically as an "Extensive form game" (EFG). We'll also need to consider types of games where there is imperfect information - players do not necessarily have access to the full state of the game. An example of this is one-card poker: (1) Each player draws a single card from a 13-card deck (ignore suits) (2) Player 1 decides whether to bet/hold (3) Player 2 decides whether to call/raise (4) Player 1 must either call/fold if Player 2 raised. From this description, player 1 has [math]\displaystyle{ 2^{13} }[/math] possible first moves (all combinations of (card, raise/hold)) and has [math]\displaystyle{ 2^{13} }[/math] possible second moves (whenever player 1 gets a second move) for a total of [math]\displaystyle{ 2^{26} }[/math] possible strategies. In addition, Player 1 never knows what cards player 2 has and vice versa. So instead of representing the game with a huge payoff matrix we can instead represent it as a simple decision tree (for a single drawn card of player 1):
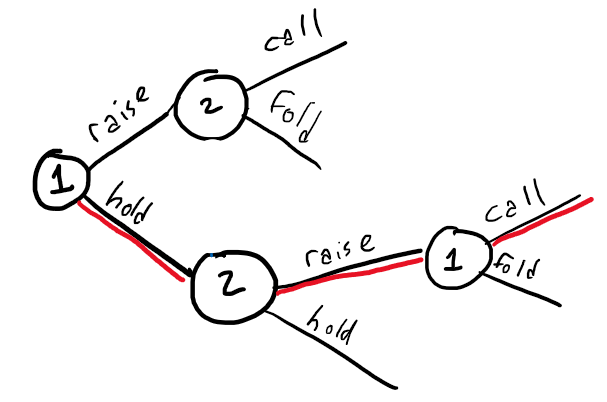
where player 1 is represented by "1", a node that has two branches corresponding to the allowed moves of player 1. However there must also be a notion of information available to either player: While this tree might correspond to say, player 1 holding a "9", it contains no information on what card player 2 is holding (and is much simpler because of this). This leads to the definition of an information set: the set of all nodes belonging to a single player for which the other player cannot distinguish which node has been reached. The information set may therefore be treated as a node itself, for which actions stemming from the node must be chosen in ignorance to what the other player did immediately before arriving at the node. In the poker example, the full game tree consists of a much more complex version of the tree shown above (containing repetitions of the given tree for every possible combination of cards dealt) and the and an example of an information set for player 1 is the set of all of nodes owned by player 2 that immediately follow player 1's decision to hold. In other words, if player 1 holds there are 13 possible nodes describing the responses of player 2 (raise/hold for player 2 having card = ace, 1, ... King) and all 13 of these nodes are indistinguishable to player 1, and so form an information set for player 1.
The following is a review of important concepts for extensive form games first formalized in [2]. Let [math]\displaystyle{ \mathcal{I}_i }[/math] be the set of all information sets for player i, and for each [math]\displaystyle{ t \in \mathcal{I}_i }[/math] let [math]\displaystyle{ \sigma_t }[/math] be the actions taken by player i to arrive at [math]\displaystyle{ t }[/math] and [math]\displaystyle{ C_t }[/math] be the actions that player i can take from [math]\displaystyle{ u }[/math]. Then the set of all possible sequences that can be taken by player i is given by
$$ S_i = \{\emptyset \} \cup \{ \sigma_t c | u\in \mathcal{I}_i, c \in C_t \} $$
So for the one-card poker we would have [math]\displaystyle{ S_1 = \{\emptyset, \text{raise}, \text{hold}, \text{hold-call}, \text{hold-fold\} } }[/math]. From the possible sequences follows two important concepts:
- The EFG payoff matrix [math]\displaystyle{ P }[/math] is size [math]\displaystyle{ |S_1| \times |S_2| }[/math] (this is all possible actions available to either player), is populated with rewards from each leaf of the tree (or "zero" for each [math]\displaystyle{ (s_1, s_2) }[/math] that is an invalid pair), and the expected payoff for realization plans [math]\displaystyle{ (u, v) }[/math] is given by [math]\displaystyle{ u^T P v }[/math]
- A realization plan [math]\displaystyle{ u \in \mathbb{R}^{|S_1|} }[/math] for player 1 ([math]\displaystyle{ v \in \mathbb{R}^{|S_2|} }[/math] for player 2 ) will describe probabilities for players to carry out each possible sequence, and each realization plan must be constrained by (i) compatibility of sequences (e.g. "raise" is not compatible with "hold-call") and (ii) information sets available to the player. These constraints are linear: $$ Eu = e \\ Fv = f $$ where [math]\displaystyle{ e = f = (1, 0, ..., 0)^T }[/math] and [math]\displaystyle{ E, F }[/math] contain entries in [math]\displaystyle{ {-1, 0, 1} }[/math] describing compatibility and information sets.
The paper's main contribution is to develop a minmax problem for extensive form games:
$$
\min_u \max_v u^T P v + \sum_{t\in \mathcal{I}_1} \sum_{c \in C_t} u_c \log \frac{u_c}{u_{p_t}} - \sum_{t\in \mathcal{I}_2} \sum_{c \in C_t} v_c \log \frac{v_c}{v_{p_t}}
$$
where [math]\displaystyle{ p_t }[/math] is the action immediately preceding information set [math]\displaystyle{ t }[/math]. Intuitively, each sum resembles a cross entropy over the distribution of probabilities in the realization plan comparing each probability to proceed from an information set to the probability to arrive at that information set. Importantly, these entropies are strictly convex or concave (for player 1 and player 2 respectively) [3] so that the minmax problem will have a unique solution and the objective function is continuous and continuously differntiable - this means there is a way to optimize the function. As noted in Theorem 1 of [1], the solution to this problem is equivalently a solution for the QRE of the game in reduced normal form.
Having decided on a cost function, the method of Lagrange multipliers my be used to construct the Lagrangian that encodes the known constraints ([math]\displaystyle{ Eu = e \,, Fv = f }[/math], and [math]\displaystyle{ u, v \geq 0 }[/math]), and then optimize the Lagrangian using Newton's method (identically to the previous section). Accounting for the constraints, the Lagrangian becomes
$$
\mathcal{L} = g(u, v) + \sum_i \mu_i(Eu - e)_i + \sum_i \nu_i (Fv - f)_i
$$
where [math]\displaystyle{ g }[/math] is the argument from the minmax statement above and [math]\displaystyle{ u, v \geq 0 }[/math] become KKT conditions. The general update rule for Newton's method may be written in terms of the derivatives of [math]\displaystyle{ \mathcal{L} }[/math] with respect to primal variables [math]\displaystyle{ u, v }[/math] and dual variables [math]\displaystyle{ \mu, \nu }[/math], yielding:
$$ \nabla_{u,v,\mu,\nu}^2 \mathcal{L} \cdot (\Delta u, \Delta v, \Delta \mu, \Delta \nu)^T= - \nabla_{u,v,\mu,\nu} \mathcal{L} $$ where [math]\displaystyle{ \nabla_{u,v,\mu,\nu}^2 \mathcal{L} }[/math] is the Hessian of the Lagrangian and [math]\displaystyle{ \nabla_{u,v,\mu,\nu} \mathcal{L} }[/math] is simply a column vector of the KKT stationarity conditions. Combined with the previous section, this completes the goal of the paper: To construct a differentiable problem for learning normal form and extensive form games.
Experiments
The authors demonstrated learning on extensive form games in the presence of side information, with partial observations using three experiments. In all cases, the goal was to maximize the likelihood of realizing an observed sequence from the player, assuming they act in accordance to the QRE.
Rock, Paper, Scissors
The first experiment was to learn a non-symmetric variant of Rock, Paper, Scissors with incomplete information with the following payoff matrix:
| Rock | Paper | Scissors | |
|---|---|---|---|
| Rock | 0 | [math]\displaystyle{ -b_1 }[/math] | [math]\displaystyle{ b_2 }[/math] |
| Paper | [math]\displaystyle{ b_1 }[/math] | 0 | [math]\displaystyle{ -b_3 }[/math] |
| Scissors | [math]\displaystyle{ -b_2 }[/math] | [math]\displaystyle{ b_3 }[/math] | 0 |
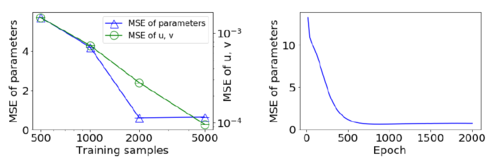
where each of the [math]\displaystyle{ b }[/math] ’s are linear function of some features [math]\displaystyle{ x \in \mathbb{R}^{2} }[/math] (i.e., [math]\displaystyle{ b_y = x^Tw_y }[/math], [math]\displaystyle{ y \in }[/math] {[math]\displaystyle{ 1,2,3 }[/math]} , where [math]\displaystyle{ w_y }[/math] are to be learned by the algorithm). Using many trials of random rewards the technique produced the following results for optimal strategies[1]:
From the graphs above, we can tell 1) both parameters learned and predicted strategies improve with larger dataset; and 2) with a reasonably sized dataset, >1000 here, convergence is stable and is fairly quick.
One-Card Poker
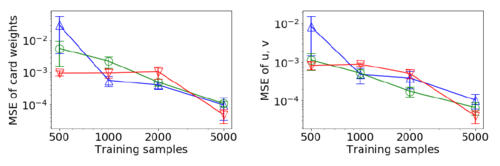
Next they investigated extensive form games using the one-Card Poker (with imperfect information) introduced in the previous section. In the experimental setup, they used a deck stacked non-uniformly (meaning repeat cards were allowed). Their goal was to learn this distribution of cards from observations of many rounds of the play. In this case, they needed to know the player’s perceived or believed distribution of cards may be different from the distribution of cards dealt. Three experiments were run with [math]\displaystyle{ n=4 }[/math]. Each experiment comprised 5 runs of training, with same weights but different training sets. Let [math]\displaystyle{ d \in \mathbb{R}^{n}, d \ge 0, \sum_{i} d_i = 1 }[/math] be the weights of the cards. The probability that the players are dealt cards [math]\displaystyle{ (i,j) }[/math] is [math]\displaystyle{ \frac{d_i d_j}{1-d_i} }[/math]. This distribution is asymmetric between players. Matrix [math]\displaystyle{ P, E, F }[/math] for the case [math]\displaystyle{ n=4 }[/math] are presented in [1]. With training for 2500 epochs, the mean squared error of learned parameters (card weights, [math]\displaystyle{ u, v }[/math] ) are averaged over all runs of and are presented as following [1]:
Security Resource Allocation Game
From Security Resource Allocation Game, they demonstrated the ability to learn from imperfect observations. The defender possesses [math]\displaystyle{ k }[/math] indistinguishable and indivisible defensive resources which he splits among [math]\displaystyle{ n }[/math] targets, { [math]\displaystyle{ T_1, ……, T_n }[/math]}. The attacker chooses one target. If the attack succeeds, the attacker gets [math]\displaystyle{ R_i }[/math] reward and defender gets [math]\displaystyle{ -R_i }[/math], otherwise zero payoff for both. If there are n defenders guarding [math]\displaystyle{ T_i }[/math], probability of successful attack on [math]\displaystyle{ T_i }[/math] is [math]\displaystyle{ \frac{1}{2^n} }[/math]. The expected payoff matrix when [math]\displaystyle{ n = 2, k = 3 }[/math], where the attackers are the row players is:
| {#[math]\displaystyle{ D_1 }[/math],#[math]\displaystyle{ D_2 }[/math]} | {0, 3} | {1, 2} | {2, 1} | {3, 0} |
|---|---|---|---|---|
| [math]\displaystyle{ T_1 }[/math] | [math]\displaystyle{ -R_1 }[/math] | [math]\displaystyle{ -\frac{1}{2}R_1 }[/math] | [math]\displaystyle{ -\frac{1}{4}R_1 }[/math] | [math]\displaystyle{ -\frac{1}{8}R_1 }[/math] |
| [math]\displaystyle{ T_2 }[/math] | [math]\displaystyle{ -\frac{1}{8}R_2 }[/math] | [math]\displaystyle{ -\frac{1}{4}R_2 }[/math] | [math]\displaystyle{ -\frac{1}{2}R_2 }[/math] | [math]\displaystyle{ -R_2 }[/math] |
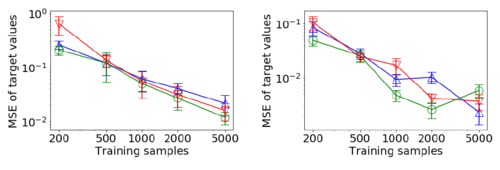
For a multi-stage game the attacker can launch [math]\displaystyle{ t }[/math] attacks, one in each stage while defender can only stick with stage 1. The attacker may change target if the attack in stage 1 is failed. Three experiments are run with [math]\displaystyle{ n = 2, k = 5 }[/math] for games with single attack and double attack, i.e, [math]\displaystyle{ t = 1 }[/math] and [math]\displaystyle{ t = 2 }[/math]. The results of simulated experiments are shown below [1]:
They learned [math]\displaystyle{ R_i }[/math] only based on observations of the defender’s actions and could still recover the game setting by only observing the defender’s actions. Same as expectation, the larger dataset size improves the learned parameters. Two outliers are 1) Security Game, the green plot for when [math]\displaystyle{ t = 2 }[/math]; and 2) RPS, when comparing between training sizes of 2000 and 5000.
Conclusion
This paper presents an end-to-end framework for implementing a game solver, for both extensive and normal form, as a module in a deep neural network for zero-sum games. This method, unlike many previous works in this area, does not require the parameters of the game to be known to the agent prior to the start of the game. The two-part method analytically computes both the optimal solution and the parameters of the game. Future work involves taking advantage of the KKT matrix structure to increase computation speed, and extensions to the area of learning general-sum games.
References
[1] Ling, C. K., Fang, F., & Kolter, J. Z. (2018). What game are we playing? end-to-end learning in normal and extensive form games. arXiv preprint arXiv:1805.02777.
[2] B. von Stengel. Efficient computation of behavior strategies.Games and Economics Behavior,14(0050):220–246, 1996.
[3] Boyd, S., Boyd, S. P., & Vandenberghe, L. (2004). Convex optimization. Cambridge university press.