very Deep Convoloutional Networks for Large-Scale Image Recognition: Difference between revisions
| Line 68: | Line 68: | ||
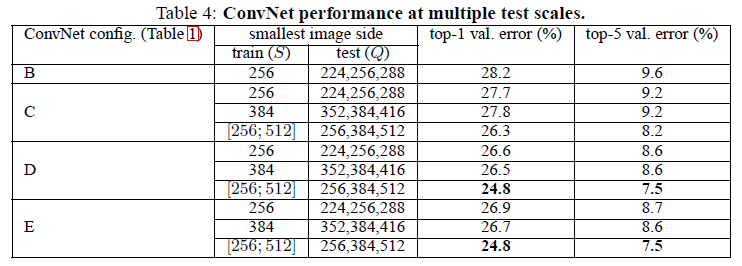
In addition to single scale evaluation stated in the previous section, in this paper, the effect of scale jittering at test time is assessed by running a model over several rescaled versions of a test image (corresponding to different values of Q), followed by averaging the resulting class posteriors. The results indicate that scale jittering at test time leads to better performance (as compared to evaluating the same model at a single scale). | In addition to single scale evaluation stated in the previous section, in this paper, the effect of scale jittering at test time is assessed by running a model over several rescaled versions of a test image (corresponding to different values of Q), followed by averaging the resulting class posteriors. The results indicate that scale jittering at test time leads to better performance (as compared to evaluating the same model at a single scale). | ||
Their best single-network performance on the validation set is 24.8%/7.5% top-1/top-5 error. On the test set, the configuration E achieves 7.3% top-5 error. | |||
[[File:ConvNet2.PNG | center]] | |||
== Appendix A: Localization== | == Appendix A: Localization== | ||
Revision as of 19:41, 5 December 2015
Introduction
In this paper the effect of the convolutional network depth on its accuracy in the large-scale image recognition setting is investigated. It was demonstrated that the representation depth is beneficial for the classification accuracy and the main contribution is a thorough evaluation of networks of increasing depth using a certain architecture with very small (3×3) convolution filters. Basically, they fix other parameters of the architecture, and steadily increase the depth of the network by adding more convolutional layers, which is feasible due to the use of very small (3 × 3) convolution filters in all layers. As a result, they come up with significantly more accurate ConvNet architectures.
Conv.Net Configurations
Architecture:
During training, the image is passed through a stack of convolutional (conv.) layers with filters with a very small receptive field: 3 × 3. Spatial pooling is carried out by five max-pooling layers, which follow some of the conv. Layers. Max-pooling is performed over a 2 × 2 pixel window, with stride 2. A stack of convolutional layers (which has a different depth in different architectures) is followed by three Fully-Connected (FC) layers. The final layer is the soft-max layer and all hidden layers are equipped with the rectification non-linearity.
They don't implement Local Response Normalization (LRN) as they found such normalization does not improve the performance on the ILSVRC dataset, but leads to increased memory consumption and computation time.
Configuration:
The ConvNet configurations, evaluated in this paper, are outlined in the following table:
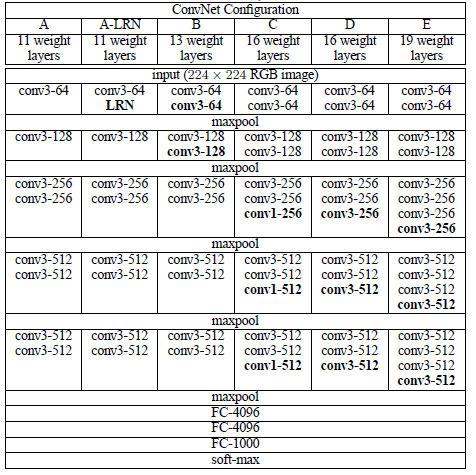
All configurations follow the aforementioned architecture and differ only in the depth from 11 weight layers in the network A (8 conv. and 3 FC layers) to 19 weight layers in the network E (16 conv. and 3 FC layers) (the added layers are shown in bold). Besides, the width of conv. layers (the number of channels) is rather small, starting from 64 in the first layer and then increasing by a factor of 2 after each max-pooling layer, until it reaches 512.
As stated in the table, multiple convolutional layers with small filters are used without any maxpooling layer between them. It is easy to show that a stack of two 3×3 conv. layers (without spatial pooling in between) has an effective receptive field of 5×5, but using two/three stack of conv. layers have 2 main advantages: 1) Two/three non-linear rectification layers are incorporated instead of a single one, which makes the decision function more discriminative. 2) the number of parameters is decreased.
In the meantime, Since the 1×1 convolution is essentially a linear projection onto the space of the same dimensionality, the incorporation of 1 × 1 conv. layers (configuration C) is a way to increase the nonlinearity of the decision function without affecting the receptive fields of the conv. layers because of the rectification function.
Classification Framework
In this section, the details of classification ConvNet training and evaluation is described.
Training:
Training is carried out by optimizing the multinomial logistic regression objective using mini-batch gradient descent with momentum. Initial weights for some layers were obtained from configuration “A” which is shallow enough to be trained with random initialization. The intermediate layers in deep models were initialized randomly. In spite of the larger number of parameters and the greater depth of the introduced nets, these nets required relatively less epochs to converge due to the following reasons: (a) implicit regularisation imposed by greater depth and smaller conv. filter sizes. (b) using pre-initialisation of certain layers.
During training, the input to the ConvNets is a fixed-size 224 × 224 RGB image. To obtain this fixed-size image, rescaling has been done while training (one crop per image per SGD iteration). In order to rescale the input image, a training scale, from which the ConvNet input is cropped, should be determined. Two approaches for setting the training scale S (Let S be the smallest side of an isotropically-rescaled training image) is considered: 1) single-scale training, that requires a fixed S. 2) multi-scale training, where each training image is individually rescaled by randomly sampling S from a certain range [Smin, Smax] .
It took 2–3 weeks to train a single net by using four NVIDIA Titan Black GPUs.
Testing:
At test time, in order to classify the input image: First, it is isotropically rescaled to a pre-defined smallest image side, denoted as Q. Then, the network is applied densely over the rescaled test image in a way that the fully-connected layers are first converted to convolutional layers (the first FC layer to a 7 × 7 conv. layer, the last two FC layers to 1 × 1 conv. layers). Then The resulting fully-convolutional net is then applied to the whole (uncropped) image.
Classification Experiments
In this section, the image classification results on the ILSVRC-2012 dataset are described:
Single-Scale Evaluation:
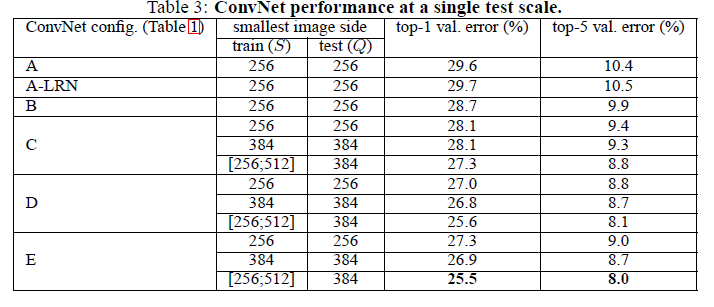
In the first part of the experiment, the test image size was set as Q = S for fixed S, and Q = 0.5(Smin + Smax) for jittered. One important result of this evaluation was that that the classification error decreases with the increased ConvNet depth. Moreover, The worse performance of the configuration with 1x1 filter (C ) in comparison with the one with 3x3 filter (D) indicates that while the additional non-linearity does help (C is better than B), it is also important to capture spatial context by using conv. filters with non-trivial receptive fields (D is better than C). Finally, scale jittering at training time leads to significantly better results than training on images with fixed smallest side. This confirms that training set augmentation by scale jittering is indeed helpful for capturing multi-scale image statistics.
Multi-Scale Evaluation
In addition to single scale evaluation stated in the previous section, in this paper, the effect of scale jittering at test time is assessed by running a model over several rescaled versions of a test image (corresponding to different values of Q), followed by averaging the resulting class posteriors. The results indicate that scale jittering at test time leads to better performance (as compared to evaluating the same model at a single scale).
Their best single-network performance on the validation set is 24.8%/7.5% top-1/top-5 error. On the test set, the configuration E achieves 7.3% top-5 error.
Appendix A: Localization
In addition to classification, the introduced architectures have been used for localization purposes. To perform object localisation, a very deep ConvNet, where the last fully connected layer predicts the bounding box location instead of the class scores is used. Apart from the last bounding box prediction layer, the ConvNet architecture D which was found to be the best-performing in the classification task is implemented and training of localisation ConvNets is similar to that of the classification ConvNets. The main difference is that the logistic regression objective is replaced with a Euclidean loss, which penalises the deviation of the predicted bounding box parameters from the ground-truth. Two testing protocols are considered: The first is used for comparing different network modifications on the validation set, and considers only the bounding box prediction for the ground truth class. (The bounding box is obtained by applying the network only to the central crop of the image.) The second, fully-fledged, testing procedure is based on the dense application of the localization ConvNet to the whole image, similarly to the classification task.
the localization experiments indicate that performance advancement brought by the introduced very deep ConvNets produces considerably better results with a simpler localization method, but a more powerful representation.
Conclusion
Very deep ConvNets are introduced in this paper. The results show that the configuration has good performance on classification and localization and significantly outperform the previous generation of models, which achieved the best results in the ILSVRC-2012 and ILSVRC-2013 competitions. They also showed that their configuration is applicable to some other datasets.