the Wake-Sleep Algorithm for Unsupervised Neural Networks: Difference between revisions
No edit summary |
No edit summary |
||
| Line 14: | Line 14: | ||
In order to see how the MDL criterion is to be implemented in this context, we must first specify a more precise network structure. The authors restrict the network to consist of stochastic binary units taking values in {0,1}, where the probability of unit ''v'' being active is given by | In order to see how the MDL criterion is to be implemented in this context, we must first specify a more precise network structure. The authors restrict the network to consist of stochastic binary units taking values in {0,1}, where the probability of unit ''v'' being active is given by | ||
::<math> P(s_v = 1) = (1 + exp(-b_v - \sum_{u}^{} s_u w_uv))^-1 </math> <br/> | ::<math> P(s_v = 1) = (1 + exp(-b_v - \sum_{u}^{} s_u w_uv))^{-1} </math> <br/> | ||
Revision as of 17:15, 18 November 2015
Introduction
In considering general learning procedures, supervised methods for neural networks are limited in that they can only be executed in specifically-structured environments. For these systems to learn, the environment must be equipped with an external "teacher" providing the network with explicit feedback on its predictive performance. From there, the system needs a means for circulating this error information across the entire network, so that the weights can be adjusted accordingly. To apply neural networks in contexts not satisfying these specific requirements, the authors purpose the wake-sleep algorithm, a two-phase procedure in which each network layer effectively learns representations of the activity in adjacent hidden layers. Here, the network is composed of feed-forward "recognition" connections used to generate an internal representation of the input, and feed-back generative connections used to produce an estimated reconstruction of the original input based on this learned internal representation. The goal is to learn an efficient representation which accurately characterizes the input to the system.
Model Structure
The wake-sleep algorithm is used to train Helmholtz machines, networks possessing the feed-forward and feed-back connections as described above. In deploying a Helmholtz machine, we hope to encode an abstraction capturing the relevant properties of the data, and using this representation, find a generative reconstruction of the original input. This is analogous to learning a data-driven "bottom-up" representation of the input that is used to inform the higher-order "top-down" reconstruction.
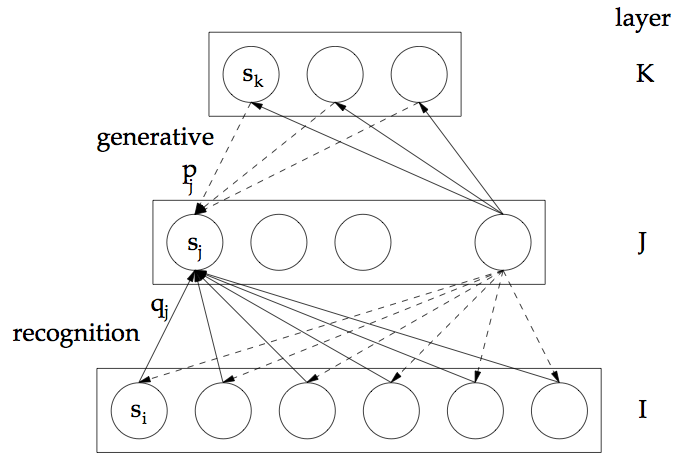
To enforce the requirement that the network produces efficient reconstructions of the data, the cost function is selected by viewing the problem as a task of information transmission. In this task, the original input vector is to be indirectly communicated from the sender to the receiver via first sending the internal representation of the datum learned by the system, and then passing along the deviation of the original input from its approximation produced by the generative reconstruction of the internal representation. Naturally, the objective then becomes to minimize the length of the sequence of bits that is needed to express the original input in this indirect manner. This corresponds to adopting the minimum description length (MDL) principle to guide the process of learning the representation. MDL is a general methodological principle stating that among a set of candidate models for the data, the one which can be represented in the fewest number of bits in the process of communication ought to be selected (see http://papers.nips.cc/paper/798-autoencoders-minimum-description-length-and-helmholtz-free-energy.pdf).
In order to see how the MDL criterion is to be implemented in this context, we must first specify a more precise network structure. The authors restrict the network to consist of stochastic binary units taking values in {0,1}, where the probability of unit v being active is given by
- [math]\displaystyle{ P(s_v = 1) = (1 + exp(-b_v - \sum_{u}^{} s_u w_uv))^{-1} }[/math]
- [math]\displaystyle{ P(s_v = 1) = (1 + exp(-b_v - \sum_{u}^{} s_u w_uv))^{-1} }[/math]