stat946w18/Predicting Floor-Level for 911 Calls with Neural Networks and Smartphone Sensor Data
Introduction
During emergency 911 calls, knowing the exact position of the victim is crucial to a fast response and a successful rescue. Problems arise when the caller is unable to give their position accurately. This can happen, for instance, when the caller is disoriented, held in hostage, or a child calling for the victim. GPS in our smartphones can give the rescuers the geographic location. However, in a tall building, GPS fails to give an accurate floor level. Previous works have explored using Wi-Fi signal or beacons placed inside the buildings, but these methods are not self-contained and require prior infrastructure knowledge.
Fortunately, today’s smartphones are equipped with many more sensors including barometer and magnetometer. Deep learning can be applied to predict floor level based on these sensor readings. Firstly, an LSTM is trained to classify whether the caller is indoor or outdoor using GPS, RSSI, and magnetometer sensor readings. Next, an unsupervised clustering algorithm is used to predict the floor level depending on the barometric pressure difference. With these two parts working together, a self-contained floor level prediction system can achieve 100% accuracy, without any outside knowledge.
Data Description
The author developed an iOS app called Sensory and used it to collect data on an iPhone 6. The following sensor readings are recorded: indoors, created at, session id, floor, RSSI strength, GPS latitude, GPS longitude, GPS vertical accuracy, GPS horizontal accuracy, GPS course, GPS speed, barometric relative altitude, barometric pressure, environment context, environment mean building floors, environment activity, city name, country name, magnet x, magnet y, magnet z, magnet total.
The indoor-outdoor data has to be manually entered as soon as the user enters or exits a building. To gather the data for floor level prediction, the authors conducted 63 trials among five different buildings throughout New York City. The actual floor level was recorded manually for validation purposes only, since unsupervised learning is being used.
Methods
The proposed method first determines if the user is indoors or outdoors, and detect the instances of transition between them. Then, vertical height is estimated from the barometer. Finally, the exact floor level is predicted through clustering techniques. Indoor/outdoor classification is critical to the working of this method. Once the user is detected to be outdoors, he is assumed to be at the ground level. The vertical height and floor estimations are applied only when the user is indoors. The indoor/outdoor transitions are used to save the barometer readings at the ground level for use as reference pressure.
Indoor/Outdoor Classification
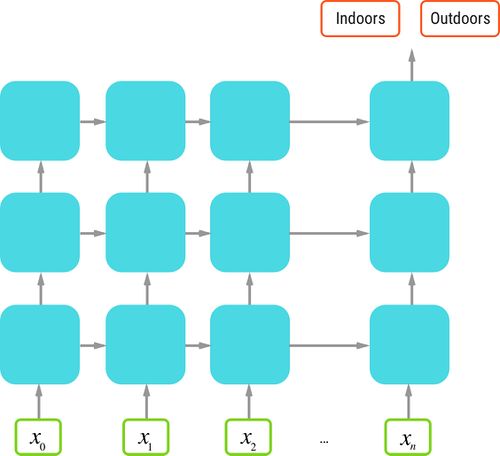
An LSTM network is used to solve the indoor-outdoor classification problem. Here is a diagram of the network architecture.
Figure 1: LSTM network architecture. A 3-layer LSTM. Inputs are sensor readings for d consecutive time-steps. Target is y = 1 if indoors and y = 0 if outdoors.
[math]\displaystyle{ X_i }[/math] contains a set of [math]\displaystyle{ d }[/math] consecutive sensor readings, i.e. [math]\displaystyle{ X_i = [x_1, x_2,...,x_d] }[/math]. [math]\displaystyle{ Y }[/math] is labelled as 0 for outdoors and 1 for indoors. [math]\displaystyle{ d }[/math] is chosen to be 3 by random-search so that [math]\displaystyle{ X }[/math] has 3 points [math]\displaystyle{ X_i = [x_{j-1}, x_j, x_{j+1}] }[/math] and the middle [math]\displaystyle{ x_j }[/math] is used for the [math]\displaystyle{ y }[/math] label. The LSTM contains three layers. Layers one and two have 50 neurons followed by a dropout layer set to 0.2. Layer 3 has two neurons fed directly into a one-neuron feedforward layer with a sigmoid activation function. The input is the sensor readings, and the output is the indoor-outdoor label. The objective function is the cross-entropy between the true label and the prediction.
\begin{equation} C(y_i, \hat{y}_i) = \frac{1}{n} \sum_{i=1}^{n} -(y_i log(\hat{y_i}) + (1 - y_i) log(1 - \hat{y_i})) \label{equation:binCE} \end{equation}
The main reason why the neural network is able to predict whether the user is indoor or outdoor is that walls of buildings interfere with the GPS signals. The LSTM is able to find the pattern in the GPS signal strength in combination with other sensor readings to give an accurate prediction. However, the change in GPS signal does not happen instantaneously as the user walks indoor. Thus, a window of 20 seconds is allowed, and the minimum barometric pressure reading within that window is recorded as the ground floor.
Indoor/Outdoor Transition
To determine the exact time the user makes an indoor-outdoor transition, two vector masks are convolved across the LSTM predictions.
\begin{equation} V_1 = [1, 1, 1, 1, 1, 0, 0, 0, 0, 0] \end{equation}
\begin{equation} V_2 = [0, 0, 0, 0, 0, 1, 1, 1, 1, 1] \end{equation}
The Jaccard distances is then calculated by the following equation:
\begin{equation} J_j = J(s_i, V_j) = \frac{|s_i \cap V_j|}{|s_i| + |V_j| - |s_i \cap V_j|} \label{equation:Jaccard} \end{equation}
If the Jaccard distance is greater than the threshold 0.4, it means the transition occurred in the vicinity of the range of the vector mask. These sets of transition windows are then merged if they are close together, and the center of the merged windows are marked as the transition points.
Vertical Height Estimation
Once the barometric pressure of the ground floor is known, the user’s current relative altitude can be calculated by the international pressure equation, where [math]\displaystyle{ m_\Delta }[/math] is the estimated height, [math]\displaystyle{ p_1 }[/math] is the pressure reading of the device, and [math]\displaystyle{ p_0 }[/math] is the reference pressure at ground level while transitioning from outdoor to indoor.
\begin{equation} m_\Delta = f_{floor}(p_0, p_1) = 44330 (1 - (\frac{p_1}{p_0})^{\frac{1}{5.255}}) \label{equation:baroHeight} \end{equation}
Floor Estimation
Given the user’s relative altitude, the floor level can be determined. However, this is not a straightforward task because different buildings have different floor heights, different floor labeling (E.g. not including the 13th floor), and floor heights within the same building can vary from floor to floor. To solve these problems, altitudes data collected are clustered into groups. Each cluster represent the approximate altitude of a floor.
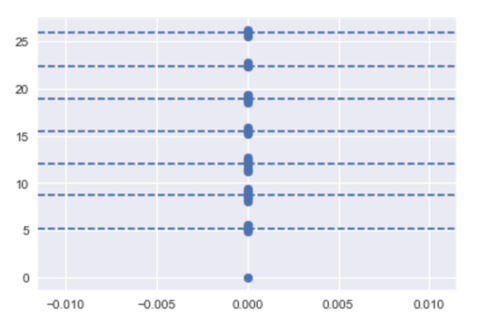
Here is an example of altitude data collected across 41 trials in the Uris Hall building in New York City. Each dashed line represent the center of a cluster.
Figure 2: Distribution of measurements across 41 trials in the Uris Hall building in New York City. A clear size difference is specially noticeable at the lobby. Each dotted line corresponds to an actual floor in the building learned from clustered data-points.
Here is the algorithm for the floor level prediction.
Experiments and Results
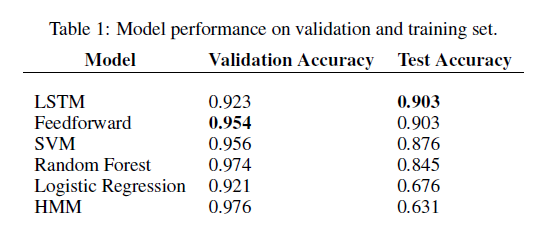
Here are the results for the indoor-outdoor classification problem using different machine learning techniques. LSTM has the best performance on the test set. The LSTM is trained for 24 epochs with a batch size of 128. All the hyper-parameters such as learning rate(0.006), number of layers, d size, number of hidden units and dropout rate were searched through random search algorithm.
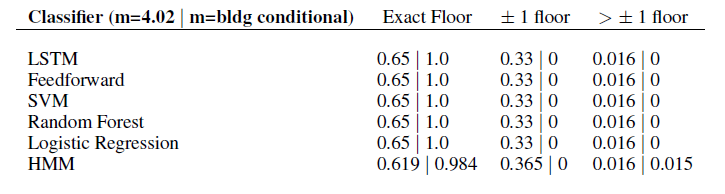
The following are the results for the floor level prediction. The left side shows the accuracy using a fixed floor height, where the right side uses clustering. When clustering is used, 100% accuracy can be achieved.
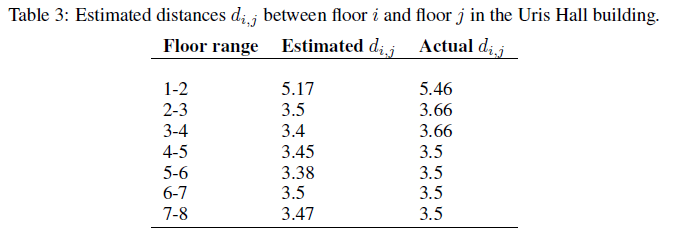
Here is the comparison between the estimated floor height and the ground truth in the Uris Hall building.
Criticism
This paper is an interesting application of deep learning and achieved an outstanding result of 100% accuracy. However, it offers no new theoretical discoveries. The machine learning techniques used are fairly standard. The neural networks used only contains 3 layers, and the clustering is applied on a one-dimensional data. This makes me question whether deep learning is suitable for this task.
It was explained in the paper that there are many cases where the system does not work. Some cases that were mentioned include: buildings with glass walls, delayed GPS signals, and pressure changes caused by air conditioning. Other examples I can think of are: uneven floors with some area higher than others, floors rarely visited, and tunnels from one building to another. These special cases are not mentioned in the paper.
Another weakness of the method comes from the clustering technique. It requires a fair bit of training data. The author suggested two approaches. First, the data can be stored in the individual smartphone. This is not realistic as most people do not visit every single floor of every building, even if it is their own apartment buildings. The second approach is to let a central system (emergency department) to collect data from multiple users (witch is what the paper’s results are based on). This is a serious violation of personal privacy and should not be legal.
An additional issue is the use of barometer to estimate floor height indoors. Many buildings in modern architecture have windowless designs and air circulation is performed by the HVAC system. Such system could have a dramatic impact to indoor barometer readings which is based on atmospheric pressure. The author performed the tests at the Uris Hall building which clearly has windows.
Aside from all the technical issues, would it not be easier to just let the response team carry a barometer with them and search for the floor with the transmitted pressure reading?