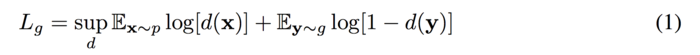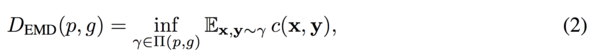stat946w18/IMPROVING GANS USING OPTIMAL TRANSPORT: Difference between revisions
| Line 42: | Line 42: | ||
[[File: equation5.png|550px]] | [[File: equation5.png|550px]] | ||
where the <math> | where the <math> \mathcal{M} </math> is the set of all joint distribution over <math> X </math> and <math> Y </math> | ||
Revision as of 12:50, 13 March 2018
Introduction
Generative Adversarial Networks (GANs) are powerful generative models. A GAN model consists of a generator and a discriminator or critic. The generator is a neural network which is trained to generate data having a distribution matched with the distribution of the real data. The critic is also a neural network, which is trained to separate the generated data from the real data. A loss function that measures the distribution distance between the generated data and the real one is important to train the generator.
Optimal transport theory evaluates the distribution distance based on metric, which provides another method for generator training. The main advantage of optimal transport theory over the distance measurement in GAN is its closed form solution for having a tractable training process. But the theory might also result in inconsistency in statistical estimation due to the given biased gradients if the mini-batches method is applied.
This paper presents a variant GANs named OT-GAN, which incorporates a discriminative metric called 'MIni-batch Energy Distance' into its critic in order to overcome the issue of biased gradients.
GANs and Optimal Transport
Generative Adversarial Nets
Original GAN was firstly reviewed. The objective function of the GAN:
The goal of GANs is to train the generator g and the discriminator d finding a pair of (g,d) to achieve Nash equilibrium. However, it could cause failure of converging since the generator and the discriminator are trained based on gradient descent techniques.
Wasserstein distance (Earth-Mover Distance)
In order to solve the problem of convergence failure, Arjovsky et. al. (2017) suggested Wasserstein distance (Earth-Mover distance) based on the optimal transport theory.
where [math]\displaystyle{ \prod (p,g) }[/math] is the set of all joint distributions [math]\displaystyle{ \gamma (x,y) }[/math] with marginals [math]\displaystyle{ p(x), g(y) }[/math] and [math]\displaystyle{ c(x,y) }[/math] is a cost function which takes to be the Euclidean distance.
The Earth-Mover Distance can be considered as moving the minimum amount of points between distribution [math]\displaystyle{ g(y) }[/math] and [math]\displaystyle{ p(x) }[/math] such that the generator distribution [math]\displaystyle{ g(y) }[/math] is similar to the real data distribution [math]\displaystyle{ p(x) }[/math].
Consider that solving the Wasserstein distance is usually not possible, the proposed Wasserstein GAN (W-GAN) provides an estimated solution by switching the optimal transport problem into dual formulation using a set of 1-Lipschitz functions. A neural network can then be used to obtain an estimation.
W-GAN solves the unstable training process of original GAN and it can solve the optimal transport problem approximately, but it is still intractable.
The training process becomes traceable and a fully connected multi-layer network is sufficient for the training. However, the calculation of the Wasserstein distance is still an approximation and we can not have a fine-optimized critic.
Sinklhorn Distance
Genevay et al. (2017) proposed to use the primal formulation of optimal transport instead of the dual formulation to generative modeling. They introduced Sinkhorn distance which is a smoothed generalization of the Earth Mover distance.
![]()
It introduced a constant [math]\displaystyle{ \beta }[/math] to restricted the entropy of the joint distribution [math]\displaystyle{ \prod_{\beta} (p,g) }[/math]. This distanc could generalize to approximate the mini-batches of data [math]\displaystyle{ X ,Y }[/math] with [math]\displaystyle{ K }[/math] vectors of [math]\displaystyle{ x, y }[/math]. The [math]\displaystyle{ i, j }[/math] th entry of the cost matrix [math]\displaystyle{ C }[/math] can be interpreted as the cost it needs to transport the [math]\displaystyle{ x_i }[/math] in mini-batch X to the [math]\displaystyle{ y_i }[/math] in mini-batch [math]\displaystyle{ Y }[/math]. The resulting distance will be:
where the [math]\displaystyle{ \mathcal{M} }[/math] is the set of all joint distribution over [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math]