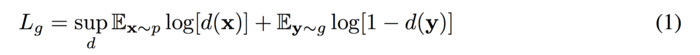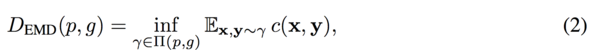stat946w18/IMPROVING GANS USING OPTIMAL TRANSPORT: Difference between revisions
| Line 1: | Line 1: | ||
== Introduction == | == Introduction == | ||
Generative Adversarial Networks (GANs) are powerful generative models. A GAN model consists of a generator and a discriminator or critic. The generator is a neural network which is trained to generate data having a distribution matched with the | Generative Adversarial Networks (GANs) are powerful generative models. A GAN model consists of a generator and a discriminator or critic. The generator is a neural network which is trained to generate data having a distribution matched with the distribution of the real data. The critic is also a neural network, which is trained to separate the generated data from the real data. A loss function that measures the distribution distance between the generated data and the real one is important to train the generator. | ||
Optimal transport theory | Optimal transport theory evaluates the distribution distance based on metric, which provides another method for generator training. The main advantage of optimal transport theory over the distance measurement in GAN is its closed form solution for having a tractable training process. But the theory might also result in inconsistency in statistical estimation due to the given biased gradients if the mini-batches method is applied. | ||
This paper presents a variant GANs named OT-GAN, which incorporates a MIni-batch Energy Distance into its critic | This paper presents a variant GANs named OT-GAN, which incorporates a discriminative metric called 'MIni-batch Energy Distance' into its critic in order to overcome the issue of biased gradients. | ||
== GANs AND OPTIMAL TRANSPORT == | == GANs AND OPTIMAL TRANSPORT == | ||
Revision as of 01:41, 13 March 2018
Introduction
Generative Adversarial Networks (GANs) are powerful generative models. A GAN model consists of a generator and a discriminator or critic. The generator is a neural network which is trained to generate data having a distribution matched with the distribution of the real data. The critic is also a neural network, which is trained to separate the generated data from the real data. A loss function that measures the distribution distance between the generated data and the real one is important to train the generator.
Optimal transport theory evaluates the distribution distance based on metric, which provides another method for generator training. The main advantage of optimal transport theory over the distance measurement in GAN is its closed form solution for having a tractable training process. But the theory might also result in inconsistency in statistical estimation due to the given biased gradients if the mini-batches method is applied.
This paper presents a variant GANs named OT-GAN, which incorporates a discriminative metric called 'MIni-batch Energy Distance' into its critic in order to overcome the issue of biased gradients.
GANs AND OPTIMAL TRANSPORT
Generative Adversarial Nets
The objective function of the GAN:
The goal of GANs is to train the generator g and the discriminator d and find a pair of (g,d) which the game reaches a Nash equilibrium. However, it could cause failure to converge since the generator and the discriminator is trained using gradient descent techniques which are not used to find a Nash equilibrium of a game.
In order to solve this problem, Arjovsky et al (2017) suggested a new GAN with the optimal transport theory.