stat946f11: Difference between revisions
| Line 4: | Line 4: | ||
===Notation=== | ===Notation=== | ||
We will begin with short section about the notation used in these notes. | We will begin with short section about the notation used in these notes. | ||
Capital letters will be used to denote random variables and lower case letters denote observations for those random variables: | Capital letters will be used to denote random variables and lower case letters denote observations for those random variables: | ||
Revision as of 11:54, 4 October 2011
Sign up for your presentation
Introduction
Notation
We will begin with short section about the notation used in these notes. Capital letters will be used to denote random variables and lower case letters denote observations for those random variables:
- [math]\displaystyle{ \{X_1,\ X_2,\ \dots,\ X_n\} }[/math] random variables
- [math]\displaystyle{ \{x_1,\ x_2,\ \dots,\ x_n\} }[/math] observations of the random variables
The joint probability mass function can be written as:
or as shorthand, we can write this as [math]\displaystyle{ p( x_1, x_2, \dots, x_n ) }[/math]. In these notes both types of notation will be used. We can also define a set of random variables [math]\displaystyle{ X_Q }[/math] where [math]\displaystyle{ Q }[/math] represents a set of subscripts.
Example
Let [math]\displaystyle{ A = \{1,4\} }[/math], so [math]\displaystyle{ X_A = \{X_1, X_4\} }[/math]; [math]\displaystyle{ A }[/math] is the set of indices for
the r.v. [math]\displaystyle{ X_A }[/math].
Also let [math]\displaystyle{ B = \{2\},\ X_B = \{X_2\} }[/math] so we can write
Graphical Models
Graphs can be represented as a pair of vertices and edges: [math]\displaystyle{ G = (V, E). }[/math]
Two branches of graphical representations of distributions are commonly used in graphical models; Bayesian networks and Markov networks. Both families encompass the properties of factorization and independence, but they differ in the factorization of the distribution that they induce.
- [math]\displaystyle{ V }[/math] is the set of nodes (vertices).
- [math]\displaystyle{ E }[/math] is the set of edges.
If the edges have a direction associated with them then we consider the graph to be directed as in Figure 1, otherwise the graph is undirected as in Figure 2.
We will use graphs in this course to represent the relationship between different random variables.
Directed graphical models (Bayesian networks)
In the case of directed graphs, the direction of the arrow indicates "causation". For example:
[math]\displaystyle{ A \longrightarrow B }[/math]: [math]\displaystyle{ A\,\! }[/math] "causes" [math]\displaystyle{ B\,\! }[/math].
In this case we must assume that our directed graphs are acyclic. If our causation graph contains a cycle then it would mean that for example:
- [math]\displaystyle{ A }[/math] causes [math]\displaystyle{ B }[/math]
- [math]\displaystyle{ B }[/math] causes [math]\displaystyle{ C }[/math]
- [math]\displaystyle{ C }[/math] causes [math]\displaystyle{ A }[/math], again.
Clearly, this would confuse the order of the events. An example of a graph with a cycle can be seen in Figure 3. Such a graph could not be used to represent causation. The graph in Figure 4 does not have cycle and we can say that the node [math]\displaystyle{ X_1 }[/math] causes, or affects, [math]\displaystyle{ X_2 }[/math] and [math]\displaystyle{ X_3 }[/math] while they in turn cause [math]\displaystyle{ X_4 }[/math].
We will consider a 1-1 map between our graph's vertices and a set of random variables. Consider the following example that uses boolean random variables. It is important to note that the variables need not be boolean and can indeed be discrete over a range or even continuous.
Speaking about random variables, we can now refer to the relationship between random variables in terms of dependence. Therefore, the direction of the arrow indicates "conditional dependence". For example:
[math]\displaystyle{ A \longrightarrow B }[/math]: [math]\displaystyle{ B\,\! }[/math] "is dependent on" [math]\displaystyle{ A\,\! }[/math].
Example
In this example we will consider the possible causes for wet grass.
The wet grass could be caused by rain, or a sprinkler. Rain can be caused by clouds. On the other hand one can not say that clouds cause the use of a sprinkler. However, the causation exists because the presence of clouds does affect whether or not a sprinkler will be used. If there are more clouds there is a smaller probability that one will rely on a sprinkler to water the grass. As we can see from this example the relationship between two variables can also act like a negative correlation. The corresponding graphical model is shown in Figure 5.
This directed graph shows the relation between the 4 random variables. If we have the joint probability [math]\displaystyle{ P(C,R,S,W) }[/math], then we can answer many queries about this system.
This all seems very simple at first but then we must consider the fact that in the discrete case the joint probability function grows exponentially with the number of variables. If we consider the wet grass example once more we can see that we need to define [math]\displaystyle{ 2^4 = 16 }[/math] different probabilities for this simple example. The table bellow that contains all of the probabilities and their corresponding boolean values for each random variable is called an interaction table.
Example:
Now consider an example where there are not 4 such random variables but 400. The interaction table would become too large to manage. In fact, it would require [math]\displaystyle{ 2^{400} }[/math] rows! The purpose of the graph is to help avoid this intractability by considering only the variables that are directly related. In the wet grass example Sprinkler (S) and Rain (R) are not directly related.
To solve the intractability problem we need to consider the way those relationships are represented in the graph. Let us define the following parameters. For each vertex [math]\displaystyle{ i \in V }[/math],
- [math]\displaystyle{ \pi_i }[/math]: is the set of parents of [math]\displaystyle{ i }[/math]
- ex. [math]\displaystyle{ \pi_R = C }[/math] \ (the parent of [math]\displaystyle{ R = C }[/math])
- [math]\displaystyle{ f_i(x_i, x_{\pi_i}) }[/math]: is the joint p.d.f. of [math]\displaystyle{ i }[/math] and [math]\displaystyle{ \pi_i }[/math] for which it is true that:
- [math]\displaystyle{ f_i }[/math] is nonnegative for all [math]\displaystyle{ i }[/math]
- [math]\displaystyle{ \displaystyle\sum_{x_i} f_i(x_i, x_{\pi_i}) = 1 }[/math]
Claim: There is a family of probability functions [math]\displaystyle{ P(X_V) = \prod_{i=1}^n f_i(x_i, x_{\pi_i}) }[/math] where this function is nonnegative, and
To show the power of this claim we can prove the equation (\ref{eqn:WetGrass}) for our wet grass example:
We want to show that
Consider factors [math]\displaystyle{ f(C) }[/math], [math]\displaystyle{ f(R,C) }[/math], [math]\displaystyle{ f(S,C) }[/math]: they do not depend on [math]\displaystyle{ W }[/math], so we can write this all as
since we had already set [math]\displaystyle{ \displaystyle \sum_{x_i} f_i(x_i, x_{\pi_i}) = 1 }[/math].
Let us consider another example with a different directed graph.
Example:
Consider the simple directed graph in Figure 6.

Assume that we would like to calculate the following: [math]\displaystyle{ p(x_3|x_2) }[/math]. We know that we can write the joint probability as:
We can also make use of Bayes' Rule here:
We also need
Thus,
Theorem 1.
.
In our simple graph, the joint probability can be written as
Instead, had we used the chain rule we would have obtained a far more complex equation:
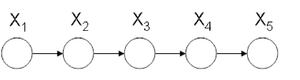
The Markov Property, or Memoryless Property is when the variable [math]\displaystyle{ X_i }[/math] is only affected by [math]\displaystyle{ X_j }[/math] and so the random variable [math]\displaystyle{ X_i }[/math] given [math]\displaystyle{ X_j }[/math] is independent of every other random variable. In our example the history of [math]\displaystyle{ x_4 }[/math] is completely determined by [math]\displaystyle{ x_3 }[/math].
By simply applying the Markov Property to the chain-rule formula we would also have obtained the same result.
Now let us consider the joint probability of the following six-node example found in Figure 7.
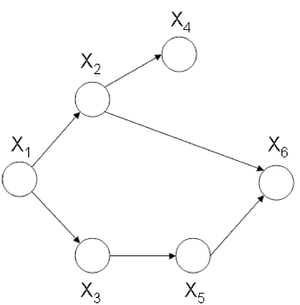
If we use Theorem 1 it can be seen that the joint probability density function for Figure 7 can be written as follows:
Once again, we can apply the Chain Rule and then the Markov Property and arrive at the same result.
Independence
Marginal independence
We can say that [math]\displaystyle{ X_A }[/math] is marginally independent of [math]\displaystyle{ X_B }[/math] if:
Conditional independence
We can say that [math]\displaystyle{ X_A }[/math] is conditionally independent of [math]\displaystyle{ X_B }[/math] given [math]\displaystyle{ X_C }[/math] if:
Aside: Before we move on further, we first define the following terms:
- I is defined as an ordering for the nodes in graph C.
- For each [math]\displaystyle{ i \in V }[/math], [math]\displaystyle{ V_i }[/math] is defined as a set of all nodes that appear earlier than i excluding [math]\displaystyle{ \pi_i }[/math].
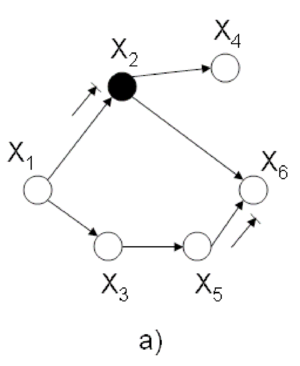
Let us consider the example of the six node figure given above (Figure 7). We can define [math]\displaystyle{ I }[/math] as follows:
We can then easily compute [math]\displaystyle{ V_i }[/math] for say [math]\displaystyle{ i=3,6 }[/math].
We would be interested in finding the conditional independence between random variables in this graph. We know [math]\displaystyle{ X_i \perp X_{v_i} | X_{\pi_i} }[/math] for each [math]\displaystyle{ i }[/math]. So:
[math]\displaystyle{ X_1 \perp \phi | \phi }[/math],
[math]\displaystyle{ X_2 \perp \phi | X_1 }[/math],
[math]\displaystyle{ X_3 \perp X_2 | X_1 }[/math],
[math]\displaystyle{ X_4 \perp \{X_1,X_3\} | X_2 }[/math],
[math]\displaystyle{ X_5 \perp \{X_1,X_2,X_4\} | X_3 }[/math],
[math]\displaystyle{ X_6 \perp \{X_1,X_3,X_4\} | \{X_2,X_5\} }[/math]
To illustrate why this is true we can take a simple example. Show that:
Proof: first, we know [math]\displaystyle{ P(X_1,X_2,X_3,X_4,X_5,X_6) = P(X_1)P(X_2|X_1)P(X_3|X_1)P(X_4|X_2)P(X_5|X_3)P(X_6|X_5,X_2)\,\! }[/math]
then
The other conditional independences can be proven through a similar process.
Sampling
Even if using graphical models helps a lot facilitate obtaining the joint probability, exact inference is not always feasible. Exact inference is feasible in small to medium-sized networks only. Exact inference consumes such a long time in large networks. Therefore, we resort to approximate inference techniques which are much faster and usually give pretty good results.
In sampling, random samples are generated and values of interest are computed from samples, not original work.
As an input you have a Bayesian network with set of nodes [math]\displaystyle{ X\,\! }[/math]. The sample taken may include all variables (except evidence E) or a subset. Sample schemas dictate how to generate samples (tuples). Ideally samples are distributed according to [math]\displaystyle{ P(X|E)\,\! }[/math]
Some sampling algorithms:
- Forward Sampling
- Likelihood weighting
- Gibbs Sampling (MCMC)
- Blocking
- Rao-Blackwellised
- Importance Sampling
Bayes Ball
The Bayes Ball algorithm can be used to determine if two random variables represented in a graph are independent. The algorithm can show that either two nodes in a graph are independent OR that they are not necessarily independent. The Bayes Ball algorithm can not show that two nodes are dependant. The algorithm will be discussed further in later parts of this section.
Canonical Graphs
In order to understand the Bayes Ball algorithm we need to first introduce 3 canonical graphs.
Markov Chain (also called serial connection)
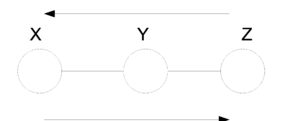
In the following graph (Figure 8 X is independent of Z given Y.
We say that: [math]\displaystyle{ X }[/math] [math]\displaystyle{ \perp }[/math] [math]\displaystyle{ Z }[/math] [math]\displaystyle{ | }[/math] [math]\displaystyle{ Y }[/math]
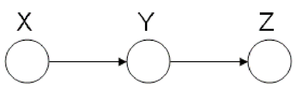
We can prove this independence:
Where
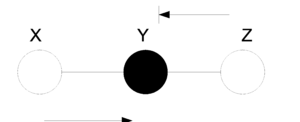
Hidden Cause (diverging connection)
In the Hidden Cause case we can say that X is independent of Z given Y. In this case Y is the hidden cause and if it is known then Z and X are considered independent.
We say that: [math]\displaystyle{ X }[/math] [math]\displaystyle{ \perp }[/math] [math]\displaystyle{ Z }[/math] [math]\displaystyle{ | }[/math] [math]\displaystyle{ Y }[/math]
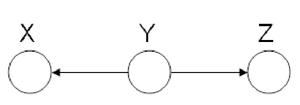
The proof of the independence:
The Hidden Cause case is best illustrated with an example:
In Figure 10 it can be seen that both "Shoe Size" and "Grey Hair" are dependant on the age of a person. The variables of "Shoe size" and "Grey hair" are dependent in some sense, if there is no "Age" in the picture. Without the age information we must conclude that those with a large shoe size also have a greater chance of having gray hair. However, when "Age" is observed, there is no dependence between "Shoe size" and "Grey hair" because we can deduce both based only on the "Age" variable.
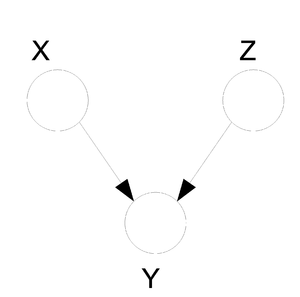
Explaining-Away (converging connection)
Finally, we look at the third type of canonical graph: Explaining-Away Graphs. This type of graph arises when a phenomena has multiple explanations. Here, the conditional independence statement is actually a statement of marginal independence: [math]\displaystyle{ X \amalg Z }[/math].
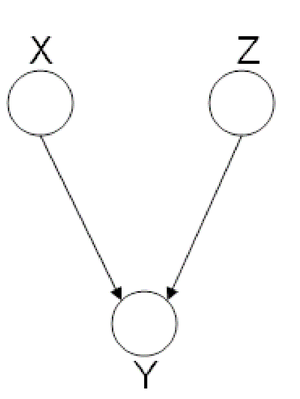
In these types of scenarios, variables X and Z are independent. However, once the third variable Y is observed, X and Z become dependent (Fig. 11).
To clarify these concepts, suppose Bob and Mary are supposed to meet for a noontime lunch. Consider the following events:
If Mary is late, then she could have been kidnapped by aliens. Alternatively, Bob may have forgotten to adjust his watch for daylight savings time, making him early. Clearly, both of these events are independent. Now, consider the following probabilities:
We expect [math]\displaystyle{ P( late = 1 ) \lt P( aliens = 1 ~|~ late = 1 ) }[/math] since [math]\displaystyle{ P( aliens = 1 ~|~ late = 1 ) }[/math] does not provide any information regarding Bob's watch. Similarly, we expect [math]\displaystyle{ P( aliens = 1 ~|~ late = 1 ) \lt P( aliens = 1 ~|~ late = 1, watch = 0 ) }[/math]. Since [math]\displaystyle{ P( aliens = 1 ~|~ late = 1 ) \neq P( aliens = 1 ~|~ late = 1, watch = 0 ) }[/math], aliens and watch are not independent given late. To summarize,
- If we do not observe late, then aliens [math]\displaystyle{ ~\amalg~ watch }[/math] ([math]\displaystyle{ X~\amalg~ Z }[/math])
- If we do observe late, then aliens [math]\displaystyle{ ~\cancel{\amalg}~ watch ~|~ late }[/math] ([math]\displaystyle{ X ~\cancel{\amalg}~ Z ~|~ Y }[/math])
Bayes Ball Algorithm
Goal: We wish to determine whether a given conditional statement such as [math]\displaystyle{ X_{A} ~\amalg~ X_{B} ~|~ X_{C} }[/math] is true given a directed graph.
The algorithm is as follows:
- Shade nodes, [math]\displaystyle{ X_{C} }[/math], that are conditioned on.
- The initial position of the ball is [math]\displaystyle{ X_{A} }[/math].
- If the ball cannot reach [math]\displaystyle{ X_{B} }[/math], then the nodes [math]\displaystyle{ X_{A} }[/math] and [math]\displaystyle{ X_{B} }[/math] must be conditionally independent.
- If the ball can reach [math]\displaystyle{ X_{B} }[/math], then the nodes [math]\displaystyle{ X_{A} }[/math] and [math]\displaystyle{ X_{B} }[/math] are not necessarily independent.
The biggest challenge in the Bayes Ball Algorithm is to determine what happens to a ball going from node X to node Z as it passes through node Y. The ball could continue its route to Z or it could be blocked. It is important to note that the balls are allowed to travel in any direction, independent of the direction of the edges in the graph.
We use the canonical graphs previously studied to determine the route of a ball traveling through a graph. Using these three graphs we establish base rules which can be extended upon for more general graphs.
Markov Chain
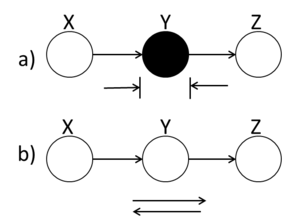
A ball traveling from X to Z or from Z to X will be blocked at node Y if this node is shaded. Alternatively, if Y is unshaded, the ball will pass through.
In (Fig. 12(a)), X and Z are conditionally independent ( [math]\displaystyle{ X ~\amalg~ Z ~|~ Y }[/math] ) while in (Fig.12(b)) X and Z are not necessarily independent.
Hidden Cause
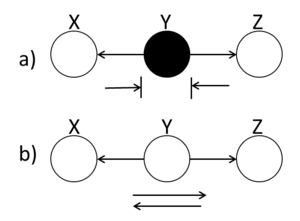
A ball traveling through Y will be blocked at Y if it is shaded. If Y is unshaded, then the ball passes through.
(Fig. 13(a)) demonstrates that X and Z are conditionally independent when Y is shaded.
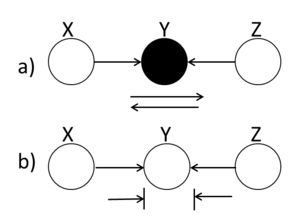
Explaining-Away
A ball traveling through Y is blocked when Y is unshaded. If Y is shaded, then the ball passes through. Hence, X and Z are conditionally independent when Y is unshaded.
Bayes Ball Examples
Example 1
In this first example, we wish to identify the behavior of a ball going from X to Y in two-node graphs.
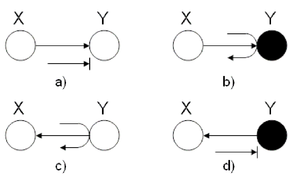
The four graphs in (Fig. 15 show different scenarios. In (a), the ball is blocked at Y. In (b) the ball passes through Y. In both of these cases, we use the rules of the Explaining Away Canonical Graph (refer to Fig. 14.) Finally, for the last two graphs, we used the rules of the Hidden Cause Canonical Graph (Fig. 13). In (c), the ball passes through Y while in (d), the ball is blocked at Y.
Example 2
Suppose your home is equipped with an alarm system. There are two possible causes for the alarm to ring:
- Your house is being burglarized
- There is an earthquake
Hence, we define the following events:
The burglary and earthquake events are independent
if the alarm does not ring. However, if the alarm does ring, then
the burglary and the earthquake events are not
necessarily independent. Also, if the alarm rings then it is
possible for a police report to be issued.
We can use the Bayes Ball Algorithm to deduce conditional independence properties from the graph. Firstly, consider figure (16(a)) and assume we are trying to determine whether there is conditional independence between the burglary and earthquake events. In figure (\ref{fig:AlarmExample1}(a)), a ball starting at the burglary event is blocked at the alarm node.
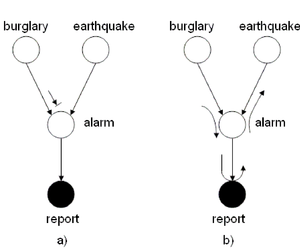
Nonetheless, this does not prove that the burglary and earthquake events are independent. Indeed, (Fig. 16(b)) disproves this as we have found an alternate path from burglary to earthquake passing through report. It follows that [math]\displaystyle{ burglary ~\cancel{\amalg}~ earthquake ~|~ report }[/math]
Example 3
Referring to figure (Fig. 17), we wish to determine whether the following conditional probabilities are true:
To determine if the conditional probability Eq.\ref{eq:c1} is true, we shade node [math]\displaystyle{ X_{2} }[/math]. This blocks balls traveling from [math]\displaystyle{ X_{1} }[/math] to [math]\displaystyle{ X_{3} }[/math] and proves that Eq.\ref{eq:c1} is valid.
After shading nodes [math]\displaystyle{ X_{3} }[/math] and [math]\displaystyle{ X_{4} }[/math] and applying the Bayes Balls Algorithm}, we find that the ball travelling from [math]\displaystyle{ X_{1} }[/math] to [math]\displaystyle{ X_{5} }[/math] is blocked at [math]\displaystyle{ X_{3} }[/math]. Similarly, a ball going from [math]\displaystyle{ X_{5} }[/math] to [math]\displaystyle{ X_{1} }[/math] is blocked at [math]\displaystyle{ X_{4} }[/math]. This proves that Eq.\ref{eq:c2 also holds.
Example 4

Consider figure (Fig. 18). Using the Bayes Ball Algorithm we wish to determine if each of the following statements are valid:
To disprove Eq.\ref{eq:c3}, we must find a path from [math]\displaystyle{ X_{4} }[/math] to [math]\displaystyle{ X_{1} }[/math] and [math]\displaystyle{ X_{3} }[/math] when [math]\displaystyle{ X_{2} }[/math] is shaded (Refer to Fig. 19(a)). Since there is no route from [math]\displaystyle{ X_{4} }[/math] to [math]\displaystyle{ X_{1} }[/math] and [math]\displaystyle{ X_{3} }[/math] we conclude that Eq.\ref{eq:c3} is true.
Similarly, we can show that there does not exist a path between [math]\displaystyle{ X_{1} }[/math] and [math]\displaystyle{ X_{6} }[/math] when [math]\displaystyle{ X_{2} }[/math] and [math]\displaystyle{ X_{3} }[/math] are shaded (Refer to Fig.19(b)). Hence, Eq.\ref{eq:c4} is true.
Finally, (Fig. 19(c)) shows that there is a route from [math]\displaystyle{ X_{2} }[/math] to [math]\displaystyle{ X_{3} }[/math] when [math]\displaystyle{ X_{1} }[/math] and [math]\displaystyle{ X_{6} }[/math] are shaded. This proves that the statement \ref{eq:c4} is false.
Theorem 2.
Define [math]\displaystyle{ p(x_{v}) = \prod_{i=1}^{n}{p(x_{i} ~|~ x_{\pi_{i}})} }[/math] to be the factorization as a multiplication of some local probability of a directed graph.
Let [math]\displaystyle{ D_{1} = \{ p(x_{v}) = \prod_{i=1}^{n}{p(x_{i} ~|~ x_{\pi_{i}})}\} }[/math]
Let [math]\displaystyle{ D_{2} = \{ p(x_{v}): }[/math]satisfy all conditional independence statements associated with a graph [math]\displaystyle{ \} }[/math].
Then [math]\displaystyle{ D_{1} = D_{2} }[/math].
Example 5
Given the following Bayesian network (Fig.19 ): Determine whether the following statements are true or false?
a.) [math]\displaystyle{ x4\perp \{x1,x3\} }[/math]
Ans. True
b.) [math]\displaystyle{ x1\perp x6\{x2,x3\} }[/math]
Ans. True
c.) [math]\displaystyle{ x2\perp x3 \{x1,x6\} }[/math]
Ans. False
Undirected Graphical Model
Generally, the graphical model is divided into two major classes, directed graphs and undirected graphs. Directed graphs and its characteristics was described previously. In this section we discuss undirected graphical model which is also known as Markov random fields. We can define an undirected graphical model with a graph [math]\displaystyle{ G = (V, E) }[/math] where [math]\displaystyle{ V }[/math] is a set of vertices corresponding to a set of random variables and [math]\displaystyle{ E }[/math] is a set of undirected edges as shown in (Fig.20)
Conditional independence
For directed graphs Bayes ball method was defined to determine the conditional independence properties of a given graph. We can also employ the Bayes ball algorithm to examine the conditional independency of undirected graphs. Here the Bayes ball rule is simpler and more intuitive. Considering (Fig.21) , a ball can be thrown either from x to z or from z to x if y is not observed. In other words, if y is not observed a ball thrown from x can reach z and vice versa. On the contrary, given a shaded y, the node can block the ball and make x and z conditionally independent. With this definition one can declare that in an undirected graph, a node is conditionally independent of non-neighbors given neighbors. Technically speaking, [math]\displaystyle{ X_A }[/math] is independent of [math]\displaystyle{ X_C }[/math] given [math]\displaystyle{ X_B }[/math] if the set of nodes [math]\displaystyle{ X_B }[/math] separates the nodes [math]\displaystyle{ X_A }[/math] from the nodes [math]\displaystyle{ X_C }[/math]. Hence, if every path from a node in [math]\displaystyle{ X_A }[/math] to a node in [math]\displaystyle{ X_C }[/math] includes at least one node in [math]\displaystyle{ X_B }[/math], then we claim that [math]\displaystyle{ X_A \perp X_c | X_B }[/math].
Question
Is it possible to convert undirected models to directed models or vice versa?
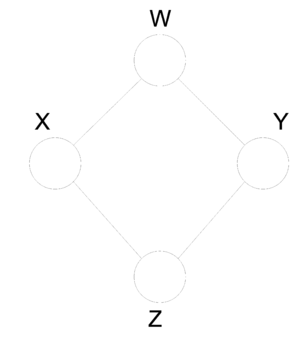
In order to answer this question, consider (Fig.22 ) which illustrates an undirected graph with four nodes - [math]\displaystyle{ X }[/math], [math]\displaystyle{ Y }[/math],[math]\displaystyle{ Z }[/math] and [math]\displaystyle{ W }[/math]. We can define two facts using Bayes ball method:
It is simple to see there is no directed graph satisfying both conditional independence properties. Recalling that directed graphs are acyclic, converting undirected graphs to directed graphs result in at least one node in which the arrows are inward-pointing(a v structure). Without loss of generality we can assume that node [math]\displaystyle{ Z }[/math] has two inward-pointing arrows. By conditional independence semantics of directed graphs, we have [math]\displaystyle{ X \perp Y|W }[/math], yet the [math]\displaystyle{ X \perp Y|\{W,Z\} }[/math] property does not hold. On the other hand, (Fig.23 ) depicts a directed graph which is characterized by the singleton independence statement [math]\displaystyle{ X \perp Y }[/math]. There is no undirected graph on three nodes which can be characterized by this singleton statement. Basically, if we consider the set of all distribution over [math]\displaystyle{ n }[/math] random variables, a subset of which can be represented by directed graphical models while there is another subset which undirected graphs are able to model that. There is a narrow intersection region between these two subsets in which probabilistic graphical models may be represented by either directed or undirected graphs.
Undirected Graphical Models
In the previous sections we discussed the Bayes Ball algorithm and the way we can use it to determine if there exists a conditional independence between two nodes in the graph. This algorithm can be easily modified to allow us to determine the same information in an undirected graph. An undirected graph that provides information about the relationships between different random variables can also be called a "Markov Random Field".
As before we must define a set of canonical graphs. The nice thing is that for undirected graphs there is really only one type of canonical graph:
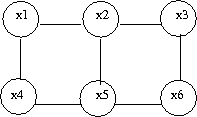
In the first figure (Fig. 21) we have no information about the node Y and so we can not say if the nodes X and Z are independent since the ball can pass from one to the other. On the other hand, in (Fig. 22) the value of Y is known and so the ball can not pass from X to Z or from Z to X. In this case we can say the X and Z are independent given Y.
Now that we have a type of Bayes Ball algorithm for both directed and undirected graphs we can ask ourselves the question: Is there an algorithm or method that we can use to convert between directed and undirected graphs?
In general: NO.
In fact, not only does there not exist a method for conversion but some graphs do not have an equivalent and may exist only in the undirected or directed form. Take the following undirected graph (Fig. 23). We can see that the radom variables that are represented in this graph have the following properties:
Now try building a directed graph with the same properties taking into consideration that directed graphs cannot contain a cycle. Under this restriction it is in fact impossible to find an equivalent directed graph that satisfies all of the above properties. Similarly, consider the following directed graph (Fig. 24). It can not be represented by any undirected graph with 3 nodes.
When we want to graph the relationships between a set of random variables it is important to consider both graph types since some relationships can only be graphed on a certain type of graph. We must therefore conclude that undirected graphs are just as important as the directed ones. For the directed graphs we have an expression for [math]\displaystyle{ P(x_V) }[/math]. We should try to develop a similar statement for the undirected graphs.
In order to develop the expression we need to introduce more terminology.
- Clique -
A subset of fully connected nodes in a graph G. Every node in the clique C is directly connected to every other node in C.
- Maximal Clique -
A clique where if any other node from the graph G is added to it then the new set is no longer a clique.
Let [math]\displaystyle{ C = /{ Set of all Maximal Cliques /}. }[/math]
Let [math]\displaystyle{ \psi_{c_i} }[/math] = A non-negative real valued function.
Now associate one [math]\displaystyle{ \psi_{c_i} }[/math] with each clique [math]\displaystyle{ c_i }[/math] then,
Where,
Conditional independence
For directed graphs Bayes ball method was defined to determine the conditional independence properties of a given graph. We can also employ the Bayes ball algorithm to examine the conditional independency of undirected graphs. Here the Bayes ball rule is simpler and more intuitive. Considering Figure.... , a ball can be thrown either from x to z or from z to x if y is not observed. In other words, if y is not observed a ball thrown from x can reach z and vice versa. On the contrary, given a shaded y, the node can block the ball and make x and z conditionally independent. With this definition one can declare that in an undirected graph, a node is conditionally independent of non-neighbors given neighbours. Technically speaking, [math]\displaystyle{ X_A }[/math] is independent of [math]\displaystyle{ X_C }[/math] given [math]\displaystyle{ X_B }[/math] if the set of nodes [math]\displaystyle{ X_B }[/math] separates the nodes [math]\displaystyle{ X_A }[/math] from the nodes [math]\displaystyle{ X_C }[/math]. Hence, if every path from a node in [math]\displaystyle{ X_A }[/math] to a node in [math]\displaystyle{ X_C }[/math] includes at least one node in [math]\displaystyle{ X_B }[/math], then we claim that [math]\displaystyle{ X_A \perp X_c | X_B }[/math].
Graphical Algorithms
In the previous chapter there were two kinds of graphical models that were used to represent dependencies between variables. One is a directed graphical model while the other is an undirected graphical model. In the case of directed graphs we can define the joint probability distribution based on a product of conditional probabilities where each node is conditioned on the value(s) of its parent(s). In the case of the undirected graphs we can define the joint probability distribution based on the normalized product of [math]\displaystyle{ \psi }[/math] functions based on the nodes that form maximal cliques in the graph. A maximal clique is a clique where we can not add an additional node such that the clique remains fully connected.
In the previous chapter we also developed the following two expressions for [math]\displaystyle{ P(x_V) }[/math]:
For Directed Graphs:
[math]\displaystyle{ P(x_V) = \prod_{i=1}^{n} P(x_i | x_{\pi_i}) }[/math]
For Undirected Graphs:
[math]\displaystyle{ P(x_{V}) = \frac{1}{Z(\Psi)} \prod_{c_i \epsilon C} \psi_{c_i} (x_{c_i}) }[/math]
Theorem: Hammersley - Clifford
If we allow [math]\displaystyle{ U_1 }[/math] to represent the set of all the decompositions of [math]\displaystyle{ P(x_{V}) }[/math] based on a certain graphical representation and we allow [math]\displaystyle{ U_2 }[/math] to represent all possible conditional probabilities of those nodes then we will find that the sets [math]\displaystyle{ U_1 }[/math] and [math]\displaystyle{ U_2 }[/math] are in fact the same set.
[math]\displaystyle{ U_{1} = \left \{ P(x_{V}) = \frac{1}{Z(\psi)} \prod_{c_i \epsilon C} \psi_{c_i} (x_{c_i}) \right \} }[/math]
[math]\displaystyle{ U_{2} = \left \{ P(x_{V}) | P(x_{V}) \mbox{ satisfies all conditional probabilities} \right \} }[/math]
Then: [math]\displaystyle{ U_{1} = U_{2} }[/math]
There is a lot of information contained in the joint probability distribution [math]\displaystyle{ P(x_{V}) }[/math]. We have defined 6 tasks (listed bellow) that we would like to accomplish with various algorithms for a given disribution [math]\displaystyle{ P(x_{V}) }[/math]. These algorithms may each be able to perform a subset of the tasks listed bellow.
Tasks:
- Marginalization
Given [math]\displaystyle{ P(x_{V}) }[/math] find [math]\displaystyle{ P(x_{A}) }[/math]
\underline{ex.} Given [math]\displaystyle{ P(x_1, x_2, ... , x_6) }[/math] find [math]\displaystyle{ P(x_2, x_6) }[/math]
- Conditioning
Given [math]\displaystyle{ P(x_V) }[/math] find [math]\displaystyle{ P(x_A|x_B) = \frac{P(x_A, x_B)}{P(x_B)} }[/math] .
- Evaluation
Evaluate the probability for a certain configuration.
- Completion
Compute the most probable configuration. In other words, which of the [math]\displaystyle{ P(x_A|x_B) }[/math] is the largest for a specific combinations of [math]\displaystyle{ A }[/math] and [math]\displaystyle{ B }[/math].
- Simulation
Generate a random configuration for [math]\displaystyle{ P(x_V) }[/math] .
- Learning
We would like to find parameters for [math]\displaystyle{ P(x_V) }[/math] .
Exact Algorithms:
We will be looking at three exact algorithms. An exact algorithm is an algorithm that will find the exact answer to one of the above tasks. The main disadvantage to the exact algorithms approach is that for large graphs which have a large number of nodes these algorithms take a long time to produce a result. When this occurs we can use inexact algorithms to more efficiently find a useful estimate.
- Elimination
- Sum-Product
- Junction Tree
General Inference:
Let us first define a set of nodes called Evidence Nodes. We will denote evidence nodes with [math]\displaystyle{ x_E }[/math]. These nodes represent the random varibles about which we have information. Similarily, let us define the set of nodes [math]\displaystyle{ x_F }[/math] as Query Nodes. These are the set of nodes for which we seek information. By Bayes Theorem we know that:
Let [math]\displaystyle{ G(V, \epsilon) }[/math] be a graph with vertices [math]\displaystyle{ V }[/math] and edges [math]\displaystyle{ \epsilon }[/math]
The group of nodes [math]\displaystyle{ V }[/math] is made up of the evidence nodes [math]\displaystyle{ E }[/math], the query nodes [math]\displaystyle{ F }[/math] and the nodes that are neither query nor evidence nodes [math]\displaystyle{ R }[/math]. We can just call [math]\displaystyle{ R }[/math] the remainder nodes. All of these sets are mutually exclusive therefore,
[math]\displaystyle{ V = E \cup F \cup R }[/math] and [math]\displaystyle{ R = V / (E \cup F) }[/math]
[math]\displaystyle{ P(x_F, x_E) = \sum_{R} P(x_V) = \sum_{R} P(x_E, x_F, x_R) }[/math]
Example:
Consider once again the example from Figure \ref{fig:ClassicExample1}. Suppose we want to calculate [math]\displaystyle{ P(x_1|\bar{x}_6) }[/math]. Where [math]\displaystyle{ \bar{x}_6 }[/math] refers to a fixed value of [math]\displaystyle{ x_6 }[/math].
If we represent the joint probabilities normally we have, \[ P(x_1, x_2, ..., x_5) = \sum_{x_6}P(x_1, x_2, ..., x_6) \] which represents a table of probabilities of size [math]\displaystyle{ 2^6 }[/math]. In general this table is of size [math]\displaystyle{ k^n }[/math] where [math]\displaystyle{ k }[/math] is the number of values each variable can take on and [math]\displaystyle{ n }[/math] is the number of vertices. In a computer algorithm this is exponential: [math]\displaystyle{ O(k^n) }[/math]
We can reduce the complexity if we represent the probabilities in factored form.
Where the computational complexity is only [math]\displaystyle{ O(nk^r) }[/math] where [math]\displaystyle{ r }[/math] is the number of parents of a node. In our case the table has been reduced to [math]\displaystyle{ 2^3 }[/math] from [math]\displaystyle{ 2^6 }[/math].
Let [math]\displaystyle{ m_i(x_{s_i}) }[/math] be the expression that arises when we perform [math]\displaystyle{ \sum_{x_i} P(x_i|x_{s_i}) }[/math] where [math]\displaystyle{ x_{s_i} }[/math] represents a set of variables other than [math]\displaystyle{ x_i }[/math].
For instance, in our example we can say that [math]\displaystyle{ m_6(x_1, x_2) = \sum_{x_6} P(x_6|x_1, x_2) }[/math] .
We know that according to Bayes Theorem we can calculate [math]\displaystyle{ P(x_1, \bar{x}_6) }[/math] and [math]\displaystyle{ P(\bar{x}_6) }[/math] separately in order to find the desired conditional probability.
Let us begin by calculating [math]\displaystyle{ P(x_1, \bar{x}_6) }[/math] .
And then we can use the above result to calculate the next desired probability. : [math]\displaystyle{ P(\bar{x}_6) = \sum_{x_1}P(x_1|\bar{x}_6) }[/math].
Finally, by using the above two results we can calculate [math]\displaystyle{ P(x_1|\bar{x}_6) = \frac{P(x_1, \bar{x}_6)}{P(\bar{x}_6)} }[/math].
Evaluation
Define [math]\displaystyle{ X_i }[/math] as an evidence node whose observed value is
[math]\displaystyle{ \overline{x_i} }[/math]. To show that [math]\displaystyle{ X_i }[/math] is fixed at the
value [math]\displaystyle{ \overline{x_i} }[/math], we define an evidence potential
[math]\displaystyle{ \delta{(x_i,\overline{x_i})} }[/math]
whose value is 1 if [math]\displaystyle{ x_i }[/math] = [math]\displaystyle{ \overline{x_i} }[/math] and 0 otherwise.
So
When we have more than one variable such as p(F[math]\displaystyle{ |\overline{E} }[/math]), the total evidence potential is:
Elimination and Directed Graphs
Given a graph G =(V,E), an evidence set E, and a query node F, we first choose an elimination ordering I such that F appears last in this ordering.
Example:
For the graph in (Fig. \ref{fig:ClassicExample1}): [math]\displaystyle{ G =(V,''E'') }[/math]. Consider once again that node [math]\displaystyle{ x_1 }[/math] is the query node and [math]\displaystyle{ x_6 }[/math] is the evidence node.
[math]\displaystyle{ I = \left\{6,5,4,3,2,1\right\} }[/math] (1 should be the last node, ordering is crucial)
We must now crete an active list. There are two rules that must be followed in order to create this list.
- For i[math]\displaystyle{ \in{V} }[/math] put [math]\displaystyle{ p(x_i|x_{\pi_i}) }[/math] in active list.
- For i[math]\displaystyle{ \in }[/math]{E} put [math]\displaystyle{ p(x_i|\overline{x_i}) }[/math] in active list.
Here, our active list is: [math]\displaystyle{ p(x_1), p(x_2|x_1), p(x_3|x_1), p(x_3|x_2), p(x_5|x_3),\underbrace{p(x_6|x_2, x_5)\delta{(\overline{x_6},x_6)}}_{\phi_6(x_2,x_5, x_6), \sum_{x6}{\phi_6}=m_{6}(x2,x5) } }[/math]
We first eliminate node [math]\displaystyle{ X_6 }[/math]. We place [math]\displaystyle{ m_{6}(x_2,x_5) }[/math] on the active list, having removed [math]\displaystyle{ X_6 }[/math]. We now eliminate [math]\displaystyle{ X_5 }[/math].
Likewise, we can also eliminate [math]\displaystyle{ X_4, X_3, X_2 }[/math](which yields the unnormalized conditional probability [math]\displaystyle{ p(x_1|\overline{x_6}) }[/math] and [math]\displaystyle{ X_1 }[/math]. Then it yields [math]\displaystyle{ m_1 = \sum_{x_1}{\phi_1(x_1)} }[/math] which is the normalization factor, [math]\displaystyle{ p(\overline{x_6}) }[/math].
Elimination and Undirected Graphs
We would also like to do this elimination on undirected graphs such as G'.
The first task is to find the maximal cliques and their associated potential functions.
maximal clique: [math]\displaystyle{ \left\{x_1, x_2\right\} }[/math], [math]\displaystyle{ \left\{x_1, x_3\right\} }[/math], [math]\displaystyle{ \left\{x_2, x_4\right\} }[/math], [math]\displaystyle{ \left\{x_3, x_5\right\} }[/math], [math]\displaystyle{ \left\{x_2,x_5,x_6\right\} }[/math]
potential functions: [math]\displaystyle{ \varphi{(x_1,x_2)},\varphi{(x_1,x_3)},\varphi{(x_2,x_4)}, \varphi{(x_3,x_5)} }[/math] and [math]\displaystyle{ \varphi{(x_2,x_3,x_6)} }[/math]
[math]\displaystyle{ p(x_1|\overline{x_6})=p(x_1,\overline{x_6})/p(\overline{x_6})\cdots\cdots\cdots\cdots\cdots(*) }[/math]
[math]\displaystyle{ p(x_1,x_6)=\frac{1}{Z}\sum_{x_2,x_3,x_4,x_5,x_6}\varphi{(x_1,x_2)}\varphi{(x_1,x_3)}\varphi{(x_2,x_4)}\varphi{(x_3,x_5)}\varphi{(x_2,x_3,x_6)}\delta{(x_6,\overline{x_6})} }[/math]
The [math]\displaystyle{ \frac{1}{Z} }[/math] looks crucial, but in fact it has no effect because for (*) both the numerator and the denominator have the [math]\displaystyle{ \frac{1}{Z} }[/math] term. So in this case we can just cancel it.
The general rule for elimination in an undirected graph is that we can remove a node as long as we connect all of the parents of that node together. Effectively, we form a clique out of the parents of that node.
Example:
For the graph G in (Fig. \ref{fig:Ex1Lab})
when we remove x1, G becomes (Fig. \ref{fig:Ex2Lab})
if we remove x2, G becomes (Fig. \ref{fig:Ex3Lab})
An interesting thing to point out is that the order of the elimination matters a great deal. Consider the two results. If we remove one node the graph complexity is slightly reduced. (Fig. \ref{fig:Ex2Lab}). But if we try to remove another node the complexity is significantly increased. (Fig. \ref{fig:Ex3Lab}). The reason why we even care about the complexity of the graph is because the complexity of a graph denotes the number of calculations that are required to answer questions about that graph. If we had a huge graph with thousands of nodes the order of the node removal would be key in the complexity of the algorithm. Unfortunately, there is no efficient algorithm that can produce the optimal node removal order such that the elimination algorithm would run quickly.
Moralization
So far we have shown how to use elimination to successively remove nodes from an undirected graph. We know that this is useful in the process of marginalization. We can now turn to the question of what will happen when we have a directed graph. It would be nice if we could somehow reduce the directed graph to an undirected form and then apply the previous elimination algorithm. This reduction is called moralization and the graph that is produced is called a moral graph.
To moralize a graph we first need to connect the parents of each node together. This makes sense intuitively because the parents of a node need to be considered together in the undirected graph and this is only done if they form a type of clique. By connecting them together we create this clique.
After the parents are connected together we can just drop the orientation on the edges in the directed graph. By removing the directions we force the graph to become undirected.
The previous elimination algorithm can now be applied to the new moral graph. We can do this by assuming that the probability functions in directed graph [math]\displaystyle{ P(x_i|\pi_{x_i}) }[/math] are the same as the mass functions from the undirected graph. [math]\displaystyle{ \psi_{c_i}(c_{x_i}) }[/math]
Example:
I = [math]\displaystyle{ \left\{x_6,x_5,x_4,x_3,x_2,x_1\right\} }[/math]
When we moralize the directed graph (Fig. \ref{fig:Moral1}), then it becomes the
undirected graph (Fig. \ref{fig:Moral2}).
Sum Product Algorithm
One of the main disadvantages to the elimination algorithm is that the ordering of the nodes defines the number of calculations that are required to produce a result. The optimal ordering is difficult to calculate and without a decent ordering the algorithm may become very slow. In response to this we can introduce the sum product algorithm. It has one major advantage over the elimination algorithm: it is faster. The sum product algorithm has the same complexity when it has to compute the probability of one node as it does to compute the probability of all the nodes in the graph. Unfortunately, the sum product algorithm also has one disadvantage. Unlike the elimination algorithm it can not be used on any graph. The sum product algorithm works only on trees.
For undirected graphs if there is only one path between any two pair of nodes then that graph is a tree (Fig. \ref{fig:UnDirTree}). If we have a directed graph then we must moralize it first. If the moral graph is a tree then the directed graph is also considered a tree (Fig. \ref{fig:DirTree}).
For the undirected graph [math]\displaystyle{ G(v, \varepsilon) }[/math] (Fig. \ref{fig:UnDirTree}) we can write the joint probability distribution function in the following way.
We know that in general we can not convert a directed graph into an undirected graph. There is however an exception to this rule when it comes to trees. In the case of a directed tree there is an algorithm that allows us to convert it to an undirected tree with the same properties.
Take the above example (Fig. \ref{fig:DirTree}) of a directed tree. We can write the joint probability distribution function as:
If we want to convert this graph to the undirected form shown in (Fig. \ref{fig:UnDirTree}) then we can use the following set of rules. \begin{thinlist}
- If [math]\displaystyle{ \gamma }[/math] is the root then: [math]\displaystyle{ \psi(x_\gamma) = P(x_\gamma) }[/math].
- If [math]\displaystyle{ \gamma }[/math] is NOT the root then: [math]\displaystyle{ \psi(x_\gamma) = 1 }[/math].
- If [math]\displaystyle{ \left\lbrace i \right\rbrace }[/math] = [math]\displaystyle{ \pi_j }[/math] then: [math]\displaystyle{ \psi(x_i, x_j) = P(x_j | x_i) }[/math].
\end{thinlist} So now we can rewrite the above equation for (Fig. \ref{fig:DirTree}) as:
Elimination Algorithm on a Tree
We will derive \textsc{Sum-Product} algorithm from the point of view of the \textsc{Eliminate} algorithm. To marginalize [math]\displaystyle{ x_1 }[/math] in (Fig. \ref{fig:TreeStdEx}),
where,
which is essentially (potential of the node)[math]\displaystyle{ \times }[/math](potential of the edge)[math]\displaystyle{ \times }[/math](message from the child).
The term "[math]\displaystyle{ m_{ji}(x_i) }[/math]" represents the intermediate factor between the eliminated variable, j, and the remaining neighbor of the variable, i. Thus, in the above case, we will use [math]\displaystyle{ m_{53}(x_3) }[/math] to denote [math]\displaystyle{ m_5(x_3) }[/math], [math]\displaystyle{ m_{42}(x_2) }[/math] to denote [math]\displaystyle{ m_4(x_2) }[/math], and [math]\displaystyle{ m_{32}(x_2) }[/math] to denote [math]\displaystyle{ m_3(x_2) }[/math]. We refer to the intermediate factor [math]\displaystyle{ m_{ji}(x_i) }[/math] as a "message" that j sends to i. (Fig. \ref{fig:TreeStdEx})
In general,Elimination To Sum Product Algorithm
The Sum-Product algorithm allows us to compute all marginals in the tree by passing messages inward from the leaves of the tree to an (arbitrary) root, and then passing it outward from the root to the leaves, again using (\ref{equ:MsgEquation}) at each step. The net effect is that a single message will flow in both directions along each edge. (See Figure \ref{fig:SumProdEx}) Once all such messages have been computed using (\ref{equ:MsgEquation}), we can compute desired marginals.
As shown in Figure \ref{fig:SumProdEx}, to compute the marginal of [math]\displaystyle{ X_1 }[/math] using elimination, we eliminate [math]\displaystyle{ X_5 }[/math], which involves computing a message [math]\displaystyle{ m_{53}(x_3) }[/math], then eliminate [math]\displaystyle{ X_4 }[/math] and [math]\displaystyle{ X_3 }[/math] which involves messages [math]\displaystyle{ m_{32}(x_2) }[/math] and [math]\displaystyle{ m_{42}(x_2) }[/math]. We subsequently eliminate [math]\displaystyle{ X_2 }[/math], which creates a message [math]\displaystyle{ m_{21}(x_1) }[/math].
Suppose that we want to compute the marginal of [math]\displaystyle{ X_2 }[/math]. As shown in Figure \ref{fig:MsgsFormed}, we first eliminate [math]\displaystyle{ X_5 }[/math], which creates [math]\displaystyle{ m_{53}(x_3) }[/math], and then eliminate [math]\displaystyle{ X_3 }[/math], [math]\displaystyle{ X_4 }[/math], and [math]\displaystyle{ X_1 }[/math], passing messages [math]\displaystyle{ m_{32}(x_2) }[/math], [math]\displaystyle{ m_{42}(x_2) }[/math] and [math]\displaystyle{ m_{12}(x_2) }[/math] to [math]\displaystyle{ X_2 }[/math].
Since the messages can be "reused", marginals over all possible elimination orderings can be computed by computing all possible messages which is small in numbers compared to the number of possible elimination orderings.
The Sum-Product algorithm is not only based on equation (\ref{equ:MsgEquation}), but also Message-Passing Protocol. Message-Passing Protocol tells us that \textit{a node can send a message to a neighbouring node when (and only when) it has received messages from all of its other neighbors}.
For Directed Graph
Previously we stated that:
Using the above equation (\ref{eqn:Marginal}), we find the marginal of [math]\displaystyle{ \bar{x}_E }[/math].
Now we denote:
Since the sets, F and E, add up to [math]\displaystyle{ \mathcal{V} }[/math], [math]\displaystyle{ p(x_v) }[/math] is equal to [math]\displaystyle{ p(x_F,x_E) }[/math]. Thus we can substitute the equation (\ref{eqn:Dir8}) into (\ref{eqn:Marginal}) and (\ref{eqn:Dir7}), and they become:
We are interested in finding the conditional probability. We substitute previous results, (\ref{eqn:Dir9}) and (\ref{eqn:Dir10}) into the conditional probability equation.
[math]\displaystyle{ p^E(x_v) }[/math] is an unnormalized version of conditional probability, [math]\displaystyle{ p(x_F|\bar{x}_E) }[/math].
For Undirected Graphs
We denote [math]\displaystyle{ \psi^E }[/math] to be:
Max-Product
We would like to find the Maximum probability that can be achieved by some set of random variables given a set of configurations. The algorithm is similar to the sum product except we replace the sum with max.
[math]\displaystyle{ p(x_F|\bar{x}_E) }[/math]
Example:
Consider the graph in Figure \ref{fig:MaxProdEx}.
Maximum configuration
We would also like to find the value of the [math]\displaystyle{ x_i }[/math]s which produces the largest value for the given expression. To do this we replace the max from the previous section with argmax.
[math]\displaystyle{ m_{53}(x_5)= argmax_{x_5}\psi{(x_5)}\psi{(x_5,x_3)} }[/math]
[math]\displaystyle{ \log{m^{max}_{ji}(x_i)}=\max_{x_j}{\log{\psi^{E}{(x_j)}}}+\log{\psi{(x_i,x_j)}}+\sum_{k\in{N(j)\backslash{i}}}\log{m^{max}_{kj}{(x_j)}} }[/math]
In many cases we want to use the log of this expression because the numbers tend to be very high. Also, it is important to note that this also works in the continuous case where we replace the summation sign with an integral.
Basic Statistical Problems
In statistics there are a number of different 'standard' problems that always appear in one form or another. They are as follows: \begin{thinlist}
- Regression
- Classification
- Clustering
- Density Estimation
\end{thinlist}
Regression
In regression we have a set of data points [math]\displaystyle{ (x_i, y_i) }[/math] for [math]\displaystyle{ i = 1...n }[/math] and we would like to determine the way that the variables x and y are related. In certain cases such as (Fig. \ref{img:regression.eps}) we try to fit a line (or other type of function) through the points in such a way that it describes the relationship between the two variables.
Once the relationship has been determined we can give a functional value to the following expression. In this way we can determine the value (or distribution) of y if we have the value for x. [math]\displaystyle{ P(y|x)=\frac{P(y,x)}{P(x)} = \frac{P(y,x)}{\int_{y}{P(y,x)dy}} }[/math]
Classification
In classification we also have a set of points [math]\displaystyle{ (x_i, y_i) }[/math] for [math]\displaystyle{ i = 1...n }[/math] but we would like to use the x and y values to determine if a certain point belongs in group A or in group B. Consider the example in (Fig. \ref{img:Classification.eps}) where two sets of points have been divided into the set + and the set - by a line. The purpose of classification is to find this line and then place any new points into one group or the other.
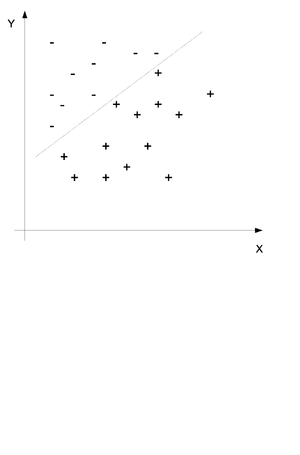
We would like to obtain the probability distribution of to following equation where c is the class and x and y are the data points. In simple terms we would like to find the probability that this point is in class c when we know that the values of X and Y are x and y.
Clustering
Clustering is somewhat like classification only that we do not know the groups before we gather and examine the data. We would like to find the probability distribution of the following equation without knowing the value of y.
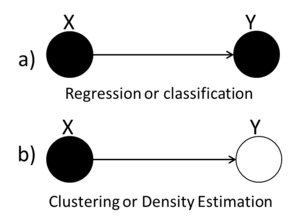
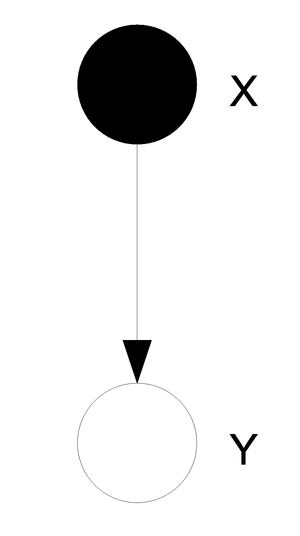
We can use graphs to represent the three types of statistical problems that have been introduced so far. The first graph (Fig. \ref{fig:RegClass} can be used to represent either the Regression or the Classification problem because both the X and the Y variables are known. The second graph (Fig. \ref{fig:Clustering}) we see that the value of the Y variable is unknown and so we can tell that this graph represents the Clustering situation.
Classification example: Naive Bayes classifier
First define a set of boolean random variables [math]\displaystyle{ X_i }[/math] and [math]\displaystyle{ Y }[/math] for [math]\displaystyle{ i = 1...n }[/math].
Then we will say that a certain pattern of Xs can either be classified as a 1 or a 0. The result of this classification will be represented by the variable Y. The graphical representation is shown in (Fig. \ref{img:classifi.eps}). One important thing to note here is that the two diagrams represent the same graph. The one on the right uses plate notation to simplify the representation of the graph for variables that are indexed. Such plate notation will also be used later in these notes.
\begin{tabular}{ccc}
[math]\displaystyle{ \stackrel{x}{\underbrace{\lt 01110\gt }_{n}} }[/math] & [math]\displaystyle{ \rightarrow }[/math] & [math]\displaystyle{ \stackrel{Y}{1} }[/math]
[math]\displaystyle{ \lt 01110\gt }[/math] & [math]\displaystyle{ \rightarrow }[/math] & [math]\displaystyle{ 0 }[/math]
\end{tabular}
We are interested in finding the following:
The classification is very intuitive in this case. We will calculate the probability that we are in class 1 and we will calculate the probability that we are in class 0. The higher probability will decide the class. For example if we have a higher probability of being in class 1 then we will place this set of Xs in class 1.
\begin{tabular}{ ccc }
[math]\displaystyle{ \widehat{y}=1 }[/math] & [math]\displaystyle{ \Leftrightarrow }[/math] & [math]\displaystyle{ P(y=1|x_1.....x_n) \gt P(y=0|x_1.....x_n) }[/math]
[math]\displaystyle{ \widehat{y}=1 }[/math] & [math]\displaystyle{ \Leftrightarrow }[/math] & [math]\displaystyle{ \frac{P(y=1|x_1.....x_n)}{P(y=0|x_1.....x_n)} \gt 1 }[/math]
& [math]\displaystyle{ \Leftrightarrow }[/math] & [math]\displaystyle{ \log{\frac{P(y=1)}{P(y=0)}} + \sum_{i=1..n}{\log{\frac{P(x_i|y=1)}{P(x_i|y=0)}}}\gt 0 }[/math]
\end{tabular}
Now if we define the following:
[math]\displaystyle{ P(y=1) =p }[/math]
[math]\displaystyle{ P(x_i|y=1)=P_{i1} }[/math]
[math]\displaystyle{ P(x_i|y=0)=P_{i0} }[/math]
We can continue with the above simplification and we arrive at the solution:
\begin{tabular}{ ccc }
[math]\displaystyle{ \widehat{y}=1 }[/math] & [math]\displaystyle{ \Leftrightarrow }[/math] & [math]\displaystyle{ x_i\log{\frac{P_{i1}}{P_{i0}}}+ (1-x_i)\log{\frac{(1-P_{i1})}{(1-P_{i0})}} \gt 0 }[/math]
& [math]\displaystyle{ \Leftrightarrow }[/math] & [math]\displaystyle{ =x_i\underbrace{\log{\frac{P_{i1}(1-P_{i0})}{P_{i0}(1-P_{i1})}}}_{slope} + \underbrace{ \log{\frac{(1-P_{i1})}{(1-P_{i0})}} }_{intercept} }[/math]
\end{tabular}
Example from last class
John is not a professional trader. However he trades in the copper market. Copper stock increase if demand for copper is more than supply, and decrease if supply is more than demand. Given supply and demand, the price of copper stock is not completely determined because some unknown factors such as prediction of political stability of countries, which supply copper or news about potential new use of copper, may impact the market.
If copper stock increases and John makes a right strategy, he will win; otherwise he will lose. Since John is not a professional trader sometimes he uses a bad trade strategy and in spite of increase of stock price he loses. S: A discrete variable which represents increasing or decreasing in copper supply.
D: A discrete variable which represents increasing or decreasing in copper demand.
C: A discrete variable which represents increasing or decreasing in stack price.
P: A discrete variable that shows whether John wins or loses in his trade.
J: A discrete variable which is 1 when John makes a right choice in his trade strategy and 0 otherwise.
p(S=1)=0.6, p(D=1)=0.7, p(J=1)=0.4
\begin{tabular}{|c|c|}
\hline % after
: \hline or \cline{col1-col2} \cline{col3-col4} ... S D & p(c=1)
\hline 1 1 & 0.5
\hline 1 0 & 0.1
\hline 0 1 & 0.85
\hline 0 0 & 0.5
\hline
\end{tabular} \begin{tabular}{|c|c|}
\hline % after
: \hline or \cline{col1-col2} \cline{col3-col4} ... J C & p(p=1)
\hline 1 1 & 0.85
\hline 1 0 & 0.5
\hline 0 1 & 0.2
\hline 0 0 & 0.1
\hline
\end{tabular} \[ p(S,D,C,J,P) = p(S)p(D)p(J)p(C|S,D)p(P|J,C) \] \end{comment}
Bayesian and Frequentist Statistics
There are two approaches of parameter estimation: the Bayesian and the Frequentist. This section focuses on the distinctions between these two approaches. We begin with a simple example,
Example:
Consider the following table of 1s and 2s. We would like to teach the computer to distinguish between the two sets of numbers so that when a person writes down a number the computer can use a statistical tool to decide if the written digit is a 1 or a 2.
\begin{tabular}{|c|c|c|}
\hline [math]\displaystyle{ \theta }[/math] & 1 & 2
\hline X & 1 & 2
\hline X & 1 & 2
\hline X & 1 & 2
\hline
\end{tabular}
The question that arises is: Given a written number what is the probability that that number belongs to the group of ones and what is the probability that that number belongs to the group of twos. In the Frequentist approach we use [math]\displaystyle{ p(x|\theta) }[/math]. We view the model [math]\displaystyle{ p(x|\theta) }[/math] as a conditional probability distribution. Here, [math]\displaystyle{ \theta }[/math] is known and X is unknown. However, Bayesian approach views X as known and [math]\displaystyle{ \theta }[/math] as unknown, which gives
Where [math]\displaystyle{ p(\theta|x) }[/math] is the posterior probability , [math]\displaystyle{ p(x|\theta) }[/math] is likelihood, and [math]\displaystyle{ p(\theta) }[/math] is the prior probability of the parameter. There are some important assumptions about this equation. First, we view [math]\displaystyle{ \theta }[/math] as a random variable. This is characteristic of the Bayesian approach, which is that all unknown quantities are treated as random variables. Second, we view the data x as a quantity to be conditioned on. Our inference is conditional on the event [math]\displaystyle{ \lbrace X=x \rbrace }[/math]. Third, in order to calculate [math]\displaystyle{ p(\theta|x) }[/math] we need [math]\displaystyle{ p(\theta) }[/math]. Finally, note that Bayes rule yields a distribution over [math]\displaystyle{ \theta }[/math], not a single estimate of [math]\displaystyle{ \theta }[/math].
The Frequentist approach tries to avoid the use of prior probabilities. The goal of Frequentist methodology is to develop an "objective" statistical theory, in which two statisticians employing the methodology must necessarily draw the same conclusions from a particular set of data.
Consider a coin-tossing experiment as an example. The model is the Bernoulli distribution, [math]\displaystyle{ p(x|\theta) = \theta^x(1-\theta)^{1-x} }[/math]. Bayesian approach requires us to assign a prior probability to [math]\displaystyle{ \theta }[/math] before observing the outcome from tossing the coin. Different conclusions may be obtained from the experiment if different priors are assigned to [math]\displaystyle{ \theta }[/math]. The Frequentist statistician wishes to avoid such "subjectivity". From another point of view, a Frequentist may claim that [math]\displaystyle{ \theta }[/math] is a fixed property of the coin, and that it makes no sense to assign probability to it. A Bayesian would believe that [math]\displaystyle{ p(\theta|x) }[/math] represents the statistician's uncertainty about the value of [math]\displaystyle{ \theta }[/math]. Bayesian statistics views the posterior probability and the prior probability alike as subjective.
Maximum Likelihood Estimator
There is one particular estimator that is widely used in Frequentist statistics, namely the maximum likelihood estimator. Recall that the probability model [math]\displaystyle{ p(x|\theta) }[/math] has the intuitive interpretation of assigning probability to X for each fixed value of [math]\displaystyle{ \theta }[/math]. In the Bayesian approach this intuition is formalized by treating [math]\displaystyle{ p(x|\theta) }[/math] as a conditional probability distribution. In the Frequentist approach, however, we treat [math]\displaystyle{ p(x|\theta) }[/math] as a function of [math]\displaystyle{ \theta }[/math] for fixed x, and refer to [math]\displaystyle{ p(x|\theta) }[/math] as the likelihood function. \[ \hat{\theta}_{ML}=argmax_{\theta}p(x|\theta) \] where [math]\displaystyle{ p(x|\theta) }[/math] is the likelihood L([math]\displaystyle{ \theta, x }[/math]) \[ \hat{\theta}_{ML}=argmax_{\theta}log(p(x|\theta)) \] where [math]\displaystyle{ log(p(x|\theta)) }[/math] is the log likelihood [math]\displaystyle{ l(\theta, x) }[/math]
Since [math]\displaystyle{ p(x) }[/math] in the denominator of Bayes Rule is independent of [math]\displaystyle{ \theta }[/math] we can consider it as a constant and we can draw the conclusion that:
Symbolically, we can interpret this as follows:
where we see that in the Bayesian approach the likelihood can be viewed as a data-dependent operator that transforms between the prior probability and the posterior probability.
Connection between Bayesian and Frequentist Statistics
Suppose in particular that we force the Bayesian to choose a particular value of [math]\displaystyle{ \theta }[/math]; that is, to remove the posterior distribution [math]\displaystyle{ p(\theta|x) }[/math] to a point estimate. Various possibilities present themselves; in particular one could choose the mean of the posterior distribution or perhaps the mode.
(i) the mean of the posterior (expectation):
is called Bayes estimate.
OR
(ii) the mode of posterior:
Note that MAP is \textsl{Maximum a posterior}.
When the prior probabilities, [math]\displaystyle{ p(\theta) }[/math] is taken to be uniform on [math]\displaystyle{ \theta }[/math], the MAP estimate reduces to the maximum likelihood estimate, [math]\displaystyle{ \hat{\theta}_{ML} }[/math].
When the prior is not taken to be uniform, the MAP estimate will be the maximization over probability distributions(the fact that the logarithm is a monotonic function implies that it does not alter the optimizing value).
Thus, one has:
as an alternative expression for the MAP estimate.
Here, [math]\displaystyle{ log (p(x|\theta)) }[/math] is log likelihood and the "penalty" is the additive term [math]\displaystyle{ log(p(\theta)) }[/math]. Penalized log likelihoods are widely used in Frequentist statistics to improve on maximum likelihood estimates in small sample settings.
Information for an Event
Consider that we have a given event E. The event has a probability P(E). As the probability of that event decreases we say that we have more information about that event. We calculate the information as:
Binomial Example
Probability Example:
Consider the set of observations [math]\displaystyle{ x = (x_1, x_2, \cdots, x_n) }[/math] which are iid, where [math]\displaystyle{ x_1, x_2, \cdots, x_n }[/math] are the different observations of [math]\displaystyle{ X }[/math]. We can also say that this random variable is parameterized by a [math]\displaystyle{ \theta }[/math] such that:
In our example we will use the following model:
Suppose now that we also have some data [math]\displaystyle{ D }[/math]:
e.g. [math]\displaystyle{ D = \left\lbrace 1,1,0,1,0,0,0,1,1,1,1,\cdots,0,1,0 \right\rbrace }[/math]
We want to use this data to estimate [math]\displaystyle{ \theta }[/math].
We would now like to use the ML technique. To do this we can construct the following graphical model:
Shade the random variables that we have already observed
Since all of the variables are iid then there are no dependencies between the variables and so we have no edges from one node to another.
How do we find the joint probability distribution function for these variables? Well since they are all independent we can just multiply the marginal probabilities and we get the joint probability.
This is in fact the likelihood that we want to work with. Now let us try to maximise it:
Take the derivative and set it to zero:
Where:
\begin{center} H = \# of all [math]\displaystyle{ x_i = 1 }[/math], e.g. \# of heads
T = \# of all [math]\displaystyle{ x_i = 0 }[/math], e.g. \# of tails
Hence, [math]\displaystyle{ T + H = n }[/math]
\end{center}
And now we can solve for [math]\displaystyle{ \theta }[/math]:
Univariate Normal
Now let us assume that the observed values come from normal distribution.
\includegraphics{images/fig4Feb6.eps}
\newline
Our new model looks like:
Now to find the likelihood we once again multiply the independent marginal probabilities to obtain the joint probability and the likelihood function.
Now, since our parameter theta is in fact a set of two parameters,
we must estimate each of the parameters separately.
Bayesian
Now we can take a look at the Bayesian approach to the same problem. Assume [math]\displaystyle{ \theta }[/math] is a random variable, and we want to find [math]\displaystyle{ P(\theta | x) }[/math]. Also, assume [math]\displaystyle{ \theta }[/math] is the mean and variance of a Gaussian distribution like in the previous example.
The graphical model is shown in Figure \ref{fig:fig5Feb6}.
We can begin with the estimation of [math]\displaystyle{ \mu }[/math]. If we assume [math]\displaystyle{ \mu }[/math] as uniform, then we become a Frequentist and the result matches the one from the ML estimation. But, if we assume [math]\displaystyle{ \mu }[/math] is normal, then we get an interesting result.
Assume [math]\displaystyle{ \mu }[/math] as normal, then
We want to find [math]\displaystyle{ P(\mu | x) }[/math] and take expectation.
Where
is a linear combination of the sample mean and the mean of the prior.
[math]\displaystyle{ P(\mu | x) }[/math] shows a distribution of [math]\displaystyle{ \mu }[/math], not just a single value. Also if we were to do the calculations for the sigma we would find the following result:
ML Estimate for Completely Observed Graphical Models
For a given graph G(V, E) each node represents a random variable. We can observe these variables and write down data for each one. If for example we had n nodes in the graph one observation would be [math]\displaystyle{ (x_1, x_2, ... , x_n) }[/math]. We can consider that these observations are independent and identically distributed. Note that [math]\displaystyle{ x_i }[/math] is not necessarily independent from [math]\displaystyle{ x_j }[/math].
Directed Graph Example
Consider the following directed graph (Fig. \ref{img:DirGraphObs.eps}).
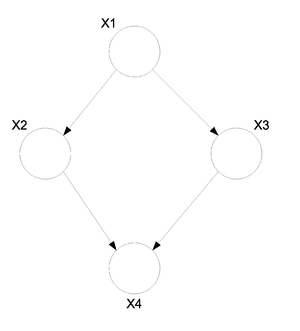
We can assume that we have made a number of observations, say n, for each of the random variables in this graph.
\begin{tabular}{ccccc}
Observation & [math]\displaystyle{ X_1 }[/math] & [math]\displaystyle{ X_2 }[/math] & [math]\displaystyle{ X_3 }[/math] & [math]\displaystyle{ X_4 }[/math]
1 & [math]\displaystyle{ x_{11} }[/math] & [math]\displaystyle{ x_{12} }[/math] & [math]\displaystyle{ x_{13} }[/math] & [math]\displaystyle{ x_{14} }[/math]
2 & [math]\displaystyle{ x_{21} }[/math] & [math]\displaystyle{ x_{22} }[/math] & [math]\displaystyle{ x_{23} }[/math] & [math]\displaystyle{ x_{24} }[/math]
3 & [math]\displaystyle{ x_{31} }[/math] & [math]\displaystyle{ x_{32} }[/math] & [math]\displaystyle{ x_{33} }[/math] & [math]\displaystyle{ x_{34} }[/math]
& & ... & &
n & [math]\displaystyle{ x_{n1} }[/math] & [math]\displaystyle{ x_{n2} }[/math] & [math]\displaystyle{ x_{n3} }[/math] & [math]\displaystyle{ x_{n4} }[/math]
\end{tabular}
Armed with this new information we would like to estimate [math]\displaystyle{ \theta = (\theta_1, \theta_2, \theta_3, \theta_4) }[/math].
We know from before that we can write the joint distribution function as:
Which means that our likelihood function is:
And our log likelihood is:
To maximise [math]\displaystyle{ \theta }[/math] we must maximise each of the [math]\displaystyle{ \theta_i }[/math] individually. The good thing is that each of our parameters appears in a different term and so the maximization of each [math]\displaystyle{ \theta_i }[/math] can be carried out independently of the others.
For discrete random variables we can use Bayes Rule. For example:
Intuitively, this means that we count the number of times that both of the variables satisfy their conditions and then divide by the number of times that only one of them satisfies the condition. Then we know what proportion of time the variables satisfy the conditions together. The proportion is in fact the [math]\displaystyle{ \theta_i }[/math] we are looking for.
We can consider another example. We can try to find:
\begin{tabular}{cccc}
[math]\displaystyle{ x_3 }[/math] & [math]\displaystyle{ x_2 }[/math] & [math]\displaystyle{ P(x_4=0|x_3, x_2) }[/math] & [math]\displaystyle{ P(x_4=1|x_3, x_2) }[/math]
0 & 0 & [math]\displaystyle{ \theta_{400} }[/math] & [math]\displaystyle{ 1 - \theta_{400} }[/math]
0 & 1 & [math]\displaystyle{ \theta_{401} }[/math] & [math]\displaystyle{ 1 - \theta_{401} }[/math]
1 & 0 & [math]\displaystyle{ \theta_{410} }[/math] & [math]\displaystyle{ 1 - \theta_{410} }[/math]
1 & 1 & [math]\displaystyle{ \theta_{411} }[/math] & [math]\displaystyle{ 1 - \theta_{411} }[/math]
\end{tabular}
For the exponential family of distributions there is a general formula for the ML estimates but it does not have a closed form solution. To get around this, one can use the Interactive Reweighted Least Squares (IRLS) method also called the Newton Raphson method to find these parameters.
In the case of the undirected model things get a little more complicated. The [math]\displaystyle{ \theta_i }[/math]s do not decouple and so they can not be calculated separately. To solve this we can use KL divergence which is a method that considers the distance between two distributions.
EM Algorithm
Let us once again consider the above example only this time the data that was supposed to be collected was not done so properly. Instead of having complete data about every random variable at every step some data points are missing.
\begin{tabular}{ccccc}
Observation & [math]\displaystyle{ X_1 }[/math] & [math]\displaystyle{ X_2 }[/math] & [math]\displaystyle{ X_3 }[/math] & [math]\displaystyle{ X_4 }[/math]
1 & [math]\displaystyle{ x_{11} }[/math] & [math]\displaystyle{ x_{12} }[/math] & [math]\displaystyle{ Z_{13} }[/math] & [math]\displaystyle{ x_{14} }[/math]
2 & [math]\displaystyle{ x_{21} }[/math] & [math]\displaystyle{ x_{22} }[/math] & [math]\displaystyle{ x_{23} }[/math] & [math]\displaystyle{ x_{24} }[/math]
3 & [math]\displaystyle{ Z_{31} }[/math] & [math]\displaystyle{ x_{32} }[/math] & [math]\displaystyle{ x_{33} }[/math] & [math]\displaystyle{ x_{34} }[/math]
4 & [math]\displaystyle{ Z_{41} }[/math] & [math]\displaystyle{ x_{42} }[/math] & [math]\displaystyle{ x_{43} }[/math] & [math]\displaystyle{ Z_{44} }[/math]
& & ... & &
n & [math]\displaystyle{ x_{n1} }[/math] & [math]\displaystyle{ x_{n2} }[/math] & [math]\displaystyle{ x_{n3} }[/math] & [math]\displaystyle{ x_{n4} }[/math]
\end{tabular}
In the above table the x values represent data as before and the Z values represent missing data (sometimes called latent data) at that point. Now the question here is how do we calculate the values of the parameters [math]\displaystyle{ \theta_i }[/math] if we do not have all the data we need. We can use the Expectation Maximization (or EM) Algorithm to estimate the parameters for the model even though we do not have a complete data set.
One thing to note here is that in the case of missing values we now have multiple local maxima in the likelihood function and as a result the EM Algorithm does not always reach the global maximum. Instead it may find one of a number of local maxima. Multiple runs of the EM Algorithm with different starting values will possibly produce different results since it may reach a different local maxima.
Define the following types of likelihoods:
complete log likelihood = [math]\displaystyle{ l_c(\theta; x, z) = log(P(x, z|\theta)) }[/math].
incomplete log likelihood = [math]\displaystyle{ l(\theta; x) = log(P(x | \theta)) }[/math].
Derivation of EM
We can rewrite the incomplete likelihood in terms of the complete likelihood. This equation is in fact the discrete case but to convert to the continuous case all we have to do is turn the summation into an integral.
Since the z has not been observed that means that [math]\displaystyle{ l_c }[/math] is in fact a random quantity. In that case we can define the expectation of [math]\displaystyle{ l_c }[/math] in terms of some arbitrary density function [math]\displaystyle{ q(z|x) }[/math].
Jensen's Inequality
In order to properly derive the formula for the EM algorithm we need to first introduce the following theorem.
For any convex function f:
This can be shown intuitively through a graph. In the (Fig. \ref{img:JensenIneq.eps}) point A is the point on the function f and point B is the value represented by the right side of the inequality. On the graph one can see why point A will be smaller than point B in a convex graph.
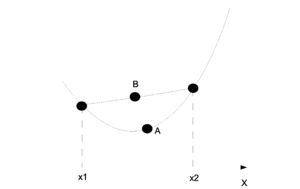
For us it is important that the log function is concave and so we must inverse the sign on the equation. Jensen's inequality is used in step (\ref{UseJensen}) of the EM derivation but for the concave log function.
Derivation
The function [math]\displaystyle{ \mathfrak{L}(q;\theta) }[/math] is called the axillary function and it is used in the EM algorithm. For the EM algorithm we have two steps that we repeat one after the other in order to get better estimates for [math]\displaystyle{ q(z|x) }[/math] and [math]\displaystyle{ \theta }[/math]. As the steps are repeated the parmeters converge to a local maximum in the likelihood function.
E-Step
M-Step
Notes About M-Step
Since the second part of the equation is only a constant with respect to [math]\displaystyle{ \theta }[/math], in the M-step we only need to maximise the expectation of the complete likelihood. The complete likelihood is the only part that still depends on [math]\displaystyle{ \theta }[/math].
Notes About E-Step
In this step we are trying to find an estimate for [math]\displaystyle{ q(z|x) }[/math]. To do this we have to maximise [math]\displaystyle{ \mathfrak{L}(q;\theta^{(t)}) }[/math].
It can be shown that [math]\displaystyle{ q(z|x) = P(z|x,\theta^{(t)}) }[/math]. So, replace [math]\displaystyle{ q(z|x) }[/math] with [math]\displaystyle{ P(z|x,\theta^{(t)}) }[/math].
But [math]\displaystyle{ \mathfrak{L}(q;\theta^{(t)}) }[/math] is the lower bound of [math]\displaystyle{ l(\theta, x) }[/math] so that means that [math]\displaystyle{ P(z|x,\theta^{(t)}) }[/math] is in fact the maximum for [math]\displaystyle{ \mathfrak{L} }[/math]. We can therefore see that we only need to do the E-Step once and then we can use that result for each repetition of the M-Step.
From the above results we can find that we have an alternative representation for the EM algorithm. We can reduce it to:
E-Step
Find [math]\displaystyle{ E[l_c(\theta; x, z)]_{P(z|x, \theta)} }[/math] only once.
M-Step
Maximise [math]\displaystyle{ E[l_c(\theta; x, z)]_{P(z|x, \theta)} }[/math] with respect to [math]\displaystyle{ theta }[/math].
The EM Algorithm is probably best understood through examples.
EM Algorithm Example
Suppose we have the two independent and identically distributed random variables:
In our case [math]\displaystyle{ y_1 = 5 }[/math] has been observed but [math]\displaystyle{ y_2 = ? }[/math] has not. Our task is to find an estimate for [math]\displaystyle{ \theta }[/math]. We will try to solve the problem first without the EM algorithm. Luckily this problem is simple enough to be solveable without the need for EM.
We take our derivative:
And now we can try the same problem with the EM Algorithm.
E-Step
M-Step
Now we pick an initial value for [math]\displaystyle{ \theta }[/math]. Usually we want to pick something reasonable. In this case it does not matter that much and we can pick [math]\displaystyle{ \theta = 10 }[/math]. Now we repeat the M-Step until the value converges.
And as we can see after a number of steps the value converges to the correct answer of 0.2. In the next section we will discuss a more complex model where it would be difficult to solve the problem without the EM Algorithm.
Mixture Models
In this section we discuss what will happen if the random variables are not identically distributed. The data will now sometimes be sampled from one distribution and sometimes from another.
Mixture of Gaussian
Given [math]\displaystyle{ P(x|\theta) = \alpha N(x;\mu_1,\sigma_1) + (1-\alpha)N(x;\mu_2,\sigma_2) }[/math]. We sample the data, [math]\displaystyle{ Data = \{x_1,x_2...x_n\} }[/math] and we know that [math]\displaystyle{ x_1,x_2...x_n }[/math] are iid. from [math]\displaystyle{ P(x|\theta) }[/math].
We would like to find:
We have no missing data here so we can try to find the parameter estimates using the ML method.
And then we need to take the log to find [math]\displaystyle{ l(\theta, Data) }[/math] and then we take the derivative for each parameter and then we set that derivative equal to zero. That sounds like a lot of work because the Gaussian is not a nice distribution to work with and we do have 5 parameters.
It is actually easier to apply the EM algorithm. The only thing is that the EM algorithm works with missing data and here we have all of our data. The solution is to introduce a latent variable z. We are basically introducing missing data to make the calculation easier to compute.
Now we have a data set that includes our latent variable [math]\displaystyle{ z_i }[/math]:
We can calculate the joint pdf by:
Let,
[math]\displaystyle{ }[/math] P(x_i|z_i,\theta)=
\left\{ \begin{tabular}{l l l}
[math]\displaystyle{ \phi_1(x_i)=N(x;\mu_1,\sigma_1) }[/math] & if & [math]\displaystyle{ z_i = 1 }[/math]
[math]\displaystyle{ \phi_2(x_i)=N(x;\mu_2,\sigma_2) }[/math] & if & [math]\displaystyle{ z_i = 0 }[/math]
\end{tabular} \right. [math]\displaystyle{ }[/math]
Now we can write
and
We can write the joint pdf as:
From the joint pdf we can get the likelihood function as:
Then take the log and find the log likelihood:
In the E-step we need to find the expectation of [math]\displaystyle{ l_c }[/math]
For now we can assume that [math]\displaystyle{ \lt z_i\gt }[/math] is known and assign it a value, let [math]\displaystyle{ \lt z_i\gt =w_i }[/math]
In M-step, we have to update our data by assuming the expectation is fixed
Taking partial derivatives of the complete log likelihood with respect to the parameters and set them equal to zero, we get our estimated parameters at (t+1).
We can verify that the results of the estimated parameters all make sense by considering what we know about the ML estimates from the standard Gaussian. But we are not done yet. We still need to compute [math]\displaystyle{ \lt z_i\gt =w_i }[/math] in the E-step.
We can now combine the two steps and we get the expectation
Using the above results for the estimated parameters in the M-step we can evaluate the parameters at (t+2),(t+3)...until they converge and we get our estimated value for each of the parameters.
The mixture model can be summarized as:
- In each step, a state will be selected according to [math]\displaystyle{ p(z) }[/math].
- Given a state, a data vector is drawn from [math]\displaystyle{ p(x|z) }[/math].
- The value of each state is independent from the previous state.
A good example of a mixture model can be seen in this example with two coins. Assume that there are two different coins that are not fair. Suppose that the probabilities for each coin are as shown in the table.
\begin{tabular}{|c|c|c|}
\hline & H & T
coin1 & 0.3 & 0.7
coin2 & 0.1 & 0.9
\hline
\end{tabular}
We can choose one coin at random and toss it in the air to see the outcome. Then we place the con back in the pocket with the other one and once again select one coin at random to toss. The resulting outcome of: HHTH \dots HTTHT is a mixture model. In this model the probability depends on which coin was used to make the toss and the probability with which we select each coin. For example, if we were to select coin1 most of the time then we would see more Heads than if we were to choose coin2 most of the time.
Hidden Markov Models
In a Hidden Markov Model (HMM) we consider that we have two levels of random variables. The first level is called the hidden layer because the random variables in that level cannot be observed. The second layer is the observed or output layer. We can sample from the output layer but not the hidden layer. The only information we know about the hidden layer is that it affects the output layer. The HMM model can be graphed as shown in Figure \ref{fig:HMM}.
In the model the [math]\displaystyle{ q_i }[/math]s are the hidden layer and the [math]\displaystyle{ y_i }[/math]s are the output layer. The [math]\displaystyle{ y_i }[/math]s are shaded because they have been observed. The parameters that need to be estimated are [math]\displaystyle{ \theta = (\pi, A, \eta) }[/math]. Where [math]\displaystyle{ \pi }[/math] represents the starting state for [math]\displaystyle{ q_0 }[/math]. In general [math]\displaystyle{ \pi_i }[/math] represents the state that [math]\displaystyle{ q_i }[/math] is in. The matrix [math]\displaystyle{ A }[/math] is the transition matrix for the states [math]\displaystyle{ q_t }[/math] and [math]\displaystyle{ q_{t+1} }[/math] and shows the probability of changing states as we move from one step to the next. Finally, [math]\displaystyle{ \eta }[/math] represents the parameter that decides the probability that [math]\displaystyle{ y_i }[/math] will produce [math]\displaystyle{ y^* }[/math] given that [math]\displaystyle{ q_i }[/math] is in state [math]\displaystyle{ q^* }[/math].
For the HMM our data comes from the output layer:
We can now write the joint pdf as:
We can use [math]\displaystyle{ a_{ij} }[/math] to represent the i,j entry in the matrix A. We can then define:
We can also define:
Now, if we take Y to be multinomial we get:
The random variable Y does not have to be multinomial, this is just an example. We can combine the first two of these definitions back into the joint pdf to produce:
We can go on to the E-Step with this new joint pdf. In the E-Step we need to find the expectation of the missing data given the observed data and the initial values of the parameters. Suppose that we only sample once so [math]\displaystyle{ n=1 }[/math]. Take the log of our pdf and we get:
Then we take the expectation for the E-Step:
If we continue with our multinomial example then we would get:
So now we need to calculate [math]\displaystyle{ E[q_0^i] }[/math] and [math]\displaystyle{ E[q_i^t q_j^{t+1}] }[/math] in order to find the expectation of the log likelihood. Let's define some variables to represent each of these quantities.
Let [math]\displaystyle{ \gamma_0^i = E[q_0^i] = P(q_0^i=1|y, \theta^{(t)}) }[/math].
Let [math]\displaystyle{ \xi_{t,t+1}^{ij} = E[q_i^t q_j^{t+1}] = P(q_t^iq_{t+1}^j|y, \theta^{(t)}) }[/math] .
We could use the sum product algorithm to calculate these equations but in this case we will introduce a new algorithm that is called the [math]\displaystyle{ \alpha }[/math] - [math]\displaystyle{ \beta }[/math] Algorithm.
The [math]\displaystyle{ \alpha }[/math] - [math]\displaystyle{ \beta }[/math] Algorithm
We have from before the expectation:
As usual we take the derivative with respect to [math]\displaystyle{ \theta }[/math] and then we set that equal to zero and solve. We obtain the following results (You can check these...) . Note that for [math]\displaystyle{ \eta }[/math] we are using a specific [math]\displaystyle{ y* }[/math] that is given.
For [math]\displaystyle{ \eta }[/math] we can think of this intuitively. It represents the proportion of times that state i prodices [math]\displaystyle{ y^* }[/math]. For example we can think of the multinomial case for y where:
Notice here that all of these parameters have been solved in terms of [math]\displaystyle{ \gamma_t^i }[/math] and [math]\displaystyle{ \xi_{t,t+1}^{ij} }[/math]. If we were to be able to calculate those two parameters then we could calculate everything in this model. This is where the [math]\displaystyle{ \alpha }[/math] - [math]\displaystyle{ \beta }[/math] Algorithm comes in.
Now due to the Markovian Memoryless property.
Define [math]\displaystyle{ \alpha }[/math] and [math]\displaystyle{ \beta }[/math] as follows:
Once we have [math]\displaystyle{ \alpha }[/math] and [math]\displaystyle{ \beta }[/math] then computing [math]\displaystyle{ P(y) }[/math] is easy.
To calculate [math]\displaystyle{ \alpha }[/math] and [math]\displaystyle{ \beta }[/math] themselves we can use:
For [math]\displaystyle{ \alpha }[/math]:
Where we begin with:
Then for [math]\displaystyle{ \beta }[/math]:
Where we now begin from the other end:
Once both [math]\displaystyle{ \alpha }[/math] and [math]\displaystyle{ \beta }[/math] have been calculated we can use them to find:
Sampling Methods
A fundamental problem in statistics has always been to find the expectation of [math]\displaystyle{ f(x) }[/math] with respect to [math]\displaystyle{ P(x) }[/math].
In many cases this integral is quite difficult to compute directly and so certain methods have been developed in an attempt to estimate the value without the need to actually do the integration. One such method is the Monte Carlo method where the integral is estimated by a sum.
We can also find the mean and standard deviation for the estimate. In fact, the mean is the correct mean for [math]\displaystyle{ f(x) }[/math].
So the only setback is that we have to be able to sample from [math]\displaystyle{ P(x) }[/math].
Sampling from Uniform
Let us assume that we want to sample from UNIF(0, 1). How would we go about doing this? Sampling from a uniform distribution that is truly random is very difficult. We are only going to look at the way it is done on a computer. On a computer we have a function that looks something like [math]\displaystyle{ D \equiv ax + b\ mod\ m }[/math] for some constants a, b and m. The choice of a, b and m is very important for the simulation of random numbers to work. The computer is also provided with a seed which will become the first term of the sequence [math]\displaystyle{ seed = x_0 }[/math]. The seed is usually chosen from the CPU clock. After that every 'random' number is generated by [math]\displaystyle{ D(x_i) = x_{i+1} }[/math]. If one were to know the seed and the constants a, b and m then the series of 'random' numbers could be predicted exactly. That is why we call random numbers that are generated by a computer Pseudo Random Numbers.
For the rest of this section we will assume that we know how to draw from a uniform distribution. It will provide us with the 'randomness' that is needed by each of our algorithms.
Inverse Method for Sampling
This is a two step method:
Step 1: Draw [math]\displaystyle{ u \sim UNIF(0,1) }[/math].
Step 2: Compute [math]\displaystyle{ x = F^{-1}(u) }[/math] where [math]\displaystyle{ F = \int^\infty_{-\infty} {P(u)du} }[/math].
Example:
Suppose that we want to draw a sample from [math]\displaystyle{ P(x) = \theta e^{-\theta x} }[/math] where [math]\displaystyle{ x\gt 0 }[/math]. We need to first find [math]\displaystyle{ F(x) }[/math] and then [math]\displaystyle{ F^{-1} }[/math].
Now we can generate our random sample [math]\displaystyle{ i=1...n }[/math] from [math]\displaystyle{ P(x) }[/math] by:
The [math]\displaystyle{ x_i }[/math] are now a random sample from [math]\displaystyle{ P(x) }[/math].
The major problem with this approach is that we have to find [math]\displaystyle{ F^{-1} }[/math] and for many distributions, such as the Gaussian for instance, it is too difficult to find the inverse of [math]\displaystyle{ F(x) }[/math].
Here [math]\displaystyle{ F^{-1}(x) }[/math] is too hard to compute.
Box-Muller
This is a method for sampling from a Gaussian Distribution. This is a unique method and it only works for this particular distribution.
- Draw [math]\displaystyle{ x_1 }[/math] and [math]\displaystyle{ x_2 }[/math] from a UNIF(0, 1).
- Accept the above values only if [math]\displaystyle{ x_1^2+x_2^2 \leq 1 }[/math]. Otherwise repeat the above step until this condition is met.
- Calculate [math]\displaystyle{ y_1 }[/math] and [math]\displaystyle{ y_2 }[/math]:
- [math]\displaystyle{ y_1 }[/math] and [math]\displaystyle{ y_2 }[/math] are now independent and distributed N(0,1).
Rejection Sampling
Suppose that we want to sample from [math]\displaystyle{ P(x) }[/math] and we are not in the Gaussian case and we can not find [math]\displaystyle{ F^{-1} }[/math]. Suppose also that there exists a [math]\displaystyle{ q(x) }[/math] that is easy to sample from. For instance the [math]\displaystyle{ UNIF(0,1) }[/math] is easy to sample from. Then if there exists a [math]\displaystyle{ k }[/math] such that [math]\displaystyle{ kq(x)\geq p(x) }[/math] for all x then we can use rejection sampling.
To present the problem intuitively we can observe the graph (Fig. \ref{fig:RejectSample}) where the top line represents [math]\displaystyle{ kq(x) }[/math] and the bottom line represents [math]\displaystyle{ p(x) }[/math]. We have in our example two points [math]\displaystyle{ x_1 }[/math] and [math]\displaystyle{ x_2 }[/math]. Consider first [math]\displaystyle{ x_1 }[/math]. From the graph we can tell that values around [math]\displaystyle{ x_1 }[/math] will be sampled more often under [math]\displaystyle{ kq(x) }[/math] than under [math]\displaystyle{ p(x) }[/math] and since we are sampling from [math]\displaystyle{ kq(x) }[/math] we expect to see many more samples in this region than we actually need. We therefore must reject most of the values drawn from around [math]\displaystyle{ x_1 }[/math] and only keep a few. If we now look at [math]\displaystyle{ x_2 }[/math] we see that the number of samples that are drawn from that region and the number we need are in fact much closer and we only have to reject a few of the values that are sampled from that area. So the question is: when we get an [math]\displaystyle{ x_i }[/math] from [math]\displaystyle{ kq(x) }[/math] how do we know if we should keep the value or if we should throw it away? In regions where [math]\displaystyle{ kq(x_i) }[/math] is far from [math]\displaystyle{ p(x_i) }[/math] we must reject many more values than in regions where [math]\displaystyle{ kq(x_i) }[/math] is close to [math]\displaystyle{ p(x_i) }[/math]. This is how rejection sampling works.
- Draw [math]\displaystyle{ x_i }[/math] from [math]\displaystyle{ q(x) }[/math].
- Accept [math]\displaystyle{ x_i }[/math] with probability [math]\displaystyle{ \frac{p(x_i)}{kq(x_i)} }[/math] and reject the value otherwise.
- The accepted values are now a random sample from your [math]\displaystyle{ P(x) }[/math].
Proof:
What we need to show is that [math]\displaystyle{ P(x_i|accept) \sim P(x_i) }[/math].
We know from the definition of the algorithm that [math]\displaystyle{ P(accept|x_i) = \frac{p(x_i)}{kq(x_i)} }[/math].
We have proven that rejection sampling works. But this type of sampling has some disadvantages too. For one thing we can look at the acceptance rate [math]\displaystyle{ P(accept) = \frac{1}{k} }[/math]. For a large k we are discarding many values and so this method is very inefficient. Also, there are distributions [math]\displaystyle{ P(x) }[/math] where it would be difficult to find a suitable [math]\displaystyle{ q(x) }[/math] or [math]\displaystyle{ k }[/math] that would allow us to sample from [math]\displaystyle{ P(x) }[/math].
Example of Rejection Sampling:
Suppose we want to sample from a [math]\displaystyle{ BETA(2, 1) }[/math].
Now we must find a [math]\displaystyle{ k }[/math] and a [math]\displaystyle{ q(x) }[/math]. We can use the [math]\displaystyle{ UNIF(0,1) }[/math] as our [math]\displaystyle{ q(x) }[/math] because it is easy to sample from. For the value of [math]\displaystyle{ k }[/math] we must find the maximum value of [math]\displaystyle{ \frac{P(x)}{q(x)} }[/math]. In this case:
So we will choose our [math]\displaystyle{ k=2 }[/math] for this example and now we can run the algorithm.
- Draw [math]\displaystyle{ x_i }[/math] from [math]\displaystyle{ UNIF(0,1) }[/math].
- Accept [math]\displaystyle{ x_i }[/math] with probability [math]\displaystyle{ \frac{2x_i}{2*1} = x_i }[/math] and reject the value otherwise.
- The accepted values are now a random sample from [math]\displaystyle{ BETA(2,1) }[/math].
Importance Sampling
We return once again to our problem of finding the expectation of [math]\displaystyle{ f(x) }[/math].
which can be approximated by:
We can try to rewrite the first equation so that we sample from [math]\displaystyle{ q(x) }[/math] and not [math]\displaystyle{ P(x) }[/math].
which can be approximated by:
The algorithm is as follows:
- Draw [math]\displaystyle{ x_i }[/math] from [math]\displaystyle{ q(x) }[/math].
- Find the weight for [math]\displaystyle{ x_i }[/math], [math]\displaystyle{ w_i = \frac{P(x_i)}{q(x_i)} }[/math].
- The set [math]\displaystyle{ w_ix_i }[/math] can now be used to estimate [math]\displaystyle{ E[f] }[/math].
The main disadvantage is that in many cases we can have the weight very close to zero and the sample itself will become almost useless. We need to have a [math]\displaystyle{ P(x) }[/math] and a [math]\displaystyle{ q(x) }[/math] that are very close for this algorithm to be more efficient. This technique does turn out to be unbiased but due to the problem of low weights the variance tends to be very high.
Greedy Importance Sampling
This method, as the name indicates, is somewhat similar to the method in the previous section. The difference from the previous algorithm is that we need to find the maximum point in [math]\displaystyle{ P(x) }[/math]. The algorithm works as follows:
- Draw [math]\displaystyle{ x_{i1} }[/math] from [math]\displaystyle{ q(x) }[/math].
- Move from [math]\displaystyle{ x_{i1} }[/math] towards the maximum point in [math]\displaystyle{ P(x) }[/math] and sample along the way. The new sample set [math]\displaystyle{ x_{i1},..., x_{ik} }[/math] must have the property that [math]\displaystyle{ \sum_{j=1}^k w_{ij} = 1 }[/math] where [math]\displaystyle{ w_{ij} }[/math] is the weight of the sample [math]\displaystyle{ x_{ij} }[/math].
- The set [math]\displaystyle{ w_{ij}x_{ij} }[/math] can now be used to estimate [math]\displaystyle{ E[f] }[/math].
This method is more difficult to compute but it is unbiased and has the advantage that it also has a low variance. In short this algorithm is more complex than the regular Importance Sampling but it has a lower variance.
Markov Chain Monte Carlo
This is best explained with an example. Say that we have a series random variables that each have a boolean state. Between two states [math]\displaystyle{ s_i }[/math] and [math]\displaystyle{ s_{i+1} }[/math] we have a set of transition probabilities.
- If [math]\displaystyle{ s_i=0 }[/math] then [math]\displaystyle{ s_{i+1}=0 }[/math] with probability [math]\displaystyle{ \frac{2}{3} }[/math].
- If [math]\displaystyle{ s_i=0 }[/math] then [math]\displaystyle{ s_{i+1}=1 }[/math] with probability [math]\displaystyle{ \frac{1}{3} }[/math].
- If [math]\displaystyle{ s_i=1 }[/math] then [math]\displaystyle{ s_{i+1}=0 }[/math] with probability [math]\displaystyle{ \frac{1}{3} }[/math].
- If [math]\displaystyle{ s_i=1 }[/math] then [math]\displaystyle{ s_{i+1}=1 }[/math] with probability [math]\displaystyle{ \frac{2}{3} }[/math].
We can say that the initial value for [math]\displaystyle{ s_0 = 1 }[/math]. From that we can deduce that:
- [math]\displaystyle{ P(s_1=1) = \frac{2}{3} }[/math] and [math]\displaystyle{ P(s_1=0) = \frac{1}{3} }[/math]
- [math]\displaystyle{ P(s_2=1) = \frac{5}{9} }[/math] and [math]\displaystyle{ P(s_2=0) = \frac{4}{9} }[/math]
- [math]\displaystyle{ P(s_3=1) = \frac{14}{27} }[/math] and [math]\displaystyle{ P(s_3=0) = \frac{13}{27} }[/math]
- ...
- [math]\displaystyle{ P(s_\infty=1) = \frac{1}{2} }[/math] and [math]\displaystyle{ P(s_\infty=0) = \frac{1}{2} }[/math]
We can see that the probabilities converge to 0.5 each. This is called the equilibrium probability distribution for this particular MCMC. If we have a [math]\displaystyle{ P(x) }[/math] we want to sample from but don't know how, there may be a way to make that [math]\displaystyle{ P(x) }[/math] the equilibrium probability for a MCMC and then sample from the tail end of the chain to get our random samples.
Metropolis Algorithm
We would like to sample from some [math]\displaystyle{ P(x) }[/math] and this time use the metropolis algorithm, which is a type of MCMC, to do it. In order for this algorithm to work we first need a number of things.
- We need some staring value [math]\displaystyle{ x }[/math]. This value can come from anywhere.
- We need to find a value [math]\displaystyle{ y }[/math] that comes from the function [math]\displaystyle{ T(x, y) }[/math].
- We need the function [math]\displaystyle{ T }[/math] to be symmetrical. [math]\displaystyle{ T(x,y)=T(y,x) }[/math].
- We also need [math]\displaystyle{ T(x,y) = P(y|x) }[/math].
Once we have all of these conditions we can run the algorithm to find our random sample.
- Get a staring value [math]\displaystyle{ x }[/math].
- Find the [math]\displaystyle{ y }[/math] value from the function [math]\displaystyle{ T(x, y) }[/math].
- Accept [math]\displaystyle{ y }[/math] with the probability [math]\displaystyle{ min(\frac{P(x)}{P(y)}, 1) }[/math].
- If the [math]\displaystyle{ y }[/math] is accepted it becomes the new x value.
- After a large number of accepted values the series will converge.
- When the series has converged any new accepted values can be treated as random samples from [math]\displaystyle{ P(x) }[/math].
The point at which the series converges is called the 'burn in point'. We must always burn in a series before we can use it to sample because we have to make sure that the series has converged. The number of values before the burn in point depends on the functions we are using since some converge faster than others.
We want to prove that the Metropolis Algorithm works. How do we know that [math]\displaystyle{ P(x) }[/math] is in fact the equilibrium distribution for this MC? We have a condition called the detailed balance condition that is sufficient but not necessary when we want to prove that [math]\displaystyle{ P(x) }[/math] is the equilibrium distribution.
Theorem 3 If [math]\displaystyle{ P(x)A(x, y) = P(y)A(y,x) }[/math] and [math]\displaystyle{ A(x,y) }[/math] is the transformation matrix for the MC then [math]\displaystyle{ P(x) }[/math] is the equilibrium distribution. This is called the Detailed Balance Condition.
Proof of Sufficiency for Detailed Balance Condition:
Need to show:
We need to show that Metropolis satisfies the detailed balance condition. We can define [math]\displaystyle{ A(x, y) }[/math] as follows:
Then,
Therefore the detailed balance condition holds for the Metropolis Algorithm and we can say that [math]\displaystyle{ P(x) }[/math] is the equilibrium distribution.
Example:
Suppose that we want to sample from a [math]\displaystyle{ Poisson(\lambda) }[/math].
Now define [math]\displaystyle{ T(x,y) : y=x+\epsilon }[/math] where [math]\displaystyle{ P(\epsilon=-1) = 0.5 }[/math] and [math]\displaystyle{ P(\epsilon=1) = 0.5 }[/math]. This type of [math]\displaystyle{ T }[/math] is called a random walk. We can select any [math]\displaystyle{ x^{(0)} }[/math] from the range of x as a starting value. Then we can calculate a y value based on our [math]\displaystyle{ T }[/math] function. We will accept the y value as our new [math]\displaystyle{ x^{(i)} }[/math] with the probability [math]\displaystyle{ min(\frac{P(x)}{P(y)}, 1) }[/math]. Once we have gathered many accepted values, say 10000, and the series has converged we can begin to sample from that point on in the series. That sample is now the random sample from a [math]\displaystyle{ Poisson(\lambda) }[/math].
Metropolis Hastings
As the name suggests the Metropolis Hastings algorithm is related to the Metropolis algorithm. It is a more generalized version of the Metropolis algorithm where we no longer require the condition that the function [math]\displaystyle{ T(x, y) }[/math] be symmetric. The algorithm can be outlined as:
- Get a staring value [math]\displaystyle{ x }[/math]. This value can be chosen at random.
- Find the [math]\displaystyle{ y }[/math] value from the function [math]\displaystyle{ T(x, y) }[/math]. Note that [math]\displaystyle{ T(x, y) }[/math] no longer has to be symmetric.
- Accept [math]\displaystyle{ y }[/math] with the probability [math]\displaystyle{ min(\frac{P(y)T(y, x)}{P(x)T(x, y)}, 1) }[/math]. Notice how the acceptance probability now contains the function [math]\displaystyle{ T(x, y) }[/math].
- If the [math]\displaystyle{ y }[/math] is accepted it becomes the new [math]\displaystyle{ x }[/math] value.
- After a large number of accepted values the series will converge.
- When the series has converged any new accepted values can be treated as random samples from [math]\displaystyle{ P(x) }[/math].
To prove that Metropolis Hastings algorithm works we once again need to show that the Detailed Balance Condition holds.
Proof:
If [math]\displaystyle{ T(x, y) = T(y, x) }[/math] then this reduces to the Metropolis algorithm which we have already proven. Otherwise,
Which means that the Detailed Balance Condition holds and therefore [math]\displaystyle{ P(x) }[/math] is the equilibrium.
Gibbs Sampling
Suppose we want to sample from the joint probability [math]\displaystyle{ P(x_1, x_2, x_3) }[/math] but we cannot sample from it directly. We can however sample from the conditional distribution [math]\displaystyle{ P(x_1 | x_2, x_3) }[/math]. The process can be defined as follows:
- Start with a randomly chosen [math]\displaystyle{ x^{(0)} }[/math] where [math]\displaystyle{ x^{(0)}=(x_1^{(0)}, x_2^{(0)}, x_3^{(0)}) }[/math].
- Once we have an [math]\displaystyle{ x^{(t)} }[/math] we can find an [math]\displaystyle{ x^{(t+1)} }[/math] by sampling from the conditional probability distribution.
- We continue this process until the burn-in point, after which we are sampling from [math]\displaystyle{ P(x) }[/math].
This process may seem different from the previous methods but in fact Gibbs Sampling is only a special case of Metropolis Hastings. Suppose one would like to sample from [math]\displaystyle{ P(x) }[/math] where [math]\displaystyle{ x=(x_1, x_2, x_3 \dots x_d) \varepsilon R^d }[/math]. Propose a [math]\displaystyle{ y_{-q} = (x_1, \dots, x_{q-1}, x_{q+1}, \dots, x_d) }[/math] and a [math]\displaystyle{ y_q = x_q }[/math]. We can define the [math]\displaystyle{ T(x, y) }[/math] function from the Metropolis Hastings algorithm as [math]\displaystyle{ T(x,y) = P(y_q | y_{-q}) = P(y_q | x_{-q}) }[/math]. In Gibbs Sampling we do not reject any of the values we sampled because our rejection probability is:
This quality makes Gibbs Sampling quite popular because we use everything we sample.
Example:
Say that we want to sample from:
[math]\displaystyle{ }[/math] N \left[
\left( \begin{array}{c}
u_1
u_2 \end{array} \right),
\left( \begin{array}{cc}
\Sigma_{11} & \Sigma_{12}
\Sigma_{21} & \Sigma_{22} \end{array} \right)
\right ] [math]\displaystyle{ }[/math]
And we know that we can find the parameters with:
For this example suppose we want to sample from :
[math]\displaystyle{ }[/math] N \left[
\left( \begin{array}{c}
0
0 \end{array} \right),
\left( \begin{array}{cc}
1 & L
L & 1 \end{array} \right)
\right ] [math]\displaystyle{ }[/math]
Then we can calculate:
The sampling process is then done with:
Independence Chains
In the Metropolis Hastings algorithm we used a [math]\displaystyle{ T(x, y) }[/math] to get the next values in the sample. Suppose now that [math]\displaystyle{ T(x, y) = T(y) }[/math]. In other words, the function [math]\displaystyle{ T }[/math] does not depend on [math]\displaystyle{ x }[/math]. The acceptance probability would now become [math]\displaystyle{ min(1, \frac{P(y)T(x)}{P(x)T(y)}) }[/math].
Bayesian Inference
In Bayesian Inference we would like to find [math]\displaystyle{ P(\theta | Data) }[/math]. Suppose we use the prior on [math]\displaystyle{ \theta }[/math] as the transition function and then we apply Metropolis Hastings. Our acceptance probability would become:
Now, recall that using Bayes rule we can write [math]\displaystyle{ P(\theta|Data) =\frac{ P(Data|\theta)P(\theta) } {P(Data)} }[/math]. We also know that [math]\displaystyle{ P(Data|\theta) = Likelihood }[/math]. From that we can rewrite the above Bayes formula as [math]\displaystyle{ P(\theta|Data) =\frac{ L(Data;\theta)P(\theta) } {P(Data)} }[/math].
Therefore, to sample from the posterior in a Bayesian Inference we can simply propose a [math]\displaystyle{ \theta^{(t+1)} }[/math] from the prior and then we accept with probability:
Example:
We would like to sample from:
and from:
The problem is that we are missing the parameter [math]\displaystyle{ \alpha }[/math]. We do however know that [math]\displaystyle{ P(\alpha) = UNIF(0,1) }[/math]. The best way to sample from the above distribution is to start with a randomly chosen [math]\displaystyle{ \alpha^{(t)} }[/math] and accept with probability [math]\displaystyle{ min \left( 1, \frac{L(Data; \theta^{(t+1)})} { L(Data; \theta^{(t)})} \right) }[/math]. When we reject we simply use the previous value again. This method also requires a burn in time so we must wait before we can begin sampling.
Simulated Annealing
Consider the general optimization problem [math]\displaystyle{ min_x h(x) }[/math] and the distribution [math]\displaystyle{ P(x) }[/math]. Instead of finding the minimum of [math]\displaystyle{ h(x) }[/math] we can try to find the maximum of [math]\displaystyle{ P(x)\propto exp\left\lbrace \frac{-h(x)}{T} \right\rbrace }[/math]. In this case [math]\displaystyle{ T }[/math] is called the temperature and it determines the shape of the distribution. As [math]\displaystyle{ T }[/math] increases the distribution expands but as [math]\displaystyle{ T\rightarrow0 }[/math] then the [math]\displaystyle{ x_i }[/math] that we sample from the [math]\displaystyle{ P(x) }[/math] are very close to the global min.
Note: If [math]\displaystyle{ x }[/math] is the minimum of [math]\displaystyle{ h(x) }[/math] then [math]\displaystyle{ x }[/math] is also the maximum of [math]\displaystyle{ P(x) }[/math].
We can define the steps to the problem as:
- Start with a randomly chosen [math]\displaystyle{ x }[/math] and set [math]\displaystyle{ T }[/math] to a large value.
- Propose a [math]\displaystyle{ y \neq x }[/math] from the function [math]\displaystyle{ T(x, y) = T(y, x) }[/math].
- Accept the [math]\displaystyle{ y }[/math] value with probability [math]\displaystyle{ min(1, \frac{P(y)}{P(x)}) }[/math].
- Decrease the value of [math]\displaystyle{ T }[/math] and return to step 1.
But what exactly does [math]\displaystyle{ \frac{P(x)}{P(y)} }[/math] mean? We can estimate each of these probabilities with the [math]\displaystyle{ exp\left\lbrace \frac{-h(x)}{T} \right\rbrace }[/math] expression we introduced earlier.
We are now left with two possible cases. If [math]\displaystyle{ h(y) \lt h(x) }[/math] then [math]\displaystyle{ P(y) \gt P(x) }[/math] which is desired and so we will always accept the new [math]\displaystyle{ y }[/math]. Otherwise, if [math]\displaystyle{ h(y) \gt h(x) }[/math] we may not accept the new [math]\displaystyle{ y }[/math] value and we can see that as [math]\displaystyle{ T \rightarrow 0 }[/math] then [math]\displaystyle{ e^{\frac{h(x) - h(y)}{T}} }[/math] will also go to zero and so the acceptance probability will go to zero.
For this method we can write down a rough algorithm:
Start with [math]\displaystyle{ x_0 }[/math] and consider a set [math]\displaystyle{ T_1 \gt T_2 \gt \dots \gt T_k }[/math] of [math]\displaystyle{ K }[/math] values.
for [math]\displaystyle{ k=1 }[/math] to [math]\displaystyle{ K }[/math]
\hspace*{20pt}for [math]\displaystyle{ j=1 }[/math] to [math]\displaystyle{ N_k }[/math]
\hspace*{20pt}Propose a [math]\displaystyle{ y }[/math] from [math]\displaystyle{ T(y, x) }[/math].
\hspace*{20pt}[math]\displaystyle{ U = UNIF(0, 1) }[/math]
\hspace*{20pt}if [math]\displaystyle{ U \leq min(1, \frac{P(y)}{P(x_{j-1})}) }[/math]
\hspace*{30pt}[math]\displaystyle{ x_j = y }[/math]
\hspace*{20pt}else
\hspace*{30pt}[math]\displaystyle{ x_j = x_{j-1} }[/math]
\hspace*{20pt}endif
endfor
endfor
Bootstrap
In data analysis we usually have an observed set of data [math]\displaystyle{ \left\lbrace x_1, x_2, \dots, x_n \right\rbrace }[/math] from a probability distribution [math]\displaystyle{ P }[/math] and we have an estimator [math]\displaystyle{ \hat{\theta} }[/math] for our parameter of interest [math]\displaystyle{ \theta }[/math]. In general it would be useful to know the distribution of our [math]\displaystyle{ \hat{\theta} }[/math]. For instance, if the estimator has a larger variance then we know that it is not very accurate. The problem is that it is not always easy to determine the distribution of an estimator. Ideally we would like to be able to sample directly from [math]\displaystyle{ P }[/math] and then for each sample of size [math]\displaystyle{ n }[/math] we can calculate a [math]\displaystyle{ \hat{\theta} }[/math]. In this way a number of estimates for [math]\displaystyle{ \theta }[/math] can be found and their distribution can be determined from the samples.
For Example:
Based on [math]\displaystyle{ \lbrace \hat{\theta_1}, \hat{\theta_2}, \dots, \hat{\theta_B} \rbrace }[/math] we can try to determine the distribution of [math]\displaystyle{ \hat{\theta} }[/math].
However, this idea is unrealistic because we don't know [math]\displaystyle{ P }[/math] and so we cannot sample from it. This is where the Bootstrap idea comes in. Assume that we have a set of data [math]\displaystyle{ \left\lbrace x_1, x_2, \dots, x_n \right\rbrace }[/math] from an unknown distribution [math]\displaystyle{ P }[/math]. To simulate sampling from [math]\displaystyle{ P }[/math] we can resample with replacement from the set of [math]\displaystyle{ n }[/math] data points. Every sample we get in this way we can use to estimate a different [math]\displaystyle{ \hat{\theta} }[/math]. We can use this method to find a collection of [math]\displaystyle{ \hat{\theta_i} }[/math] parameters from which we can:
- Find the expectation of [math]\displaystyle{ \hat{\theta} }[/math].
- Find the variance of [math]\displaystyle{ \hat{\theta} }[/math].
- Find a confidence interval.
- Find the bias.
- Bias correction.
At first, this method seems strange. We are sampling from the sample itself and not the distribution. However, it has been shown that the Bootstrap method does indeed work and can provide more useful information on top of what the raw data could have provided.
This kind of Bootstrap is called the Naive Bootstrap because the values are sampled one at a time independently and this destroys any kind of correlation in the initial distribution. The correct Bootstrap method requires the selection of blocks of data in order to keep the correlation in the data. These blocks are sampled with replacement and may overlap.