stat946f11: Difference between revisions
m (Conversion script moved page Stat946f11 to stat946f11: Converting page titles to lowercase) |
|||
| (446 intermediate revisions by 12 users not shown) | |||
| Line 1: | Line 1: | ||
==[[f11stat946EditorSignUp| Editor Sign Up]]== | |||
==[[f11Stat946presentation| Sign up for your presentation]]== | ==[[f11Stat946presentation| Sign up for your presentation]]== | ||
==[[f11Stat946papers| paper summaries]]== | |||
==[[f11Stat946ass| Assignments]]== | |||
==Introduction== | ==Introduction== | ||
===Motivation=== | |||
Graphical probabilistic models provide a concise representation of various probabilistic distributions that are found in many | |||
real world applications. Some interesting areas include medical diagnosis, computer vision, language, analyzing gene expression | |||
data, etc. A problem related to medical diagnosis is, "detecting and quantifying the causes of a disease". This question can | |||
be addressed through the graphical representation of relationships between various random variables (both observed and hidden). | |||
This is an efficient way of representing a joint probability distribution. | |||
Graphical models are excellent tools to burden the computational load of probabilistic models. Suppose we want to model a binary image. If we have 256 by 256 image then our distribution function has <math>2^{256*256}=2^{65536}</math> outcomes. Even very simple tasks such as marginalization of such a probability distribution over some variables can be computationally intractable and the load grows exponentially versus number of the variables. In practice and in real world applications we generally have some kind of dependency or relation between the variables. Using such information, can help us to simplify the calculations. For example for the same problem if all the image pixels can be assumed to be independent, marginalization can be done easily. One of the good tools to depict such relations are graphs. Using some rules we can indicate a probability distribution uniquely by a graph, and then it will be easier to study the graph instead of the probability distribution function (PDF). We can take advantage of graph theory tools to design some algorithms. Though it may seem simple but this approach will simplify the commutations and as mentioned help us to solve a lot of problems in different research areas. | |||
===Notation=== | ===Notation=== | ||
| Line 22: | Line 35: | ||
===Graphical Models=== | ===Graphical Models=== | ||
Graphical models provide a compact representation of the joint distribution where V vertices (nodes) represent random variables and edges E represent the dependency between the variables. There are two forms of graphical models (Directed and Undirected graphical model). Directed graphical (Figure 1) models consist of arcs and nodes where arcs indicate that the parent is a explanatory variable for the child. Undirected graphical models (Figure 2) are based on the assumptions that two nodes or two set of nodes are conditionally independent given their neighbour[http://www.cs.ubc.ca/~murphyk/Bayes/bnintro.html 1]. | |||
Similiar types of analysis predate the area of Probablistic Graphical Models and it's terminology. Bayesian Network and Belief Network are preceeding terms used to a describe directed acyclical graphical model. Similarly Markov Random Field (MRF) and Markov Network are preceeding terms used to decribe a undirected graphical model. Probablistic Graphical Models have united some of the theory from these older theories and allow for more generalized distributions than were possible in the previous methods. | |||
[[File:directed.png|thumb|right|Fig.1 A directed graph.]] | [[File:directed.png|thumb|right|Fig.1 A directed graph.]] | ||
| Line 35: | Line 43: | ||
We will use graphs in this course to represent the relationship between different random variables. | We will use graphs in this course to represent the relationship between different random variables. | ||
{{Cleanup|date=October 2011|reason= It is worth noting that both Bayesian networks and Markov networks existed before introduction of graphical models but graphical models helps us to provide a unified theory for both cases and more generalized distributions.}} | |||
====Directed graphical models (Bayesian networks)==== | ====Directed graphical models (Bayesian networks)==== | ||
In the case of directed graphs, the direction of the arrow indicates "causation". For example: | In the case of directed graphs, the direction of the arrow indicates "causation". This assumption makes these networks useful for the cases that we want to model causality. So these models are more useful for applications such as computational biology and bioinformatics, where we study effect (cause) of some variables on another variable. For example: | ||
<br /> | <br /> | ||
<math>A \longrightarrow B</math>: <math>A\,\!</math> "causes" <math>B\,\!</math>. | <math>A \longrightarrow B</math>: <math>A\,\!</math> "causes" <math>B\,\!</math>. | ||
In this case we must assume that our directed graphs are ''acyclic''. If our causation graph contains a cycle then it would mean that for example: | In this case we must assume that our directed graphs are ''acyclic''. An example of an acyclic graphical model from medicine is shown in Figure 2a. | ||
[[File:acyclicgraph.png|thumb|right|Fig.2a Sample acyclic directed graph.]] | |||
Exposure to ionizing radiation (such as CT scans, X-rays, etc) and also to environment might lead to gene mutations that eventually give rise to cancer. Figure 2a can be called as a causation graph. | |||
If our causation graph contains a cycle then it would mean that for example: | |||
* <math>A</math> causes <math>B</math> | * <math>A</math> causes <math>B</math> | ||
| Line 53: | Line 67: | ||
[[File:acyclic.png|thumb|right|Fig.4 An acyclic graph.]] | [[File:acyclic.png|thumb|right|Fig.4 An acyclic graph.]] | ||
In directed acyclic graphical models each vertex represents a random variable; a random variable associated with one vertex is distinct from the random variables associated with other vertices. Consider the following example that uses boolean random variables. It is important to note that the variables need not be boolean and can indeed be discrete over a range or even continuous. | |||
Speaking about random variables, we can now refer to the relationship between random variables in terms of dependence. Therefore, the direction of the arrow indicates "conditional dependence". For example: | Speaking about random variables, we can now refer to the relationship between random variables in terms of dependence. Therefore, the direction of the arrow indicates "conditional dependence". For example: | ||
<br /> | <br /> | ||
<math>A \longrightarrow B</math>: <math>B\,\!</math> "is dependent on" <math>A\,\!</math>. | <math>A \longrightarrow B</math>: <math>B\,\!</math> "is dependent on" <math>A\,\!</math>. | ||
Note if we do not have any conditional independence, the corresponding graph will be complete, i.e., all possible edges will be present. Whereas if we have full independence our graph will have no edge. Between these two extreme cases there exist a large class. Graphical models are more useful when the graph be sparse, i.e., only a small number of edges exist. The topology of this graph is important and later we will see some examples that we can use graph theory tools to solve some probabilistic problems. On the other hand this representation makes it easier to model causality between variables in real world phenomena. | |||
====Example==== | ====Example==== | ||
| Line 200: | Line 216: | ||
===Independence=== | ===Independence=== | ||
Sept.22.2011 <br /> | |||
The intuition behind the concept of independence is that when considering two variables, we say that they are independent of each other if knowing the value of one of them gives no extra information about the other variable than what we already know about it. Formaly, this can be expressed as follows: | |||
<math>\, p(X|Y) = p(X)</math> | |||
<math>\, p(Y|X) = p(Y)</math> | |||
====Marginal independence==== | ====Marginal independence==== | ||
We can say that <math>X_A</math> is marginally independent of <math>X_B</math> if: | We can say that <math>X_A</math> is marginally independent of <math>X_B</math> if: | ||
| Line 216: | Line 235: | ||
P(X_A|X_B,X_C) & = & P(X_A|X_C) | P(X_A|X_B,X_C) & = & P(X_A|X_C) | ||
\end{matrix}</math></center> | \end{matrix}</math></center> | ||
Note: Both equations are equivalent. | |||
'''Aside:''' Before we move on further, | '''Aside:''' Before we move on further, lets first define the following terms: | ||
# I is defined as an ordering for the nodes in graph | # I is defined as an ordering for the nodes in graph G where G=(V,E)(vertices and edges). | ||
# For each <math>i \in V</math>, <math>V_i</math> is defined as a set of all nodes that appear earlier than i excluding <math>\pi_i</math>. | # For each <math>i \in V</math>, <math>V_i</math> which is defined as a set of all nodes that appear earlier than i excluding its parents <math>\pi_i</math>. | ||
Let us consider the example of the six node figure given above (Figure 7). We can define <math>I</math> as follows: | Let us consider the example of the six node figure given above (Figure 7). We can define <math>I</math> as follows: | ||
| Line 225: | Line 245: | ||
We can then easily compute <math>V_i</math> for say <math>i=3,6</math>. <br /> | We can then easily compute <math>V_i</math> for say <math>i=3,6</math>. <br /> | ||
<center><math> V_3 = \{2\}, V_6 = \{1,3,4\}\,\!</math></center> | <center><math> V_3 = \{2\}, V_6 = \{1,3,4\}\,\!</math></center> | ||
while <math>\pi_i</math> for <math> i=3,6</math> will be. <br /> | |||
<center><math> \pi_3 = \{1\}, \pi_6 = \{2,5\}\,\!</math></center> | |||
We would be interested in finding the conditional independence between random variables in this graph. We know <math>X_i \perp X_{v_i} | X_{\pi_i}</math> for each <math>i</math>. So:<br /> | We would be interested in finding the conditional independence between random variables in this graph. We know <math>X_i \perp X_{v_i} | X_{\pi_i}</math> for each <math>i</math>. In other words, given its parents the node is independent of all earlier nodes. So:<br /> | ||
<math>X_1 \perp \phi | \phi</math>, <br /> | <math>X_1 \perp \phi | \phi</math>, <br /> | ||
<math>X_2 \perp \phi | X_1</math>, <br /> | <math>X_2 \perp \phi | X_1</math>, <br /> | ||
| Line 251: | Line 273: | ||
====Sampling==== | ====Sampling==== | ||
Even if using graphical models helps a lot facilitate obtaining the joint probability, exact inference is not always feasible. Exact inference is feasible in small to medium-sized networks only. Exact inference consumes such a long time in large networks. Therefore, we resort to approximate inference techniques which are much faster and usually give pretty good results. | Inference on graphical models can be defined as the task of answering a query about a number of variables that we are interested in conditioned on the set of observed variables (evidence). Even if using graphical models helps a lot facilitate obtaining the joint probability, exact inference is not always feasible. "Exact inference is feasible in small to medium-sized networks only. Exact inference consumes such a long time in large networks. Therefore, we resort to approximate inference techniques which are much faster and usually give pretty good results". It is known that exact inference on graphical models is NP-Hard in most of the cases. | ||
<ref>Weng-Keen Wong, "Bayesian Networks: A Tutorial", School of Electrical Engineering and Computer Science, Oregon State University, 2005. Available: [http://dimacs.rutgers.edu/Workshops/Surveillance/slides/wong.ppt]</ref> | |||
In sampling, random samples are generated and values of interest are computed from samples, not original work. | In sampling, random samples are generated and values of interest are computed from samples, not original work. | ||
As an input you have a Bayesian network with set of nodes <math>X\,\!</math>. The sample taken may include all variables (except evidence E) or a subset. Sample schemas dictate how to generate samples (tuples). Ideally samples are distributed according to <math>P(X|E)\,\!</math> | As an input you have a Bayesian network with set of nodes <math>X\,\!</math>. The sample taken may include all variables (except evidence E) or a subset. "Sample schemas dictate how to generate samples (tuples). Ideally samples are distributed according to <math>P(X|E)\,\!</math>" <ref>"Sample Bayesian Networks", 2005. Available: [http://docs.google.com/viewer?a=v&q=cache:ZB6zFHWcz34J:www.ics.uci.edu/~dechter/courses/ics-275b/spring-05/handouts/Sampling_ICS275b_2005.ppt+Sample+schemas+dictate+how+to+generate+samples+%28tuples%29&hl=en&pid=bl&srcid=ADGEESj0xCSmNdteIObRF7wCqBOxeWhRWoMik_tszbOZgCZTn-e1A_77Itc5RAWc_MqSdYttnRZyvPjYNdzTKXnlxJcYmv3wglclnzp_B8q0XT58CUB0QY3m--XD3LnWzVeFoRJP3rRQ&sig=AHIEtbRsgiT7VVpAAur2QRDSM3wxLqQRsA] </ref> | ||
Some sampling algorithms: | Some sampling algorithms: | ||
| Line 266: | Line 289: | ||
==Bayes Ball== | ==Bayes Ball== | ||
The Bayes Ball algorithm can be used to determine if two random variables represented in a graph are independent. The algorithm can show that either two nodes in a graph are independent OR that they are not necessarily independent. The Bayes Ball algorithm can not show that two nodes are | The Bayes Ball algorithm can be used to determine if two random variables represented in a graph are independent. The algorithm can show that either two nodes in a graph are independent OR that they are not necessarily independent. The Bayes Ball algorithm can not show that two nodes are dependent. In other word it provides some rules which enables us to do this task using the graph without the need to use the probability distributions. The algorithm will be discussed further in later parts of this section. | ||
===Canonical Graphs=== | ===Canonical Graphs=== | ||
In order to understand the Bayes Ball algorithm we need to first introduce 3 canonical graphs. | In order to understand the Bayes Ball algorithm we need to first introduce 3 canonical graphs. Since our graphs are acyclic, we can represent them using these 3 canonical graphs. | ||
====Markov Chain (also called serial connection)==== | ====Markov Chain (also called serial connection)==== | ||
In the following graph (Figure 8 X is independent of Z given Y. | In the following graph (Figure. 8), variable X is independent of Z given Y. | ||
We say that: <math>X</math> <math>\perp</math> <math>Z</math> <math>|</math> <math>Y</math> | We say that: <math>X</math> <math>\perp</math> <math>Z</math> <math>|</math> <math>Y</math> | ||
| Line 293: | Line 316: | ||
& = & P(X)P(Y | X)\\ | & = & P(X)P(Y | X)\\ | ||
\end{matrix}</math></center> | \end{matrix}</math></center> | ||
Markov chains are an important class of distributions with applications in communications, information theory and image processing. They are suitable to model memory in phenomenon. For example suppose we want to study the frequency of appearance of English letters in a text. Most likely when "q" appears, the next letter will be "u", this shows dependency between these letters. Markov chains are suitable model for this kind of relations. Markov chains are also the main building block for one of the most famous and widely used statistical models called Hidden Markov Model, which usually used for Time Series. | |||
[[File:Markovexample.png|thumb|right|Fig.8a Example of a Markov chain.]] | |||
Markov chains play a significant role in biological applications. It is widely used in the study of carcinogenesis (initiation of cancer formation). A gene has to undergo several mutations before it becomes cancerous, which can be addressed through Markov chains. An example is given in Figure 8a which shows only two gene mutations. | |||
====Hidden Cause (diverging connection)==== | ====Hidden Cause (diverging connection)==== | ||
| Line 321: | Line 351: | ||
phenomena has multiple explanations. Here, the conditional | phenomena has multiple explanations. Here, the conditional | ||
independence statement is actually a statement of marginal | independence statement is actually a statement of marginal | ||
independence: <math>X \ | independence: <math>X \perp Z</math>. This type of graphs is also called "V-structure" or "V-shape" because of its illustration (Fig. 11). | ||
[[File:ExplainingAway.png|thumb|right|Fig.11 The missing edge between node X and node Z implies that | [[File:ExplainingAway.png|thumb|right|Fig.11 The missing edge between node X and node Z implies that | ||
there is a marginal independence between the two: <math>X \ | there is a marginal independence between the two: <math>X \perp Z</math>.]] | ||
In these types of scenarios, variables X and Z are independent. | In these types of scenarios, variables X and Z are independent. | ||
| Line 372: | Line 402: | ||
<math>P( aliens = 1 ~|~ late = 1 ) \neq P( aliens = 1 ~|~ late = 1, watch = 0 )</math>, ''aliens'' and | <math>P( aliens = 1 ~|~ late = 1 ) \neq P( aliens = 1 ~|~ late = 1, watch = 0 )</math>, ''aliens'' and | ||
''watch'' are not independent given ''late''. To summarize, | ''watch'' are not independent given ''late''. To summarize, | ||
* If we do not observe ''late'', then ''aliens'' <math>~\ | * If we do not observe ''late'', then ''aliens'' <math>~\perp~ watch</math> (<math>X~\perp~ Z</math>) | ||
* If we do observe ''late'', then ''aliens'' <math> ~\cancel{\ | * If we do observe ''late'', then ''aliens'' <math> ~\cancel{\perp}~ watch ~|~ late</math> (<math>X ~\cancel{\perp}~ Z ~|~ Y</math>) | ||
===Bayes Ball Algorithm=== | ===Bayes Ball Algorithm=== | ||
Sept. 27.2011<br /> | |||
'''Goal:''' We wish to determine whether a given conditional | '''Goal:''' We wish to determine whether a given conditional | ||
statement such as <math>X_{A} ~\ | statement such as <math>X_{A} ~\perp~ X_{B} ~|~ X_{C}</math> is true given a directed graph. | ||
The algorithm is as follows: | The algorithm is as follows: | ||
# Shade nodes, <math>X_{C}</math>, that are conditioned on. | # Shade nodes, <math>~X_{C}~</math>, that are conditioned on, i.e. they have been observed. | ||
# | # Assuming that the initial position of the ball is <math>~X_{A}~</math>: | ||
# If the ball cannot reach <math>X_{B}</math>, then the nodes <math>X_{A}</math> and <math>X_{B}</math> must be conditionally independent. | # If the ball cannot reach <math>~X_{B}~</math>, then the nodes <math>~X_{A}~</math> and <math>~X_{B}~</math> must be conditionally independent. | ||
# If the ball can reach <math>X_{B}</math>, then the nodes <math>X_{A}</math> and <math>X_{B}</math> are not necessarily independent. | # If the ball can reach <math>~X_{B}~</math>, then the nodes <math>~X_{A}~</math> and <math>~X_{B}~</math> are not necessarily independent. | ||
The biggest challenge in the ''Bayes Ball Algorithm'' is to | The biggest challenge in the ''Bayes Ball Algorithm'' is to | ||
| Line 396: | Line 426: | ||
We use the canonical graphs previously studied to determine the | We use the canonical graphs previously studied to determine the | ||
route of a ball traveling through a graph. Using these three | route of a ball traveling through a graph. Using these three | ||
graphs we establish | graphs, we establish the Bayes ball rules which can be extended for more | ||
graphical models. | |||
====Markov Chain==== | ====Markov Chain (serial connection)==== | ||
[[File:BB_Markov.png|thumb|right|Fig.12 (a) When the middle node is shaded, the ball is blocked. (b) When the middle ball is not shaded, the ball passes through Y.]] | [[File:BB_Markov.png|thumb|right|Fig.12 (a) When the middle node is shaded, the ball is blocked. (b) When the middle ball is not shaded, the ball passes through Y.]] | ||
| Line 407: | Line 437: | ||
In (Fig. 12(a)), X and Z are conditionally | In (Fig. 12(a)), X and Z are conditionally | ||
independent ( <math>X ~\ | independent ( <math>X ~\perp~ Z ~|~ Y</math> ) while in | ||
(Fig.12(b)) X and Z are not necessarily | (Fig.12(b)) X and Z are not necessarily | ||
independent. | independent. | ||
====Hidden Cause==== | ====Hidden Cause (diverging connection)==== | ||
[[File:BB_Hidden.png|thumb|right|Fig.13 (a) When the middle node is shaded, the ball is blocked. (b) When the middle ball is not shaded, the ball passes through Y.]] | [[File:BB_Hidden.png|thumb|right|Fig.13 (a) When the middle node is shaded, the ball is blocked. (b) When the middle ball is not shaded, the ball passes through Y.]] | ||
| Line 420: | Line 450: | ||
conditionally independent when Y is shaded. | conditionally independent when Y is shaded. | ||
====Explaining-Away==== | ====Explaining-Away (converging connection)==== | ||
Unlike the last two cases in which the Bayes ball rule was intuitively understandable, in this case a ball traveling through Y is blocked when Y is UNSHADED!. If Y is | |||
shaded, then the ball passes through. Hence, X and Z are | shaded, then the ball passes through. Hence, X and Z are | ||
conditionally independent when Y is unshaded. | conditionally independent when Y is unshaded. | ||
[[File:BB_ExplainingAway.png|thumb|right|Fig.14 (a) When the middle node is shaded, the ball passes through Y. (b) When the middle ball is unshaded, the ball is blocked.]] | [[File:BB_ExplainingAway.png|thumb|right|Fig.14 (a) When the middle node is shaded, the ball passes through Y. (b) When the middle ball is unshaded, the ball is blocked.]] | ||
===Bayes Ball Examples=== | ===Bayes Ball Examples=== | ||
====Example 1==== | ====Example 1==== | ||
In this first example, we wish to identify the behavior of a ball | In this first example, we wish to identify the behavior of leaves in the graphical models using two-nodes graphs. Let a ball be | ||
going from X to Y in two-node graphs. | going from X to Y in two-node graphs. To employ the Bayes ball method mentioned above, we have to implicitly add one extra node to the two-node structure since we introduced the Bayes rules for three nodes configuration. We add the third node exactly symmetric to node X with respect to node Y. For example in (Fig. 15) (a) we can think of a hidden node in the right hand side of node Y with a hidden arrow from the hidden node to Y. Then, we are able to utilize the Bayes ball method considering the fact that a ball thrown from X cannot reach Y, and thus it will be blocked. On the contrary, following the same rule in (Fig. 15) (b) turns out that if there was a hidden node in right hand side of Y, a ball could pass from X to that hidden node according to explaining-away structure. Of course, there is no real node and in this case we conventionally say that the ball will be bounced back to node X. | ||
[[File:TwoNodesExample.png|thumb|right|Fig.15 (a)The ball is blocked at Y. (b)The ball passes through Y. (c)The ball passes through Y. (d) The ball is blocked at Y.]] | [[File:TwoNodesExample.png|thumb|right|Fig.15 (a)The ball is blocked at Y. (b)The ball passes through Y. (c)The ball passes through Y. (d) The ball is blocked at Y.]] | ||
Finally, for the last two graphs, we used the rules of the ''Hidden Cause Canonical Graph'' (Fig. 13). In (c), the ball passes through | |||
graphs, we used the rules of the ''Hidden Cause Canonical | |||
Graph'' (Fig. 13). In (c), the ball passes through | |||
Y while in (d), the ball is blocked at Y. | Y while in (d), the ball is blocked at Y. | ||
| Line 486: | Line 509: | ||
the ''burglary'' and the ''earthquake'' events are not | the ''burglary'' and the ''earthquake'' events are not | ||
necessarily independent. Also, if the alarm rings then it is | necessarily independent. Also, if the alarm rings then it is | ||
possible | more possible that a police report will be issued. | ||
We can use the ''Bayes Ball Algorithm'' to deduce conditional | We can use the ''Bayes Ball Algorithm'' to deduce conditional | ||
| Line 571: | Line 594: | ||
Ans. False | Ans. False | ||
== Undirected Graphical Model == | == Undirected Graphical Model == | ||
Sept.29.2011<br /> | |||
[[File:UnDirGraphCanon.png|thumb|right|Fig.20a Connecting three nodes in an undirected graph.]] | |||
[[File:UnDirGraphCanonlattice.png|thumb|right|Fig.20b Undirected graph on a lattice.]] | |||
Generally, the graphical model is divided into two major classes, directed graphs and undirected graphs. Directed graphs and its characteristics was described previously. In this section we discuss undirected graphical model which is also known as Markov random fields. In some applications there are relations between variables but these relation are bilateral and we don't encounter causality. For example consider a natural image. In natural images the value of a pixel has correlations with neighboring pixel values but this is bilateral and not a causality relations. | |||
Markov random fields are suitable to model such processes and have found applications in fields such as vision and image processing.We can define an undirected graphical model with a graph <math> G = (V, E)</math> where <math> V </math> is a set of vertices corresponding to a set of random variables and <math> E </math> is a set of undirected edges as shown in (Fig.20a). An another example is displayed in (Fig.20b) that shows part of a lattice. Couple of observations from the two examples are the following: there is no parent and child relationship; potentials are defined on several cliques of a graph which will be discussed in the subsequent sections. | |||
==== Conditional independence ==== | ==== Conditional independence ==== | ||
[[File:UnDirGraphCase1.png|thumb|right|Fig.21a Ball can pass through the center node.]] | |||
For directed graphs Bayes ball method was defined to determine the conditional independence properties of a given graph. We can also employ the Bayes ball algorithm to examine the conditional independency of undirected graphs. Here the Bayes ball rule is simpler and more intuitive. Considering (Fig. | [[File:UnDirGraphCase2.png|thumb|right|Fig.21b Ball cannot pass through the center node.]] | ||
For directed graphs Bayes ball method was defined to determine the conditional independence properties of a given graph. We can also employ the Bayes ball algorithm to examine the conditional independency of undirected graphs. Here the Bayes ball rule is simpler and more intuitive. | |||
Considering (Fig.21a) , a ball can be thrown either from x to z or from z to x if y is not observed. In other words, if y is not observed (Fig.21b) a ball thrown from x can reach z and vice versa. On the contrary, given a shaded y, the node can block the ball and make x and z conditionally independent. With this definition one can declare that in an undirected graph, a node is conditionally independent of non-neighbors given neighbors. Technically speaking, <math>X_A</math> is independent of <math>X_C</math> given <math>X_B</math> if the set of nodes <math>X_B</math> separates the nodes <math>X_A</math> from the nodes <math>X_C</math>. Hence, if every path from a node in <math>X_A</math> to a node in <math>X_C</math> includes at least one node in <math>X_B</math>, then we claim that <math> X_A \perp X_c | X_B </math>. | |||
==== Question ==== | ==== Question ==== | ||
| Line 591: | Line 619: | ||
W \perp Z | \{X,Y\} \\ | W \perp Z | \{X,Y\} \\ | ||
\end{matrix}</math></center> | \end{matrix}</math></center> | ||
[[File:UnDirGraphUnconvert.png|thumb|right|Fig.22 There is no directed equivalent to this graph.]] | |||
It is simple to see there is no directed graph satisfying both conditional independence properties. Recalling that directed graphs are acyclic, converting undirected graphs to directed graphs result in at least one node in which the arrows are inward-pointing(a v structure). Without loss of generality we can assume that node <math>Z</math> has two inward-pointing arrows. By conditional independence semantics of directed graphs, we have <math> X \perp Y|W</math>, yet the <math>X \perp Y|\{W,Z\}</math> property does not hold. On the other hand, (Fig.23 ) depicts a directed graph which is characterized by the singleton independence statement <math>X \perp Y </math>. There is no undirected graph on three nodes which can be characterized by this singleton statement. Basically, if we consider the set of all distribution over <math>n</math> random variables, a subset of which can be represented by directed graphical models while there is another subset which undirected graphs are able to model that. There is a narrow intersection region between these two subsets in which probabilistic graphical models may be represented by either directed or undirected graphs. | It is simple to see there is no directed graph satisfying both conditional independence properties. Recalling that directed graphs are acyclic, converting undirected graphs to directed graphs result in at least one node in which the arrows are inward-pointing(a v structure). Without loss of generality we can assume that node <math>Z</math> has two inward-pointing arrows. By conditional independence semantics of directed graphs, we have <math> X \perp Y|W</math>, yet the <math>X \perp Y|\{W,Z\}</math> property does not hold. On the other hand, (Fig.23 ) depicts a directed graph which is characterized by the singleton independence statement <math>X \perp Y </math>. There is no undirected graph on three nodes which can be characterized by this singleton statement. Basically, if we consider the set of all distribution over <math>n</math> random variables, a subset of which can be represented by directed graphical models while there is another subset which undirected graphs are able to model that. There is a narrow intersection region between these two subsets in which probabilistic graphical models may be represented by either directed or undirected graphs. | ||
[[File:DirGraphUnconvert.png|thumb|right|Fig.23 There is no undirected equivalent to this graph.]] | |||
==== Parameterization ==== | |||
Having undirected graphical models, we would like to obtain "local" parameterization like what we did in the case of directed graphical models. For directed graphical models, "local" had the interpretation of a set of node and its parents, <math> \{i, \pi_i\} </math>. The joint probability and the marginals are defined as a product of such local probabilities which was inspired from the chain rule in the probability theory. | |||
In undirected GMs "local" functions cannot be represented using conditional probabilities, and we must abandon conditional probabilities altogether. Therefore, the factors do not have probabilistic interpretation any more, but we can choose the "local" functions arbitrarily. However, any "local" function for undirected graphical models should satisfy the following condition: | |||
- Consider <math> X_i </math> and <math> X_j </math> that are not linked, they are conditionally independent given all other nodes. As a result, the "local" function should be able to do the factorization on the joint probability such that <math> X_i </math> and <math> X_j </math> are placed in different factors. | |||
It can be shown that definition of local functions based only a node and its corresponding edges (similar to directed graphical models) is not tractable and we need to follow a different approach. Before defining the "local" functions, we have to introduce a new terminology in graph theory called clique. Clique is | |||
a subset of fully connected nodes in a graph G. Every node in the clique C is directly connected to every other node in C. In addition, maximal clique is a clique where if any other node from the graph G is added to it then the new set is no longer a clique. Consider the undirected graph shown in (Fig. 24), we can list all the cliques as follow: | |||
[[File:graph.png|thumb|right|Fig.24 Undirected graph]] | |||
- <math> \{X_1, X_3\} </math> | |||
- <math> \{X_1, X_2\} </math> | |||
- <math> \{X_3, X_5\} </math> | |||
- <math> \{X_2, X_4\} </math> | |||
- <math> \{X_5, X_6\} </math> | |||
- <math> \{X_2, X_5\} </math> | |||
- <math> \{X_2, X_5, X_6\} </math> | |||
According to the definition, <math> \{X_2,X_5\} </math> is not a maximal clique since we can add one more node, <math> X_6 </math> and still have a clique. Let C be set of all maximal cliques in <math> G(V, E) </math>: | |||
<center><math> | |||
C = \{c_1, c_2,..., c_n\} | |||
</math></center> | |||
where in aforementioned example <math> c_1 </math> would be <math> \{X_1, X_3\} </math>, and so on. We define the joint probability over all nodes as: | |||
<center><math> | |||
P(x_{V}) = \frac{1}{Z} \prod_{c_i \epsilon C} \psi_{c_i} (x_{c_i}) | |||
</math></center> | |||
where <math> \psi_{c_i} (x_{c_i})</math> is an arbitrarily function with some restrictions. This function is not necessarily probability and is defined over each clique. There are only two restrictions for this function, non-negative and real-valued. Usually <math> \psi_{c_i} (x_{c_i})</math> is called potential function. The <math> Z </math> is normalization factor and determined by: | |||
<center><math> | |||
Z = \sum_{X_V} { \prod_{c_i \epsilon C} \psi_{c_i} (x_{c_i})} | |||
</math></center> | |||
As a matter of fact, normalization factor, <math> Z </math>, is not very important since in most of the time is canceled out during computation. For instance, to calculate conditional probability <math> P(X_A | X_B) </math>, <math> Z </math> is crossed out between the nominator <math> P(X_A, X_B) </math> and the denominator <math> P(X_B) </math>. | |||
As was mentioned above, sum-product of the potential functions determines the joint probability over all nodes. Because of the fact that potential functions are arbitrarily defined, assuming exponential functions for <math> \psi_{c_i} (x_{c_i})</math> simplifies and reduces the computations. Let potential function be: | |||
= | <center><math> | ||
\psi_{c_i} (x_{c_i}) = exp (- H(x_i)) | |||
</math></center> | |||
the joint probability is given by: | |||
<center><math> | |||
P(x_{V}) = \frac{1}{Z} \prod_{c_i \epsilon C} exp(-H(x_i)) = \frac{1}{Z} exp (- \sum_{c_i} {H_{c_i} (x_i)}) | |||
</math></center> | |||
- | |||
There is a lot of information contained in the joint probability distribution <math> P(x_{V}) </math>. We define 6 tasks listed bellow that we would like to accomplish with various algorithms for a given distribution <math> P(x_{V}) </math>. | |||
There is a lot of information contained in the joint probability distribution <math> P(x_{V}) </math>. We | |||
===Tasks:=== | ===Tasks:=== | ||
* Marginalization <br /> | * Marginalization <br /> | ||
Given <math> P(x_{V}) </math> find <math> P(x_{A}) </math> <br /> | Given <math> P(x_{V}) </math> find <math> P(x_{A}) </math> where A ⊂ V<br /> | ||
Given <math> P(x_1, x_2, ... , x_6) </math> find <math> P(x_2, x_6) </math> | |||
* Conditioning <br /> | * Conditioning <br /> | ||
Given <math> P(x_V) </math> find <math>P(x_A|x_B) = \frac{P(x_A, x_B)}{P(x_B)}</math> . | Given <math> P(x_V) </math> find <math>P(x_A|x_B) = \frac{P(x_A, x_B)}{P(x_B)}</math> if A ⊂ V and B ⊂ V . | ||
* Evaluation <br /> | * Evaluation <br /> | ||
Evaluate the probability for a certain configuration. | Evaluate the probability for a certain configuration. | ||
| Line 679: | Line 696: | ||
We would like to find parameters for <math> P(x_V) </math> . | We would like to find parameters for <math> P(x_V) </math> . | ||
===Exact Algorithms=== | |||
To compute the probabilistic inference or the conditional probability of a variable <math>X</math> we need to marginalize over all the random variables <math>X_i</math> and the possible values of <math>X_i</math> which might take long running time. To reduce the computational complexity of preforming such marginalization the next section presents different exact algorithms that find the exact solutions for algorithmic problem in a Polynomial time(fast) which are: | |||
* Elimination | * Elimination | ||
* Sum-Product | * Sum-Product | ||
* Max-Product | |||
* Junction Tree | * Junction Tree | ||
== | = Elimination Algorithm= | ||
Oct. 4. 2011 <br /> | |||
In this section we will see how we could overcome the problem of probabilistic inference on graphical models. In other words, we discuss the problem of computing conditional and marginal probabilities in graphical models. | |||
Variable Elimination as an exact inference algorithm. It uses dynamic programming technique to reduce the number of required computations needed to answer an inference query. The basic idea behind Variable Elimination Algorithm is to push the summations over random variables as far as possible and replace the resulted terms with new factors. For a Markov chain this algorithm guaranteed that the number of computations needed to answer an inference query would always be linear with the length of the chain. | |||
== Elimination Algorithm on Directed Graphs<ref name="Pool">[http://www.wikicoursenote.com/wiki/Stat946f11pool]</ref>== | |||
First we assume that E and F are disjoint subsets of the node indices of a graphical model, i.e. <math> X_E </math> and <math> X_F </math> are disjoint subsets of the random variables. Given a graph G =(V,''E''), we aim to calculate <math> p(x_F | x_E) </math> where <math> X_E </math> and <math> X_F </math> represents evidence and query nodes, respectively. Here and in this section <math> X_F </math> should be only one node; however, later on a more powerful inference method will be introduced which is able to make inference on multi-variables. In order to compute <math> p(x_F | x_E) </math> we have to first marginalize the joint probability on nodes which are neither <math> X_F </math> nor <math> X_E </math> denoted by <math> R = V - ( E U F)</math>. | |||
<center><math> | |||
p(x_E, x_F) = \sum_{x_R} {p(x_E, x_F, x_R)} | |||
</math></center> | |||
which can be further marginalized to yield <math> p(E) </math>: | |||
<center><math> | |||
p(x_E) = \sum_{x_F} {p(x_E, x_F)} | |||
</math></center> | |||
and then the desired conditional probability is given by: | |||
<center><math> | <center><math> | ||
p(x_F|x_E) = \frac{p(x_E, x_F)}{p(x_E)} | |||
</math></center> | |||
== Example == | |||
Let | Let assume that we are interested in <math> p(x_1 | \bar{x_6)} </math> in (Fig. 21) where <math> x_6 </math> is an observation of <math> X_6 </math> , and thus we may assume that it is a constant. According to the rule mentioned above we have to marginalized the joint probability over non-evidence and non-query nodes: | ||
<center><math>\begin{matrix} | <center><math>\begin{matrix} | ||
p(x_1, \bar{x_6})& = &\sum_{x_2} \sum_{x_3} \sum_{x_4} \sum_{x_5} p(x_1)p(x_2|x_1)p(x_3|x_1)p(x_4|x_2)p(x_5|x_3)p(\bar{x_6}|x_2,x_5)\\ | |||
&= | & = & p(x_1) \sum_{x_2} p(x_2|x_1) \sum_{x_3} p(x_3|x_1) \sum_{x_4} p(x_4|x_2) \sum_{x_5} p(x_5|x_3)p(\bar{x_6}|x_2,x_3)\\ | ||
&= | & = & p(x_1) \sum_{x_2} p(x_2|x_1) \sum_{x_3} p(x_3|x_1) \sum_{x_4} p(x_4|x_2) m_5(x_2, x_3) | ||
& | |||
\end{matrix}</math></center> | \end{matrix}</math></center> | ||
where to simplify the notations we define <math> m_5(x_2, x_3) </math> which is the result of the last summation. The last summation is over <math> x_5 </math> , and thus the result is only depend on <math> x_2 </math> and <math> x_3</math>. In particular, let <math> m_i(x_{s_i}) </math> denote the expression that arises from performing the <math> \sum_{x_i} </math>, where <math> x_{S_i} </math> are the variables, other than <math> x_i </math>, that appear in the summand. Continuing the derivations we have: | |||
<center><math>\begin{matrix} | |||
p(x_1, \bar{x_6})& = &p(x_1) \sum_{x_2} p(x_2|x_1) \sum_{x_3} p(x_3|x_1)m_5(x_2,x_3)\sum_{x_4} p(x_4|x_2)\\ | |||
& = & p(x_1) \sum_{x_2} p(x_2|x_1)m_4(x_2)\sum_{x_3}p(x_3|x_1)m_5(x_2,x_3)\\ | |||
& = & p(x_1) \sum_{x_2} p(x_2|x_1)m_4(x_2)m_3(x_1,x_2)\\ | |||
& = & p(x_1)m_2(x_1) | |||
\end{matrix}</math></center> | |||
= | Therefore, the conditional probability is given by: | ||
<center><math> | |||
<math>\ | p(x_1|\bar{x_6}) = \frac{p(x_1)m_2(x_1)}{\sum_{x_1} p(x_1)m_2(x_1)} | ||
</math></center> | |||
<math>\delta | |||
At the beginning of our computation we had the assumption which says <math> X_6 </math> is observed, and thus the notation <math> \bar{x_6} </math> was used to express this fact. Let <math> X_i </math> be an evidence node whose observed value is <math> \bar{x_i} </math>, we define an evidence potential function, <math> \delta(x_i, \bar{x_i}) </math>, which its value is one if <math> x_i = \bar{x_i} </math> and zero elsewhere. | |||
This function allows us to use summation over <math> x_6 </math> yielding: | |||
<center><math> | |||
m_6(x_2, x_5) = \sum_{x_6} p(x_6|x_2, x_5) \delta(x_6, \bar{x_6}) | |||
</math></center> | |||
We can define an algorithm to make inference on directed graphs using elimination techniques. | |||
Let E and F be an evidence set and a query node, respectively. We first choose an elimination ordering I such that F appears last in this ordering. The following figure shows the steps required to perform the elimination algorithm for probabilistic inference on directed graphs: | |||
<code> | |||
ELIMINATE (G,E,F)<br/> | |||
INITIALIZE (G,F)<br/> | |||
EVIDENCE(E)<br/> | |||
UPDATE(G)<br/> | |||
NORMALIZE(F)<br/> | |||
INITIALIZE(G,F)<br/> | |||
Choose an ordering <math>I</math> such that <math>F</math> appear last <br/> | |||
:'''For''' each node <math>X_i</math> in <math>V</math> <br/> | |||
::Place <math>p(x_i|x_{\pi_i})</math> on the active list <br/> | |||
:'''End'''<br/> | |||
EVIDENCE(E)<br/> | |||
:'''For''' each <math>i</math> in <math>E</math> <br/> | |||
::Place <math>\delta(x_i|\overline{x_i})</math> on the active list <br/> | |||
:'''End''' <br/> | |||
Update(G)<br/> | |||
:''' For''' each <math>i</math> in <math>I</math> <br/> | |||
::Find all potentials from the active list that reference <math>x_i</math> and remove them from the active list <br/> | |||
::Let <math>\phi_i(x_Ti)</math> denote the product of these potentials <br/> | |||
::Let <math>m_i(x_Si)=\sum_{x_i}\phi_i(x_Ti)</math> <br/> | |||
::Place <math>m_i(x_Si)</math> on the active list <br/> | |||
:'''End''' <br/> | |||
Normalize(F) <br/> | |||
:<math> p(x_F|\overline{x_E})</math> ← <math>\phi_F(x_F)/\sum_{x_F}\phi_F(x_F)</math><br/> | |||
</code> | |||
'''Example:''' <br /> | '''Example:''' <br /> | ||
For the graph in | For the graph in figure 21 <math>G =(V,''E'')</math>. Consider once again that node <math>x_1</math> is the query node and <math>x_6</math> is the evidence node. <br /> | ||
<math>I = \left\{6,5,4,3,2,1\right\}</math> (1 should be the last node, ordering is crucial)<br /> | <math>I = \left\{6,5,4,3,2,1\right\}</math> (1 should be the last node, ordering is crucial)<br /> | ||
We must now | [[File:ClassicExample1.png|thumb|right|Fig.21 Six node example.]] | ||
We must now create an active list. There are two rules that must be followed in order to create this list. | |||
# For i<math>\in{V}</math> | # For i<math>\in{V}</math> place <math>p(x_i|x_{\pi_i})</math> in active list. | ||
# For i<math>\in</math>{E} | # For i<math>\in</math>{E} place <math>\delta(x_i|\overline{x_i})</math> in active list. | ||
Here, our active list is: | Here, our active list is: | ||
<math> p(x_1), p(x_2|x_1), p(x_3|x_1), p( | <math> p(x_1), p(x_2|x_1), p(x_3|x_1), p(x_4|x_2), p(x_5|x_3),\underbrace{p(x_6|x_2, x_5)\delta{(\overline{x_6},x_6)}}_{\phi_6(x_2,x_5, x_6), \sum_{x6}{\phi_6}=m_{6}(x2,x5) }</math> | ||
We first eliminate node <math>X_6</math>. We place <math>m_{6}(x_2,x_5)</math> on the active list, having removed <math>X_6</math>. We now eliminate <math>X_5</math>. | We first eliminate node <math>X_6</math>. We place <math>m_{6}(x_2,x_5)</math> on the active list, having removed <math>X_6</math>. We now eliminate <math>X_5</math>. | ||
| Line 767: | Line 814: | ||
Likewise, we can also eliminate <math>X_4, X_3, X_2</math>(which yields the unnormalized conditional probability <math>p(x_1|\overline{x_6})</math> and <math>X_1</math>. Then it yields <math>m_1 = \sum_{x_1}{\phi_1(x_1)}</math> which is the normalization factor, <math>p(\overline{x_6})</math>. | Likewise, we can also eliminate <math>X_4, X_3, X_2</math>(which yields the unnormalized conditional probability <math>p(x_1|\overline{x_6})</math> and <math>X_1</math>. Then it yields <math>m_1 = \sum_{x_1}{\phi_1(x_1)}</math> which is the normalization factor, <math>p(\overline{x_6})</math>. | ||
[[File:threetwograph.png|thumb|right|Fig.21 3x2 graph ]] | |||
Note: the complexity of elimination is determined by the maximum message size or in other word by tree-width. | |||
Tree width= (the minimum of the maximal clique created during graph elimination)-1. For example the tree-width of 3x2 graph in figure 21 is 3-1=2. | |||
==Elimination Algorithm on Undirected Graphs== | |||
Oct.6 .2011<br /> | |||
[[File:graph.png|thumb|right|Fig. | [[File:graph.png|thumb|right|Fig.22 Undirected graph G']] | ||
The first task is to find the maximal cliques and their associated potential functions. <br /> | The first task is to find the maximal cliques and their associated potential functions. <br /> | ||
| Line 783: | Line 833: | ||
The <math>\frac{1}{Z}</math> looks crucial, but in fact it has no effect because for (*) both the numerator and the denominator have the <math>\frac{1}{Z}</math> term. So in this case we can just cancel it. <br /> | The <math>\frac{1}{Z}</math> looks crucial, but in fact it has no effect because for (*) both the numerator and the denominator have the <math>\frac{1}{Z}</math> term. So in this case we can just cancel it. <br /> | ||
The general rule for elimination in an undirected graph is that we can remove a node as long as we connect all of the parents of that node together. Effectively, we form a clique out of the parents of that node. | The general rule for elimination in an undirected graph is that we can remove a node as long as we connect all of the parents of that node together. Effectively, we form a clique out of the parents of that node. | ||
The algorithm used to eliminate nodes in an undirected graph is: | |||
<code> | |||
<br/> | |||
UndirectedGraphElimination(G,l) | |||
:For each node <math>X_i</math> in <math>I</math> | |||
::Connect all of the remaining neighbours of <math>X_i</math> | |||
::Remove <math>X_i</math> from the graph | |||
:End | |||
<br/> | |||
</code> | |||
'''Example: ''' <br /> | '''Example: ''' <br /> | ||
For the graph G in | For the graph G in figure 24 <br /> | ||
when we remove x1, G becomes | when we remove x1, G becomes as in figure 25 <br /> | ||
if we remove x2, G becomes | while if we remove x2, G becomes as in figure 26 | ||
[[File:ex.png|thumb|right|Fig. | [[File:ex.png|thumb|right|Fig.24 ]] | ||
[[File:ex2.png|thumb|right|Fig. | [[File:ex2.png|thumb|right|Fig.25 ]] | ||
[[File:ex3.png|thumb|right|Fig. | [[File:ex3.png|thumb|right|Fig.26 ]] | ||
An interesting thing to point out is that the order of the elimination matters a great deal. Consider the two results. If we remove one node the graph complexity is slightly reduced | An interesting thing to point out is that the order of the elimination matters a great deal. Consider the two results. If we remove one node the graph complexity is slightly reduced. But if we try to remove another node the complexity is significantly increased. The reason why we even care about the complexity of the graph is because the complexity of a graph denotes the number of calculations that are required to answer questions about that graph. If we had a huge graph with thousands of nodes the order of the node removal would be key in the complexity of the algorithm. Unfortunately, there is no efficient algorithm that can produce the optimal node removal order such that the elimination algorithm would run quickly. If we remove one of the leaf first, then the largest clique is two and computational complexity is of order <math>N^2</math>. And removing the center node gives the largest clique size to be five and complexity is of order <math>N^5</math>. Hence, it is very hard to find an optimal ordering, due to which this is an NP problem. | ||
==Moralization== | |||
So far we have shown how to use elimination to successively remove nodes from an undirected graph. We know that this is useful in the process of marginalization. We can now turn to the question of what will happen when we have a directed graph. It would be nice if we could somehow reduce the directed graph to an undirected form and then apply the previous elimination algorithm. This reduction is called moralization and the graph that is produced is called a moral graph. | So far we have shown how to use elimination to successively remove nodes from an undirected graph. We know that this is useful in the process of marginalization. We can now turn to the question of what will happen when we have a directed graph. It would be nice if we could somehow reduce the directed graph to an undirected form and then apply the previous elimination algorithm. This reduction is called moralization and the graph that is produced is called a moral graph. | ||
| Line 807: | Line 872: | ||
'''Example:'''<br /> | '''Example:'''<br /> | ||
I = <math>\left\{x_6,x_5,x_4,x_3,x_2,x_1\right\}</math><br /> | I = <math>\left\{x_6,x_5,x_4,x_3,x_2,x_1\right\}</math><br /> | ||
When we moralize the directed graph | When we moralize the directed graph in figure 27, we obtain the | ||
undirected graph | undirected graph in figure 28. | ||
[[File:moral.png|thumb|right|Fig. | [[File:moral.png|thumb|right|Fig.27 Original Directed Graph]] | ||
[[File:moral3.png|thumb|right|Fig. | [[File:moral3.png|thumb|right|Fig.28 Moral Undirected Graph]] | ||
===Sum Product Algorithm | =Elimination Algorithm on Trees= | ||
'''Definition of a tree:'''<br /> | |||
A tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree. | |||
If we have a directed graph then we must moralize it first. If the moral graph is a tree then the directed graph is also considered a tree. | |||
==Belief Propagation Algorithm (Sum Product Algorithm)== | |||
One of the main disadvantages to the elimination algorithm is that the ordering of the nodes defines the number of calculations that are required to produce a result. The optimal ordering is difficult to calculate and without a decent ordering the algorithm may become very slow. In response to this we can introduce the sum product algorithm. It has one major advantage over the elimination algorithm: it is faster. The sum product algorithm has the same complexity when it has to compute the probability of one node as it does to compute the probability of all the nodes in the graph. Unfortunately, the sum product algorithm also has one disadvantage. Unlike the elimination algorithm it can not be used on any graph. The sum product algorithm works only on trees. | One of the main disadvantages to the elimination algorithm is that the ordering of the nodes defines the number of calculations that are required to produce a result. The optimal ordering is difficult to calculate and without a decent ordering the algorithm may become very slow. In response to this we can introduce the sum product algorithm. It has one major advantage over the elimination algorithm: it is faster. The sum product algorithm has the same complexity when it has to compute the probability of one node as it does to compute the probability of all the nodes in the graph. Unfortunately, the sum product algorithm also has one disadvantage. Unlike the elimination algorithm it can not be used on any graph. The sum product algorithm works only on trees. | ||
For undirected graphs if there is only one path between any two pair of nodes then that graph is a tree (Fig. | For undirected graphs if there is only one path between any two pair of nodes then that graph is a tree (Fig.29). If we have a directed graph then we must moralize it first. If the moral graph is a tree then the directed graph is also considered a tree (Fig.30). | ||
[[File:UnDirTree.png|thumb|right|Fig. | [[File:UnDirTree.png|thumb|right|Fig.29 Undirected tree]] | ||
[[File:Dir_Tree.png|thumb|right|Fig. | [[File:Dir_Tree.png|thumb|right|Fig.30 Directed tree]] | ||
For the undirected graph <math>G(v, \varepsilon)</math> (Fig. | For the undirected graph <math>G(v, \varepsilon)</math> (Fig.30) we can write the joint probability distribution function in the following way. | ||
<center><math> P(x_v) = \frac{1}{Z(\psi)}\prod_{i \varepsilon v}\psi(x_i)\prod_{i,j \varepsilon \varepsilon}\psi(x_i, x_j)</math></center> | <center><math> P(x_v) = \frac{1}{Z(\psi)}\prod_{i \varepsilon v}\psi(x_i)\prod_{i,j \varepsilon \varepsilon}\psi(x_i, x_j)</math></center> | ||
We know that in general we can not convert a directed graph into an undirected graph. There is however an exception to this rule when it comes to trees. In the case of a directed tree there is an algorithm that allows us to convert it to an undirected tree with the same properties. <br /> | We know that in general we can not convert a directed graph into an undirected graph. There is however an exception to this rule when it comes to trees. In the case of a directed tree there is an algorithm that allows us to convert it to an undirected tree with the same properties. <br /> | ||
Take the above example (Fig. | Take the above example (Fig.30) of a directed tree. We can write the joint probability distribution function as: | ||
<center><math> P(x_v) = P(x_1)P(x_2|x_1)P(x_3|x_1)P(x_4|x_2)P(x_5|x_2) </math></center> | <center><math> P(x_v) = P(x_1)P(x_2|x_1)P(x_3|x_1)P(x_4|x_2)P(x_5|x_2) </math></center> | ||
If we want to convert this graph to the undirected form shown in (Fig. | If we want to convert this graph to the undirected form shown in (Fig. 29) then we can use the following set of rules. | ||
\begin{thinlist} | \begin{thinlist} | ||
* If <math>\gamma</math> is the root then: <math> \psi(x_\gamma) = P(x_\gamma) </math>. | * If <math>\gamma</math> is the root then: <math> \psi(x_\gamma) = P(x_\gamma) </math>. | ||
* If <math>\gamma</math> is NOT the root then: <math> \psi(x_\gamma) = 1 </math>. | * If <math>\gamma</math> is NOT the root then: <math> \psi(x_\gamma) = 1 </math>. | ||
* If <math>\left\lbrace i \right\rbrace</math> = <math>\pi_j</math> then: <math> \psi(x_i, x_j) = P(x_j | x_i) </math>. | * If <math>\left\lbrace i \right\rbrace</math> = <math>\pi_j</math> then: <math> \psi(x_i, x_j) = P(x_j | x_i) </math>. | ||
So now we can rewrite the above equation for (Fig. | |||
So now we can rewrite the above equation for (Fig.30) as: | |||
<center><math> P(x_v) = \frac{1}{Z(\psi)}\psi(x_1)...\psi(x_5)\psi(x_1, x_2)\psi(x_1, x_3)\psi(x_2, x_4)\psi(x_2, x_5) </math></center> | <center><math> P(x_v) = \frac{1}{Z(\psi)}\psi(x_1)...\psi(x_5)\psi(x_1, x_2)\psi(x_1, x_3)\psi(x_2, x_4)\psi(x_2, x_5) </math></center> | ||
<center><math> = \frac{1}{Z(\psi)}P(x_1)P(x_2|x_1)P(x_3|x_1)P(x_4|x_2)P(x_5|x_2) </math></center> | <center><math> = \frac{1}{Z(\psi)}P(x_1)P(x_2|x_1)P(x_3|x_1)P(x_4|x_2)P(x_5|x_2) </math></center> | ||
==Elimination Algorithm on a Tree<ref name="Pool"/>== | |||
[[File:fig1.png|thumb|right|Fig. | [[File:fig1.png|thumb|right|Fig.31 Message-passing in Elimination Algorithm]] | ||
We will derive | We will derive the Sum-Product algorithm from the point of view | ||
of the | of the Eliminate algorithm. To marginalize <math>x_1</math> in | ||
Fig.31, | |||
<center><math>\begin{matrix} | <center><math>\begin{matrix} | ||
p(x_i)&=&\sum_{x_2}\sum_{x_3}\sum_{x_4}\sum_{x_5}p(x_1)p(x_2|x_1)p(x_3|x_2)p(x_4|x_2)p(x_5|x_3) \\ | p(x_i)&=&\sum_{x_2}\sum_{x_3}\sum_{x_4}\sum_{x_5}p(x_1)p(x_2|x_1)p(x_3|x_2)p(x_4|x_2)p(x_5|x_3) \\ | ||
| Line 873: | Line 947: | ||
\end{matrix}</math></center> | \end{matrix}</math></center> | ||
Note: It is important to know that BP algorithm gives us the exact solution only if the graph is a tree, however experiments have shown that BP leads to acceptable approximate answer even when the graphs has some loops. | |||
==Elimination To Sum Product Algorithm<ref name="Pool"/>== | |||
[[File:fig2.png|thumb|right|Fig. | [[File:fig2.png|thumb|right|Fig.32 All of the messages needed to compute all singleton | ||
marginals]] | marginals]] | ||
| Line 881: | Line 957: | ||
marginals in the tree by passing messages inward from the leaves of | marginals in the tree by passing messages inward from the leaves of | ||
the tree to an (arbitrary) root, and then passing it outward from the | the tree to an (arbitrary) root, and then passing it outward from the | ||
root to the leaves, again using | root to the leaves, again using the above equation at each step. The net effect is | ||
that a single message will flow in both directions along each edge. | that a single message will flow in both directions along each edge. | ||
(See | (See Fig.32) Once all such messages have been computed using the above equation, | ||
we can compute desired marginals. | we can compute desired marginals. One of the major advantages of this algorithm is that | ||
messages can be reused which reduces the computational cost heavily. | |||
As shown in | As shown in Fig.32, to compute the marginal of <math>X_1</math> using | ||
elimination, we eliminate <math>X_5</math>, which involves computing a message | elimination, we eliminate <math>X_5</math>, which involves computing a message | ||
<math>m_{53}(x_3)</math>, then eliminate <math>X_4</math> and <math>X_3</math> which involves | <math>m_{53}(x_3)</math>, then eliminate <math>X_4</math> and <math>X_3</math> which involves | ||
| Line 893: | Line 970: | ||
Suppose that we want to compute the marginal of <math>X_2</math>. As shown in | Suppose that we want to compute the marginal of <math>X_2</math>. As shown in | ||
Fig.33, we first eliminate <math>X_5</math>, which creates <math>m_{53}(x_3)</math>, and | |||
then eliminate <math>X_3</math>, <math>X_4</math>, and <math>X_1</math>, passing messages | then eliminate <math>X_3</math>, <math>X_4</math>, and <math>X_1</math>, passing messages | ||
<math>m_{32}(x_2)</math>, <math>m_{42}(x_2)</math> and <math>m_{12}(x_2)</math> to <math>X_2</math>. | <math>m_{32}(x_2)</math>, <math>m_{42}(x_2)</math> and <math>m_{12}(x_2)</math> to <math>X_2</math>. | ||
[[File:fig3.png|thumb|right|Fig. | [[File:fig3.png|thumb|right|Fig.33 The messages formed when computing the marginal of <math>X_2</math>]] | ||
Since the messages can be "reused", marginals over all possible | Since the messages can be "reused", marginals over all possible | ||
| Line 904: | Line 981: | ||
possible elimination orderings. | possible elimination orderings. | ||
The Sum-Product algorithm is not only based on equation | The Sum-Product algorithm is not only based on the above equation, but also ''Message-Passing Protocol''. | ||
'''Message-Passing Protocol''' tells us that a node can | |||
'''Message-Passing Protocol''' tells us that | send a message to a neighboring node when (and only when) it has | ||
send a message to a | received messages from all of its other neighbors. | ||
received messages from all of its other neighbors | |||
===For Directed Graph=== | |||
Previously we stated that: | Previously we stated that: | ||
<center><math> | <center><math> | ||
| Line 947: | Line 1,024: | ||
<math>p(x_F|\bar{x}_E)</math>. | <math>p(x_F|\bar{x}_E)</math>. | ||
===For Undirected Graphs=== | |||
We denote <math>\psi^E</math> to be: | We denote <math>\psi^E</math> to be: | ||
| Line 955: | Line 1,032: | ||
\end{matrix}</math></center> | \end{matrix}</math></center> | ||
==Max-Product== | |||
Because multiplication distributes over max as well as sum: | |||
<center><math>\begin{matrix} | |||
max(ab,ac) = a & \max(b,c) | |||
\end{matrix}</math></center> | |||
Formally, both the sum-product and max-product are commutative semirings. | |||
We would like to find the Maximum probability that can be achieved by some set of random variables given a set of configurations. The algorithm is similar to the sum product except we replace the sum with max. <br /> | We would like to find the Maximum probability that can be achieved by some set of random variables given a set of configurations. The algorithm is similar to the sum product except we replace the sum with max. <br /> | ||
[[File:suks.png|thumb|right|Fig. | [[File:suks.png|thumb|right|Fig.33 Max Product Example]] | ||
<center><math>\begin{matrix} | <center><math>\begin{matrix} | ||
| Line 979: | Line 1,057: | ||
'''Example:''' | '''Example:''' | ||
Consider the graph in Figure | Consider the graph in Figure.33. | ||
<center><math> m^{max}_{53}(x_5)=\max_{x_5}{\psi^{E}{(x_5)}\psi{(x_3,x_5)}} </math></center> | <center><math> m^{max}_{53}(x_5)=\max_{x_5}{\psi^{E}{(x_5)}\psi{(x_3,x_5)}} </math></center> | ||
<center><math> m^{max}_{32}(x_3)=\max_{x_3}{\psi^{E}{(x_3)}\psi{(x_3,x_5)}m^{max}_{5,3}} </math></center> | <center><math> m^{max}_{32}(x_3)=\max_{x_3}{\psi^{E}{(x_3)}\psi{(x_3,x_5)}m^{max}_{5,3}} </math></center> | ||
==Maximum configuration== | |||
We would also like to find the value of the <math>x_i</math>s which produces the largest value for the given expression. To do this we replace the max from the previous section with argmax. <br /> | We would also like to find the value of the <math>x_i</math>s which produces the largest value for the given expression. To do this we replace the max from the previous section with argmax. <br /> | ||
<math>m_{53}(x_5)= argmax_{x_5}\psi{(x_5)}\psi{(x_5,x_3)}</math><br /> | <math>m_{53}(x_5)= argmax_{x_5}\psi{(x_5)}\psi{(x_5,x_3)}</math><br /> | ||
<math>\log{m^{max}_{ji}(x_i)}=\max_{x_j}{\log{\psi^{E}{(x_j)}}}+\log{\psi{(x_i,x_j)}}+\sum_{k\in{N(j)\backslash{i}}}\log{m^{max}_{kj}{(x_j)}}</math><br /> | <math>\log{m^{max}_{ji}(x_i)}=\max_{x_j}{\log{\psi^{E}{(x_j)}}}+\log{\psi{(x_i,x_j)}}+\sum_{k\in{N(j)\backslash{i}}}\log{m^{max}_{kj}{(x_j)}}</math><br /> | ||
In many cases we want to use the log of this expression because the numbers tend to be very high. Also, it is important to note that this also works in the continuous case where we replace the summation sign with an integral. | In many cases we want to use the log of this expression because the numbers tend to be very high. Also, it is important to note that this also works in the continuous case where we replace the summation sign with an integral. | ||
=Parameter Learning= | |||
Oct .11.2011 <br /> | |||
The goal of graphical models is to build a useful representation of the input data to understand and design learning algorithm. Thereby, graphical model provide a representation of joint probability distribution over nodes (random variables). One of the most important features of a graphical model is representing the conditional independence between the graph nodes. This is achieved using local functions which are gathered to compose factorizations. Such factorizations, in turn, represent the joint probability distributions and hence, the conditional independence lying in such distributions. However that doesn’t mean the graphical model represent all the necessary independence assumptions. | |||
==Basic Statistical Problems== | ==Basic Statistical Problems== | ||
In statistics there are a number of different 'standard' problems that always appear in one form or another. They are as follows: | In statistics there are a number of different 'standard' problems that always appear in one form or another. They are as follows: | ||
* Regression | * Regression | ||
* Classification | * Classification | ||
* Clustering | * Clustering | ||
* Density Estimation | * Density Estimation | ||
===Regression=== | ===Regression=== | ||
In regression we have a set of data points <math> (x_i, y_i) </math> for <math> i = 1...n </math> and we would like to determine the way that the variables x and y are related. In certain cases such as (Fig. | In regression we have a set of data points <math> (x_i, y_i) </math> for <math> i = 1...n </math> and we would like to determine the way that the variables x and y are related. In certain cases such as (Fig.34) we try to fit a line (or other type of function) through the points in such a way that it describes the relationship between the two variables. | ||
[[File:regression.png|thumb|right|Fig. | [[File:regression.png|thumb|right|Fig.34 Regression]] | ||
Once the relationship has been determined we can give a functional value to the following expression. In this way we can determine the value (or distribution) of y if we have the value for x. | Once the relationship has been determined we can give a functional value to the following expression. In this way we can determine the value (or distribution) of y if we have the value for x. | ||
| Line 1,008: | Line 1,090: | ||
===Classification=== | ===Classification=== | ||
In classification we also have a set of points <math> (x_i | In classification we also have a set of data points which each contain set features <math> (x_1, x_2,.. ,x_i) </math> for <math> i = 1...n </math> and we would like to assign the data points into one of a given number of classes y. Consider the example in (Fig.35) where two sets of features have been divided into the set + and - by a line. The purpose of classification is to find this line and then place any new points into one group or the other. | ||
[[File:Classification.png|thumb|right|Fig. | [[File:Classification.png|thumb|right|Fig.35 Classify Points into Two Sets]] | ||
We would like to obtain the probability distribution of | We would like to obtain the probability distribution of the following equation where c is the class and x and y are the data points. In simple terms we would like to find the probability that this point is in class c when we know that the values of x and Y are x and y. | ||
<center><math> P(c|x,y)=\frac{P(c,x,y)}{P(x,y)} = \frac{P(c,x,y)}{\sum_{c}{P(c,x,y)}} </math></center> | <center><math> P(c|x,y)=\frac{P(c,x,y)}{P(x,y)} = \frac{P(c,x,y)}{\sum_{c}{P(c,x,y)}} </math></center> | ||
===Clustering=== | ===Clustering=== | ||
Clustering is | Clustering is unsupervised learning method that assign different a set of data point into a group or cluster based on the similarity between the data points. Clustering is somehow like classification only that we do not know the groups before we gather and examine the data. We would like to find the probability distribution of the following equation without knowing the value of c. | ||
<center><math> P( | <center><math> P(c|x)=\frac{P(c,x)}{P(x)}\ \ c\ unknown </math></center> | ||
===Density Estimation=== | |||
Density Estimation is the problem of modeling a probability density function p(x), given a finite number of data points | |||
drawn from that density function. | |||
<center><math> P(y|x)=\frac{P(y,x)}{P(x)} \ \ x\ unknown </math></center> | |||
We can use graphs to represent the four types of statistical problems that have been introduced so far. The first graph (Fig.36(a)) can be used to represent either the Regression or the Classification problem because both the X and the Y variables are known. The second graph (Fig.36(b)) we see that the value of the Y variable is unknown and so we can tell that this graph represents the Clustering and Density Estimation situation. | |||
[[File:RegClass.png|thumb|right|Fig.36(a) Regression or classification (b) Clustering or Density Estimation]] | |||
==Likelihood Function== | |||
Recall that the probability model <math>p(x|\theta)</math> has the intuitive interpretation of assigning probability to X for each fixed value of <math>\theta</math>. In the Bayesian approach this intuition is formalized by treating <math>p(x|\theta)</math> as a conditional probability distribution. In the Frequentist approach, however, we treat <math>p(x|\theta)</math> as a function of <math>\theta</math> for fixed x, and refer to <math>p(x|\theta)</math> as the likelihood function. | |||
<center><math> | |||
L(\theta;x)= p(x|\theta)</math></center> | |||
where <math>p(x|\theta)</math> is the likelihood L(<math>\theta, x</math>) | |||
<center><math> | |||
l(\theta,x)=log(p(x|\theta)) | |||
</math></center> | |||
where <math>log(p(x|\theta))</math> is the log likelihood <math>l(\theta, x)</math> | |||
Since <math>p(x)</math> in the denominator of Bayes Rule is independent of <math>\theta</math> we can consider it as a constant and we can draw the conclusion that: | |||
<center><math> | |||
< | p(\theta|x) \propto p(x|\theta)p(\theta) | ||
</math></center> | |||
Symbolically, we can interpret this as follows: | |||
< | <center><math> | ||
< | Posterior \propto likelihood \times prior | ||
</math></center> | |||
where we see that in the Bayesian approach the likelihood can be | |||
viewed as a data-dependent operator that transforms between the | |||
prior probability and the posterior probability. | |||
===Maximum likelihood=== | |||
The idea of estimating the maximum is to find the optimum values for the parameters by maximizing a likelihood function form the training data. Suppose in particular that we force the Bayesian to choose a | |||
particular value of <math>\theta</math>; that is, to remove the posterior | |||
distribution <math>p(\theta|x)</math> to a point estimate. Various | |||
possibilities present themselves; in particular one could choose the | |||
mean of the posterior distribution or perhaps the mode. | |||
(i) the mean of the posterior (expectation): | |||
<center><math> | |||
\hat{\theta}_{Bayes}=\int \theta p(\theta|x)\,d\theta | |||
</math></center> | |||
is called ''Bayes estimate''. | |||
OR | |||
(ii) the mode of posterior: | |||
<center><math>\begin{matrix} | |||
\hat{\theta}_{MAP}&=&argmax_{\theta} p(\theta|x) \\ | |||
&=&argmax_{\theta}p(x|\theta)p(\theta) | |||
\end{matrix}</math></center> | |||
Note that MAP is '''Maximum a posterior'''. | |||
<center><math> MAP -------> \hat\theta_{ML}</math></center> | |||
When the prior probabilities, <math>p(\theta)</math> is taken to be uniform on <math>\theta</math>, the MAP estimate reduces to the maximum likelihood estimate, <math>\hat{\theta}_{ML}</math>. | |||
= | <center><math> MAP = argmax_{\theta} p(x|\theta) p(\theta) </math></center> | ||
When the prior is not taken to be uniform, the MAP estimate will be the maximization over probability distributions(the fact that the logarithm is a monotonic function implies that it does not alter the optimizing value). | |||
Thus, one has: | |||
<center><math> | <center><math> | ||
\hat{\theta}_{MAP}=argmax_{\theta} \{ log p(x|\theta) + log | |||
p(\theta) \} | |||
</math></center> | </math></center> | ||
as an alternative expression for the MAP estimate. | |||
Here, <math>log (p(x|\theta))</math> is log likelihood and the "penalty" is the | |||
additive term <math>log(p(\theta))</math>. Penalized log likelihoods are widely | |||
used in Frequentist statistics to improve on maximum likelihood | |||
estimates in small sample settings. | |||
===Example : Bernoulli trials=== | |||
Consider the simple experiment where a biased coin is tossed four times. Suppose now that we also have some data <math>D</math>: <br />e.g. <math>D = \left\lbrace h,h,h,t\right\rbrace </math>. We want to use this data to estimate <math>\theta</math>. The probability of observing head is <math> p(H)= \theta</math> and the probability of observing a tail is <math> p(T)= 1-\theta</math>. | |||
where the conditional probability is <center><math> P(x|\theta) = \theta^{x_i}(1-\theta)^{(1-x_i)} </math></center> | |||
where <math> | |||
We would now like to use the ML technique.Since all of the variables are iid then there are no dependencies between the variables and so we have no edges from one node to another. | |||
How do we find the joint probability distribution function for these variables? Well since they are all independent we can just multiply the marginal probabilities and we get the joint probability. | |||
<center><math>L(\theta;x) = \prod_{i=1}^n P(x_i|\theta)</math></center> | |||
This is in fact the likelihood that we want to work with. Now let us try to maximise it: | |||
<center><math>\begin{matrix} | |||
l(\theta;x) & = & log(\prod_{i=1}^n P(x_i|\theta)) \\ | |||
& = & \sum_{i=1}^n log(P(x_i|\theta)) \\ | |||
& = & \sum_{i=1}^n log(\theta^{x_i}(1-\theta)^{1-x_i}) \\ | |||
& = & \sum_{i=1}^n x_ilog(\theta) + \sum_{i=1}^n (1-x_i)log(1-\theta) \\ | |||
\end{matrix}</math></center> | |||
Take the derivative and set it to zero: | |||
<center><math> | <center><math> \frac{\partial l}{\partial\theta} = 0 </math></center> | ||
<center><math> \frac{\partial l}{\partial\theta} = \sum_{i=0}^{n}\frac{x_i}{\theta} - \sum_{i=0}^{n}\frac{1-x_i}{1-\theta} = 0 </math></center> | |||
</math></center> | <center><math> \Rightarrow \frac{\sum_{i=0}^{n}x_i}{\theta} = \frac{\sum_{i=0}^{n}(1-x_i)}{1-\theta} </math></center> | ||
<center><math> \frac{NH}{\theta} = \frac{NT}{1-\theta} </math></center> | |||
Where: | |||
NH = number of all the observed of heads <br /> | |||
NT = number of all the observed tails <br /> | |||
Hence, <math>NT + NH = n</math> <br /> | |||
And now we can solve for <math>\theta</math>: | |||
</math> | |||
<center><math>\begin{matrix} | |||
\theta & = & \frac{(1-\theta)NH}{NT} \\ | |||
\theta + \theta\frac{NH}{NT} & = & \frac{NH}{NT} \\ | |||
\theta(\frac{NT+NH}{NT}) & = & \frac{NH}{NT} \\ | |||
\theta & = & \frac{\frac{NH}{NT}}{\frac{n}{NT}} = \frac{NH}{n} | |||
\end{matrix}</math></center> | |||
=== | ===Example : Multinomial trials=== | ||
Recall from the previous example that a Bernoulli trial has only two outcomes (e.g. Head/Tail, Failure/Success,…). A Multinomial trial is a multivariate generalization of the Bernoulli trial with K number of possible outcomes, where K > 2. Let <math> p(k) = \theta_k </math> be the probability of outcome k. All the <math>\theta_k</math> parameters must be: | |||
<math> 0 \leq \theta_k \leq 1</math> | |||
and | |||
<math> \sum_k \theta_k = 1</math> | |||
\ | |||
</math | |||
Consider the example of rolling a die M times and recording the number of times each of the six die's faces observed. Let <math> N_k </math> be the number of times that face k was observed. | |||
Let <math>[x^m = k]</math> be a binary indicator, such that the whole term would equals one if <math>x^m = k</math>, and zero otherwise. The likelihood function for the Multinomial distribution is: | |||
<math>l(\theta; D) = log( p(D|\theta) )</math> | |||
<math>= log(\prod_m \theta_{x^m}^{x})</math> | |||
<math>= log(\prod_m \theta_{1}^{[x^m = 1]} ... \theta_{k}^{[x^m = k]})</math> | |||
<math>= \sum_k log(\theta_k) \sum_m [x^m = k]</math> | |||
<math>= \sum_k N_k log(\theta_k)</math> | |||
Take the derivatives and set it to zero: | |||
<math>\frac{\partial l}{\partial\theta_k} = 0</math> | |||
<math>\frac{\partial l}{\partial\theta_k} = \frac{N_k}{\theta_k} - M = 0</math> | |||
<math>\Rightarrow \theta_k = \frac{N_k}{M}</math> | |||
===Example: Univariate Normal=== | |||
Now let us assume that the observed values come from normal distribution. <br /> | |||
\includegraphics{images/fig4Feb6.eps} | |||
\newline | |||
Our new model looks like: | |||
<center><math>P(x_i|\theta) = \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{1}{2}(\frac{x_i-\mu}{\sigma})^{2}} </math></center> | |||
Now to find the likelihood we once again multiply the independent marginal probabilities to obtain the joint probability and the likelihood function. | |||
<center><math> L(\theta;x) = \prod_{i=1}^{n}\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{1}{2}(\frac{x_i-\mu}{\sigma})^{2}}</math></center> | |||
<center><math> \max_{\theta}l(\theta;x) = \max_{\theta}\sum_{i=1}^{n}(-\frac{1}{2}(\frac{x_i-\mu}{\sigma})^{2}+log\frac{1}{\sqrt{2\pi}\sigma} </math></center> | |||
Now, since our parameter theta is in fact a set of two parameters, | |||
<center><math>\theta = (\mu, \sigma)</math></center> | |||
we must estimate each of the parameters separately. | |||
<center><math>\frac{\partial}{\partial u} = \sum_{i=1}^{n} \left( \frac{\mu - x_i}{\sigma} \right) = 0 \Rightarrow \hat{\mu} = \frac{1}{n}\sum_{i=1}^{n}x_i</math></center> | |||
<center><math>\frac{\partial}{\partial \mu ^{2}} = -\frac{1}{2\sigma ^4} \sum _{i=1}^{n}(x_i-\mu)^2 + \frac{n}{2} \frac{1}{\sigma ^2} = 0</math></center> | |||
<center><math> \Rightarrow \hat{\sigma} ^2 = \frac{1}{n}\sum_{i=1}{n}(x_i - \hat{\mu})^2 </math></center> | |||
== | ==Discriminative vs Generative Models== | ||
[[File:GenerativeModel.png|thumb|right|Fig.36i Generative Model represented in a graph.]] | |||
(beginning of Oct. 18) | |||
If we call the evidence/features variable <math>X\,\!</math> and the output variable <math>Y\,\!</math>, one way to model a classifier is to base the definition of the joint distribution on <math>p(X|Y)\,\!</math> and another one is to do it based on <math>p(Y|X)\,\!</math>. The first of this two approaches is called generative, as the second one is called discriminative. The philosophy behind this naming might be clear by looking at the way each conditional probability function tries to present a model. Based on the experience, using generative models (e.g. Bayes Classifier) in many cases leads to taking some assumptions which may not be valid according to the nature of the problem and hence make a model depart from the primary intentions of a design. This may not be the case for discriminative models (e.g. Logistic Regression), as they do not depend on many assumptions besides the given data. | |||
[[File:DiscriminativeModel.png|thumb|right|Fig.36ii Discriminative Model represented in a graph.]] | |||
Given <math>N</math> variables, we have a full joint distribution in a generative model. In this model we can identify the conditional independencies between various random variables. This joint distribution can be factorized into various conditional distributions. One can also define the prior distributions that affect the variables. | |||
Here is an example that represents generative model for classification in terms of a directed graphical model shown in Figure 36i. The following have to be estimated to fit the model: conditional probability, i.e. <math>P(Y|X)</math>, marginal and the prior probabilities. Examples that use generative approaches are Hidden Markov models, Markov random fields, etc. | |||
Discriminative approach used in classification is displayed in terms of a graph in Figure 36ii. However, in discriminative models the dependencies between various random variables are not explicitly defined. We need to estimate the conditional probability, i.e. <math>P(X|Y)</math>. Examples that use discriminative approach are neural networks, logistic regression, etc. | |||
Sometimes, it becomes very hard to compute <math>P(X|Y)</math> if <math>X</math> is of higher dimensional (like data from images). Hence, we tend to omit the intermediate step and calculate directly. In higher dimensions, we assume that they are independent to that it does not over fit. | |||
==Markov Models== | |||
Markov models, introduced by Andrey (Andrei) Andreyevich Markov as a way of modeling Russian poetry, are known as a good way of modeling those processes which progress over time or space. Basically, a Markov model can be formulated as follows: | |||
<center><math> | |||
y_t=f(y_{t-1},y_{t-2},\ldots,y_{t-k}) | |||
</math></center> | |||
And the joint distribution of t observations of Markov model is: | |||
<math>P(y_1,y_2,....y_T)=P(y_1,y_2,....y_k)\prod^t_{t=k+1} P(y_t,y_{t-1},....y_{t-k})</math> | |||
Which can be interpreted by the dependence of the current state of a variable on its last <math>k</math> states. (Fig. 37) | |||
Maximum Entropy Markov model is a type of Markov model, which makes the current state of a variable dependant on some global variables, besides the local dependencies. As an example, we can define the sequence of words in a context as a local variable, as the appearance of each word depends mostly on the words that have come before (n-grams). However, the role of POS (part of speech tagging) can not be denied, as it affect the sequence of words very clearly. In this example, POS are global dependencies, whereas last words in a row are those of local. | |||
===Markov Chain=== | |||
"The simplest Markov model is the Markov chain. It models the state of a system with a random variable that changes through time. In this context, the Markov property suggests that the distribution for this variable depends only on the distribution of the previous state." <ref>[http://en.wikipedia.org/wiki/Markov_model#Markov_chain]</ref> It is worth to note that alternatively Markov property can be explained as:"Given the current state the previous and future states are independent.". | |||
[[File:HMMorder1.png|thumb|right|Fig.37 Markov model of order 1.]] | |||
An example of a Markov model of oder 1 is displayed in Figure 37. Most common example is in the study of gene analysis or gene sequencing, and the joint probability is given by | |||
<center><math> P(y1,y2,y3,y4,y5) = P(y1)P(y2|y1)P(y3|y2)P(y4|y3)P(y5|y4). </math></center> | |||
[[File:HMMorder2.png|thumb|right|Fig.38 Markov model of order 2.]] | |||
A Markov model of order 2 is displayed in Figure 38. Joint probability is given by | |||
<center><math> P(y1,y2,y3,y4) = P(y1,y2)P(y3|y1,y2)P(y4|y2,y3). </math></center> | |||
==Hidden Markov Models (HMM)== | |||
Markov models fail to address a scenario, in which, a series of states cannot be observed except they are probabilistic function of those hidden states. Markov models are extended in these scenarios where observation is a probability function of state. An example of a HMM is the formation of DNA sequence. There is a hidden process that generates amino acids depending on some probabilities to determine an exact sequence. Main questions that can be answered with HMM are the following: | |||
* How can one estimate the probability of occurrence of an observation sequence? | |||
* How can we choose the state sequence such that the joint probability of the observation sequence is maximized? | |||
* How can we describe an observation sequence through the model parameters? | |||
A Hidden Markov Model (HMM) is a directed graphical model with two layers of nodes. The hidden layer of nodes represents a set of unobserved discrete random variables with some state space as the support. Isolated the first layer represents as a discrete time Markov Chain. These random variables are sequentially connected and which can often represent a temporal dependancy. In this model we do not observe the states (nodes in layer 1) we instead observe features that may be dependant on the states; this set of features represents the second observed layer of nodes. Thus for each node in layer 1 we have a corresponding dependant node in layer 2 which represents the observed features. Please see the Figure 39 for a visual depiction of the graphical structure. | |||
In other words, in HMM, it's guaranteed that, given the present state, the future state is independent of the past. The future state depends only on the present state. | |||
[[File:HMM.png|thumb|right|Fig.39 Hidden Markov Model]] | |||
The nodes in the first and second layers are denoted by <math> {q_0, q_1, ... , q_T} </math> (which are always discrete) and <math>{y_0, y_1, ... , y_T}</math> (which can be discrete or continuous) respectively. The <math>y_i</math>s are shaded because they are observed. | |||
The | The parameters that need to be estimated are <math> \theta = (\pi, A, \eta)</math>. Where <math>\pi</math> represents the initial states distributions, i.e <math>P(q_0)</math>. In general <math>\pi_i</math> represents the state that <math>q_i</math> is in. The matrix <math>A</math> is the transition matrix for the states <math>q_t</math> and <math>q_{t+1}</math> and shows the probability of changing states as we move from one step to the next. Finally, <math>\eta</math> represents the parameter that decides the probability that <math>y_i</math> will produce <math>y^*</math> given that <math>q_i</math> is in state <math>q^*</math>. <br /> | ||
Defining some notation: | |||
Note that we will be using a homogeneous descrete time Markov Chain with finite state space for the first layer. | |||
<math> \ q_t^j = \begin{cases} 1 & \text{if } q_t = j \\ 0 & \text{otherwise } \end{cases} | |||
</math> | |||
<math> | |||
\pi_i = P(q_0 = i) = P(q_0^i = 1) | |||
</math> | |||
==== | <math> | ||
a_{ij} = P(q_{t+1} = j | q_t = i) = P(q_{t+1}^j = 1 | q_t^i = 1) | |||
</math> | |||
For the HMM our data comes from the output layer: | |||
<center><math>\ Data = (y_{0i}, y_{1i}, y_{2i}, ... , y_{Ti}) \text{ for } i = 1...n </math></center> | |||
We can use <math>a_{ij}</math> to represent the i,j entry in the transition matrix A. We can then define: | |||
<center><math> P(q_{t-1}|q_t) = \prod_{i,j=1}^M (a_{ij})^{q_i^t q_j^{t+1}} </math></center> | |||
We can also define: | |||
<center><math> p(q_0) = \prod_{i=1}^M (\pi_i)^{q_0^i} </math></center> | |||
Now, if we take Y to be multinomial we get: | |||
<center><math> P(y_t|q_t) = \prod_{i,j=1}^M (\eta_{ij})^{y_t^i q_t^j} </math> | |||
where <math>n_{ij} = P(y_{t+1} = j | q_t = i) = P(y_{t+1}^j = 1 | q_t^i = 1) </math> | |||
</center> | |||
The random variable Y does not have to be multinomial, this is just an example. | |||
We can write the joint pdf using the structure of the HMM model graphical structure. | |||
<center><math> P(q, y) = p(q_0)\prod_{t=0}^{T-1}P(q_{t-1}|q_t)\prod_{t=0}^{T}P(y_t|q_t) </math></center> | |||
Substituting our representations for the 3 probabilities: | |||
<center><math> P(q, y) = \prod_{i=1}^M (\pi_i)^{q_0^i}\prod_{t=0}^{T-1} \prod_{i,j=1}^M (a_{ij})^{q_i^t q_j^{t+1}} \prod_{t=0}^{T}P(y_t|q_t) </math></center> | |||
We can go on to the E-Step with this new joint pdf. In the E-Step we need to find the expectation of the missing data given the observed data and the initial values of the parameters. Suppose that we only sample once so <math>n=1</math>. Take the log of our pdf and we get: | |||
<center><math> l_c(\theta, q, y) = \sum_{i=1}^M {q_0^i}log(\pi_i)\sum_{t=0}^{T-1} \sum_{i,j=1}^M {q_i^t q_j^{t+1}} log(a_{ij}) \sum_{t=0}^{T}log(P(y_t|q_t)) </math></center> | |||
Then we take the expectation for the E-Step: | |||
<center><math> E[l_c(\theta, q, y)] = \sum_{i=1}^M E[q_0^i]log(\pi_i)\sum_{t=0}^{T-1} \sum_{i,j=1}^M E[q_i^t q_j^{t+1}] log(a_{ij}) \sum_{t=0}^{T}E[log(P(y_t|q_t))] </math></center> | |||
If we continue with our multinomial example then we would get: | |||
<center><math> \sum_{t=0}^{T}E[log(P(y_t|q_t))] = \sum_{t=0}^{T}\sum_{i,j=1}^M E[q_t^j] y_t^i log(\eta_{ij}) </math></center> | |||
So now we need to calculate <math>E[q_0^i]</math> and <math> E[q_i^t q_j^{t+1}] </math> in order to find the expectation of the log likelihood. Let's define some variables to represent each of these quantities. <br /> | |||
Let <math> \gamma_0^i = E[q_0^i] = P(q_0^i=1|y, \theta^{(t)}) </math>. <br /> | |||
Let <math> \xi_{t,t+1}^{ij} = E[q_i^t q_j^{t+1}] = P(q_t^iq_{t+1}^j|y, \theta^{(t)}) </math> .<br /> | |||
We could use the sum product algorithm to calculate these equations but in this case we will introduce a new algorithm that is called the <math>\alpha</math> - <math>\beta</math> Algorithm. | |||
===The <math>\alpha</math> - <math>\beta</math> Algorithm=== | |||
We | We have from before the expectation: | ||
<center><math> | <center><math> E[l_c(\theta, q, y)] = \sum_{i=1}^M \gamma_0^i log(\pi_i)\sum_{t=0}^{T-1} \sum_{i,j=1}^M \xi_{t,t+1}^{ij} log(a_{ij}) \sum_{t=0}^{T}E[log(P(y_t|q_t))] </math></center> | ||
As usual we take the derivative with respect to <math>\theta</math> and then we set that equal to zero and solve. We obtain the following results (You can check these...) . Note that for <math>\eta</math> we are using a specific <math>y*</math> that is given. | |||
<center><math>\begin{matrix} | <center><math>\begin{matrix} | ||
\hat \pi_0 & = & \frac{\gamma_0^i}{\sum_{k=1}^M \gamma_0^k} \\ | |||
\hat a_{ij} & = & \frac{\sum_{t=0}^{T-1}\xi_{t,t+1}^{ij}}{\sum_{k=1}^M\sum_{t=0}^{T-1}\xi_{t,t+1}^{ij}} \\ | |||
\end{matrix}</math></center> | \hat \eta_i(y^*) & = & \frac{\sum_{t|y_t=y^*}\gamma_t^i}{\sum_{t=0}^T\gamma_t^i} | ||
\end{matrix}</math></center> | |||
For <math>\eta</math> we can think of this intuitively. It represents the proportion of times that state i prodices <math>y^*</math>. For example we can think of the multinomial case for y where: | |||
<center><math> P( | <center><math> \hat \eta_{ij} = \frac{\sum_{t=0}^T\gamma_t^i y_t^j}{\sum_{t=0}^T\gamma_t^i} </math></center> | ||
\begin{ | Notice here that all of these parameters have been solved in terms of <math>\gamma_t^i</math> and <math>\xi_{t,t+1}^{ij}</math>. If we were to be able to calculate those two parameters then we could calculate everything in this model. This is where the <math>\alpha</math> - <math>\beta</math> Algorithm comes in. | ||
<math> | <center><math>\begin{matrix} | ||
\gamma_t^i & = & P(q_t^i = 1|y) \\ | |||
& = & \frac{P(y|q_t)P(q_t)}{P(y)} | |||
\end{matrix}</math></center> | |||
Now due to the Markovian Memoryless property. | |||
\ | <center><math>\begin{matrix} | ||
\gamma_t^i & = & \frac{P(y_0...y_t|q_t)P(y_{t+1}...y_T|q_t)P(q_t)}{P(y)} \\ | |||
& = & \frac{P(y_0...y_t|q_t)P(q_t)P(y_{t+1}...y_T|q_t)}{P(y)} \\ | |||
& = & \frac{P(y_0...y_t, q_t)P(y_{t+1}...y_T|q_t)}{P(y)} | |||
\end{matrix}</math></center> | |||
Define <math>\alpha</math> and <math>\beta</math> as follows: | |||
<center><math>\ \alpha(q_t) = P(y_0...y_t, q_t) </math></center> | |||
<center><math>\ \beta(q_t) = P(y_{t+1}...y_T|q_t) </math></center> | |||
Once we have <math>\alpha</math> and <math>\beta</math> then computing <math>P(y)</math> is easy. | |||
<center><math>\ P(y) = \sum_{q_t}\alpha(q_t)\beta(q_t) </math></center> | |||
To calculate <math>\alpha</math> and <math>\beta</math> themselves we can use:<br /> | |||
For <math>\alpha</math>: | |||
<center><math>\ \alpha(q_{t+1}) = \sum_{q_t}\alpha(q_t)a_{q_t,q_{t+1}}P(y_{t+1}|q_{t+1}) </math></center> | |||
Where we begin with: | |||
<center><math>\ \alpha(q_0) = P(y_0, q_0) = P(y_0| q_0)\pi_0 </math></center> | |||
Then for <math>\beta</math>: | |||
<center><math>\ \beta(q_t) = \sum_{q_t+1}\beta(q_{t+1})a_{q_t,q_{t+1}}P(y_{t+1}|q_{t+1}) </math></center> | |||
Where we now begin from the other end: | |||
<center><math>\ \beta(q_T) = (1,1,.....1) = \text{A Vector of Ones} </math></center> | |||
Once both <math>\alpha</math> and <math>\beta</math> have been calculated we can use them to find: | |||
<center><math>\ \gamma_t^i = \frac{\alpha(q_t)\beta(q_t)}{\sum_{q_t}\alpha(q_t)\beta(q_t)} </math></center> | |||
<center><math>\ \xi_{t,t+1}^{ij} = \frac{\alpha(q_t)P(y_{t+1}, q_{t+1}) \beta(q_{t+1}) a_{q_t,q_{t+1}}}{P(y)} </math></center> | |||
In order to find the hidden state given the observations, if we are | |||
conditioning over the state <math>q_t</math> using Bayes rule we have: | |||
<math>p(q_t|y)= \frac{p(y|q_t)p(q_t)}{p(y)}</math> | |||
<math>p(q_t|y)=\frac{p(y_0 y_1,... y_t|q_t) p(y_{t+1} ... y_t|q_t) p(q_t)}{p(y)}</math> | |||
= | <math>p(q_t|y)=\frac{p(y_0 y_1 ... y_t,q_t) p(y_{t+1} ... y_t|q_t) | ||
p(q_t)}{p(y)}</math> | |||
We | We represent <math>p(y_0 y_1 ... y_t,q_t)</math> as <math>\alpha(q_t)</math> and | ||
< | <math>p(y_{t+1} ... y_t|q_t)</math> as <math>\beta(q_t)</math> | ||
<math>\alpha(q_t)</math> and <math>\beta(q_t)</math> are independent and they can be computed | |||
recursively. Forward recursive manner in <math>\alpha(q_t)</math> and backward recursive manner in <math>\beta(q_t)</math> to reduce the computational complexity to O(M<sup>2</sup>T) in alpha recursion . | |||
Where <math>\alpha(q_t)</math> represents: what is the chance of hearing a | |||
sequence like <math>y_0 y_1 ... y_t</math> and being in state <math>q_t</math> | |||
and | |||
<math>\beta(q_t)</math> represents: Given in state <math>q_t</math>, what is the chance of | |||
hearing the specific sequence. | |||
The following two equations represent the relationship between | |||
<math>\alpha(q_t)</math> with <math>\alpha(q_{t+1})</math> and <math>\beta(q_t)</math> with <math>\beta(q_{t+1})</math> | |||
<math>\alpha(q_{t+1})=\sum_{q_{t}}\alpha(q_t) a_{q_t} , q_{t+1} p (y_{t+1}|q_{t+1})</math> | |||
<math>\beta(q_t)=\sum_{q_{t+1}} \beta (q_{t+1}) a_{q_t} , q_{t+1} | |||
p(y_{t+1}|q_{t+1})</math> | |||
' | HMM's are widely used in speech recognition applications as their temporal nature is ideal for such applications. | ||
== | ==Graph Structure== | ||
Up to this point, we have covered many topics about graphical models, assuming that the graph structure is given. However, finding an optimal structure for a graphical model is a challenging problem all by itself. In this section, we assume that the graphical model that we are looking for is expressible in a form of tree. And to remind ourselves of the concept of tree, an undirected graph will be a tree, if there is one and only one path between each pair of nodes. For the case of directed graphs, however, on top of the mentioned condition, we also need to check if all the nodes have at most one parent - which is in other words no explaining away kinds of structures. | |||
Firstly, let us show you how it does not affect the joint distribution function, if a graph is directed or undirected, as long as it is tree. Here is how one can write down the joint ditribution of the graph of Fig. XX. | |||
<center><math> | <center><math> | ||
p(x_1,x_2,x_3,x_4)=p(x_1)p(x_2|x_1)p(x_3|x_2)p(x_4|x_2).\,\! | |||
</math></center> | </math></center> | ||
Now, if we change the direction of the connecting edge between <math>x_1</math> and <math>x_2</math>, we will have the graph of Fig. XX and the corresponding joint distribution function will change as follows: | |||
<center><math> | |||
p(x_1,x_2,x_3,x_4)=p(x_2)p(x_1|x_2)p(x_3|x_2)p(x_4|x_2),\,\! | |||
</math></center> | |||
which can be simply re-written as: | |||
<center><math> | |||
p(x_1,x_2,x_3,x_4)=p(x_1,x_2)p(x_3|x_2)p(x_4|x_2),\,\! | |||
</math></center> | |||
which is the same as the first function. We will depend on this very simplistic observation and leave the proof to the enthusiast reader. | |||
=== | ===Maximum Likelihood Tree=== | ||
We want to compute the tree that maximizes the likelihood for a given set of data. Optimality of a tree structure can be discussed in terms of likelihood of the set of variables. By doing so, we can define a fully connected, weighted graph by setting the edge weights to the likelihood of the occurrence of the connecting nodes/random variables and then by running the maximum weight spanning tree. Here is how it works. | |||
We have defined the joint distribution as follows: | |||
<center><math> | <center><math> | ||
p(x)=\prod_{i\in V}p(x_i)\prod_{i,j\in E}\frac{p(x_i,x_j)}{p(x_i)p(x_j)} | |||
< | </math></center> | ||
Where <math>V</math> and <math>E</math> are respectively the sets of vertices and edges of the corresponding graph. This holds as long as the tree structure for the graphical model is concerned, as the dependence of <math>x_i</math> on <math>x_j</math> has been chosen arbitrarily and this is not the case for non-tree graphical models. | |||
Maximizing the joint probability distribution over the given set of data samples <math>X</math> with the objective of parameter estimation we will have (MLE): | |||
<center><math> | |||
<center><math> | L(\theta|X):p(X|\theta)=\prod_{i\in V}p(x_i|\theta)\prod_{i,j\in E}\frac{p(x_i,x_j|\theta)}{p(x_i|\theta)p(x_j|\theta)} | ||
</math></center> | |||
And by taking the logarithm of <math>L(\theta|X)</math> (log-likelihood), we will get: | |||
<center><math> | |||
l=\sum_{i\in V}\log p(x_i)+\sum_{i,j\in E}\log\frac{p(x_i,x_j|\theta)}{p(x_i|\theta)p(x_j|\theta)} | |||
</math></center> | |||
The first term in the above equation does not convey anything about the topology or the structure of the tree as it is defined over single nodes. As much as the optimization of the tree structure is concerned, the probability of the single nodes may not play any role in the optimization, so we can define the cost function for our optimization problem as such: | |||
<center><math> | |||
l_r=\sum_{i,j\in E}\log\frac{p(x_i,x_j|\theta)}{p(x_i|\theta)p(x_j|\theta)} | |||
<center><math> | </math></center> | ||
\ | Where the sub r is for reduced. By replacing the probability functions with the frequency of occurence of each state, we will have: | ||
<center><math>\ | |||
\ | |||
\theta | |||
\theta | |||
= | <center><math> | ||
l_r=\sum_{s,t}N_{ijst}\log\frac{N_{ijst}}{N_{is}N_{jt}} | |||
</math></center> | |||
=== | Where we have assumed that <math>p(x_i,x_j)=\frac{N_{ijst}}{N}</math>, <math>p(x_i)=\frac{N_{is}}{N}</math>, and <math>p(x_j)=\frac{N_{jt}}{N}</math>. The resulting statement is the definition of the mutual information of the two random variables <math>x_i</math> and <math>x_j</math>, where the former is in state <math>s</math> and the latter in <math>t</math>. | ||
This is how it has been figured out how to define weights for the edges of a fully connected graph. Now, it is required to run the maximum weight spanning tree on the resulting graph to find the optimal structure for the tree. | |||
It is important to note that before developing graphical models this problem has been solved in graph theory. Here our problem was completely a probabilistic problem but using graphical models we could find an equivalent graph theory problem. This show how graphical models can help us to use powerful graph theory tools to solve probabilistic problems. | |||
==Latent Variable Models== | |||
(beginning of Oct. 20) | |||
Learning refers to either estimating the parameters or the structures of the models, which can be in four forms: known structure and fully observed variables, known structure and partially observed variables, unknown structure and fully observed variables, and unknown structure and partially observed variables. | |||
Assuming that we have thoroughly observed, or even identified all of the random variables of a model can be a very naive assumption, as one can think of many instances of contrary cases. To make a model as rich as possible -there is always a trade-off between richness and complexity, so we do not like to inject unnecessary complexity to our model either- the concept of latent variables has been introduced to the graphical models. | |||
First let's define latent variables. "Latent variables are variables that are not directly observed but are rather inferred (through a mathematical model) from other variables that are observed (directly measured). Mathematical models that aim to explain observed variables in terms of latent variables are called latent variable models."<ref>[http://en.wikipedia.org/wiki/Latent_variable]</ref> | |||
Depending on the position of an unobserved variable, <math>z</math>, we take different actions. If there is no variable conditioned on <math>z</math>, we can integrate/sum it out and it will never be noticed, as it is not either an evidence or a querey. However, we will require to model an unobserved variable like <math>z</math>, if it is bound to some conditions. | |||
<math></math> | The use of latent variables makes a model harder to analyze and to learn. The use of log-likelihood used to make the target function easier to obtain, as the log of product will change to sum of logs, but this will not be the case, when one introduces latent variables to a model, as the resulting joint probability function comes with a sum, which makes the effect of log on product impossible. | ||
<center><math> | |||
l(\theta,D) = \log\sum_{z}p(x,z|\theta). | |||
</math></center> | |||
As an example of latent variables, one can think of a mixture density model. There are different models come together to build the final model, but it takes one more random variable to say which one of those models to use at the presence of each new sample point. This will affect both the learning and recalling phases. | |||
< | == EM Algorithm == | ||
Oct. 25th | |||
< | === Introduction === | ||
In last section the graphical models with latent variables were discussed. It was mentioned that, for example, if fitting typical distributions on a data set is too complex, one may think of modeling the data set using a mixture of famous distribution such as Gaussian. Therefore, a hidden variable is needed to determine weight of each Gaussian model. Parameter learning in graphical models with latent variables is more complicated in comparison with the models with no latent variable.\\ | |||
Consider Fig.40 which depicts a simple graphical model with two nodes. As the convention, unobserved variable <math> Z </math> is unshaded. To compare complexity between fully observed models and the models with hidden variables, lets suppose variables <math> Z </math> and <math> X </math> are both observed. We may like to interpret this problem as a classification problem where <math> Z </math> is class label and <math> X </math> is the data set. In addition, we assume the distribution over members of each group is Gaussian. Thus, the learning process is to determine label <math> Z </math> out of the training set by maximizing the posterior: | |||
[[File:GMwithLatent.png|thumb|right|Fig.40 A simple graphical model with a latent variable.]] | |||
<center><math> | |||
P(z|x) = \frac{P(x|z)P(z)}{P(x)}, | |||
<center><math> | </math></center> | ||
For simplicity, we assume there are two classes generating the data set <math> X</math>, <math> Z = 1 </math> and <math> Z = 0 </math>. The posterior <math> P(z=1|x) </math> can be easily computed using: | |||
<center><math> | |||
P(z = 1|x) = \frac{N(x; \mu_1, \sigma_1)}{N(x; \mu_1, \sigma_1)\pi_1 + N(x; \mu_0, \sigma_0)\pi_0}, | |||
</math></center> | |||
On the contrary, if <math> Z </math> is unknown we are not able to easily write the posterior and consequently parameter estimation is more difficult. In the case of graphical models with latent variables, we first assume the latent variable is somehow known, and thus writing the posterior becomes easy. Then, we are going to make the estimation of <math> Z </math> more accurate. For instance, if the task is to fit a set of data derived from unknown sources with mixtures of Gaussian distribution, we may assume the data is derived from two sources whose distributions are Gaussian. The first estimation might not be accurate, yet we introduce an algorithm by which the estimation is becoming more accurate using an iterative approach. In this section we see how the parameter learning for these graphical models is performed using EM algorithm. | |||
=== EM Method === | |||
EM (Expectation-Maximization) algorithm is "an iterative method for finding maximum likelihood or maximum a posterior (MAP) estimates of parameters in statistical models, where the model depends on unobserved latent variables."<ref name="Em">[http://en.wikipedia.org/wiki/Expectation%E2%80%93maximization_algorithm]</ref> | |||
There are two applications of the EM algorithm. The first is when the data has missing variables. The second occurs when obtaining the maximum likelihood estimate is very complicated and hence introducing a new variable while assuming that its value is unknown (hidden) considerably simplifies computations.<ref>Jeff A. Bilmes, "A Gentle Tutorial of the EM Algorithm and its Application to Parameter Estimation for Gaussian Mixture and Hidden Markov Models", 1998</ref> | |||
"The EM iteration alternates between performing an expectation (E) step, which computes the expectation of the log-likelihood evaluated using the current estimate for the parameters, and a maximization (M) step, which computes parameters maximizing the expected log-likelihood found on the E step. These parameter-estimates are then used to determine the distribution of the latent variables in the next E step."<ref name="Em"/> Consider a probabilistic model in which we collectively denote all of the observed variables by X and all of the hidden variables by Z resulting in a simple graphical model with two nodes (Fig. 40). The joint distribution | |||
<math> p(X,Z|θ) </math> is governed by a set of parameters,θ. The task is to maximize the likelihood function that is given by: | |||
<center><math> | |||
l_c(\theta; x,z) = log P(x,z | \theta) | |||
</math></center> | |||
which is called "complete log likelihood". In the above equation the x values represent data as before and the Z values represent missing data (sometimes called latent data) at that point. Now the question here is how do we calculate the values of the parameters <math>\theta_i</math> if we do not have all the data we need. We can use the Expectation Maximization (or EM) Algorithm to estimate the parameters for the model even though we do not have a complete data set. <br /> | |||
To simplify the problem we define the following type of likelihood: | |||
<center><math> | |||
l(\theta; x) = log(P(x | \theta)) | |||
</math></center> | |||
which is called "incomplete log likelihood". We can rewrite the incomplete likelihood in terms of the complete likelihood. This equation is in fact the discrete case but to convert to the continuous case all we have to do is turn the summation into an integral. | |||
<center><math> l(\theta; x) = log(P(x | \theta)) = log(\sum_zP(x, z|\theta)) </math></center> | |||
Since the z has not been observed that means that <math>l_c</math> is in fact a random quantity. In that case we can define the expectation of <math>l_c</math> in terms of some arbitrary density function <math>q(z|x)</math>. | |||
<center><math> l(\theta;x) = P(x|\theta) = log \sum_z P(x,z|\theta) = log \sum_z q(z|x) \frac{P(x,z|\theta)}{q(z|x)} = \sum_z q(z|x)log\frac{P(x, z|\theta)}{q(z|x)} </math></center> | |||
====Jensen's Inequality==== | |||
In order to properly derive the formula for the EM algorithm we need to first introduce the following theorem. | |||
For any '''concave''' function f: | |||
<center>any point between points <math>x_1 \,\!</math>&<math>x_2 \,\!</math> in Fig. 41 can be written as <math> \alpha x_1 + (1-\alpha)x_2 \,\!</math></center> | |||
<center><math> f(\alpha x_1 + (1-\alpha)x_2) \geqslant \alpha f(x_1) + (1-\alpha)f(x_2) </math></center> | |||
This can be shown intuitively through a graph. In the (Fig. 41) point A is the point on the function f and point B is the value represented by the right side of the inequality. On the graph one can see why point A will be smaller than point B in a convex graph. | |||
[[File:inequality.png|thumb|right|Fig.41 Jensen's Inequality]] | |||
\ | |||
For us it is important that the log function is '''concave''' , and thus: | |||
<center><math> | |||
log \sum_z q(z|x) \frac{P(x,z|\theta)}{q(z|x)} \geqslant \sum_z q(z|x) log \frac{P(x,z|\theta)}{q(z|x)} = F(\theta, q) | |||
</math></center> | |||
The function <math> F (\theta, q) </math> is called the auxiliary function and it is used in the EM algorithm. As seen in above equation <math> F(\theta, q) </math> is the lower bound of the incomplete log likelihood and one way to maximize the incomplete likelihood is to increase its lower bound. For the EM algorithm we have two steps repeating one after the other to give better estimation for <math>q(z|x)</math> and <math>\theta</math>. As the steps are repeated the parameters converge to a local maximum in the likelihood function. | |||
In the first step we assume <math> \theta </math> is known and then the goal is to find <math> q </math> to maximize the lower bound. Second, suppose <math> q </math> is known and find the <math> \theta </math>. In other words: | |||
'''E-Step''' | |||
<center><math> q^{t+1} = argmax_{q} F(\theta^t, q) </math></center> | |||
= | '''M-Step''' | ||
<center><math> \theta^{t+1} = argmax_{\theta} F(\theta, q^{t+1}) </math></center> | |||
==== M-Step Explanation ==== | |||
<center><math>\begin{matrix} | |||
F(q;\theta) & = & \sum_z q(z|x) log \frac{P(x,z|\theta)}{q(z|x)} \\ | |||
<center><math> | & = & \sum_z q(z|x)log(P(x,z|\theta)) - \sum_z q(z|x)log(q(z|x))\\ | ||
\end{matrix}</math></center> | |||
Since the second part of the equation is only a constant with respect to <math>\theta</math>, in the M-step we only need to maximize the expectation of the COMPLETE likelihood. The complete likelihood is the only part that still depends on <math>\theta</math>. | |||
==== E-Step Explanation ==== | |||
In this step we are trying to find an estimate for <math>q(z|x)</math>. To do this we have to maximize <math> F(q;\theta^{(t)})</math>. | |||
<center><math> | |||
F(q;\theta^{t}) = \sum_z q(z|x) log(\frac{P(x,z|\theta)}{q(z|x)}) | |||
</math></center> | |||
'''Claim:''' It can be shown that to maximize the auxiliary function one should set <math>q(z|x)</math> to <math> p(z|x,\theta^{(t)})</math>. Replacing <math>q(z|x)</math> with <math>P(z|x,\theta^{(t)})</math> results in: | |||
<center><math>\begin{matrix} | <center><math>\begin{matrix} | ||
\ | F(q;\theta^{t}) & = & \sum_z P(z|x,\theta^{(t)}) log(\frac{P(x,z|\theta)}{P(z|x,\theta^{(t)})}) \\ | ||
& = & \sum_z P(z|x,\theta^{(t)}) log(\frac{P(z|x,\theta^{(t)})P(x|\theta^{(t)})}{P(z|x,\theta^{(t)})}) \\ | |||
& = & \sum_z P(z|x,\theta^{(t)}) log(P(x|\theta^{(t)})) \\ | |||
& = & log(P(x|\theta^{(t)})) \\ | |||
& = & l(\theta; x) | |||
\end{matrix}</math></center> | \end{matrix}</math></center> | ||
Recall that <math>F(q;\theta^{(t)})</math> is the lower bound of <math> l(\theta, x) </math> determines that <math>P(z|x,\theta^{(t)})</math> is in fact the maximum for <math>F(q;\theta)</math>. Therefore we only need to do the E-Step once and then use the result for each iteration of the M-Step. | |||
The EM algorithm is a two-stage iterative optimization technique for finding | |||
maximum likelihood solutions. Suppose that the current value of the parameter vector is <math> \theta^t </math>. In the E step, the | |||
lower bound <math> F(q, \theta^t) </math> is maximized with respect to <math> q(z|x) </math> while <math> \theta^t </math> is fixed. | |||
As was mentioned above the solution to this maximization problem is to set the <math> q(z|x) </math> to <math> p(z|x,\theta^t) </math> since the value of incomplete likelihood,<math> log p(X|\theta^t) </math> does not depend on <math> q(z|x) </math> and so the largest value of <math> F(q, \theta^t) </math> will be achieved using this parameter. In this case the lower bound will equal the incomplete log likelihood. | |||
=== Alternative steps for the EM algorithms === | |||
From the above results we can find an alternative representation for the EM algorithm reproducing it to: | |||
'''E-Step''' <br /> | |||
Find <math> E[l_c(\theta; x, z)]_{P(z|x, \theta)} </math> only once. <br /> | |||
'''M-Step''' <br /> | |||
Maximise <math> E[l_c(\theta; x, z)]_{P(z|x, \theta)} </math> with respect to <math>theta</math>. | |||
The EM Algorithm is probably best understood through examples. | |||
=== | ====EM Algorithm Example==== | ||
Suppose we have the two independent and identically distributed random variables: | |||
<center><math> Y_1, Y_2 \sim P(y|\theta) = \theta e^{-\theta y} </math></center> | |||
In our case <math>y_1 = 5</math> has been observed but <math>y_2 = ?</math> has not. Our task is to find an estimate for <math>\theta</math>. We will try to solve the problem first without the EM algorithm. Luckily this problem is simple enough to be solveable without the need for EM. | |||
<center><math>\begin{matrix} | |||
L(\theta; Data) & = & \theta e^{-5\theta} \\ | |||
l(\theta; Data) & = & log(\theta)- 5\theta | |||
<center><math> | \end{matrix}</math></center> | ||
<center><math> | We take our derivative: | ||
<center><math>\begin{matrix} | |||
& \frac{dl}{d\theta} & = 0 \\ | |||
\Rightarrow & \frac{1}{\theta}-5 & = 0 \\ | |||
\Rightarrow & \theta & = 0.2 | |||
\end{matrix}</math></center> | |||
<center><math> | And now we can try the same problem with the EM Algorithm. | ||
<center><math>\begin{matrix} | |||
L(\theta; Data) & = & \theta e^{-5\theta}\theta e^{-y_2\theta} \\ | |||
= | l(\theta; Data) & = & 2log(\theta) - 5\theta - y_2\theta | ||
\end{matrix}</math></center> | |||
E-Step | |||
<center><math> E[l_c(\theta; Data)]_{P(y_2|y_1, \theta)} = 2log(\theta) - 5\theta - \frac{\theta}{\theta^{(t)}}</math></center> | |||
M-Step | |||
<center><math>\begin{matrix} | |||
<center><math> | & \frac{dl_c}{d\theta} & = 0 \\ | ||
<center><math> | \Rightarrow & \frac{2}{\theta}-5 - \frac{1}{\theta^{(t)}} & = 0 \\ | ||
\Rightarrow & \theta^{(t+1)} & = \frac{2\theta^{(t)}}{5\theta^{(t)}+1} | |||
\end{matrix}</math></center> | |||
Now we pick an initial value for <math>\theta</math>. Usually we want to pick something reasonable. In this case it does not matter that much and we can pick <math>\theta = 10</math>. Now we repeat the M-Step until the value converges. | |||
<center><math>\begin{matrix} | |||
\theta^{(1)} & = & 10 \\ | |||
\theta^{(2)} & = & 0.392 \\ | |||
\theta^{(3)} & = & 0.2648 \\ | |||
... & & \\ | |||
\theta^{(k)} & \simeq & 0.2 | |||
\end{matrix}</math></center> | |||
And as we can see after a number of steps the value converges to the correct answer of 0.2. In the next section we will discuss a more complex model where it would be difficult to solve the problem without the EM Algorithm. | |||
===Mixture Models=== | |||
Mixture models is a statistical model that has different sub-population within the overall population which use to compute the probability distribution in clustering. In this section we discuss what will happen if the random variables are not identically distributed. The data will now sometimes be sampled from one distribution and sometimes from another. | |||
====Mixture of Gaussian ==== | |||
In Gaussian mixture model the probability distribution function is computed by summing all the component of Gaussian mixtures. | |||
Given <math>P(x|\theta) = \alpha N(x;\mu_1,\sigma_1) + (1-\alpha)N(x;\mu_2,\sigma_2)</math>. We sample the data, <math>Data = \{x_1,x_2...x_n\} </math> and we know that <math>x_1,x_2...x_n</math> are iid. from <math>P(x|\theta)</math>.<br /> | |||
We would like to compute the variance<math>\sigma_i</math> and the mean<math>\mu_i</math> of each distribution : | |||
<center><math>\theta = \{\alpha,\mu_1,\sigma_1,\mu_2,\sigma_2\} </math></center> | |||
We have no missing data here so we can try to find the parameter estimates using the ML method. | |||
<center><math> L(\theta; Data) = \prod_i=1...n (\alpha N(x_i, \mu_1, \sigma_1) + (1 - \alpha) N(x_i, \mu_2, \sigma_2)) </math></center> | |||
<center><math> | And then we need to take the log to find <math>l(\theta, Data)</math> and then we take the derivative for each parameter and then we set that derivative equal to zero. That sounds like a lot of work because the Gaussian is not a nice distribution to work with and we do have 5 parameters. <br /> | ||
It is actually easier to apply the EM algorithm. The only thing is that the EM algorithm works with missing data and here we have all of our data. The solution is to introduce a latent variable z. We are basically introducing missing data to make the calculation easier to compute. | |||
<center><math> z_i = 1 \text{ with prob. } \alpha </math></center> | |||
<center><math> z_i = 0 \text{ with prob. } (1-\alpha) </math></center> | |||
Now we have a dataset that includes our latent variables <math>z_i</math>: | |||
<center><math> Data = \{(x_1,z_1),(x_2,z_2)...(x_n,z_n)\} </math></center> | |||
We can calculate the joint pdf by: | |||
<center><math> P(x_i,z_i|\theta)=P(x_i|z_i,\theta)P(z_i|\theta) </math></center> | |||
Let, | |||
<math> P(x_i|z_i,\theta)=</math> | |||
We | |||
<center><math> | <math> \phi_1(x_i)=N(x;\mu_1,\sigma_1)</math> & if & <math> z_i = 1 </math> <br /> | ||
<math> \phi_2(x_i)=N(x;\mu_2,\sigma_2)</math> & if & <math> z_i = 0 </math> | |||
<center><math> | |||
<center><math> | |||
<center><math> \ | |||
Now we can write | |||
<center><math> P(x_i|z_i,\theta)=\phi_1(x_i)^{z_i} \phi_2(x_i)^{1-z_i} </math></center> | |||
and | |||
<center><math> P(z_i)=\alpha^{z_i}(1-\alpha)^{1-z_i} </math></center> | |||
We can write the joint pdf as: | |||
<center><math> P(x_i,z_i|\theta)=\phi_1(x_i)^{z_i}\phi_2(x_i)^{1-z_i}\alpha^{z_i}(1-\alpha)^{1-z_i} </math></center> | |||
From the joint pdf we can get the '''likelihood function''' as: | |||
<center><math> L(\theta;D)=\prod_{i=1}^n \phi_1(x_i)^{z_i}\phi_2(x_i)^{1-z_i}\alpha^{z_i}(1-\alpha)^{1-z_i} </math></center> | |||
Then take the log and find the log likelihood: | |||
<center><math> l_c(\theta;D)=\sum_{i=1}^n z_i log\phi_1(x_i) + (1-z_i)log\phi_2(x_i) + z_ilog\alpha + (1-z_i)log(1-\alpha) </math></center> | |||
In the''' E-step''' we need to find the expectation of <math>l_c</math> | |||
<center><math> E[l_c(\theta;D)] = \sum_{i=1}^n E[z_i]log\phi_1(x_i)+(1-E[z_i])log\phi_2(x_i)+E[z_i]log\alpha+(1-E[z_i])log(1-\alpha) </math></center> | |||
For now we can assume that <math><z_i></math> is known and assign it a value, let <math> <z_i>=w_i</math><br /> | |||
'''In M-step''', we have to update our data by assuming the expectation is fixed | |||
<center><math> \theta^{(t+1)} <-- argmax_{\theta} E[l_c(\theta;D)] </math></center> | |||
Taking partial derivatives of the complete log likelihood with respect to the parameters and set them equal to zero, we get our estimated parameters at (t+1). | |||
<center><math>\begin{matrix} | |||
\frac{d}{d\alpha} = 0 \Rightarrow & \sum_{i=1}^n \frac{w_i}{\alpha}-\frac{1-w_i}{1-\alpha} = 0 & \Rightarrow \alpha=\frac{\sum_{i=1}^n w_i}{n} \\ | |||
\frac{d}{d\mu_1} = 0 \Rightarrow & \sum_{i=1}^n w_i(x_i-\mu_1)=0 & \Rightarrow \mu_1=\frac{\sum_{i=1}^n w_ix_i}{\sum_{i=1}^n w_i} \\ | |||
\frac{d}{d\mu_2}=0 \Rightarrow & \sum_{i=1}^n (1-w_i)(x_i-\mu_2)=0 & \Rightarrow \mu_2=\frac{\sum_{i=1}^n (1-w_i)x_i}{\sum_{i=1}^n (1-w_i)} \\ | |||
\frac{d}{d\sigma_1} = 0 \Rightarrow & \sum_{i=1}^n w_i(-\frac{1}{2\sigma_1^{2}}+\frac{(x_i-\mu_1)^2}{2\sigma_1^4})=0 & \Rightarrow \sigma_1=\frac{\sum_{i=1}^n w_i(x_i-\mu_1)^2}{\sum_{i=1}^n w_i} \\ | |||
\frac{d}{d\sigma_2} = 0 \Rightarrow & \sum_{i=1}^n (1-w_i)(-\frac{1}{2\sigma_2^{2}}+\frac{(x_i-\mu_2)^2}{2\sigma_2^4})=0 & \Rightarrow \sigma_2=\frac{\sum_{i=1}^n (1-w_i)(x_i-\mu_2)^2}{\sum_{i=1}^n (1-w_i)} | |||
\end{matrix}</math></center> | |||
We can verify that the results of the estimated parameters all make sense by considering what we know about the ML estimates from the standard Gaussian. But we are not done yet. We still need to compute <math><z_i>=w_i</math> in the E-step. | |||
<center><math>\begin{matrix} | |||
<z_i> & = & E_{z_i|x_i,\theta^{(t)}}(z_i) \\ | |||
& = & \sum_z z_i P(z_i|x_i,\theta^{(t)}) \\ | |||
& = & 1\times P(z_i=1|x_i,\theta^{(t)}) + 0\times P(z_i=0|x_i,\theta^{(t)}) \\ | |||
& = & P(z_i=1|x_i,\theta^{(t)}) \\ | |||
P(z_i=1|x_i,\theta^{(t)}) & = & \frac{P(z_i=1,x_i|\theta^{(t)})}{P(x_i|\theta^{(t)})} \\ | |||
& = & \frac {P(z_i=1,x_i|\theta^{(t)})}{P(z_i=1,x_i|\theta^{(t)}) + P(z_i=0,x_i|\theta^{(t)})} \\ | |||
& = & \frac{\alpha^{(t)}N(x_i,\mu_1^{(t)},\sigma_1^{(t)}) }{\alpha^{(t)}N(x_i,\mu_1^{(t)},\sigma_1^{(t)}) +(1-\alpha^{(t)})N(x_i,\mu_2^{(t)},\sigma_2^{(t)})} | |||
\end{matrix}</math></center> | |||
We can now combine the two steps and we get the expectation | |||
<center><math>E[z_i] =\frac{\alpha^{(t)}N(x_i,\mu_1^{(t)},\sigma_1^{(t)}) }{\alpha^{(t)}N(x_i,\mu_1^{(t)},\sigma_1^{(t)}) +(1-\alpha^{(t)})N(x_i,\mu_2^{(t)},\sigma_2^{(t)})} </math></center> | |||
Using the above results for the estimated parameters in the M-step we can evaluate the parameters at (t+2),(t+3)...until they converge and we get our estimated value for each of the parameters. | |||
The mixture model can be summarized as: | |||
* In each step, a state will be selected according to <math>p(z)</math>. | |||
* Given a state, a data vector is drawn from <math>p(x|z)</math>. | |||
* The value of each state is independent from the previous state. | |||
A good example of a mixture model can be seen in this example with two coins. Assume that there are two different coins that are not fair. Suppose that the probabilities for each coin are as shown in the table. <br /> | |||
\begin{tabular}{|c|c|c|} | |||
\hline | |||
& H & T <br /> | |||
coin1 & 0.3 & 0.7 <br /> | |||
coin2 & 0.1 & 0.9 <br /> | |||
\hline | |||
\end{tabular}<br /> | |||
We can choose one coin at random and toss it in the air to see the outcome. Then we place the con back in the pocket with the other one and once again select one coin at random to toss. The resulting outcome of: HHTH \dots HTTHT is a mixture model. In this model the probability depends on which coin was used to make the toss and the probability with which we select each coin. For example, if we were to select coin1 most of the time then we would see more Heads than if we were to choose coin2 most of the time. | |||
[[File:dired.png|thumb|right|Fig.1 A directed graph.]] | |||
===Alternative Algorithms=== | |||
There has been different algorithms proposed, besides the EM algorithm, which try to fulfill the same objective as EM algorithm does. The objective is to make an inference, based on the given joint distribution. It involves approximating marginal distribution of a subset of variables, where there might exist a number of latent variable. One of those algorithms which is a deterministic algorithm just like EM, is variational Bayesian method. This algorithm can be seen as a variety of EM algorithm, which applies to the maximum a posterior (MAP), instead of class-conditional. <ref>[http://en.wikipedia.org/wiki/Variational_Bayes]</ref> | |||
Another approach which is, unlike the two previous ones, a randomized algorithm is the Gibbs Sampling algorithm. The basic idea behind this algorithm is that it can be more convenient to start generating samples of a distribution in order to find a marginal distribution, rather than getting involved in some troublesome optimization problems. The random nature of this algorithms leads to different answers each time that one runs the algorithm, given the same problem and the same initial solution. Gibbs sampling can be thought of as a special case of Markov Chain Monte Carlo algorithm.<ref>[http://en.wikipedia.org/wiki/Gibbs_sampling]</ref> | |||
=Conditional random fields= | |||
(Nov 3rd lecture) | |||
===Motivation=== | |||
Hidden Markov models (HMMs) are widely used in computation biology to analyze genome sequences. These models | |||
are described by a joint probability distribution to the observed and label sequences. The joint distribution should be | |||
defined over all possible observation sequences; which is a complex process in many applications. This lead to the | |||
introduction of conditional random fields (CRF), which is a statistical framework used to build various probabilistic models to analyze gene sequence data. One of the main advantages over HMM's is to relax the conditions on independencies over several random variables. For a given observed sequence, CRF's estimates the probabilities for a possible label sequence. and also allows multiple interacting features. "CRF's are usually used for labelling or parsing of sequential data, such as natural language text and are also used in computer vision" <ref>[http://en.wikipedia.org/wiki/Conditional_random_field]</ref>. Another property of CRF is that they can be used to model non-causal phenomena. HMM assumes causality and thus we have a notion of time in the model. In applications we have signals that does not obey causality. Image are one important class of such signals. In an image most probably a single pixel has correlation with neighboring pixels but we can't define notion of order and thus causality on this relation. That's why we need concept of the random field rather than simple rv's. | |||
===Conditional distribution of CRF=== | |||
CRF is an undirected graphical model that defines a distribution over labels for a given observation sequence. Let <math> G=(V,E)</math> be an undirected graph (this is natural since as explained notion of causality is not applied in CDF's), and <math>{v_1,...v_n} \in V</math> are the nodes of a graph that represent a random variables <math>{Y_1,...,Y_n}</math> respectively. Suppose X is an observed sequence which is conditioned globally on the graph <math> G</math>. | |||
[[File:CRF.png|thumb|right|Fig.42 An example of a CRF graph]] | |||
If <math>x</math> is any realization of the observed sequence and <math>{y_1,...,y_n}</math> is any realization of the label sequence. So, the joint distribution of the graph is given by <math>P(y_1,y_2,...,y_n|x)</math>. Then <math>(X,Y)</math> is called conditional random field if all random variables <math>{Y_1,...,Y_n}</math> obey Markov property with respect to the graph G, then | |||
<center><math> P(Y_v|X,Y_w,w\neq v)=P(Y_v|X,Y_w,w\sim v)</math></center> | |||
where <math>w\sim v</math> represents that <math>w</math> and <math>v</math> are neighbors in the graph. | |||
[[File:CRFchain.png|thumb|right|Fig.43 An example of a linear chain CRF]] | |||
An example is displayed in figure 42, which denotes Markov chain. The graph consists of only random variables <math>Y_1,...,Y_n</math>. Observe that there is no graphical structure for the random variables <math>X_1,...,X_n</math>, which states that there are no independence assumptions that are made on the radom variable <math>X</math>. We try to address the probability distribution of <math>P(y|x)</math>. Figure 43 is an example of a linear chain structured CRF, where <math>X={X_1,...,X_n}</math> | |||
An application of the above example can be taken from computational biology, where the random variables <math>Y_1,...,Y_n</math> represents a sequence of gene mutations that occur due to various reasons denoted by <math>X_1,...,X_n</math>. | |||
The joint distribution over all the random variables <math>Y_1,...,Y_n</math> can be factorized using local potential functions. As we know, potential functions are defined on the vertices of the graph that form the maximal clique. From the figure 42, potential functions are defined on <math>Y_i</math> and <math>Y_{i+1}</math> (<math>1\leq i\leq n</math>). If <math> Z </math> is normalization factor and <math> C </math> is the set of all maximal cliques of <math> G </math>. For a given observable realization <math> X </math>, the joint probability is given by: | |||
<center><math> | |||
P(X,Y) = \psi_{X}(x)\frac{1}{Z} \prod_{c_i \epsilon C,C \neq {X}} \psi_{c_i} (x,y) | |||
</math></center> | |||
Joint distribution can be defined in terms of exponential terms as follows: | |||
<center><math> | |||
P(X,Y) = \frac{1}{Z} \exp{(\sum_i\lambda_i \psi_i(X,Y))} | |||
</math></center> | |||
Since, it is hard to account for all possible realizations of <math> X </math>, we define conditional distribution of a particular observed sequence on the whole graph <math> G </math> as: | |||
<center><math> | |||
P(y_1,y_2,...y_n|x) = \frac{1}{Z(X)} \prod_{c_i \epsilon C,C \neq {X}} \psi_{c_i} (x,y) | |||
</math></center> | |||
Notice that the normalization constant <math> Z </math> is now observable specific. In terms of an exponential function, the conditional distribution is given by | |||
<center><math> | |||
P(y_1,y_2,...y_n|X) = \frac{1}{Z(X)} \exp{(\sum_i\lambda_i \psi_i(Y,X))} | |||
</math></center> | |||
or, it can be rewritten as follows: | |||
<center><math> | |||
P(y_1,y_2,...y_n|X) = \frac{1}{Z(X)} \exp{(\sum_j\sum_i\lambda_i \psi_i(y_{j-1},y_{j},X),j)} | |||
</math></center> | |||
In the above equation <math>j</math> gives the position of the observed sequence. Further simplification can be done by moving the two sums outside the exponential function to obtain, | |||
<center><math> | |||
P(y_1,y_2,...y_n|X) = \frac{1}{Z(X)}\prod_{i}\prod_{j} \exp{(\lambda_i \psi_i(y_{j-1},y_{j},X),j)} | |||
</math></center> | |||
Replacing the normalization factor with the exponential term, we obtain: | |||
<center><math> | |||
P(y_1,y_2,...y_n|X) = \frac{\exp{(\sum_i\lambda_i \psi_i(y_1,y_2,...y_n,x))}} {\sum_Y \exp{(\sum_i\lambda_i \psi_i(Y,X))}} | |||
</math></center> | |||
The summation over <math>Y</math> resembles all the possible label sequences. | |||
Main advantages are: | |||
* It is mainly used in classification given by: <math>P(class|input)</math> | |||
* We don't need to model distribution over inputs. | |||
If <math>\psi_{i1}(Y,X) </math> depends on at least one variable in X and <math>\psi_{i2}(X) </math> depends on the evidence <math>X</math>, the conditional distribution can be simplified to the following: | |||
<center><math>\begin{matrix} | |||
P(Y|X) & = & \displaystyle{\frac{\exp{(\sum_{i1}\lambda_{i1} \psi_{i1}(Y,X)+\sum_{i2}\lambda_{i2} \psi_{i2}(X))}} {\sum_X\exp{(\sum_{i1}\lambda_{i1} \psi_{i1}(Y,X)+\sum_{i2}\lambda_{i2} \psi_{i2}(X))}}} \\[2ex] | |||
& = & \displaystyle{\frac{\exp{(\sum_{i1}\lambda_{i1} \psi_{i1}(Y,X)}\exp{\sum_{i2}\lambda_{i2} \psi_{i2}(X))}} {\sum_X\exp{(\sum_{i1}\lambda_{i1} \psi_{i1}(Y,X)}\exp{\sum_{i2}\lambda_{i2} \psi_{i2}(X))}}} \\[2ex] | |||
& = & \frac{1}{Z(X)} \exp{(\sum_{i1}\lambda_{i1} \psi_{i1}(Y,X))} | |||
\end{matrix}</math></center> | |||
===Parameter estimation=== | |||
Questions that can be posed are the following: | |||
* What is the possible label sequence for a given observation sequence? | |||
* What are the parameters to maximize the conditional distribution? | |||
Let <math>D</math> be the training data set and we apply the log-likelihood on the D and maximize it as follows: | |||
<center><math>\begin{matrix} | |||
L(D) & = & \sum_{(X,Y)\in D}\log{P(Y|X)}\\[2ex] | |||
& = & \sum_{(X,Y)\in D}\log{(\frac{\exp{(\sum_i\lambda_i \psi_i(y_1,y_2,...y_n,x))}} {\sum_Y \exp{(\sum_i\lambda_i \psi_i(Y,X))}})} | |||
\end{matrix}</math></center> | |||
Notice that log-likelihood function is concave and the parameter <math>\lambda</math> can be chosen such that, we obtain the global maximum and differentiating the function gives us zero. | |||
Then, differentiating the log-likelihood estimation with respect to <math>\lambda_i</math> we obtain the following: | |||
<center><math>\begin{matrix} | |||
\frac{\partial{L(D)}}{{\partial \lambda_i}} = \tilde{E}_{P(Y,X)}(\psi_i)-\sum_i E_{P(Y|x_i,\lambda)}(\psi_i) | |||
\end{matrix}</math></center> | |||
where, <math>\tilde{E}(\psi_i)</math> represents the expectation of the empirical distribution of the training data <math>D</math>; and <math>E_{P(Y|x_i,\lambda)}(\psi_i)</math> denotes the expectation with respect to the conditional distribution. Most of the times, it is not quite possible to estimate all the parameters analytically such that the derivative is zero, i.e., we do not necessarily obtain a closed form solution. Therefore, some iterative techniques and gradient based methodologies are used to estimate the parameters. | |||
=Markov logic networks= | |||
A new technique developed by the artificial intelligence community is to combine first order logic with probability theory, called as Markov logic network (MLN). One of the main reasons to arrive at this method is to represent large amounts of data in a compact and precise manner. Markov logic networks generalize first-order logic, in the sense that, in a certain limit, all unsatisfiable statements have a probability of zero, and all tautologies have probability one. First order logic is a set of formulas f, and a weight is attached to each of these formulas w. Each formula is made up of predicates, constants, variables and functions. Predicates are used to represent various relationships between objects in the specified domain. A first order knowledge base (KB) is a set of formulas using first order logic. | |||
A logical knowledge base can only handle hard constraints that covers limited possible worlds. If a world (specific configuration of all the formulas) violated a formula in a logical knowledge base, this world would be considered impossible to occur. Markov logic network, on the other hand, will assign wights <math>\, w </math> to each formula, such that when a formula being violated in a world, that world wouldn't become impossible, but would become less probable with a probability that is proportional to that weight of the violated formula. | |||
Some of the main applications of Markov logic networks are tasks in statistical relational learning, like collective classification, link prediction, link-based clustering, social network modeling and object identification. <ref>Matthew Richardson, Pedro Domingos, "Markov Logic Networks", Department of Computer Science and Engineering, University of Washington. Available: [http://www.cs.washington.edu/homes/pedrod/kbmn.pdf] </ref> | |||
It is quite evident that KB can take only boolean values, which can be thought of a hard constraint. The main purpose of MLN is to soften these constraints. Each formula is given a weight denoting the strength of that constraint in the domain. Hence higher the weight implies that constraint is strong. Markov networks and Bayesian networks can also be represented by MLN. The goal of inference in a Markov logic network is to find the stationary distribution of the system, or one that is close to it | |||
Definition: MLN is a set of pairs <math>(F,W)</math> where <math>F</math> denotes formulas in the first order logic and <math>W</math> is a real number that denotes the weight associated with the formula. Incorporating a set of constraints into MLN turns out to be a Markov network. Each binary node in MLN has grounding for each predicate and has one feature associated for each grounding of <math>F_i</math> and the corresponding <math>W_i</math>. Inference in MLNs can be performed using standard Markov network inference techniques over the minimal subset of the relevant Markov network required for answering the query. These techniques include Gibbs sampling, which is effective but may be excessively slow for large networks, belief propagation, or approximation via pseudolikelihood. | |||
One common example is the following: | |||
* Smoking causes cancer | |||
* Friends have similar smoking habits | |||
Step1: | |||
We write the above two statements in terms of formulas using logical operators as follows: | |||
* <math>\forall x, smokes(x) \implies cancer(x)</math> | |||
* <math>\forall x,y, Friends(x,y) \implies (smokes(x)\iff smokes(y)</math> | |||
Step2: | |||
We associate weights to each of the above formulas, say <math>W_1=1.75</math> and <math>W_2=1.25</math> respectively. | |||
Suppose A and B (represent persons) are any two constants, then the above set of formulas are represented in terms of an Markov ground network as follows: | |||
[[File:MLN.png|thumb|right|Fig.44 An example of a Markov network]] | |||
Each node resembles an ground atom, and an edge between a pair of atoms. Several questions can be answered from the ground network designed in Figure 44 such as: if A is a friend of B and B does not smoke, then What is the probability that A has cancer? | |||
MLN are frame works to address Markov networks. Probability distribution of a world is given by: | |||
<center><math> | |||
P(X=x) = \frac{1}{Z} \exp{(\sum_i W_i n_i(X))} | |||
</math></center> | |||
where, <math>n_i(x)</math> is the number of true groundings of the formula and <math>W_i</math> is the weight of formula <math>i</math>. | |||
[[File:MLN2.png|thumb|right|Fig.45 Another example of a Markov network]] | |||
Here is another example: | |||
* Smoking causes cancer | |||
* If there are two friends and one among them has smoking habit, then there is a chance that other friend might also get cancer (assuming the biological system is weak and inhaling might lead to mutations) | |||
The above sentences can be written in terms of formulas as follows: | |||
* <math>\forall x, smokes(x) \implies cancer(x)</math> | |||
* <math>\forall x,y, Friends(x,y) \and smokes(x) \implies cancer(y)</math> | |||
Alchemy is an open source AI software, hosted at the department of computer science, university of Washington, which makes use of the Logic Markov Networks. [http://alchemy.cs.washington.edu/] | |||
=Kernel Belief Propagation= | |||
We have talked about the belief propogation in previous lectures. | |||
In papers <ref name="kdp"> [http://jmlr.csail.mit.edu/proceedings/papers/v15/song11a/song11a.pdf] </ref> and <ref> [http://jmlr.csail.mit.edu/proceedings/papers/v9/song10a/song10a.pdf] </ref> Song et.al. talk about Kernel Belief | |||
Propagation. As we know a lot of linear methods can be used for nonlinear problems using notion of kernel. In most applications the variable space is not linear but it is linear in space of some kernel functions. This is the main reason behind using the notion of kernel but not until recently this notion has been used in BP. The intuition of the two papers on kernelizing BP is as follows: | |||
If we have two different distributions with different means as in Figure 46 , <math>\mu</math> | |||
is not a good measure to compare the two distributions and higher moments of distributions are needed for comparing the distributions. | |||
It turns out that expectation of some samples of these distributions in a higher dimensional feature space (Hilbert space) is a good measure for characterizing and comparing the distributions (Though it may seem counter-intuition but it can be shown mathematically a general distribution can be shown and recovered uniquely by only one point in a proper Hilbert space): | |||
<math>E(\phi(x))</math>, where <math>\phi(.)</math> represents the mapping function to a Hilbert space. | |||
[[File:Figure_1.png|thumb|right|Fig.46 Different distributions.]] | |||
Expectation of the mapped samples points <math>\phi(x)</math> is then computed as: <math>E(\phi(x))\approx | |||
\frac{1}{m} \sum^m_{i=1} \phi(x_i) =\mu_x</math> | |||
[[File:Figur2.png|thumb|right|Fig.47 Function <math>\phi(x)</math> maps the point into Hilbert space and each distribution is mapped to one point in the new space F.]] | |||
The idea is to represent the distribution with a point in the feature space (expectation of the mapped samples of the distribution)such that the distribution is summarized in this point and the point can be used to recover the distribution. Therefore, there is a one-to-one relation between | |||
<math>E(\phi(x))</math> and <math>dist(x)</math>. Hence, distance between two distributions p and q can be computed as the distance between their corresponding expected values in a Hilbert space. One important advantage is that the distance can be calculated based on samples of the distribution and thus is nonparametric and there is no need to know the mathematical form of the distribution. | |||
The question is: what is a proper mapping function <math>\phi(x)</math>? | |||
The function <math>\phi</math> is an injective mapping.. It turns out that we need to only implicitly transfer the sampled point to the Hilbert space, and there is no need to explicitly define the mapping function <math>\phi(x)</math> and instead the mapping can be done in terms of kernel functions. Suppose, we need to find distance between two distributions p and q: | |||
<math>|p-q|^2</math> | |||
where <math>x \thicksim p</math> and <math>y \thicksim q</math>, then | |||
<math>|E (\phi (x_i))-E (\phi (y_i))|^2</math> gives us the measure of similarity or dissimilarity of the two distributions. | |||
we can expand this and write it in terms of kernels, | |||
<center> | |||
<math>\begin{matrix} | |||
((E (\phi (x_i))-E (\phi (y_i)))^T(E (\phi (x_i))-E (\phi (y_i)))) &=& [\frac{1}{n}\sum_{i=1}^n \phi(x_i) -\frac{1}{m}\sum_{j=1}^m \phi(y_j)]^T [\frac{1}{n}\sum_{i=1}^n \phi(x_i) -\frac{1}{m}\sum_{j=1}^m \phi(y_j)]\\[2ex] | |||
&=& \frac{1}{n^2} \sum_{ij} k(x_i,x_j)+\frac{1}{m^2} \sum_{ij}k(y_i,y_j) - \sum\frac{2}{nm} k(x_i,y_j) | |||
\end{matrix}</math> | |||
</center> | |||
In addition to distance between the distibutions, we can quantify the independence between two random variables using Hilbert Schmidt Independent Criterion (HSIC) defined as: | |||
<math> | |||
\begin{align} | |||
P_{xy} = P_x * P_y \rightarrow |P_{xy}-P_x * P_y|^2 &\propto (HSIC)\\ | |||
& \propto Tr (KHLH) | |||
\end{align} | |||
</math> | |||
Where <math>H=(I-\frac{1}{m} e e^T)</math> is the constant matrix that centralizes where row mean and column mean are zero; and <math>K</math> is a kernel over <math>x</math> and <math>L</math> is a kernel over <math>y</math>. | |||
The introduced is an empirical measure for HSIC. For a thorough explanation and details of the measure, you can refer to the original work, Measuring Statistical Dependence with Hilbert-Schmidt Norms <ref>[http://www.kyb.mpg.de/fileadmin/user_upload/files/publications/attachments/hsicALT05_%5b0%5d.pdf]</ref>. | |||
If the result is equal to zero then we induce that they are | |||
independent, otherwise we can measure their dependency. | |||
If instead of <math>p(x)</math> we have conditional distribution (<math>p(x|y)</math>) (or a family of distributions) | |||
then how we can project to Hilbert space? | |||
If the distribution is binary it is not hard, we can find | |||
expectation for points with <math>y=0</math> and then for the ones with <math>y=1</math>. | |||
What should we do in the case that there is multinomial distribution | |||
for <math>y</math> or if <math>y</math> is continues: | |||
Please look at the following Example: | |||
We have two distributions which are conditioned on <math>y_1</math> and <math>y_2</math>, | |||
respectively as seen in Figure 48. We can map to space <math>G</math> as can be seen in the figure 47. | |||
[[File:multinomial.png|thumb|right|Fig.47 if <math>y_1 \thicksim y_2 \Rightarrow </math> mapping would be similar.]] | |||
If the points that we are conditioning on, are close to each other; | |||
we expect points to be similar and so their mapping. Therefore, in | |||
the space <math>G</math> we find the expectation of each point in this space. | |||
The idea is to have a linear transformation that if we apply in | |||
space <math>G</math> then we can get to space <math>F</math>. Going from space <math>G</math> to <math>F</math> | |||
is done through a linear transformation. | |||
Suppose <math>z</math> is a multidimentional Gaussian: <math>z=[x,y]^T</math>. We can then derive that <math>p(y|x)</math> is Gaussian as well, defined as follows: <math>N (C_{yx} C_{xx}^{-1} x, | |||
C_{yy}-C_{yx} C_{xx}^{-1} C_{xy})</math> | |||
Where <math>C_{yx} C_{xx}^{-1} x</math> is mean (mean is a linear operator | |||
times the point that we conditioned on) and <math>C_{yy}-C_{yx} | |||
C_{xx}^{-1} C_{xy}</math> is covariance. | |||
<math>C</math> is covariance of <math>x</math> and <math>y</math>. | |||
Therefore, to be able to obtain this linear transformation, we need to come up with the definition of covariance in Hilbert space. The Covariance of two objects of two Hilbert space: | |||
<math>C_{xy} = E_{xy} [\phi(x) \otimes \phi(y)] - E_x [\phi(x)] | |||
\otimes E_y [\phi(y)]</math> | |||
In other words, We can define KBP intuitively as a transformation that, rather than maps our functions into a linear space, it maps them into a Gaussian space, where it is much easier and straightforward to perform classification or some other task. | |||
"A direct implementation of kernel BP has the following computational cost: each message update costs <math>O(m^2d_{max})</math> when computed exactly, whereas <math>m</math> is the number of training examples and <math>d_{max}</math> is the maximum degree of a node in the graphical model." <ref name="kbp"/> | |||
As Song et al noted, one of the main differences between Kernel Belief Propagation (KBP) and BP is that it is used also on graphs with loops (not only on trees) and therefore it iterates until convergence is achieved <ref name="kbp"/>. KBP is computationally more complex but the main advantage is that it is nonparametric and doesn't have limitations of BP. | |||
=Markov Chain Monte Carlo (MCMC)= | |||
Markov chain Monte Carlo (MCMC) methods are a class of algorithms for sampling from probability distributions based on constructing a Markov chain that has the desired distribution as its equilibrium distribution. The state of the chain after a large number of steps is then used as a sample of the desired distribution. The quality of the sample improves as a function of the number of steps. It is very useful when direct sampling of a distribution is not possible but it is possible to sample another distribution. | |||
Usually it is not hard to construct a Markov chain with the desired properties. The more difficult problem is to determine how many steps are needed to converge to the stationary distribution within an acceptable error. A good chain will have rapid mixing—the stationary distribution is reached quickly starting from an arbitrary position—described further under Markov chain mixing time. | |||
Typical use of MCMC sampling can only approximate the target distribution, as there is always some residual effect of the starting position. More sophisticated MCMC-based algorithms such as coupling from the past can produce exact samples, at the cost of additional computation and an unbounded (though finite in expectation) running time. | |||
The most common application of these algorithms is numerically calculating multi-dimensional integrals. In these methods, an ensemble of "walkers" moves around randomly. At each point where the walker steps, the integrand value at that point is counted towards the integral. The walker then may make a number of tentative steps around the area, looking for a place with reasonably high contribution to the integral to move into next. Random walk methods are a kind of random simulation or Monte Carlo method. However, whereas the random samples of the integrand used in a conventional Monte Carlo integration are statistically independent, those used in MCMC are correlated. A Markov chain is constructed in such a way as to have the integrand as its equilibrium distribution. Surprisingly, this is often easy to do. | |||
Multi-dimensional integrals often arise in Bayesian statistics, computational physics, computational biology and computational linguistics, so Markov chain Monte Carlo methods are widely used in those fields. Here we try to give a brief review on basic MCMC concepts and few related algorithms. | |||
==Markov chain basic concepts== | |||
A Markov chain, named after Andrey Markov, is a mathematical system that undergoes transitions from one state to another, between a finite or countable number of possible states. It is a random process characterized as memoryless: the next state depends only on the current state and not on the sequence of events that preceded it. This specific kind of "memorylessness" is called the Markov property. Markov chains have many applications as statistical models of real-world processes. Since it is a random variable depending on a deterministic variable, mathematically is a stochastic process. | |||
Definition 1:Stochastic process: It is a set of random variable defined on an indexed set: | |||
<center><math> \{x_t|t \in T\}</math></center> | |||
The index set <math>\ T</math> in general can be discrete or continuous. Here first we assume discrete case first. | |||
Definition 2: Markov Chain (MC): Is a stochastic process for which the distribution of Definition <math>\ x_{t-1}</math> only depends on <math>\ T</math> or mathematically: | |||
<center><math>\ P(x_t|x_0,x_1,...,x_{t-1})=P(x_t|x_{t-1})</math></center> | |||
In terms of graphical model representation it is represents in Fig. 48. | |||
[[File:HMMorder1.png|thumb|right|Fig.48 Graphical Model for a Markov Chain]] | |||
Often, the term "Markov chain" is used to mean a Markov process which has a discrete (finite or countable) state-space. Usually a Markov chain is defined for a discrete set of times (i.e., a discrete-time Markov chain). MC in can be generalized for the cases the current states depends on two or more previous states but always it is casual model. Here we consider the simplest case with memory length of one. MC involves a system which is in a certain state at each step, with the state changing randomly between steps. The steps are often thought of as moments in time, but they can equally well refer to physical distance or any other discrete measurement; formally, the steps are the integers or natural numbers, and the random process is a mapping of these to states. The Markov property states that the conditional probability distribution for the system at the next step (and in fact at all future steps) depends only on the current state of the system, and not additionally on the state of the system at previous steps. Since the system changes randomly, it is generally impossible to predict with certainty the state of a Markov chain at a given point in the future. However, the statistical properties of the system's future can be predicted. In many applications, it is these statistical properties that are important. We assume that the value of states are an ordered subset of natural numbers. | |||
The changes of state of the system are called transitions, and the probabilities associated with various state-changes are called transition probabilities. The set of all states and transition probabilities completely characterizes a Markov chain. By convention, we assume all possible states and transitions have been included in the definition of the processes, so there is always a next state and the process goes on forever. These concepts bring the following definitions: | |||
Definition 3: Transition Probability: It measure the possibility of going to a state given the current state. Formally: | |||
<center><math>\ p_{ij}=P(x_{t+1}=j|x_{t}=i)</math></center> | |||
Definition 4: Transition Matrix: The matrix whose <math>\ (i,j)</math> elements is <math>\ p_{ij}</math>. It is obvious that <math>\ \sum_i p_{ij}=1</math> since each row corresponds to a pmf. | |||
One important property of MC is Homogeneous property: | |||
<center><math>\ P(x_t|x_{t-1})=P(x_1|x_0)</math></center> | |||
It is easy to verify that knowing the initial state and also transition matrix is enough to study the behavior of MC. | |||
Example: One of the famous MC's is Random Walk. The corresponding matrix has the following form: | |||
<center><math>\ \begin{bmatrix} | |||
1 & 0 & 0 & \cdots & 0 \\ | |||
1-p & 0 & p &\cdots & 0 \\ | |||
0 & 1-p & 0 &\cdots & 0 \\ | |||
\vdots & \ddots & \vdots \\ | |||
0 & 0 & 0 & \cdots & 1 | |||
\end{bmatrix}</math></center> | |||
We can generalize the study of MC and consider the case when we want to go from one state to another in more than one step. Here come the following two extensions for definitions 3,4: | |||
*Let<math>\ p_{ij}(n)=P(x_{t+n}=j|x_{t}=i)</math> | |||
*Let <math>\ P_n </math> to be a matrix such that its <math>\ (i,j)</math> elements is <math>\ p_{ij}(n)</math>. This is called n-step transition probability matrix. It is easy to show by induction that: | |||
<center><math>\ P_n=P^n</math></center> | |||
Definition 5: Let <math>\ \mu_t=(mu_t(1),...,\mu_t(n))</math> a row vector where <math>\ \mu_t(i)=P(x_t=i)</math>. This is called marginal probability that chain is in each sate at time t. It shows the possibility of being in each state after running the MC t steps. | |||
Therorem 1: The marginal probability is given by: | |||
<center><math>\ \mu_t=\mu_0 P^t</math></center> | |||
Proof is very easy and straight forward using induction. | |||
====Steady-state analysis and limiting distributions==== | |||
It is interesting that under some assumptions Markov chains tends to a stationary situation as time tends to infinity. This property is very important and can be used for our main purpose for sampling. | |||
* Let <math>\ \pi=[\pi_i, i\in X]</math> be a vector of non-negative numbers that sum to one. (Equivalently it is a PMF) | |||
Definition 6: <math>\ \pi</math> is stationary distribution (invariant) of a MC if: | |||
<center><math>\ \pi=\pi P</math></center> | |||
This means that we have reached to a condition that possibility of each state occurrence doesn't change with time. | |||
Definition 7: Limiting distribution of a chain, A chain has a limiting distribution if | |||
<center><math>\ lim_{n\rightarrow \infty}P^n=[\pi,\pi,...,\pi]^T</math></center> | |||
Example: Consider the following transition matrix: | |||
<center><math>\ P= \begin{bmatrix} | |||
0.2 & 0.3 & 0.5 \\ | |||
0.6 & 0 & 0.4 \\ | |||
0.7 & 0.1 & 0.2 \\ | |||
\end{bmatrix}</math></center> | |||
Now Note: | |||
<center><math>\ P^5= \begin{bmatrix} | |||
0.4451 & 0.1795 & 0.3754 \\ | |||
0.4594 & 0.1711 & 0.3695 \\ | |||
0.4653 & 0.1677 & 0.3670 \\ | |||
\end{bmatrix}</math></center> | |||
<center><math>\ P^{10}= \begin{bmatrix} | |||
0.4553 & 0.1736 & 0.3712 \\ | |||
0.4550 & 0.1737 & 0.3713 \\ | |||
0.4549 & 0.1738 & 0.3713 \\ | |||
\end{bmatrix}</math></center> | |||
<center><math>\ P^{100}= \begin{bmatrix} | |||
0.4451 & 0.1737 & 0.3713 \\ | |||
0.4551 & 0.1737 & 0.3713 \\ | |||
0.4551 & 0.1737 & 0.3713 \\ | |||
\end{bmatrix}</math></center> | |||
This example shows convergence behavior of this MC and also we can conclude: <math>\ \mu=[0.4451 , 0.1737 , 0.3713]</math> | |||
This property is not valid for all MC. Consider the following example: | |||
Example: | |||
<center><math>\ P= \begin{bmatrix} | |||
0 & 1 & 0 \\ | |||
0 & 0 & 1 \\ | |||
1 & 0 & 0 \\ | |||
\end{bmatrix}</math></center> | |||
It is easy to check that <math>\ \mu=[0.3333 , 0.3333 , 0.3333]</math> is stationary distribution of this MC, but the chain doesn't have limiting distribution. | |||
Definition 7: Detailed balance: A chain has detailed balance property if:<math>\ \pi_i p_{ij}=p_{ji}\pi_j</math> and we say the chain satisfies detailed balance property. | |||
Theorem2: If <math>\ \pi</math> satisfies detailed balance property then it is stationary distribution. | |||
Proof: | |||
<center><math>\ \pi=\pi P</math></center> | |||
<center><math>\ [\pi P]_j=\sum_i \pi_i P_{ij}=\sum_i P_{ji} \pi_j \pi_j=\sum_i P_{ji}=\pi_j</math></center> | |||
Which is the desired result. | |||
Knowing these basic MC definitions and properties we are ready to study some MCMC sampling algorithms. | |||
==Metropolis Algorithm== | |||
We would like to sample from some <math>P(x)</math> and this time use the metropolis algorithm, which is a type of MCMC, to do it. In order for this algorithm to work we first need a number of things. | |||
# We need some staring value <math>x</math>. This value can come from anywhere. | |||
# We need to find a value <math>y</math> that comes from the function <math>T(x, y)</math>. | |||
# We need the function <math>T</math> to be symmetrical. <math>T(x,y)=T(y,x)</math>. | |||
# We also need <math>T(x,y) = P(y|x)</math>. | |||
Once we have all of these conditions we can run the algorithm to find our random sample. | |||
# Get a staring value <math>x</math>. | |||
# Find the <math>y</math> value from the function <math>T(x, y)</math>. | |||
# Accept <math>y</math> with the probability <math>min(\frac{P(x)}{P(y)}, 1)</math>. | |||
# If the <math>y</math> is accepted it becomes the new x value. | |||
# After a large number of accepted values the series will converge. | |||
# When the series has converged any new accepted values can be treated as random samples from <math>P(x)</math>. | |||
The point at which the series converges is called the 'burn in point'. We must always burn in a series before we can use it to sample because we have to make sure that the series has converged. The number of values before the burn in point depends on the functions we are using since some converge faster than others. <br /> | |||
We want to prove that the Metropolis Algorithm works. How do we know that <math>P(x)</math> is in fact the equilibrium distribution for this MC? We have a condition called the detailed balance condition that is sufficient but not necessary when we want to prove that <math>P(x)</math> is the equilibrium distribution. | |||
'''Theorem 3''' | |||
If <math> P(x)A(x, y) = P(y)A(y,x) </math> and <math>A(x,y)</math> is the transformation matrix for the MC then <math>P(x)</math> is the equilibrium distribution. This is called the Detailed Balance Condition. | |||
'''Proof of Sufficiency for Detailed Balance Condition:''' <br /> | |||
Need to show: | |||
<center><math> \int_y P(y)A(x, y) = P(x) </math></center> | |||
<center><math> \int_y P(y)A(y, x) = \int_y P(x)A(x, y) = P(x) \int_y A(x, y) = P(x) </math></center> | |||
We need to show that Metropolis satisfies the detailed balance condition. We can define <math>A(x, y)</math> as follows: | |||
<center><math> A(x, y) = T(x, y) min(\frac{P(x)}{P(y)}, 1) </math></center> | |||
Then, | |||
<center><math>\begin{matrix} | |||
P(x)A(x, y) & = & P(x) T(x, y) min(1 , \frac{P(x)}{P(y)}) \\ | |||
& = & min (P(x) T(x, y), P(y)T(x, y)) \\ | |||
& = & min (P(x) T(y, x), P(y)T(y, x)) \\ | |||
& = & P(y) T(y, x) min(\frac{P(x)}{P(y)}, 1) \\ | |||
& = & P(y) A(y, x) | |||
\end{matrix}</math></center> | |||
Therefore the detailed balance condition holds for the Metropolis Algorithm and we can say that <math>P(x)</math> is the equilibrium distribution. | |||
'''Example:''' <br /> | |||
Suppose that we want to sample from a <math> Poisson(\lambda) </math>. | |||
<center><math> P(x) = \frac{\lambda^x}{x!}e^{-\lambda} \text{ for } x = 0,1,2,3, ... </math></center> | |||
Now define <math>T(x,y) : y=x+\epsilon</math> where <math>P(\epsilon=-1) = 0.5</math> and <math>P(\epsilon=1) = 0.5</math>. This type of <math>T</math> is called a random walk. We can select any <math>x^{(0)}</math> from the range of x as a starting value. Then we can calculate a y value based on our <math>T</math> function. We will accept the y value as our new <math>x^{(i)}</math> with the probability <math>min(\frac{P(x)}{P(y)}, 1)</math>. | |||
Once we have gathered many accepted values, say 10000, and the series has converged we can begin to sample from that point on in the series. That sample is now the random sample from a <math> Poisson(\lambda) </math>. | |||
==Metropolis Hastings== | |||
As the name suggests the ''Metropolis Hastings'' algorithm is related to the ''Metropolis'' algorithm. It is a more generalized version of the ''Metropolis'' algorithm to sample from F where we no longer require the condition that the function <math>T(x, y)</math> be symmetric. The algorithm can be outlined as: | |||
# Get a staring value <math>x</math>. This value can be chosen at random. | |||
# Find the <math>y</math> value from the function <math>T(x, y)</math>. Note that <math>T(x, y)</math> no longer has to be symmetric. | |||
# Accept <math>y</math> with the probability <math>min(\frac{P(y)T(y, x)}{P(x)T(x, y)}, 1)</math>. Notice how the acceptance probability now contains the function <math>T(x, y)</math>. | |||
# If the <math>y</math> is accepted it becomes the new <math>x</math> value. | |||
# After a large number of accepted values the series will converge. | |||
# When the series has converged any new accepted values can be treated as random samples from <math>P(x)</math>. | |||
To prove that ''Metropolis Hastings'' algorithm works we once again need to show that the Detailed Balance Condition holds. | |||
'''Proof:'''<br /> | |||
If <math>T(x, y) = T(y, x)</math> then this reduces to the ''Metropolis'' algorithm which we have already proven. Otherwise, | |||
<center><math>\begin{matrix} | |||
A(x, y) & = & T(x,y) min(\frac{P(y)T(y, x)}{P(x)T(x, y)}, 1) \\ | |||
P(x)A(x, y) & = & P(x)T(x,y) min(\frac{P(y)T(y, x)}{P(x)T(x, y)}, 1) \\ | |||
& = & min(P(y)T(y, x), P(x)T(x,y)) \\ | |||
& = & P(y)T(y, x) min(1, \frac{P(x)T(x, y)}{P(y)T(y, x)}) \\ | |||
& = & P(y)A(y, x) | |||
\end{matrix}</math></center> | |||
Which means that the Detailed Balance Condition holds and therefore <math>P(x)</math> is the equilibrium. | |||
== Metropolis Hastings - Dec. 6th == | |||
Metropolis Hastings is an MCMC algorithm that is used for sampling from a given distribution. Metropolis Hastings proceeds as follows: | |||
# Choose an initial point <math>X_o</math> and set <math>i = 0</math> | |||
# Generate <math>Y\thicksim q(y|x_i)</math> | |||
# Compute <math>r(X_i,Y)</math> to decide whether to accept the generated Y based on the criterion in step 5. | |||
<center><math>\min(\frac{f(y)}{f(x)}\frac{q(x|y)}{q(y|x)},1)</math></center> | |||
# Generate <math>U \thicksim Unif(0,1)</math> | |||
# Accept the generated Y as follows: | |||
<center><math> | |||
X_{i+1} =\begin{cases} | |||
Y, & \hbox{if U is less than or equal to r}, \\ | |||
X_i, & \hbox{otherwise}. | |||
\end{cases} | |||
</math></center> | |||
# <math>i = i + 1</math> and go to step 2. | |||
Repeat the above procedure up to a burning point and consider the points sampled after the burning points. Usually a very large number of iterations are considered before the burning point is reached. | |||
Examples: | |||
consider <math>f(x) = \frac{1}{\pi} \frac{1}{1+x^2}</math> | |||
<math>f(x) \propto \frac{1}{1+x^2}</math> | |||
Let's choose a normal distribution with a mean <math>X</math> and variance <math>b^2</math> to be a proposal distribution representing <math>q(y|x)</math> | |||
<math>q(y|x) = N(X,b^2)</math> | |||
Therefore, <math>\frac {q(x|y)}{q(y|x)} = 1</math> | |||
and <math>\frac{f(y)}{f(x)}\frac{q(x|y)}{q(y|x)} = \frac{1+x^2}{1+y^2}.1 = \frac{1+x^2}{1+y^2}</math> | |||
The Matlab code for Metropolis Hastings sampling technique for the given distribution in this example is as follows: | |||
<pre style="align:left; width: 75%; padding: 2% 2%"> | |||
X(1) = randn; | |||
b = 0.1; | |||
for i = 2:10000 | |||
Y = b*randn+X(i-1); | |||
r = min((1+X(i-1)^2)/(1+Y^2),1); | |||
U =rand; | |||
if U <= r | |||
X(i) = Y; | |||
else | |||
X(i) = X(i-1); | |||
end | |||
end | |||
% to check the distrubtion of the sampled points | |||
hist(X) | |||
</pre> | |||
By Proper selection of b we can see that the algorithm works. The following figure depicts histogram of some instances for some values of b. | |||
[[File:100.png|thumb|right|Fig.49 Sample histogram for instances of the algorithm]] | |||
A close look confirms that for b=0.5 the histogram is very similar to what we expect. | |||
Now we investigate why the above procedure would work? | |||
if a Markov chain satisfied a detailed balance criterion: | |||
<math>\pi_i P_{ij} = \pi_j P_{ji}</math> | |||
The stationary distribution of the chain will be <math>\pi</math>. This is true for discrete and continuous case. | |||
In continuous case, the detailed balance is: | |||
<math>f(x)P(x \rightarrow y) = f(y) P(y \rightarrow x)</math> | |||
\ | |||
Proof: | |||
Suppose we have two points<math>x</math> and <math>y</math> | |||
the quantity <math>\frac{f(y)}{f(x)}\frac{q(x|y)}{q(y|x)} </math> is eigher <math> <1 </math> or <math> >1 </math> | |||
Without the loss of generality, we assume that the above quantity is less than 1. | |||
Therefore, | |||
<math>r(x,y) = \frac{f(y)}{f(x)}\frac{q(x|y)}{q(y|x)}</math> | |||
and | |||
<math>r(y,x) = 1</math> | |||
Compute the probability of transitioning from point x to y: <math>P(x \rightarrow y)</math>. For this, we need to: | |||
# Generate <math>y \thicksim q(y|x)</math> | |||
# Accept <math>y</math> with the probability <math>r(x,y)</math>. <math>r(x,y)</math> is the change of accepting <math>y</math>. | |||
Then, we have: | |||
<math>P(x \rightarrow y) = q(y|x).r(x,y) | |||
f(x)q(y|x)\frac{f(y)}{f(x)}\frac{q(x|y)}{q(y|x)}= f(y).q(x|y) \Rightarrow </math>L.H.S of the detailed balance equation | |||
<math>f(y)q(x|y)r(y,x) = f(y).q(x|y)\Rightarrow </math>R.H.S of the detailed balance equation | |||
<math>R.H.S = L.H.S</math>; hence the detailed balance is satisfied and the stationary distribution of the chain is <math>f(y)</math>. | |||
== | == Gibbs Sampling == | ||
Although Metropolis-Hasting is a general and useful sampling algorithm, the proposal distribution must be tuned in such a way that makes it suite the target distribution well. The proposal distribution should not be too broad or too narrow than the target distribution; otherwise most of the proposed samples will be rejected. | |||
A method called Gibbs sampling was introduced by Geman in 1984 in the context of image processing. This method allows us to generate samples from the full joint distribution given that the full conditional distribution is known. That is, we can generate samples from the joint distribution <math>\, P(\theta_1, \theta_2, ..., \theta_n | D)</math>, using Gibbs sampling, if samples from the conditional distributions <math>\, P(\theta_i | \theta_{-i}, D) </math> can be generated, where <math>\, i \in {1, ...,n}</math> and <math>\, \theta_{-i}</math> are all parameters except parameter number i. | |||
The Gibbs sampling algorithms is as follows: | |||
# set j = 0 | |||
# initialize all the random variables <math>\, \theta_{i}^{j}</math>, where <math>\, i \in {1,..., n} </math> | |||
# Repeat for i from 1 to n: | |||
## j = j + 1 | |||
## Generate a sample for <math>\, \theta_{i}^{j} </math> from <math>\, p(\theta_{i}^{j-1}|\theta_{i}) </math> | |||
Note that <math>\, \theta_{i} </math> is always take the last value that was assigned to it. Also note that on the contrary to the Metropolis-Hasting, all the samples are accepted in Gibbs sapling. | |||
=Appendix: Graph Drawing Tools= | |||
===Graphviz=== | |||
[http://www.graphviz.org/ Website] | |||
"Graphviz is open source graph visualization software. Graph visualization is a way of representing structural information as diagrams of abstract graphs and networks. It has important applications in networking, bioinformatics, software engineering, database and web design, machine learning, and in visual interfaces for other technical domains." | |||
<ref>http://www.graphviz.org/</ref> | |||
There is a wiki extension developed, called Wikitex, which makes it possible to make use of this package in wiki pages. [http://wikisophia.org/wiki/Wikitex#Graph Here] is an example. | |||
=== | ===AISee=== | ||
[http://www.aisee.com/ Website] | |||
AISee is a commercial graph visualization software. The free trial version has almost all the features of the full version except that it should not be used for commercial purposes. | |||
===TikZ=== | |||
[http://www.texample.net/tikz/ Website] | |||
"TikZ and PGF are TeX packages for creating graphics programmatically. TikZ is build on top of PGF and allows you to create sophisticated graphics in a rather intuitive and easy manner." <ref> | |||
http://www.texample.net/tikz/ | |||
</ref> | |||
===Xfig=== | |||
"Xfig" is an open source drawing software used to create objects of various geometry. It can be installed on both windows and unix based machines. | |||
[http://www.xfig.org/ Website] | |||
==References== | |||
<references /> | |||
Latest revision as of 09:45, 30 August 2017
Editor Sign Up
Sign up for your presentation
paper summaries
Assignments
Introduction
Motivation
Graphical probabilistic models provide a concise representation of various probabilistic distributions that are found in many real world applications. Some interesting areas include medical diagnosis, computer vision, language, analyzing gene expression data, etc. A problem related to medical diagnosis is, "detecting and quantifying the causes of a disease". This question can be addressed through the graphical representation of relationships between various random variables (both observed and hidden). This is an efficient way of representing a joint probability distribution.
Graphical models are excellent tools to burden the computational load of probabilistic models. Suppose we want to model a binary image. If we have 256 by 256 image then our distribution function has [math]\displaystyle{ 2^{256*256}=2^{65536} }[/math] outcomes. Even very simple tasks such as marginalization of such a probability distribution over some variables can be computationally intractable and the load grows exponentially versus number of the variables. In practice and in real world applications we generally have some kind of dependency or relation between the variables. Using such information, can help us to simplify the calculations. For example for the same problem if all the image pixels can be assumed to be independent, marginalization can be done easily. One of the good tools to depict such relations are graphs. Using some rules we can indicate a probability distribution uniquely by a graph, and then it will be easier to study the graph instead of the probability distribution function (PDF). We can take advantage of graph theory tools to design some algorithms. Though it may seem simple but this approach will simplify the commutations and as mentioned help us to solve a lot of problems in different research areas.
Notation
We will begin with short section about the notation used in these notes. Capital letters will be used to denote random variables and lower case letters denote observations for those random variables:
- [math]\displaystyle{ \{X_1,\ X_2,\ \dots,\ X_n\} }[/math] random variables
- [math]\displaystyle{ \{x_1,\ x_2,\ \dots,\ x_n\} }[/math] observations of the random variables
The joint probability mass function can be written as:
or as shorthand, we can write this as [math]\displaystyle{ p( x_1, x_2, \dots, x_n ) }[/math]. In these notes both types of notation will be used. We can also define a set of random variables [math]\displaystyle{ X_Q }[/math] where [math]\displaystyle{ Q }[/math] represents a set of subscripts.
Example
Let [math]\displaystyle{ A = \{1,4\} }[/math], so [math]\displaystyle{ X_A = \{X_1, X_4\} }[/math]; [math]\displaystyle{ A }[/math] is the set of indices for
the r.v. [math]\displaystyle{ X_A }[/math].
Also let [math]\displaystyle{ B = \{2\},\ X_B = \{X_2\} }[/math] so we can write
Graphical Models
Graphical models provide a compact representation of the joint distribution where V vertices (nodes) represent random variables and edges E represent the dependency between the variables. There are two forms of graphical models (Directed and Undirected graphical model). Directed graphical (Figure 1) models consist of arcs and nodes where arcs indicate that the parent is a explanatory variable for the child. Undirected graphical models (Figure 2) are based on the assumptions that two nodes or two set of nodes are conditionally independent given their neighbour1.
Similiar types of analysis predate the area of Probablistic Graphical Models and it's terminology. Bayesian Network and Belief Network are preceeding terms used to a describe directed acyclical graphical model. Similarly Markov Random Field (MRF) and Markov Network are preceeding terms used to decribe a undirected graphical model. Probablistic Graphical Models have united some of the theory from these older theories and allow for more generalized distributions than were possible in the previous methods.
We will use graphs in this course to represent the relationship between different random variables. {{
Template:namespace detect
| type = style | image = | imageright = | style = | textstyle = | text = This article may require cleanup to meet Wikicoursenote's quality standards. The specific problem is: It is worth noting that both Bayesian networks and Markov networks existed before introduction of graphical models but graphical models helps us to provide a unified theory for both cases and more generalized distributions.. Please improve this article if you can. (October 2011) | small = | smallimage = | smallimageright = | smalltext = }}
Directed graphical models (Bayesian networks)
In the case of directed graphs, the direction of the arrow indicates "causation". This assumption makes these networks useful for the cases that we want to model causality. So these models are more useful for applications such as computational biology and bioinformatics, where we study effect (cause) of some variables on another variable. For example:
[math]\displaystyle{ A \longrightarrow B }[/math]: [math]\displaystyle{ A\,\! }[/math] "causes" [math]\displaystyle{ B\,\! }[/math].
In this case we must assume that our directed graphs are acyclic. An example of an acyclic graphical model from medicine is shown in Figure 2a.
Exposure to ionizing radiation (such as CT scans, X-rays, etc) and also to environment might lead to gene mutations that eventually give rise to cancer. Figure 2a can be called as a causation graph.
If our causation graph contains a cycle then it would mean that for example:
- [math]\displaystyle{ A }[/math] causes [math]\displaystyle{ B }[/math]
- [math]\displaystyle{ B }[/math] causes [math]\displaystyle{ C }[/math]
- [math]\displaystyle{ C }[/math] causes [math]\displaystyle{ A }[/math], again.
Clearly, this would confuse the order of the events. An example of a graph with a cycle can be seen in Figure 3. Such a graph could not be used to represent causation. The graph in Figure 4 does not have cycle and we can say that the node [math]\displaystyle{ X_1 }[/math] causes, or affects, [math]\displaystyle{ X_2 }[/math] and [math]\displaystyle{ X_3 }[/math] while they in turn cause [math]\displaystyle{ X_4 }[/math].
In directed acyclic graphical models each vertex represents a random variable; a random variable associated with one vertex is distinct from the random variables associated with other vertices. Consider the following example that uses boolean random variables. It is important to note that the variables need not be boolean and can indeed be discrete over a range or even continuous.
Speaking about random variables, we can now refer to the relationship between random variables in terms of dependence. Therefore, the direction of the arrow indicates "conditional dependence". For example:
[math]\displaystyle{ A \longrightarrow B }[/math]: [math]\displaystyle{ B\,\! }[/math] "is dependent on" [math]\displaystyle{ A\,\! }[/math].
Note if we do not have any conditional independence, the corresponding graph will be complete, i.e., all possible edges will be present. Whereas if we have full independence our graph will have no edge. Between these two extreme cases there exist a large class. Graphical models are more useful when the graph be sparse, i.e., only a small number of edges exist. The topology of this graph is important and later we will see some examples that we can use graph theory tools to solve some probabilistic problems. On the other hand this representation makes it easier to model causality between variables in real world phenomena.
Example
In this example we will consider the possible causes for wet grass.
The wet grass could be caused by rain, or a sprinkler. Rain can be caused by clouds. On the other hand one can not say that clouds cause the use of a sprinkler. However, the causation exists because the presence of clouds does affect whether or not a sprinkler will be used. If there are more clouds there is a smaller probability that one will rely on a sprinkler to water the grass. As we can see from this example the relationship between two variables can also act like a negative correlation. The corresponding graphical model is shown in Figure 5.
This directed graph shows the relation between the 4 random variables. If we have the joint probability [math]\displaystyle{ P(C,R,S,W) }[/math], then we can answer many queries about this system.
This all seems very simple at first but then we must consider the fact that in the discrete case the joint probability function grows exponentially with the number of variables. If we consider the wet grass example once more we can see that we need to define [math]\displaystyle{ 2^4 = 16 }[/math] different probabilities for this simple example. The table bellow that contains all of the probabilities and their corresponding boolean values for each random variable is called an interaction table.
Example:
Now consider an example where there are not 4 such random variables but 400. The interaction table would become too large to manage. In fact, it would require [math]\displaystyle{ 2^{400} }[/math] rows! The purpose of the graph is to help avoid this intractability by considering only the variables that are directly related. In the wet grass example Sprinkler (S) and Rain (R) are not directly related.
To solve the intractability problem we need to consider the way those relationships are represented in the graph. Let us define the following parameters. For each vertex [math]\displaystyle{ i \in V }[/math],
- [math]\displaystyle{ \pi_i }[/math]: is the set of parents of [math]\displaystyle{ i }[/math]
- ex. [math]\displaystyle{ \pi_R = C }[/math] \ (the parent of [math]\displaystyle{ R = C }[/math])
- [math]\displaystyle{ f_i(x_i, x_{\pi_i}) }[/math]: is the joint p.d.f. of [math]\displaystyle{ i }[/math] and [math]\displaystyle{ \pi_i }[/math] for which it is true that:
- [math]\displaystyle{ f_i }[/math] is nonnegative for all [math]\displaystyle{ i }[/math]
- [math]\displaystyle{ \displaystyle\sum_{x_i} f_i(x_i, x_{\pi_i}) = 1 }[/math]
Claim: There is a family of probability functions [math]\displaystyle{ P(X_V) = \prod_{i=1}^n f_i(x_i, x_{\pi_i}) }[/math] where this function is nonnegative, and
To show the power of this claim we can prove the equation (\ref{eqn:WetGrass}) for our wet grass example:
We want to show that
Consider factors [math]\displaystyle{ f(C) }[/math], [math]\displaystyle{ f(R,C) }[/math], [math]\displaystyle{ f(S,C) }[/math]: they do not depend on [math]\displaystyle{ W }[/math], so we can write this all as
since we had already set [math]\displaystyle{ \displaystyle \sum_{x_i} f_i(x_i, x_{\pi_i}) = 1 }[/math].
Let us consider another example with a different directed graph.
Example:
Consider the simple directed graph in Figure 6.

Assume that we would like to calculate the following: [math]\displaystyle{ p(x_3|x_2) }[/math]. We know that we can write the joint probability as:
We can also make use of Bayes' Rule here:
We also need
Thus,
Theorem 1.
.
In our simple graph, the joint probability can be written as
Instead, had we used the chain rule we would have obtained a far more complex equation:
The Markov Property, or Memoryless Property is when the variable [math]\displaystyle{ X_i }[/math] is only affected by [math]\displaystyle{ X_j }[/math] and so the random variable [math]\displaystyle{ X_i }[/math] given [math]\displaystyle{ X_j }[/math] is independent of every other random variable. In our example the history of [math]\displaystyle{ x_4 }[/math] is completely determined by [math]\displaystyle{ x_3 }[/math].
By simply applying the Markov Property to the chain-rule formula we would also have obtained the same result.
Now let us consider the joint probability of the following six-node example found in Figure 7.
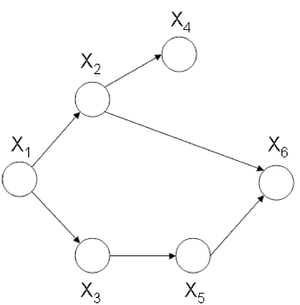
If we use Theorem 1 it can be seen that the joint probability density function for Figure 7 can be written as follows:
Once again, we can apply the Chain Rule and then the Markov Property and arrive at the same result.
Independence
Sept.22.2011
The intuition behind the concept of independence is that when considering two variables, we say that they are independent of each other if knowing the value of one of them gives no extra information about the other variable than what we already know about it. Formaly, this can be expressed as follows: [math]\displaystyle{ \, p(X|Y) = p(X) }[/math] [math]\displaystyle{ \, p(Y|X) = p(Y) }[/math]
Marginal independence
We can say that [math]\displaystyle{ X_A }[/math] is marginally independent of [math]\displaystyle{ X_B }[/math] if:
Conditional independence
We can say that [math]\displaystyle{ X_A }[/math] is conditionally independent of [math]\displaystyle{ X_B }[/math] given [math]\displaystyle{ X_C }[/math] if:
Note: Both equations are equivalent.
Aside: Before we move on further, lets first define the following terms:
- I is defined as an ordering for the nodes in graph G where G=(V,E)(vertices and edges).
- For each [math]\displaystyle{ i \in V }[/math], [math]\displaystyle{ V_i }[/math] which is defined as a set of all nodes that appear earlier than i excluding its parents [math]\displaystyle{ \pi_i }[/math].
Let us consider the example of the six node figure given above (Figure 7). We can define [math]\displaystyle{ I }[/math] as follows:
We can then easily compute [math]\displaystyle{ V_i }[/math] for say [math]\displaystyle{ i=3,6 }[/math].
while [math]\displaystyle{ \pi_i }[/math] for [math]\displaystyle{ i=3,6 }[/math] will be.
We would be interested in finding the conditional independence between random variables in this graph. We know [math]\displaystyle{ X_i \perp X_{v_i} | X_{\pi_i} }[/math] for each [math]\displaystyle{ i }[/math]. In other words, given its parents the node is independent of all earlier nodes. So:
[math]\displaystyle{ X_1 \perp \phi | \phi }[/math],
[math]\displaystyle{ X_2 \perp \phi | X_1 }[/math],
[math]\displaystyle{ X_3 \perp X_2 | X_1 }[/math],
[math]\displaystyle{ X_4 \perp \{X_1,X_3\} | X_2 }[/math],
[math]\displaystyle{ X_5 \perp \{X_1,X_2,X_4\} | X_3 }[/math],
[math]\displaystyle{ X_6 \perp \{X_1,X_3,X_4\} | \{X_2,X_5\} }[/math]
To illustrate why this is true we can take a simple example. Show that:
Proof: first, we know [math]\displaystyle{ P(X_1,X_2,X_3,X_4,X_5,X_6) = P(X_1)P(X_2|X_1)P(X_3|X_1)P(X_4|X_2)P(X_5|X_3)P(X_6|X_5,X_2)\,\! }[/math]
then
The other conditional independences can be proven through a similar process.
Sampling
Inference on graphical models can be defined as the task of answering a query about a number of variables that we are interested in conditioned on the set of observed variables (evidence). Even if using graphical models helps a lot facilitate obtaining the joint probability, exact inference is not always feasible. "Exact inference is feasible in small to medium-sized networks only. Exact inference consumes such a long time in large networks. Therefore, we resort to approximate inference techniques which are much faster and usually give pretty good results". It is known that exact inference on graphical models is NP-Hard in most of the cases.
<ref>Weng-Keen Wong, "Bayesian Networks: A Tutorial", School of Electrical Engineering and Computer Science, Oregon State University, 2005. Available: [1]</ref> In sampling, random samples are generated and values of interest are computed from samples, not original work.
As an input you have a Bayesian network with set of nodes [math]\displaystyle{ X\,\! }[/math]. The sample taken may include all variables (except evidence E) or a subset. "Sample schemas dictate how to generate samples (tuples). Ideally samples are distributed according to [math]\displaystyle{ P(X|E)\,\! }[/math]" <ref>"Sample Bayesian Networks", 2005. Available: [2] </ref>
Some sampling algorithms:
- Forward Sampling
- Likelihood weighting
- Gibbs Sampling (MCMC)
- Blocking
- Rao-Blackwellised
- Importance Sampling
Bayes Ball
The Bayes Ball algorithm can be used to determine if two random variables represented in a graph are independent. The algorithm can show that either two nodes in a graph are independent OR that they are not necessarily independent. The Bayes Ball algorithm can not show that two nodes are dependent. In other word it provides some rules which enables us to do this task using the graph without the need to use the probability distributions. The algorithm will be discussed further in later parts of this section.
Canonical Graphs
In order to understand the Bayes Ball algorithm we need to first introduce 3 canonical graphs. Since our graphs are acyclic, we can represent them using these 3 canonical graphs.
Markov Chain (also called serial connection)
In the following graph (Figure. 8), variable X is independent of Z given Y.
We say that: [math]\displaystyle{ X }[/math] [math]\displaystyle{ \perp }[/math] [math]\displaystyle{ Z }[/math] [math]\displaystyle{ | }[/math] [math]\displaystyle{ Y }[/math]
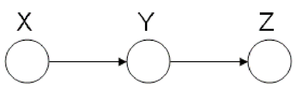
We can prove this independence:
Where
Markov chains are an important class of distributions with applications in communications, information theory and image processing. They are suitable to model memory in phenomenon. For example suppose we want to study the frequency of appearance of English letters in a text. Most likely when "q" appears, the next letter will be "u", this shows dependency between these letters. Markov chains are suitable model for this kind of relations. Markov chains are also the main building block for one of the most famous and widely used statistical models called Hidden Markov Model, which usually used for Time Series.

Markov chains play a significant role in biological applications. It is widely used in the study of carcinogenesis (initiation of cancer formation). A gene has to undergo several mutations before it becomes cancerous, which can be addressed through Markov chains. An example is given in Figure 8a which shows only two gene mutations.
Hidden Cause (diverging connection)
In the Hidden Cause case we can say that X is independent of Z given Y. In this case Y is the hidden cause and if it is known then Z and X are considered independent.
We say that: [math]\displaystyle{ X }[/math] [math]\displaystyle{ \perp }[/math] [math]\displaystyle{ Z }[/math] [math]\displaystyle{ | }[/math] [math]\displaystyle{ Y }[/math]
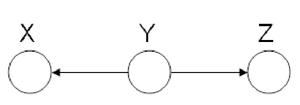
The proof of the independence:
The Hidden Cause case is best illustrated with an example:
In Figure 10 it can be seen that both "Shoe Size" and "Grey Hair" are dependant on the age of a person. The variables of "Shoe size" and "Grey hair" are dependent in some sense, if there is no "Age" in the picture. Without the age information we must conclude that those with a large shoe size also have a greater chance of having gray hair. However, when "Age" is observed, there is no dependence between "Shoe size" and "Grey hair" because we can deduce both based only on the "Age" variable.
Explaining-Away (converging connection)
Finally, we look at the third type of canonical graph: Explaining-Away Graphs. This type of graph arises when a phenomena has multiple explanations. Here, the conditional independence statement is actually a statement of marginal independence: [math]\displaystyle{ X \perp Z }[/math]. This type of graphs is also called "V-structure" or "V-shape" because of its illustration (Fig. 11).
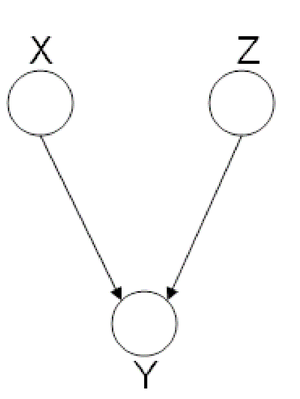
In these types of scenarios, variables X and Z are independent. However, once the third variable Y is observed, X and Z become dependent (Fig. 11).
To clarify these concepts, suppose Bob and Mary are supposed to meet for a noontime lunch. Consider the following events:
If Mary is late, then she could have been kidnapped by aliens. Alternatively, Bob may have forgotten to adjust his watch for daylight savings time, making him early. Clearly, both of these events are independent. Now, consider the following probabilities:
We expect [math]\displaystyle{ P( late = 1 ) \lt P( aliens = 1 ~|~ late = 1 ) }[/math] since [math]\displaystyle{ P( aliens = 1 ~|~ late = 1 ) }[/math] does not provide any information regarding Bob's watch. Similarly, we expect [math]\displaystyle{ P( aliens = 1 ~|~ late = 1 ) \lt P( aliens = 1 ~|~ late = 1, watch = 0 ) }[/math]. Since [math]\displaystyle{ P( aliens = 1 ~|~ late = 1 ) \neq P( aliens = 1 ~|~ late = 1, watch = 0 ) }[/math], aliens and watch are not independent given late. To summarize,
- If we do not observe late, then aliens [math]\displaystyle{ ~\perp~ watch }[/math] ([math]\displaystyle{ X~\perp~ Z }[/math])
- If we do observe late, then aliens [math]\displaystyle{ ~\cancel{\perp}~ watch ~|~ late }[/math] ([math]\displaystyle{ X ~\cancel{\perp}~ Z ~|~ Y }[/math])
Bayes Ball Algorithm
Sept. 27.2011
Goal: We wish to determine whether a given conditional
statement such as [math]\displaystyle{ X_{A} ~\perp~ X_{B} ~|~ X_{C} }[/math] is true given a directed graph.
The algorithm is as follows:
- Shade nodes, [math]\displaystyle{ ~X_{C}~ }[/math], that are conditioned on, i.e. they have been observed.
- Assuming that the initial position of the ball is [math]\displaystyle{ ~X_{A}~ }[/math]:
- If the ball cannot reach [math]\displaystyle{ ~X_{B}~ }[/math], then the nodes [math]\displaystyle{ ~X_{A}~ }[/math] and [math]\displaystyle{ ~X_{B}~ }[/math] must be conditionally independent.
- If the ball can reach [math]\displaystyle{ ~X_{B}~ }[/math], then the nodes [math]\displaystyle{ ~X_{A}~ }[/math] and [math]\displaystyle{ ~X_{B}~ }[/math] are not necessarily independent.
The biggest challenge in the Bayes Ball Algorithm is to determine what happens to a ball going from node X to node Z as it passes through node Y. The ball could continue its route to Z or it could be blocked. It is important to note that the balls are allowed to travel in any direction, independent of the direction of the edges in the graph.
We use the canonical graphs previously studied to determine the route of a ball traveling through a graph. Using these three graphs, we establish the Bayes ball rules which can be extended for more graphical models.
Markov Chain (serial connection)
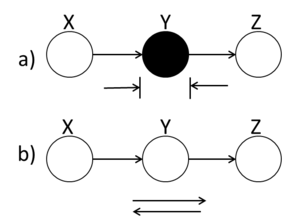
A ball traveling from X to Z or from Z to X will be blocked at node Y if this node is shaded. Alternatively, if Y is unshaded, the ball will pass through.
In (Fig. 12(a)), X and Z are conditionally independent ( [math]\displaystyle{ X ~\perp~ Z ~|~ Y }[/math] ) while in (Fig.12(b)) X and Z are not necessarily independent.
Hidden Cause (diverging connection)
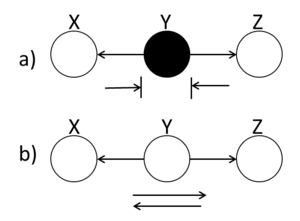
A ball traveling through Y will be blocked at Y if it is shaded. If Y is unshaded, then the ball passes through.
(Fig. 13(a)) demonstrates that X and Z are conditionally independent when Y is shaded.
Explaining-Away (converging connection)
Unlike the last two cases in which the Bayes ball rule was intuitively understandable, in this case a ball traveling through Y is blocked when Y is UNSHADED!. If Y is shaded, then the ball passes through. Hence, X and Z are conditionally independent when Y is unshaded.
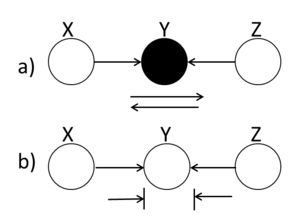
Bayes Ball Examples
Example 1
In this first example, we wish to identify the behavior of leaves in the graphical models using two-nodes graphs. Let a ball be going from X to Y in two-node graphs. To employ the Bayes ball method mentioned above, we have to implicitly add one extra node to the two-node structure since we introduced the Bayes rules for three nodes configuration. We add the third node exactly symmetric to node X with respect to node Y. For example in (Fig. 15) (a) we can think of a hidden node in the right hand side of node Y with a hidden arrow from the hidden node to Y. Then, we are able to utilize the Bayes ball method considering the fact that a ball thrown from X cannot reach Y, and thus it will be blocked. On the contrary, following the same rule in (Fig. 15) (b) turns out that if there was a hidden node in right hand side of Y, a ball could pass from X to that hidden node according to explaining-away structure. Of course, there is no real node and in this case we conventionally say that the ball will be bounced back to node X.
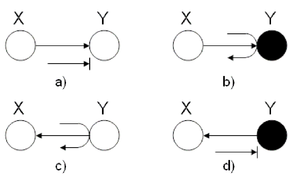
Finally, for the last two graphs, we used the rules of the Hidden Cause Canonical Graph (Fig. 13). In (c), the ball passes through Y while in (d), the ball is blocked at Y.
Example 2
Suppose your home is equipped with an alarm system. There are two possible causes for the alarm to ring:
- Your house is being burglarized
- There is an earthquake
Hence, we define the following events:
The burglary and earthquake events are independent
if the alarm does not ring. However, if the alarm does ring, then
the burglary and the earthquake events are not
necessarily independent. Also, if the alarm rings then it is
more possible that a police report will be issued.
We can use the Bayes Ball Algorithm to deduce conditional independence properties from the graph. Firstly, consider figure (16(a)) and assume we are trying to determine whether there is conditional independence between the burglary and earthquake events. In figure (\ref{fig:AlarmExample1}(a)), a ball starting at the burglary event is blocked at the alarm node.
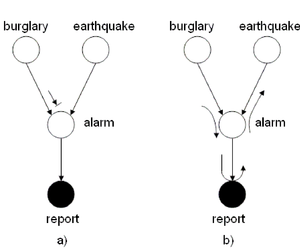
Nonetheless, this does not prove that the burglary and earthquake events are independent. Indeed, (Fig. 16(b)) disproves this as we have found an alternate path from burglary to earthquake passing through report. It follows that [math]\displaystyle{ burglary ~\cancel{\amalg}~ earthquake ~|~ report }[/math]
Example 3
Referring to figure (Fig. 17), we wish to determine whether the following conditional probabilities are true:
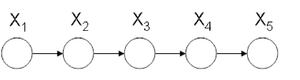
To determine if the conditional probability Eq.\ref{eq:c1} is true, we shade node [math]\displaystyle{ X_{2} }[/math]. This blocks balls traveling from [math]\displaystyle{ X_{1} }[/math] to [math]\displaystyle{ X_{3} }[/math] and proves that Eq.\ref{eq:c1} is valid.
After shading nodes [math]\displaystyle{ X_{3} }[/math] and [math]\displaystyle{ X_{4} }[/math] and applying the Bayes Balls Algorithm}, we find that the ball travelling from [math]\displaystyle{ X_{1} }[/math] to [math]\displaystyle{ X_{5} }[/math] is blocked at [math]\displaystyle{ X_{3} }[/math]. Similarly, a ball going from [math]\displaystyle{ X_{5} }[/math] to [math]\displaystyle{ X_{1} }[/math] is blocked at [math]\displaystyle{ X_{4} }[/math]. This proves that Eq.\ref{eq:c2 also holds.
Example 4

Consider figure (Fig. 18). Using the Bayes Ball Algorithm we wish to determine if each of the following statements are valid:
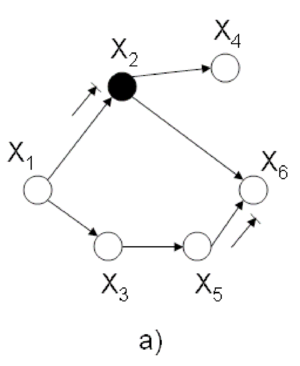
To disprove Eq.\ref{eq:c3}, we must find a path from [math]\displaystyle{ X_{4} }[/math] to [math]\displaystyle{ X_{1} }[/math] and [math]\displaystyle{ X_{3} }[/math] when [math]\displaystyle{ X_{2} }[/math] is shaded (Refer to Fig. 19(a)). Since there is no route from [math]\displaystyle{ X_{4} }[/math] to [math]\displaystyle{ X_{1} }[/math] and [math]\displaystyle{ X_{3} }[/math] we conclude that Eq.\ref{eq:c3} is true.
Similarly, we can show that there does not exist a path between [math]\displaystyle{ X_{1} }[/math] and [math]\displaystyle{ X_{6} }[/math] when [math]\displaystyle{ X_{2} }[/math] and [math]\displaystyle{ X_{3} }[/math] are shaded (Refer to Fig.19(b)). Hence, Eq.\ref{eq:c4} is true.
Finally, (Fig. 19(c)) shows that there is a route from [math]\displaystyle{ X_{2} }[/math] to [math]\displaystyle{ X_{3} }[/math] when [math]\displaystyle{ X_{1} }[/math] and [math]\displaystyle{ X_{6} }[/math] are shaded. This proves that the statement \ref{eq:c4} is false.
Theorem 2.
Define [math]\displaystyle{ p(x_{v}) = \prod_{i=1}^{n}{p(x_{i} ~|~ x_{\pi_{i}})} }[/math] to be the factorization as a multiplication of some local probability of a directed graph.
Let [math]\displaystyle{ D_{1} = \{ p(x_{v}) = \prod_{i=1}^{n}{p(x_{i} ~|~ x_{\pi_{i}})}\} }[/math]
Let [math]\displaystyle{ D_{2} = \{ p(x_{v}): }[/math]satisfy all conditional independence statements associated with a graph [math]\displaystyle{ \} }[/math].
Then [math]\displaystyle{ D_{1} = D_{2} }[/math].
Example 5
Given the following Bayesian network (Fig.19 ): Determine whether the following statements are true or false?
a.) [math]\displaystyle{ x4\perp \{x1,x3\} }[/math]
Ans. True
b.) [math]\displaystyle{ x1\perp x6\{x2,x3\} }[/math]
Ans. True
c.) [math]\displaystyle{ x2\perp x3 \{x1,x6\} }[/math]
Ans. False
Undirected Graphical Model
Sept.29.2011
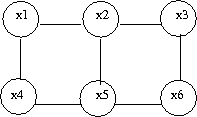
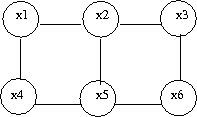
Generally, the graphical model is divided into two major classes, directed graphs and undirected graphs. Directed graphs and its characteristics was described previously. In this section we discuss undirected graphical model which is also known as Markov random fields. In some applications there are relations between variables but these relation are bilateral and we don't encounter causality. For example consider a natural image. In natural images the value of a pixel has correlations with neighboring pixel values but this is bilateral and not a causality relations. Markov random fields are suitable to model such processes and have found applications in fields such as vision and image processing.We can define an undirected graphical model with a graph [math]\displaystyle{ G = (V, E) }[/math] where [math]\displaystyle{ V }[/math] is a set of vertices corresponding to a set of random variables and [math]\displaystyle{ E }[/math] is a set of undirected edges as shown in (Fig.20a). An another example is displayed in (Fig.20b) that shows part of a lattice. Couple of observations from the two examples are the following: there is no parent and child relationship; potentials are defined on several cliques of a graph which will be discussed in the subsequent sections.
Conditional independence
For directed graphs Bayes ball method was defined to determine the conditional independence properties of a given graph. We can also employ the Bayes ball algorithm to examine the conditional independency of undirected graphs. Here the Bayes ball rule is simpler and more intuitive. Considering (Fig.21a) , a ball can be thrown either from x to z or from z to x if y is not observed. In other words, if y is not observed (Fig.21b) a ball thrown from x can reach z and vice versa. On the contrary, given a shaded y, the node can block the ball and make x and z conditionally independent. With this definition one can declare that in an undirected graph, a node is conditionally independent of non-neighbors given neighbors. Technically speaking, [math]\displaystyle{ X_A }[/math] is independent of [math]\displaystyle{ X_C }[/math] given [math]\displaystyle{ X_B }[/math] if the set of nodes [math]\displaystyle{ X_B }[/math] separates the nodes [math]\displaystyle{ X_A }[/math] from the nodes [math]\displaystyle{ X_C }[/math]. Hence, if every path from a node in [math]\displaystyle{ X_A }[/math] to a node in [math]\displaystyle{ X_C }[/math] includes at least one node in [math]\displaystyle{ X_B }[/math], then we claim that [math]\displaystyle{ X_A \perp X_c | X_B }[/math].
Question
Is it possible to convert undirected models to directed models or vice versa?
In order to answer this question, consider (Fig.22 ) which illustrates an undirected graph with four nodes - [math]\displaystyle{ X }[/math], [math]\displaystyle{ Y }[/math],[math]\displaystyle{ Z }[/math] and [math]\displaystyle{ W }[/math]. We can define two facts using Bayes ball method:
It is simple to see there is no directed graph satisfying both conditional independence properties. Recalling that directed graphs are acyclic, converting undirected graphs to directed graphs result in at least one node in which the arrows are inward-pointing(a v structure). Without loss of generality we can assume that node [math]\displaystyle{ Z }[/math] has two inward-pointing arrows. By conditional independence semantics of directed graphs, we have [math]\displaystyle{ X \perp Y|W }[/math], yet the [math]\displaystyle{ X \perp Y|\{W,Z\} }[/math] property does not hold. On the other hand, (Fig.23 ) depicts a directed graph which is characterized by the singleton independence statement [math]\displaystyle{ X \perp Y }[/math]. There is no undirected graph on three nodes which can be characterized by this singleton statement. Basically, if we consider the set of all distribution over [math]\displaystyle{ n }[/math] random variables, a subset of which can be represented by directed graphical models while there is another subset which undirected graphs are able to model that. There is a narrow intersection region between these two subsets in which probabilistic graphical models may be represented by either directed or undirected graphs.
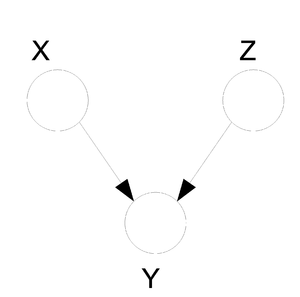
Parameterization
Having undirected graphical models, we would like to obtain "local" parameterization like what we did in the case of directed graphical models. For directed graphical models, "local" had the interpretation of a set of node and its parents, [math]\displaystyle{ \{i, \pi_i\} }[/math]. The joint probability and the marginals are defined as a product of such local probabilities which was inspired from the chain rule in the probability theory. In undirected GMs "local" functions cannot be represented using conditional probabilities, and we must abandon conditional probabilities altogether. Therefore, the factors do not have probabilistic interpretation any more, but we can choose the "local" functions arbitrarily. However, any "local" function for undirected graphical models should satisfy the following condition: - Consider [math]\displaystyle{ X_i }[/math] and [math]\displaystyle{ X_j }[/math] that are not linked, they are conditionally independent given all other nodes. As a result, the "local" function should be able to do the factorization on the joint probability such that [math]\displaystyle{ X_i }[/math] and [math]\displaystyle{ X_j }[/math] are placed in different factors.
It can be shown that definition of local functions based only a node and its corresponding edges (similar to directed graphical models) is not tractable and we need to follow a different approach. Before defining the "local" functions, we have to introduce a new terminology in graph theory called clique. Clique is a subset of fully connected nodes in a graph G. Every node in the clique C is directly connected to every other node in C. In addition, maximal clique is a clique where if any other node from the graph G is added to it then the new set is no longer a clique. Consider the undirected graph shown in (Fig. 24), we can list all the cliques as follow:
- [math]\displaystyle{ \{X_1, X_3\} }[/math] - [math]\displaystyle{ \{X_1, X_2\} }[/math] - [math]\displaystyle{ \{X_3, X_5\} }[/math] - [math]\displaystyle{ \{X_2, X_4\} }[/math] - [math]\displaystyle{ \{X_5, X_6\} }[/math] - [math]\displaystyle{ \{X_2, X_5\} }[/math] - [math]\displaystyle{ \{X_2, X_5, X_6\} }[/math]
According to the definition, [math]\displaystyle{ \{X_2,X_5\} }[/math] is not a maximal clique since we can add one more node, [math]\displaystyle{ X_6 }[/math] and still have a clique. Let C be set of all maximal cliques in [math]\displaystyle{ G(V, E) }[/math]:
where in aforementioned example [math]\displaystyle{ c_1 }[/math] would be [math]\displaystyle{ \{X_1, X_3\} }[/math], and so on. We define the joint probability over all nodes as:
where [math]\displaystyle{ \psi_{c_i} (x_{c_i}) }[/math] is an arbitrarily function with some restrictions. This function is not necessarily probability and is defined over each clique. There are only two restrictions for this function, non-negative and real-valued. Usually [math]\displaystyle{ \psi_{c_i} (x_{c_i}) }[/math] is called potential function. The [math]\displaystyle{ Z }[/math] is normalization factor and determined by:
As a matter of fact, normalization factor, [math]\displaystyle{ Z }[/math], is not very important since in most of the time is canceled out during computation. For instance, to calculate conditional probability [math]\displaystyle{ P(X_A | X_B) }[/math], [math]\displaystyle{ Z }[/math] is crossed out between the nominator [math]\displaystyle{ P(X_A, X_B) }[/math] and the denominator [math]\displaystyle{ P(X_B) }[/math].
As was mentioned above, sum-product of the potential functions determines the joint probability over all nodes. Because of the fact that potential functions are arbitrarily defined, assuming exponential functions for [math]\displaystyle{ \psi_{c_i} (x_{c_i}) }[/math] simplifies and reduces the computations. Let potential function be:
the joint probability is given by:
-
There is a lot of information contained in the joint probability distribution [math]\displaystyle{ P(x_{V}) }[/math]. We define 6 tasks listed bellow that we would like to accomplish with various algorithms for a given distribution [math]\displaystyle{ P(x_{V}) }[/math].
Tasks:
- Marginalization
Given [math]\displaystyle{ P(x_{V}) }[/math] find [math]\displaystyle{ P(x_{A}) }[/math] where A ⊂ V
Given [math]\displaystyle{ P(x_1, x_2, ... , x_6) }[/math] find [math]\displaystyle{ P(x_2, x_6) }[/math]
- Conditioning
Given [math]\displaystyle{ P(x_V) }[/math] find [math]\displaystyle{ P(x_A|x_B) = \frac{P(x_A, x_B)}{P(x_B)} }[/math] if A ⊂ V and B ⊂ V .
- Evaluation
Evaluate the probability for a certain configuration.
- Completion
Compute the most probable configuration. In other words, which of the [math]\displaystyle{ P(x_A|x_B) }[/math] is the largest for a specific combinations of [math]\displaystyle{ A }[/math] and [math]\displaystyle{ B }[/math].
- Simulation
Generate a random configuration for [math]\displaystyle{ P(x_V) }[/math] .
- Learning
We would like to find parameters for [math]\displaystyle{ P(x_V) }[/math] .
Exact Algorithms
To compute the probabilistic inference or the conditional probability of a variable [math]\displaystyle{ X }[/math] we need to marginalize over all the random variables [math]\displaystyle{ X_i }[/math] and the possible values of [math]\displaystyle{ X_i }[/math] which might take long running time. To reduce the computational complexity of preforming such marginalization the next section presents different exact algorithms that find the exact solutions for algorithmic problem in a Polynomial time(fast) which are:
- Elimination
- Sum-Product
- Max-Product
- Junction Tree
Elimination Algorithm
Oct. 4. 2011
In this section we will see how we could overcome the problem of probabilistic inference on graphical models. In other words, we discuss the problem of computing conditional and marginal probabilities in graphical models.
Variable Elimination as an exact inference algorithm. It uses dynamic programming technique to reduce the number of required computations needed to answer an inference query. The basic idea behind Variable Elimination Algorithm is to push the summations over random variables as far as possible and replace the resulted terms with new factors. For a Markov chain this algorithm guaranteed that the number of computations needed to answer an inference query would always be linear with the length of the chain.
Elimination Algorithm on Directed Graphs<ref name="Pool">[3]</ref>
First we assume that E and F are disjoint subsets of the node indices of a graphical model, i.e. [math]\displaystyle{ X_E }[/math] and [math]\displaystyle{ X_F }[/math] are disjoint subsets of the random variables. Given a graph G =(V,E), we aim to calculate [math]\displaystyle{ p(x_F | x_E) }[/math] where [math]\displaystyle{ X_E }[/math] and [math]\displaystyle{ X_F }[/math] represents evidence and query nodes, respectively. Here and in this section [math]\displaystyle{ X_F }[/math] should be only one node; however, later on a more powerful inference method will be introduced which is able to make inference on multi-variables. In order to compute [math]\displaystyle{ p(x_F | x_E) }[/math] we have to first marginalize the joint probability on nodes which are neither [math]\displaystyle{ X_F }[/math] nor [math]\displaystyle{ X_E }[/math] denoted by [math]\displaystyle{ R = V - ( E U F) }[/math].
which can be further marginalized to yield [math]\displaystyle{ p(E) }[/math]:
and then the desired conditional probability is given by:
Example
Let assume that we are interested in [math]\displaystyle{ p(x_1 | \bar{x_6)} }[/math] in (Fig. 21) where [math]\displaystyle{ x_6 }[/math] is an observation of [math]\displaystyle{ X_6 }[/math] , and thus we may assume that it is a constant. According to the rule mentioned above we have to marginalized the joint probability over non-evidence and non-query nodes:
where to simplify the notations we define [math]\displaystyle{ m_5(x_2, x_3) }[/math] which is the result of the last summation. The last summation is over [math]\displaystyle{ x_5 }[/math] , and thus the result is only depend on [math]\displaystyle{ x_2 }[/math] and [math]\displaystyle{ x_3 }[/math]. In particular, let [math]\displaystyle{ m_i(x_{s_i}) }[/math] denote the expression that arises from performing the [math]\displaystyle{ \sum_{x_i} }[/math], where [math]\displaystyle{ x_{S_i} }[/math] are the variables, other than [math]\displaystyle{ x_i }[/math], that appear in the summand. Continuing the derivations we have:
Therefore, the conditional probability is given by:
At the beginning of our computation we had the assumption which says [math]\displaystyle{ X_6 }[/math] is observed, and thus the notation [math]\displaystyle{ \bar{x_6} }[/math] was used to express this fact. Let [math]\displaystyle{ X_i }[/math] be an evidence node whose observed value is [math]\displaystyle{ \bar{x_i} }[/math], we define an evidence potential function, [math]\displaystyle{ \delta(x_i, \bar{x_i}) }[/math], which its value is one if [math]\displaystyle{ x_i = \bar{x_i} }[/math] and zero elsewhere. This function allows us to use summation over [math]\displaystyle{ x_6 }[/math] yielding:
We can define an algorithm to make inference on directed graphs using elimination techniques. Let E and F be an evidence set and a query node, respectively. We first choose an elimination ordering I such that F appears last in this ordering. The following figure shows the steps required to perform the elimination algorithm for probabilistic inference on directed graphs:
ELIMINATE (G,E,F)
INITIALIZE (G,F)
EVIDENCE(E)
UPDATE(G)
NORMALIZE(F)
INITIALIZE(G,F)
Choose an ordering [math]\displaystyle{ I }[/math] such that [math]\displaystyle{ F }[/math] appear last
- For each node [math]\displaystyle{ X_i }[/math] in [math]\displaystyle{ V }[/math]
- Place [math]\displaystyle{ p(x_i|x_{\pi_i}) }[/math] on the active list
- End
EVIDENCE(E)
- For each [math]\displaystyle{ i }[/math] in [math]\displaystyle{ E }[/math]
- Place [math]\displaystyle{ \delta(x_i|\overline{x_i}) }[/math] on the active list
- End
Update(G)
- For each [math]\displaystyle{ i }[/math] in [math]\displaystyle{ I }[/math]
- Find all potentials from the active list that reference [math]\displaystyle{ x_i }[/math] and remove them from the active list
- Let [math]\displaystyle{ \phi_i(x_Ti) }[/math] denote the product of these potentials
- Let [math]\displaystyle{ m_i(x_Si)=\sum_{x_i}\phi_i(x_Ti) }[/math]
- Place [math]\displaystyle{ m_i(x_Si) }[/math] on the active list
- End
Normalize(F)
- [math]\displaystyle{ p(x_F|\overline{x_E}) }[/math] ← [math]\displaystyle{ \phi_F(x_F)/\sum_{x_F}\phi_F(x_F) }[/math]
Example:
For the graph in figure 21 [math]\displaystyle{ G =(V,''E'') }[/math]. Consider once again that node [math]\displaystyle{ x_1 }[/math] is the query node and [math]\displaystyle{ x_6 }[/math] is the evidence node.
[math]\displaystyle{ I = \left\{6,5,4,3,2,1\right\} }[/math] (1 should be the last node, ordering is crucial)

We must now create an active list. There are two rules that must be followed in order to create this list.
- For i[math]\displaystyle{ \in{V} }[/math] place [math]\displaystyle{ p(x_i|x_{\pi_i}) }[/math] in active list.
- For i[math]\displaystyle{ \in }[/math]{E} place [math]\displaystyle{ \delta(x_i|\overline{x_i}) }[/math] in active list.
Here, our active list is: [math]\displaystyle{ p(x_1), p(x_2|x_1), p(x_3|x_1), p(x_4|x_2), p(x_5|x_3),\underbrace{p(x_6|x_2, x_5)\delta{(\overline{x_6},x_6)}}_{\phi_6(x_2,x_5, x_6), \sum_{x6}{\phi_6}=m_{6}(x2,x5) } }[/math]
We first eliminate node [math]\displaystyle{ X_6 }[/math]. We place [math]\displaystyle{ m_{6}(x_2,x_5) }[/math] on the active list, having removed [math]\displaystyle{ X_6 }[/math]. We now eliminate [math]\displaystyle{ X_5 }[/math].
Likewise, we can also eliminate [math]\displaystyle{ X_4, X_3, X_2 }[/math](which yields the unnormalized conditional probability [math]\displaystyle{ p(x_1|\overline{x_6}) }[/math] and [math]\displaystyle{ X_1 }[/math]. Then it yields [math]\displaystyle{ m_1 = \sum_{x_1}{\phi_1(x_1)} }[/math] which is the normalization factor, [math]\displaystyle{ p(\overline{x_6}) }[/math].
Note: the complexity of elimination is determined by the maximum message size or in other word by tree-width. Tree width= (the minimum of the maximal clique created during graph elimination)-1. For example the tree-width of 3x2 graph in figure 21 is 3-1=2.
Elimination Algorithm on Undirected Graphs
Oct.6 .2011
The first task is to find the maximal cliques and their associated potential functions.
maximal clique: [math]\displaystyle{ \left\{x_1, x_2\right\} }[/math], [math]\displaystyle{ \left\{x_1, x_3\right\} }[/math], [math]\displaystyle{ \left\{x_2, x_4\right\} }[/math], [math]\displaystyle{ \left\{x_3, x_5\right\} }[/math], [math]\displaystyle{ \left\{x_2,x_5,x_6\right\} }[/math]
potential functions: [math]\displaystyle{ \varphi{(x_1,x_2)},\varphi{(x_1,x_3)},\varphi{(x_2,x_4)}, \varphi{(x_3,x_5)} }[/math] and [math]\displaystyle{ \varphi{(x_2,x_3,x_6)} }[/math]
[math]\displaystyle{ p(x_1|\overline{x_6})=p(x_1,\overline{x_6})/p(\overline{x_6})\cdots\cdots\cdots\cdots\cdots(*) }[/math]
[math]\displaystyle{ p(x_1,x_6)=\frac{1}{Z}\sum_{x_2,x_3,x_4,x_5,x_6}\varphi{(x_1,x_2)}\varphi{(x_1,x_3)}\varphi{(x_2,x_4)}\varphi{(x_3,x_5)}\varphi{(x_2,x_3,x_6)}\delta{(x_6,\overline{x_6})} }[/math]
The [math]\displaystyle{ \frac{1}{Z} }[/math] looks crucial, but in fact it has no effect because for (*) both the numerator and the denominator have the [math]\displaystyle{ \frac{1}{Z} }[/math] term. So in this case we can just cancel it.
The general rule for elimination in an undirected graph is that we can remove a node as long as we connect all of the parents of that node together. Effectively, we form a clique out of the parents of that node.
The algorithm used to eliminate nodes in an undirected graph is:
UndirectedGraphElimination(G,l)
- For each node [math]\displaystyle{ X_i }[/math] in [math]\displaystyle{ I }[/math]
- Connect all of the remaining neighbours of [math]\displaystyle{ X_i }[/math]
- Remove [math]\displaystyle{ X_i }[/math] from the graph
- End
Example:
For the graph G in figure 24
when we remove x1, G becomes as in figure 25
while if we remove x2, G becomes as in figure 26
An interesting thing to point out is that the order of the elimination matters a great deal. Consider the two results. If we remove one node the graph complexity is slightly reduced. But if we try to remove another node the complexity is significantly increased. The reason why we even care about the complexity of the graph is because the complexity of a graph denotes the number of calculations that are required to answer questions about that graph. If we had a huge graph with thousands of nodes the order of the node removal would be key in the complexity of the algorithm. Unfortunately, there is no efficient algorithm that can produce the optimal node removal order such that the elimination algorithm would run quickly. If we remove one of the leaf first, then the largest clique is two and computational complexity is of order [math]\displaystyle{ N^2 }[/math]. And removing the center node gives the largest clique size to be five and complexity is of order [math]\displaystyle{ N^5 }[/math]. Hence, it is very hard to find an optimal ordering, due to which this is an NP problem.
Moralization
So far we have shown how to use elimination to successively remove nodes from an undirected graph. We know that this is useful in the process of marginalization. We can now turn to the question of what will happen when we have a directed graph. It would be nice if we could somehow reduce the directed graph to an undirected form and then apply the previous elimination algorithm. This reduction is called moralization and the graph that is produced is called a moral graph.
To moralize a graph we first need to connect the parents of each node together. This makes sense intuitively because the parents of a node need to be considered together in the undirected graph and this is only done if they form a type of clique. By connecting them together we create this clique.
After the parents are connected together we can just drop the orientation on the edges in the directed graph. By removing the directions we force the graph to become undirected.
The previous elimination algorithm can now be applied to the new moral graph. We can do this by assuming that the probability functions in directed graph [math]\displaystyle{ P(x_i|\pi_{x_i}) }[/math] are the same as the mass functions from the undirected graph. [math]\displaystyle{ \psi_{c_i}(c_{x_i}) }[/math]
Example:
I = [math]\displaystyle{ \left\{x_6,x_5,x_4,x_3,x_2,x_1\right\} }[/math]
When we moralize the directed graph in figure 27, we obtain the
undirected graph in figure 28.
Elimination Algorithm on Trees
Definition of a tree:
A tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree.
If we have a directed graph then we must moralize it first. If the moral graph is a tree then the directed graph is also considered a tree.
Belief Propagation Algorithm (Sum Product Algorithm)
One of the main disadvantages to the elimination algorithm is that the ordering of the nodes defines the number of calculations that are required to produce a result. The optimal ordering is difficult to calculate and without a decent ordering the algorithm may become very slow. In response to this we can introduce the sum product algorithm. It has one major advantage over the elimination algorithm: it is faster. The sum product algorithm has the same complexity when it has to compute the probability of one node as it does to compute the probability of all the nodes in the graph. Unfortunately, the sum product algorithm also has one disadvantage. Unlike the elimination algorithm it can not be used on any graph. The sum product algorithm works only on trees.
For undirected graphs if there is only one path between any two pair of nodes then that graph is a tree (Fig.29). If we have a directed graph then we must moralize it first. If the moral graph is a tree then the directed graph is also considered a tree (Fig.30).
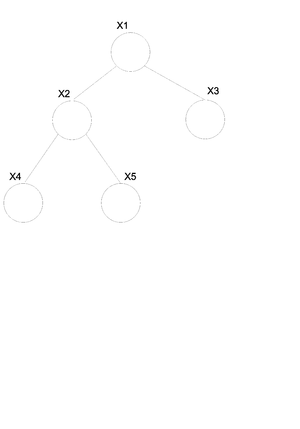
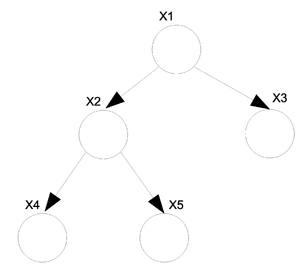
For the undirected graph [math]\displaystyle{ G(v, \varepsilon) }[/math] (Fig.30) we can write the joint probability distribution function in the following way.
We know that in general we can not convert a directed graph into an undirected graph. There is however an exception to this rule when it comes to trees. In the case of a directed tree there is an algorithm that allows us to convert it to an undirected tree with the same properties.
Take the above example (Fig.30) of a directed tree. We can write the joint probability distribution function as:
If we want to convert this graph to the undirected form shown in (Fig. 29) then we can use the following set of rules. \begin{thinlist}
- If [math]\displaystyle{ \gamma }[/math] is the root then: [math]\displaystyle{ \psi(x_\gamma) = P(x_\gamma) }[/math].
- If [math]\displaystyle{ \gamma }[/math] is NOT the root then: [math]\displaystyle{ \psi(x_\gamma) = 1 }[/math].
- If [math]\displaystyle{ \left\lbrace i \right\rbrace }[/math] = [math]\displaystyle{ \pi_j }[/math] then: [math]\displaystyle{ \psi(x_i, x_j) = P(x_j | x_i) }[/math].
So now we can rewrite the above equation for (Fig.30) as:
Elimination Algorithm on a Tree<ref name="Pool"/>
We will derive the Sum-Product algorithm from the point of view of the Eliminate algorithm. To marginalize [math]\displaystyle{ x_1 }[/math] in Fig.31,
where,
which is essentially (potential of the node)[math]\displaystyle{ \times }[/math](potential of the edge)[math]\displaystyle{ \times }[/math](message from the child).
The term "[math]\displaystyle{ m_{ji}(x_i) }[/math]" represents the intermediate factor between the eliminated variable, j, and the remaining neighbor of the variable, i. Thus, in the above case, we will use [math]\displaystyle{ m_{53}(x_3) }[/math] to denote [math]\displaystyle{ m_5(x_3) }[/math], [math]\displaystyle{ m_{42}(x_2) }[/math] to denote [math]\displaystyle{ m_4(x_2) }[/math], and [math]\displaystyle{ m_{32}(x_2) }[/math] to denote [math]\displaystyle{ m_3(x_2) }[/math]. We refer to the intermediate factor [math]\displaystyle{ m_{ji}(x_i) }[/math] as a "message" that j sends to i. (Fig. \ref{fig:TreeStdEx})
In general,
Note: It is important to know that BP algorithm gives us the exact solution only if the graph is a tree, however experiments have shown that BP leads to acceptable approximate answer even when the graphs has some loops.
Elimination To Sum Product Algorithm<ref name="Pool"/>
The Sum-Product algorithm allows us to compute all marginals in the tree by passing messages inward from the leaves of the tree to an (arbitrary) root, and then passing it outward from the root to the leaves, again using the above equation at each step. The net effect is that a single message will flow in both directions along each edge. (See Fig.32) Once all such messages have been computed using the above equation, we can compute desired marginals. One of the major advantages of this algorithm is that messages can be reused which reduces the computational cost heavily.
As shown in Fig.32, to compute the marginal of [math]\displaystyle{ X_1 }[/math] using elimination, we eliminate [math]\displaystyle{ X_5 }[/math], which involves computing a message [math]\displaystyle{ m_{53}(x_3) }[/math], then eliminate [math]\displaystyle{ X_4 }[/math] and [math]\displaystyle{ X_3 }[/math] which involves messages [math]\displaystyle{ m_{32}(x_2) }[/math] and [math]\displaystyle{ m_{42}(x_2) }[/math]. We subsequently eliminate [math]\displaystyle{ X_2 }[/math], which creates a message [math]\displaystyle{ m_{21}(x_1) }[/math].
Suppose that we want to compute the marginal of [math]\displaystyle{ X_2 }[/math]. As shown in Fig.33, we first eliminate [math]\displaystyle{ X_5 }[/math], which creates [math]\displaystyle{ m_{53}(x_3) }[/math], and then eliminate [math]\displaystyle{ X_3 }[/math], [math]\displaystyle{ X_4 }[/math], and [math]\displaystyle{ X_1 }[/math], passing messages [math]\displaystyle{ m_{32}(x_2) }[/math], [math]\displaystyle{ m_{42}(x_2) }[/math] and [math]\displaystyle{ m_{12}(x_2) }[/math] to [math]\displaystyle{ X_2 }[/math].
Since the messages can be "reused", marginals over all possible elimination orderings can be computed by computing all possible messages which is small in numbers compared to the number of possible elimination orderings.
The Sum-Product algorithm is not only based on the above equation, but also Message-Passing Protocol. Message-Passing Protocol tells us that a node can send a message to a neighboring node when (and only when) it has received messages from all of its other neighbors.
For Directed Graph
Previously we stated that:
Using the above equation (\ref{eqn:Marginal}), we find the marginal of [math]\displaystyle{ \bar{x}_E }[/math].
Now we denote:
Since the sets, F and E, add up to [math]\displaystyle{ \mathcal{V} }[/math], [math]\displaystyle{ p(x_v) }[/math] is equal to [math]\displaystyle{ p(x_F,x_E) }[/math]. Thus we can substitute the equation (\ref{eqn:Dir8}) into (\ref{eqn:Marginal}) and (\ref{eqn:Dir7}), and they become:
We are interested in finding the conditional probability. We substitute previous results, (\ref{eqn:Dir9}) and (\ref{eqn:Dir10}) into the conditional probability equation.
[math]\displaystyle{ p^E(x_v) }[/math] is an unnormalized version of conditional probability, [math]\displaystyle{ p(x_F|\bar{x}_E) }[/math].
For Undirected Graphs
We denote [math]\displaystyle{ \psi^E }[/math] to be:
Max-Product
Because multiplication distributes over max as well as sum:
Formally, both the sum-product and max-product are commutative semirings.
We would like to find the Maximum probability that can be achieved by some set of random variables given a set of configurations. The algorithm is similar to the sum product except we replace the sum with max.
[math]\displaystyle{ p(x_F|\bar{x}_E) }[/math]
Example:
Consider the graph in Figure.33.
Maximum configuration
We would also like to find the value of the [math]\displaystyle{ x_i }[/math]s which produces the largest value for the given expression. To do this we replace the max from the previous section with argmax.
[math]\displaystyle{ m_{53}(x_5)= argmax_{x_5}\psi{(x_5)}\psi{(x_5,x_3)} }[/math]
[math]\displaystyle{ \log{m^{max}_{ji}(x_i)}=\max_{x_j}{\log{\psi^{E}{(x_j)}}}+\log{\psi{(x_i,x_j)}}+\sum_{k\in{N(j)\backslash{i}}}\log{m^{max}_{kj}{(x_j)}} }[/math]
In many cases we want to use the log of this expression because the numbers tend to be very high. Also, it is important to note that this also works in the continuous case where we replace the summation sign with an integral.
Parameter Learning
Oct .11.2011
The goal of graphical models is to build a useful representation of the input data to understand and design learning algorithm. Thereby, graphical model provide a representation of joint probability distribution over nodes (random variables). One of the most important features of a graphical model is representing the conditional independence between the graph nodes. This is achieved using local functions which are gathered to compose factorizations. Such factorizations, in turn, represent the joint probability distributions and hence, the conditional independence lying in such distributions. However that doesn’t mean the graphical model represent all the necessary independence assumptions.
Basic Statistical Problems
In statistics there are a number of different 'standard' problems that always appear in one form or another. They are as follows:
- Regression
- Classification
- Clustering
- Density Estimation
Regression
In regression we have a set of data points [math]\displaystyle{ (x_i, y_i) }[/math] for [math]\displaystyle{ i = 1...n }[/math] and we would like to determine the way that the variables x and y are related. In certain cases such as (Fig.34) we try to fit a line (or other type of function) through the points in such a way that it describes the relationship between the two variables.
Once the relationship has been determined we can give a functional value to the following expression. In this way we can determine the value (or distribution) of y if we have the value for x. [math]\displaystyle{ P(y|x)=\frac{P(y,x)}{P(x)} = \frac{P(y,x)}{\int_{y}{P(y,x)dy}} }[/math]
Classification
In classification we also have a set of data points which each contain set features [math]\displaystyle{ (x_1, x_2,.. ,x_i) }[/math] for [math]\displaystyle{ i = 1...n }[/math] and we would like to assign the data points into one of a given number of classes y. Consider the example in (Fig.35) where two sets of features have been divided into the set + and - by a line. The purpose of classification is to find this line and then place any new points into one group or the other.
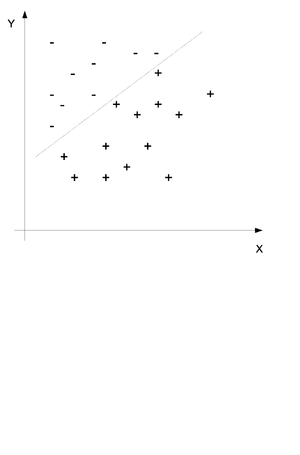
We would like to obtain the probability distribution of the following equation where c is the class and x and y are the data points. In simple terms we would like to find the probability that this point is in class c when we know that the values of x and Y are x and y.
Clustering
Clustering is unsupervised learning method that assign different a set of data point into a group or cluster based on the similarity between the data points. Clustering is somehow like classification only that we do not know the groups before we gather and examine the data. We would like to find the probability distribution of the following equation without knowing the value of c.
Density Estimation
Density Estimation is the problem of modeling a probability density function p(x), given a finite number of data points drawn from that density function.
We can use graphs to represent the four types of statistical problems that have been introduced so far. The first graph (Fig.36(a)) can be used to represent either the Regression or the Classification problem because both the X and the Y variables are known. The second graph (Fig.36(b)) we see that the value of the Y variable is unknown and so we can tell that this graph represents the Clustering and Density Estimation situation.
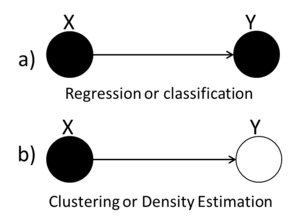
Likelihood Function
Recall that the probability model [math]\displaystyle{ p(x|\theta) }[/math] has the intuitive interpretation of assigning probability to X for each fixed value of [math]\displaystyle{ \theta }[/math]. In the Bayesian approach this intuition is formalized by treating [math]\displaystyle{ p(x|\theta) }[/math] as a conditional probability distribution. In the Frequentist approach, however, we treat [math]\displaystyle{ p(x|\theta) }[/math] as a function of [math]\displaystyle{ \theta }[/math] for fixed x, and refer to [math]\displaystyle{ p(x|\theta) }[/math] as the likelihood function.
where [math]\displaystyle{ p(x|\theta) }[/math] is the likelihood L([math]\displaystyle{ \theta, x }[/math])
where [math]\displaystyle{ log(p(x|\theta)) }[/math] is the log likelihood [math]\displaystyle{ l(\theta, x) }[/math]
Since [math]\displaystyle{ p(x) }[/math] in the denominator of Bayes Rule is independent of [math]\displaystyle{ \theta }[/math] we can consider it as a constant and we can draw the conclusion that:
Symbolically, we can interpret this as follows:
where we see that in the Bayesian approach the likelihood can be viewed as a data-dependent operator that transforms between the prior probability and the posterior probability.
Maximum likelihood
The idea of estimating the maximum is to find the optimum values for the parameters by maximizing a likelihood function form the training data. Suppose in particular that we force the Bayesian to choose a particular value of [math]\displaystyle{ \theta }[/math]; that is, to remove the posterior distribution [math]\displaystyle{ p(\theta|x) }[/math] to a point estimate. Various possibilities present themselves; in particular one could choose the mean of the posterior distribution or perhaps the mode.
(i) the mean of the posterior (expectation):
is called Bayes estimate.
OR
(ii) the mode of posterior:
Note that MAP is Maximum a posterior.
When the prior probabilities, [math]\displaystyle{ p(\theta) }[/math] is taken to be uniform on [math]\displaystyle{ \theta }[/math], the MAP estimate reduces to the maximum likelihood estimate, [math]\displaystyle{ \hat{\theta}_{ML} }[/math].
When the prior is not taken to be uniform, the MAP estimate will be the maximization over probability distributions(the fact that the logarithm is a monotonic function implies that it does not alter the optimizing value).
Thus, one has:
as an alternative expression for the MAP estimate.
Here, [math]\displaystyle{ log (p(x|\theta)) }[/math] is log likelihood and the "penalty" is the additive term [math]\displaystyle{ log(p(\theta)) }[/math]. Penalized log likelihoods are widely used in Frequentist statistics to improve on maximum likelihood estimates in small sample settings.
Example : Bernoulli trials
Consider the simple experiment where a biased coin is tossed four times. Suppose now that we also have some data [math]\displaystyle{ D }[/math]:
e.g. [math]\displaystyle{ D = \left\lbrace h,h,h,t\right\rbrace }[/math]. We want to use this data to estimate [math]\displaystyle{ \theta }[/math]. The probability of observing head is [math]\displaystyle{ p(H)= \theta }[/math] and the probability of observing a tail is [math]\displaystyle{ p(T)= 1-\theta }[/math].
where the conditional probability is
We would now like to use the ML technique.Since all of the variables are iid then there are no dependencies between the variables and so we have no edges from one node to another.
How do we find the joint probability distribution function for these variables? Well since they are all independent we can just multiply the marginal probabilities and we get the joint probability.
This is in fact the likelihood that we want to work with. Now let us try to maximise it:
Take the derivative and set it to zero:
Where:
NH = number of all the observed of heads
NT = number of all the observed tails
Hence, [math]\displaystyle{ NT + NH = n }[/math]
And now we can solve for [math]\displaystyle{ \theta }[/math]:
Example : Multinomial trials
Recall from the previous example that a Bernoulli trial has only two outcomes (e.g. Head/Tail, Failure/Success,…). A Multinomial trial is a multivariate generalization of the Bernoulli trial with K number of possible outcomes, where K > 2. Let [math]\displaystyle{ p(k) = \theta_k }[/math] be the probability of outcome k. All the [math]\displaystyle{ \theta_k }[/math] parameters must be:
[math]\displaystyle{ 0 \leq \theta_k \leq 1 }[/math]
and
[math]\displaystyle{ \sum_k \theta_k = 1 }[/math]
Consider the example of rolling a die M times and recording the number of times each of the six die's faces observed. Let [math]\displaystyle{ N_k }[/math] be the number of times that face k was observed.
Let [math]\displaystyle{ [x^m = k] }[/math] be a binary indicator, such that the whole term would equals one if [math]\displaystyle{ x^m = k }[/math], and zero otherwise. The likelihood function for the Multinomial distribution is:
[math]\displaystyle{ l(\theta; D) = log( p(D|\theta) ) }[/math]
[math]\displaystyle{ = log(\prod_m \theta_{x^m}^{x}) }[/math]
[math]\displaystyle{ = log(\prod_m \theta_{1}^{[x^m = 1]} ... \theta_{k}^{[x^m = k]}) }[/math]
[math]\displaystyle{ = \sum_k log(\theta_k) \sum_m [x^m = k] }[/math]
[math]\displaystyle{ = \sum_k N_k log(\theta_k) }[/math]
Take the derivatives and set it to zero:
[math]\displaystyle{ \frac{\partial l}{\partial\theta_k} = 0 }[/math]
[math]\displaystyle{ \frac{\partial l}{\partial\theta_k} = \frac{N_k}{\theta_k} - M = 0 }[/math]
[math]\displaystyle{ \Rightarrow \theta_k = \frac{N_k}{M} }[/math]
Example: Univariate Normal
Now let us assume that the observed values come from normal distribution.
\includegraphics{images/fig4Feb6.eps}
\newline
Our new model looks like:
Now to find the likelihood we once again multiply the independent marginal probabilities to obtain the joint probability and the likelihood function.
Now, since our parameter theta is in fact a set of two parameters,
we must estimate each of the parameters separately.
Discriminative vs Generative Models
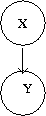
(beginning of Oct. 18)
If we call the evidence/features variable [math]\displaystyle{ X\,\! }[/math] and the output variable [math]\displaystyle{ Y\,\! }[/math], one way to model a classifier is to base the definition of the joint distribution on [math]\displaystyle{ p(X|Y)\,\! }[/math] and another one is to do it based on [math]\displaystyle{ p(Y|X)\,\! }[/math]. The first of this two approaches is called generative, as the second one is called discriminative. The philosophy behind this naming might be clear by looking at the way each conditional probability function tries to present a model. Based on the experience, using generative models (e.g. Bayes Classifier) in many cases leads to taking some assumptions which may not be valid according to the nature of the problem and hence make a model depart from the primary intentions of a design. This may not be the case for discriminative models (e.g. Logistic Regression), as they do not depend on many assumptions besides the given data.
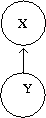
Given [math]\displaystyle{ N }[/math] variables, we have a full joint distribution in a generative model. In this model we can identify the conditional independencies between various random variables. This joint distribution can be factorized into various conditional distributions. One can also define the prior distributions that affect the variables. Here is an example that represents generative model for classification in terms of a directed graphical model shown in Figure 36i. The following have to be estimated to fit the model: conditional probability, i.e. [math]\displaystyle{ P(Y|X) }[/math], marginal and the prior probabilities. Examples that use generative approaches are Hidden Markov models, Markov random fields, etc.
Discriminative approach used in classification is displayed in terms of a graph in Figure 36ii. However, in discriminative models the dependencies between various random variables are not explicitly defined. We need to estimate the conditional probability, i.e. [math]\displaystyle{ P(X|Y) }[/math]. Examples that use discriminative approach are neural networks, logistic regression, etc.
Sometimes, it becomes very hard to compute [math]\displaystyle{ P(X|Y) }[/math] if [math]\displaystyle{ X }[/math] is of higher dimensional (like data from images). Hence, we tend to omit the intermediate step and calculate directly. In higher dimensions, we assume that they are independent to that it does not over fit.
Markov Models
Markov models, introduced by Andrey (Andrei) Andreyevich Markov as a way of modeling Russian poetry, are known as a good way of modeling those processes which progress over time or space. Basically, a Markov model can be formulated as follows:
And the joint distribution of t observations of Markov model is: [math]\displaystyle{ P(y_1,y_2,....y_T)=P(y_1,y_2,....y_k)\prod^t_{t=k+1} P(y_t,y_{t-1},....y_{t-k}) }[/math]
Which can be interpreted by the dependence of the current state of a variable on its last [math]\displaystyle{ k }[/math] states. (Fig. 37)
Maximum Entropy Markov model is a type of Markov model, which makes the current state of a variable dependant on some global variables, besides the local dependencies. As an example, we can define the sequence of words in a context as a local variable, as the appearance of each word depends mostly on the words that have come before (n-grams). However, the role of POS (part of speech tagging) can not be denied, as it affect the sequence of words very clearly. In this example, POS are global dependencies, whereas last words in a row are those of local.
Markov Chain
"The simplest Markov model is the Markov chain. It models the state of a system with a random variable that changes through time. In this context, the Markov property suggests that the distribution for this variable depends only on the distribution of the previous state." <ref>[4]</ref> It is worth to note that alternatively Markov property can be explained as:"Given the current state the previous and future states are independent.".

An example of a Markov model of oder 1 is displayed in Figure 37. Most common example is in the study of gene analysis or gene sequencing, and the joint probability is given by
A Markov model of order 2 is displayed in Figure 38. Joint probability is given by
Hidden Markov Models (HMM)
Markov models fail to address a scenario, in which, a series of states cannot be observed except they are probabilistic function of those hidden states. Markov models are extended in these scenarios where observation is a probability function of state. An example of a HMM is the formation of DNA sequence. There is a hidden process that generates amino acids depending on some probabilities to determine an exact sequence. Main questions that can be answered with HMM are the following:
- How can one estimate the probability of occurrence of an observation sequence?
- How can we choose the state sequence such that the joint probability of the observation sequence is maximized?
- How can we describe an observation sequence through the model parameters?
A Hidden Markov Model (HMM) is a directed graphical model with two layers of nodes. The hidden layer of nodes represents a set of unobserved discrete random variables with some state space as the support. Isolated the first layer represents as a discrete time Markov Chain. These random variables are sequentially connected and which can often represent a temporal dependancy. In this model we do not observe the states (nodes in layer 1) we instead observe features that may be dependant on the states; this set of features represents the second observed layer of nodes. Thus for each node in layer 1 we have a corresponding dependant node in layer 2 which represents the observed features. Please see the Figure 39 for a visual depiction of the graphical structure.
In other words, in HMM, it's guaranteed that, given the present state, the future state is independent of the past. The future state depends only on the present state.
The nodes in the first and second layers are denoted by [math]\displaystyle{ {q_0, q_1, ... , q_T} }[/math] (which are always discrete) and [math]\displaystyle{ {y_0, y_1, ... , y_T} }[/math] (which can be discrete or continuous) respectively. The [math]\displaystyle{ y_i }[/math]s are shaded because they are observed.
The parameters that need to be estimated are [math]\displaystyle{ \theta = (\pi, A, \eta) }[/math]. Where [math]\displaystyle{ \pi }[/math] represents the initial states distributions, i.e [math]\displaystyle{ P(q_0) }[/math]. In general [math]\displaystyle{ \pi_i }[/math] represents the state that [math]\displaystyle{ q_i }[/math] is in. The matrix [math]\displaystyle{ A }[/math] is the transition matrix for the states [math]\displaystyle{ q_t }[/math] and [math]\displaystyle{ q_{t+1} }[/math] and shows the probability of changing states as we move from one step to the next. Finally, [math]\displaystyle{ \eta }[/math] represents the parameter that decides the probability that [math]\displaystyle{ y_i }[/math] will produce [math]\displaystyle{ y^* }[/math] given that [math]\displaystyle{ q_i }[/math] is in state [math]\displaystyle{ q^* }[/math].
Defining some notation:
Note that we will be using a homogeneous descrete time Markov Chain with finite state space for the first layer.
[math]\displaystyle{ \ q_t^j = \begin{cases} 1 & \text{if } q_t = j \\ 0 & \text{otherwise } \end{cases} }[/math]
[math]\displaystyle{ \pi_i = P(q_0 = i) = P(q_0^i = 1) }[/math]
[math]\displaystyle{ a_{ij} = P(q_{t+1} = j | q_t = i) = P(q_{t+1}^j = 1 | q_t^i = 1) }[/math]
For the HMM our data comes from the output layer:
We can use [math]\displaystyle{ a_{ij} }[/math] to represent the i,j entry in the transition matrix A. We can then define:
We can also define:
Now, if we take Y to be multinomial we get:
where [math]\displaystyle{ n_{ij} = P(y_{t+1} = j | q_t = i) = P(y_{t+1}^j = 1 | q_t^i = 1) }[/math]
The random variable Y does not have to be multinomial, this is just an example.
We can write the joint pdf using the structure of the HMM model graphical structure.
Substituting our representations for the 3 probabilities:
We can go on to the E-Step with this new joint pdf. In the E-Step we need to find the expectation of the missing data given the observed data and the initial values of the parameters. Suppose that we only sample once so [math]\displaystyle{ n=1 }[/math]. Take the log of our pdf and we get:
Then we take the expectation for the E-Step:
If we continue with our multinomial example then we would get:
So now we need to calculate [math]\displaystyle{ E[q_0^i] }[/math] and [math]\displaystyle{ E[q_i^t q_j^{t+1}] }[/math] in order to find the expectation of the log likelihood. Let's define some variables to represent each of these quantities.
Let [math]\displaystyle{ \gamma_0^i = E[q_0^i] = P(q_0^i=1|y, \theta^{(t)}) }[/math].
Let [math]\displaystyle{ \xi_{t,t+1}^{ij} = E[q_i^t q_j^{t+1}] = P(q_t^iq_{t+1}^j|y, \theta^{(t)}) }[/math] .
We could use the sum product algorithm to calculate these equations but in this case we will introduce a new algorithm that is called the [math]\displaystyle{ \alpha }[/math] - [math]\displaystyle{ \beta }[/math] Algorithm.
The [math]\displaystyle{ \alpha }[/math] - [math]\displaystyle{ \beta }[/math] Algorithm
We have from before the expectation:
As usual we take the derivative with respect to [math]\displaystyle{ \theta }[/math] and then we set that equal to zero and solve. We obtain the following results (You can check these...) . Note that for [math]\displaystyle{ \eta }[/math] we are using a specific [math]\displaystyle{ y* }[/math] that is given.
For [math]\displaystyle{ \eta }[/math] we can think of this intuitively. It represents the proportion of times that state i prodices [math]\displaystyle{ y^* }[/math]. For example we can think of the multinomial case for y where:
Notice here that all of these parameters have been solved in terms of [math]\displaystyle{ \gamma_t^i }[/math] and [math]\displaystyle{ \xi_{t,t+1}^{ij} }[/math]. If we were to be able to calculate those two parameters then we could calculate everything in this model. This is where the [math]\displaystyle{ \alpha }[/math] - [math]\displaystyle{ \beta }[/math] Algorithm comes in.
Now due to the Markovian Memoryless property.
Define [math]\displaystyle{ \alpha }[/math] and [math]\displaystyle{ \beta }[/math] as follows:
Once we have [math]\displaystyle{ \alpha }[/math] and [math]\displaystyle{ \beta }[/math] then computing [math]\displaystyle{ P(y) }[/math] is easy.
To calculate [math]\displaystyle{ \alpha }[/math] and [math]\displaystyle{ \beta }[/math] themselves we can use:
For [math]\displaystyle{ \alpha }[/math]:
Where we begin with:
Then for [math]\displaystyle{ \beta }[/math]:
Where we now begin from the other end:
Once both [math]\displaystyle{ \alpha }[/math] and [math]\displaystyle{ \beta }[/math] have been calculated we can use them to find:
In order to find the hidden state given the observations, if we are conditioning over the state [math]\displaystyle{ q_t }[/math] using Bayes rule we have:
[math]\displaystyle{ p(q_t|y)= \frac{p(y|q_t)p(q_t)}{p(y)} }[/math]
[math]\displaystyle{ p(q_t|y)=\frac{p(y_0 y_1,... y_t|q_t) p(y_{t+1} ... y_t|q_t) p(q_t)}{p(y)} }[/math]
[math]\displaystyle{ p(q_t|y)=\frac{p(y_0 y_1 ... y_t,q_t) p(y_{t+1} ... y_t|q_t) p(q_t)}{p(y)} }[/math]
We represent [math]\displaystyle{ p(y_0 y_1 ... y_t,q_t) }[/math] as [math]\displaystyle{ \alpha(q_t) }[/math] and [math]\displaystyle{ p(y_{t+1} ... y_t|q_t) }[/math] as [math]\displaystyle{ \beta(q_t) }[/math]
[math]\displaystyle{ \alpha(q_t) }[/math] and [math]\displaystyle{ \beta(q_t) }[/math] are independent and they can be computed recursively. Forward recursive manner in [math]\displaystyle{ \alpha(q_t) }[/math] and backward recursive manner in [math]\displaystyle{ \beta(q_t) }[/math] to reduce the computational complexity to O(M2T) in alpha recursion .
Where [math]\displaystyle{ \alpha(q_t) }[/math] represents: what is the chance of hearing a sequence like [math]\displaystyle{ y_0 y_1 ... y_t }[/math] and being in state [math]\displaystyle{ q_t }[/math]
and
[math]\displaystyle{ \beta(q_t) }[/math] represents: Given in state [math]\displaystyle{ q_t }[/math], what is the chance of hearing the specific sequence.
The following two equations represent the relationship between [math]\displaystyle{ \alpha(q_t) }[/math] with [math]\displaystyle{ \alpha(q_{t+1}) }[/math] and [math]\displaystyle{ \beta(q_t) }[/math] with [math]\displaystyle{ \beta(q_{t+1}) }[/math]
[math]\displaystyle{ \alpha(q_{t+1})=\sum_{q_{t}}\alpha(q_t) a_{q_t} , q_{t+1} p (y_{t+1}|q_{t+1}) }[/math]
[math]\displaystyle{ \beta(q_t)=\sum_{q_{t+1}} \beta (q_{t+1}) a_{q_t} , q_{t+1} p(y_{t+1}|q_{t+1}) }[/math]
HMM's are widely used in speech recognition applications as their temporal nature is ideal for such applications.
Graph Structure
Up to this point, we have covered many topics about graphical models, assuming that the graph structure is given. However, finding an optimal structure for a graphical model is a challenging problem all by itself. In this section, we assume that the graphical model that we are looking for is expressible in a form of tree. And to remind ourselves of the concept of tree, an undirected graph will be a tree, if there is one and only one path between each pair of nodes. For the case of directed graphs, however, on top of the mentioned condition, we also need to check if all the nodes have at most one parent - which is in other words no explaining away kinds of structures.
Firstly, let us show you how it does not affect the joint distribution function, if a graph is directed or undirected, as long as it is tree. Here is how one can write down the joint ditribution of the graph of Fig. XX.
Now, if we change the direction of the connecting edge between [math]\displaystyle{ x_1 }[/math] and [math]\displaystyle{ x_2 }[/math], we will have the graph of Fig. XX and the corresponding joint distribution function will change as follows:
which can be simply re-written as:
which is the same as the first function. We will depend on this very simplistic observation and leave the proof to the enthusiast reader.
Maximum Likelihood Tree
We want to compute the tree that maximizes the likelihood for a given set of data. Optimality of a tree structure can be discussed in terms of likelihood of the set of variables. By doing so, we can define a fully connected, weighted graph by setting the edge weights to the likelihood of the occurrence of the connecting nodes/random variables and then by running the maximum weight spanning tree. Here is how it works.
We have defined the joint distribution as follows:
Where [math]\displaystyle{ V }[/math] and [math]\displaystyle{ E }[/math] are respectively the sets of vertices and edges of the corresponding graph. This holds as long as the tree structure for the graphical model is concerned, as the dependence of [math]\displaystyle{ x_i }[/math] on [math]\displaystyle{ x_j }[/math] has been chosen arbitrarily and this is not the case for non-tree graphical models.
Maximizing the joint probability distribution over the given set of data samples [math]\displaystyle{ X }[/math] with the objective of parameter estimation we will have (MLE):
And by taking the logarithm of [math]\displaystyle{ L(\theta|X) }[/math] (log-likelihood), we will get:
The first term in the above equation does not convey anything about the topology or the structure of the tree as it is defined over single nodes. As much as the optimization of the tree structure is concerned, the probability of the single nodes may not play any role in the optimization, so we can define the cost function for our optimization problem as such:
Where the sub r is for reduced. By replacing the probability functions with the frequency of occurence of each state, we will have:
Where we have assumed that [math]\displaystyle{ p(x_i,x_j)=\frac{N_{ijst}}{N} }[/math], [math]\displaystyle{ p(x_i)=\frac{N_{is}}{N} }[/math], and [math]\displaystyle{ p(x_j)=\frac{N_{jt}}{N} }[/math]. The resulting statement is the definition of the mutual information of the two random variables [math]\displaystyle{ x_i }[/math] and [math]\displaystyle{ x_j }[/math], where the former is in state [math]\displaystyle{ s }[/math] and the latter in [math]\displaystyle{ t }[/math].
This is how it has been figured out how to define weights for the edges of a fully connected graph. Now, it is required to run the maximum weight spanning tree on the resulting graph to find the optimal structure for the tree. It is important to note that before developing graphical models this problem has been solved in graph theory. Here our problem was completely a probabilistic problem but using graphical models we could find an equivalent graph theory problem. This show how graphical models can help us to use powerful graph theory tools to solve probabilistic problems.
Latent Variable Models
(beginning of Oct. 20)
Learning refers to either estimating the parameters or the structures of the models, which can be in four forms: known structure and fully observed variables, known structure and partially observed variables, unknown structure and fully observed variables, and unknown structure and partially observed variables.
Assuming that we have thoroughly observed, or even identified all of the random variables of a model can be a very naive assumption, as one can think of many instances of contrary cases. To make a model as rich as possible -there is always a trade-off between richness and complexity, so we do not like to inject unnecessary complexity to our model either- the concept of latent variables has been introduced to the graphical models.
First let's define latent variables. "Latent variables are variables that are not directly observed but are rather inferred (through a mathematical model) from other variables that are observed (directly measured). Mathematical models that aim to explain observed variables in terms of latent variables are called latent variable models."<ref>[5]</ref>
Depending on the position of an unobserved variable, [math]\displaystyle{ z }[/math], we take different actions. If there is no variable conditioned on [math]\displaystyle{ z }[/math], we can integrate/sum it out and it will never be noticed, as it is not either an evidence or a querey. However, we will require to model an unobserved variable like [math]\displaystyle{ z }[/math], if it is bound to some conditions.
The use of latent variables makes a model harder to analyze and to learn. The use of log-likelihood used to make the target function easier to obtain, as the log of product will change to sum of logs, but this will not be the case, when one introduces latent variables to a model, as the resulting joint probability function comes with a sum, which makes the effect of log on product impossible.
As an example of latent variables, one can think of a mixture density model. There are different models come together to build the final model, but it takes one more random variable to say which one of those models to use at the presence of each new sample point. This will affect both the learning and recalling phases.
EM Algorithm
Oct. 25th
Introduction
In last section the graphical models with latent variables were discussed. It was mentioned that, for example, if fitting typical distributions on a data set is too complex, one may think of modeling the data set using a mixture of famous distribution such as Gaussian. Therefore, a hidden variable is needed to determine weight of each Gaussian model. Parameter learning in graphical models with latent variables is more complicated in comparison with the models with no latent variable.\\
Consider Fig.40 which depicts a simple graphical model with two nodes. As the convention, unobserved variable [math]\displaystyle{ Z }[/math] is unshaded. To compare complexity between fully observed models and the models with hidden variables, lets suppose variables [math]\displaystyle{ Z }[/math] and [math]\displaystyle{ X }[/math] are both observed. We may like to interpret this problem as a classification problem where [math]\displaystyle{ Z }[/math] is class label and [math]\displaystyle{ X }[/math] is the data set. In addition, we assume the distribution over members of each group is Gaussian. Thus, the learning process is to determine label [math]\displaystyle{ Z }[/math] out of the training set by maximizing the posterior:
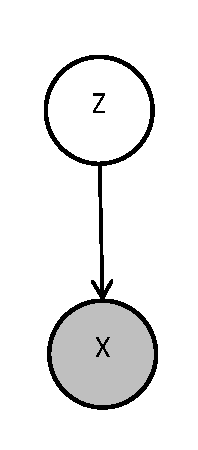
For simplicity, we assume there are two classes generating the data set [math]\displaystyle{ X }[/math], [math]\displaystyle{ Z = 1 }[/math] and [math]\displaystyle{ Z = 0 }[/math]. The posterior [math]\displaystyle{ P(z=1|x) }[/math] can be easily computed using:
On the contrary, if [math]\displaystyle{ Z }[/math] is unknown we are not able to easily write the posterior and consequently parameter estimation is more difficult. In the case of graphical models with latent variables, we first assume the latent variable is somehow known, and thus writing the posterior becomes easy. Then, we are going to make the estimation of [math]\displaystyle{ Z }[/math] more accurate. For instance, if the task is to fit a set of data derived from unknown sources with mixtures of Gaussian distribution, we may assume the data is derived from two sources whose distributions are Gaussian. The first estimation might not be accurate, yet we introduce an algorithm by which the estimation is becoming more accurate using an iterative approach. In this section we see how the parameter learning for these graphical models is performed using EM algorithm.
EM Method
EM (Expectation-Maximization) algorithm is "an iterative method for finding maximum likelihood or maximum a posterior (MAP) estimates of parameters in statistical models, where the model depends on unobserved latent variables."<ref name="Em">[6]</ref>
There are two applications of the EM algorithm. The first is when the data has missing variables. The second occurs when obtaining the maximum likelihood estimate is very complicated and hence introducing a new variable while assuming that its value is unknown (hidden) considerably simplifies computations.<ref>Jeff A. Bilmes, "A Gentle Tutorial of the EM Algorithm and its Application to Parameter Estimation for Gaussian Mixture and Hidden Markov Models", 1998</ref>
"The EM iteration alternates between performing an expectation (E) step, which computes the expectation of the log-likelihood evaluated using the current estimate for the parameters, and a maximization (M) step, which computes parameters maximizing the expected log-likelihood found on the E step. These parameter-estimates are then used to determine the distribution of the latent variables in the next E step."<ref name="Em"/> Consider a probabilistic model in which we collectively denote all of the observed variables by X and all of the hidden variables by Z resulting in a simple graphical model with two nodes (Fig. 40). The joint distribution [math]\displaystyle{ p(X,Z|θ) }[/math] is governed by a set of parameters,θ. The task is to maximize the likelihood function that is given by:
which is called "complete log likelihood". In the above equation the x values represent data as before and the Z values represent missing data (sometimes called latent data) at that point. Now the question here is how do we calculate the values of the parameters [math]\displaystyle{ \theta_i }[/math] if we do not have all the data we need. We can use the Expectation Maximization (or EM) Algorithm to estimate the parameters for the model even though we do not have a complete data set.
To simplify the problem we define the following type of likelihood:
which is called "incomplete log likelihood". We can rewrite the incomplete likelihood in terms of the complete likelihood. This equation is in fact the discrete case but to convert to the continuous case all we have to do is turn the summation into an integral.
Since the z has not been observed that means that [math]\displaystyle{ l_c }[/math] is in fact a random quantity. In that case we can define the expectation of [math]\displaystyle{ l_c }[/math] in terms of some arbitrary density function [math]\displaystyle{ q(z|x) }[/math].
Jensen's Inequality
In order to properly derive the formula for the EM algorithm we need to first introduce the following theorem.
For any concave function f:
This can be shown intuitively through a graph. In the (Fig. 41) point A is the point on the function f and point B is the value represented by the right side of the inequality. On the graph one can see why point A will be smaller than point B in a convex graph.
For us it is important that the log function is concave , and thus:
The function [math]\displaystyle{ F (\theta, q) }[/math] is called the auxiliary function and it is used in the EM algorithm. As seen in above equation [math]\displaystyle{ F(\theta, q) }[/math] is the lower bound of the incomplete log likelihood and one way to maximize the incomplete likelihood is to increase its lower bound. For the EM algorithm we have two steps repeating one after the other to give better estimation for [math]\displaystyle{ q(z|x) }[/math] and [math]\displaystyle{ \theta }[/math]. As the steps are repeated the parameters converge to a local maximum in the likelihood function.
In the first step we assume [math]\displaystyle{ \theta }[/math] is known and then the goal is to find [math]\displaystyle{ q }[/math] to maximize the lower bound. Second, suppose [math]\displaystyle{ q }[/math] is known and find the [math]\displaystyle{ \theta }[/math]. In other words:
E-Step
M-Step
M-Step Explanation
Since the second part of the equation is only a constant with respect to [math]\displaystyle{ \theta }[/math], in the M-step we only need to maximize the expectation of the COMPLETE likelihood. The complete likelihood is the only part that still depends on [math]\displaystyle{ \theta }[/math].
E-Step Explanation
In this step we are trying to find an estimate for [math]\displaystyle{ q(z|x) }[/math]. To do this we have to maximize [math]\displaystyle{ F(q;\theta^{(t)}) }[/math].
Claim: It can be shown that to maximize the auxiliary function one should set [math]\displaystyle{ q(z|x) }[/math] to [math]\displaystyle{ p(z|x,\theta^{(t)}) }[/math]. Replacing [math]\displaystyle{ q(z|x) }[/math] with [math]\displaystyle{ P(z|x,\theta^{(t)}) }[/math] results in:
Recall that [math]\displaystyle{ F(q;\theta^{(t)}) }[/math] is the lower bound of [math]\displaystyle{ l(\theta, x) }[/math] determines that [math]\displaystyle{ P(z|x,\theta^{(t)}) }[/math] is in fact the maximum for [math]\displaystyle{ F(q;\theta) }[/math]. Therefore we only need to do the E-Step once and then use the result for each iteration of the M-Step.
The EM algorithm is a two-stage iterative optimization technique for finding maximum likelihood solutions. Suppose that the current value of the parameter vector is [math]\displaystyle{ \theta^t }[/math]. In the E step, the lower bound [math]\displaystyle{ F(q, \theta^t) }[/math] is maximized with respect to [math]\displaystyle{ q(z|x) }[/math] while [math]\displaystyle{ \theta^t }[/math] is fixed. As was mentioned above the solution to this maximization problem is to set the [math]\displaystyle{ q(z|x) }[/math] to [math]\displaystyle{ p(z|x,\theta^t) }[/math] since the value of incomplete likelihood,[math]\displaystyle{ log p(X|\theta^t) }[/math] does not depend on [math]\displaystyle{ q(z|x) }[/math] and so the largest value of [math]\displaystyle{ F(q, \theta^t) }[/math] will be achieved using this parameter. In this case the lower bound will equal the incomplete log likelihood.
Alternative steps for the EM algorithms
From the above results we can find an alternative representation for the EM algorithm reproducing it to:
E-Step
Find [math]\displaystyle{ E[l_c(\theta; x, z)]_{P(z|x, \theta)} }[/math] only once.
M-Step
Maximise [math]\displaystyle{ E[l_c(\theta; x, z)]_{P(z|x, \theta)} }[/math] with respect to [math]\displaystyle{ theta }[/math].
The EM Algorithm is probably best understood through examples.
EM Algorithm Example
Suppose we have the two independent and identically distributed random variables:
In our case [math]\displaystyle{ y_1 = 5 }[/math] has been observed but [math]\displaystyle{ y_2 = ? }[/math] has not. Our task is to find an estimate for [math]\displaystyle{ \theta }[/math]. We will try to solve the problem first without the EM algorithm. Luckily this problem is simple enough to be solveable without the need for EM.
We take our derivative:
And now we can try the same problem with the EM Algorithm.
E-Step
M-Step
Now we pick an initial value for [math]\displaystyle{ \theta }[/math]. Usually we want to pick something reasonable. In this case it does not matter that much and we can pick [math]\displaystyle{ \theta = 10 }[/math]. Now we repeat the M-Step until the value converges.
And as we can see after a number of steps the value converges to the correct answer of 0.2. In the next section we will discuss a more complex model where it would be difficult to solve the problem without the EM Algorithm.
Mixture Models
Mixture models is a statistical model that has different sub-population within the overall population which use to compute the probability distribution in clustering. In this section we discuss what will happen if the random variables are not identically distributed. The data will now sometimes be sampled from one distribution and sometimes from another.
Mixture of Gaussian
In Gaussian mixture model the probability distribution function is computed by summing all the component of Gaussian mixtures.
Given [math]\displaystyle{ P(x|\theta) = \alpha N(x;\mu_1,\sigma_1) + (1-\alpha)N(x;\mu_2,\sigma_2) }[/math]. We sample the data, [math]\displaystyle{ Data = \{x_1,x_2...x_n\} }[/math] and we know that [math]\displaystyle{ x_1,x_2...x_n }[/math] are iid. from [math]\displaystyle{ P(x|\theta) }[/math].
We would like to compute the variance[math]\displaystyle{ \sigma_i }[/math] and the mean[math]\displaystyle{ \mu_i }[/math] of each distribution :
We have no missing data here so we can try to find the parameter estimates using the ML method.
And then we need to take the log to find [math]\displaystyle{ l(\theta, Data) }[/math] and then we take the derivative for each parameter and then we set that derivative equal to zero. That sounds like a lot of work because the Gaussian is not a nice distribution to work with and we do have 5 parameters.
It is actually easier to apply the EM algorithm. The only thing is that the EM algorithm works with missing data and here we have all of our data. The solution is to introduce a latent variable z. We are basically introducing missing data to make the calculation easier to compute.
Now we have a dataset that includes our latent variables [math]\displaystyle{ z_i }[/math]:
We can calculate the joint pdf by:
Let, [math]\displaystyle{ P(x_i|z_i,\theta)= }[/math]
[math]\displaystyle{ \phi_1(x_i)=N(x;\mu_1,\sigma_1) }[/math] & if & [math]\displaystyle{ z_i = 1 }[/math]
[math]\displaystyle{ \phi_2(x_i)=N(x;\mu_2,\sigma_2) }[/math] & if & [math]\displaystyle{ z_i = 0 }[/math]
Now we can write
and
We can write the joint pdf as:
From the joint pdf we can get the likelihood function as:
Then take the log and find the log likelihood:
In the E-step we need to find the expectation of [math]\displaystyle{ l_c }[/math]
For now we can assume that [math]\displaystyle{ \lt z_i\gt }[/math] is known and assign it a value, let [math]\displaystyle{ \lt z_i\gt =w_i }[/math]
In M-step, we have to update our data by assuming the expectation is fixed
Taking partial derivatives of the complete log likelihood with respect to the parameters and set them equal to zero, we get our estimated parameters at (t+1).
We can verify that the results of the estimated parameters all make sense by considering what we know about the ML estimates from the standard Gaussian. But we are not done yet. We still need to compute [math]\displaystyle{ \lt z_i\gt =w_i }[/math] in the E-step.
We can now combine the two steps and we get the expectation
Using the above results for the estimated parameters in the M-step we can evaluate the parameters at (t+2),(t+3)...until they converge and we get our estimated value for each of the parameters.
The mixture model can be summarized as:
- In each step, a state will be selected according to [math]\displaystyle{ p(z) }[/math].
- Given a state, a data vector is drawn from [math]\displaystyle{ p(x|z) }[/math].
- The value of each state is independent from the previous state.
A good example of a mixture model can be seen in this example with two coins. Assume that there are two different coins that are not fair. Suppose that the probabilities for each coin are as shown in the table.
\begin{tabular}{|c|c|c|}
\hline & H & T
coin1 & 0.3 & 0.7
coin2 & 0.1 & 0.9
\hline
\end{tabular}
We can choose one coin at random and toss it in the air to see the outcome. Then we place the con back in the pocket with the other one and once again select one coin at random to toss. The resulting outcome of: HHTH \dots HTTHT is a mixture model. In this model the probability depends on which coin was used to make the toss and the probability with which we select each coin. For example, if we were to select coin1 most of the time then we would see more Heads than if we were to choose coin2 most of the time.
Alternative Algorithms
There has been different algorithms proposed, besides the EM algorithm, which try to fulfill the same objective as EM algorithm does. The objective is to make an inference, based on the given joint distribution. It involves approximating marginal distribution of a subset of variables, where there might exist a number of latent variable. One of those algorithms which is a deterministic algorithm just like EM, is variational Bayesian method. This algorithm can be seen as a variety of EM algorithm, which applies to the maximum a posterior (MAP), instead of class-conditional. <ref>[7]</ref>
Another approach which is, unlike the two previous ones, a randomized algorithm is the Gibbs Sampling algorithm. The basic idea behind this algorithm is that it can be more convenient to start generating samples of a distribution in order to find a marginal distribution, rather than getting involved in some troublesome optimization problems. The random nature of this algorithms leads to different answers each time that one runs the algorithm, given the same problem and the same initial solution. Gibbs sampling can be thought of as a special case of Markov Chain Monte Carlo algorithm.<ref>[8]</ref>
Conditional random fields
(Nov 3rd lecture)
Motivation
Hidden Markov models (HMMs) are widely used in computation biology to analyze genome sequences. These models are described by a joint probability distribution to the observed and label sequences. The joint distribution should be defined over all possible observation sequences; which is a complex process in many applications. This lead to the introduction of conditional random fields (CRF), which is a statistical framework used to build various probabilistic models to analyze gene sequence data. One of the main advantages over HMM's is to relax the conditions on independencies over several random variables. For a given observed sequence, CRF's estimates the probabilities for a possible label sequence. and also allows multiple interacting features. "CRF's are usually used for labelling or parsing of sequential data, such as natural language text and are also used in computer vision" <ref>[9]</ref>. Another property of CRF is that they can be used to model non-causal phenomena. HMM assumes causality and thus we have a notion of time in the model. In applications we have signals that does not obey causality. Image are one important class of such signals. In an image most probably a single pixel has correlation with neighboring pixels but we can't define notion of order and thus causality on this relation. That's why we need concept of the random field rather than simple rv's.
Conditional distribution of CRF
CRF is an undirected graphical model that defines a distribution over labels for a given observation sequence. Let [math]\displaystyle{ G=(V,E) }[/math] be an undirected graph (this is natural since as explained notion of causality is not applied in CDF's), and [math]\displaystyle{ {v_1,...v_n} \in V }[/math] are the nodes of a graph that represent a random variables [math]\displaystyle{ {Y_1,...,Y_n} }[/math] respectively. Suppose X is an observed sequence which is conditioned globally on the graph [math]\displaystyle{ G }[/math].
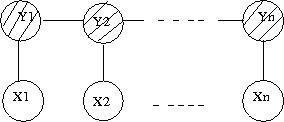
If [math]\displaystyle{ x }[/math] is any realization of the observed sequence and [math]\displaystyle{ {y_1,...,y_n} }[/math] is any realization of the label sequence. So, the joint distribution of the graph is given by [math]\displaystyle{ P(y_1,y_2,...,y_n|x) }[/math]. Then [math]\displaystyle{ (X,Y) }[/math] is called conditional random field if all random variables [math]\displaystyle{ {Y_1,...,Y_n} }[/math] obey Markov property with respect to the graph G, then
where [math]\displaystyle{ w\sim v }[/math] represents that [math]\displaystyle{ w }[/math] and [math]\displaystyle{ v }[/math] are neighbors in the graph.
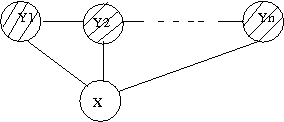
An example is displayed in figure 42, which denotes Markov chain. The graph consists of only random variables [math]\displaystyle{ Y_1,...,Y_n }[/math]. Observe that there is no graphical structure for the random variables [math]\displaystyle{ X_1,...,X_n }[/math], which states that there are no independence assumptions that are made on the radom variable [math]\displaystyle{ X }[/math]. We try to address the probability distribution of [math]\displaystyle{ P(y|x) }[/math]. Figure 43 is an example of a linear chain structured CRF, where [math]\displaystyle{ X={X_1,...,X_n} }[/math] An application of the above example can be taken from computational biology, where the random variables [math]\displaystyle{ Y_1,...,Y_n }[/math] represents a sequence of gene mutations that occur due to various reasons denoted by [math]\displaystyle{ X_1,...,X_n }[/math]. The joint distribution over all the random variables [math]\displaystyle{ Y_1,...,Y_n }[/math] can be factorized using local potential functions. As we know, potential functions are defined on the vertices of the graph that form the maximal clique. From the figure 42, potential functions are defined on [math]\displaystyle{ Y_i }[/math] and [math]\displaystyle{ Y_{i+1} }[/math] ([math]\displaystyle{ 1\leq i\leq n }[/math]). If [math]\displaystyle{ Z }[/math] is normalization factor and [math]\displaystyle{ C }[/math] is the set of all maximal cliques of [math]\displaystyle{ G }[/math]. For a given observable realization [math]\displaystyle{ X }[/math], the joint probability is given by:
Joint distribution can be defined in terms of exponential terms as follows:
Since, it is hard to account for all possible realizations of [math]\displaystyle{ X }[/math], we define conditional distribution of a particular observed sequence on the whole graph [math]\displaystyle{ G }[/math] as:
Notice that the normalization constant [math]\displaystyle{ Z }[/math] is now observable specific. In terms of an exponential function, the conditional distribution is given by
or, it can be rewritten as follows:
In the above equation [math]\displaystyle{ j }[/math] gives the position of the observed sequence. Further simplification can be done by moving the two sums outside the exponential function to obtain,
Replacing the normalization factor with the exponential term, we obtain:
The summation over [math]\displaystyle{ Y }[/math] resembles all the possible label sequences. Main advantages are:
- It is mainly used in classification given by: [math]\displaystyle{ P(class|input) }[/math]
- We don't need to model distribution over inputs.
If [math]\displaystyle{ \psi_{i1}(Y,X) }[/math] depends on at least one variable in X and [math]\displaystyle{ \psi_{i2}(X) }[/math] depends on the evidence [math]\displaystyle{ X }[/math], the conditional distribution can be simplified to the following:
Parameter estimation
Questions that can be posed are the following:
- What is the possible label sequence for a given observation sequence?
- What are the parameters to maximize the conditional distribution?
Let [math]\displaystyle{ D }[/math] be the training data set and we apply the log-likelihood on the D and maximize it as follows:
Notice that log-likelihood function is concave and the parameter [math]\displaystyle{ \lambda }[/math] can be chosen such that, we obtain the global maximum and differentiating the function gives us zero. Then, differentiating the log-likelihood estimation with respect to [math]\displaystyle{ \lambda_i }[/math] we obtain the following:
where, [math]\displaystyle{ \tilde{E}(\psi_i) }[/math] represents the expectation of the empirical distribution of the training data [math]\displaystyle{ D }[/math]; and [math]\displaystyle{ E_{P(Y|x_i,\lambda)}(\psi_i) }[/math] denotes the expectation with respect to the conditional distribution. Most of the times, it is not quite possible to estimate all the parameters analytically such that the derivative is zero, i.e., we do not necessarily obtain a closed form solution. Therefore, some iterative techniques and gradient based methodologies are used to estimate the parameters.
Markov logic networks
A new technique developed by the artificial intelligence community is to combine first order logic with probability theory, called as Markov logic network (MLN). One of the main reasons to arrive at this method is to represent large amounts of data in a compact and precise manner. Markov logic networks generalize first-order logic, in the sense that, in a certain limit, all unsatisfiable statements have a probability of zero, and all tautologies have probability one. First order logic is a set of formulas f, and a weight is attached to each of these formulas w. Each formula is made up of predicates, constants, variables and functions. Predicates are used to represent various relationships between objects in the specified domain. A first order knowledge base (KB) is a set of formulas using first order logic.
A logical knowledge base can only handle hard constraints that covers limited possible worlds. If a world (specific configuration of all the formulas) violated a formula in a logical knowledge base, this world would be considered impossible to occur. Markov logic network, on the other hand, will assign wights [math]\displaystyle{ \, w }[/math] to each formula, such that when a formula being violated in a world, that world wouldn't become impossible, but would become less probable with a probability that is proportional to that weight of the violated formula.
Some of the main applications of Markov logic networks are tasks in statistical relational learning, like collective classification, link prediction, link-based clustering, social network modeling and object identification. <ref>Matthew Richardson, Pedro Domingos, "Markov Logic Networks", Department of Computer Science and Engineering, University of Washington. Available: [10] </ref>
It is quite evident that KB can take only boolean values, which can be thought of a hard constraint. The main purpose of MLN is to soften these constraints. Each formula is given a weight denoting the strength of that constraint in the domain. Hence higher the weight implies that constraint is strong. Markov networks and Bayesian networks can also be represented by MLN. The goal of inference in a Markov logic network is to find the stationary distribution of the system, or one that is close to it
Definition: MLN is a set of pairs [math]\displaystyle{ (F,W) }[/math] where [math]\displaystyle{ F }[/math] denotes formulas in the first order logic and [math]\displaystyle{ W }[/math] is a real number that denotes the weight associated with the formula. Incorporating a set of constraints into MLN turns out to be a Markov network. Each binary node in MLN has grounding for each predicate and has one feature associated for each grounding of [math]\displaystyle{ F_i }[/math] and the corresponding [math]\displaystyle{ W_i }[/math]. Inference in MLNs can be performed using standard Markov network inference techniques over the minimal subset of the relevant Markov network required for answering the query. These techniques include Gibbs sampling, which is effective but may be excessively slow for large networks, belief propagation, or approximation via pseudolikelihood.
One common example is the following:
- Smoking causes cancer
- Friends have similar smoking habits
Step1: We write the above two statements in terms of formulas using logical operators as follows:
- [math]\displaystyle{ \forall x, smokes(x) \implies cancer(x) }[/math]
- [math]\displaystyle{ \forall x,y, Friends(x,y) \implies (smokes(x)\iff smokes(y) }[/math]
Step2: We associate weights to each of the above formulas, say [math]\displaystyle{ W_1=1.75 }[/math] and [math]\displaystyle{ W_2=1.25 }[/math] respectively.
Suppose A and B (represent persons) are any two constants, then the above set of formulas are represented in terms of an Markov ground network as follows:
Each node resembles an ground atom, and an edge between a pair of atoms. Several questions can be answered from the ground network designed in Figure 44 such as: if A is a friend of B and B does not smoke, then What is the probability that A has cancer? MLN are frame works to address Markov networks. Probability distribution of a world is given by:
where, [math]\displaystyle{ n_i(x) }[/math] is the number of true groundings of the formula and [math]\displaystyle{ W_i }[/math] is the weight of formula [math]\displaystyle{ i }[/math].
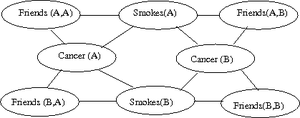
Here is another example:
- Smoking causes cancer
- If there are two friends and one among them has smoking habit, then there is a chance that other friend might also get cancer (assuming the biological system is weak and inhaling might lead to mutations)
The above sentences can be written in terms of formulas as follows:
- [math]\displaystyle{ \forall x, smokes(x) \implies cancer(x) }[/math]
- [math]\displaystyle{ \forall x,y, Friends(x,y) \and smokes(x) \implies cancer(y) }[/math]
Alchemy is an open source AI software, hosted at the department of computer science, university of Washington, which makes use of the Logic Markov Networks. [11]
Kernel Belief Propagation
We have talked about the belief propogation in previous lectures.
In papers <ref name="kdp"> [12] </ref> and <ref> [13] </ref> Song et.al. talk about Kernel Belief Propagation. As we know a lot of linear methods can be used for nonlinear problems using notion of kernel. In most applications the variable space is not linear but it is linear in space of some kernel functions. This is the main reason behind using the notion of kernel but not until recently this notion has been used in BP. The intuition of the two papers on kernelizing BP is as follows:
If we have two different distributions with different means as in Figure 46 , [math]\displaystyle{ \mu }[/math]
is not a good measure to compare the two distributions and higher moments of distributions are needed for comparing the distributions.
It turns out that expectation of some samples of these distributions in a higher dimensional feature space (Hilbert space) is a good measure for characterizing and comparing the distributions (Though it may seem counter-intuition but it can be shown mathematically a general distribution can be shown and recovered uniquely by only one point in a proper Hilbert space):
[math]\displaystyle{ E(\phi(x)) }[/math], where [math]\displaystyle{ \phi(.) }[/math] represents the mapping function to a Hilbert space.
Expectation of the mapped samples points [math]\displaystyle{ \phi(x) }[/math] is then computed as: [math]\displaystyle{ E(\phi(x))\approx \frac{1}{m} \sum^m_{i=1} \phi(x_i) =\mu_x }[/math]
The idea is to represent the distribution with a point in the feature space (expectation of the mapped samples of the distribution)such that the distribution is summarized in this point and the point can be used to recover the distribution. Therefore, there is a one-to-one relation between [math]\displaystyle{ E(\phi(x)) }[/math] and [math]\displaystyle{ dist(x) }[/math]. Hence, distance between two distributions p and q can be computed as the distance between their corresponding expected values in a Hilbert space. One important advantage is that the distance can be calculated based on samples of the distribution and thus is nonparametric and there is no need to know the mathematical form of the distribution. The question is: what is a proper mapping function [math]\displaystyle{ \phi(x) }[/math]? The function [math]\displaystyle{ \phi }[/math] is an injective mapping.. It turns out that we need to only implicitly transfer the sampled point to the Hilbert space, and there is no need to explicitly define the mapping function [math]\displaystyle{ \phi(x) }[/math] and instead the mapping can be done in terms of kernel functions. Suppose, we need to find distance between two distributions p and q:
[math]\displaystyle{ |p-q|^2 }[/math] where [math]\displaystyle{ x \thicksim p }[/math] and [math]\displaystyle{ y \thicksim q }[/math], then [math]\displaystyle{ |E (\phi (x_i))-E (\phi (y_i))|^2 }[/math] gives us the measure of similarity or dissimilarity of the two distributions.
we can expand this and write it in terms of kernels,
[math]\displaystyle{ \begin{matrix} ((E (\phi (x_i))-E (\phi (y_i)))^T(E (\phi (x_i))-E (\phi (y_i)))) &=& [\frac{1}{n}\sum_{i=1}^n \phi(x_i) -\frac{1}{m}\sum_{j=1}^m \phi(y_j)]^T [\frac{1}{n}\sum_{i=1}^n \phi(x_i) -\frac{1}{m}\sum_{j=1}^m \phi(y_j)]\\[2ex] &=& \frac{1}{n^2} \sum_{ij} k(x_i,x_j)+\frac{1}{m^2} \sum_{ij}k(y_i,y_j) - \sum\frac{2}{nm} k(x_i,y_j) \end{matrix} }[/math]
In addition to distance between the distibutions, we can quantify the independence between two random variables using Hilbert Schmidt Independent Criterion (HSIC) defined as:
[math]\displaystyle{ \begin{align} P_{xy} = P_x * P_y \rightarrow |P_{xy}-P_x * P_y|^2 &\propto (HSIC)\\ & \propto Tr (KHLH) \end{align} }[/math]
Where [math]\displaystyle{ H=(I-\frac{1}{m} e e^T) }[/math] is the constant matrix that centralizes where row mean and column mean are zero; and [math]\displaystyle{ K }[/math] is a kernel over [math]\displaystyle{ x }[/math] and [math]\displaystyle{ L }[/math] is a kernel over [math]\displaystyle{ y }[/math].
The introduced is an empirical measure for HSIC. For a thorough explanation and details of the measure, you can refer to the original work, Measuring Statistical Dependence with Hilbert-Schmidt Norms <ref>[14]</ref>.
If the result is equal to zero then we induce that they are independent, otherwise we can measure their dependency.
If instead of [math]\displaystyle{ p(x) }[/math] we have conditional distribution ([math]\displaystyle{ p(x|y) }[/math]) (or a family of distributions) then how we can project to Hilbert space?
If the distribution is binary it is not hard, we can find expectation for points with [math]\displaystyle{ y=0 }[/math] and then for the ones with [math]\displaystyle{ y=1 }[/math].
What should we do in the case that there is multinomial distribution for [math]\displaystyle{ y }[/math] or if [math]\displaystyle{ y }[/math] is continues:
Please look at the following Example:
We have two distributions which are conditioned on [math]\displaystyle{ y_1 }[/math] and [math]\displaystyle{ y_2 }[/math], respectively as seen in Figure 48. We can map to space [math]\displaystyle{ G }[/math] as can be seen in the figure 47.
If the points that we are conditioning on, are close to each other; we expect points to be similar and so their mapping. Therefore, in the space [math]\displaystyle{ G }[/math] we find the expectation of each point in this space.
The idea is to have a linear transformation that if we apply in space [math]\displaystyle{ G }[/math] then we can get to space [math]\displaystyle{ F }[/math]. Going from space [math]\displaystyle{ G }[/math] to [math]\displaystyle{ F }[/math] is done through a linear transformation.
Suppose [math]\displaystyle{ z }[/math] is a multidimentional Gaussian: [math]\displaystyle{ z=[x,y]^T }[/math]. We can then derive that [math]\displaystyle{ p(y|x) }[/math] is Gaussian as well, defined as follows: [math]\displaystyle{ N (C_{yx} C_{xx}^{-1} x,
C_{yy}-C_{yx} C_{xx}^{-1} C_{xy}) }[/math]
Where [math]\displaystyle{ C_{yx} C_{xx}^{-1} x }[/math] is mean (mean is a linear operator times the point that we conditioned on) and [math]\displaystyle{ C_{yy}-C_{yx} C_{xx}^{-1} C_{xy} }[/math] is covariance.
[math]\displaystyle{ C }[/math] is covariance of [math]\displaystyle{ x }[/math] and [math]\displaystyle{ y }[/math].
Therefore, to be able to obtain this linear transformation, we need to come up with the definition of covariance in Hilbert space. The Covariance of two objects of two Hilbert space:
[math]\displaystyle{ C_{xy} = E_{xy} [\phi(x) \otimes \phi(y)] - E_x [\phi(x)] \otimes E_y [\phi(y)] }[/math]
In other words, We can define KBP intuitively as a transformation that, rather than maps our functions into a linear space, it maps them into a Gaussian space, where it is much easier and straightforward to perform classification or some other task.
"A direct implementation of kernel BP has the following computational cost: each message update costs [math]\displaystyle{ O(m^2d_{max}) }[/math] when computed exactly, whereas [math]\displaystyle{ m }[/math] is the number of training examples and [math]\displaystyle{ d_{max} }[/math] is the maximum degree of a node in the graphical model." <ref name="kbp"/>
As Song et al noted, one of the main differences between Kernel Belief Propagation (KBP) and BP is that it is used also on graphs with loops (not only on trees) and therefore it iterates until convergence is achieved <ref name="kbp"/>. KBP is computationally more complex but the main advantage is that it is nonparametric and doesn't have limitations of BP.
Markov Chain Monte Carlo (MCMC)
Markov chain Monte Carlo (MCMC) methods are a class of algorithms for sampling from probability distributions based on constructing a Markov chain that has the desired distribution as its equilibrium distribution. The state of the chain after a large number of steps is then used as a sample of the desired distribution. The quality of the sample improves as a function of the number of steps. It is very useful when direct sampling of a distribution is not possible but it is possible to sample another distribution. Usually it is not hard to construct a Markov chain with the desired properties. The more difficult problem is to determine how many steps are needed to converge to the stationary distribution within an acceptable error. A good chain will have rapid mixing—the stationary distribution is reached quickly starting from an arbitrary position—described further under Markov chain mixing time. Typical use of MCMC sampling can only approximate the target distribution, as there is always some residual effect of the starting position. More sophisticated MCMC-based algorithms such as coupling from the past can produce exact samples, at the cost of additional computation and an unbounded (though finite in expectation) running time. The most common application of these algorithms is numerically calculating multi-dimensional integrals. In these methods, an ensemble of "walkers" moves around randomly. At each point where the walker steps, the integrand value at that point is counted towards the integral. The walker then may make a number of tentative steps around the area, looking for a place with reasonably high contribution to the integral to move into next. Random walk methods are a kind of random simulation or Monte Carlo method. However, whereas the random samples of the integrand used in a conventional Monte Carlo integration are statistically independent, those used in MCMC are correlated. A Markov chain is constructed in such a way as to have the integrand as its equilibrium distribution. Surprisingly, this is often easy to do. Multi-dimensional integrals often arise in Bayesian statistics, computational physics, computational biology and computational linguistics, so Markov chain Monte Carlo methods are widely used in those fields. Here we try to give a brief review on basic MCMC concepts and few related algorithms.
Markov chain basic concepts
A Markov chain, named after Andrey Markov, is a mathematical system that undergoes transitions from one state to another, between a finite or countable number of possible states. It is a random process characterized as memoryless: the next state depends only on the current state and not on the sequence of events that preceded it. This specific kind of "memorylessness" is called the Markov property. Markov chains have many applications as statistical models of real-world processes. Since it is a random variable depending on a deterministic variable, mathematically is a stochastic process.
Definition 1:Stochastic process: It is a set of random variable defined on an indexed set:
The index set [math]\displaystyle{ \ T }[/math] in general can be discrete or continuous. Here first we assume discrete case first.
Definition 2: Markov Chain (MC): Is a stochastic process for which the distribution of Definition [math]\displaystyle{ \ x_{t-1} }[/math] only depends on [math]\displaystyle{ \ T }[/math] or mathematically:
In terms of graphical model representation it is represents in Fig. 48.

Often, the term "Markov chain" is used to mean a Markov process which has a discrete (finite or countable) state-space. Usually a Markov chain is defined for a discrete set of times (i.e., a discrete-time Markov chain). MC in can be generalized for the cases the current states depends on two or more previous states but always it is casual model. Here we consider the simplest case with memory length of one. MC involves a system which is in a certain state at each step, with the state changing randomly between steps. The steps are often thought of as moments in time, but they can equally well refer to physical distance or any other discrete measurement; formally, the steps are the integers or natural numbers, and the random process is a mapping of these to states. The Markov property states that the conditional probability distribution for the system at the next step (and in fact at all future steps) depends only on the current state of the system, and not additionally on the state of the system at previous steps. Since the system changes randomly, it is generally impossible to predict with certainty the state of a Markov chain at a given point in the future. However, the statistical properties of the system's future can be predicted. In many applications, it is these statistical properties that are important. We assume that the value of states are an ordered subset of natural numbers. The changes of state of the system are called transitions, and the probabilities associated with various state-changes are called transition probabilities. The set of all states and transition probabilities completely characterizes a Markov chain. By convention, we assume all possible states and transitions have been included in the definition of the processes, so there is always a next state and the process goes on forever. These concepts bring the following definitions: Definition 3: Transition Probability: It measure the possibility of going to a state given the current state. Formally:
Definition 4: Transition Matrix: The matrix whose [math]\displaystyle{ \ (i,j) }[/math] elements is [math]\displaystyle{ \ p_{ij} }[/math]. It is obvious that [math]\displaystyle{ \ \sum_i p_{ij}=1 }[/math] since each row corresponds to a pmf.
One important property of MC is Homogeneous property:
It is easy to verify that knowing the initial state and also transition matrix is enough to study the behavior of MC.
Example: One of the famous MC's is Random Walk. The corresponding matrix has the following form:
We can generalize the study of MC and consider the case when we want to go from one state to another in more than one step. Here come the following two extensions for definitions 3,4:
- Let[math]\displaystyle{ \ p_{ij}(n)=P(x_{t+n}=j|x_{t}=i) }[/math]
- Let [math]\displaystyle{ \ P_n }[/math] to be a matrix such that its [math]\displaystyle{ \ (i,j) }[/math] elements is [math]\displaystyle{ \ p_{ij}(n) }[/math]. This is called n-step transition probability matrix. It is easy to show by induction that:
Definition 5: Let [math]\displaystyle{ \ \mu_t=(mu_t(1),...,\mu_t(n)) }[/math] a row vector where [math]\displaystyle{ \ \mu_t(i)=P(x_t=i) }[/math]. This is called marginal probability that chain is in each sate at time t. It shows the possibility of being in each state after running the MC t steps.
Therorem 1: The marginal probability is given by:
Proof is very easy and straight forward using induction.
Steady-state analysis and limiting distributions
It is interesting that under some assumptions Markov chains tends to a stationary situation as time tends to infinity. This property is very important and can be used for our main purpose for sampling.
- Let [math]\displaystyle{ \ \pi=[\pi_i, i\in X] }[/math] be a vector of non-negative numbers that sum to one. (Equivalently it is a PMF)
Definition 6: [math]\displaystyle{ \ \pi }[/math] is stationary distribution (invariant) of a MC if:
This means that we have reached to a condition that possibility of each state occurrence doesn't change with time. Definition 7: Limiting distribution of a chain, A chain has a limiting distribution if
Example: Consider the following transition matrix:
Now Note:
This example shows convergence behavior of this MC and also we can conclude: [math]\displaystyle{ \ \mu=[0.4451 , 0.1737 , 0.3713] }[/math]
This property is not valid for all MC. Consider the following example: Example:
It is easy to check that [math]\displaystyle{ \ \mu=[0.3333 , 0.3333 , 0.3333] }[/math] is stationary distribution of this MC, but the chain doesn't have limiting distribution.
Definition 7: Detailed balance: A chain has detailed balance property if:[math]\displaystyle{ \ \pi_i p_{ij}=p_{ji}\pi_j }[/math] and we say the chain satisfies detailed balance property.
Theorem2: If [math]\displaystyle{ \ \pi }[/math] satisfies detailed balance property then it is stationary distribution. Proof:
Which is the desired result.
Knowing these basic MC definitions and properties we are ready to study some MCMC sampling algorithms.
Metropolis Algorithm
We would like to sample from some [math]\displaystyle{ P(x) }[/math] and this time use the metropolis algorithm, which is a type of MCMC, to do it. In order for this algorithm to work we first need a number of things.
- We need some staring value [math]\displaystyle{ x }[/math]. This value can come from anywhere.
- We need to find a value [math]\displaystyle{ y }[/math] that comes from the function [math]\displaystyle{ T(x, y) }[/math].
- We need the function [math]\displaystyle{ T }[/math] to be symmetrical. [math]\displaystyle{ T(x,y)=T(y,x) }[/math].
- We also need [math]\displaystyle{ T(x,y) = P(y|x) }[/math].
Once we have all of these conditions we can run the algorithm to find our random sample.
- Get a staring value [math]\displaystyle{ x }[/math].
- Find the [math]\displaystyle{ y }[/math] value from the function [math]\displaystyle{ T(x, y) }[/math].
- Accept [math]\displaystyle{ y }[/math] with the probability [math]\displaystyle{ min(\frac{P(x)}{P(y)}, 1) }[/math].
- If the [math]\displaystyle{ y }[/math] is accepted it becomes the new x value.
- After a large number of accepted values the series will converge.
- When the series has converged any new accepted values can be treated as random samples from [math]\displaystyle{ P(x) }[/math].
The point at which the series converges is called the 'burn in point'. We must always burn in a series before we can use it to sample because we have to make sure that the series has converged. The number of values before the burn in point depends on the functions we are using since some converge faster than others.
We want to prove that the Metropolis Algorithm works. How do we know that [math]\displaystyle{ P(x) }[/math] is in fact the equilibrium distribution for this MC? We have a condition called the detailed balance condition that is sufficient but not necessary when we want to prove that [math]\displaystyle{ P(x) }[/math] is the equilibrium distribution.
Theorem 3 If [math]\displaystyle{ P(x)A(x, y) = P(y)A(y,x) }[/math] and [math]\displaystyle{ A(x,y) }[/math] is the transformation matrix for the MC then [math]\displaystyle{ P(x) }[/math] is the equilibrium distribution. This is called the Detailed Balance Condition.
Proof of Sufficiency for Detailed Balance Condition:
Need to show:
We need to show that Metropolis satisfies the detailed balance condition. We can define [math]\displaystyle{ A(x, y) }[/math] as follows:
Then,
Therefore the detailed balance condition holds for the Metropolis Algorithm and we can say that [math]\displaystyle{ P(x) }[/math] is the equilibrium distribution.
Example:
Suppose that we want to sample from a [math]\displaystyle{ Poisson(\lambda) }[/math].
Now define [math]\displaystyle{ T(x,y) : y=x+\epsilon }[/math] where [math]\displaystyle{ P(\epsilon=-1) = 0.5 }[/math] and [math]\displaystyle{ P(\epsilon=1) = 0.5 }[/math]. This type of [math]\displaystyle{ T }[/math] is called a random walk. We can select any [math]\displaystyle{ x^{(0)} }[/math] from the range of x as a starting value. Then we can calculate a y value based on our [math]\displaystyle{ T }[/math] function. We will accept the y value as our new [math]\displaystyle{ x^{(i)} }[/math] with the probability [math]\displaystyle{ min(\frac{P(x)}{P(y)}, 1) }[/math]. Once we have gathered many accepted values, say 10000, and the series has converged we can begin to sample from that point on in the series. That sample is now the random sample from a [math]\displaystyle{ Poisson(\lambda) }[/math].
Metropolis Hastings
As the name suggests the Metropolis Hastings algorithm is related to the Metropolis algorithm. It is a more generalized version of the Metropolis algorithm to sample from F where we no longer require the condition that the function [math]\displaystyle{ T(x, y) }[/math] be symmetric. The algorithm can be outlined as:
- Get a staring value [math]\displaystyle{ x }[/math]. This value can be chosen at random.
- Find the [math]\displaystyle{ y }[/math] value from the function [math]\displaystyle{ T(x, y) }[/math]. Note that [math]\displaystyle{ T(x, y) }[/math] no longer has to be symmetric.
- Accept [math]\displaystyle{ y }[/math] with the probability [math]\displaystyle{ min(\frac{P(y)T(y, x)}{P(x)T(x, y)}, 1) }[/math]. Notice how the acceptance probability now contains the function [math]\displaystyle{ T(x, y) }[/math].
- If the [math]\displaystyle{ y }[/math] is accepted it becomes the new [math]\displaystyle{ x }[/math] value.
- After a large number of accepted values the series will converge.
- When the series has converged any new accepted values can be treated as random samples from [math]\displaystyle{ P(x) }[/math].
To prove that Metropolis Hastings algorithm works we once again need to show that the Detailed Balance Condition holds.
Proof:
If [math]\displaystyle{ T(x, y) = T(y, x) }[/math] then this reduces to the Metropolis algorithm which we have already proven. Otherwise,
Which means that the Detailed Balance Condition holds and therefore [math]\displaystyle{ P(x) }[/math] is the equilibrium.
Metropolis Hastings - Dec. 6th
Metropolis Hastings is an MCMC algorithm that is used for sampling from a given distribution. Metropolis Hastings proceeds as follows:
- Choose an initial point [math]\displaystyle{ X_o }[/math] and set [math]\displaystyle{ i = 0 }[/math]
- Generate [math]\displaystyle{ Y\thicksim q(y|x_i) }[/math]
- Compute [math]\displaystyle{ r(X_i,Y) }[/math] to decide whether to accept the generated Y based on the criterion in step 5.
- Generate [math]\displaystyle{ U \thicksim Unif(0,1) }[/math]
- Accept the generated Y as follows:
- [math]\displaystyle{ i = i + 1 }[/math] and go to step 2.
Repeat the above procedure up to a burning point and consider the points sampled after the burning points. Usually a very large number of iterations are considered before the burning point is reached.
Examples:
consider [math]\displaystyle{ f(x) = \frac{1}{\pi} \frac{1}{1+x^2} }[/math] [math]\displaystyle{ f(x) \propto \frac{1}{1+x^2} }[/math] Let's choose a normal distribution with a mean [math]\displaystyle{ X }[/math] and variance [math]\displaystyle{ b^2 }[/math] to be a proposal distribution representing [math]\displaystyle{ q(y|x) }[/math] [math]\displaystyle{ q(y|x) = N(X,b^2) }[/math] Therefore, [math]\displaystyle{ \frac {q(x|y)}{q(y|x)} = 1 }[/math] and [math]\displaystyle{ \frac{f(y)}{f(x)}\frac{q(x|y)}{q(y|x)} = \frac{1+x^2}{1+y^2}.1 = \frac{1+x^2}{1+y^2} }[/math]
The Matlab code for Metropolis Hastings sampling technique for the given distribution in this example is as follows:
X(1) = randn;
b = 0.1;
for i = 2:10000
Y = b*randn+X(i-1);
r = min((1+X(i-1)^2)/(1+Y^2),1);
U =rand;
if U <= r
X(i) = Y;
else
X(i) = X(i-1);
end
end
% to check the distrubtion of the sampled points
hist(X)
By Proper selection of b we can see that the algorithm works. The following figure depicts histogram of some instances for some values of b.
A close look confirms that for b=0.5 the histogram is very similar to what we expect.
Now we investigate why the above procedure would work?
if a Markov chain satisfied a detailed balance criterion:
[math]\displaystyle{ \pi_i P_{ij} = \pi_j P_{ji} }[/math]
The stationary distribution of the chain will be [math]\displaystyle{ \pi }[/math]. This is true for discrete and continuous case.
In continuous case, the detailed balance is:
[math]\displaystyle{ f(x)P(x \rightarrow y) = f(y) P(y \rightarrow x) }[/math]
Proof: Suppose we have two points[math]\displaystyle{ x }[/math] and [math]\displaystyle{ y }[/math] the quantity [math]\displaystyle{ \frac{f(y)}{f(x)}\frac{q(x|y)}{q(y|x)} }[/math] is eigher [math]\displaystyle{ \lt 1 }[/math] or [math]\displaystyle{ \gt 1 }[/math]
Without the loss of generality, we assume that the above quantity is less than 1.
Therefore,
[math]\displaystyle{ r(x,y) = \frac{f(y)}{f(x)}\frac{q(x|y)}{q(y|x)} }[/math]
and
[math]\displaystyle{ r(y,x) = 1 }[/math]
Compute the probability of transitioning from point x to y: [math]\displaystyle{ P(x \rightarrow y) }[/math]. For this, we need to:
- Generate [math]\displaystyle{ y \thicksim q(y|x) }[/math]
- Accept [math]\displaystyle{ y }[/math] with the probability [math]\displaystyle{ r(x,y) }[/math]. [math]\displaystyle{ r(x,y) }[/math] is the change of accepting [math]\displaystyle{ y }[/math].
Then, we have:
[math]\displaystyle{ P(x \rightarrow y) = q(y|x).r(x,y) f(x)q(y|x)\frac{f(y)}{f(x)}\frac{q(x|y)}{q(y|x)}= f(y).q(x|y) \Rightarrow }[/math]L.H.S of the detailed balance equation
[math]\displaystyle{ f(y)q(x|y)r(y,x) = f(y).q(x|y)\Rightarrow }[/math]R.H.S of the detailed balance equation
[math]\displaystyle{ R.H.S = L.H.S }[/math]; hence the detailed balance is satisfied and the stationary distribution of the chain is [math]\displaystyle{ f(y) }[/math].
Gibbs Sampling
Although Metropolis-Hasting is a general and useful sampling algorithm, the proposal distribution must be tuned in such a way that makes it suite the target distribution well. The proposal distribution should not be too broad or too narrow than the target distribution; otherwise most of the proposed samples will be rejected.
A method called Gibbs sampling was introduced by Geman in 1984 in the context of image processing. This method allows us to generate samples from the full joint distribution given that the full conditional distribution is known. That is, we can generate samples from the joint distribution [math]\displaystyle{ \, P(\theta_1, \theta_2, ..., \theta_n | D) }[/math], using Gibbs sampling, if samples from the conditional distributions [math]\displaystyle{ \, P(\theta_i | \theta_{-i}, D) }[/math] can be generated, where [math]\displaystyle{ \, i \in {1, ...,n} }[/math] and [math]\displaystyle{ \, \theta_{-i} }[/math] are all parameters except parameter number i.
The Gibbs sampling algorithms is as follows:
- set j = 0
- initialize all the random variables [math]\displaystyle{ \, \theta_{i}^{j} }[/math], where [math]\displaystyle{ \, i \in {1,..., n} }[/math]
- Repeat for i from 1 to n:
- j = j + 1
- Generate a sample for [math]\displaystyle{ \, \theta_{i}^{j} }[/math] from [math]\displaystyle{ \, p(\theta_{i}^{j-1}|\theta_{i}) }[/math]
Note that [math]\displaystyle{ \, \theta_{i} }[/math] is always take the last value that was assigned to it. Also note that on the contrary to the Metropolis-Hasting, all the samples are accepted in Gibbs sapling.
Appendix: Graph Drawing Tools
Graphviz
"Graphviz is open source graph visualization software. Graph visualization is a way of representing structural information as diagrams of abstract graphs and networks. It has important applications in networking, bioinformatics, software engineering, database and web design, machine learning, and in visual interfaces for other technical domains." <ref>http://www.graphviz.org/</ref>
There is a wiki extension developed, called Wikitex, which makes it possible to make use of this package in wiki pages. Here is an example.
AISee
AISee is a commercial graph visualization software. The free trial version has almost all the features of the full version except that it should not be used for commercial purposes.
TikZ
"TikZ and PGF are TeX packages for creating graphics programmatically. TikZ is build on top of PGF and allows you to create sophisticated graphics in a rather intuitive and easy manner." <ref> http://www.texample.net/tikz/ </ref>
Xfig
"Xfig" is an open source drawing software used to create objects of various geometry. It can be installed on both windows and unix based machines. Website
References
<references />