stat946F18/Beyond Word Importance Contextual Decomposition to Extract Interactions from LSTMs
Introduction
The main reason behind the recent success of LSTM (Long Short-Term Memory Networks) and deep neural networks, in general, has been their ability to model complex and non-linear interactions. Our inability to fully comprehend these relationships has led to these state-of-the-art models being regarded as black-boxes. The paper "Beyond Word Importance: Contextual Decomposition to Extract Interactions from LSTMs" by W. James Murdoch, Peter J. Liu, and Bin Yu propose an interpretation algorithm called Contextual Decomposition(CD) for analyzing individual predictions made by the LSTMs without any change to the underlying original model. The problem of sentiment analysis is chosen for the evaluation of the model.
Overview of previous work
There has been research towards developing methods to understand the evaluations provided by LSTMs. Some of them are in line with the work done in this particular paper while others have followed some different approaches.
Approaches similar to the one provided in this paper - All of the approaches in this category have tried to look into computing just the word-level importance scores with varying evaluation methods.
- Murdoch & Szlam (2017): introduced a decomposition of the LSTM's output embedding and learned the importance score of certain words and phrases from those words (sum of the importance of words). A classifier is then built that searches for these learned phrases that are important and predicts the associated class which is then compared with the output of the LSTMs for validation.
- Li et al. (2016): (Leave one out) They observed the change in log probability of a function by replacing a word vector (with zero) and studying the change in the prediction of the LSTM. It is completely anecdotal. Additionally provided an RL model to find the minimal set of words that must be erased to change the model's decision (although this is irrelevant to interpretability).
- Sundararajan et al. 2017 (Integrated Gradients): a general gradient based technique to learn importance evaluated theoretically and empirically. Built up as an improvement to methods which were trying to do something quite similar. It is tested on image, text and chemistry models.
Decomposition-based approaches for CNN:
- Bach et al. 2015: proposed a solution to the problem of understanding classification decisions of CNNs by pixel-wise decomposition. Pixel contributions are visualized as heat maps.
- Shrikumar et al. 2016 (DeepLift): an algorithm based on a method similar to backpropagation to learn the importance score for the inputs for a given output. The algorithm to learn these input scores is not dependent on the gradient therefore learning can also happen if the gradient is zero during backpropagation.
Focussing on analyzing the gate activations:
- Karpathy et al. (2015) worked with character generating LSTMs and tried to study activation and firing in certain hidden units for meaningful attributes. For eg. a cell being activated for keeping track of open parathesis or quotes.
- Strobelt et al. 2016: built a visual tool for understanding and analyzing raw gate activations.
Attention-based models:
- Bahdanau et al. (2014): These are a different class of models which use attention modules(different architectures) to help focus the neural network to decide the parts of the input that it should look more closely or give more importance to. But the problem with it is twofold. Firstly, it is only an indirect indicator of importance and does not provide directionality. Secondly, they have not been evaluated empirically or otherwise as an interpretation technique. Although they have been used in multiple other applications and architectures for solving a variety of problems.
Long Short-Term Memory Networks
Over the past few years, LSTM has become a core component of neural NLP systems and sequence modeling systems in general. LSTMs are a special kind of Recurrent Neural Network(RNNs) which in many cases work better than the standard RNN by solving the vanishing gradient problem. To put it simply they are much more efficient in learning long-term dependencies. Like a standard RNN, LSTMs are made up of chains of repeating modules. The difference is that the modules are little more complicated. Instead of having a single tanh layer like in an RNN, they have four (called gates), interacting in a special way. Additionally, they have a cell state which runs through the entire chain of the network. It helps in managing the information from the previous cells in the chain.
Let's now define it more formally and mathematically. Given a sequence of word embeddings [math]\displaystyle{ x_1, ..., x_T \in R^{d_1} }[/math], a cell and state vector [math]\displaystyle{ c_t, h_t \in R^{d_2} }[/math] are computed for each element by iteratively applying the below equations, with initializations [math]\displaystyle{ h_0 = c_0 = 0 }[/math].
\begin{align} o_t = \sigma(W_ox_t + V_oh_{t−1} + b_o) \end{align} \begin{align} f_t = \sigma(W_fx_t + V_fh_{t−1} + b_f) \end{align} \begin{align} i_t = \sigma(W_ix_t + V_ih_{t−1} + b_i) \end{align} \begin{align} g_t = tanh(W_gx_t + V_gh_{t−1} + b_g) \end{align} \begin{align} c_t = f_t \odot c_{t−1} + i_t \odot g_t \end{align} \begin{align} h_t = o_t \odot tanh(c_t) \end{align}
Where [math]\displaystyle{ W_o, W_i, W_f , W_g \in R^{{d_1}×{d_2}} , V_o, V_f , V_i , V_g \in R^{{d_2}×{d_2}}, b_o, b_g, b_i, b_g \in R^{d_2} }[/math] and [math]\displaystyle{ \odot }[/math] denotes element-wise multiplication. [math]\displaystyle{ o_t, f_t }[/math] and [math]\displaystyle{ i_t }[/math] are often referred to as output, forget and input gates, respectively, due to the fact that their values are bounded between 0 and 1, and that they are used in element-wise multiplication. Intuitively we can think of the forget gate as how much previous memory(information) do we want to forget; input gate as controlling whether or not to let new input in; g gate controlling what do we want to add and finally the output gate as controlling how much the current information(at current time step) should flow out.
After processing the full sequence of words, the final state [math]\displaystyle{ h_T }[/math] is fed to a multinomial logistic regression, to return a probability distribution over C classes.
\begin{align} p_j = SoftMax(Wh_T)_j = \frac{\exp(W_jh_T)}{\sum_{k=1}^C\exp(W_kh_T) } \end{align}
Contextual Decomposition(CD) of LSTM
CD decomposes the output of the LSTM into a sum of two contributions:
- those resulting solely from the given phrase
- those involving other factors
One important thing that is crucial to understand is that this method does not affect the architecture or the predictive accuracy of the model in any way. It just takes the trained model and tries to break it down into the two components mentioned above. It takes in a particular phrase that the user wants to understand or the entire sentence and returns the vectors with the contributions.
Now let's define this more formally. Let the arbitrary input phrase be [math]\displaystyle{ x_q, ..., x_r }[/math], where [math]\displaystyle{ 1 \leq q \leq r \leq T }[/math], where T represents the length of the sentence. CD decomposes the output and cell state ([math]\displaystyle{ c_t, h_t }[/math]) of each cell into a sum of 2 contributions as shown in the equations below.
\begin{align} h_t = \beta_t + \gamma_t \end{align} \begin{align} c_t = \beta_t^c + \gamma_t^c \end{align}
In the decomposition [math]\displaystyle{ \beta_t }[/math] corresponds to the contributions given to [math]\displaystyle{ h_t }[/math] solely from the given phrase while [math]\displaystyle{ \gamma_t }[/math] denotes contribution atleast in part from the other factors. Similarly, [math]\displaystyle{ \beta_t^c }[/math] and [math]\displaystyle{ \gamma_t^c }[/math] represents the contributions given to [math]\displaystyle{ c_t }[/math] solely from the given phrase and atleast in part from the other factors respectively.
Using this decomposition the softmax function can be represented as follows \begin{align} p = SoftMax(W\beta_T + W\gamma_T) \end{align}
As this score corresponds to the input to a logistic regression, it may be interpreted in the same way as a standard logistic regression coefficient.
Disambiguation Interaction between gates
In the equations for the calculation of [math]\displaystyle{ i_t }[/math] and [math]\displaystyle{ g_t }[/math] in the LSTM, we use the contribution at that time step, [math]\displaystyle{ x_t }[/math] as well the output of the previous state [math]\displaystyle{ h_t }[/math]. Therefore when the [math]\displaystyle{ i_t \odot g_t }[/math] is calculated, the contributions made by [math]\displaystyle{ x_t }[/math] to [math]\displaystyle{ i_t }[/math] interact with contributions made by [math]\displaystyle{ h_t }[/math] to [math]\displaystyle{ g_t }[/math] and vice versa. This insight is used to construct the decomposition.
At this stage we need to make an assumption that the non-linear operations at the gate can be represented in a linear fashion. How this is done will be explained in a later part of the summary. Therefore writing equations 1 as a linear sum of contributions from the inputs we have \begin{align} i_t &= \sigma(W_ix_t + V_ih_{t−1} + b_i) \\ & = L_\sigma(W_ix_t) + L_\sigma(V_ih_{t−1}) + L_\sigma(b_i) \end{align}
The important thing to notice now is that after using this linearization, the products between gates also become linear sums of contributions from the 2 factors mentioned above. To expand we can learn whether they resulted solely from the phrase ([math]\displaystyle{ L_\sigma(V_i\beta_{t-1}) \odot L_{tanh}(V_g\beta_{t-1}) }[/math]), solely from the other factors ([math]\displaystyle{ L_\sigma(b_i) \odot L_{tanh}(V_g\gamma_{t-1}) }[/math]) or as an interaction between the phrase and other factors ([math]\displaystyle{ L_\sigma(V_i\beta_{t-1}) \odot L_{tanh}(V_g\gamma_{t-1}) }[/math]).
Since we are able to calculate gradients values recursively in LSTMs, we would use the same procedure to recursively compute the decompositions with the initializations [math]\displaystyle{ \beta_0 = \beta_0^c = \gamma_0 = \gamma_0^c = 0 }[/math]. The derivations can vary a little depending on cases whether the current time step is contained within the phrase ([math]\displaystyle{ q \leq t \leq r }[/math]) or not([math]\displaystyle{ t \lt q, t \gt r }[/math]). In this summary, we will derive the equations for the former case.
So essentially what we are going to do now is linearize each of the gates, then expand the product of sums of these gates and then finally group the terms we get depending on which type of interaction they represent (solely from phase, solely from other factors and a combination of both).
Terms are determined to be derived solely from the specific phrase if they involve products from some combination of [math]\displaystyle{ \beta_{t-1}, \beta_{t-1}^c, x_t }[/math] and [math]\displaystyle{ b_i }[/math] or [math]\displaystyle{ b_g }[/math](but not both). In the other case when t is not within the phrase, products involving [math]\displaystyle{ x_t }[/math] are treated as not deriving from the phrase. This(the other case) can be observed by seeing the equations for this specific case in the appendix of the original paper.
\begin{align} f_t\odot c_{t-1} &= (L_\sigma(W_fx_t) + L_\sigma(V_f\beta_{t-1}) + L_\sigma(V_f\gamma_{t-1}) + L_\sigma(b_f)) \odot (\beta_{t-1}^c + \gamma_{t-1}^c) \\ & = ([L_\sigma(W_fx_t) + L_\sigma(V_f\beta_{t-1}) + L_\sigma(b_f)] \odot \beta_{t-1}^c) + (L_\sigma(V_f\gamma_{t-1}) \odot \beta_{t-1}^c + f_t \odot \gamma_{t-1}^c) \\ & = \beta_t^f + \gamma_t^f \end{align}
Similarly
\begin{align} i_t\odot g_t &= [(L_\sigma(W_ix_t) + L_\sigma(V_i\beta_{t-1}) + L_\sigma(V_i\gamma_{t-1}) + L_\sigma(b_i))] \\ & \odot [(L_{tanh}(W_gx_t) + L_{tanh}(V_g\beta_{t-1}) + L_{tanh}(V_g\gamma_{t-1}) + L_{tanh}(b_g))] \\ & = ([L_\sigma(W_ix_t) \odot [(L_{tanh}(W_gx_t) + L_{tanh}(V_g\beta_{t-1}) + L_{tanh}(b_g))] \\ &+ L_\sigma(V_f\beta_{t-1}) + L_\sigma(V_i\beta_{t-1}) \odot [(L_{tanh}(W_gx_t) + L_{tanh}(V_g\beta_{t-1}) + L_{tanh}(b_g))] \\ &+ L_\sigma(b_i) \odot [(L_{tanh}(W_gx_t) + L_{tanh}(V_g\beta_{t-1})] \\ &+ [L_\sigma(V_i\gamma_{t-1}) \odot g_t + i_t \odot L_{tanh}(V_g\gamma_{t-1}) - L_\sigma(V_i\gamma_{t-1}) \odot L_{tanh}(V_g\gamma_{t-1}) \\ &+ L_\sigma(b_i) \odot L_{tanh}(b_g)] \\ & = \beta_t^u + \gamma_t^u \end{align}
Thus we can represent [math]\displaystyle{ c_t }[/math] as
\begin{align} c_t &= \beta_t^f + \gamma_t^f + \beta_t^u + \gamma_t^u \\ & = \beta_t^f + \beta_t^u + \gamma_t^f + \gamma_t^u \\ & = \beta_t^c + \gamma_t^c \end{align}
So once we have the decomposition of [math]\displaystyle{ c_t }[/math], then we can rather simply calculate the transformation of [math]\displaystyle{ h_t }[/math] by linearizing the [math]\displaystyle{ tanh }[/math] function. Again at this point, we just assume that a linearizing function for [math]\displaystyle{ tanh }[/math] exists. Similar to the decomposition of the forget and input gate we can decompose the output gate as well but empirically it was found that it did not produce improved results. So finally [math]\displaystyle{ h_t }[/math] can be written as
\begin{align} h_t &= o_t \odot tanh(c_t) \\ & = o_t \odot [L_{tanh}(\beta_t^c) + L_{tanh}(\gamma_t^c)] \\ & = o_t \odot L_{tanh}(\beta_t^c) + o_t \odot L_{tanh}(\gamma_t^c) \\ & = \beta_t + \gamma_t \end{align}
Linearizing activation functions
This section will explain the big assumption that we took earlier about the linearizing functions [math]\displaystyle{ L_{\sigma} }[/math] and [math]\displaystyle{ L_{tanh} }[/math]. For arbitrary { [math]\displaystyle{ y_1, ..., y_N }[/math] } [math]\displaystyle{ \in R }[/math], the problem that we intend to solve is essentially \begin{align} tanh(\sum_{i=1}^Ny_i) = \sum_{i=1}^NL_{tanh}(y_i) \end{align}
In cases where {[math]\displaystyle{ y_i }[/math]} follow a natural ordering, work in Murdoch & Szlam, 2017 where the difference of partial sums is utilized as a linearization technique could be used. This could be shown by the equation below \begin{align} L^{'}_{tanh}(y_k) = tanh(\sum_{j=1}^ky_j) - tanh(\sum_{j=1}^{k-1}y_j) \end{align}
But in our case the terms do not follow any particular ordering, for e.g. while calculating [math]\displaystyle{ o_t }[/math] we could write it as a sum of [math]\displaystyle{ W_ox_t, V_oh_{t−1}, b_o }[/math] or [math]\displaystyle{ b_o, V_oh_{t−1}, W_ox_t }[/math]. Thus, we average over all the possible orderings. Let [math]\displaystyle{ \pi_i, ..., \pi_{M_n} }[/math] denote the set of all permutations of [math]\displaystyle{ 1, ..., N }[/math], then the score could be given as below
\begin{align} L_{tanh}(y_k) = \frac{1}{M_N}\sum_{i=1}^{M_N}[tanh(\sum_{j=1}^{\pi_i^{-1}(k)}y_{\pi_i(j)}) - tanh(\sum_{j=1}^{\pi_i^{-1}(k) - 1}y_{\pi_i(j)})] \end{align}
We can similarly derive [math]\displaystyle{ L_{\sigma} }[/math]. An important empirical observation to note here is that in the case when one of the terms of the decomposition is a bias, improvements were seen when restricting to permutations where the bias was the first term. In our case, the value of N only ranges from 2 to 4, which makes the linearization take very simple forms. An example of a case where N=2 is shown below.
\begin{align} L_{tanh}(y_1) = \frac{1}{2}([tanh(y_1) - tanh(0)] + [tanh(y_2 + y_1) - tanh(y_1)]) \end{align}
Experiments
As mentioned earlier, the empirical validation of CD is done on the task of sentiment analysis. The paper verifies the following 3 tasks with the experiments:
- It should work on the standard problem of word-level importance scores
- It should behave for words as well as phrases especially in situations involving compositionality.
- It should be able to extract instances of positive and negative negation.
An important fact worth mentioning again is that the primary objective of the paper is to produce meaningful interpretations on a pre-trained LSTM model rather than achieving the state-of-the-art results on the task of sentiment analysis. Therefore standard practices are used for tuning the models. The models are implemented in Torch using default parameters for weight initializations. The code can be found at "https://github.com/jamie-murdoch/ContextualDecomposition". The model was trained using Adam with the learning rate of 0.001 and using early stopping on the validation set. Additionally, a bag of words linear model was used.
All the experiments were performed on the Stanford Sentiment Treebank(SST) [Socher et al., 2013] dataset and the Yelp Polarity(YP) [Zhang et al., 2015] dataset. SST is a standard NLP benchmark which consists of movie reviews ranging from 2 to 52 words long. It is important to note that the SST dataset has one key feature that is perfect for this task, which is in addition to review-level labels, it also provides labels for each phrase in the binarized constituency parse tree. This enables us to examine that if the model can identify negative phrases out of a positive review, or vice versa. The word embedding used in LSTM is pretrained Glove vectors with length equal to 300, and the hidden representations of the LSTM is set to be 168. The LSTM model attained an accuracy of 87.2% whereas the logistic regression model with the bag of words features attained an accuracy of 83.2%. In the case of YP, the task is to perform a binary sentiment classification task. The reviews considered were only which were of at most 40 words. The LSTM model attained a 4.6% error as compared the 5.7% error for the regression model.
Baselines
The interpretations are compared with 4 state-of-the-art baselines for interpretability.
- Cell Decomposition(Murdoch & Szlam, 2017),
- Integrated Gradients (Sundararajan et al., 2017),
- Leave One Out (Li et al., 2016),
- Gradient times input [gradient of the output probability with respect to the word embeddings is computed which is finally reported as a dot product with the word vector]
To obtain phrase scores for word-based baselines integrated gradients, cell decomposition, and gradients, the paper sums the scores of the words contained within the phrase.
Unigram(Word) Scores
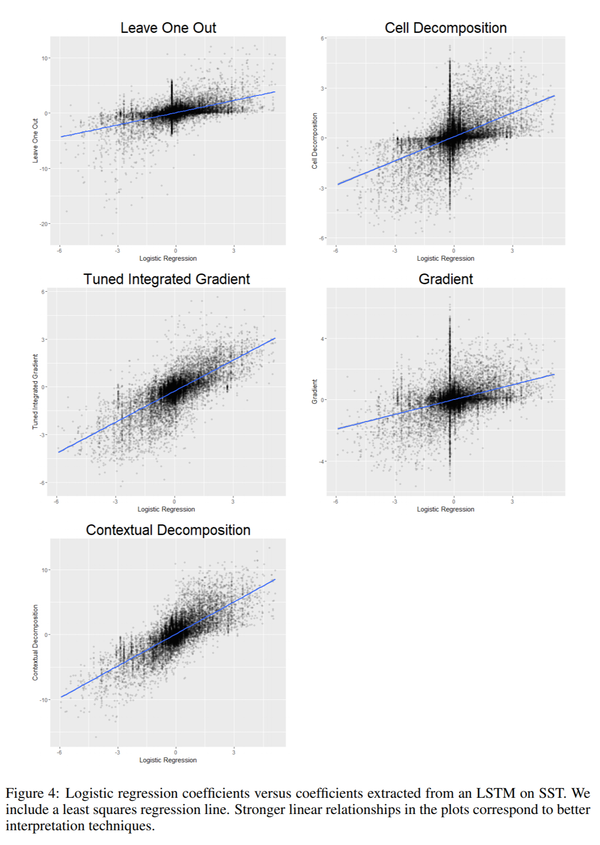
Logistic regression(LR) coefficients while being sufficiently accurate for prediction are considered the gold standard for interpretability. For the task of sentiment analysis, the importance of the words is given by their coefficient values. Thus we would expect the CD scores extracted from an LSTM, to have meaningful relationships and comparison with the logistic regression coefficients. This comparison is done using scatter plots(Fig 4) which measures the Pearson correlation coefficient between the importance scores extracted by LR coefficients and LSTM. This is done for multiple words which are represented as a point in the scatter plots. For SST, CD and Integrated Gradients, with correlations of 0.76 and 0.72, respectively, are substantially better than other methods, which have correlations of at most 0.51. On Yelp, the gap is not as big, but CD is still very competitive, having correlation 0.52 with other methods ranging from 0.34 to 0.56. The complete results are shown in Table 4.

Benefits
Having verified reasonably strong results in the base case, the paper then proceeds to show the benefits of CD.
Identifying Dissenting Subphrases
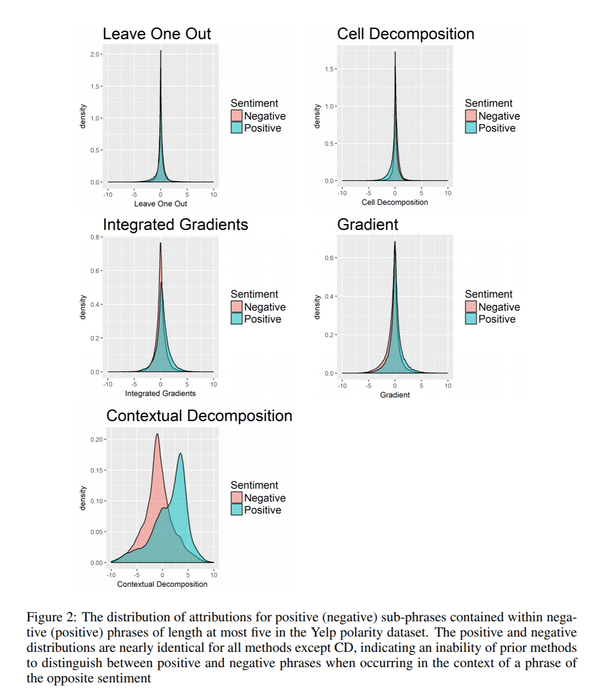
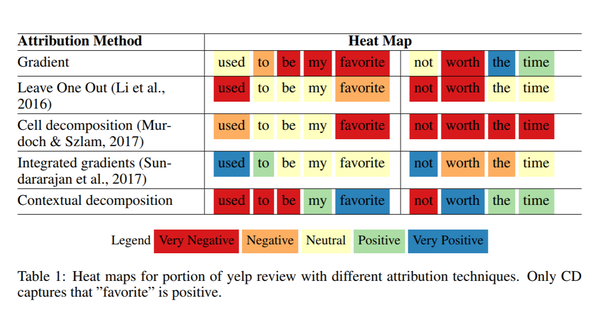
First, the paper shows that the existing methods are not able to recognize sub-phrases in a phrase(a phrase is considered to be of at most 5 words) with different sentiments. For example, consider the phrase "used to be my favorite". The word "favorite" is strongly positive which is also shown by it having a high linear regression coefficient. Nonetheless, the existing methods identify "favorite" as being highly negative or neutral in this context. However, as shown in table 1 CD is able to correctly identify it being strongly positive, and the subphrase "used to be" as highly negative. This particular identification is itself the main reason for using the LSTMs over other methods in text comprehension. Thus, it is quite important that an interpretation algorithm is able to properly uncover how these interactions are being handled. A search across the datasets is done to find similar cases where a negative phrase contains a positive sub-phrase and vice versa. Phrases are scored using the logistic regression over n-gram features and included if their overall score is over 1.5.
It is to be noted that for an efficient interpretation algorithm the distribution of scores for these positive and negative dissenting subphrases should be significantly separate with the positive subphrases having positive scores and vice-versa. However, as shown in figure 2, this is not the case with the previous interpretation algorithms.
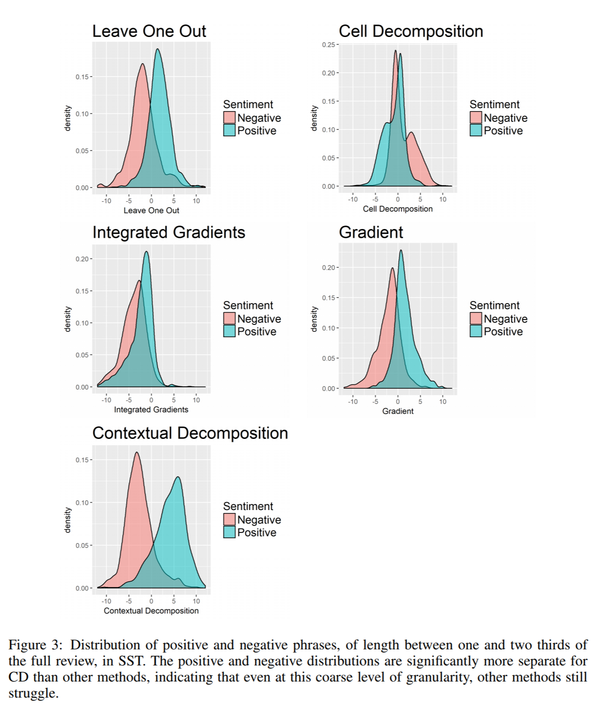
Examining High-Level Compositionality
The paper now studies the cases where a sizable portion of a review(between one and two-thirds) has a different polarity from the final sentiment. An example is shown in Table 2. SST contains phrase-level sentiment labels too. Therefore the authors conduct a search in SST where a sizable phrase in a review is of the opposite polarity than the review-level label. The figure shows the distribution of the resulting positive and negative phrases for different attribution methods. We should note that a successful interpretation method would have a sizeable gap between these two distributions. Notice that the previous methods fail to satisfy this criterion. The paper additionally provides a two-sample Kolmogorov-Smirnov one-sided test statistic, to quantify this difference in performance. This statistic is a common difference measure for the difference of distributions with values ranging from 0 to 1. As shown in Figure 3 CD gets a score of 0.74 while the other models achieve a score of 0(Cell decomposition), 0.33(Integrated Gradients), 0.58(Leave One Out) and 0.61(gradient). The methods leave one out and gradient perform relatively better than the other 2 baselines but they were the weakest performers in the unigram scores. This inconsistency in other methods performance further strengthens the superiority of CD.

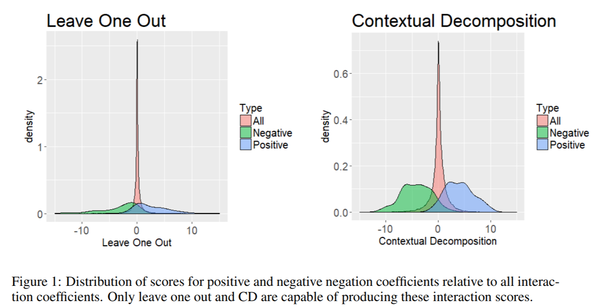
Capturing Negation
The paper also shows a way to empirically show how the LSTMs capture negations in a sentence. To search for negations, the following list of negation words were used: not, n’t, lacks, nobody, nor, nothing, neither, never, none, nowhere, remotely. Again using the phrase labels present in SST, the authors search over the training set for instances of negation. Both the positive as well as negative negations are identified. For a given negation phrase, they extract a negation interaction by computing the CD score of the entire phrase and subtracting the CD scores of the phrase being negated and the negation term itself. The resulting score can be interpreted as an n-gram feature. Apart from CD, only leave one out is capable of producing such interaction scores. The distribution of extracted scores is presented in Figure 1. For CD there is a clear distinction between positive and negative negations. Leave one out is able to capture some of the interactions, but has a noticeable overlap between positive and negative negations around zero, indicating a high rate of false negatives.
Identifying Similar Phrases
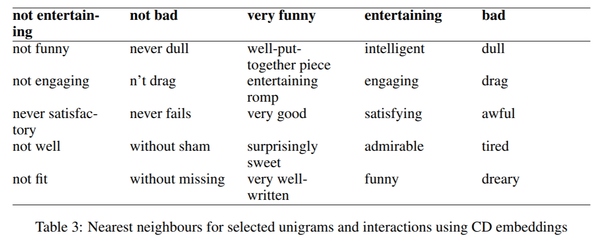
A key aspect of the CD algorithm is that it helps us learn the value of [math]\displaystyle{ \beta_t }[/math] which is essentially a dense embedding vector for a word or a phrase. The way the authors did in the paper is to calculate the AVG([math]\displaystyle{ \beta_t }[/math] ), and then, using similarity measures in the embedding space(eg. cosine similarity) we can easily find similar phrases/words given a phrase/word. The results as shown in Table 3 are qualitatively sensible for 3 different kinds of interactions: positive negation, negative negation and modification, as well as positive and negative words.
Conclusions
The paper provides an algorithm called Contextual Decomposition(CD) to interpret predictions made by LSTMs without modifying their architecture. It takes in a trained LSTM and breaks it down in components and quantifies the interpretability of its decision. In both NLP and in general applications CD produces importance scores for words (single variables in general), phrases (several variables together) and word interactions (variable interactions). It also compares the algorithm with state-of-the-art baselines and shows that it performs favorably. It also shows that CD is capable of identifying phrases of varying sentiment and extracting meaningful word (or variable) interactions. It shows the shortcomings of the traditional word-based interpretability approaches for understanding LSTMs and advances the state-of-the-art.
Critique/Future Work
While the method itself is novel in the sense that it moves past the traditional approach of looking just at word level importance scores; it only looks at one specific architecture which is applied to a very simple problem. The authors don't talk about any future directions for this work in the paper itself but a discussion about it happened during the Oral presentation of the paper at ICLR 2018. Following are the importance points:
- We could look at interpreting a more complex model, for example, say seq2seq. The author pointed out that he was affirmative that this model could be extended for such purposes although the computational complexity would increase since we would be predicting multiple outputs in this case.
- We could also look at whether this approach could be generalized to completely different architectures like CNN. As of now given a new model, we need to manually work out the math for the specific model. Could we develop some general approach towards this? Although the author pointed out that they are working towards using this approach to interpret CNNs.
References
W. James Murdoch, Peter J. Liu, Bin Yu. Beyond Word Importance: Contextual Decomposition to Extract Interactions from LSTMs. ICLR 2018
Sebastian Bach, Alexander Binder, Gregoire Montavon, Frederick Klauschen, Klaus-Robert Muller, and Wojciech Samek. On pixel-wise explanations for non-linear classifier decisions by layer-wise relevance propagation. PloS one, 10(7):e0130140, 2015.
Dzmitry Bahdanau, Kyunghyun Cho, and Yoshua Bengio. Neural machine translation by jointly learning to align and translate. arXiv preprint arXiv:1409.0473, 2014.
Sepp Hochreiter and Jurgen Schmidhuber. Long short-term memory. ¨ Neural Computation, 9(8): 1735–1780, 1997.
Andrej Karpathy, Justin Johnson, and Li Fei-Fei. Visualizing and understanding recurrent networks. arXiv preprint arXiv:1506.02078, 2015.
Jiwei Li, Will Monroe, and Dan Jurafsky. Understanding neural networks through representation erasure. CoRR, abs/1612.08220, 2016. URL http://arxiv.org/abs/1612.08220.
W James Murdoch and Arthur Szlam. Automatic rule extraction from long short-term memory networks. ICLR, 2017.
Jeffrey Pennington, Richard Socher, and Christopher Manning. Glove: Global vectors for word representation. In Proceedings of the 2014 conference on empirical methods in natural language processing (EMNLP), pp. 1532–1543, 2014.
Avanti Shrikumar, Peyton Greenside, and Anshul Kundaje. Learning important features through propagating activation differences. arXiv preprint arXiv:1704.02685, 2017
Richard Socher, Alex Perelygin, Jean Wu, Jason Chuang, Christopher D Manning, Andrew Ng, and Christopher Potts. Recursive deep models for semantic compositionality over a sentiment treebank. In Proceedings of the 2013 conference on empirical methods in natural language processing, pp. 1631–1642, 2013.
Hendrik Strobelt, Sebastian Gehrmann, Bernd Huber, Hanspeter Pfister, and Alexander M Rush. Visual analysis of hidden state dynamics in recurrent neural networks. arXiv preprint arXiv:1606.07461, 2016.
Mukund Sundararajan, Ankur Taly, and Qiqi Yan. Axiomatic attribution for deep networks. CoRR, abs/1703.01365, 2017. URL http://arxiv.org/abs/1703.01365
Xiang Zhang, Junbo Zhao, and Yann LeCun. Character-level convolutional networks for text classification. In Advances in neural information processing systems, pp. 649–657, 2015
Appendix