stat946F18/Autoregressive Convolutional Neural Networks for Asynchronous Time Series
This page is a summary of the paper "Autoregressive Convolutional Neural Networks for Asynchronous Time Series" by Mikołaj Binkowski, Gautier Marti, Philippe Donnat. It was published at ICML in 2018.
Introduction
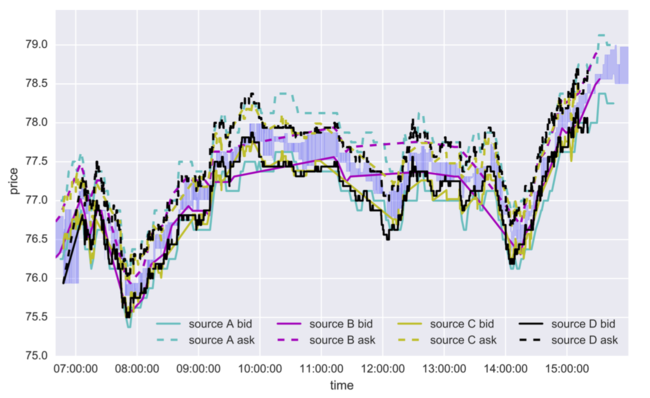
In this paper, the authors proposed a deep convolutional network architecture called Significance-Offset Convolutional Neural Network, for regression of multivariate asynchronous time series. The model is inspired by standard autoregressive(AR) models and gating systems used in recurrent neural networks, and is evaluated on such datasets: a hedge fund proprietary dataset of over 2 million quotes for a credit derivative index, an artificially generated noisy autoregressive series and UCI household electricity consumption dataset. This paper focused on time series with multivariate and noisy signals, especially the financial data. Financial time series are challenging to predict due to their low signal-to-noise ratio and heavy-tailed distributions. For example, same signal (e.g. price of stock) is obtained from different sources (e.g. financial news, investment bank, financial analyst etc.) in asynchronous moment of time. Each source has different different bias and noise.(Figure 1) The investment bank with more clients can update their information more precisely than the investment bank with fewer clients, then the significance of each past observations may depend on other factors that changes in time. Therefore, the traditional econometric models such as AR, VAR, VARMA[1] might not be sufficient. However, their relatively good performance could allow us to combine such linear econometric models with deep neural networks that can learn highly nonlinear relationships.
The time series forecasting problem can be expressed as a conditional probability distribution below, we focused on modeling the predictors of future values of time series given their past:
The predictability of financial dataset still remains an open problem and is discussed in various publications. ([2])
Related Work
Time series forecasting
From recent proceedings in main machine learning venues i.e. ICML, NIPS, AISTATS, UAI, we can notice that time series are often forecast using Gaussian processes[3,4], especially for irregularly sampled time series[5]. Though still largely independent, combined models have started to appear, for example, the Gaussian Copula Process Volatility model[6]. Although prediction of the next character or word in Natural Language Processing seems to be related to our forecasting problem, the nature of the sequences is too different to use the same cost functions and architectures, same to the adversarial training proposed by Mathieu et al. [7] for video frame prediction.
More recently, the papers include Sirignano (2016)[8] that used 4-layer perceptrons in modeling price change distributions in Limit Order Books, and Borovykh et al. (2017)[9] who applied more recent WaveNet architecture to several short univariate and bivariate time-series (including financial ones). Heaton et al. (2016)[10] claimed to use autoencoders with a single hidden layer to compress multivariate financial data. Neil et al. (2016)[11] presented augmentation of LSTM architecture suitable for asynchronous series, which stimulates learning dependencies of different frequencies through time gate.
Gating and weighting mechanisms
Gating mechanisms for neural networks has ability to overcome the problem of vanishing gradient, and can be expressed as [math]\displaystyle{ f(x)=c(x) \otimes \sigma(x) }[/math], where [math]\displaystyle{ f }[/math] is the output function, [math]\displaystyle{ c }[/math] is a "candidate output" (a nonlinear function of [math]\displaystyle{ x }[/math]), [math]\displaystyle{ \otimes }[/math] is an element-wise matrix product, and [math]\displaystyle{ \sigma : \mathbb{R} \rightarrow [0,1] }[/math] is a sigmoid nonlinearity that controls the amount of output passed to the next layer. This composition of functions may lead to popular recurrent architecture such as LSTM and GRU.
The idea of the gating system is aimed to weight outputs of the intermediate layers within neural networks, and is most closely related to softmax gating used in MuFuRu(Multi-Function Recurrent Unit)[12], i.e. [math]\displaystyle{ f(x) = \sum_{l=1}^L p^l(x) \otimes f^l(x), p(x)=softmax(\widehat{p}(x)), }[/math], where [math]\displaystyle{ (f^l)_{l=1}^L }[/math]are candidate outputs(composition operators in MuFuRu), [math]\displaystyle{ (\widehat{p}^l)_{l=1}^L }[/math]are linear functions of inputs. This idea is also used in attention networks[13] such as image captioning and machine translation.

Motivation
There are mainly five motivations they stated in the paper:
- The forecasting problem in this paper has done almost independently by econometrics and machine learning communities. Unlike in machine learning, research in econometrics are more likely to explain variables rather than improving out-of-sample prediction power. These models tend to 'over-fit' on financial time series, their parameters are unstable and have poor performance on out-of-sample prediction.
- Although Gaussian processes provide useful theoretical framework that is able to handle asynchronous data, they often follow heavy-tailed distribution for financial datasets.
- Predictions of autoregressive time series may involve highly nonlinear functions if sampled irregularly. For AR time series with higher order and have more past observations, the expectation of it [math]\displaystyle{ \mathbb{E}[X(t)|{X(t-m), m=1,...,M}] }[/math] may involve more complicated functions that in general may not allow closed-form expression.
- In practice, the dimensions of multivariate time series are often observed separately and asynchronously, such series at fixed frequency may lead to lose information or enlarge the dataset, which is shown in Figure 2(a). Therefore, the core of proposed architecture SOCNN represents separate dimensions as a single one with dimension and duration indicators as additional features(Figure 2(b)).
- Given a series of pairs of consecutive input values and corresponding durations, [math]\displaystyle{ x_n = (X(t_n),t_n-t_{n-1}) }[/math]. One may expect that LSTM may memorize the input values in each step and weight them at the output according to the durations, but this approach may lead to imbalance between the needs for memory and for linearity. The weights that are assigned to the memorized observations potentially require several layers of nonlinearity to be computed properly, while past observations might just need to be memorized as they are.
Model Architecture
Suppose there's a multivariate time series [math]\displaystyle{ (x_n)_{n=0}^{\infty} \subset \mathbb{R}^d }[/math], we want to predict the conditional future values of a subset of elements of [math]\displaystyle{ x_n }[/math]
where [math]\displaystyle{ I=\{i_1,i_2,...i_{d_I}\} \subset \{1,2,...,d\} }[/math] is a subset of features of [math]\displaystyle{ x_n }[/math]. Let [math]\displaystyle{ \textbf{x}_n^{-M} = (x_{n-m})_{m=1}^M }[/math]. The estimator of [math]\displaystyle{ y_n }[/math] can be expressed as:
where
- [math]\displaystyle{ F,S : \mathbb{R}^{d \times M} \rightarrow \mathbb{R}^{d_I \times M} }[/math] are neural networks. S is a fully convolutional network which is composed of convolutional layers only. [math]\displaystyle{ F }[/math] is in the form of
[math]\displaystyle{ F(\textbf{x}_n^{-M}) = W \otimes [off(x_{n-m}) + x_{n-m}^I)]_{m=1}^M }[/math] where [math]\displaystyle{ W \in \mathbb{R}^{d_I \times M} }[/math] and [math]\displaystyle{ off: \mathbb{R}^d \rightarrow \mathbb{R}^{d_I} }[/math] is a multilayer perceptron.
- [math]\displaystyle{ \sigma }[/math] is a normalized activation function independent at each row, i.e. [math]\displaystyle{ \sigma ((a_1^T,...,a_{d_I}^T)^T)=(\sigma(a_1)^T,...\sigma(a_{d_I})^T)^T }[/math]
- [math]\displaystyle{ \otimes }[/math] is element-wise matrix multiplication.
- [math]\displaystyle{ A.,_m }[/math] denotes the m-th column of a matrix A, and [math]\displaystyle{ \sum_{m=1}^M A.,_m=A(1,1,...,1)^T }[/math], there are M 1s.
Relation to asynchronous data
One common problem of time series is that durations are varying between consecutive observations, the paper states two ways to solve this problem
- Data preprocessing: aligning the observations at some fixed frequency e.g. duplicating and interpolating observations as shown in Figure 2(a). However, as mentioned in the figure, this approach will tend to loss of information and enlarge the size of the dataset and model complexity.
- Add additional features: Treating duration or time of the observations as additional features, it is the core of SOCNN, which is shown in Figure 2(b).
Loss function
Experiments
The paper evaluated SOCNN architecture on three datasets: artificial generated datasets, household electric power consumption dataset, and the financial dataset of bid/ask quotes sent by several market participants active in the credit derivatives market. Comparing its performance with simple CNN, single and multiplayer LSTM and 25-layer ResNet. The code and datasets are available here
Datasets
Artificial data: They generated 4 artificial series, [math]\displaystyle{ X_{K \times N} }[/math], where [math]\displaystyle{ K \in \{16,64\} }[/math]. Therefore there is a synchronous and a asynchronous series for each K value.
Electricity data: This UCI dataset contains 7 different features excluding date and time. The features include global active power, global reactive power, voltage, global intensity, sub- metering 1, sub-metering 2 and sub-metering 3, recorded every minute for 47 months. In order to represent the data for the SOCNN architecture, the data has been altered so that one observation contains only the value of one of 7 features, while durations between consecutive observations are ranged from 1 to 7 minutes. The goal of the regression is to predict all 7 features for the next time step.
Non-anonymous quotes: The dataset contains 2.1 million quotes from 28 different sources, i.e. market participants such as analysts, banks etc. Each quote is characterized by 31 features: the offered price, 28 indicators of the quoting source, the direction indicator (the quote refers to either a buy or a sell offer) and duration from the previous quote. For each source and direction we aim at predicting the next quoted price from this given source and direction considering the last 60 quotes. We