stat841F18/: Difference between revisions
| (14 intermediate revisions by one other user not shown) | |||
| Line 1: | Line 1: | ||
== Presented by == | == Presented by == | ||
Zhaoran Hou, Pei wei Wang, Chi Zhang, Daoyi Chen, Yiming Li,Ying Chi | |||
== Introduction == | == Introduction == | ||
| Line 31: | Line 31: | ||
== Model Architecture == | == Model Architecture == | ||
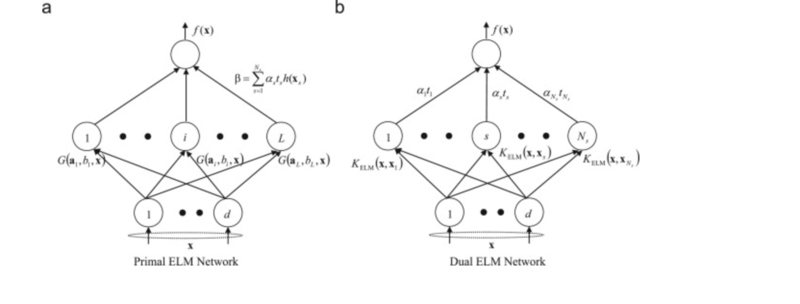
The extreme learning machine (ELM) is a particular kind of machine learning setup in which a single layer or multiple layers apply. The ELM includes numbers of hidden neurons where the input weights are assigned randomly. Extreme learning machines use the concept of random projection and early perceptron models to do specific kinds of problem-solving. | |||
Given a single hidden layer of ELM, suppose that the output function of the <math>i</math>-th hidden node is <math>h_i(\mathbf{x})=G(\mathbf{a}_i,b_i,\mathbf{x})</math>, where <math>\mathbf{a}_i</math> and <math>b_i</math> are the parameters of the <math>i</math>-th hidden node. The output function of the ELM for SLFNs with <math>L</math> hidden nodes is: | |||
<math>f_L({\bf x})=\sum_{i=1}^L{\boldsymbol \beta}_ih_i({\bf x})</math>, where is the output weight of the <math>i</math>-th hidden node. | |||
<math>\mathbf{h}(\mathbf{x})=[G(h_i(\mathbf{x}),...,h_L(\mathbf{x}))]</math> is the hidden layer output mapping of ELM. Given <math>N</math> training samples, the hidden layer output matrix <math>\mathbf{H}</math> of ELM is given as: <math>{\bf H}=\left[\begin{matrix} | |||
{\bf h}({\bf x}_1)\\ | |||
\vdots\\ | |||
{\bf h}({\bf x}_N) | |||
\end{matrix}\right]=\left[\begin{matrix} | |||
G({\bf a}_1, b_1, {\bf x}_1) &\cdots & G({\bf a}_L, b_L, {\bf x}_1)\\ | |||
\vdots &\vdots&\vdots\\ | |||
G({\bf a}_1, b_1, {\bf x}_N) &\cdots & G({\bf a}_L, b_L, {\bf x}_N) | |||
\end{matrix}\right] | |||
</math> | |||
and <math>\mathbf{T}</math> is the training data target matrix: <math>{\bf T}=\left[\begin{matrix} | |||
{\bf t}_1\\ | |||
\vdots\\ | |||
{\bf t}_N | |||
\end{matrix}\right] | |||
</math> | |||
General speaking, ELM is a kind of regularization neural networks but with non-tuned hidden layer mappings (formed by either random hidden nodes, kernels or other implementations), its objective function is: | |||
<math> | |||
\text{Minimize: } \|{\boldsymbol \beta}\|_p^{\sigma_1}+C\|{\bf H}{\boldsymbol \beta}-{\bf T}\|_q^{\sigma_2} | |||
</math> | |||
where <math>\sigma_1>0, \sigma_2>0, p,q=0, \frac{1}{2}, 1, 2, \cdots, +\infty</math>. | |||
Different combinations of <math>\sigma_1</math>, <math>\sigma_2</math>, <math>p</math> and <math>q</math> can be used and result in different learning algorithms for regression, classification, sparse coding, compression, feature learning and clustering. | |||
As a special case, a simplest ELM training algorithm learns a model of the form (for single hidden layer sigmoid neural networks): | |||
:<math>\mathbf{\hat{Y}} = \mathbf{W}_2 \sigma(\mathbf{W}_1 x)</math> | |||
where is the matrix of input-to-hidden-layer weights, <math>\sigma</math> is an activation function, and is the matrix of hidden-to-output-layer weights. The algorithm proceeds as follows: | |||
# Fill with random values (e.g, Gaussian noise|Gaussian random noise); | |||
# estimate by least-squares fit to a matrix of response variables, computed using the Moore–Penrose pseudoinverse|pseudoinverse, given a design matrix]] : | |||
#:<math>\mathbf{W}_2 = \sigma(\mathbf{W}_1 \mathbf{X})^+ \mathbf{Y}</math> | |||
<center> | <center> | ||
[[File:aa.png|800px]] | [[File:aa.png|800px]] | ||
| Line 42: | Line 88: | ||
<center> | <center> | ||
[[File:cc.png| | [[File:cc.png|400px]] | ||
Fig. 1. | |||
</center> | </center> | ||
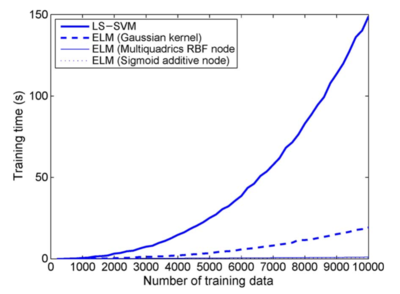
Fig. 1 shows the scalability of different classifiers: An example on letter data set. training time spent by LS-SVM and ELM (Gaussian kernel) increases sharply when the number of training data increases. However, the training time spent by ELM with Sigmoid additive node and multiquadric function node increases very slowly when the number of training data increases. | |||
== Conclusion == | == Conclusion == | ||
<center> | |||
[[File:dd.png|800px]] | |||
</center> | |||
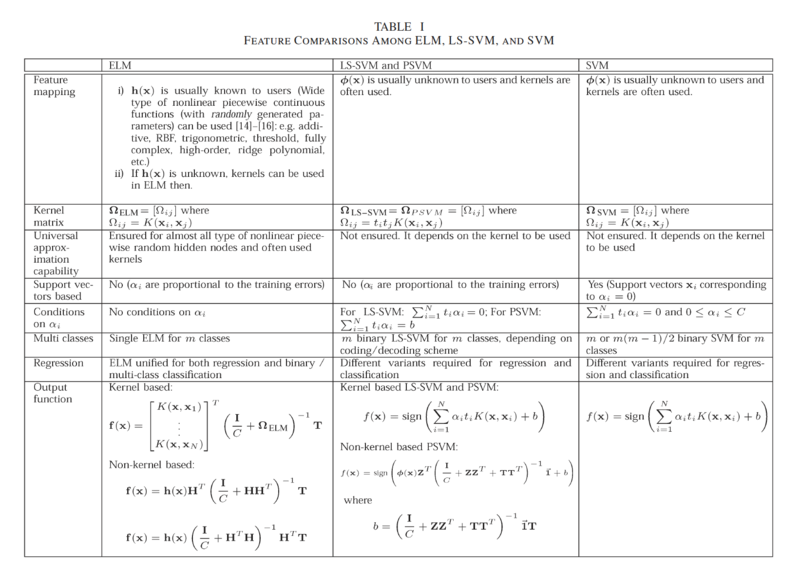
ELM is a learning mechanism for the generalized SLFNs, where learning is made without iterative tuning. The essence of ELM is that the hidden layer of the generalized SLFNs should not be tuned. This paper has shown that both LS-SVM and PSVM can be simplified by removing the term bias b and the resultant learning algorithms are unified with ELM. Instead of different variants requested for different types of applications, ELM can be applied in regression and multiclass classification appli- cations directly. | |||
ELM requires less human intervention than SVM and LS- SVM/PSVM. If the feature mappings h(x) are known to users, in ELM, only one parameter C needs to be specified by users. The generalization performance of ELM is not sensitive to the dimensionality L of the feature space (the number of hidden nodes) as long as L is set large enough (e.g., L ≥ 1000 for all the real-world cases tested in our simulations). Different from SVM, LS-SVM, and PSVM which usually request two parameters (C,γ) to be specified by users, single-parameter setting makes ELM be used easily and efficiently. If feature mappings are unknown to users, similar to SVM, LS-SVM, and PSVM, kernels can be applied in ELM as well. Different from LS-SVM and PSVM, ELM does not have con- straints on the Lagrange multipliers αi’s. Since LS-SVM and ELM have the same optimization objective functions and LS- SVM has some optimization constraints on Lagrange multipli- ers αi’s, in this sense, LS-SVM tends to obtain a solution which is suboptimal to ELM. | |||
As verified by the simulation results, compared to SVM and LS-SVM ELM achieves similar or better generalization performance for regression and binary class classification cases, and much better generalization performance for multiclass clas- sification cases. ELM has better scalability and runs at much faster learning speed (up to thousands of times) than traditional SVM and LS-SVM. | |||
== Critiques == | == Critiques == | ||
An ELM is basically a 2-layer neural net in which the first layer is fixed and random, and the second layer is trained. There is a number of issues with this idea. | |||
Firstly, Algrithms such as SVM and Deep Learning are focusing on fitting a complex function with less parameters while ELM uses more parameters to fit a relatively simple function | |||
Secondly, the name: an ELM is *exactly* what Minsky & Papert call a Gamba Perceptron (a Perceptron whose first layer is a bunch of linear threshold units). The original 1958 Rosenblatt perceptron was an ELM in that the first layer was randomly connected. | |||
Thirdly, the method: connecting the first layer randomly is just about the stupidest thing you could do. People have spent the almost 60 years since the Perceptron to come up with better schemes to non-linearly expand the dimension of an input vector so as to make the data more separable (many of which are documented in the 1974 edition of Duda & Hart). | |||
== References == | == References == | ||
Latest revision as of 17:50, 9 November 2018
Presented by
Zhaoran Hou, Pei wei Wang, Chi Zhang, Daoyi Chen, Yiming Li,Ying Chi
Introduction
In the past two decades, due to their surprising classi- fication capability, support vector machine (SVM) [1] and its variants [2]–[4] have been extensively used in classification applications. Least square support vector machine (LS-SVM) and proximal sup- port vector machine (PSVM) have been widely used in binary classification applications. The conventional LS-SVM and PSVM cannot be used in regression and multiclass classification appli- cations directly, although variants of LS-SVM and PSVM have been proposed to handle such cases.
Motivation
There are several issues on BP learning algorithms:
(1) When the learning rate Z is too small, the learning algorithm converges very slowly. However, when Z is too large, the algorithm becomes unstable and diverges.
(2) Another peculiarity of the error surface that impacts the performance of the BP learning algorithm is the presence of local minima [6]. It is undesirable that the learning algorithm stops at a local minima if it is located far above a global minima.
(3) Neural network may be over-trained by using BP algorithms and obtain worse generalization performance. Thus, validation and suitable stopping methods are required in the cost function minimization procedure.
(4) Gradient-based learning is very time-consuming in most applications.
Due to the simplicity of their implementations, least square support vector machine (LS-SVM) and proximal support vector machine (PSVM) have been widely used in binary classification applications. The conventional LS-SVM and PSVM cannot be used in regression and multiclass classification applications directly, although variants of LS-SVM and PSVM have been proposed to handle such cases. This paper shows that both LS-SVM and PSVM can be simplified further and a unified learning framework of LS-SVM, PSVM, and other regularization algorithms referred to extreme learning machine (ELM) can be built.
Previous Work
As the training of SVMs involves a quadratic programming problem, the computational complexity of SVM training al- gorithms is usually intensive, which is at least quadratic with respect to the number of training examples
Least square SVM (LS-SVM) [2] and proximal SVM (PSVM) [3] provide fast implementations of the traditional SVM. Both LS-SVM and PSVM use equality optimization constraints instead of inequalities from the traditional SVM, which results in a direct least square solution by avoiding quadratic programming.
SVM, LS-SVM, and PSVM are originally proposed for bi- nary classification. Different methods have been proposed in or- der for them to be applied in multiclass classification problems. One-against-all (OAA) and one-against-one (OAO) methods are mainly used in the implementation of SVM in multiclass classification applications [8].
extreme learning machine (ELM) for single hidden layer feedforward neural networks (SLFNs) which randomly chooses the input weights and analytically determines the output weights of SLFNs. In theory, this algorithm tends to provide the best generalization performance at extremely fast learning speed. The experimental results based on real world benchmarking function approximation and classification problems including large complex applications show that the new algorithm can produce best generalization performance in some cases and can learn much faster than traditional popular learning algorithms for feedforward neural networks.
Model Architecture
The extreme learning machine (ELM) is a particular kind of machine learning setup in which a single layer or multiple layers apply. The ELM includes numbers of hidden neurons where the input weights are assigned randomly. Extreme learning machines use the concept of random projection and early perceptron models to do specific kinds of problem-solving.
Given a single hidden layer of ELM, suppose that the output function of the [math]\displaystyle{ i }[/math]-th hidden node is [math]\displaystyle{ h_i(\mathbf{x})=G(\mathbf{a}_i,b_i,\mathbf{x}) }[/math], where [math]\displaystyle{ \mathbf{a}_i }[/math] and [math]\displaystyle{ b_i }[/math] are the parameters of the [math]\displaystyle{ i }[/math]-th hidden node. The output function of the ELM for SLFNs with [math]\displaystyle{ L }[/math] hidden nodes is:
[math]\displaystyle{ f_L({\bf x})=\sum_{i=1}^L{\boldsymbol \beta}_ih_i({\bf x}) }[/math], where is the output weight of the [math]\displaystyle{ i }[/math]-th hidden node.
[math]\displaystyle{ \mathbf{h}(\mathbf{x})=[G(h_i(\mathbf{x}),...,h_L(\mathbf{x}))] }[/math] is the hidden layer output mapping of ELM. Given [math]\displaystyle{ N }[/math] training samples, the hidden layer output matrix [math]\displaystyle{ \mathbf{H} }[/math] of ELM is given as: [math]\displaystyle{ {\bf H}=\left[\begin{matrix} {\bf h}({\bf x}_1)\\ \vdots\\ {\bf h}({\bf x}_N) \end{matrix}\right]=\left[\begin{matrix} G({\bf a}_1, b_1, {\bf x}_1) &\cdots & G({\bf a}_L, b_L, {\bf x}_1)\\ \vdots &\vdots&\vdots\\ G({\bf a}_1, b_1, {\bf x}_N) &\cdots & G({\bf a}_L, b_L, {\bf x}_N) \end{matrix}\right] }[/math]
and [math]\displaystyle{ \mathbf{T} }[/math] is the training data target matrix: [math]\displaystyle{ {\bf T}=\left[\begin{matrix} {\bf t}_1\\ \vdots\\ {\bf t}_N \end{matrix}\right] }[/math]
General speaking, ELM is a kind of regularization neural networks but with non-tuned hidden layer mappings (formed by either random hidden nodes, kernels or other implementations), its objective function is:
[math]\displaystyle{ \text{Minimize: } \|{\boldsymbol \beta}\|_p^{\sigma_1}+C\|{\bf H}{\boldsymbol \beta}-{\bf T}\|_q^{\sigma_2} }[/math]
where [math]\displaystyle{ \sigma_1\gt 0, \sigma_2\gt 0, p,q=0, \frac{1}{2}, 1, 2, \cdots, +\infty }[/math].
Different combinations of [math]\displaystyle{ \sigma_1 }[/math], [math]\displaystyle{ \sigma_2 }[/math], [math]\displaystyle{ p }[/math] and [math]\displaystyle{ q }[/math] can be used and result in different learning algorithms for regression, classification, sparse coding, compression, feature learning and clustering.
As a special case, a simplest ELM training algorithm learns a model of the form (for single hidden layer sigmoid neural networks):
- [math]\displaystyle{ \mathbf{\hat{Y}} = \mathbf{W}_2 \sigma(\mathbf{W}_1 x) }[/math]
where is the matrix of input-to-hidden-layer weights, [math]\displaystyle{ \sigma }[/math] is an activation function, and is the matrix of hidden-to-output-layer weights. The algorithm proceeds as follows:
- Fill with random values (e.g, Gaussian noise|Gaussian random noise);
- estimate by least-squares fit to a matrix of response variables, computed using the Moore–Penrose pseudoinverse|pseudoinverse, given a design matrix]] :
- [math]\displaystyle{ \mathbf{W}_2 = \sigma(\mathbf{W}_1 \mathbf{X})^+ \mathbf{Y} }[/math]
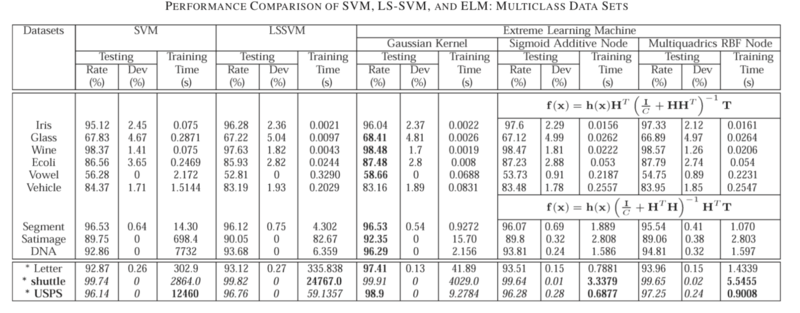
Performance Verification
Fig. 1.
Fig. 1 shows the scalability of different classifiers: An example on letter data set. training time spent by LS-SVM and ELM (Gaussian kernel) increases sharply when the number of training data increases. However, the training time spent by ELM with Sigmoid additive node and multiquadric function node increases very slowly when the number of training data increases.
Conclusion
ELM is a learning mechanism for the generalized SLFNs, where learning is made without iterative tuning. The essence of ELM is that the hidden layer of the generalized SLFNs should not be tuned. This paper has shown that both LS-SVM and PSVM can be simplified by removing the term bias b and the resultant learning algorithms are unified with ELM. Instead of different variants requested for different types of applications, ELM can be applied in regression and multiclass classification appli- cations directly.
ELM requires less human intervention than SVM and LS- SVM/PSVM. If the feature mappings h(x) are known to users, in ELM, only one parameter C needs to be specified by users. The generalization performance of ELM is not sensitive to the dimensionality L of the feature space (the number of hidden nodes) as long as L is set large enough (e.g., L ≥ 1000 for all the real-world cases tested in our simulations). Different from SVM, LS-SVM, and PSVM which usually request two parameters (C,γ) to be specified by users, single-parameter setting makes ELM be used easily and efficiently. If feature mappings are unknown to users, similar to SVM, LS-SVM, and PSVM, kernels can be applied in ELM as well. Different from LS-SVM and PSVM, ELM does not have con- straints on the Lagrange multipliers αi’s. Since LS-SVM and ELM have the same optimization objective functions and LS- SVM has some optimization constraints on Lagrange multipli- ers αi’s, in this sense, LS-SVM tends to obtain a solution which is suboptimal to ELM.
As verified by the simulation results, compared to SVM and LS-SVM ELM achieves similar or better generalization performance for regression and binary class classification cases, and much better generalization performance for multiclass clas- sification cases. ELM has better scalability and runs at much faster learning speed (up to thousands of times) than traditional SVM and LS-SVM.
Critiques
An ELM is basically a 2-layer neural net in which the first layer is fixed and random, and the second layer is trained. There is a number of issues with this idea.
Firstly, Algrithms such as SVM and Deep Learning are focusing on fitting a complex function with less parameters while ELM uses more parameters to fit a relatively simple function
Secondly, the name: an ELM is *exactly* what Minsky & Papert call a Gamba Perceptron (a Perceptron whose first layer is a bunch of linear threshold units). The original 1958 Rosenblatt perceptron was an ELM in that the first layer was randomly connected.
Thirdly, the method: connecting the first layer randomly is just about the stupidest thing you could do. People have spent the almost 60 years since the Perceptron to come up with better schemes to non-linearly expand the dimension of an input vector so as to make the data more separable (many of which are documented in the 1974 edition of Duda & Hart).
References
- [1]G.-B. Huang, Q.-Y. Zhu, and C.-K. Siew, “Extreme learning machine: A new learning scheme of feedforward neural networks,” in Proc. IJCNN,Budapest, Hungary, Jul. 25–29, 2004, vol. 2, pp. 985–990.
- [2]G.-B. Huang, X.Ding, and H.Zhou, Optimization method based extreme learning machine for classification," Neurocomputing, vol. 74, no. 1-3, pp. 155-163, Dec. 2010.