stat841: Difference between revisions
| Line 1,709: | Line 1,709: | ||
We can propagate the error calculated in the output back through the previous layers and adjust weights to minimize error. | We can propagate the error calculated in the output back through the previous layers and adjust weights to minimize error. | ||
Back-Propagation neural network is a good method for following situations: | |||
*The problem is very complex and the number of input or output data points is very large, and have no idea to relate the input to the output. | |||
*The solution varies over time within the bounds of the given input and output data, or the output is not easy to measure. | |||
==Neural Networks (NN) - October 30, 2009 == | ==Neural Networks (NN) - October 30, 2009 == | ||
Revision as of 01:23, 26 November 2009
Proposal
Mark your contribution here
Scribe sign up
Classfication-2009.9.30
Classification
With the rise of fields such as data-mining, bioinformatics, and machine learning, classification has becomes a fast-developing topic. In the age of information, vast amounts of data are generated constantly, and the goal of classification is to learn from data. Potential application areas include handwritten post codes recognition, medical diagnosis, face recognition, human language processing and so on.
Definition: The problem of Prediction a discrete random variable [math]\displaystyle{ \mathcal{Y} }[/math] from another random variable [math]\displaystyle{ \mathcal{X} }[/math] is called Classification.
In classification,, we attempt to approximate a function [math]\displaystyle{ \,h }[/math], by using a training data set, which will then be able to accurately classify new data inputs.
Given [math]\displaystyle{ \mathcal{X} \subset \mathbb{R}^{d} }[/math], a subset of the [math]\displaystyle{ d }[/math]-dimensional real vectors and [math]\displaystyle{ \mathcal{Y} }[/math], a finite set of labels, We try to determine a 'classification rule' [math]\displaystyle{ \,h }[/math] such that,
- [math]\displaystyle{ \,h: \mathcal{X} \mapsto \mathcal{Y} }[/math]
We use [math]\displaystyle{ \,n }[/math] ordered pairs of training data which are identical independent distributions, [math]\displaystyle{ \,\{(X_{1},Y_{1}), (X_{2},Y_{2}), \dots , (X_{n},Y_{n})\} }[/math] where [math]\displaystyle{ \,X_{i} \in \mathcal{X} }[/math],[math]\displaystyle{ \,Y_{i} \in \mathcal{Y} }[/math], to approximate [math]\displaystyle{ \,h }[/math].
Thus, given a new input, [math]\displaystyle{ \,X \in \mathcal{X} }[/math]
by using the classification rule we can predict a corresponding [math]\displaystyle{ \,\hat{Y}=h(X) }[/math].
- Example Suppose we wish to classify fruits into apples and oranges by considering certain features of the fruit, for instance, color, diameter, and weight.
Let [math]\displaystyle{ \mathcal{X}= (\mathrm{colour}, \mathrm{diameter}, \mathrm{weight}) }[/math] and [math]\displaystyle{ \mathcal{Y}=\{\mathrm{apple}, \mathrm{orange}\} }[/math]. The goal is to find a classification rule such that when a new fruit [math]\displaystyle{ \,X }[/math] is presented based on its features, [math]\displaystyle{ (\,X_{\mathrm{color}}, X_{\mathrm{diameter}}, X{_\mathrm{weight}}) }[/math], our classification rule [math]\displaystyle{ \,h }[/math] can classify it as either an apple or an orange, i.e., [math]\displaystyle{ \,h(X_{\mathrm{color}}, X_{\mathrm{diameter}}, X_{\mathrm{weight}}) }[/math] be the fruit type of [math]\displaystyle{ \,X }[/math].
Error rate
- 'True error rate' of a classifier(h) is defined as the probability that [math]\displaystyle{ \,h }[/math] does not correctly classify the points of [math]\displaystyle{ \,\mathcal{X} }[/math], i.e.,
- [math]\displaystyle{ \, L(h)=P(h(X) \neq Y) }[/math]
- 'Empirical error rate(training error rate)' of a classifier(h) is defined as the frequency that [math]\displaystyle{ \,h }[/math] does not correctly classify the points in the training set, i.e.,
- [math]\displaystyle{ \, L_{h}= \frac{1}{n} \sum_{i=1}^{n} I(h(X_{i}) \neq Y_{i}) }[/math], where [math]\displaystyle{ \,I }[/math] is an indicator that [math]\displaystyle{ \, I= \left\{\begin{matrix} 1 & h(X_i) \neq Y_i \\ 0 & h(X_i)=Y_i \end{matrix}\right. }[/math].
Bayes Classifier
The principle of Bayes Classifier is to calculate the posterior probability of a given object from its prior probability via Bayes formula, and then place the object in the class with the largest posterior probability. Intuitively speaking, to classify [math]\displaystyle{ \,x\in \mathcal{X} }[/math] we find [math]\displaystyle{ y \in \mathcal{Y} }[/math] such that [math]\displaystyle{ \,P(Y=y|X=x) }[/math] is maximum over all the members of [math]\displaystyle{ \mathcal{Y} }[/math].
Mathematically, for [math]\displaystyle{ \,k }[/math] classes and given object [math]\displaystyle{ \,X=x }[/math], we find [math]\displaystyle{ \,y\in \mathcal{Y} }[/math] which maximizes [math]\displaystyle{ \,P(Y=y|X=x) }[/math], and classify [math]\displaystyle{ \,X }[/math] into class [math]\displaystyle{ \,y }[/math]. In order to calculate the value of [math]\displaystyle{ \,P(Y=y|X=x) }[/math], we use Bayes formula
- [math]\displaystyle{ \begin{align} P(Y=y|X=x) &= \frac{P(X=x|Y=y)P(Y=y)}{P(X=x)} \\ &=\frac{P(X=x|Y=y)P(Y=y)}{\Sigma_{\forall y \in \mathcal{Y}}P(X=x|Y=y)P(Y=y)} \end{align} }[/math]
where [math]\displaystyle{ \,P(Y=y|X=x) }[/math] is referred to as the posterior probability, [math]\displaystyle{ \,P(Y=y) }[/math] as the prior probability, [math]\displaystyle{ \,P(X=x|Y=y) }[/math] as the likelihood, and [math]\displaystyle{ \,P(X=x) }[/math] as the evidence.
For the special case that [math]\displaystyle{ \,Y }[/math] has only two classes, that is, [math]\displaystyle{ \, \mathcal{Y}=\{0, 1\} }[/math]. Consider the probability that [math]\displaystyle{ \,r(X)=P\{Y=1|X=x\} }[/math]. Given [math]\displaystyle{ \,X=x }[/math], By Bayes formula, we have
- [math]\displaystyle{ \begin{align} r(X)&=P(Y=1|X=x) \\ &=\frac{P(X=x|Y=1)P(Y=1)}{P(X=x)}\\ &=\frac{P(X=x|Y=1)P(Y=1)}{P(X=x|Y=1)P(Y=1)+P(X=x|Y=0)P(Y=0)} \end{align} }[/math]
Definition:
The Bayes classification rule [math]\displaystyle{ \,h }[/math] is
- [math]\displaystyle{ \, h(X)= \left\{\begin{matrix} 1 & r(x)\gt \frac{1}{2} \\ 0 & \mathrm{otherwise} \end{matrix}\right. }[/math]
3 different approaches to classification:
1) Empirical Risk Minimization: Choose a set fo classifier [math]\displaystyle{ \mathcal{H} }[/math] and find [math]\displaystyle{ \,h^*\in \mathcal{H} }[/math] that minimizes some estimate of [math]\displaystyle{ \,L(h) }[/math]
2) Regression: Find an estimate [math]\displaystyle{ (\hat r) }[/math] of the function [math]\displaystyle{ r }[/math] and define
- [math]\displaystyle{ \, h(X)= \left\{\begin{matrix} 1 & \hat r(x)\gt \frac{1}{2} \\ 0 & \mathrm{otherwise} \end{matrix}\right. }[/math]
3) Density Estimation: estimate [math]\displaystyle{ \,P(X=x|Y=0) }[/math] and [math]\displaystyle{ \,P(X=x|Y=1) }[/math] (less popular in high-dimension cases)
Bayes Classification Rule Optimality Theorem: The Bayes rule is optimal in true error rate, that is for any other classification rule [math]\displaystyle{ \, \overline{h} }[/math], we have [math]\displaystyle{ \,L(h) \le L(\overline{h}) }[/math]. Intuitively speaking this theorem is saying we cannot do better than classifying [math]\displaystyle{ \,x\in \mathcal{X} }[/math] to [math]\displaystyle{ \,y }[/math] when[math]\displaystyle{ }[/math] the probability of being of type [math]\displaystyle{ \,y }[/math] for [math]\displaystyle{ \,x }[/math] is more than probability of being any other type.
Definition:
The set [math]\displaystyle{ \,D(h)=\{x: P(Y=1|X=x)=P(Y=0|X=x)\} }[/math] is called the decision boundary.
- [math]\displaystyle{ \, h^*(X)= \left\{\begin{matrix} 1 & if P(Y=1|X=x)\gt P(Y=0|X=x) \\ 0 & \mathrm{otherwise} \end{matrix}\right. }[/math]
Remark:
1)Bayes classification rule is optimal. Proof:[1]
2)We still need any other method, since we cannot define prior probability in realistic.
Example:
We’re going to predict if a particular student will pass STAT441/841.
We have data on past student performance. For each student we know:
If student’s GPA > 3.0 (G)
If student had a strong math background (M)
If student is a hard worker (H)
If student passed or failed course
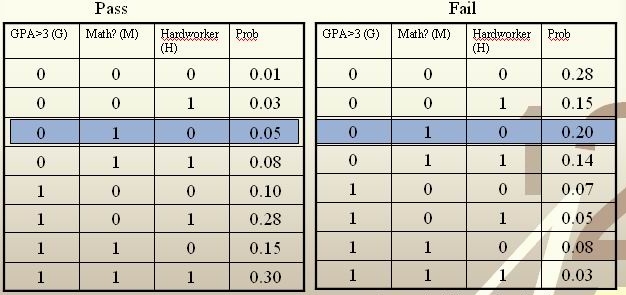
[math]\displaystyle{ \, \mathcal{Y}= \{ 0,1 \} }[/math], where 1 refers to pass and 0 refers to fail. Assume that [math]\displaystyle{ \,P(Y=1)=P(Y=0)=0.5 }[/math]
For a new student comes along with values [math]\displaystyle{ \,G=0, M=1, H=0 }[/math], we calculate [math]\displaystyle{ \,r(X)=P(Y=1|X=(0,1,0)) }[/math] as
[math]\displaystyle{ \,r(X)=P(Y=1|X=(0,1,0))=\frac{P(X=(0,1,0)|Y=1)P(Y=1)}{P(X=(0,1,0)|Y=1)P(Y=1)+P(X=(0,1,0)|Y=0)P(Y=0)}=\frac{0.025}{0.125}=0.2\lt \frac{1}{2} }[/math]
Thus, we classify the new student into class 0, namely, we predict him to fail in this course.
- Notice: Although the Bayes rule is optimal, we still need other methods, since it is generally impossible for us to know the prior [math]\displaystyle{ \,P(Y=1) }[/math], and class conditional density [math]\displaystyle{ \,P(X=x|Y=1) }[/math] and ultimately calculate the value of [math]\displaystyle{ \,r(X) }[/math], which makes Bayes rule inconvenient in practice.
Currently, there are four primary classifier based on Bayes Classifier: Naive Bayes classifier[2], tree-augmented naive Bayes (TAN), Bayesian network augmented naive Bayes (BAN) and general Bayesian network (GBN).
useful link:Decision Theory, Bayes Classifier
Bayesian vs. Frequentist
Intuitively, to solve a two-class problem, we may have the following two approaches:
1) If [math]\displaystyle{ \,P(Y=1|X=x)\gt P(Y=0|X=x) }[/math], then [math]\displaystyle{ \,h(x)=1 }[/math], otherwise [math]\displaystyle{ \,h(x)=0 }[/math].
2) If [math]\displaystyle{ \,P(X=x|Y=1)\gt P(X=x|Y=0) }[/math], then [math]\displaystyle{ \,h(x)=1 }[/math], otherwise [math]\displaystyle{ \,h(x)=0 }[/math].
One obvious difference between these two methods is that the first one considers probability as changing based on observation while the second one considers probablity as having objective existence. Actually, they represent two different schools in statistics.
During the history of statistics, there are two major classification methods : Bayesian and frequentist. The two methods represent two different ways of thoughts and hold different view to define probability. The followings are the main differences between Bayes and Frequentist.
Frequentist
- Probability is objective.
- Data is a repeatable random sample(there is a frequency).
- Parameters are fixed and unknown constant.
- Not applicable to single event. For example, a frequentist cannot predict the weather of tomorrow because tomorrow is only one unique event, and cannot be referred to a frequency in a lot of samples.
Bayesian
- Probability is subjective.
- Data are fixed.
- Parameters are unknown and random variables that have a given distribution and other probability statements can be made about them.
- Can be applied to single events based on degree of confidence or beliefs. For example, Bayesian can predict tomorrow's weather, such as having the probability of [math]\displaystyle{ \,50% }[/math] of rain.
Example
Suppose there is a man named Jack. In Bayesian method, at first, one can see this man (object), and then judge whether his name is Jack (label). On the other hand, in Frequentist method, one doesn’t see the man (object), but can see the photos (label) of this man to judge whether he is Jack.
Linear and Quadratic Discriminant Analysis - October 2,2009
Introduction
Notation
Let us first introduce some new notation for the following sections.
Multi-class Classification:
Y takes on more than two values.
Recall that in the discussion of the Bayes Classifier, we introduced Bayes Formula:
- [math]\displaystyle{ \begin{align} P(Y=y|X=x) &=\frac{P(X=x|Y=y)P(Y=y)}{\Sigma_{\forall y \in \mathcal{Y}}P(X=x|Y=y)P(Y=y)} \end{align} }[/math]
We will use new labels for the following equivalent formula:
- [math]\displaystyle{ \begin{align} P(Y=k|X=x) &=\frac{f_k(x)\pi_k}{\Sigma_kf_k(x)\pi_k} \end{align} }[/math]
- [math]\displaystyle{ \,f_k }[/math] is called the class conditional density; also referred to previously as the likelihood function. Essentially, this is the function that allows us to reason about a parameter given a certain outcome.
- [math]\displaystyle{ \,\pi_k }[/math] is called the prior probability. This is a probability distribution that represents what we know (or believe we know) about a population.
- [math]\displaystyle{ \,\Sigma_k }[/math] is the sum with respect to all [math]\displaystyle{ \,k }[/math] classes.
Approaches
Representing the optimal method, Bayes classifier cannot be used in the most practical situations though, since usually the prior probability is unknown. Fortunately, other methods of classification have been evolved. These methods fall into three general categories.
1 Empirical Risk Minimization:Choose a set fo classifier [math]\displaystyle{ \mathcal{H} }[/math] and find [math]\displaystyle{ \,h^* \epsilon H }[/math], minimize some estimate of [math]\displaystyle{ \,L(H) }[/math].
2 Regression:Find an estimate [math]\displaystyle{ (\hat r) }[/math] of the function [math]\displaystyle{ \ r }[/math] and deifne
- [math]\displaystyle{ \, h(X)= \left\{\begin{matrix} 1 & \hat r(x)\gt \frac{1}{2} \\ 0 & \mathrm{otherwise} \end{matrix}\right. }[/math]
3 Density estimation, estimate [math]\displaystyle{ \ P(X = x|Y = 0) }[/math] and [math]\displaystyle{ \ P(X = x|Y = 1) }[/math]
Note:
The third approach, in this form, is not popular because density estimation doesn't work very well with dimension greater than 2. However this approach is the simplest and we can assume a parametric model for the densities.
Linear Discriminate Analysis and Quadratic Discriminate Analysis are examples of the third approach, density estimation.
LDA
Motivation
The Bayes classifier is optimal. Unfortunately, the prior and conditional density of most data is not known. Some estimation of these should be made if we want to classify some data.
The simplest way to achieve this is to assume that all the class densities are approximately a multivariate normal distribution, find the parameters of each such distribution, and use them to calculate the conditional density and prior for unknown points, thus approximating the Bayesian classifier to choose the most likely class. In addition, if the covariance of each class density is assumed to be the same, the number of unknown parameters is reduced and the model is easy to fit and use, as seen later.
History
The name Linear Discriminant Analysis comes from the fact that these simplifications produce a linear model, which is used to discriminate between classes. In many cases, this simple model is sufficient to provide a near optimal classification - for example, the Z-Score credit risk model, designed by Edward Altman in 1968, which is essentially a weighted LDA, revisited in 2000, has shown an 85-90% success rate predicting bankruptcy, and is still in use today.
Purpose
1 feature selection
2 which classification rule best seperate the classes
Definition
To perform LDA we make two assumptions.
- The clusters belonging to all classes each follow a multivariate normal distribution.
[math]\displaystyle{ x \in \mathbb{R}^d }[/math] [math]\displaystyle{ f_k(x)=\frac{1}{ (2\pi)^{d/2}|\Sigma_k|^{1/2} }\exp\left( -\frac{1}{2} [x - \mu_k]^\top \Sigma_k^{-1} [x - \mu_k] \right) }[/math]
where [math]\displaystyle{ \ f_k(x) }[/math] is a class conditional density
- Simplification Assumption: Each cluster has the same covariance matrix [math]\displaystyle{ \,\Sigma }[/math] equal to the covariance of [math]\displaystyle{ \Sigma_k \forall k }[/math].
We wish to solve for the decision boundary where the error rates for classifying a point are equal, where one side of the boundary gives a lower error rate for one class and the other side gives a lower error rate for the other class.
So we solve [math]\displaystyle{ \,r_k(x)=r_l(x) }[/math] for all the pairwise combinations of classes.
[math]\displaystyle{ \,\Rightarrow Pr(Y=k|X=x)=Pr(Y=l|X=x) }[/math]
[math]\displaystyle{ \,\Rightarrow \frac{Pr(X=x|Y=k)Pr(Y=k)}{Pr(X=x)}=\frac{Pr(X=x|Y=l)Pr(Y=l)}{Pr(X=x)} }[/math] using Bayes' Theorem
[math]\displaystyle{ \,\Rightarrow Pr(X=x|Y=k)Pr(Y=k)=Pr(X=x|Y=l)Pr(Y=l) }[/math] by canceling denominators
[math]\displaystyle{ \,\Rightarrow f_k(x)\pi_k=f_l(x)\pi_l }[/math]
[math]\displaystyle{ \,\Rightarrow \frac{1}{ (2\pi)^{d/2}|\Sigma|^{1/2} }\exp\left( -\frac{1}{2} [x - \mu_k]^\top \Sigma^{-1} [x - \mu_k] \right)\pi_k=\frac{1}{ (2\pi)^{d/2}|\Sigma|^{1/2} }\exp\left( -\frac{1}{2} [x - \mu_l]^\top \Sigma^{-1} [x - \mu_l] \right)\pi_l }[/math]
[math]\displaystyle{ \,\Rightarrow \exp\left( -\frac{1}{2} [x - \mu_k]^\top \Sigma^{-1} [x - \mu_k] \right)\pi_k=\exp\left( -\frac{1}{2} [x - \mu_l]^\top \Sigma^{-1} [x - \mu_l] \right)\pi_l }[/math] Since both [math]\displaystyle{ \Sigma }[/math] are equal based on the assumptions specific to LDA.
[math]\displaystyle{ \,\Rightarrow -\frac{1}{2} [x - \mu_k]^\top \Sigma^{-1} [x - \mu_k] + \log(\pi_k)=-\frac{1}{2} [x - \mu_l]^\top \Sigma^{-1} [x - \mu_l] +\log(\pi_l) }[/math] taking the log of both sides.
[math]\displaystyle{ \,\Rightarrow \log(\frac{\pi_k}{\pi_l})-\frac{1}{2}\left( x^\top\Sigma^{-1}x + \mu_k^\top\Sigma^{-1}\mu_k - 2x^\top\Sigma^{-1}\mu_k - x^\top\Sigma^{-1}x - \mu_l^\top\Sigma^{-1}\mu_l + 2x^\top\Sigma^{-1}\mu_l \right)=0 }[/math] by expanding out
[math]\displaystyle{ \,\Rightarrow \log(\frac{\pi_k}{\pi_l})-\frac{1}{2}\left( \mu_k^\top\Sigma^{-1}\mu_k-\mu_l^\top\Sigma^{-1}\mu_l - 2x^\top\Sigma^{-1}(\mu_k-\mu_l) \right)=0 }[/math] after canceling out like terms and factoring.
We can see that this is a linear function in [math]\displaystyle{ \ x }[/math] with general form [math]\displaystyle{ \,ax+b=0 }[/math].
Actually, this linear log function shows that the decision boundary between class [math]\displaystyle{ \ k }[/math] and class [math]\displaystyle{ \ l }[/math], i.e. [math]\displaystyle{ \ P(G=k|X=x)=P(G=l|X=x) }[/math], is linear in [math]\displaystyle{ \ x }[/math]. Given any pair of classes, decision boundaries are always linear. In [math]\displaystyle{ \ d }[/math] dimensions, we separate regions by hyperplanes.
In the special case where the number of samples from each class are equal ([math]\displaystyle{ \,\pi_k=\pi_l }[/math]), the boundary surface or line lies halfway between [math]\displaystyle{ \,\mu_l }[/math] and [math]\displaystyle{ \,\mu_k }[/math]
QDA
The concept uses a same idea as LDA of finding a boundary where the error rate for classification between classes are equal, except the assumption that each cluster has the same variance [math]\displaystyle{ \,\Sigma }[/math] equal to the mean variance of [math]\displaystyle{ \Sigma_k \forall k }[/math] is removed. We can use a hypothesis test with [math]\displaystyle{ \ H_0 }[/math]: [math]\displaystyle{ \Sigma_k \forall k }[/math]=[math]\displaystyle{ \,\Sigma }[/math].The best method is likelihood ratio test.
Following along from where QDA diverges from LDA.
[math]\displaystyle{ \,f_k(x)\pi_k=f_l(x)\pi_l }[/math]
[math]\displaystyle{ \,\Rightarrow \frac{1}{ (2\pi)^{d/2}|\Sigma_k|^{1/2} }\exp\left( -\frac{1}{2} [x - \mu_k]^\top \Sigma_k^{-1} [x - \mu_k] \right)\pi_k=\frac{1}{ (2\pi)^{d/2}|\Sigma_l|^{1/2} }\exp\left( -\frac{1}{2} [x - \mu_l]^\top \Sigma_l^{-1} [x - \mu_l] \right)\pi_l }[/math]
[math]\displaystyle{ \,\Rightarrow \frac{1}{|\Sigma_k|^{1/2} }\exp\left( -\frac{1}{2} [x - \mu_k]^\top \Sigma_k^{-1} [x - \mu_k] \right)\pi_k=\frac{1}{|\Sigma_l|^{1/2} }\exp\left( -\frac{1}{2} [x - \mu_l]^\top \Sigma_l^{-1} [x - \mu_l] \right)\pi_l }[/math] by cancellation
[math]\displaystyle{ \,\Rightarrow -\frac{1}{2}\log(|\Sigma_k|)-\frac{1}{2} [x - \mu_k]^\top \Sigma_k^{-1} [x - \mu_k]+\log(\pi_k)=-\frac{1}{2}\log(|\Sigma_l|)-\frac{1}{2} [x - \mu_l]^\top \Sigma_l^{-1} [x - \mu_l]+\log(\pi_l) }[/math] by taking the log of both sides
[math]\displaystyle{ \,\Rightarrow \log(\frac{\pi_k}{\pi_l})-\frac{1}{2}\log(\frac{|\Sigma_k|}{|\Sigma_l|})-\frac{1}{2}\left( x^\top\Sigma_k^{-1}x + \mu_k^\top\Sigma_k^{-1}\mu_k - 2x^\top\Sigma_k^{-1}\mu_k - x^\top\Sigma_l^{-1}x - \mu_l^\top\Sigma_l^{-1}\mu_l + 2x^\top\Sigma_l^{-1}\mu_l \right)=0 }[/math] by expanding out
[math]\displaystyle{ \,\Rightarrow \log(\frac{\pi_k}{\pi_l})-\frac{1}{2}\log(\frac{|\Sigma_k|}{|\Sigma_l|})-\frac{1}{2}\left( x^\top(\Sigma_k^{-1}-\Sigma_l^{-1})x + \mu_k^\top\Sigma_k^{-1}\mu_k - \mu_l^\top\Sigma_l^{-1}\mu_l - 2x^\top(\Sigma_k^{-1}\mu_k-\Sigma_l^{-1}\mu_l) \right)=0 }[/math] this time there are no cancellations, so we can only factor
The final result is a quadratic equation specifying a curved boundary between classes with general form [math]\displaystyle{ \,ax^2+bx+c=0 }[/math].
It is quadratic because there is no boundaries.
Linear and Quadratic Discriminant Analysis cont'd - October 5, 2009
Summarizing LDA and QDA
We can summarize what we have learned on LDA and QDA so far into the following theorem.
Theorem:
Suppose that [math]\displaystyle{ \,Y \in \{1,\dots,k\} }[/math], if [math]\displaystyle{ \,f_k(x) = Pr(X=x|Y=k) }[/math] is Gaussian, the Bayes Classifier rule is
- [math]\displaystyle{ \,h(X) = \arg\max_{k} \delta_k(x) }[/math]
where
- [math]\displaystyle{ \,\delta_k = - \frac{1}{2}log(|\Sigma_k|) - \frac{1}{2}(x-\mu_k)^\top\Sigma_k^{-1}(x-\mu_k) + log (\pi_k) }[/math] (quadratic)
- Note The decision boundary between classes [math]\displaystyle{ k }[/math] and [math]\displaystyle{ l }[/math] is quadratic in [math]\displaystyle{ x }[/math].
If the covariance of the Gaussians are the same, this becomes
- [math]\displaystyle{ \,\delta_k = x^\top\Sigma^{-1}\mu_k - \frac{1}{2}\mu_k^\top\Sigma^{-1}\mu_k + log (\pi_k) }[/math] (linear)
- Note [math]\displaystyle{ \,\arg\max_{k} \delta_k(x) }[/math]returns the set of k for which [math]\displaystyle{ \,\delta_k(x) }[/math] attains its largest value.
In practice
We need to estimate the prior, so in order to do this, we use the sample estimates of [math]\displaystyle{ \,\pi,\mu_k,\Sigma_k }[/math] in place of the true values, i.e.
[math]\displaystyle{ \,\hat{\pi_k} = \hat{Pr}(y=k) = \frac{n_k}{n} }[/math]
[math]\displaystyle{ \,\hat{\mu_k} = \frac{1}{n_k}\sum_{i:y_i=k}x_i }[/math]
[math]\displaystyle{ \,\hat{\Sigma_k} = \frac{1}{n_k}\sum_{i:y_i=k}(x_i-\hat{\mu_k})(x_i-\hat{\mu_k})^\top }[/math]
In the case where we have a common covariance matrix, we get the ML estimate to be
[math]\displaystyle{ \,\Sigma=\frac{\sum_{r=1}^{k}(n_r\Sigma_r)}{\sum_{l=1}^{k}(n_l)} }[/math]
Computation
Case 1: (Example) [math]\displaystyle{ \, \Sigma_k = I }[/math]
This means that the data is distributed symmetrically around the center [math]\displaystyle{ \mu }[/math], i.e. the isocontours are all circles.
We have:
[math]\displaystyle{ \,\delta_k = - \frac{1}{2}log(|I|) - \frac{1}{2}(x-\mu_k)^\top I(x-\mu_k) + log (\pi_k) }[/math]
We see that the first term in the above equation, [math]\displaystyle{ \,\frac{1}{2}log(|I|) }[/math], is zero. The second term contains [math]\displaystyle{ \, (x-\mu_k)^\top I(x-\mu_k) = (x-\mu_k)^\top(x-\mu_k) }[/math], which is the squared Euclidean distance between [math]\displaystyle{ \,x }[/math] and [math]\displaystyle{ \,\mu_k }[/math]. Therefore we can find the distance between a point and each center and adjust it with the log of the prior, [math]\displaystyle{ \,log(\pi_k) }[/math]. The class that has the minimum distance will maximise [math]\displaystyle{ \,\delta_k }[/math]. According to the theorem, we can then classify the point to a specific class [math]\displaystyle{ \,k }[/math]. In addition, [math]\displaystyle{ \, \Sigma_k = I }[/math] implies that our data is spherical.
Case 2: (General Case) [math]\displaystyle{ \, \Sigma_k \ne I }[/math]
We can decompose this as:
[math]\displaystyle{ \, \Sigma_k = USV^\top = USU^\top }[/math] (In general when [math]\displaystyle{ \,X=USV^\top }[/math], [math]\displaystyle{ \,U }[/math] is the eigenvectors of [math]\displaystyle{ \,XX^T }[/math] and [math]\displaystyle{ \,V }[/math] is the eigenvectors of [math]\displaystyle{ \,X^\top X }[/math]. So if [math]\displaystyle{ \, X }[/math] is symmetric, we will have [math]\displaystyle{ \, U=V }[/math]. Here [math]\displaystyle{ \, \Sigma }[/math] is symmetric)
and the inverse of [math]\displaystyle{ \,\Sigma_k }[/math] is
[math]\displaystyle{ \, \Sigma_k^{-1} = (USU^\top)^{-1} = (U^\top)^{-1}S^{-1}U^{-1} = US^{-1}U^\top }[/math] (since [math]\displaystyle{ \,U }[/math] is orthonormal)
So from the formula for [math]\displaystyle{ \,\delta_k }[/math], the second term is
- [math]\displaystyle{ \begin{align} (x-\mu_k)^\top\Sigma_k^{-1}(x-\mu_k)&= (x-\mu_k)^\top US^{-1}U^T(x-\mu_k)\\ & = (U^\top x-U^\top\mu_k)^\top S^{-1}(U^\top x-U^\top \mu_k)\\ & = (U^\top x-U^\top\mu_k)^\top S^{-\frac{1}{2}}S^{-\frac{1}{2}}(U^\top x-U^\top\mu_k) \\ & = (S^{-\frac{1}{2}}U^\top x-S^{-\frac{1}{2}}U^\top\mu_k)^\top I(S^{-\frac{1}{2}}U^\top x-S^{-\frac{1}{2}}U^\top \mu_k) \\ & = (S^{-\frac{1}{2}}U^\top x-S^{-\frac{1}{2}}U^\top\mu_k)^\top(S^{-\frac{1}{2}}U^\top x-S^{-\frac{1}{2}}U^\top \mu_k) \\ \end{align} }[/math]
where we have the Euclidean distance between [math]\displaystyle{ \, S^{-\frac{1}{2}}U^\top x }[/math] and [math]\displaystyle{ \, S^{-\frac{1}{2}}U^\top\mu_k }[/math].
A transformation of all the data points can be done from [math]\displaystyle{ \,x }[/math] to [math]\displaystyle{ \,x^* }[/math] where [math]\displaystyle{ \, x^* \leftarrow S^{-\frac{1}{2}}U^\top x }[/math].
It is now possible to do classification with [math]\displaystyle{ \,x^* }[/math], treating it as in Case 1 above.
Note that when we have multiple classes, they must all have the same transformation, else, ahead of time we would have to assume a data point belongs to one class or the other. All classes therefore need to have the same shape for classification to be applicable using this method. So this method works for LDA.
If the classes have different shapes, in another word, have different covariance [math]\displaystyle{ \,\Sigma_k }[/math], can we use the same method to transform all data points [math]\displaystyle{ \,x }[/math] to [math]\displaystyle{ \,x^* }[/math]?
The answer is NO. Consider that you have two classes with different shapes, then consider transforming them to the same shape. Given a data point, justify which class this point belongs to. The question is, which transformation can you use? For example, if you use the transformation of class A, then you have assumed that this data point belongs to class A.
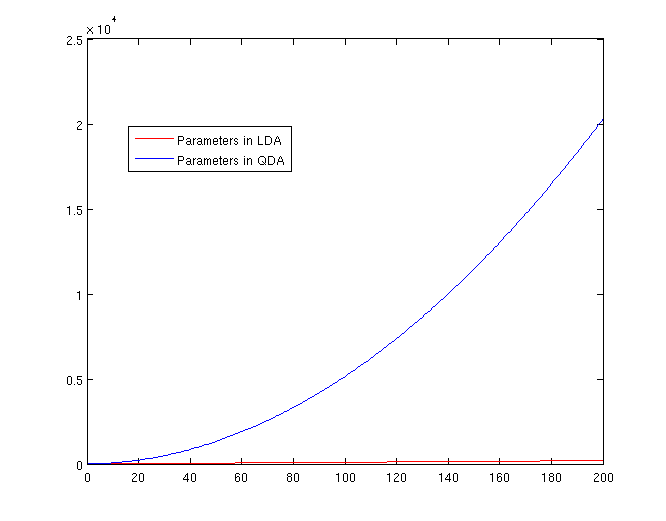
The Number of Parameters in LDA and QDA
Both LDA and QDA require us to estimate parameters. The more estimation we have to do, the less robust our classification algorithm will be.
LDA: Since we just need to compare the differences between one given class and remaining [math]\displaystyle{ \,K-1 }[/math] classes, totally, there are [math]\displaystyle{ \,K-1 }[/math] differences. For each of them, [math]\displaystyle{ \,a^{T}x+b }[/math] requires [math]\displaystyle{ \,d+1 }[/math] parameters. Therefore, there are [math]\displaystyle{ \,(K-1)\times(d+1) }[/math] parameters.
QDA: For each of the differences, [math]\displaystyle{ \,x^{T}ax + b^{T}x + c }[/math] requires [math]\displaystyle{ \frac{1}{2}(d+1)\times d + d + 1 = \frac{d(d+3)}{2}+1 }[/math] parameters. Therefore, there are [math]\displaystyle{ (K-1)(\frac{d(d+3)}{2}+1) }[/math] parameters.
LDA and QDA in Matlab - October 7, 2009
We have examined the theory behind Linear Discriminant Analysis (LDA) and Quadratic Discriminant Analysis (QDA) above; how do we use these algorithms in practice? Matlab offers us a function called classify that allows us to perform LDA and QDA quickly and easily.
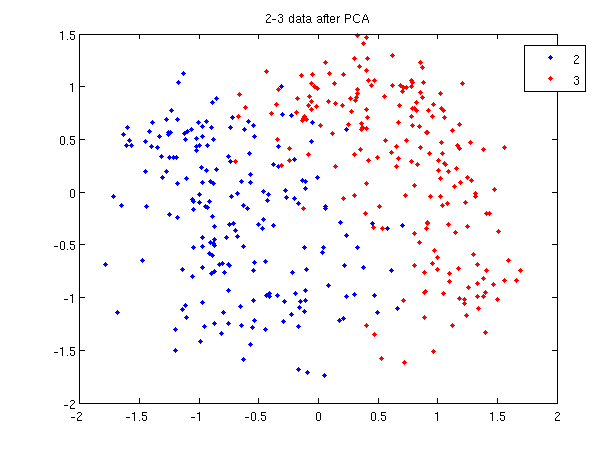
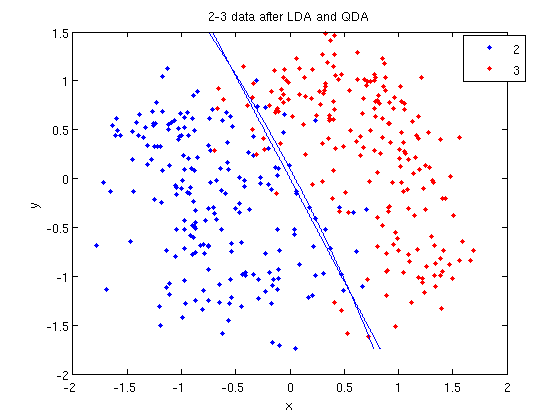
In class, we were shown an example of using LDA and QDA on the 2_3 data that is used in the first assignment. The code below reproduces that example, slightly modified, and explains each step.
>> load 2_3; >> [U, sample] = princomp(X'); >> sample = sample(:,1:2);
- First, we do principal component analysis (PCA) on the 2_3 data to reduce the dimensionality of the original data from 64 dimensions to 2. Doing this makes it much easier to visualize the results of the LDA and QDA algorithms.
>> plot (sample(1:200,1), sample(1:200,2), '.'); >> hold on; >> plot (sample(201:400,1), sample(201:400,2), 'r.');
- Recall that in the 2_3 data, the first 200 elements are images of the number two handwritten and the last 200 elements are images of the number three handwritten. This code sets up a plot of the data such that the points that represent a 2 are blue, while the points that represent a 3 are red.
title and legend for information on adding the title and legend.- Before using
classifywe can set up a vector that contains the actual labels for our data, to train the classification algorithm. If we don't know the labels for the data, then the element in thegroupvector should be an empty string orNaN. (See grouping data for more information.)
>> group = ones(400,1); >> group(201:400) = 2;
- We can now classify our data.
>> [class, error, POSTERIOR, logp, coeff] = classify(sample, sample, group, 'linear');
- The full details of this line can be examined in the Matlab help file linked above. What we care about are
class, which contains the labels that the algorithm thinks that each data point belongs to, andcoeff, which contains information about the line that algorithm created to separate the data into each class.
- We can see the efficacy of the algorithm by comparing
classtogroup.
>> sum (class==group) ans = 369
- This compares the value in
classto the value ingroup. The answer of 369 tells us that the algorithm correctly determined the class of the point 369 times, out of a possible 400 data points. This gives us an empirical error rate of 0.0775.
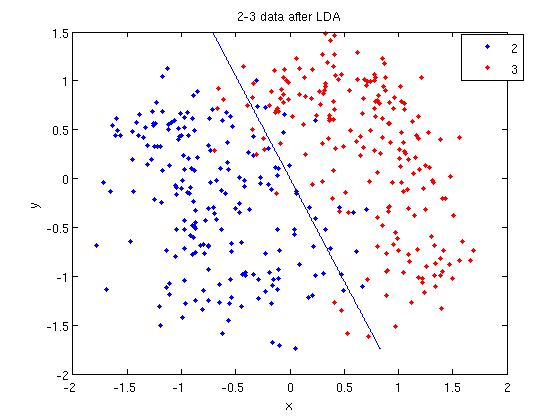
- We can see the line produced by LDA using
coeff.
>> k = coeff(1,2).const;
>> l = coeff(1,2).linear;
>> f = sprintf('0 = %g+%g*x+%g*y', k, l(1), l(2));
>> ezplot(f, [min(sample(:,1)), max(sample(:,1)), min(sample(:,2)), max(sample(:,2))]);
- Those familiar with the programming language C will find the
sprintfline refreshingly familiar; those with no exposure to C are directed to Matlab'ssprintfpage. Essentially, this code sets up the equation of the line in the form0 = a + bx + cy. We then use theezplotfunction to plot the line.
- Let's perform the same steps, except this time using QDA. The main difference with QDA is a slightly different call to
classify, and a more complicated procedure to plot the line.
>> [class, error, POSTERIOR, logp, coeff] = classify(sample, sample, group, 'quadratic');
>> sum (class==group)
ans =
371
>> k = coeff(1,2).const;
>> l = coeff(1,2).linear;
>> q = coeff(1,2).quadratic;
>> f = sprintf('0 = %g+%g*x+%g*y+%g*x^2+%g*x.*y+%g*y.^2', k, l, q(1,1), q(1,2)+q(2,1), q(2,2));
>> ezplot(f, [min(sample(:,1)), max(sample(:,1)), min(sample(:,2)), max(sample(:,2))]);
classify can also be used with other discriminant analysis algorithms. The steps laid out above would only need to be modified slightly for those algorithms.
Recall: An analysis of the function of princomp in matlab.
In our assignment 1, we have learnt that how to perform Principal Component Analysis using SVD method. In fact, the matlab offers us a function called princomp which can perform PCA conveniently. From the matlab help file on princomp, you can find the details about this function. But here we will analyze the code of the function of princomp() in matlab to find something different when comparing with SVD method. The following is the code of princomp and explanations to some emphasized steps.
function [pc, score, latent, tsquare] = princomp(x);
% PRINCOMP Principal Component Analysis (centered and scaled data).
% [PC, SCORE, LATENT, TSQUARE] = PRINCOMP(X) takes a data matrix X and
% returns the principal components in PC, the so-called Z-scores in SC
% ORES, the eigenvalues of the covariance matrix of X in LATENT,
% and Hotelling's T-squared statistic for each data point in TSQUARE.
% Reference: J. Edward Jackson, A User's Guide to Principal Components
% John Wiley & Sons, Inc. 1991 pp. 1-25.
% B. Jones 3-17-94
% Copyright 1993-2002 The MathWorks, Inc.
% $Revision: 2.9 $ $Date: 2002/01/17 21:31:45 $
[m,n] = size(x); % get the lengh of the rows and columns of matrix x.
r = min(m-1,n); % max possible rank of X
avg = mean(x); % the mean of every column of X
centerx = (x - avg(ones(m,1),:));
% centers X by subtracting off column means
[U,latent,pc] = svd(centerx./sqrt(m-1),0);
% "economy size" decomposition
score = centerx*pc;
% the representation of X in the principal component space
if nargout < 3
return;
end
latent = diag(latent).^2;
if (r latent = [latent(1:r); zeros(n-r,1)];
score(:,r+1:end) = 0;
end
if nargout < 4
return;
end
tmp = sqrt(diag(1./latent(1:r)))*score(:,1:r)';
tsquare = sum(tmp.*tmp)';
From the above code, we should pay attention to the following aspects when comparing with SVD method:
First, Rows of [math]\displaystyle{ \,X }[/math] correspond to observations, columns to variables. When using princomp on 2_3 data in assignment 1, note that we take the transpose of [math]\displaystyle{ \,X }[/math].
>> load 2_3; >> [U, score] = princomp(X');
Second, princomp centers X by subtracting off column means.
The third, when [math]\displaystyle{ \,X=UdV' }[/math], princomp uses [math]\displaystyle{ \,V }[/math] as coefficients for principal components, rather than [math]\displaystyle{ \,U }[/math].
The following is an example to perform PCA using princomp and SVD respectively to get the same results.
- SVD method
>> load 2_3 >> mn=mean(X,2); >> X1=X-repmat(mn,1,400); >> [s d v]=svd(X1'); >> y=X1'*v;
- princomp
>>[U score]=princomp(X');
Then we can see that y=score, v=U.
Trick: Using LDA to do QDA - October 7, 2009
There is a trick that allows us to use the linear discriminant analysis (LDA) algorithm to generate as its output a quadratic function that can be used to classify data. This trick is similar to, but more primitive than, the Kernel trick that will be discussed later in the course.
Essentially, the trick involves adding one or more new features (i.e. new dimensions) that just contain our original data projected to that dimension. We then do LDA on our new higher-dimensional data. The answer provided by LDA can then be collapsed onto a lower dimension, giving us a quadratic answer.
Motivation
Why would we want to use LDA over QDA? In situations where we have fewer data points, LDA turns out to be more robust.
If we look back at the equations for LDA and QDA, we see that in LDA we must estimate [math]\displaystyle{ \,\mu_1 }[/math], [math]\displaystyle{ \,\mu_2 }[/math] and [math]\displaystyle{ \,\Sigma }[/math]. In QDA we must estimate all of those, plus another [math]\displaystyle{ \,\Sigma }[/math]; the extra [math]\displaystyle{ \,\frac{d(d-1)}{2} }[/math] estimations make QDA less robust with fewer data points.
Theoretically
Suppose we can estimate some vector [math]\displaystyle{ \underline{w}^T }[/math] such that
[math]\displaystyle{ y = \underline{w}^Tx }[/math]
where [math]\displaystyle{ \underline{w} }[/math] is a d-dimensional column vector, and [math]\displaystyle{ x\ \epsilon\ \Re^d }[/math] (vector in d dimensions).
We also have a non-linear function [math]\displaystyle{ g(x) = y = x^Tvx + \underline{w}^Tx }[/math] that we cannot estimate.
Using our trick, we create two new vectors, [math]\displaystyle{ \,\underline{w}^* }[/math] and [math]\displaystyle{ \,x^* }[/math] such that:
[math]\displaystyle{ \underline{w}^{*T} = [w_1,w_2,...,w_d,v_1,v_2,...,v_d] }[/math]
and
[math]\displaystyle{ x^{*T} = [x_1,x_2,...,x_d,{x_1}^2,{x_2}^2,...,{x_d}^2] }[/math]
We can then estimate a new function, [math]\displaystyle{ g^*(x,x^2) = y^* = \underline{w}^{*T}x^* }[/math].
Note that we can do this for any [math]\displaystyle{ x }[/math] and in any dimension; we could extend a [math]\displaystyle{ D \times n }[/math] matrix to a quadratic dimension by appending another [math]\displaystyle{ D \times n }[/math] matrix with the original matrix squared, to a cubic dimension with the original matrix cubed, or even with a different function altogether, such as a [math]\displaystyle{ \,sin(x) }[/math] dimension.
By Example
Let's use our trick to do a quadratic analysis of the 2_3 data using LDA.
>> load 2_3; >> [U, sample] = princomp(X'); >> sample = sample(:,1:2);
- We start off the same way, by using PCA to reduce the dimensionality of our data to 2.
>> X_star = zeros(400,4);
>> X_star(:,1:2) = sample(:,:);
>> for i=1:400
for j=1:2
X_star(i,j+2) = X_star(i,j)^2;
end
end
- This projects our sample into two more dimensions by squaring our initial two dimensional data set.
>> group = ones(400,1); >> group(201:400) = 2; >> [class, error, POSTERIOR, logp, coeff] = classify(X_star, X_star, group, 'linear'); >> sum (class==group) ans = 375
- We can now display our results.
>> k = coeff(1,2).const;
>> l = coeff(1,2).linear;
>> f = sprintf('0 = %g+%g*x+%g*y+%g*(x)^2+%g*(y)^2', k, l(1), l(2),l(3),l(4));
>> ezplot(f,[min(sample(:,1)), max(sample(:,1)), min(sample(:,2)), max(sample(:,2))]);
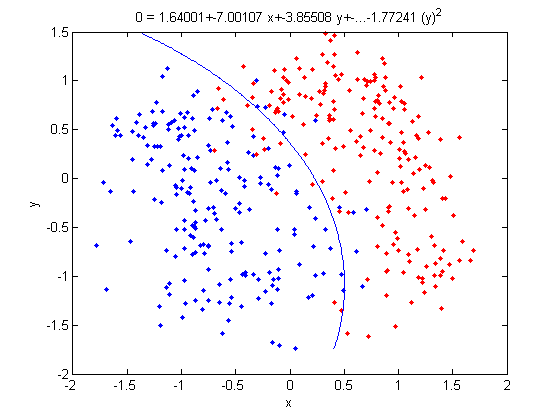
- Not only does LDA give us a better result than it did previously, it actually beats QDA, which only correctly classified 371 data points for this data set. Continuing this procedure by adding another two dimensions with [math]\displaystyle{ x^4 }[/math] (i.e. we set
X_star(i,j+2) = X_star(i,j)^4) we can correctly classify 376 points.
Introduction to Fisher's Discriminant Analysis - October 7, 2009
Fisher's Discriminant Analysis (FDA), also known as Fisher's Linear Discriminant Analysis (LDA) in some sources, is a classical feature extraction technique. It was originally described in 1936 by Sir Ronald Aylmer Fisher, an English statistician and eugenicist who has been described as one of the founders of modern statistical science. His original paper describing FDA can be found here; a Wikipedia article summarizing the algorithm can be found here.
LDA is for classification and FDA is used for feature extraction.
Contrasting FDA with PCA
The goal of FDA is in contrast to our other main feature extraction technique, principal component analysis (PCA).
- In PCA, we map data to lower dimensions to maximize the variation in those dimensions.
- In FDA, we map data to lower dimensions to best separate data in different classes.
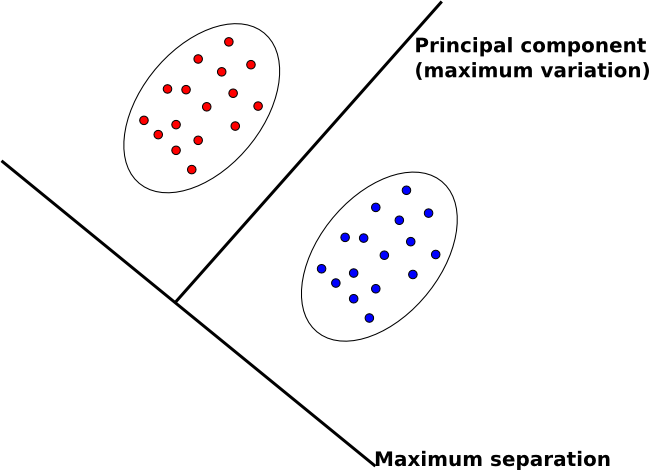
Because we are concerned with identifying which class data belongs to, FDA is often a better feature extraction algorithm for classification.
Another difference between PCA and FDA is that FDA is a supervised algorithm; that is, we know what class data belongs to, and we exploit that knowledge to find a good projection to lower dimensions.
Intuitive Description of FDA
An intuitive description of FDA can be given by visualizing two clouds of data, as shown above. Ideally, we would like to collapse all of the data points in each cloud onto one point on some projected line, then make those two points as far apart as possible. In doing so, we make it very easy to tell which class a data point belongs to. In practice, it is not possible to collapse all of the points in a cloud to one point, but we attempt to make all of the points in a cloud close to each other while simultaneously far from the points in the other cloud.
Example in R
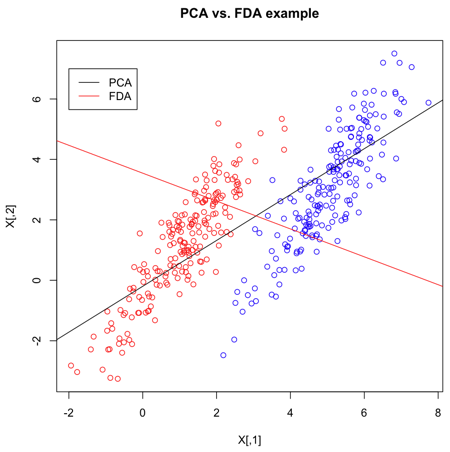
>> X = matrix(nrow=400,ncol=2)
>> X[1:200,] = mvrnorm(n=200,mu=c(1,1),Sigma=matrix(c(1,1.5,1.5,3),2))
>> X[201:400,] = mvrnorm(n=200,mu=c(5,3),Sigma=matrix(c(1,1.5,1.5,3),2))
>> Y = c(rep("red",200),rep("blue",200))
- Create 2 multivariate normal random variables with [math]\displaystyle{ \, \mu_1 = \left( \begin{array}{c}1 \\ 1 \end{array} \right), \mu_2 = \left( \begin{array}{c}5 \\ 3 \end{array} \right). ~\textrm{Cov} = \left( \begin{array}{cc} 1 & 1.5 \\ 1.5 & 3 \end{array} \right) }[/math]. Create
Y, an index indicating which class they belong to.
>> s <- svd(X,nu=1,nv=1)
- Calculate the singular value decomposition of X. The most significant direction is in
s$v[,1], and is displayed as a black line.
>> s2 <- lda(X,grouping=Y)
- The
ldafunction, given the group for each item, uses Fischer's Linear Discriminant Analysis (FLDA) to find the most discriminant direction. This can be found ins2$scaling.
Now that we've calculated the PCA and FLDA decompositions, we create a plot to demonstrate the differences between the two algorithms. FLDA is clearly better suited to discriminating between two classes whereas PCA is primarily good for reducing the number of dimensions when data is high-dimensional.
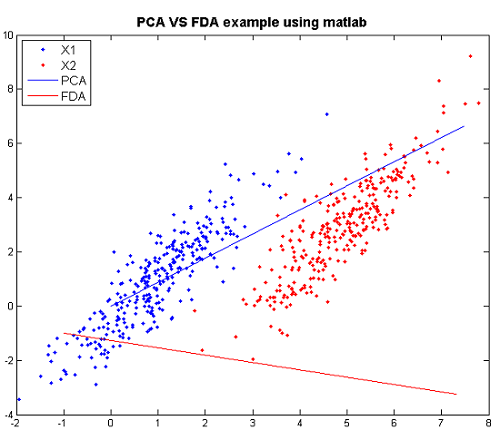
>> plot(X,col=Y,main="PCA vs. FDA example")
- Plot the set of points, according to colours given in Y.
>> slope = s$v[2]/s$v[1] >> intercept = mean(X[,2])-slope*mean(X[,1]) >> abline(a=intercept,b=slope)
- Plot the main PCA direction, drawn through the mean of the dataset. Only the direction is significant.
>> slope2 = s2$scaling[2]/s2$scaling[1] >> intercept2 = mean(X[,2])-slope2*mean(X[,1]) >> abline(a=intercept2,b=slope2,col="red")
- Plot the FLDA direction, again through the mean.
>> legend(-2,7,legend=c("PCA","FDA"),col=c("black","red"),lty=1)
- Labeling the lines directly on the graph makes it easier to interpret.
Ficher's Discriminant Analysis (FDA)
The goal of FDA is to reduce the dimensionality of data in order to have separable data points in a new space. We can consider two kinds of problems:
- 2-class problem
- multi-class problem
Two-class problem - October 9, 2009
In the two-class problem, we have the pre-knowledge that data points belong to two classes. Intuitively speaking points of each class form a cloud around the mean of the class, with each class having possibly different size. To be able to separate the two classes we must determine the class whose mean is closest to a given point while also accounting for the different size of each class, which is represented by the covariance of each class.
Assume [math]\displaystyle{ \underline{\mu_{1}}=\frac{1}{n_{1}}\displaystyle\sum_{i:y_{i}=1}\underline{x_{i}} }[/math] and [math]\displaystyle{ \displaystyle\Sigma_{1} }[/math], represent the mean and covariance of the 1st class, and [math]\displaystyle{ \underline{\mu_{2}}=\frac{1}{n_{2}}\displaystyle\sum_{i:y_{i}=2}\underline{x_{i}} }[/math] and [math]\displaystyle{ \displaystyle\Sigma_{2} }[/math] represent the mean and covariance of the 2nd class. We have to find a transformation which satisfies the following goals:
1.To make the means of these two classes as far apart as possible
- In other words, the goal is to maximize the distance after projection between class 1 and class 2. This can be done by maximizing the distance between the means of the classes after projection. When projecting the data points to a one-dimensional space, all points will be projected to a single line; the line we seek is the one with the direction that achieves maximum separation of classes upon projetion. If the original points are [math]\displaystyle{ \underline{x_{i}} \in \mathbb{R}^{d} }[/math]and the projected points are [math]\displaystyle{ \underline{w}^T \underline{x_{i}} }[/math] then the mean of the projected points will be [math]\displaystyle{ \underline{w}^T \underline{\mu_{1}} }[/math] and [math]\displaystyle{ \underline{w}^T \underline{\mu_{2}} }[/math] for class 1 and class 2 respectively. The goal now becomes to maximize the Euclidean distance between projected means, [math]\displaystyle{ (\underline{w}^T\underline{\mu_{1}}-\underline{w}^T\underline{\mu_{2}})^T (\underline{w}^T\underline{\mu_{1}}-\underline{w}^T\underline{\mu_{2}}) }[/math]. The steps of this maximization are given below.
2.We want to collapse all data points of each class to a single point, i.e., minimize the covariance within classes
- Notice that the variance of the projected classes 1 and 2 are given by [math]\displaystyle{ \underline{w}^T\Sigma_{1}\underline{w} }[/math] and [math]\displaystyle{ \underline{w}^T\Sigma_{2}\underline{w} }[/math]. The second goal is to minimize the sum of these two covariances.
As is demonstrated below, both of these goals can be accomplished simultaneously.
Original points are [math]\displaystyle{ \underline{x_{i}} \in \mathbb{R}^{d} }[/math]
Projected points are [math]\displaystyle{ \underline{z_{i}} \in \mathbb{R}^{1} }[/math] with [math]\displaystyle{ \underline{z_{i}} = \underline{w}^T \cdot\underline{x_{i}} }[/math]
Between class covariance
In this particular case, we want to project all the data points in one dimensional space.
We want to maximize the Euclidean distance between projected means, which is
- [math]\displaystyle{ \begin{align} (\underline{w}^T \underline{\mu_{1}} - \underline{w}^T \underline{\mu_{2}})^T(\underline{w}^T \underline{\mu_{1}} - \underline{w}^T \underline{\mu_{2}}) &= (\underline{\mu_{1}}-\underline{\mu_{2}})^T\underline{w} . \underline{w}^T(\underline{\mu_{1}}-\underline{\mu_{2}})\\ &= \underline{w}^T(\underline{\mu_{1}}-\underline{\mu_{2}})(\underline{\mu_{1}}-\underline{\mu_{2}})^T\underline{w} \end{align} }[/math]
The quantity [math]\displaystyle{ (\underline{\mu_{1}}-\underline{\mu_{2}})(\underline{\mu_{1}}-\underline{\mu_{2}})^T }[/math] is called between class covariance or [math]\displaystyle{ \,S_{B} }[/math].
The goal is to maximize : [math]\displaystyle{ \underline{w}^T S_{B} \underline{w} }[/math]
Within class covariance
Covariance of class 1 is [math]\displaystyle{ \,\Sigma_{1} }[/math] Covariance of class 2 is [math]\displaystyle{ \,\Sigma_{2} }[/math] So covariance of projected points will be [math]\displaystyle{ \,\underline{w}^T \Sigma_{1} \underline{w} }[/math] and [math]\displaystyle{ \underline{w}^T \Sigma_{2} \underline{w} }[/math]
If we sum this two quantities we have
- [math]\displaystyle{ \begin{align} \underline{w}^T \Sigma_{1} \underline{w} + \underline{w}^T \Sigma_{2} \underline{w} &= \underline{w}^T(\Sigma_{1} + \Sigma_{2})\underline{w} \end{align} }[/math]
The quantity [math]\displaystyle{ \,(\Sigma_{1} + \Sigma_{2}) }[/math] is called within class covariance or [math]\displaystyle{ \,S_{W} }[/math]
The goal is to minimize [math]\displaystyle{ \underline{w}^T S_{W} \underline{w} }[/math]
Objective Function
Instead of maximizing [math]\displaystyle{ \underline{w}^T S_{B} \underline{w} }[/math] and minimizing [math]\displaystyle{ \underline{w}^T S_{W} \underline{w} }[/math] we can define the following objective function:
- [math]\displaystyle{ \underset{\underline{w}}{max}\ \frac{\underline{w}^T S_{B} \underline{w}}{\underline{w}^T S_{W} \underline{w}} }[/math]
This maximization problem is equivalent to [math]\displaystyle{ \underset{\underline{w}}{max}\ \underline{w}^T S_{B} \underline{w} }[/math] subject to constraint [math]\displaystyle{ \underline{w}^T S_{W} \underline{w} = 1 }[/math]. We can use the Lagrange multiplier method to solve it:
- [math]\displaystyle{ L(\underline{w},\lambda) = \underline{w}^T S_{B} \underline{w} - \lambda(\underline{w}^T S_{W} \underline{w} - 1) }[/math]
With [math]\displaystyle{ \frac{\part L}{\part \underline{w}} = 0 }[/math] we get:
- [math]\displaystyle{ \begin{align} &\Rightarrow\ 2\ S_{B}\ \underline{w}\ - 2\lambda\ S_{W}\ \underline{w}\ = 0\\ &\Rightarrow\ S_{B}\ \underline{w}\ =\ \lambda\ S_{W}\ \underline{w} \\ &\Rightarrow\ S_{W}^{-1}\ S_{B}\ \underline{w}\ =\ \lambda\ \underline{w} \end{align} }[/math]
Note that [math]\displaystyle{ \, S_{W}=\Sigma_1+\Sigma_2 }[/math] is sum of two positive matrices and so it has an inverse.
Here [math]\displaystyle{ \underline{w} }[/math] is the eigenvector of [math]\displaystyle{ S_{w}^{-1}\ S_{B} }[/math] corresponding to the largest eigenvalue.
In facts, this expression can be simplified even more.
- [math]\displaystyle{ \Rightarrow\ S_{w}^{-1}\ S_{B}\ \underline{w}\ =\ \lambda\ \underline{w} }[/math] with [math]\displaystyle{ S_{B}\ =\ (\underline{\mu_{1}}-\underline{\mu_{2}})(\underline{\mu_{1}}-\underline{\mu_{2}})^T }[/math]
- [math]\displaystyle{ \Rightarrow\ S_{w}^{-1}\ (\underline{\mu_{1}}-\underline{\mu_{2}})(\underline{\mu_{1}}-\underline{\mu_{2}})^T \underline{w}\ =\ \lambda\ \underline{w} }[/math]
The quantity [math]\displaystyle{ (\underline{\mu_{1}}-\underline{\mu_{2}})^T \underline{w} }[/math] and [math]\displaystyle{ \lambda }[/math] are scalars.
So we can say the quantity [math]\displaystyle{ S_{w}^{-1}\ (\underline{\mu_{1}}-\underline{\mu_{2}}) }[/math] is proportional to [math]\displaystyle{ \underline{w} }[/math]
FDA vs. PCA Example in Matlab
We can compare PCA and FDA through the figure produced by matlab.
The following are the code to produce the figure step by step and the explanation for steps.
>>X1=mvnrnd([1,1],[1 1.5;1.5 3],300); >>X2=mvnrnd([5,3],[1 1.5;1.5 3],300); >>X=[X1;X2];
- Create two multivariate normal random variables with [math]\displaystyle{ \, \mu_1 = \left( \begin{array}{c}1 \\ 1 \end{array} \right), \mu_2 = \left( \begin{array}{c}5 \\ 3 \end{array} \right). ~\textrm{Cov} = \left( \begin{array}{cc} 1 & 1.5 \\ 1.5 & 3 \end{array} \right) }[/math].
>>plot(X(1:300,1),X(1:300,2),'.'); >>hold on >>p1=plot(X(301:600,1),X(301:600,2),'r.');
- Plot the the data of the two classes respectively.
>>[U Y]=princomp(X); >>plot([0 U(1,1)*10],[0 U(2,1)*10]);
- Using PCA to find the principal component and plot it.
>>sw=2*[1 1.5;1.5 3]; >>sb=([1; 1]-[5 ;3])*([1; 1]-[5; 3])'; >>g =inv(sw)*sb; >>[v w]=eigs(g); >>plot([v(1,1)*5 0],[v(2,1)*5 0],'r')
- Using FDA to find the principal component and plot it.
Now we can compare them through the figure.
Practical example of 2_3
In this matlab example we explore FDA using our familiar data set 2_3 which consists of 200 handwritten "2" and 200 handwritten "3".
X is a matrix of size 64*400 and each column represents an 8*8 image of "2" or "3". Here X1 gets all "2" and X2 gets all "3".
>>load 2_3 >>X1 = X(:, 1:200); >>X2 = X(:, 201:400);
Next we calculate within class covariance and between class covariance as before.
>>mu1 = mean(X1, 2); >>mu2 = mean(X2, 2); >>sb = (mu1 - mu2) * (mu1 - mu2)'; >>sw = cov(X1') + cov(X2');
We use the first two eigenvectors to project the dato in a two-dimensional space.
>>[v d] = eigs( inv(sw) * sb ); >>w = v(:, 1:2); >>X_hat = w'*X;
Finally we plot the data and visualize the effect of FDA.
>> scatter(ones(1,200),X_hat(1:200)) >> hold on >> scatter(ones(1,200),X_hat(201:400),'r')
FDA for Multi-class Problems - October 14, 2009
For the [math]\displaystyle{ k }[/math]-class problem, we need to find a projection from [math]\displaystyle{ d }[/math]-dimensional space to a [math]\displaystyle{ (k-1) }[/math]-dimensional space.
(It is more reasonable to have at least 2 directions)
Basically, the within class covariance matrix [math]\displaystyle{ \mathbf{S}_{W} }[/math] is easily to obtain:
- [math]\displaystyle{ \begin{align} \mathbf{S}_{W} = \sum_{i=1}^{k} \mathbf{S}_{W,i} \end{align} }[/math]
where [math]\displaystyle{ \mathbf{S}_{W,i} = \frac{1}{n_{i}}\sum_{j: y_{j}=i}(\mathbf{x}_{j} - \mathbf{\mu}_{i})(\mathbf{x}_{j} - \mathbf{\mu}_{i})^{T} }[/math] and [math]\displaystyle{ \mathbf{\mu}_{i} = \frac{\sum_{j: y_{j}=i}\mathbf{x}_{j}}{n_{i}} }[/math].
However, the between class covariance matrix [math]\displaystyle{ \mathbf{S}_{B} }[/math] is not easy to obtain. One of the simplifications is that we may assume that the total covariance [math]\displaystyle{ \mathbf{S}_{T} }[/math] of the data is constant, since [math]\displaystyle{ \mathbf{S}_{W} }[/math] is easy to compute, we can get [math]\displaystyle{ \mathbf{S}_{B} }[/math] using the following relationship:
- [math]\displaystyle{ \begin{align} \mathbf{S}_{B} = \mathbf{S}_{T} - \mathbf{S}_{W} \end{align} }[/math]
Actually, there is another generation for [math]\displaystyle{ \mathbf{S}_{B} }[/math]. Denote a total mean vector [math]\displaystyle{ \mathbf{\mu} }[/math] by
- [math]\displaystyle{ \begin{align} \mathbf{\mu} = \frac{1}{n}\sum_{i}\mathbf{x_{i}} = \frac{1}{n}\sum_{j=1}^{k}n_{j}\mathbf{\mu}_{j} \end{align} }[/math]
Thus the total covariance matrix [math]\displaystyle{ \mathbf{S}_{T} }[/math] is
- [math]\displaystyle{ \begin{align} \mathbf{S}_{T} = \sum_{i}(\mathbf{x_{i}-\mu})(\mathbf{x_{i}-\mu})^{T} \end{align} }[/math]
Thus we obtain
- [math]\displaystyle{ \begin{align} & \mathbf{S}_{T} = \sum_{i=1}^{k}\sum_{j: y_{j}=i}(\mathbf{x}_{j} - \mathbf{\mu}_{i} + \mathbf{\mu}_{i} - \mathbf{\mu})(\mathbf{x}_{j} - \mathbf{\mu}_{i} + \mathbf{\mu}_{i} - \mathbf{\mu})^{T} \\& = \sum_{i=1}^{k}\sum_{j: y_{j}=i}(\mathbf{x}_{j}-\mathbf{\mu}_{i})(\mathbf{x}_{j}-\mathbf{\mu}_{i})^{T}+ \sum_{i=1}^{k}\sum_{j: y_{j}=i}(\mathbf{\mu}_{i}-\mathbf{\mu})(\mathbf{\mu}_{i}-\mathbf{\mu})^{T} \\& = \mathbf{S}_{W} + \sum_{i=1}^{k} n_{i}(\mathbf{\mu}_{i}-\mathbf{\mu})(\mathbf{\mu}_{i}-\mathbf{\mu})^{T} \end{align} }[/math]
Since the total covariance [math]\displaystyle{ \mathbf{S}_{T} }[/math] is the sum of the within class covariance [math]\displaystyle{ \mathbf{S}_{W} }[/math] and the between class covariance [math]\displaystyle{ \mathbf{S}_{B} }[/math], we can denote the second term as the general between class covariance matrix [math]\displaystyle{ \mathbf{S}_{B} }[/math], thus we obtain
- [math]\displaystyle{ \begin{align} \mathbf{S}_{B} = \sum_{i=1}^{k} n_{i}(\mathbf{\mu}_{i}-\mathbf{\mu})(\mathbf{\mu}_{i}-\mathbf{\mu})^{T} \end{align} }[/math]
Therefore,
- [math]\displaystyle{ \begin{align} \mathbf{S}_{T} = \mathbf{S}_{W} + \mathbf{S}_{B} \end{align} }[/math]
Recall that in the two class case problem, we have
- [math]\displaystyle{ \begin{align} & \mathbf{S}_{B^{\ast}} = (\mathbf{\mu}_{1}-\mathbf{\mu}_{2})(\mathbf{\mu}_{1}-\mathbf{\mu}_{2})^{T} \\ & = (\mathbf{\mu}_{1}-\mathbf{\mu}+\mathbf{\mu}-\mathbf{\mu}_{2})(\mathbf{\mu}_{1}-\mathbf{\mu}+\mathbf{\mu}-\mathbf{\mu}_{2})^{T} \\ & = ((\mathbf{\mu}_{1}-\mathbf{\mu})-(\mathbf{\mu}_{2}-\mathbf{\mu}))((\mathbf{\mu}_{1}-\mathbf{\mu})-(\mathbf{\mu}_{2}-\mathbf{\mu}))^{T} \\ & = (\mathbf{\mu}_{1}-\mathbf{\mu})(\mathbf{\mu}_{1}-\mathbf{\mu})^{T}+(\mathbf{\mu}_{2}-\mathbf{\mu})(\mathbf{\mu}_{2}-\mathbf{\mu})^{T} \end{align} }[/math]
From the general form,
- [math]\displaystyle{ \begin{align} & \mathbf{S}_{B} = n_{1}(\mathbf{\mu}_{1}-\mathbf{\mu})(\mathbf{\mu}_{1}-\mathbf{\mu})^{T} + n_{2}(\mathbf{\mu}_{2}-\mathbf{\mu})(\mathbf{\mu}_{2}-\mathbf{\mu})^{T} \end{align} }[/math]
Apparently, they are very similar.
Now, we are trying to find the optimal transformation. Basically, we have
- [math]\displaystyle{ \begin{align} \mathbf{z}_{i} = \mathbf{W}^{T}\mathbf{x}_{i}, i=1,2,...,k-1 \end{align} }[/math]
where [math]\displaystyle{ \mathbf{z}_{i} }[/math] is a [math]\displaystyle{ (k-1)\times 1 }[/math] vector, [math]\displaystyle{ \mathbf{W} }[/math] is a [math]\displaystyle{ d\times (k-1) }[/math] transformation matrix, i.e. [math]\displaystyle{ \mathbf{W} = [\mathbf{w}_{1}, \mathbf{w}_{2},..., \mathbf{w}_{k-1}] }[/math], and [math]\displaystyle{ \mathbf{x}_{i} }[/math] is a [math]\displaystyle{ d\times 1 }[/math] column vector.
Thus we obtain
- [math]\displaystyle{ \begin{align} & \mathbf{S}_{W}^{\ast} = \sum_{i=1}^{k}\sum_{j: y_{j}=i}(\mathbf{W}^{T}\mathbf{x}_{j}-\mathbf{W}^{T}\mathbf{\mu}_{i})(\mathbf{W}^{T}\mathbf{x}_{j}-\mathbf{W}^{T}\mathbf{\mu}_{i})^{T} \\ & = \sum_{i=1}^{k}\sum_{j: y_{j}=i}\mathbf{W}^{T}(\mathbf{x}_{j}-\mathbf{\mu}_{i})(\mathbf{x}_{j}-\mathbf{\mu}_{i})\mathbf{W} \\ & = \mathbf{W}^{T}\left[\sum_{i=1}^{k}\sum_{j: y_{j}=i}(\mathbf{x}_{j}-\mathbf{\mu}_{i})(\mathbf{x}_{j}-\mathbf{\mu}_{i})\right]\mathbf{W} \\ & = \mathbf{W}^{T}\mathbf{S}_{W}\mathbf{W} \end{align} }[/math]
Similarly, we obtain
- [math]\displaystyle{ \begin{align} & \mathbf{S}_{B}^{\ast} = \sum_{i=1}^{k}n_{i}(\mathbf{W}^{T}\mathbf{\mu}_{i}-\mathbf{W}^{T}\mathbf{\mu})(\mathbf{W}^{T}\mathbf{\mu}_{i}-\mathbf{W}^{T}\mathbf{\mu})^{T} \\ & = \sum_{i=1}^{k}n_{i}\mathbf{W}^{T}(\mathbf{\mu}_{i}-\mathbf{\mu})(\mathbf{\mu}_{i}-\mathbf{\mu})^{T}\mathbf{W} \\ & = \mathbf{W}^{T}\left[ \sum_{i=1}^{k}n_{i}(\mathbf{\mu}_{i}-\mathbf{\mu})(\mathbf{\mu}_{i}-\mathbf{\mu})^{T}\right]\mathbf{W} \\ & = \mathbf{W}^{T}\mathbf{S}_{B}\mathbf{W} \end{align} }[/math]
Now, we use the determinant of the matrix, i.e. the product of the eigenvalues of the matrix, as our measure.
- [math]\displaystyle{ \begin{align} \phi(\mathbf{W}) = \frac{|\mathbf{S}_{B}^{\ast}|}{|\mathbf{S}_{W}^{\ast}|} = \frac{\mathbf{W}^{T}\mathbf{S}_{B}\mathbf{W}}{\mathbf{W}^{T}\mathbf{S}_{W}\mathbf{W}} \end{align} }[/math]
The solution for this question is that the columns of the transformation matrix [math]\displaystyle{ \mathbf{W} }[/math] are exactly the eigenvectors that correspond to largest [math]\displaystyle{ k-1 }[/math] eigenvalues with respect to
- [math]\displaystyle{ \begin{align} \mathbf{S}_{W}^{-1}\mathbf{S}_{B}\mathbf{w}_{i} = \lambda_{i}\mathbf{w}_{i} \end{align} }[/math]
Also, note that we can use
- [math]\displaystyle{ \begin{align} \sum_{i=1}^{k}n_{i}\|(\mathbf{W}^{T}\mathbf{\mu}_{i}-\mathbf{W}^{T}\mathbf{\mu})^{T}\|^{2} \end{align} }[/math]
as our measure.
Recall that
- [math]\displaystyle{ \begin{align} \|\mathbf{X}\|^2 = Tr(\mathbf{X}^{T}\mathbf{X}) \end{align} }[/math]
Thus we obtain that
- [math]\displaystyle{ \begin{align} & \sum_{i=1}^{k}n_{i}\|(\mathbf{W}^{T}\mathbf{\mu}_{i}-\mathbf{W}^{T}\mathbf{\mu})^{T}\|^{2} \\ & = \sum_{i=1}^{k}n_{i}Tr[(\mathbf{W}^{T}\mathbf{\mu}_{i}-\mathbf{W}^{T}\mathbf{\mu})(\mathbf{W}^{T}\mathbf{\mu}_{i}-\mathbf{W}^{T}\mathbf{\mu})^{T}] \\ & = Tr[\sum_{i=1}^{k}n_{i}(\mathbf{W}^{T}\mathbf{\mu}_{i}-\mathbf{W}^{T}\mathbf{\mu})(\mathbf{W}^{T}\mathbf{\mu}_{i}-\mathbf{W}^{T}\mathbf{\mu})^{T}] \\ & = Tr[\sum_{i=1}^{k}n_{i}\mathbf{W}^{T}(\mathbf{\mu}_{i}-\mathbf{\mu})(\mathbf{\mu}_{i}-\mathbf{\mu})^{T}\mathbf{W}] \\ & = Tr[\mathbf{W}^{T}\sum_{i=1}^{k}n_{i}(\mathbf{\mu}_{i}-\mathbf{\mu})(\mathbf{\mu}_{i}-\mathbf{\mu})^{T}\mathbf{W}] \\ & = Tr[\mathbf{W}^{T}\mathbf{S}_{B}\mathbf{W}] \end{align} }[/math]
Similarly, we can get [math]\displaystyle{ Tr[\mathbf{W}^{T}\mathbf{S}_{W}\mathbf{W}] }[/math]. Thus we have following criterion function
- [math]\displaystyle{ \begin{align} \phi(\mathbf{W}) = \frac{Tr[\mathbf{W}^{T}\mathbf{S}_{B}\mathbf{W}]}{Tr[\mathbf{W}^{T}\mathbf{S}_{W}\mathbf{W}]} \end{align} }[/math]
Similar to the two class case problem, we have:
max [math]\displaystyle{ Tr[\mathbf{W}^{T}\mathbf{S}_{B}\mathbf{W}] }[/math] subject to [math]\displaystyle{ Tr[\mathbf{W}^{T}\mathbf{S}_{W}\mathbf{W}]=1 }[/math]
To solve this optimization problem a Lagrange multiplier [math]\displaystyle{ \Lambda }[/math], which actually is a [math]\displaystyle{ d \times d }[/math] diagonal matrix, is introduced:
- [math]\displaystyle{ \begin{align} L(\mathbf{W},\Lambda) = Tr[\mathbf{W}^{T}\mathbf{S}_{W}\mathbf{B}] - \Lambda\left\{ Tr[\mathbf{W}^{T}\mathbf{S}_{W}\mathbf{W}] - 1 \right\} \end{align} }[/math]
Differentiating with respect to [math]\displaystyle{ \mathbf{W} }[/math] we obtain:
- [math]\displaystyle{ \begin{align} \frac{\partial L}{\partial \mathbf{W}} = (\mathbf{S}_{B} + \mathbf{S}_{B}^{T})\mathbf{W} - \Lambda (\mathbf{S}_{W} + \mathbf{S}_{W}^{T})\mathbf{W} \end{align} }[/math]
Note that the [math]\displaystyle{ \mathbf{S}_{B} }[/math] and [math]\displaystyle{ \mathbf{S}_{W} }[/math] are both symmetric matrices, thus set the first derivative to zero, we obtain:
- [math]\displaystyle{ \begin{align} \mathbf{S}_{B}\mathbf{W} - \Lambda\mathbf{S}_{W}\mathbf{W}=0 \end{align} }[/math]
Thus,
- [math]\displaystyle{ \begin{align} \mathbf{S}_{B}\mathbf{W} = \Lambda\mathbf{S}_{W}\mathbf{W} \end{align} }[/math]
where
- [math]\displaystyle{ \mathbf{\Lambda} = \begin{pmatrix} \lambda_{1} & & 0\\ &\ddots&\\ 0 & &\lambda_{d} \end{pmatrix} }[/math]
and [math]\displaystyle{ \mathbf{W} = [\mathbf{w}_{1}, \mathbf{w}_{2},..., \mathbf{w}_{k-1}] }[/math].
As a matter of fact, [math]\displaystyle{ \mathbf{\Lambda} }[/math] must have [math]\displaystyle{ \mathbf{k-1} }[/math] nonzero eigenvalues, because [math]\displaystyle{ rank({S}_{W}^{-1}\mathbf{S}_{B})=k-1 }[/math].
Therefore, the solution for this question is as same as the previous case. The columns of the transformation matrix [math]\displaystyle{ \mathbf{W} }[/math] are exactly the eigenvectors that correspond to largest [math]\displaystyle{ k-1 }[/math] eigenvalues with respect to
- [math]\displaystyle{ \begin{align} \mathbf{S}_{W}^{-1}\mathbf{S}_{B}\mathbf{w}_{i} = \lambda_{i}\mathbf{w}_{i} \end{align} }[/math]
Linear Regression Models - October 14, 2009
Regression analysis is a general statistical technique for modelling and analyzing how a dependent variable changes according to changes in independent variables. In classification, we are interested in how a label, [math]\displaystyle{ \,y }[/math], changes according to changes in [math]\displaystyle{ \,X }[/math].
We will start by considering a very simple regression model, the linear regression model.
General information on linear regression can be found at the University of South Florida and this MIT lecture.
For the purpose of classification, the linear regression model assumes that the regression function [math]\displaystyle{ \,E(Y|X) }[/math] is linear in the inputs [math]\displaystyle{ \,\mathbf{x}_{1}, ..., \mathbf{x}_{p} }[/math].
The linear regression model has the general form:
- [math]\displaystyle{ \begin{align} f(x) = \beta^{T}\mathbf{x}_{i}+\beta_{0} \end{align} }[/math]
where [math]\displaystyle{ \,\beta }[/math] is a [math]\displaystyle{ 1 \times d }[/math] vector.
Given input data [math]\displaystyle{ \,\mathbf{x}_{1}, ..., \mathbf{x}_{p} }[/math] and [math]\displaystyle{ \,y_{1}, ..., y_{p} }[/math] our goal is to find [math]\displaystyle{ \,\beta }[/math] and [math]\displaystyle{ \,\beta_0 }[/math] such that the linear model fits the data while minimizing sum of squared errors using the Least Squares method.
Note that vectors [math]\displaystyle{ \mathbf{x}_{i} }[/math] could be numerical inputs, transformations of the original data, i.e. [math]\displaystyle{ \log \mathbf{x}_{i} }[/math] or [math]\displaystyle{ \sin \mathbf{x}_{i} }[/math], or basis expansions, i.e. [math]\displaystyle{ \mathbf{x}_{i}^{2} }[/math] or [math]\displaystyle{ \mathbf{x}_{i}\times \mathbf{x}_{j} }[/math].
Denote [math]\displaystyle{ \mathbf{X} }[/math] as a [math]\displaystyle{ n\times(d+1) }[/math] matrix with each row an input vector (with 1 in the first position), [math]\displaystyle{ \,\beta = (\beta_0, \beta_1,..., \beta_{d})^{T} }[/math] and [math]\displaystyle{ \mathbf{y} }[/math] as a [math]\displaystyle{ n \times 1 }[/math] vector of outputs. We then try to minimize the residual sum-of-squares
- [math]\displaystyle{ \begin{align} \mathrm{RSS}(\beta)=(\mathbf{y}-\mathbf{X}\beta)(\mathbf{y}-\mathbf{X}\beta)^{T} \end{align} }[/math]
This is a quadratic function in the [math]\displaystyle{ \,d+1 }[/math] parameters. Differentiating with respect to [math]\displaystyle{ \,\beta }[/math] we obtain
- [math]\displaystyle{ \begin{align} \frac{\partial \mathrm{RSS}}{\partial \beta} = -2\mathbf{X}^{T}(\mathbf{y}-\mathbf{X}\beta) \end{align} }[/math]
- [math]\displaystyle{ \begin{align} \frac{\partial^{2}\mathrm{RSS}}{\partial \beta \partial \beta^{T}}=2\mathbf{X}^{T}\mathbf{X} \end{align} }[/math]
Set the first derivative to zero
- [math]\displaystyle{ \begin{align} \mathbf{X}^{T}(\mathbf{y}-\mathbf{X}\beta)=0 \end{align} }[/math]
we obtain the solution
- [math]\displaystyle{ \begin{align} \hat \beta = (\mathbf{X}^{T}\mathbf{X})^{-1}\mathbf{X}^{T}\mathbf{y} \end{align} }[/math]
Thus the fitted values at the inputs are
- [math]\displaystyle{ \begin{align} \mathbf{\hat y} = \mathbf{X}\hat\beta = \mathbf{X} (\mathbf{X}^{T}\mathbf{X})^{-1}\mathbf{X}^{T}\mathbf{y} \end{align} }[/math]
where [math]\displaystyle{ \mathbf{H} = \mathbf{X} (\mathbf{X}^{T}\mathbf{X})^{-1}\mathbf{X}^{T} }[/math] is called the hat matrix.
- Note For classification purposes, this is not a correct model. Recall the following application of Bayes classifier:
[math]\displaystyle{ r(x)= P( Y=k | X=x )= \frac{f_{k}(x)\pi_{k}}{\Sigma_{k}f_{k}(x)\pi_{k}} }[/math]
It is clear that to make sense mathematically, [math]\displaystyle{ \displaystyle r(x) }[/math] must be a value between 0 and 1. If this is estimated with the
regression function [math]\displaystyle{ \displaystyle r(x)=E(Y|X=x) }[/math] and [math]\displaystyle{ \mathbf{\hat\beta} }[/math] is learned as above, then there is nothing that would restrict [math]\displaystyle{ \displaystyle r(x) }[/math] to taking values between 0 and 1.
A linear regression example in Matlab
We can see how linear regression works through the following example in Matlab. The following is the code and the explanation for each step.
Again, we use the data in 2_3.m.
>>load 2_3; >>[U, sample] = princomp(X'); >>sample = sample(:,1:2);
We carry out Principal Component Analysis (PCA) to reduce the dimensionality from 64 to 2.
>>y = zeros(400,1); >>y(201:400) = 1;
We let y represent the set of labels coded as 0 and 1.
>>x=[sample;ones(1,400)];
Construct x by adding a row of vector 1 to data.
>>b=inv(x*x')*x*y;
Calculate b, which represents [math]\displaystyle{ \beta }[/math] in the linear regression model.
>>x1=x';
>>for i=1:400
if x1(i,:)*b>0.5
plot(x1(i,1),x1(i,2),'.')
hold on
elseif x1(i,:)*b < 0.5
plot(x1(i,1),x1(i,2),'r.')
end
end
Plot the fitted y values.
Logistic Regression- October 16, 2009
logistic function
A logistic function or logistic curve is the most common sigmoid curve.
- [math]\displaystyle{ y = \frac{1}{1+e^{-x}} }[/math]
1. [math]\displaystyle{ \frac{dy}{dx} = y(1-y)=\frac{e^{x}}{(1+e^{x})^{2}} }[/math]
2. [math]\displaystyle{ y(0) = \frac{1}{2} }[/math]
3. [math]\displaystyle{ \int y dx = ln(1 + e^{x}) }[/math]
4. [math]\displaystyle{ y(x) = \frac{1}{2} + \frac{1}{4}x - \frac{1}{48}x^{3} + \frac{1}{48}x^{5} \cdots }[/math]
5. The logistic curve shows early exponential growth for negative t, which slows to linear growth of slope 1/4 near t = 0, then approaches y = 1 with an exponentially decaying gap.
Intuition behind Logistic Regression
Recall that, for classification purposes, the linear regression model presented in the above section is not correct because it does not force [math]\displaystyle{ \,r(x) }[/math] to be between 0 and 1 and sum to 1. Consider the following log odds model (for two classes):
- [math]\displaystyle{ \log\left(\frac{P(Y=1|X=x)}{P(Y=0|X=x)}\right)=\beta^Tx }[/math]
Calculating [math]\displaystyle{ \,P(Y=1|X=x) }[/math] leads us to the logistic regression model, which as opposed to the linear regression model, allows the modelling of the posterior probabilities of the classes through linear methods and at the same time ensures that they sum to one and are between 0 and 1. It is a type of Generalized Linear Model (GLM).
The Logistic Regression Model
The logistic regression model for the two class case is defined as
Class 1

- [math]\displaystyle{ P(Y=1 | X=x) =\frac{\exp(\underline{\beta}^T \underline{x})}{1+\exp(\underline{\beta}^T \underline{x})}=P(x;\underline{\beta}) }[/math]
Then we have that
Class 0

- [math]\displaystyle{ P(Y=0 | X=x) = 1-P(Y=1 | X=x)=1-\frac{\exp(\underline{\beta}^T \underline{x})}{1+\exp(\underline{\beta}^T \underline{x})}=\frac{1}{1+\exp(\underline{\beta}^T \underline{x})} }[/math]
Fitting a Logistic Regression
Logistic regression tries to fit a distribution. The fitting of logistic regression models is usually accomplished by maximum likelihood, using Pr(Y|X). The maximum likelihood of [math]\displaystyle{ \underline\beta }[/math] maximizes the probability of obtaining the data [math]\displaystyle{ \displaystyle{x_{1},...,x_{n}} }[/math] from the known distribution. Combining [math]\displaystyle{ \displaystyle P(Y=1 | X=x) }[/math] and [math]\displaystyle{ \displaystyle P(Y=0 | X=x) }[/math] as follows, we can consider the two classes at the same time:
- [math]\displaystyle{ p(\underline{x_{i}};\underline{\beta}) = \left(\frac{\exp(\underline{\beta}^T \underline{x_i})}{1+\exp(\underline{\beta}^T \underline{x_i})}\right)^{y_i} \left(\frac{1}{1+\exp(\underline{\beta}^T \underline{x_i})}\right)^{1-y_i} }[/math]
Assuming the data [math]\displaystyle{ \displaystyle {x_{1},...,x_{n}} }[/math] is drawn independently, the likelihood function is
- [math]\displaystyle{ \begin{align} \mathcal{L}(\theta)&=p({x_{1},...,x_{n}};\theta)\\ &=\displaystyle p(x_{1};\theta) p(x_{2};\theta)... p(x_{n};\theta) \quad \mbox{(by independence)}\\ &= \prod_{i=1}^n p(x_{i};\theta) \end{align} }[/math]
Since it is more convenient to work with the log-likelihood function, take the log of both sides, we get
- [math]\displaystyle{ \displaystyle l(\theta)=\displaystyle \sum_{i=1}^n \log p(x_{i};\theta) }[/math]
So,
- [math]\displaystyle{ \begin{align} l(\underline\beta)&=\displaystyle\sum_{i=1}^n y_{i}\log\left(\frac{\exp(\underline{\beta}^T \underline{x_i})}{1+\exp(\underline{\beta}^T \underline{x_i})}\right)+(1-y_{i})\log\left(\frac{1}{1+\exp(\underline{\beta}^T\underline{x_i})}\right)\\ &= \displaystyle\sum_{i=1}^n y_{i}(\underline{\beta}^T\underline{x_i}-\log(1+\exp(\underline{\beta}^T\underline{x_i}))+(1-y_{i})(-\log(1+\exp(\underline{\beta}^T\underline{x_i}))\\ &= \displaystyle\sum_{i=1}^n y_{i}\underline{\beta}^T\underline{x_i}-y_{i} \log(1+\exp(\underline{\beta}^T\underline{x_i}))- \log(1+\exp(\underline{\beta}^T\underline{x_i}))+y_{i} \log(1+\exp(\underline{\beta}^T\underline{x_i}))\\ &=\displaystyle\sum_{i=1}^n y_{i}\underline{\beta}^T\underline{x_i}- \log(1+\exp(\underline{\beta}^T\underline{x_i}))\\ \end{align} }[/math]
To maximize the log-likelihood, set its derivative to 0.
- [math]\displaystyle{ \begin{align} \frac{\partial l}{\partial \underline{\beta}} &= \sum_{i=1}^n \left[{y_i} \underline{x}_i- \frac{\exp(\underline{\beta}^T \underline{x_i})}{1+\exp(\underline{\beta}^T \underline{x}_i)}\underline{x}_i\right]\\ &=\sum_{i=1}^n \left[{y_i} \underline{x}_i - p(\underline{x}_i;\underline{\beta})\underline{x}_i\right] \end{align} }[/math]
To solve this equation, the Newton-Raphson algorithm is used which requires the second derivative in addition to the first derivative. This is demonstrated in the next section.
Logistic Regression(2) - October 19, 2009
Logistic Regression Model
Recall that in the last lecture, we learned the logistic regression model.
- [math]\displaystyle{ P(Y=1 | X=x)=P(\underline{x}_i;\underline{\beta})=\frac{exp(\underline{\beta}^T \underline{x})}{1+exp(\underline{\beta}^T \underline{x})} }[/math]
- [math]\displaystyle{ P(Y=0 | X=x)=1-P(\underline{x}_i;\underline{\beta})=\frac{1}{1+exp(\underline{\beta}^T \underline{x})} }[/math]
Find [math]\displaystyle{ \underline{\beta} }[/math]
Criteria: find a [math]\displaystyle{ \underline{\beta} }[/math] that maximizes the conditional likelihood of Y given X using the training data.
From above, we have the first derivative of the log-likelihood:
[math]\displaystyle{ \frac{\partial l}{\partial \underline{\beta}} = \sum_{i=1}^n \left[{y_i} \underline{x}_i- \frac{exp(\underline{\beta}^T \underline{x_i})}{1+exp(\underline{\beta}^T \underline{x}_i)}\underline{x}_i\right] }[/math] [math]\displaystyle{ =\sum_{i=1}^n \left[{y_i} \underline{x}_i - P(\underline{x}_i;\underline{\beta})\underline{x}_i\right] }[/math]
The Newton-Raphson algorithm requires the second-derivative or Hessian matrix.
[math]\displaystyle{ \frac{\partial^{2} l}{\partial \underline{\beta} \partial \underline{\beta}^T }= \sum_{i=1}^n - \underline{x_i} \frac{(exp(\underline{\beta}^T\underline{x}_i) \underline{x}_i^T)(1+exp(\underline{\beta}^T \underline{x}_i))-\underline{x}_i exp(\underline{\beta}^T\underline{x}_i)exp(\underline{\beta}^T\underline{x}_i)}{(1+exp(\underline{\beta}^T \underline{x}))^2} }[/math]
(note: [math]\displaystyle{ \frac{\partial\underline{\beta}^T\underline{x}_i}{\partial \underline{\beta}^T}=\underline{x}_i^T }[/math] you can check it here, it's a very useful website including a Matrix Reference Manual that you can find information about linear algebra and the properties of real and complex matrices.)
- [math]\displaystyle{ =\sum_{i=1}^n - \underline{x}_i \frac{(-\underline{x}_i exp(\underline{\beta}^T\underline{x}_i) \underline{x}_i^T)}{(1+exp(\underline{\beta}^T \underline{x}))(1+exp(\underline{\beta}^T \underline{x}))} }[/math] (by cancellation)
- [math]\displaystyle{ =\sum_{i=1}^n - \underline{x}_i \underline{x}_i^T P(\underline{x}_i;\underline{\beta}))[1-P(\underline{x}_i;\underline{\beta})]) }[/math](since [math]\displaystyle{ P(\underline{x}_i;\underline{\beta})=\frac{exp(\underline{\beta}^T \underline{x})}{1+exp(\underline{\beta}^T \underline{x})} }[/math] and [math]\displaystyle{ 1-P(\underline{x}_i;\underline{\beta})=\frac{1}{1+exp(\underline{\beta}^T \underline{x})} }[/math])
The same second derivative can be achieved if we reduce the occurrences of beta to 1 by the identity[math]\displaystyle{ \frac{a}{1+a}=1-\frac{1}{1+a} }[/math]
And solving [math]\displaystyle{ \frac{\partial}{\partial \underline{\beta}^T}\sum_{i=1}^n \left[{y_i} \underline{x}_i-\left[1-\frac{1}{1+exp(\underline{\beta}^T \underline{x}_i)}\right]\underline{x}_i\right] }[/math]
Starting with [math]\displaystyle{ \,\underline{\beta}^{old} }[/math], the Newton-Raphson update is
[math]\displaystyle{ \,\underline{\beta}^{new}\leftarrow \,\underline{\beta}^{old}- (\frac{\partial ^2 l}{\partial \underline{\beta}\partial \underline{\beta}^T})^{-1}(\frac{\partial l}{\partial \underline{\beta}}) }[/math] where the derivatives are evaluated at [math]\displaystyle{ \,\underline{\beta}^{old} }[/math]
The iteration will terminate when [math]\displaystyle{ \underline{\beta}^{new} }[/math] is very close to [math]\displaystyle{ \underline{\beta}^{old} }[/math].
The iteration can be described in matrix form.
- Let [math]\displaystyle{ \,\underline{Y} }[/math] be the column vector of [math]\displaystyle{ \,y_i }[/math]. ([math]\displaystyle{ n\times1 }[/math])
- Let [math]\displaystyle{ \,X }[/math] be the [math]\displaystyle{ {d}\times{n} }[/math] input matrix.
- Let [math]\displaystyle{ \,\underline{P} }[/math] be the [math]\displaystyle{ {n}\times{1} }[/math] vector with [math]\displaystyle{ i }[/math]th element [math]\displaystyle{ P(\underline{x}_i;\underline{\beta}^{old}) }[/math].
- Let [math]\displaystyle{ \,W }[/math] be an [math]\displaystyle{ {n}\times{n} }[/math] diagonal matrix with [math]\displaystyle{ i }[/math]th element [math]\displaystyle{ P(\underline{x}_i;\underline{\beta}^{old})[1-P(\underline{x}_i;\underline{\beta}^{old})] }[/math]
then
[math]\displaystyle{ \frac{\partial l}{\partial \underline{\beta}} = X(\underline{Y}-\underline{P}) }[/math]
[math]\displaystyle{ \frac{\partial ^2 l}{\partial \underline{\beta}\partial \underline{\beta}^T} = -XWX^T }[/math]
The Newton-Raphson step is
[math]\displaystyle{ \underline{\beta}^{new} \leftarrow \underline{\beta}^{old}+(XWX^T)^{-1}X(\underline{Y}-\underline{P}) }[/math]
This equation is sufficient for computation of the logistic regression model. However, we can simplify further to uncover an interesting feature of this equation.
[math]\displaystyle{ \begin{align} \underline{\beta}^{new} &= (XWX^T)^{-1}(XWX^T)\underline{\beta}^{old}+(XWX^T)^{-1}XWW^{-1}(\underline{Y}-\underline{P})\\ &=(XWX^T)^{-1}XW[X^T\underline{\beta}^{old}+W^{-1}(\underline{Y}-\underline{P})]\\ &=(XWX^T)^{-1}XWZ \end{align} }[/math]
where [math]\displaystyle{ Z=X^T\underline{\beta}^{old}+W^{-1}(\underline{Y}-\underline{P}) }[/math]
Recall that linear regression by least square finds the following minimum: [math]\displaystyle{ \min_{\underline{\beta}}(\underline{y}-\underline{\beta}^T X)^T(\underline{y}-\underline{\beta}^TX) }[/math]
we have [math]\displaystyle{ \underline\hat{\beta}=(XX^T)^{-1}X\underline{y} }[/math]
Similarly, we can say that [math]\displaystyle{ \underline{\beta}^{new} }[/math] is the solution of a weighted least square problem:
[math]\displaystyle{ \underline{\beta}^{new} \leftarrow \min_{\underline{\beta}}(Z-X\underline{\beta}^T)W(Z-X\underline{\beta}) }[/math]
WLS
Actually, the weighted least squares estimator minimizes the weighted sum of squared errors [math]\displaystyle{ S(\beta) = \sum_{i=1}^{n}w_{i}[y_{i}-\mathbf{x}_{i}^{T}\beta]^{2} }[/math] where [math]\displaystyle{ \displaystyle w_{i}\gt 0 }[/math]. Hence the WLS estimator is given by [math]\displaystyle{ \hat\beta^{WLS}=\left[\sum_{i=1}^{n}w_{i}\mathbf{x}_{i}\mathbf{x}_{i}^{T} \right]^{-1}\left[ \sum_{i=1}^{n}w_{i}\mathbf{x}_{i}y_{i}\right] }[/math]
A weighted linear regression of the iteratively computed response [math]\displaystyle{ \mathbf{z}=\mathbf{X}^{T}\beta^{old}+\mathbf{W}^{-1}(\mathbf{y}-\mathbf{p}) }[/math]
Therefore, we obtain
- [math]\displaystyle{ \begin{align} & \hat\beta^{WLS}=\left[\sum_{i=1}^{n}w_{i}\mathbf{x}_{i}\mathbf{x}_{i}^{T} \right]^{-1}\left[ \sum_{i=1}^{n}w_{i}\mathbf{x}_{i}z_{i}\right] \\& = \left[ \mathbf{XWX}^{T}\right]^{-1}\left[ \mathbf{XWz}\right] \\& = \left[ \mathbf{XWX}^{T}\right]^{-1}\mathbf{XW}(\mathbf{X}^{T}\beta^{old}+\mathbf{W}^{-1}(\mathbf{y}-\mathbf{p})) \\& = \beta^{old}+ \left[ \mathbf{XWX}^{T}\right]^{-1}\mathbf{X}(\mathbf{y}-\mathbf{p}) \end{align} }[/math]
note:Here we obtain [math]\displaystyle{ \underline{\beta} }[/math], which is a [math]\displaystyle{ d\times{1} }[/math] vector, because we construct the model like [math]\displaystyle{ \underline{\beta}^T\underline{x} }[/math]. If we construct the model like [math]\displaystyle{ \underline{\beta}_0+ \underline{\beta}^T\underline{x} }[/math], then similar to linear regression, [math]\displaystyle{ \underline{\beta} }[/math] will be a [math]\displaystyle{ (d+1)\times{1} }[/math] vector.
- Choosing [math]\displaystyle{ \displaystyle\beta=0 }[/math] seems to be a suitable starting value for the Newton-Raphson iteration procedure in this case. However, this does not guarantee convergence. The procedure will usually converge since the log-likelihood function is concave(or convex). In the case that it does not, we can just prove the local convergence of the method, which means the iteration would converge only if the initial point is closed enough to the exact solution. However, in practice, choosing an appropriate initial value is really trivial, namely, it is not often to find a initial too far from the exact solution to make the iteration invalid. <ref>C. T. Kelley, Iterative Methods for Linear and Nonlinear Equations, chapter 5 </ref> Besides, step-size halving will solve this problem. <ref>H. Trevor, R. Tibshirani, J. Friedman, The Elements of Statistical Learning (Springer
2009),121.</ref>
Pseudo Code
- [math]\displaystyle{ \underline{\beta} \leftarrow 0 }[/math]
- Set [math]\displaystyle{ \,\underline{Y} }[/math], the label associated with each observation [math]\displaystyle{ \,i=1...n }[/math].
- Compute [math]\displaystyle{ \,\underline{P} }[/math] according to the equation [math]\displaystyle{ P(\underline{x}_i;\underline{\beta})=\frac{exp(\underline{\beta}^T \underline{x})}{1+exp(\underline{\beta}^T \underline{x})} }[/math] for all [math]\displaystyle{ \,i=1...n }[/math].
- Compute the diagonal matrix [math]\displaystyle{ \,W }[/math] by setting [math]\displaystyle{ \,w_i,i }[/math] to [math]\displaystyle{ P(\underline{x}_i;\underline{\beta}))[1-P(\underline{x}_i;\underline{\beta})] }[/math] for all [math]\displaystyle{ \,i=1...n }[/math].
- [math]\displaystyle{ Z \leftarrow X^T\underline{\beta}+W^{-1}(\underline{Y}-\underline{P}) }[/math].
- [math]\displaystyle{ \underline{\beta} \leftarrow (XWX^T)^{-1}XWZ }[/math].
- If the new [math]\displaystyle{ \underline{\beta} }[/math] value is sufficiently close to the old value, stop; otherwise go back to step 3.
Comparison with Linear Regression
- Similarities
- They are both to attempt to estimate [math]\displaystyle{ \,P(Y=k|X=x) }[/math] (For logistic regression, we just mentioned about the case that [math]\displaystyle{ \,k=0 }[/math] or [math]\displaystyle{ \,k=1 }[/math] now).
- They are both have linear boundaris.
- note:For linear regression, we assume the model is linear. The boundary is [math]\displaystyle{ P(Y=k|X=x)=\underline{\beta}^T\underline{x}_i+\underline{\beta}_0=0.5 }[/math] (linear)
- For logistic regression, the boundary is [math]\displaystyle{ P(Y=k|X=x)=\frac{exp(\underline{\beta}^T \underline{x})}{1+exp(\underline{\beta}^T \underline{x})}=0.5 \Rightarrow exp(\underline{\beta}^T \underline{x})=1\Rightarrow \underline{\beta}^T \underline{x}=0 }[/math] (linear)
- Differences
- Linear regression: [math]\displaystyle{ \,P(Y=k|X=x) }[/math] is linear function of [math]\displaystyle{ \,x }[/math], [math]\displaystyle{ \,P(Y=k|X=x) }[/math] is not guaranteed to fall between 0 and 1 and to sum up to 1.
- Logistic regression: [math]\displaystyle{ \,P(Y=k|X=x) }[/math] is a nonlinear function of [math]\displaystyle{ \,x }[/math], and it is guaranteed to range from 0 to 1 and to sum up to 1.
Comparison with LDA
- The linear logistic model only consider the conditional distribution [math]\displaystyle{ \,P(Y=k|X=x) }[/math]. No assumption is made about [math]\displaystyle{ \,P(X=x) }[/math].
- The LDA model specifies the joint distribution of [math]\displaystyle{ \,X }[/math] and [math]\displaystyle{ \,Y }[/math].
- Logistic regression maximizes the conditional likelihood of [math]\displaystyle{ \,Y }[/math] given [math]\displaystyle{ \,X }[/math]: [math]\displaystyle{ \,P(Y=k|X=x) }[/math]
- LDA maximizes the joint likelihood of [math]\displaystyle{ \,Y }[/math] and [math]\displaystyle{ \,X }[/math]: [math]\displaystyle{ \,P(Y=k,X=x) }[/math].
- If [math]\displaystyle{ \,\underline{x} }[/math] is d-dimensional,the number of adjustable parameter in logistic regression is [math]\displaystyle{ \,d }[/math]. The number of parameters grows linearly w.r.t dimension.
- If [math]\displaystyle{ \,\underline{x} }[/math] is d-dimensional,the number of adjustable parameter in LDA is [math]\displaystyle{ \,(2d)+d(d+1)/2+2=(d^2+5d+4)/2 }[/math]. The number of parameters grows quardratically w.r.t dimension.
- As logistic regression relies on fewer assumptions, it seems to be more robust.
- In practice, Logistic regression and LDA often give the similar results.
By example
Now we compare LDA and Logistic regression by an example. Again, we use them on the 2_3 data.
>>load 2_3; >>[U, sample] = princomp(X'); >>sample = sample(:,1:2); >>plot (sample(1:200,1), sample(1:200,2), '.'); >>hold on; >>plot (sample(201:400,1), sample(201:400,2), 'r.');
- First, we do PCA on the data and plot the data points that represent 2 or 3 in different colors. See the previous example for more details.
>>group = ones(400,1); >>group(201:400) = 2;
- Group the data points.
>>[B,dev,stats] = mnrfit(sample,group); >>x=[ones(1,400); sample'];
- Now we use mnrfit to use logistic regression to classfy the data. This function can return B which is a [math]\displaystyle{ (d+1)\times{(k–1)} }[/math] matrix of estimates, where each column corresponds to the estimated intercept term and predictor coefficients. In this case, B is a [math]\displaystyle{ 3\times{1} }[/math] matrix.
>> B B =0.1861 -5.5917 -3.0547
- This is our [math]\displaystyle{ \underline{\beta} }[/math]. So the posterior probabilities are:
- [math]\displaystyle{ P(Y=1 | X=x)=\frac{exp(0.1861-5.5917X_1-3.0547X_2)}{1+exp(0.1861-5.5917X_1-3.0547X_2)} }[/math].
- [math]\displaystyle{ P(Y=2 | X=x)=\frac{1}{1+exp(0.1861-5.5917X_1-3.0547X_2)} }[/math]
- The classification rule is:
- [math]\displaystyle{ \hat Y = 1 }[/math], if [math]\displaystyle{ \,0.1861-5.5917X_1-3.0547X_2\gt =0 }[/math]
- [math]\displaystyle{ \hat Y = 2 }[/math], if [math]\displaystyle{ \,0.1861-5.5917X_1-3.0547X_2\lt 0 }[/math]
>>f = sprintf('0 = %g+%g*x+%g*y', B(1), B(2), B(3));
>>ezplot(f,[min(sample(:,1)), max(sample(:,1)), min(sample(:,2)), max(sample(:,2))])
- Plot the decision boundary by logistic regression.
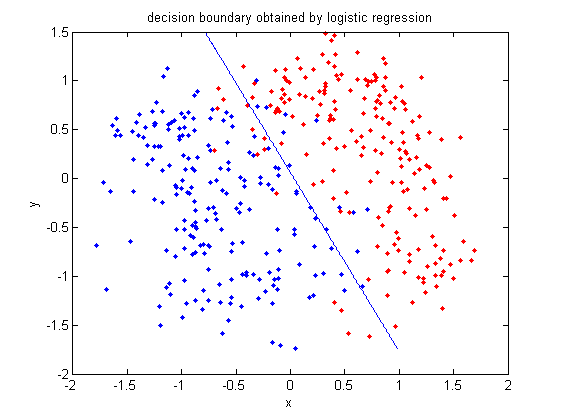
>>[class, error, POSTERIOR, logp, coeff] = classify(sample, sample, group, 'linear');
>>k = coeff(1,2).const;
>>l = coeff(1,2).linear;
>>f = sprintf('0 = %g+%g*x+%g*y', k, l(1), l(2));
>>h=ezplot(f, [min(sample(:,1)), max(sample(:,1)), min(sample(:,2)), max(sample(:,2))]);
- Plot the decision boundary by LDA. See the previous example for more information about LDA in matlab.
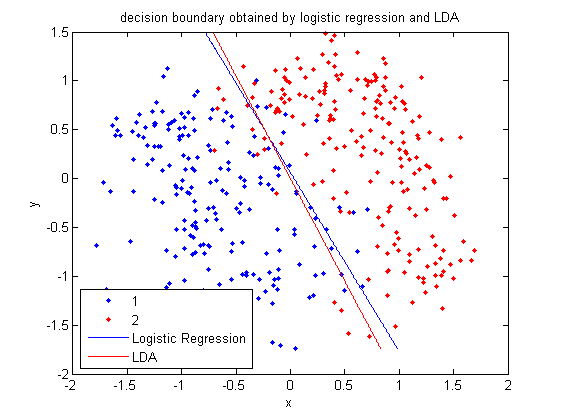
2009.10.21
Multi-Class Logistic Regression
Our earlier goal with logistic regression was to model the posteriors for a 2 class classification problem with a linear function bounded by the interval [0,1]. In that case our model was,
[math]\displaystyle{ \log\left(\frac{P(Y=1|X=x)}{P(Y=0|X=x)}\right)= \log\left(\frac{\frac{\exp(\beta^T x)}{1+\exp(\beta^T x)}}{\frac{1}{1+\exp(\beta^T x)}}\right) =\beta^Tx }[/math]
We can extend this idea to the more general case with K-classes. This model is specified with K - 1 terms where the Kth class in the denominator can be chosen arbitrarily.
[math]\displaystyle{ \log\left(\frac{P(Y=i|X=x)}{P(Y=K|X=x)}\right)=\beta_i^Tx,\quad i \in \{1,\dots,K-1\} }[/math]
The posteriors for each class are given by,
[math]\displaystyle{ P(Y=i|X=x) = \frac{\exp(\beta_i^T x)}{1+\sum_{k=1}^{K-1}\exp(\beta_k^T x)}, \quad i \in \{1,\dots,K-1\} }[/math]
[math]\displaystyle{ P(Y=K|X=x) = \frac{1}{1+\sum_{k=1}^{K-1}\exp(\beta_k^T x)} }[/math]
Seeing these equations as a weighted least squares problem makes them easier to derivate.
Note that we still retain the property that the sum of the posteriors is 1. In general the posteriors are no longer complements of each other as in true in the 2 class problem where we could express [math]\displaystyle{ \displaystyle P(Y=1|X=x)=1-P(Y=0|X=x) }[/math]. Fitting a Logistic model for the K>2 class problem isn't as 'nice' as in the 2 class problem since we don't have the same simplification.
Perceptron (Foundation of Neural Network)
Separating Hyperplane Classifiers
Separating hyperplane trys to separate the data using linear decision boundaries. When the classes overlap, it can be generalized to support vector machine, which constructs nonlinear boundaries by constructing a linear boundary in an enlarged and transformed feature space.
Perceptron
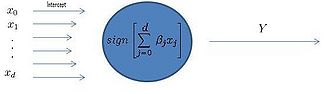
Recall the use of Least Squares regression as a classifier, shown to be identical to LDA. To classify points with least squares we take the sign of a linear combination of data points and assign a label equivalent to +1 or -1.
Least Squares returns the sign of a linear combination of data points as the class label
[math]\displaystyle{ sign(\underline{\beta}^T \underline{x} + {\beta}_0) = sign(\beta_{0}+\beta_{1}x_{1}+\beta_{2}x_{2}) }[/math]
In the 1950s Frank Rosenblatt developed an iterative linear classifier while at Cornell University known as the Perceptron. The concept of a perceptron was fundamental to the later development of the Artificial Neural Network models. The perceptron is a simple type of neural network which models the electrical signals of biological neurons. In fact, it was the first neural network to be algorithmically described. <ref>Simon S. Haykin, Neural Networks and Learning Machines, (Prentice Hall 2008). </ref>
As in other linear classification methods like Least Squares, Rosenblatt's classifier determines a hyperplane for the decision boundary. Linear methods all determine slightly different decision boundaries, Rosenblatt's algorithm seeks to minimize the distance between the decision boundary and the misclassified points <ref>H. Trevor, R. Tibshirani, J. Friedman, The Elements of Statistical Learning (Springer 2009),156.</ref>.
Particular to the iterative nature of the solution, the problem has no global mean (not convex). It does not converge to give a unique hyperplane, and the solutions depend on the size of the gap between classes. If the classes are separable then the algorithm is shown to converge to a local mean. The proof of this convergence is known as the perceptron convergence theorem. However, for overlapping classes convergence to a local mean cannot be guaranteed.
If we find a hyperplane that is not unique between 2 classes, there will be infinitely many solutions obtained from the perceptron algorithm.
As seen in Figure 1, after training, the perceptron determines the label of the data by computing the sign of a linear combination of components.
A Perceptron Example
The perceptron network can figure out the decision boundray line even if we dont know how to draw the line. We just have to give it some examples first. For example:
| Features:x1, x2, x3 | Answer |
|---|---|
| 1,0,0 | +1 |
| 1,0,1 | +1 |
| 1,1,0 | +1 |
| 0,0,1 | -1 |
| 0,1,1 | -1 |
| 1,1,1 | -1 |
Then the perceptron starts out not knowing how to separate the answers so it guesses. For example we input 1,0,0 and it guesses -1. But the right answer is +1. So the perceptron adjusts its line and we try the next example. Eventually the perceptron will have all the answers right.
y=[1;1;1;-1;-1;-1];
x=[1,0,0;1,0,1;,1,1,0;0,0,1;0,1,1;1,1,1]';
b_0=0;
b=[1;1;1];
rho=.5;
for j=1:100;
changed=0;
for i=1:6
d=(b'*x(:,i)+b_0)*y(i);
if d<0
b=b+rho*x(:,i)*y(i);
b_0=b_0+rho*y(i);
changed=1;
end
end
if changed==0
break;
end
end
The Perceptron (Lecture October 23, 2009)
A Perceptron can be modeled as shown in Figure 1 of the previous lecture where[math]\displaystyle{ \,x_0 }[/math] is the model intercept and [math]\displaystyle{ x_{1},\ldots,x_{d} }[/math] represent the feature data, [math]\displaystyle{ \sum_{i=0}^d \beta_{j}x_{j} }[/math] is a linear combination of some weights of these inputs, and [math]\displaystyle{ I(\sum_{i=1}^d \beta_{j}x_{j}) }[/math], where [math]\displaystyle{ \,I }[/math] indicates the sign of the expression and returns the label of the data point.
The Perceptron algorithm seeks a linear boundary between two classes. A linear decision boundary can be represented by[math]\displaystyle{ \underline{\beta}^T\underline{x}+\beta_{0}. }[/math] The algorithm begins with an arbitrary hyperplane [math]\displaystyle{ \underline{\beta}^T\underline{x}+\beta_{0} }[/math] (initial guess). Its goal is to minimize the distance between the decision boundary and the misclassified data points. This is illustrated in Figure 2. It attempts to find the optimal [math]\displaystyle{ \underline\beta }[/math] by iteratively adjusting the decision boundary until all points are on the correct side of the boundary. It terminates when there are no misclassified points.
Derivation: The distance between the decision boundary and misclassified points.
If [math]\displaystyle{ \underline{x_{1}} }[/math] and [math]\displaystyle{ \underline{x_{2}} }[/math]both lie on the decision boundary then,
- [math]\displaystyle{ \begin{align} \underline{\beta}^T\underline{x_{1}}+\beta_{0} &= \underline{\beta}^T\underline{x_{2}}+\beta_{0} \\ \underline{\beta}^T (x_{1}-x_{2})&=0 \end{align} }[/math]
[math]\displaystyle{ \underline{\beta}^T (x_{1}-x_{2}) }[/math] denotes an inner product. Since the inner product is 0 and [math]\displaystyle{ (\underline{x_{1}}-\underline{x_{2}}) }[/math] is a vector lying on the decision boundary, [math]\displaystyle{ \underline{\beta} }[/math] is orthogonal to the decision boundary.
Let [math]\displaystyle{ \underline{x_{i}} }[/math] be a misclassified point.
Then the projection of the vector [math]\displaystyle{ \underline{x_{i}} }[/math] on the direction that is orthogonal to the decision boundary is [math]\displaystyle{ \underline{\beta}^T\underline{x_{i}} }[/math].
Now, if [math]\displaystyle{ \underline{x_{0}} }[/math] is also on the decision boundary, then [math]\displaystyle{ \underline{\beta}^T\underline{x_{0}}+\beta_{0}=0 }[/math] and so [math]\displaystyle{ \underline{\beta}^T\underline{x_{0}}= -\beta_{0} }[/math]. Looking at Figure 3, it can be seen that the distance between [math]\displaystyle{ \underline{x_{i}} }[/math] and the decision boundary is the absolute value of [math]\displaystyle{ \underline{\beta}^T\underline{x_{i}}+\beta_{0}. }[/math]
Consider [math]\displaystyle{ y_{i}(\underline{\beta}^T\underline{x_{i}}+\beta_{0}). }[/math]
- Notice that if [math]\displaystyle{ \underline{x_{i}} }[/math] is classified correctly then this product is positive. This is because if it is classified correctly, then either both ([math]\displaystyle{ \underline{\beta}^T\underline{x_{i}}+\beta_{0}) }[/math] and[math]\displaystyle{ \displaystyle y_{i} }[/math] are positive or they are both negative. However, if [math]\displaystyle{ \underline{x_{i}} }[/math] is classified incorrectly then one of [math]\displaystyle{ (\underline{\beta}^T\underline{x_{i}}+\beta_{0}) }[/math] and [math]\displaystyle{ \displaystyle y_{i} }[/math] is positive and the other is negative. The result is that the above product is negative for a point that is misclassified.
For the algorithm, we need only consider the distance between the misclassified points and the decision boundary.
- Consider [math]\displaystyle{ \phi(\underline{\beta},\beta_{0})= -\displaystyle\sum_{i\in M} –y_{i}(\underline{\beta}^T\underline{x_{i}}+\beta_{0}) }[/math]
which is a summation of positive numbers and where [math]\displaystyle{ \displaystyle M }[/math] is the set of all misclassified points.
The goal now becomes to [math]\displaystyle{ \min_{\underline{\beta},\beta_{0}} \phi(\underline{\beta},\beta_{0}). }[/math]
This can be done using a gradient descent approach, which is a numerical method that takes one predetermined step in the direction of the gradient, getting closer to a minimum at each step, until the gradient is zero. A problem with this algorithm is the possibility of getting stuck in a local minimum. To continue, the following derivatives are needed:
- [math]\displaystyle{ \frac{\partial \phi}{\partial \underline{\beta}}= -\displaystyle\sum_{i \in M}y_{i}\underline{x_{i}} \ \ \ \ \ \ \ \ \ \ \ \frac{\partial \phi}{\partial \beta_{0}}= -\displaystyle\sum_{i \in M}y_{i} }[/math]
Then the gradient descent type algorithm (Perceptron Algorithm) is
- [math]\displaystyle{ \begin{pmatrix} \underline{\beta}^{\mathrm{new}}\\ \underline{\beta_0}^{\mathrm{new}} \end{pmatrix} = \begin{pmatrix} \underline{\beta}^{\mathrm{old}}\\ \underline{\beta_0}^{\mathrm{old}} \end{pmatrix} +\rho \begin{pmatrix} y_i \underline{x_i}\\ y_i \end{pmatrix} }[/math]
where [math]\displaystyle{ \displaystyle\rho }[/math] is the magnitude of each step called the "learning rate" or the "convergence rate". The algorithm continues until [math]\displaystyle{
\begin{pmatrix}
\underline{\beta}^{\mathrm{new}}\\
\underline{\beta_0}^{\mathrm{new}}
\end{pmatrix}
=
\begin{pmatrix}
\underline{\beta}^{\mathrm{old}}\\
\underline{\beta_0}^{\mathrm{old}}
\end{pmatrix} }[/math]
or until it has iterated a specified number of times. If the algorithm converges, it has found a linear classifier, ie., there are no misclassified points.
Problems with the Algorithm and Issues Affecting Convergence
- If the data is not separable, then the Perceptron algorithm will not converge since it cannot find a linear classifier that classifies all of the points correctly.
- Convergence rates depend on the size of the gap between classes. If the gap is large, then the algorithm converges quickly. However, if the gap is small, the algorithm converges slowly. This problem can be eliminated by using basis expansions technique. To be specific, we try to find a hyperplane not in the original space, but in the enlarged space obtained by using some basis functions.
- If the classes are separable, there exists infinitely many solutions to Perceptron, all of which are hyperplanes.
- The speed of convergence of the algorithm is also dependent on the value of [math]\displaystyle{ \displaystyle\rho }[/math], the learning rate. A larger value of [math]\displaystyle{ \displaystyle\rho }[/math] could yield quicker convergence, but if this value is too large, it may also result in “skipping over” the minimum that the algorithm is trying to find and possibly oscillating forever between the last two points, before and after the min.
- A perfect separation is not always available even desirable. If observations comes from different classes sharing the same imput, the classification model seems to be overfitting and will generally have poor predictive performance.
- The perceptron convergence theorem states that if there exists an exact solution (in other words, if the training data set is linearly separable), then the perceptron learning algorithm is guaranteed to find an exact solution in a finite number of steps. Proofs of this theorem can be found for example in Rosenblatt (1962), Block (1962), Nilsson (1965), Minsky and Papert (1969), Hertz et al. (1991), and Bishop (1995a). Note, however, that the number of steps required to achieve convergence could still be substantial, and in practice, until convergence is achieved we will not be able to distinguish between a nonseparable problem and one that is simply slow to converge<ref>
Pattern Recognition and Machine Learning,Christopher M. Bishop,194
</ref>.
Comment on gradient descent algorithm
Consider yourself on the peak and you want to get to the land as fast as possible. So which direction should you step? Intuitively it should be the direction in which the height decreases fastest, which is given by the gradient. However, if the mountain has a saddle shape and you initially stand in the middle, then you will finally arrive at the saddle point (local minimum) and get stuck there.
In addition, note that in the final form of our gradient descent algorithm, we get rid of the summation over [math]\displaystyle{ \,i }[/math] (all data points). Actually, this is an alternative of the original gradient descent algorithm (sometimes called batch gradient descent) known as Stochastic gradient descent, where we approximate the true gradient by only evaluating on a single training example. This means that [math]\displaystyle{ \,{\beta} }[/math] gets improved by computation of only one sample. When there is a large data set, say, population database, it's very time-consuming to do summation over millions of samples. By Stochastic gradient descent, we can treat the problem sample by sample and still get decent result in practice.
- A Perceptron applet can be found at http://isl.ira.uka.de/neuralNetCourse/2004/VL_11_5/Perceptron.html .
Neural Networks (NN) - October 28, 2009
Introduction
A neural network is a two stage regression for classification model. It can be represented by a network diagram. It is a parallel, distributed information processing structure consisting of processing elements interconnected together with signal channels called connections. Each processing element has a single output connection with branches that "fan out" onto as many connections as desired, each carrying the same signal - the processing element output signal.
<ref> Haykin, Simon (2009). Neural Networks and Learning Machines. Pearson Education, Inc. </ref> A neural network resembles the brain in two respects:
1. Knowledge is acquired by the network from its environment through a learning process.
2. Interneuron connection strengths, known as synaptic weights, are used to store the acquired knowledge.
<ref> Theory of the Backpropagation Neural Network, R. Necht-Nielsen </ref> It is a multistage regression or classification model represented by a network. Figure 1 is an example of a typical neural network but it can have many different forms. It network applies both to regression or classification.
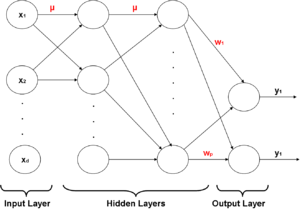
- A regression problem typically has only one unit [math]\displaystyle{ \ y_1 }[/math] in the output layer, but these networks can handle multiple quantitative responses in a seamless fashion.
- In a k-class classification problem, there are usually k target measurements units [math]\displaystyle{ \ y_1,...,y_k }[/math] in the output layer that each represent the probability of class k and each [math]\displaystyle{ \displaystyle y_k }[/math] is coded (0,1).
Activation Function
Activation Function is a term that is frequently used in classification by NN.
In perceptron, we have a "sign" function that takes the sign of a weighted sum of input features.
File:signfuncperceptron.png
The sign function is of the form File:signfunc1.png ; it is not continuous at 0 and we cannot take derivative of it. Thus, we replace it by a smooth function [math]\displaystyle{ \displaystyle \sigma }[/math] of the form File:signfunc2.png and call it the activation function.
The choice of this function [math]\displaystyle{ \displaystyle \sigma }[/math] is determined by the properties of the data and the assumed distribution of target variables, but for multiple binary classification problems the logistic function, also known as inverse-logit (sigmoid function), is often used:
[math]\displaystyle{ \sigma(a)=\frac {1}{1+e^{-a}} }[/math]
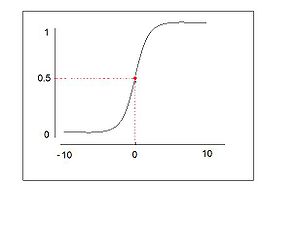
There are some important properties for the activation function.
- Activation function is nonlinear. It can be shown that if the activation function of the hidden units is linear, a three-layer neural network is equivalent to a two layer one.
- Activation function saturate, which means there are maximum and minimum output value. This property ensures that the weights are bounded and therefore the searching time is limited.
- Activation function is continuous and smooth.
- Activation function is monotonic. This property is not necessary, since we know that RBF networks is also a kind of power model.
Note: A key difference between a perceptron and a neural network is that a neural network uses continuous nonlinearities in the units, for the purpose of differentiation, whereas the perceptron often uses a non-differentiable activation function. The neural network function is differentiable with respect to the network parameters so that a gradient descent method can be used in training. Moreover, a perceptron is a linear classifier, whereas a neural network,by introducting the nonlinear transformation [math]\displaystyle{ \ sigma }[/math],it greatly enlarges the class of linear models and by combining layers of perceptrons, neural network is able to classify non-linear problems through proper training.
By assigning some weights to the connectors in the neural network (see diagram above) we weigh the input that comes into the perceptron, to get an output that in turn acts as an input to the next layer of perceptrons, and so on for each layer. This type of neural network is called Feed-Forward Neural Network. Applications to Feed-Forward Neural Networks include data reduction, speech recognition, sensor signal processing, and ECG abnormality detection, to name a few. <ref>J. Annema, Feed-Forward Neural Networks, (Springer 1995), pp. 9 </ref>
Back-propagation
For a while, the Neural Network model was just an idea, since there were no algorithms for training the model until 1986, when Geoffrey Hinton <ref> http://www.cs.toronto.edu/~hinton/backprop.html </ref> devised an algorithm called back-propagation [3]. After that, a number of other training algorithms and various configurations of neural networks were implemented.
When we were talking about perceptrons, we applied a gradient descent algorithm for optimizing weights. Back-propagation uses this idea of gradient descent to train a neural network based on the chain rule in calculus.
Assume that the last output layer has only one unit, so we are working with a regression problem. Later we will see how this can be extended to more output layers and thus turn into a classificaiton problem.
For simplicity, there is only 1 unit at the end and assume for the moment we are doing regression.
Note that we make a distinction between the input weights [math]\displaystyle{ \displaystyle (w_i) }[/math] and hidden weights [math]\displaystyle{ \displaystyle (u_i) }[/math].
Within each unit we have a function [math]\displaystyle{ \displaystyle z_i=\sigma(a_i) }[/math] that takes input [math]\displaystyle{ \displaystyle a_i }[/math] (linear sum of previous level) and outputs [math]\displaystyle{ \displaystyle z_i's }[/math]. The [math]\displaystyle{ \displaystyle z_i's }[/math] are the inputs into the final output of the model [math]\displaystyle{ \Rightarrow \hat y_i=\sum_{i=1}^p w_i z_i }[/math]
We can find the error of the neural network output by evaluating the squared difference between the true classification and the resulting classification output [math]\displaystyle{ \Rightarrow \displaystyle error=||y-\hat y ||^2 }[/math]
First find derivative of the model error with respect to output weights [math]\displaystyle{ \displaystyle w_i }[/math]
[math]\displaystyle{ \frac{\partial err}{\partial w_i}=\frac{\partial err}{\partial \hat y} \cdot \frac{\partial \hat y}{\partial w_i} }[/math]
[math]\displaystyle{ \frac{\partial err}{\partial w_i}=2(y-\hat y) \cdot z_i }[/math]
Now we need to find the derivative of the model error with respect to hidden weights [math]\displaystyle{ \displaystyle u_i's }[/math]
Consider the following diagram that opens up the hidden layers of the neural network:
i j are reversed!
Notice that the weighted sum on the output of the perceptrons at layer [math]\displaystyle{ \displaystyle l }[/math] are the inputs into the perceptrons at layer [math]\displaystyle{ \displaystyle j }[/math] and so on for all hidden layers.
So, using the chain rule
[math]\displaystyle{ \frac{\partial err}{\partial u_{jl}}=\frac{\partial err}{\partial a_j} \cdot \frac{\partial a_j}{\partial u_{jl}} }[/math]
[math]\displaystyle{ \frac{\partial err}{\partial u_{jl}}=\delta_j \cdot z_l }[/math]
Note that a change in [math]\displaystyle{ \,a_j }[/math] causes changes in all [math]\displaystyle{ \,a_i }[/math] in the next layer on which the error is based, so we need to sum over i in the chain:
[math]\displaystyle{ \delta_j = \frac{\partial err}{\partial a_j} = \sum_i \frac{\partial err}{\partial a_i} \cdot \frac{\partial a_i}{\partial a_j} =\sum_i \delta_i \cdot \frac{\partial a_i}{\partial a_j} }[/math]
[math]\displaystyle{ \,\frac{\partial a_i}{\partial a_j}=\frac{\partial a_i}{\partial z_j} \cdot \frac{\partial z_j}{\partial a_j}=u_{ij} \cdot \sigma'(a_j) }[/math] Using the activation function [math]\displaystyle{ \,\sigma(\cdot) }[/math]
So [math]\displaystyle{ \delta_j = \sum_i \delta_i \cdot u_{ij} \cdot \sigma'(a_j) }[/math]
[math]\displaystyle{ \delta_j = \sigma'(a_j)\sum_i \delta_i \cdot u_{ij} }[/math]
We can propagate the error calculated in the output back through the previous layers and adjust weights to minimize error.
Back-Propagation neural network is a good method for following situations:
- The problem is very complex and the number of input or output data points is very large, and have no idea to relate the input to the output.
- The solution varies over time within the bounds of the given input and output data, or the output is not easy to measure.
Neural Networks (NN) - October 30, 2009
Back-propagation
The idea is that we first feed an input from the training set to the Neural Network, then find the error rate at the output and then we propagate the error to previous layers and for each edge of weight [math]\displaystyle{ \,u_{ij} }[/math] we find [math]\displaystyle{ \frac{\partial \mathrm{err}}{\partial u_{ij}} }[/math]. Having the error rates at hand we adjust the weight of each edge by taking steps proportional to the negative of the gradient to decrease the error at output. The next step is to apply the next input from the training set and go through the described adjustment procedure. The overview of Back-propagation algorithm:
- Feed a point [math]\displaystyle{ \,x }[/math] in the training set to the network, and find the output of all the nodes.
- Evaluate [math]\displaystyle{ \,\delta_k=y_k-\hat{y_k} }[/math] for all output units, where [math]\displaystyle{ y_k }[/math] is the expected output and [math]\displaystyle{ \hat{y_k} }[/math] is the real output.
- By propagating to the previous layers evaluate all [math]\displaystyle{ \,\delta_j }[/math]s for hidden units: [math]\displaystyle{ \,\delta_j=\sigma'(a_j)\sum_i \delta_i u_{ij} }[/math] where [math]\displaystyle{ i }[/math] is associated to the previous layer.
- Using [math]\displaystyle{ \frac{\partial \mathrm{err}}{\partial u_{jl}} = \delta_j\cdot z_l }[/math] find all the derivatives.
- Adjust each weight by taking steps proportional to the negative of the gradient: [math]\displaystyle{ u_{jl}^{\mathrm{new}} \leftarrow u_{jl}^{\mathrm{old}} -\rho \frac{\partial \mathrm{err}}{u_{ij}} }[/math]
- Feed the next point in the training set and repeat the above steps.
How to initialize the weights
This still leaves the question of how to initialize the weights [math]\displaystyle{ \,u_{ij}, w_i }[/math]. The method of choosing weights mentioned in class was to randomize the weights before the first step. This is not likely to be near the optimal solution in every case, but is simple to implement. To be more specific, random values near zero will be a good choice for the initial weights(usually from [-1,1]). In this case, the model evolves from a nearly linear one to a nonlinear one as we desired. An alternative is to use an orthogonal least squares method to find the initial weights <ref>http://www.mitpressjournals.org/doi/abs/10.1162/neco.1995.7.5.982</ref>. Regression is performed on the weights and output by using a linear approximation of [math]\displaystyle{ \,\sigma(a_i) }[/math], and finds optimal weights in the linear model. Back propagation is used afterward to find the optimal solution, since the NN is non-linear.
How to set learning rates
The learning rate [math]\displaystyle{ \,\rho }[/math] is usually a constant.
If we use On-line learning, as a form of stochastic approximation process, [math]\displaystyle{ \,\rho }[/math] should decrease as the iteration increase.
Choosing too large learning rate may cause the unstability of the system, while the too small learning rate may lead to a very slow convergence rate(very long time in learning phase). However, the advantage of small learning rate is that it can guarantee the convergence. Thus, generally, it is better to choose a relatively small learning rate to ensure the stability. Usually, choose [math]\displaystyle{ \,\rho }[/math] between 0.01 and 0.7
Here we will mainly discuss how to estimate the number of hidden units at very beginning. Obviously, we should adjust it to be more precise using CV, LOO or other complexity control methods.
Basically, if the patterns are well separated, few hidden units are fairly enough. If the patterns are drawn from some highly complicated mixture models, more hidden units are really needed.
Actually, the number of hidden units determines the size of the model, and therefore the total number of the weights in the model. Typically speaking, the number of weights should not be larger than the number of training data, say N. Thus, sometimes, N/10 is a good choice. However, in pratice, many well performed models will use more hidden units.
Dimensionality reduction application
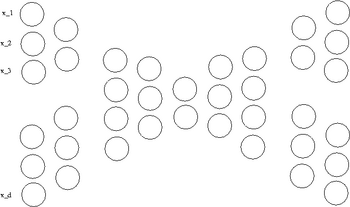
One possible application of Neural Networks is to perform dimensionality reduction, like other techniques, e.g., PCA, MDS, LLE and Isomap.
Consider the following configuration as shown in figure 1: As we go forward in layers of this Neural Network, the number of nodes is reduced, until we reach a layer with the number of nodes representing the desired dimensionality. However, note that at the very first few layers the number of nodes may not be strictly decreasing, as long as finally it can reach a layer with less nodes. From now on in the Neural Network the previous layers are mirrored. So at the output layer we have the same number of states as we have in the input layer. Now note that if we feed the network with each point and get an output approximately equal to the fed input, that means at the output the same input is reconstructed from the middle layer units. So the output of the middle layer units can represent the input with less dimensions.
To train this Neural Network, we feed the network with a training point and through back propagation we adjust the network weights based on the error between the input layer and the reconstruction at the output layer. Our low dimensional mapping will be the observed output from the middle layer. Data reconstruction consists of putting the low dimensional data through the second half of the network.
Deep Neural Network
Back-propagation in practice may not work well when there are too many hidden layers, since the [math]\displaystyle{ \,\delta }[/math] may become negligible and the errors vanish. This is a numerical problem, where it is difficult to estimate the errors. So in practice configuring a Neural Network with Back-propagation faces some subtleties. Deep Neural Networks became popular two or three years ago, when introduced by Bradford Nill in his PhD thesis. Deep Neural Network training algorithm deals with the training of a Neural Network with a large number of layers.
The approach of training the deep network is to assume the network has only two layers first and train these two layers. After that we train the next two layers, so on and so forth.
Although we know the input and we expect a particular output, we do not know the correct output of the hidden layers, and this will be the issue that the algorithm mainly deals with. There are two major techniques to resolve this problem: using Boltzman machine to minimize the energy function, which is inspired from the theory in atom physics concerning the most stable condition; or somehow finding out what output of the second layer is most likely to lead us to the expected output at the output layer.
Neural Networks in Practice
Now that we know so much about Neural Networks, what are suitable real world applications? Neural Networks have already been successfully applied in many industries.
Since neural networks are good at identifying patterns or trends in data, they are well suited for prediction or forecasting needs, such as customer research, sales forecasting, risk management and so on.
Take a specific marketing case for example. A feedforward neural network was trained using back-propagation to assist the marketing control of airline seat allocations. The neural approach was adaptive to the rule. The system is used to monitor and recommend booking advice for each departure.
Issues with Neural Network
When Neural Networks was first introduced they were thought to be modeling human brains, hence they were given the fancy name "Neural Network". But now we know that they are just logistic regression layers on top of each other but have nothing to do with the real function principle in the brain.
We do not know why deep networks turn out to work quite well in practice. Some people claim that they mimic the human brains, but this is unfounded. As a result of these kinds of claims it is important to keep the right perspective on what this field of study is trying to accomplish. For example, the goal of machine learning may be to mimic the 'learning' function of the brain, but necessarily the processes the brain uses to learn.
As for the algorithm, since it does not have a convex form, we still face the problem of local minimum, although people have devised other techniques to avoid this dilemma.
In sum, Neural Network lacks a strong learning theory to back up its "success", thus it's hard for people to wisely apply and adjust it. Having said that, it is not an active research area in machine learning. NN still has wide applications in the engineering field such as in control.
Complexity Control October 30, 2009
There are two issues that we have to avoid in Machine Learning:
- Overfitting
- Underfitting
Overfitting occurs when our model is heavily complex with so many degrees of freedom, that we can learn every detail of the training set. Such a model will have very high precision on the training set but will show very poor ability to predict outcomes of new instances, especially outside the domain of the training set.
In a Neural Network if the depth is too much, the network will have many degrees of freedom and will learn every characteristic of the training data set. That means it will show a very precise outcome of the training set but will not be able to generalize the commonality of the training set to predict the outcome of new cases.
Underfitting occurs when the model we picked to describe the data is not complex enough, and has high error rate on the training set. There is always a trade-off. If our model is too simple, underfitting could occur and if it is too complex, overfitting can occur.
Example
- Consider the example showed in the figure. We have a training set and we want to find a model which fits it the best. We can find a polynomial of high degree which almost passes through all the points in the training set. But, in fact the training set is coming from a line model. Now the problem is although the complex model has less error on the training set it diverges from the line in other ranges which we have no training point. Because of that the high degree polynomail has very poor predictive result on test cases. This is an example of overfitting model.
- Now consider a training set which comes from a polynomial of degree two model. If we model this training set with a polynomial of degree one, our model will have high error rate on the training set, and is not complex enough to describe the problem.
- Consider a simple classification example. If our classification rule takes as input only the colour of a fruit and concludes that it is a banana, then it is not a good classifier. The reason is that just because a fruit is a yellow, does not mean that it is a banana. We can add complexity to our model to make it a better classifier by considering more features typical of bananas, such as size and shape. If we continue to make our model more and more complex in order to improve our classifier, we will eventually reach a point where the quality of our classifier no longer improves, ie., we have overfit the data. This occurs when we have considered so many features that we have perfectly described the existing bananas, but if presented with a new banana of slightly different shape than the existing bananas, for example, it cannot be detected. This is the tradeoff; what is the right level of complexity?
Complexity Control - Nov 2, 2009
Overfitting occurs when the model becomes too complex and underfitting occurs when it is not complex enough, both of which are not desirable. To control complexity, it is necessary to make assumptions for the model before fitting the data. Assumptions that we can make for a model are with polynomials or a neural network. There are other ways as well.

We do not want a model to get too complex, so we control it by making an assumption on the model. With complexity control, we want a model or a classifier with a low error rate.
How do we choose a good classifier?
Our goal is to find a classifier that minimizes the true error rate. Recall the empirical error rate
[math]\displaystyle{ \, L_{h}= \frac{1}{n} \sum_{i=1}^{n} I(h(x_{i}) \neq y_{i}) }[/math]
[math]\displaystyle{ \,h }[/math] is a classifier and we want to minimize the error rate. So we apply [math]\displaystyle{ \displaystyle x_1 }[/math] to [math]\displaystyle{ \displaystyle x_n }[/math] to [math]\displaystyle{ \displaystyle h }[/math], and take the average to get the empirical true error rate estimation of probability that [math]\displaystyle{ h(x_{i}) \neq y_{i} }[/math].
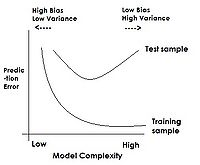
There is a downward bias to this estimate meaning that it is always less than the true error rate.
If there is a change in our complexity from low to high, our error rate is always decreasing. When we apply our model to the test data, our error rate will start to decrease to a point, but then it will increase since the model hasn't seen it before. This can be explained since training error will decrease when we fit the model better by increasing its complexity, but as we have seen, this complex model will not generalize well, resulting in a larger test error.
We use our test data (from the test sample line shown on Figure 2) to get our empirical error rate. Right complexity is defined as where error rate of the test data is minimum; and this is one idea behind complexity control.
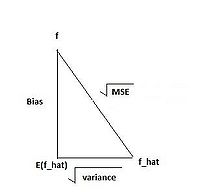
We assume that we have samples [math]\displaystyle{ \,X_1, . . . ,X_n }[/math] that follow some (possibly unknown) distribution. We want to estimate a parameter [math]\displaystyle{ \,f }[/math] of the unknown distribution. This parameter may be the mean [math]\displaystyle{ \,E(X_i) }[/math], the variance [math]\displaystyle{ \,var(X_i) }[/math] or some other quantity.
The unknown parameter [math]\displaystyle{ \,f }[/math] is a fixed real number [math]\displaystyle{ f\in R }[/math]. To estimate it, we use an estimator which is a function of our observations, [math]\displaystyle{ \hat{f}(X_1,...,X_n) }[/math].
[math]\displaystyle{ Bias (\hat{f}) = E(\hat{f}) - f }[/math]
[math]\displaystyle{ MSE (\hat{f}) = E[(\hat{f} - f)^2] }[/math]
[math]\displaystyle{ Variance (\hat{f}) = E[(\hat{f} - E(\hat{f}))^2] }[/math]
One property we desire of the estimator is that it is correct on average, that is, it is unbiased. [math]\displaystyle{ Bias (\hat{f}) = E(\hat{f}) - f=0 }[/math]. However, there is a more important property for an estimator than just being unbiased: the mean squared error. In statistics, there are problems for which it may be good to use an estimator with a small bias. In some cases, an estimator with a small bias may have lesser mean squared error or be median-unbiased (rather than mean-unbiased, the standard unbiasedness property). The property of median-unbiasedness is invariant under transformations while the property of mean-unbiasedness may be lost under nonlinear transformations. For example, while using an unbiased estimator with large mean square error to estimate the parameter, we highly risk a big error. In contrast, a biased estimator with small mean square error will well improve the precision of our prediction.
Hence, our goal is to minimize [math]\displaystyle{ MSE (\hat{f}) }[/math].
From figure 3, we can see that the relationship of the three parameters is: [math]\displaystyle{ MSE (\hat{f})=Variance (\hat{f})+Bias ^2(\hat{f}) }[/math]. Thus given the Mean Squared Error (MSE), if we have a low bias, then we will have a high variance and vice versa.
A Test error is a good estimation on MSE. We want to have a somewhat balanced bias and variance (not high on bias or variance), although it will have some bias.
Referring to Figure 2, overfitting happens after the point where training data (training sample line) starts to decrease and test data (test sample line) starts to increase. There are 2 main approaches to avoid overfitting:
1. Estimating error rate
[math]\displaystyle{ \hookrightarrow }[/math] Empirical training error is not a good estimation
[math]\displaystyle{ \hookrightarrow }[/math] Empirical test error is a better estimation
[math]\displaystyle{ \hookrightarrow }[/math] Cross-Validation is fast
[math]\displaystyle{ \hookrightarrow }[/math] Computing error bound (analytically) using some probability inequality.
We will not discuss computing the error bound in class; however, a popular method for doing this computation is called VC Dimension (short for Vapnik–Chervonenkis Dimension). Information can be found from Andrew Moore and Steve Gunn.
2. Regularization
[math]\displaystyle{ \hookrightarrow }[/math] Use of shrinkage method
[math]\displaystyle{ \hookrightarrow }[/math] Decrease the chance of overfitting by controlling the weights
Example of under and overfitting in R
To give further intuition of over and underfitting, consider this example. A simple quadratic data set with some random noise is generated, and then polynomials of varying degrees are fitted. The errors for the training set and a test set are calculated.
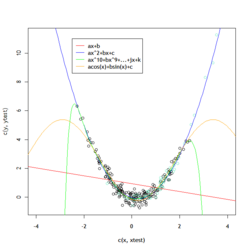
>> x <- rnorm(200,0,1) >> y <- x^2-0.5*x+rnorm(200,0,0.3) >> xtest <- rnorm(50,1,1) >> ytest <- xtest^2-0.5*xtest+rnorm(50,0,0.3) >> p1 <- lm(y~x) >> p2 <- lm(y ~ poly(x,2)) >> pn <- lm(y ~ poly(x,10)) >> psi <- lm(y~I(sin(x))+I(cos(x)))
xvalues for the training set are based on a [math]\displaystyle{ \,N(0,1) }[/math] distribution, while the test set has a [math]\displaystyle{ \,N(1,1) }[/math] distribution.yvalues are determined by [math]\displaystyle{ \,y = x^2 + x + N(0,0.3) }[/math], a quadratic function with some random variation. Polynomial least square fits of degree 1, 2, and 10 are calculated, as well as a fit of [math]\displaystyle{ \,sin(x)+cos(x) }[/math].
>> > # calculate the mean squared error of degree 1 poly >> > sum((y-predict(p1,data.frame(x)))^2)/length(y) >> [1] 1.576042 >> > sum((ytest-predict(p1,data.frame(x=xtest)))^2)/length(ytest) >> [1] 7.727615
- Training and test mean squared errors for the linear fit. These are both quite high - and since the data is non-linear, the different mean value of the test data increases the error quite a bit.
>> > # calculate the mean squared error of degree 2 poly >> > sum((y-predict(p2,data.frame(x)))^2)/length(y) >> [1] 0.08608467 >> > sum((ytest-predict(p2,data.frame(x=xtest)))^2)/length(ytest) >> [1] 0.08407432
- This fit is far better - and there is not much difference between the training and test error, either.
>> > # calculate the mean squared error of degree 10 poly >> > sum((y-predict(pn,data.frame(x)))^2)/length(y) >> [1] 0.07967558 >> > sum((ytest-predict(pn,data.frame(x=xtest)))^2)/length(ytest) >> [1] 156.7139
- With a high-degree polynomial, the training error continues to decrease, but not by much - and the test set error has risen again. The overfitting makes it a poor predictor. As the degree of the polynomial rises further, the accuracy of the computer becomes an issue - and a good fit is not even consistently produced for the training data.
>> > # calculate mse of sin/cos fit >> > sum((y-predict(psi,data.frame(x)))^2)/length(y) >> [1] 0.1105446 >> > sum((ytest-predict(psi,data.frame(x=xtest)))^2)/length(ytest) >> [1] 1.320404
- Fitting a function of the form sin(x)+cos(x) works pretty well on the training set, but because it is not the real underlying function, it fails on test data which doesn't lie on the same domain.
Cross-Validation (CV) - Introduction

Cross-Validation is used to estimate the error rate of a classifier with respect to test data rather than data used in the model. Here is a general introduction to CV:
[math]\displaystyle{ \hookrightarrow }[/math] We have a set of collected data for which we know the proper labels
[math]\displaystyle{ \hookrightarrow }[/math] We divide it into 2 parts, Training data (T) and Validation data (V)
[math]\displaystyle{ \hookrightarrow }[/math] For our calculation, we pretend that we do not know the label of V and we use data in T to train the classifier
[math]\displaystyle{ \hookrightarrow }[/math] We estimate an empirical error rate on V since the model hasn't seen V yet and we know the proper label of all elements in V to know how many were misclassified.
CV has different implementations which can reduce the variance of the calculated error rate, but sometimes with a tradeoff of a higher calculation time.
Complexity Control - Nov 4, 2009
Cross-validation
Cross-validation is the simplest and most widely used method to estimate the true error. It comes from the observation that although training error always decreases with the increasing complexity of the model, the test error starts to increase from a certain point, which is noted as overfitting (see figure 2 above). Since test error estimates MSE (mean square error) best, people came up with the idea to divide the data set into three parts: training set, validation set, and test set. training set is used to build the model, validation set is used to deside the parameters and the optimal model, and the test set is used to estimate the performance of the chosen model. A classical division is 50% for training set, and 25% each for validation set and test set. All of them are randomly selected from the original data set.
Then, we only use the part of our data marked as the "training set" to train our algorithm, while keeping the remaining marked as the "validation set" untouched. As a result, the validation set will be totally unknown to the trained model. The error rate is then estimated by:
[math]\displaystyle{ \hat L(h) = \frac{1}{|\nu|}\sum_{X_i \in \nu}(h(x_i) \neq y_i) }[/math], where [math]\displaystyle{ \,|\nu| }[/math] is the cardinality of the validation set.
When we change the complexity, the error generated by the validation set will have the same behavior as the test set, so we are able to choose the best parameters to get the lowest error.
K-fold Cross-validation
Above is the simplest form of complexity control. However, in reality, it may be hard to collect data ??and we usually suffer from the curse of dimensionality??, and a larger data set may be hard to come by. Consequently, we may not be able to afford to sacrifice part of the limited resources. In this case we use another method that addresses this problem, K-fold cross-validation. We divide the data set into [math]\displaystyle{ \,K }[/math] subsets roughly equal in size. The usual choice is [math]\displaystyle{ \,K = 10 }[/math].
Generally, how to choose [math]\displaystyle{ \,K }[/math]:
if [math]\displaystyle{ \,K=n }[/math], leave one out, low bias, high variance. Each subset contains a single element, so the model is trained with all except one point, and then validated using that point.
if [math]\displaystyle{ \,K=2 }[/math], say 2-fold, 5-fold, high bias, low variance. Each subset contains approximately [math]\displaystyle{ \,\frac{1}{2} }[/math] or [math]\displaystyle{ \,\frac{1}{5} }[/math] of the data.
For every [math]\displaystyle{ \,k }[/math]th [math]\displaystyle{ ( \,k \in [ 1, K ] ) }[/math] part, we use the other [math]\displaystyle{ \,K-1 }[/math] parts to fit the model and test on the [math]\displaystyle{ \,k }[/math]th part to estimate the prediction error [math]\displaystyle{ \hat L_k }[/math], where
[math]\displaystyle{ \hat L(h) = \frac{1}{K}\sum_{k=1}^K\hat L_k }[/math]
For example, suppose we want to fit a polynomial model to the data set and split the set into four equal subsets as shown in Figure 2. First we choose the degree to be 1, i.e. a linear model. Next we use the first three sets as training sets and the last as validation set, then the 1st, 2nd, 4th subsets as training set and the 3rd as validation set, so on and so forth until all the subsets have been the validation set once (all observations are used for both training and validation). After we get [math]\displaystyle{ \hat L_1, \hat L_2, \hat L_3, \hat L_4 }[/math], we can calculate the average [math]\displaystyle{ \hat L }[/math] for degree 1 model. Similarly, we can estimate the error for n degree model and generate a simulating curve. Now we are able to choose the right degree which corresponds to the minimum error. Also, we can use this method to find the optimal unit number of hidden layers of neural networks. We can begin with 1 unit number, then 2, 3 and so on and so forth. Then find the unit number of hidden layers with lowest average error.
Generalized Cross-validation
If the vector of observed values is denoted by [math]\displaystyle{ \mathbf{y} }[/math], and the vector of fitted values by [math]\displaystyle{ \hat\mathbf{y} }[/math].
[math]\displaystyle{ \mathbf{y} = \mathbf{H}\hat\mathbf{y} }[/math],
where the hat matrix is given by
[math]\displaystyle{ \mathbf{H} = \mathbf{X}( \mathbf{X}^{T} \mathbf{X})^{-1}\mathbf{X}^{T} }[/math],
[math]\displaystyle{ \frac{1}{N}\sum_{i=1}^{N}[y_{i} - \hat f^{-i}(\mathbf{x}_{i})]^{2}=\frac{1}{N}\sum_{i=1}^{N}[\frac{y_{i}-\hat f(x_{i})}{1-\mathbf{H}_{ii}}]^{2} }[/math],
Then the GCV approximation is given by
[math]\displaystyle{ GCV(\hat f) = \frac{1}{N}\sum_{i=1}^{N}[\frac{y_{i}-\hat f(x_{i})}{1-trace(\mathbf{H})/N}]^{2} }[/math],
Thus, one of the biggest advantages of the GCV is that the trace is more easily computed.
Leave-one-out Cross-validation
Leave-one-out cross-validation involves using all but one data point in the original training data set to train our model, then using the data point that we initially left out as a means to estimate true error. But repeating this process for every data point in our original data set, we can obtain a good estimation of true error.
In other words, leave-one-out cross-validation is k-fold cross-validation in which we set the subset number [math]\displaystyle{ \,K }[/math] to be the cardinality of the whole data set.
In the above example, we can see that k-fold cross-validation can be computationally expensive: for every possible value of the parameter, we must train the model [math]\displaystyle{ \,K }[/math] times. This deficiency is even more obvious in leave-one-out cross-validation, where we must train the model [math]\displaystyle{ \,n }[/math] times, where [math]\displaystyle{ \,n }[/math] is the number of data point in the data set.
Fortunately, when adding data points to the classifier is reversible, calculating the difference between two classifiers is computationally more efficient than calculating the two classifiers separately. So, if the classifier on all the data points is known, we simply undo the changes from a data point [math]\displaystyle{ \,K }[/math] times to calculate the leave-one-out cross-validation error rate.
Regularization for Neural Network — Weight Decay
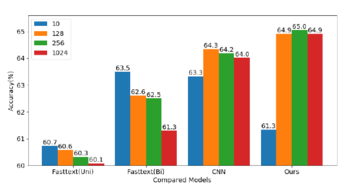
Weight decay training is suggested as an implementation for achieving a robust neural network which is insensitive to noise. Since the number of hidden layers in NN is usually decided by certain domain knowledge, it may easily get into the problem of overfitting.
It can be seen from Figure 1 that when the weight is in the vicinity of zero, the operative part of the activation function shows linear behavior. The NN then collapses to an approximately linear model. Note that a linear model is the simplest model, we can avoid overfitting by constraining the weights to be small. This gives us a hint to initialize the random weights to be close to zero.
Formally, we penalize nonlinear weights by adding a penalty term in the error function. Now the regularized error function becomes:
[math]\displaystyle{ \,REG = err + \lambda(\sum_{i}|w_i|^2 + \sum_{jk}|u_{jk}|^2) }[/math], where [math]\displaystyle{ \,err }[/math] is the original error in back-propagation; [math]\displaystyle{ \,w_i }[/math] is the weights of the output layer; [math]\displaystyle{ \,u_{jk} }[/math] is the weights of the hidden layers.
Usually, too large [math]\displaystyle{ \,\lambda }[/math] will make the weights [math]\displaystyle{ \,w_i }[/math] and [math]\displaystyle{ \,u_{jk} }[/math] too small. We can use cross validation to estimate [math]\displaystyle{ \,\lambda }[/math].
A similar penalty, weight elimination, is given by,
[math]\displaystyle{ \,REG = err + \lambda(\sum_{i}\frac{|w_i|^2}{1 + |w_i|^2} + \sum_{jk}\frac{|u_{jk}|^2}{1+|u_{jk}|^2}) }[/math].
As in back-propagation, we take partial derivative with respect to the weights:
[math]\displaystyle{ \frac{\partial REG}{\partial w_i} = \frac{\partial err}{\partial w_i} + 2\lambda w_i }[/math]
[math]\displaystyle{ \frac{\partial REG}{\partial u_{jk}} = \frac{\partial err}{\partial u_{jk}} + 2\lambda u_{jk} }[/math]
[math]\displaystyle{ w^{new} \leftarrow w^{old} - \rho\left(\frac{\partial err}{\partial w} + 2\lambda w\right) }[/math]
[math]\displaystyle{ u^{new} \leftarrow u^{old} - \rho\left(\frac{\partial err}{\partial u} + 2\lambda u\right) }[/math]
Note that here [math]\displaystyle{ \,\lambda }[/math] serves as a trade-off parameter, tuning between the error rate and the linearity. Actually, we may also set [math]\displaystyle{ \,\lambda }[/math] by cross-validation. The tuning parameter is important since weights of zero will lead to zero derivatives and the algorithm will not change. On the other hand, starting with weights that are too large means starting with a nonlinear model which can often lead to poor solutions. <ref>Trevor Hastie, Robert Tibshirani, Jerome Friedman, Elements of Statistical Learning (Springer 2009) pp.398</ref>
Radial Basis Function (RBF) Networks - November 6, 2009
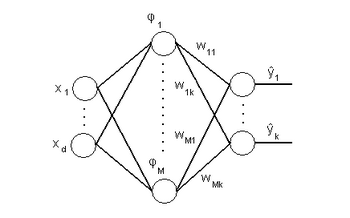
Introduction
A Radial Basis Function (RBF) network [4] is a type of artificial neural network with an output layer and a single hidden layer, with weights from the hidden layer to the output layer, and can be trained without back propagation since it has a closed-form solution. The neurons in the hidden layer contain basis functions. One choice that has been widely used is that of radial basis functions, which have the property that each basis function depends only on the radial distance (typically Euclidean) from a center [math]\displaystyle{ \displaystyle\mu_{j} }[/math], so that [math]\displaystyle{ \phi_{j}(x)= h({\Vert x - \mu_{j}\Vert}) }[/math].
The output of an RBF network can be expressed as a weighted sum of its radial basis functions as follows:
[math]\displaystyle{ \hat y_{k} = \sum_{j=1}^M\phi_{j}(x) w_{jk} }[/math]
The radial basis function is:
[math]\displaystyle{ \phi_{j}(x) = e^{\frac{-\Vert x - \mu_{j}\Vert ^2}{2\sigma_{j}^2}} }[/math]
(Gaussian without a normalization constant)
note:The hidden layer has a variable number of neurons (the optimal number is determined by the training process). As usual the more neurons in the hidden layer, the higher the model complexity. Each neuron consists of a radial basis function centered on a point with the same dimensions as the input data. The radii of the RBF functions may be different. The centers and radii can be determined through clustering or an EM algorithm. When the x vector is given from the input layer, the hidden neuron computes the radial distance from the neuron’s center point and then applies RBF function to this distance. The resulting value is passed to the the output layer and weighed together to form the output.
[math]\displaystyle{ \,y_{k} }[/math] can be expressed in matrix form as:
[math]\displaystyle{ \hat Y = \Phi W }[/math]
where
- [math]\displaystyle{ \hat{Y}_{n,k} = \left[ \begin{matrix} \hat{y}_{1,1} & \hat{y}_{1,2} & \cdots & \hat{y}_{1,k} \\ \hat{y}_{2,1} & \hat{y}_{2,2} & \cdots & \hat{y}_{2,k} \\ \vdots &\vdots & \ddots & \vdots \\ \hat{y}_{n,1} & \hat{y}_{n,2} & \cdots & \hat{y}_{n,k} \end{matrix}\right] }[/math] is the matrix of output variables.
- [math]\displaystyle{ \Phi_{n,m} = \left[ \begin{matrix} \phi_{1,1} & \phi_{1,2} & \cdots & \phi_{1,m} \\ \phi_{2,1} & \phi_{2,2} & \cdots & \phi_{2,m} \\ \vdots & \vdots & \ddots & \vdots \\ \phi_{n,1} & \phi_{n,2} & \cdots & \phi_{n,m} \end{matrix}\right] }[/math] is the matrix of Radial Basis Functions.
- [math]\displaystyle{ W_{m,k} = \left[ \begin{matrix} w_{1,1} & w_{1,2} & \cdots & w_{1,k} \\ w_{2,1} & w_{2,2} & \cdots & w_{2,k} \\ \vdots & \vdots & \ddots & \vdots \\ w_{m,1} & w_{m,2} & \cdots & w_{m,k} \end{matrix}\right] }[/math] is the matrix of weights.
Here, [math]\displaystyle{ k }[/math] is the number of outputs, [math]\displaystyle{ n }[/math] is the number of data points, and [math]\displaystyle{ m }[/math] is the number of hidden units. If [math]\displaystyle{ k = 1 }[/math], [math]\displaystyle{ \hat Y }[/math] and [math]\displaystyle{ W }[/math] are column vectors.
related reading:
Introduction of the Radial Basis Function (RBF) Networks [5]
Radial Basis Function (RBF) Networks [6] [7]
Estimation of weight matrix W
We minimize the training error, [math]\displaystyle{ \Vert Y - \hat{Y}\Vert^2 }[/math] in order to find [math]\displaystyle{ \,W }[/math].
From a previous result in linear algebra we know that
[math]\displaystyle{ \Vert A \Vert^2 = Tr(A^{T}A) }[/math]
Thus we have a problem similar to linear regression:
[math]\displaystyle{ \ err = \Vert Y - \Phi W\Vert^{2} = Tr[(Y - \Phi W)^{T}(Y - \Phi W)] }[/math]
[math]\displaystyle{ \ err = Tr[Y^{T}Y - Y^{T}\Phi W - W^{T} \Phi^{T} Y + W^{T}\Phi^{T} \Phi W] }[/math]
Useful properties of matrix differentiation
[math]\displaystyle{ \frac{\partial Tr(AX)}{\partial X} = A^{T} }[/math]
[math]\displaystyle{ \frac{\partial Tr(X^{T}A)}{\partial X} = A }[/math]
[math]\displaystyle{ \frac{\partial Tr(X^{T}AX)}{\partial X} = (A^{T} + A)X }[/math]
Solving for W
We find the minimum over [math]\displaystyle{ \,W }[/math] by setting [math]\displaystyle{ \frac{\partial err}{\partial W} }[/math] equal to zero and using the aforementioned properties of matrix differentiation.
[math]\displaystyle{ \frac{\partial err}{\partial W} = 0 }[/math]
[math]\displaystyle{ \ 0 - \Phi^{T}Y - \Phi^{T}Y + 2\Phi^{T}\Phi W = 0 }[/math]
[math]\displaystyle{ \ -2 \Phi^{T}Y + 2\Phi^{T}\Phi W = 0 }[/math]
[math]\displaystyle{ \ W = (\Phi^{T}\Phi)^{-1}\Phi^{T}Y }[/math]
[math]\displaystyle{ \hat{Y} = \Phi W = \Phi(\Phi^{T}\Phi)^{-1}\Phi^{T}Y = HY }[/math]
where [math]\displaystyle{ \ H = \Phi(\Phi^{T}\Phi)^{-1}\Phi^{T} }[/math]
[math]\displaystyle{ \,H }[/math] is the hat matrix for this model. This gives us a nice results since the solution has a closed form and we do not have to worry about convexity problems in this case.
Including an additional bias
[math]\displaystyle{ \,y_{k} }[/math] can be expressed in matrix form as:
[math]\displaystyle{ \hat Y = \Phi W }[/math]
where
- [math]\displaystyle{ \hat Y = \left[ \begin{matrix} y_{11} & y_{12} & \cdots & y_{1k} \\ y_{21} & y_{22} & \cdots & y_{2k} \\ \vdots & & \ddots & \vdots \\ y_{n1} & y_{n2} & \cdots & y_{nk} \end{matrix}\right] }[/math] is the matrix(n by k) of output variables.
- [math]\displaystyle{ \Phi = \left[ \begin{matrix} \phi_{10} &\phi_{11} & \phi_{12} & \cdots & \phi_{1M} \\ \phi_{20} & \phi_{21} & \phi_{22} & \cdots & \phi_{2M} \\ \vdots & & \ddots & \vdots \\ \phi_{n0} &\phi_{n1} & \phi_{n2} & \cdots & \phi_{nM} \end{matrix}\right] }[/math] is the matrix(n by M+1) of Radial Basis Functions.
- [math]\displaystyle{ W = \left[ \begin{matrix} w_{01} & w_{02} & \cdots & w_{0k} \\ w_{11} & w_{12} & \cdots & w_{1k} \\ w_{21} & w_{22} & \cdots & w_{2k} \\ \vdots & & \ddots & \vdots \\ w_{M1} & w_{M2} & \cdots & w_{Mk} \end{matrix}\right] }[/math] is the matrix(M+1 by k) of weights.
where the extra basis function [math]\displaystyle{ \Phi_{0} }[/math] is set to 1.
Normalized RBF
In addition to the above unnormalized architecture, the normalized RBF can be represented as:
[math]\displaystyle{ \hat{y}_{k}(X) = \frac{\sum_{j=1}^{M} w_{jk}\Phi_{j}(X)}{\sum_{r=1}^{M}\Phi_{r}(X)} }[/math]
Actually, [math]\displaystyle{ \Phi^{\ast}_{j}(X) = \frac{\Phi_{j}(X)}{\sum_{r=1}^{M}\Phi_{r}(X)} }[/math] is known as a normalized radial basis function. Giving the familiar form,
[math]\displaystyle{ \hat{y}_{k}(X) = \sum_{j=1}^{M} w_{jk}\Phi^{\ast}_{j}(X) }[/math]
Conceptualizing RBF networks
In the past, we have classified data using models that were explicitly linear, quadratic, or otherwise definite. In RBF networks, like in Neural Networks, we can fit an arbitrary model. How can we do this without changing the equations being used?
Recall a trick that was discussed in the October 7 lecture: if we add new features to our original data set, we can project into higher dimensions, use a linear algorithm, and get a quadratic result by collapsing to a lower dimension afterward. In RBF networks, something similar can happen.
Think of [math]\displaystyle{ \,\Phi }[/math], our matrix of radial basis functions, as a feature space of the input. Each hidden unit, then, can be thought to represent a feature; we can see that, if there are more hidden units than input units, we can essentially project to a higher-dimensional space, as we did in our earlier trick. However, this does not mean that an RBF network will actually do this, it is merely a way to convince yourself that RBF networks (and neural networks) can fit arbitrary models. Nevertheless, it is also noticed that just because of such great power, the problem of overfitting appears more important. We have to control its complexity so that it does not fit to an arbitrary training model but to a general one.
RBF networks for classification -- a probabilistic paradigm
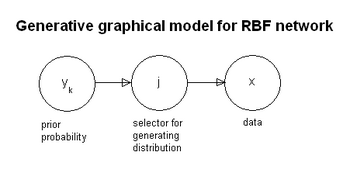
An RBF network is akin to fitting a Gaussian mixture model to data. We assume that each class can be modelled by a single function [math]\displaystyle{ \,\phi }[/math] and data is generated by a mixture model. According to Bayes Rule,
[math]\displaystyle{ Pr(Y = y_{k} | X = x) = \frac {Pr(x|y_{k})*Pr(y_{k})}{Pr(x)} }[/math]
While all classifiers that we have seen thus far in the course have been in discriminative form, the RBF network is a generative model that can be represented using a directed graph.
We can replace the class conditional density in the above conditional probability expression by marginalizing [math]\displaystyle{ \,x }[/math] over [math]\displaystyle{ \,j }[/math]: [math]\displaystyle{ \Pr(x|y_{k}) = \sum_{j} Pr(x|j)*Pr(j|y_{k}) }[/math]
- Note We made the assumption that each class can be modelled by a single function [math]\displaystyle{ \displaystyle\Phi }[/math] and that the data was generated by a mixture model. The Gaussian mixture model has the form:
[math]\displaystyle{ f(x)=\sum_{m=1}^M \alpha_m \phi(x;\mu_m,\Sigma_m) }[/math] where [math]\displaystyle{ \displaystyle\alpha_m }[/math] are mixing proportions, [math]\displaystyle{ \displaystyle\sum_m \alpha_m=1 }[/math], and [math]\displaystyle{ \displaystyle\mu_m }[/math] and [math]\displaystyle{ \displaystyle\Sigma_m }[/math] are the mean and covariance of each Gaussian density respectively. <ref>H. Trevor, R. Tibshirani, J. Friedman, The Elements of Statistical Learning (Springer 2009), pp. 214. </ref> The generative model in Figure 1 shows graphically how each Gaussian in the mixture model is chosen to sample from.
Radial Basis Function (RBF) Networks - November 9th, 2009
RBF Network for classification (A probabilistic point of view)
Using RBF Network to do classification, we usually treat it as regression problem. We want to set a threshold to decide what the data’s class membership is. However, to find some insight to the classification problem of what we are doing in terms of RBF Network, we often think of mixture models and make certain assumptions.
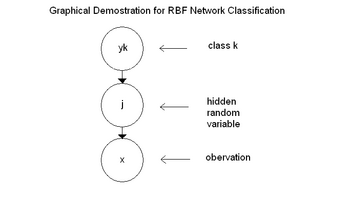
We assume, as we can see in the graph on the right hand side, that we have three random variables, [math]\displaystyle{ \displaystyle y_k }[/math], [math]\displaystyle{ \displaystyle j }[/math], and [math]\displaystyle{ \displaystyle x }[/math] where [math]\displaystyle{ \displaystyle y_k }[/math] denotes class [math]\displaystyle{ \,k }[/math], [math]\displaystyle{ \displaystyle x }[/math] is what we observed here, and [math]\displaystyle{ \displaystyle j }[/math] is some hidden random variable. There is a process that there are different classes, and each class can trigger a different hidden random variable [math]\displaystyle{ \displaystyle j }[/math]. To understand this, we can assume that, for instance, this random variable [math]\displaystyle{ \displaystyle j }[/math] has a Gaussian distribution (it could have any other distribution as well) and that all the [math]\displaystyle{ \displaystyle j }[/math]’s have the same distribution (Gaussian), but with different parameters. From each Gaussian distribution triggered by each class, we are going to sample some data points. Therefore, in the end, we are going to get a set of data, which are not strictly Gaussian, but are actually a mixture of Gaussians.
Again, we look at the posterior distribution from Bayes' Rule.
[math]\displaystyle{ Pr(Y = y_{k} | X = x) = \frac {Pr(X = x | Y = y_{k})*Pr(Y = y_{k})}{Pr(X = x)} }[/math]
Since we made the assumption that the data has been generated from a mixture model, we can estimate this conditional probability by
[math]\displaystyle{ \Pr(X = x | Y = y_{k}) = \sum_{j} Pr(X = x | j)*Pr(j | Y = y_{k}) }[/math],
which is the class conditional distribution (or probability) of the mixture model. Note, here, if we only have a simple model from [math]\displaystyle{ \displaystyle y_k }[/math] to [math]\displaystyle{ \displaystyle x }[/math], then we won’t have this summation.
We can substitute this class conditional distribution into Bayes' formula. We can see that the posterior of class [math]\displaystyle{ \displaystyle k }[/math] is the summation over [math]\displaystyle{ \displaystyle j }[/math] of the probability of [math]\displaystyle{ \displaystyle x }[/math] given [math]\displaystyle{ \displaystyle j }[/math] times the probability of [math]\displaystyle{ \displaystyle j }[/math] given [math]\displaystyle{ \displaystyle y_k }[/math], times the prior distribution of class [math]\displaystyle{ \displaystyle k }[/math], and lastly divided by the marginal probability of [math]\displaystyle{ \displaystyle x }[/math]. That is,
[math]\displaystyle{ \Pr(y_k | x) = \frac {\sum_{j} Pr(x | j)*Pr(j | y_{k})*Pr(y_{k})}{Pr(x)} }[/math].
Since, the prior probability of class [math]\displaystyle{ \displaystyle k }[/math], [math]\displaystyle{ \displaystyle Pr(y_{k}) }[/math], does not have an index of [math]\displaystyle{ \displaystyle j }[/math], it can be taken out of the summation. This yields,
[math]\displaystyle{ \Pr(y_k | x) = \frac {Pr(y_{k})\sum_{j} Pr(x | j)*Pr(j | y_{k})}{Pr(x)} }[/math].
We multiply this by [math]\displaystyle{ \displaystyle 1 = \frac {Pr(j)}{Pr(j)} }[/math]. Then, it becomes,
[math]\displaystyle{ \Pr(y_k | x) = \frac {Pr(y_{k})\sum_{j} Pr(x | j)*Pr(j | y_{k})}{Pr(x)} * \frac {Pr(j)}{Pr(j)} }[/math].
Next, note that [math]\displaystyle{ \displaystyle Pr(j | x) = \frac {Pr(x | j)*Pr(j)}{Pr(x)} }[/math], and [math]\displaystyle{ \displaystyle Pr(y_k | j) = \frac {Pr(j | y_k)*Pr(y_k)}{Pr(j)} }[/math]. Then rearranging the terms, we finally have the posterior:
[math]\displaystyle{ \displaystyle Pr(y_k | x) = \sum_{j} Pr(j | x)Pr(y_k | j) }[/math].
Interestingly, this is just the product of the posterior of the two functions that are summed.
Interpretation of RBF Network classification
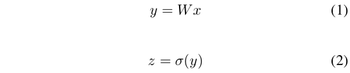
We want to relate the results that we derived above to our RBF Network. In a RBF Network, as we can see on the right hand side, we have a set of data, [math]\displaystyle{ \displaystyle x_1 }[/math] to [math]\displaystyle{ \displaystyle x_d }[/math], and the hidden basis function, [math]\displaystyle{ \displaystyle \phi_{1} }[/math] to [math]\displaystyle{ \displaystyle \phi_{M} }[/math], and then we have some output, [math]\displaystyle{ \displaystyle y_1 }[/math] to [math]\displaystyle{ \displaystyle y_k }[/math]. Also, we have weights from the hidden layer to output layer. The output is just the linear sum of [math]\displaystyle{ \displaystyle \phi }[/math]’s.
Now consider probability of [math]\displaystyle{ \displaystyle j }[/math] given [math]\displaystyle{ \displaystyle x }[/math] to be [math]\displaystyle{ \displaystyle \phi }[/math], and the probability of [math]\displaystyle{ \displaystyle y_k }[/math] given [math]\displaystyle{ \displaystyle j }[/math] to be the weights [math]\displaystyle{ \displaystyle w_{jk} }[/math], then the posterior can be written as,
[math]\displaystyle{ \displaystyle Pr(y_k | x) = \sum_{j} \phi_{j}(x)*w_{jk} }[/math].
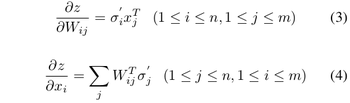
Now, let us look at an example in one dimensional case. Suppose,
[math]\displaystyle{ \phi_{j}(x) = e^{\frac{-\Vert x - \mu_{j}\Vert ^2}{2\sigma_{j}^2}} }[/math], and [math]\displaystyle{ \displaystyle j }[/math] is from 1 to 2.
We know that [math]\displaystyle{ \displaystyle \phi }[/math] is a radial basis function. It's as if we put some Gaussian over data. And for each Gaussian, we consider the center [math]\displaystyle{ \displaystyle \mu }[/math]. Then, what [math]\displaystyle{ \displaystyle \phi }[/math] computes is the similarity of any data point to the center.
We can see the graph on the left which plots the density of [math]\displaystyle{ \displaystyle \phi_{1} }[/math] and [math]\displaystyle{ \displaystyle \phi_{2} }[/math]. Take [math]\displaystyle{ \displaystyle \phi_{1} }[/math] for instance, if the point gets far from the center [math]\displaystyle{ \displaystyle \mu_{1} }[/math], then it will reduce [math]\displaystyle{ \displaystyle \phi_{1} }[/math] to become nearly zero. Remember that, we can usually find a non-linear regression or classification of input space by doing a linear one in some extended space or some feature space (more details in Aside). Here, the [math]\displaystyle{ \displaystyle \phi }[/math]’s actually produce that feature space.
So, one way to look at this is that this [math]\displaystyle{ \displaystyle \phi }[/math] is telling us that given an input, how likely the probability of presence of a particular feature is. Say, for example, we define the features as the centers of these Gaussian distributions. Then, this [math]\displaystyle{ \displaystyle \phi }[/math] function somehow computes the possibility given certain data points, of this kind of feature appearing. If the data point is right at the center, then the value of that [math]\displaystyle{ \displaystyle \phi }[/math] would be one, i.e. the probability is 1. If the point is far from the center, then the probability ([math]\displaystyle{ \displaystyle \phi }[/math] function value) will be close to zero, that is, it’s less likely. Therefore, we can treat [math]\displaystyle{ \displaystyle Pr(j | x) }[/math] as the probability of a particular feature given data.
When we have those features, then [math]\displaystyle{ \displaystyle y }[/math] is the linear combination of the features. Hence, any of the weights [math]\displaystyle{ \displaystyle w }[/math], which is equal to [math]\displaystyle{ \displaystyle Pr(y_k | j) }[/math], tells us how likely this particular [math]\displaystyle{ \displaystyle y }[/math] will appear given those features. Therefore, the weight [math]\displaystyle{ \displaystyle w_{jk} }[/math] shows the probability of class membership given feature.
Hence, we have found a probabilistic point of view to look at RBF Network!
- Note There are some inconsistencies with this probabilistic point of view. There are no restrictions that force [math]\displaystyle{ \displaystyle Pr(y_k | x) = \sum_{j} \phi_{j}(x)*w_{jk} }[/math] to be between 0 and 1. So if least squares is used to solve this, [math]\displaystyle{ \displaystyle w_{jk} }[/math] cannot be interpreted as a probability.
Aside
- Feature Space:
- One way to produce a feature space is LDA
- Suppose, we have n data points [math]\displaystyle{ \mathbf{x}_1 }[/math] to [math]\displaystyle{ \mathbf{x}_n }[/math]. Each data point has d features. And these n data points consist of the [math]\displaystyle{ X }[/math] matrix,
- [math]\displaystyle{ X = \left[ \begin{matrix} x_{11} & x_{21} & \cdots & x_{n1} \\ x_{12} & x_{22} & \cdots & x_{n2} \\ \vdots & & \ddots & \vdots \\ x_{1d} & x_{2d} & \cdots & x_{nd} \end{matrix}\right] }[/math]
- Also, we have feature space,
- [math]\displaystyle{ \Phi^{T} = \left[ \begin{matrix} \phi_{1}(\mathbf{x_1}) & \phi_{1}(\mathbf{x_2})& \cdots & \phi_{1}(\mathbf{x_n})\\ \phi_{2}(\mathbf{x_1})& \phi_{2}(\mathbf{x_2})& \cdots & \phi_{2}(\mathbf{x_n}) \\ \vdots & & \ddots & \vdots \\ \phi_{M}(\mathbf{x_1}) & \phi_{M}(\mathbf{x_2}) & \cdots & \phi_{M}(\mathbf{x_n}) \end{matrix}\right] }[/math]
- If we want to solve a regression problem for the input data, we don’t perform Least Square on this [math]\displaystyle{ \displaystyle X }[/math] matrix, we do Least Square on the feature space, i.e. on the [math]\displaystyle{ \displaystyle \Phi^{T} }[/math] matrix. The dimensionality of [math]\displaystyle{ \displaystyle \Phi^{T} }[/math] is M by n.
- Now, we still have n data points, but we define these n data points in terms of a new set of features. So, originally, we define our data points by d features, but now, we define them by M features. And what are those M features telling us?
- Let us look at the first column of [math]\displaystyle{ \displaystyle \Phi^{T} }[/math] matrix. The first entry is [math]\displaystyle{ \displaystyle \phi_1 }[/math] applied to [math]\displaystyle{ \mathbf{x_1} }[/math], and so on, until the last entry is [math]\displaystyle{ \displaystyle \phi_M }[/math] applied to [math]\displaystyle{ \mathbf{x_1} }[/math]. Suppose each of these [math]\displaystyle{ \displaystyle \phi_j }[/math] is defined by
- [math]\displaystyle{ \phi_{j}(x) = e^{\frac{-\Vert x - \mu_{j}\Vert ^2}{2\sigma_{j}^2}} }[/math].
- Then, each [math]\displaystyle{ \displaystyle \phi_j }[/math] checks the similarity of the data point with its center. Hence, the new set of features are actually representing M centers in our data set, and for each data point, its new features check how this point is similar to the first center; how it is similar to the second center; and how it is similar to the [math]\displaystyle{ \displaystyle M^{th} }[/math] center. And this checking process will apply to all data points. Therefore, feature space gives another representation of our data set.
Model selection or complexity control for RBF Network - a brief introduction
In order to obtain a better fit for the training data, we often want to increase the complexity of our RBF Network. By its construction, we know that to change the complexity of a RBF Network, the only way is to add or decrease the number of basis functions. A large number of basis function yields a more complex network. In theory, if we add enough basis functions, the RFB Network would work for any training; however, it doesn't mean this RBF Network model can generalize well. Therefore, for the purpose of avoiding overfitting problem (see Notes below), we only want to increase the number of basis function to certain point, i.e. its optimal level.
For the model selection, what we usually do is estimate the training error. After working through the training error, we’ll see that the training error in fact can be decomposed, and one component of training error is called Mean Squared Error (MSE). In the later notes, we will find that our final goal is to get a good estimate of MSE. Moreover, in order to find an optimal model for our data, we select the model with the smallest MSE.
Now, let us introduce some notations that we will use in the analysis:
- [math]\displaystyle{ \hat f }[/math] -- the prediction model estimated by a RBF network from the training data
- [math]\displaystyle{ \displaystyle f }[/math] -- the real model (not null), and ideally, we want [math]\displaystyle{ \hat f }[/math] to be close to [math]\displaystyle{ \displaystyle f }[/math]
- [math]\displaystyle{ \displaystyle err }[/math] -- the training error
- [math]\displaystyle{ \displaystyle Err }[/math] -- the testing error
- [math]\displaystyle{ \displaystyle MSE }[/math] -- the Mean Squared Error
Notes
- Being more complex isn’t always a good thing. Sometime, overfitting causes the model to lose its generality. For example in the graph on left hand side, the data points are sampled from the model [math]\displaystyle{ \displaystyle y_i= f(x_i)+\epsilon_i }[/math], where [math]\displaystyle{ \displaystyle f(x_i) }[/math] is a linear function, which is shown by the blue line, and [math]\displaystyle{ \displaystyle \epsilon_i }[/math]is additive Gaussian noise from [math]\displaystyle{ ~N(0,\sigma^2) }[/math]. The red curve displayed in the graph shows the over-fitted model. Clearly, this over-fitted model only works for any training data, and is useless for any further prediction when new data points are introduced.
> n<-20; > x<-seq(1,10,length=n); > alpha<-2.5; > beta<-1.75; > y<-alpha+beta*x+rnorm(n); > plot(y~x, pch=16, lwd=3, cex=0.5, main='Overfitting'); > abline(alpha, beta, col='blue'); > lines(spline(x, y), col = 2);
- More details on this topic later on.
Model Selection(Stein's Unbiased Risk Estimate)- November 11th, 2009
Model Selection
Model selection is a task of selecting a model of optimal complexity for a given data. Learning a radial basis function network from data is a parameter estimation problem. One difficulty with this problem is selecting parameters that show good performance on both training and testing data. In principle, a model is selected to have parameters associated with the best observed performance on training data, although our goal really is to achieve good performance on unseen testing data. Not surprisingly, a model selected on the basis of training data does not necessarily exhibit comparable performance on the testing data. When squared error is used as the performance index, a zero-error model on the training data can always be achieved by using a sufficient number of basis functions.
But, training error and testing error do not demonstrate a linear relationship. In particular, a smaller training error does do not necessarily result in a smaller testing error. In practice, one often observes that, up to a certain point, the model error on testing data tends to decrease as the training error decreases. However, if one attempts to decrease the training error too far by increasing model complexity, the testing error often can take a dramatic increase.
The basic reason behind this phenomenon is that in the process of minimizing training error, after a certain point, the model begins to over-fit the training set. Over-fitting in this context means fitting the model to training data at the expense of losing generality. In the extreme form, a set of [math]\displaystyle{ \displaystyle N }[/math] training data points can be modeled exactly with [math]\displaystyle{ \displaystyle N }[/math] radial basis functions. Such a model follows the training data perfectly. However, the model is not representative features of the true underlying data source, and this is why it fails to correctly model new data points.
In general, the training error rate will be less than the testing error on the new data. A model typically adapts to the training data, and hence the training error will be an overly optimistic estimate of the testing error. An obvious way to well estimate testing err is to add a penalty term to the training error to compensate. Actually, SURE is developed based on this.
Stein's unbiased risk estimate (SURE)
Important Notation
Let:
- [math]\displaystyle{ \hat f(X) }[/math] denote the prediction model, which is estimated from a training sample by the RBF neural network model.
- [math]\displaystyle{ \displaystyle f(X) }[/math] denote the true model.
- [math]\displaystyle{ \displaystyle err=\sum_{i=1}^N (\hat y_i-y_i)^2 }[/math] denote the training error,which is the average loss over the training sample.
- [math]\displaystyle{ \displaystyle Err=\sum_{i=1}^M (\hat y_i-y_i)^2 }[/math] denote the test error, which is the expected prediction error on an independent test sample.
- [math]\displaystyle{ \displaystyle MSE=E(\hat f-f)^2 }[/math] denote the mean squared error, where [math]\displaystyle{ \hat f(X) }[/math] is the estimated model and [math]\displaystyle{ \displaystyle f(X) }[/math] is the true model.
Suppose the observations [math]\displaystyle{ \displaystyle y_i= f(x_i)+\epsilon_i }[/math], where [math]\displaystyle{ \displaystyle \epsilon_i }[/math]is additive Gaussian noise [math]\displaystyle{ ~N(0,\sigma^2) }[/math].We need to estimate [math]\displaystyle{ \hat f }[/math] from training data set [math]\displaystyle{ T=\{(x_i,y_i)\}^2_{i=1} }[/math]. Let [math]\displaystyle{ \hat f_i=\hat f_(x_i) }[/math] and [math]\displaystyle{ \displaystyle f_i= f(x_i) }[/math], then
[math]\displaystyle{ \displaystyle E[(\hat y_i-y_i)^2 ]=E[(\hat f_i-f_i-\epsilon_i)^2] }[/math][math]\displaystyle{ =E[(\hat f_i-f_i)^2]+E[\epsilon_i^2]-2E[\epsilon_i(\hat f_i-f_i)] }[/math]
[math]\displaystyle{ \displaystyle E[(\hat y_i-y_i)^2 ]=E[(\hat f_i-f_i)^2]+\sigma^2-2E[\epsilon_i(\hat f_i-f_i)] }[/math] [math]\displaystyle{ \displaystyle (1) }[/math]
The last term can be written as:
[math]\displaystyle{ \displaystyle E[\epsilon_i(\hat f_i-f_i)]=E[(y_i-f_i)(\hat f_i-f_i)]=cov(y_i,\hat f) }[/math], where[math]\displaystyle{ \displaystyle y_i }[/math] and [math]\displaystyle{ \hat f_i }[/math] both have same mean [math]\displaystyle{ \displaystyle f_i }[/math].
Stein's Lemma
If [math]\displaystyle{ \,Z }[/math] is [math]\displaystyle{ \,N(\mu,\sigma^2) }[/math] and if [math]\displaystyle{ \displaystyle g(Z) }[/math] is weakly differentiable,such that[math]\displaystyle{ \displaystyle E[\vert g'(Z)\vert]\lt \infty }[/math], then [math]\displaystyle{ \displaystyle E[g(Z)(Z-\mu)]=\sigma^2E(g'(Z)) }[/math].
According to Stein's Lemma, the last cross term of [math]\displaystyle{ \displaystyle (1) }[/math], [math]\displaystyle{ \displaystyle E[\epsilon_i(\hat f_i-f_i)] }[/math] can be written as [math]\displaystyle{ \sigma^2 E[\frac {\partial \hat f}{\partial y_i}] }[/math]. The derivation is as follows.
[math]\displaystyle{ \displaystyle Proof }[/math]: Let [math]\displaystyle{ \,Z = \epsilon }[/math]. Then [math]\displaystyle{ g(Z) = \hat f-f }[/math], since [math]\displaystyle{ \hat y = f + \epsilon }[/math], and [math]\displaystyle{ \,f }[/math] is a constant. So [math]\displaystyle{ \,\mu = 0 }[/math] and [math]\displaystyle{ \,\sigma^2 }[/math] is the variance in [math]\displaystyle{ \,\epsilon }[/math]. [math]\displaystyle{ \displaystyle E[g(Z)(Z-\mu)]=E[(\hat f-f)\epsilon]=\sigma^2E(g'(Z))=\sigma^2 E[\frac {\partial (\hat f-f)}{\partial y_i}]=\sigma^2 E[\frac {\partial \hat f}{\partial y_i}-\frac {\partial f}{\partial y_i}] }[/math]
Since [math]\displaystyle{ \displaystyle f }[/math] is the true model, not the function of the observations [math]\displaystyle{ \displaystyle y_i }[/math], then [math]\displaystyle{ \frac {\partial f}{\partial y_i}=0 }[/math].
So,[math]\displaystyle{ \displaystyle E[\epsilon_i(\hat f_i-f_i)]=\sigma^2 E[\frac {\partial \hat f}{\partial y_i}] }[/math] [math]\displaystyle{ \displaystyle (2) }[/math]
Two Different Cases
SURE in RBF, Automatic basis selection for RBF networks using Stein’s unbiased risk estimator,Ali Ghodsi Dale Schuurmans
Case 1
Consider the case in which a new data point has been introduced to the estimated model, i.e. [math]\displaystyle{ (x_i,y_i)\not\in\tau }[/math]; this new point belong to the validation set [math]\displaystyle{ \displaystyle \nu }[/math],i.e.[math]\displaystyle{ (x_i,y_i)\in\nu }[/math]. Since [math]\displaystyle{ \displaystyle y_i }[/math] is a new point, [math]\displaystyle{ \hat f }[/math] and [math]\displaystyle{ \displaystyle y_i }[/math] are independent. Therefore [math]\displaystyle{ \displaystyle cov(y_i,\hat f)=0 }[/math] (or think about [math]\displaystyle{ \frac{\partial \hat f}{\partial y_i} }[/math], when [math]\displaystyle{ \,y_i }[/math]is a new point, then it has nothing with [math]\displaystyle{ \hat f }[/math] because the estimation of [math]\displaystyle{ \hat f }[/math] is from the training data, so [math]\displaystyle{ \frac{\partial \hat f}{\partial y_i}=0 }[/math] ) and [math]\displaystyle{ \displaystyle (1) }[/math] in this case can be written as:
[math]\displaystyle{ \displaystyle E[(\hat y_i-y_i)^2 ]=E[(\hat f_i-f_i)^2]+\sigma^2 }[/math].
This expectation means [math]\displaystyle{ \frac {1}{m}\sum_{i=1}^m (\hat y_i-y_i)^2 = \frac {1}{m}\sum_{i=1}^m (\hat f_i-f_i)^2+ \sigma^2 }[/math].
[math]\displaystyle{ \sum_{i=1}^m (\hat y_i-y_i)^2 = \sum_{i=1}^m (\hat f_i-f_i)^2+ m\sigma^2 }[/math]
Based on the notation we denote above, then we obtain: [math]\displaystyle{ \displaystyle MSE=Err-m\sigma^2 }[/math]
This is the justification behind the technique of cross validation. since [math]\displaystyle{ \displaystyle \sigma^2 }[/math] is constant, to minimize [math]\displaystyle{ \displaystyle MSE }[/math] is equal to minimize the test err [math]\displaystyle{ \displaystyle Err }[/math]. In cross vaildation to avoid overfitting or underfitting, a validation data set is independent from the estimated model.
Case 2
A more interesting case is the case in which we do not use new data points to assess the performance of the estimated model. and the training data is used for both estimating and assessing a model [math]\displaystyle{ \hat f_i }[/math]. In this case the cross term in [math]\displaystyle{ \displaystyle (1) }[/math] cannot be ignored because [math]\displaystyle{ \hat f_i }[/math] and [math]\displaystyle{ \displaystyle y_i }[/math] are not independent. Therefore the cross term can be estimated by Stein's lemma, which was originally proposed to estimated the mean of a Guassian distribution.
Suppose [math]\displaystyle{ (x_i,y_i)\in\tau }[/math], then by applying Stein's lemma, we obtain [math]\displaystyle{ \displaystyle (2) }[/math] proved above.
[math]\displaystyle{ \displaystyle E[(\hat y_i-y_i)^2 ]=E[(\hat f_i-f_i)^2]+\sigma^2-2\sigma^2E[\frac {\partial \hat f}{\partial y_i}] }[/math].
This expectation means [math]\displaystyle{ \frac {1}{N}\sum_{i=1}^N (\hat y_i-y_i)^2 = \frac {1}{N}\sum_{i=1}^N (\hat f_i-f_i)^2+ \sigma^2-\frac {2}{N}\sum_{i=1}^N \frac {\partial \hat f}{\partial y_i} }[/math].
[math]\displaystyle{ \sum_{i=1}^N (\hat y_i-y_i)^2 = \sum_{i=1}^N (\hat f_i-f_i)^2+ N\sigma^2-2\sigma^2\sum_{i=1}^N \frac {\partial \hat f}{\partial y_i} }[/math].
[math]\displaystyle{ \displaystyle err=MSE+N\sigma^2-2\sigma^2\sum_{i=1}^N \frac {\partial \hat f}{\partial y_i} }[/math]
[math]\displaystyle{ \displaystyle MSE=err-N\sigma^2+2\sigma^2\sum_{i=1}^N \frac {\partial \hat f}{\partial y_i} }[/math] [math]\displaystyle{ \displaystyle (3) }[/math]
In statistics, this is known as Stein's unbiased risk estimate (SURE) is an unbiased estimator of the mean-squared error of a given estimator, in a deterministic estimation scenario. In other words, it provides an indication of the accuracy of a given estimator. This is important since, in deterministic estimation, the true mean-squared error of an estimator generally depends on the value of the unknown parameter, and thus cannot be determined completely.
SURE for RBF Network
Based on SURE, the optimum number of basis functions should be assigned to have the minimum generalization err [math]\displaystyle{ \displaystyle err }[/math]. Based on the Radial Basis Function Network, by setting [math]\displaystyle{ \frac{\partial err}{\partial W} }[/math] equal to zero , we get the least squared solution of[math]\displaystyle{ \ W = (\Phi^{T}\Phi)^{-1}\Phi^{T}Y }[/math].Then we have [math]\displaystyle{ \hat{Y} = \Phi W = \Phi(\Phi^{T}\Phi)^{-1})\Phi^{T}Y = HY }[/math],where [math]\displaystyle{ \ H = \Phi(\Phi^{T}\Phi)^{-1})\Phi^{T} }[/math], [math]\displaystyle{ \,H }[/math] is the hat matrix for this model.
[math]\displaystyle{ \hat f=\,H_{i1}y_2+\,H_{i2}y_2+\cdots+\,H_{in}y_n }[/math] [math]\displaystyle{ \displaystyle (3) }[/math]
where [math]\displaystyle{ \,H }[/math] depends on the input vector [math]\displaystyle{ \displaystyle x_i }[/math] but not on [math]\displaystyle{ \displaystyle y_i }[/math].
By taking the derivative of [math]\displaystyle{ \hat f_i }[/math] with respect to [math]\displaystyle{ \displaystyle y_i }[/math], we can easily obtain:
[math]\displaystyle{ \sum_{i=1}^N \frac {\partial \hat f}{\partial y_i}=\sum_{i=1}^N \,H_{ii} }[/math]
Now, substituing this into[math]\displaystyle{ \displaystyle (3) }[/math] ,we get
[math]\displaystyle{ \displaystyle MSE=err-N\sigma^2+2\sigma^2\sum_{i=1}^N \,H_{ii} }[/math]
Here, we can tell that [math]\displaystyle{ \sum_{i=1}^N \,H_{ii}= \,Trace(H) }[/math], the sum of the diagonal elements of [math]\displaystyle{ \,H }[/math]. Thus, we can obtain the further simplification that [math]\displaystyle{ \,Trace(H)= Trace(\Phi(\Phi^{T}\Phi)^{-1})\Phi^{T})= Trace(\Phi^{T}\Phi(\Phi^{T}\Phi)^{-1})=d }[/math], where[math]\displaystyle{ \displaystyle d }[/math] is the dimension of [math]\displaystyle{ \displaystyle \Phi }[/math]. Since [math]\displaystyle{ \displaystyle \Phi }[/math] is a projection of input matrix [math]\displaystyle{ \,X }[/math] onto a basis set spanned by [math]\displaystyle{ \,M }[/math], the number of basis functions. If considering intercept, then [math]\displaystyle{ \,Trace(H)= M+1 }[/math].
Then,[math]\displaystyle{ \displaystyle MSE=err-N\sigma^2+2\sigma^2(M+1) }[/math].
SURE Algorithm
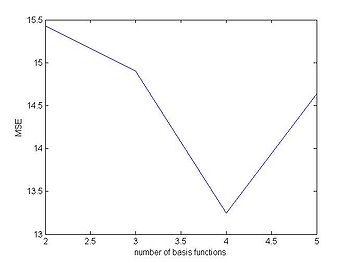
We use this method to find the optimum number of basis function by choosing the model with smallest MSE over the set of models considered. Given a set of models [math]\displaystyle{ \hat f_M(x) }[/math] indexed by the number of basis functions, [math]\displaystyle{ \displaystyle err(M) }[/math].
Then, [math]\displaystyle{ \displaystyle MSE(M)=err(M)-N\sigma^2+2\sigma^2(M+1) }[/math]
where [math]\displaystyle{ \displaystyle N }[/math] is the number of training samples and the noise,[math]\displaystyle{ \sigma^2 }[/math], can be estimated from the training data as
[math]\displaystyle{ \hat \sigma^2=\frac {1}{N-1}\sum_{i=1}^N (\hat y-y)^2 }[/math].
By applying SURE algorithm to SPECT Heart data, we get the optimal number of basis functions is [math]\displaystyle{ \displaystyle M=4 }[/math].
Pls take a look at figure 27.1 on the right, which shows that[math]\displaystyle{ \displaystyle MSE }[/math] is smallest when [math]\displaystyle{ \displaystyle M=4 }[/math].
Calculating the SURE value is easy if you have access to [math]\displaystyle{ \,\sigma }[/math].
sure_Err = error - num_data_point * sigma .^ 2 + 2 * sigma .^2 * (num_basis_functions + 1);
If [math]\displaystyle{ \,\sigma }[/math] is not known, it can be estimated using the error.
error = (output - expected_output) .^ 2; sigma = (dot(err, ones(1, num_data_point)) / (num_data_point)) / (num_data_point - 1); sure_Err = error - num_data_point * sigma .^ 2 + 2 * sigma .^2 * (num_basis_functions + 1);
SURE for RBF network & Support Vector Machine - November 13th, 2009
SURE for RBF network
Minimizing MSE
By Stein's unbiased risk estimate (SURE) for Radial Basis Function (RBF) Network we get:
[math]\displaystyle{ \displaystyle MSE=err-N\sigma^2+2\sigma^2(M+1) }[/math] (28.1)
- [math]\displaystyle{ \displaystyle MSE }[/math](mean square error)= [math]\displaystyle{ \sum_{i=1}^N (\hat y_i-y_i)^2 }[/math]
- [math]\displaystyle{ \displaystyle err }[/math](training error)= [math]\displaystyle{ \sum_{i=1}^N (\hat f_i-f_i)^2 }[/math]
- [math]\displaystyle{ \displaystyle (M+1) }[/math]( number of hidden units)= [math]\displaystyle{ \sum_{i=1}^N \frac {\partial \hat f}{\partial y_i} }[/math]
Goal: To minimize MSE
1. If [math]\displaystyle{ \displaystyle \sigma }[/math] is known, then it is no impact (i.e. a constant), and we can ignore it. Only need to minimize [math]\displaystyle{ \displaystyle MSE=err +2\sigma^2(M+1) }[/math].
2. In reality, we do not know [math]\displaystyle{ \displaystyle \sigma }[/math], and the estimate [math]\displaystyle{ \,\hat \sigma }[/math] changes when [math]\displaystyle{ \displaystyle (M+1) }[/math] changes. However, we can estimate [math]\displaystyle{ \displaystyle \sigma }[/math].
[math]\displaystyle{ \displaystyle y_i= f(x_i)+\epsilon_i }[/math], where [math]\displaystyle{ \displaystyle \epsilon_i }[/math]is additive Gaussian noise [math]\displaystyle{ ~N(0,\sigma^2) }[/math]. Suppose we do not know the variance of [math]\displaystyle{ \displaystyle \epsilon }[/math]. Then,
[math]\displaystyle{ \displaystyle \sigma^2=\frac{1}{N-1}\sum_{i=1}^N (\hat y_i-y_i)^2 =\frac{1}{N-1}err }[/math] (28.2)
Substitute (28.2) into (28.1), get
[math]\displaystyle{ \displaystyle MSE=err-N\frac{1}{N-1}err+2\frac{1}{N-1}err(M+1) }[/math]
[math]\displaystyle{ \displaystyle MSE=err(1-\frac{N}{N-1}+\frac{2(M+1)}{N-1}) }[/math]
[math]\displaystyle{ \displaystyle MSE=err(\frac{N-1-N+2M+2}{N-1}) }[/math]
[math]\displaystyle{ \displaystyle MSE=err(\frac{2M+1}{N-1}) }[/math] (28.3)
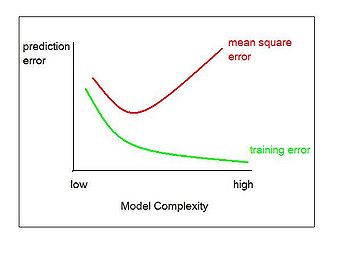
Figure 28.1: the training error will decrease and the MSE will increase when increasing the number of hidden units (i.e. the model is more complex).
When the number of hidden units gets larger and larger, the training error will decrease until it approaches to [math]\displaystyle{ \displaystyle 0 }[/math]. If training error equals [math]\displaystyle{ \displaystyle 0 }[/math], then no matter how large [math]\displaystyle{ \displaystyle (M+1) }[/math] is, from (28.3) we can see the estimate of MSE will approach [math]\displaystyle{ \displaystyle 0 }[/math] as well. However, in fact it does not happen since when training error is close to [math]\displaystyle{ \displaystyle 0 }[/math] overfitting happens, and MSE should increase instead of being close to [math]\displaystyle{ \displaystyle 0 }[/math]. We can see it from the Figure 28.1.
We can see [math]\displaystyle{ \displaystyle \sigma^2 }[/math] is the average of [math]\displaystyle{ \displaystyle err }[/math]. In order to deal with this problem, we can take the average for [math]\displaystyle{ \displaystyle err }[/math] of each hidden unit. For example: we can first take 1 hidden unit, and take 10 hidden units in the next. Since in reality the value of [math]\displaystyle{ \, \sigma^2 }[/math] is a constant adjustment to the data points, and doesn't depend on [math]\displaystyle{ \,M+1 }[/math], using the average [math]\displaystyle{ \,\sigma^2 }[/math] value for 1 to 10 hidden units has a firm theoretical basis.
We can also see that unlike the classical Cross Validation (CV) or Leave one out (LOO) techniques, the SURE technique does not need to do the validation to find the optimal model. Hence, SURE technique uses less data than CV or LOO. It is suitable for the case that there is not enough data for validation. However, to implement SURE we need to find [math]\displaystyle{ \frac {\partial \hat f}{\partial y_i} }[/math], which may not be trivial for models that do not have a closed-form solution.
Kmeans Clustering
Description:
Kmeans clustering is a method of cluster analysis which aims to partition n observations into k clusters in which each observation belongs to the cluster with the nearest mean.
- The number of hidden units is equal to the number of clusters, which is [math]\displaystyle{ \displaystyle \phi }[/math]
- [math]\displaystyle{ \displaystyle \phi_{j}(x) = e^{\frac{-\Vert x - \mu_{j}\Vert ^2}{2\sigma_{j}^2}} }[/math], we set it equal for all clusters.
The basic details for [math]\displaystyle{ K }[/math]-means clustering are given:
The [math]\displaystyle{ K }[/math] initial centers are randomly chosen from the training data.
Then the following two steps are iterated alternately until convergence.
1. For each existing center, we re-identify its cluster (every point in this cluster should be closer to this center than to others).
2. Compute the mean for each cluster and make it as the new center for each cluster.
Example:
Partition data into 2 clusters (2 hidden values)
>> X=rand(30,80); >> [IDX,C,sumD,D]=kmeans(X,2); >> size(IDX) >> 30 1 >> size(C) >> 2 80 >> size(sumD) >> 2 1 >> c1=sum(IDX==1) >> 14 >> c2=sum(IDX==2) >> 16 >> sumD >> 85.6643 >> 101.0419 >> v1=sumD(1,1)/c1 >> 6.1189 >> v2=sumD(2,1)/c2 >> 6.3151
Comments:
We create [math]\displaystyle{ X }[/math] randomly as a training set with 80 data points and 30 dimensions, and then apply “kmeans” method to separate X into 2 clusters. IDX is a vector contains 1 or 2 which indicates 2 clusters, and its size is 30*1. [math]\displaystyle{ \displaystyle C }[/math] is the center (mean) of each cluster with size 2*80; sumD is sum of the square distance between the data points and center of its cluster. The [math]\displaystyle{ \displaystyle c1 }[/math] and [math]\displaystyle{ \displaystyle c2 }[/math] indicate the number of data points in cluster 1 and 2. [math]\displaystyle{ \displaystyle V1 }[/math] is the variance of the first cluster [math]\displaystyle{ \displaystyle (v1=\sigma_1) }[/math]; [math]\displaystyle{ \displaystyle V2 }[/math] is the variance of the second cluster [math]\displaystyle{ \displaystyle (v2=\sigma_2) }[/math]. Now we can get [math]\displaystyle{ \displaystyle \phi }[/math], [math]\displaystyle{ \displaystyle w }[/math], hat matrix [math]\displaystyle{ \displaystyle H }[/math] and [math]\displaystyle{ \displaystyle \hat Y }[/math] by following equations. Finally, we will get the [math]\displaystyle{ \displaystyle MSE }[/math] and predict the test set.
[math]\displaystyle{ \displaystyle \phi_{j}(x) = e^{\frac{-\Vert x - \mu_{j}\Vert ^2}{2\sigma_{j}^2}} }[/math]
[math]\displaystyle{ \displaystyle W = (\phi^{T}\Phi)^{-1}\phi^{T}Y }[/math]
[math]\displaystyle{ \displaystyle H = \phi(\Phi^{T}\Phi)^{-1}\phi^{T} }[/math]
[math]\displaystyle{ \displaystyle \hat{Y} = \phi W = \phi(\phi^{T}\phi)^{-1}\phi^{T}Y = HY }[/math]
Aside:
Similar in spirit to [math]\displaystyle{ K }[/math]-means, there is EM algorithm with respect to Gaussian mixture model. Generally speaking, the Gaussian mixture model is referred to as a soft clustering while [math]\displaystyle{ K }[/math]-means is hard clustering.
Similar to [math]\displaystyle{ K }[/math]-means, the following two steps are iterated alternately until convergernce.
E-step, each point is assigned a weight for each cluster based on the likelihood of each of the corresponding Gaussians. Observations is assigned 1 for one cluster if they are closer to the center of that cluster, and is assigned 0 for other clusters.
M-step, compute the weighted means and covariances and make them as the new means and covariances for every cluster.
>>[P,mu,phi,1Pxtr]=mdgEM(X,2,200,0);
Support Vector Machine
Introduction
We have seen that linear discriminant analysis and logistic regression both estimate linear decision boundaries in similar but slightly different ways. Separating hyperplane classifiers provide the basis for the support vector machine (SVM). An SVM constructs linear decision boundaries that explicitly try to separate the data into different classes while maximizing the margin of separation. The techniques that make the extensions to the non-separable case, where the classes overlap, are generalized to what is known as the support vector machine. It produces nonlinear boundaries by constructing a linear boundary in a high-dimensional, transformed version of the feature space. It is also calculated based on only a fraction of the data rather than a calculation on every point in the data, much like the difference between the median and the mean.
The original basis for SVM was published in the 1960s by Vapnik, Chervonenkis et al., however the ideas did not gain any attention until strong results were shown in the early 1990s.
Definition:
Support Vector Machines (SVM) are a set of related supervised learning methods used for classification and regression. A support vector machine constructs a maximum margin hyperplane or set of hyperplanes in a higher or infinite dimensional space. The set of points near the class boundaries, support vectors, define the model which can be used for classification, regression or other tasks.
Optimal Seperating Hyperplane
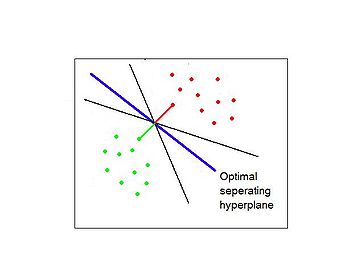
Figure 28.2 An example with two classes separated by a hyperplane. The blue line is the least squares solution, which misclassifies one of the training points. Also shown are the black separating hyperplanes found by the perceptron learning algorithm with different random starts.
We can see the data points can be separated by a linear boundary are in two classes in [math]\displaystyle{ \displaystyle \mathbb{R}^{2} }[/math]. Suppose a dataset is indeed linearly separable, then there exits infinitely many possible separating hyperplanes including the black lines in the figure as two of them for training data. However, which solution is the best when we introduce the new data.
Aside:
The blue line is the least squares solution to the problem,obtained by regressing the [math]\displaystyle{ \displaystyle -1/+1 }[/math] response [math]\displaystyle{ \displaystyle Y }[/math] on [math]\displaystyle{ \displaystyle X }[/math] (with intercept); the line is given by
[math]\displaystyle{ \displaystyle {X:\hat\beta_0+\hat\beta_1X_1+\hat\beta_2X_2=0} }[/math].
This least squares solution does not do a perfect job in separating the points, and makes one error. This is the same boundary found by linear discriminant analysis, in light of its equivalence with linear regression in the two-class case.
Classifiers such as (28.4) that compute a linear combination of the input features and return the sign were called perceptrons in the engineering literature in the late 1950s.
Identifications:
- Hyperplane: separate two classes
[math]\displaystyle{ \displaystyle x^{T}\beta+\beta_0=0 }[/math]
- Margin: the distance between the hyperplane and the closest point.
[math]\displaystyle{ \displaystyle d_i=x_i^{T}\beta+\beta_0 }[/math] where [math]\displaystyle{ \displaystyle i=1,....,N }[/math]
Note: since distance is positive, if the data is on [math]\displaystyle{ \displaystyle +1 }[/math] side the distance is [math]\displaystyle{ \displaystyle d_i(+1) }[/math]. If the data is on the [math]\displaystyle{ \displaystyle -1 }[/math] side the distance is [math]\displaystyle{ \displaystyle d_i(-1) }[/math].
- Data points: [math]\displaystyle{ \displaystyle y_i\in\{-1,+1\} }[/math]we can classify points as[math]\displaystyle{ \displaystyle sign\{d_i\} }[/math] if [math]\displaystyle{ \displaystyle \beta,\beta_0 }[/math] is known.
Maximum Margin Classifiers in the Linearly separable case
Choose the line farthest from both classes or choose the line which has the maximum distance from the closest point. (i.e maximize the margin)
[math]\displaystyle{ \displaystyle Margin=min\{y_id_i\} }[/math] [math]\displaystyle{ \displaystyle i=1,2,....,N }[/math]
where [math]\displaystyle{ \displaystyle y_i }[/math] is label and [math]\displaystyle{ \displaystyle d_i }[/math] is distance
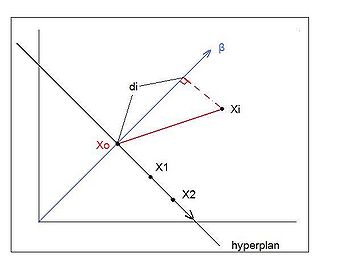
Fiqure 28.3 depicts a hyperplane defined by the equation [math]\displaystyle{ \displaystyle x^{T}\beta+\beta_0=0 }[/math]. Since they are in [math]\displaystyle{ \displaystyle \mathbb{R}^{2} }[/math], the hyperplane is a line.
Let us rewrite [math]\displaystyle{ \displaystyle Margin=min\{y_id_i\} }[/math] by using the following properties:
1. [math]\displaystyle{ \displaystyle \beta }[/math] is orthogonal to the hyperplane
Two points[math]\displaystyle{ \displaystyle x_1,x_2 }[/math] lying on the hyperplane.
[math]\displaystyle{ \displaystyle \beta^{T}x_1+\beta_0=0 }[/math]
[math]\displaystyle{ \displaystyle \beta^{T}x_2+\beta_0=0 }[/math]
[math]\displaystyle{ \displaystyle \beta^{T}x_1+\beta_0 - (\beta^{T}x_2+\beta_0)=0 }[/math]
[math]\displaystyle{ \displaystyle \beta^{T}(x_1-x_2)=0 }[/math]
Hence,[math]\displaystyle{ \displaystyle \beta }[/math] is orthogonal to [math]\displaystyle{ \displaystyle (x_1-x_2) }[/math], and[math]\displaystyle{ \displaystyle \beta^*=\frac{\beta}{\|\beta\|} }[/math] is the vector normal to the hyperplane.
2. For any point [math]\displaystyle{ \displaystyle x_1 }[/math] on the hyperplane,
[math]\displaystyle{ \displaystyle \beta^{T}x_1+\beta_0=0 }[/math]
[math]\displaystyle{ \displaystyle \beta^{T}x_1=-\beta_0 }[/math]
For any point on the hyperplane, multiplying by [math]\displaystyle{ \displaystyle \beta^{T} }[/math] gives negative value of the intercept of the hyperplane.
3. The signed distance for any point [math]\displaystyle{ \displaystyle x }[/math] to the hyperplane is [math]\displaystyle{ \displaystyle d_i=\beta^{T}(x_i-x_0) }[/math].
Since the length of [math]\displaystyle{ \displaystyle \beta }[/math] is not known, let it be unit vector.
[math]\displaystyle{ \displaystyle d_i=\frac{\beta^{T}(x_i-x_0)}{\|\beta\|} }[/math] [math]\displaystyle{ \displaystyle i=1,2,....,N }[/math]
[math]\displaystyle{ \displaystyle d_i=\frac{\beta^{T}x_i-\beta^{T}x_0}{\|\beta\|} }[/math]
by property 2
[math]\displaystyle{ \displaystyle d_i=\frac{\beta^{T}x_i+\beta_0}{\|\beta\|} }[/math]
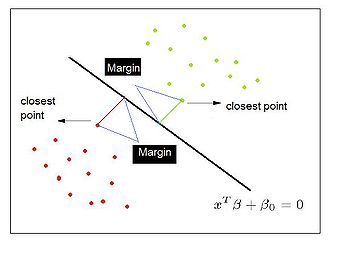
We had [math]\displaystyle{ \displaystyle Margin=min(y_id_i) }[/math] [math]\displaystyle{ \displaystyle i=1,2,....,N }[/math], and since we now know how to compute [math]\displaystyle{ \displaystyle d_i \Rightarrow }[/math]
[math]\displaystyle{ \displaystyle Margin=min\{y_i\frac{\beta^{T}x_i+\beta_0}{\|\beta\|}\} }[/math]
Suppose [math]\displaystyle{ \displaystyle x_i }[/math] is not on the hyperplane
[math]\displaystyle{ \displaystyle y_i(\beta^{T}x_i+\beta_0)\gt 0 }[/math]
[math]\displaystyle{ \displaystyle y_i(\beta^{T}x_i+\beta_0)\geq c }[/math]for [math]\displaystyle{ \displaystyle c\gt 0 }[/math]
[math]\displaystyle{ \displaystyle y_i(\frac{\beta^{T}x_i}{c}+\frac{\beta_0}{c})\geq1 }[/math]
This is known as the canonical representation of the decision hyperplane.
For [math]\displaystyle{ \displaystyle \beta^{T} }[/math] only the direction is important, so [math]\displaystyle{ \displaystyle \frac{\beta^{T}}{c} }[/math] does not change its direction, the hyperplane will be the same.
[math]\displaystyle{ \displaystyle y_i(\beta^{T}x_i+\beta_0)\geq1 }[/math]
[math]\displaystyle{ \displaystyle y_i\frac{\beta^{T}x_i+\beta_0}{\|\beta\|}\geq\frac{1}{\|\beta\|} }[/math]
[math]\displaystyle{ \displaystyle Margin=min(\frac{1}{\|\beta\|} ) }[/math]
which is equivalent as [math]\displaystyle{ \displaystyle Margin=max(\|\beta\| ) }[/math]
Reference:
Hastie,T.,Tibshirani,R., Friedman,J.,(2008).The Elements of Statistical Learning:129-130
Optimizing The Support Vector Machine - November 16th, 2009
We currently derive Support Vector Machine for the case where two classes are separable in the given feature space. This margin can be written as [math]\displaystyle{ \,min\{y_id_i\} }[/math], or the distance of each point from the hyperplane, where [math]\displaystyle{ \,d_i }[/math] is the distance and [math]\displaystyle{ \,y_i }[/math] is used as the sign.
Margin Maximizing Problem for the Support Vector Machine
[math]\displaystyle{ \,Margin=min\{y_id_i\} }[/math] can be rewritten as [math]\displaystyle{ \,min\left\{\frac{y_i\left(\beta^Tx_i+\beta_0\right)}{|\beta|}\right\} }[/math]. <br\>Note that the term [math]\displaystyle{ \,y_i\left(\beta^Tx_i+\beta_0\right) = 0 }[/math] if [math]\displaystyle{ \,x_i }[/math] is on the hyperplane, but [math]\displaystyle{ \,y_i\left(\beta^Tx_i+\beta_0\right) \gt 0 }[/math] if [math]\displaystyle{ \,x_i }[/math] is not on the hyperplane.
This implies [math]\displaystyle{ \,\exists C\gt 0 }[/math] such that [math]\displaystyle{ \,y_i\left(\beta^Tx_i+\beta_0\right) \geq C }[/math].
Divide through by C to produce [math]\displaystyle{ \,y_i\left(\frac{\beta^T}{C}x_i + \frac{\beta_0}{C}\right) \geq 1 }[/math].
[math]\displaystyle{ \,\beta, \beta_0 }[/math] compose a hyperplane that can have different values but we care about the direction, dividng through by a constant does not change the direction of the hyperplane. Thus, by assuming scaled values for [math]\displaystyle{ \,\beta, \beta_0 }[/math] we eliminate C, so that [math]\displaystyle{ \,y_i\left(\beta^Tx_i+\beta_0\right) \geq 1 }[/math]. Implying that the lower bound on [math]\displaystyle{ \,y_i\left(\beta^Tx_i+\beta_0\right) }[/math] is [math]\displaystyle{ \displaystyle 1 }[/math]
Now in order to maximize the margin, we simply need to find [math]\displaystyle{ \,min\left\{\frac{1}{|\beta|}\right\} }[/math].
In other words, our optimization problem is now to find maximum [math]\displaystyle{ \,|\beta| }[/math], under the constraint that [math]\displaystyle{ \,min_i\{y_i(\beta^Tx_i+\beta_0)\} = 1 }[/math].
Note that we're dealing with the norm of [math]\displaystyle{ \,\beta }[/math]. There are many different choices of possible norms, in general p-norm. The 1-norm of a vector is simply the sum of the absolute value of each element (also known as the taxicab or Manhattan distance), and is apparently more accurate, but also has a discontinuity in the derivative. 2-norm or the Euclidean norm (the intuitive measure of the length of a vector), is easier to work with - that is [math]\displaystyle{ \,\|\beta\|_2 = (\beta^T\beta)^{1/2} }[/math]. For convenience, we will maximize [math]\displaystyle{ \,\frac{1}{2}\|\beta\|^2 = \frac{1}{2}\beta^T\beta }[/math] where the constant 1/2 has been added for simplification and that the maximizing the function is the same as maximizing the square root of that function.
This is an example of a quadratic programming problem and we will minimize a quadratic function subject to linear inequality constraints.
Writing Lagrangian Form of Support Vector Machine
The Lagrangian form is introduced to ensure that the optimization conditions are satisfied, as well as finding an optimal solution (the optimal saddle point of the Lagrangian for the classic quadratic optimization). The problem will be solved in dual space by introducing [math]\displaystyle{ \,\alpha_i }[/math] as dual constraints, this is in contrast to solving the problem in primal space as function of the betas. A simple algorithm for iteratively solving the Lagrangian has been found to run well on very large data sets, making SVM more usable. Note that this algorithm is intended to solve Support Vector Machines with some tolerance for errors - not all points are necessarily classified correctly. Several papers by Mangasarian explore different algorithms for solving SVM.
[math]\displaystyle{ \,L(\beta,\beta_0,\alpha) = \frac{1}{2}\|\beta\|^2 - \sum_{i=1}^n{\alpha_i\left(y_i(\beta^Tx_i+\beta_0)-1\right)} }[/math]. To find the optimal value, set the derivative equal to zero.
[math]\displaystyle{ \,\frac{\partial L}{\partial \beta} = 0 }[/math], [math]\displaystyle{ \,\frac{\partial L}{\partial \beta_0} = 0 }[/math]. Note that [math]\displaystyle{ \,\frac{\partial L}{\partial \alpha_i} }[/math] is equivalent to the constraints [math]\displaystyle{ \left(y_i(\beta^Tx_i+\beta_0)-1\right) \geq 0, \,\forall\, i }[/math]
First, [math]\displaystyle{ \,\frac{\partial L}{\partial \beta} = \frac{\partial}{\partial \beta}\frac{1}{2}\|\beta\|^2 - \sum_{i=1}^n{\left\{\frac{\partial}{\partial \beta}(\alpha_iy_i\beta^Tx_i)+\frac{\partial}{\partial \beta}\alpha_iy_i\beta_0-\frac{\partial}{\partial \beta}\alpha_iy_i\right\}} }[/math]
- [math]\displaystyle{ \frac{\partial}{\partial \beta}\frac{1}{2}\|\beta\|^2 = \beta }[/math].
- [math]\displaystyle{ \,\frac{\partial}{\partial \beta}(\alpha_iy_i\beta^Tx_i) = \alpha_iy_ix_i }[/math]
- [math]\displaystyle{ \,\frac{\partial}{\partial \beta}\alpha_iy_i\beta_0 = 0 }[/math].
- [math]\displaystyle{ \,\frac{\partial}{\partial \beta}\alpha_iy_i = 0 }[/math].
So this simplifies to [math]\displaystyle{ \,\frac{\partial L}{\partial \beta} = \beta - \sum_{i=1}^n{\alpha_iy_ix_i} = 0 }[/math]. In other words,
[math]\displaystyle{ \,\beta = \sum_{i=1}^n{\alpha_iy_ix_i} }[/math], [math]\displaystyle{ \,\beta^T = \sum_{i=1}^n{\alpha_iy_ix_i^T} }[/math]
Similarly, [math]\displaystyle{ \,\frac{\partial L}{\partial \beta_0} = -\sum_{i=1}^n{\alpha_iy_i} = 0 }[/math].
This allows us to rewrite the Lagrangian without [math]\displaystyle{ \,\beta }[/math].
[math]\displaystyle{ \,\frac{1}{2}\sum_{i=1}^n{\sum_{j=1}^n{\alpha_i\alpha_jy_iy_jx_i^Tx_j}} - \sum_{i=1}^n{\alpha_iy_i(\sum_{j=1}^n{\alpha_jy_jx_j^Tx_i} + \beta_0) - 1} }[/math].
Because [math]\displaystyle{ \,\sum_{i=1}^n{\alpha_iy_i} = 0 }[/math], and [math]\displaystyle{ \,\beta_0 }[/math] is constant, [math]\displaystyle{ \,\sum_{i=1}^n{\alpha_iy_i\beta_0} = 0 }[/math]. So this simplifies further, to
[math]\displaystyle{ L(\alpha) = \,-\frac{1}{2}\sum_{i=1}^n{\sum_{j=1}^n{\alpha_i\alpha_jy_iy_jx_i^Tx_j}} + \sum_{i=1}^n{\alpha_i} }[/math] A dual representation of the maximum margin.
Because [math]\displaystyle{ \,\alpha_i }[/math] is the Lagrange multiplier, [math]\displaystyle{ \,\alpha_i \geq 0 \forall i }[/math].
This is a much simpler optimization problem.
The Support Vector Machine algorithm - November 18, 2009
Lagrange Duality
In convex optimization, consider the primal optimization problem:
[math]\displaystyle{ \,\min_\beta }[/math] [math]\displaystyle{ \,f(\omega) }[/math]
[math]\displaystyle{ \,s.t. }[/math] [math]\displaystyle{ \,g_i(\omega) \leq 0 }[/math]
[math]\displaystyle{ \,h_i(\omega) = 0 }[/math]
Define the generalized Lagrangian to be
[math]\displaystyle{ L(\omega,\alpha,\beta) = f(\omega)+\sum_{i=1}^k\alpha_ig_i(\omega)+\sum_{i=1}^k\beta_ih_i(\omega) }[/math]
Then the dual optimization problem is
[math]\displaystyle{ \max_{\alpha,\beta} }[/math] [math]\displaystyle{ \min_{\omega} }[/math] [math]\displaystyle{ L(\omega,\alpha,\beta) }[/math]
Now instead of solving the primal problem, we can solve the dual problem without changing the solution as long as it subjects to the Karush-Kuhn-Tucker (KKT) conditions:
[math]\displaystyle{ \frac{\partial}{\partial\omega_i}L(\omega,\alpha,\beta)=0 }[/math]
[math]\displaystyle{ \frac{\partial}{\partial\beta_i}L(\omega,\alpha,\beta)=0 }[/math]
[math]\displaystyle{ \,\alpha_ig_i(\omega)=0 }[/math]
[math]\displaystyle{ g_i(\omega) \leq 0 }[/math]
[math]\displaystyle{ \,\alpha_i \geq 0 }[/math]
We are interested in the dual form because it gives bound on the primal problem and in some cases is easier to solve. For more information about convex optimization, see the book by Boyd: [8]
Solving the Lagrangian
Continuing from the above derivation, we now have the equation that we need to minimize, as well as two constraints.
The Support Vector Machine problem boils down to:
[math]\displaystyle{ \min_{\alpha} L(\alpha) = \sum_{i=1}^n{\alpha_i} - \frac{1}{2}\sum_{i=1}^n{\sum_{j=1}^n{\alpha_i\alpha_jy_iy_jx_i^Tx_j}} }[/math]
- such that [math]\displaystyle{ \alpha_i \geq 0 }[/math]
- and [math]\displaystyle{ \sum_{i=1}^n{\alpha_i y_i} = 0 }[/math]
We are looking to minimize [math]\displaystyle{ \,\alpha }[/math], which is our only unknown. Once we know [math]\displaystyle{ \,\alpha }[/math], we can easily find [math]\displaystyle{ \,\beta }[/math] and [math]\displaystyle{ \,\beta_0 }[/math] (see the Support Vector algorithm below for complete details).
If we examine the Lagrangian equation, we can see that [math]\displaystyle{ \,\alpha }[/math] is multiplied by itself; that is, the Lagrangian is quadratic with respect to [math]\displaystyle{ \,\alpha }[/math]. Our constraints are linear. This is therefore a problem that can be solved through quadratic programming techniques. We will examine how to do this in Matlab shortly.
We can write the Lagrangian equation in matrix form:
[math]\displaystyle{ L(\alpha) = \underline{\alpha}^T\underline{1} - \frac{1}{2}\underline{\alpha}^TS\underline{\alpha} }[/math]
- such that [math]\displaystyle{ \underline{\alpha} \geq \underline{0} }[/math]
- and [math]\displaystyle{ \underline{\alpha}^T\underline{y} = 0 }[/math]
Where:
- [math]\displaystyle{ \underline{\alpha} }[/math] denotes an [math]\displaystyle{ \,n \times 1 }[/math] vector; [math]\displaystyle{ \underline{\alpha}^T = [\alpha_1, ..., \alpha_n] }[/math]
- Matrix [math]\displaystyle{ S = y_iy_jx_i^Tx_j = (y_ix_i)^T(y_ix_i) }[/math]
- [math]\displaystyle{ \,\underline{0} }[/math] and [math]\displaystyle{ \,\underline{1} }[/math] are vectors containing all 0s or all 1s respectively
Using this matrix notation, we can use Matlab's built in quadratic programming routine, quadprog.
Quadprog example
Let's use quadprog to find the solution to [math]\displaystyle{ \,L(\alpha) }[/math].
Matlab's quadprog function minimizes an equation of the following form:
- [math]\displaystyle{ \min_x\frac{1}{2}x^THx+f^Tx }[/math]
- such that: [math]\displaystyle{ \,A \cdot x \leq b }[/math], [math]\displaystyle{ \,Aeq \cdot x = beq }[/math] and [math]\displaystyle{ \,lb \leq x \leq ub }[/math]
We can now see why we kept the [math]\displaystyle{ \frac{1}{2} }[/math] constant in the original derivation of the equation.
The function is called as such: x = quadprog(H,f,A,b,Aeq,beq,lb,ub). The variables correspond to values in the equation above.
We can now try to find the solution to [math]\displaystyle{ \,L(\alpha) }[/math] (though, it should be noted, that in [math]\displaystyle{ \,L(\alpha) }[/math] we subtract the first term rather than add it; I'm not sure if this difference would change how we call quadprog).
We'll use a simple one-dimensional data set, which is essentially y = -1 or 1 + Gaussian noise. (Note: you could easily put the values straight into the quadprog equation; they are separated for clarity.)
x = [mvnrnd([-1],[0.01],100); mvnrnd([1],[0.01],100)]'; y = [-ones(100,1); ones(100,1)]; S = (y*x)' * (y*x); f = ones(200,1); A = -ones(1,200); b = 0; Aeq = y'; beq = 0; lb = 0; ub = []; % There is no upper bound alpha = quadprog(S,f,A,b,Aeq,beq,lb,ub);
This gives us the optimal [math]\displaystyle{ \,\alpha }[/math]... or at least I think it should, but it does not appear to work for me (that is, despite setting the lower boundary of 0, a number of values are still negative. Whether this is just the nature of quadprog or an error on my part is an exercise for the reader).
Examining K.K.T. conditions
Karush-Kuhn-Tucker conditions (more info) give us a closer look into the Lagrangian equation and the associated conditions.
Suppose we are looking to minimize [math]\displaystyle{ \,f(x) }[/math] such that [math]\displaystyle{ \,g_i(x) \geq 0, \forall{x} }[/math]. If [math]\displaystyle{ \,f }[/math] and [math]\displaystyle{ \,g }[/math] are differentiable, then the necessary conditions for [math]\displaystyle{ \hat{x} }[/math] to be a local minimum are:
- At the optimal point, [math]\displaystyle{ \frac{\partial L}{\partial \hat{x}} = 0 }[/math]; i.e. [math]\displaystyle{ f'(\hat{x}) - \sum{\alpha_ig'(\hat{x})}=0 }[/math]
- [math]\displaystyle{ \alpha_i \geq 0 }[/math]. (Dual Feasibility)
- [math]\displaystyle{ \alpha_ig_i(\hat{x}) = 0, \forall{i} }[/math] (Complementary Slackness)
- [math]\displaystyle{ g_i(\hat{x}) \geq 0 }[/math] (Primal Feasibility)
If any of these conditions are violated, then the problem is deemed not feasible.
These are all trivial except for condition 4. Let's examine it further in our support vector machine problem.
Support Vectors
Support vectors are the training points that determine the optimal separating hyperplane that we seek. Also, they are the most difficult points to classify or the most informative for the classification.
In our case, the [math]\displaystyle{ g_i(\hat{x}) }[/math] function is:
- [math]\displaystyle{ \,g_i(x) = y_i(\beta^Tx_i+\beta_0)-1 }[/math]
Substituting [math]\displaystyle{ \,g_i }[/math] into KKT condition 3, we get [math]\displaystyle{ \,\alpha_i[y_i(\beta^Tx_i+\beta_0)-1] = 0 }[/math]. <br\>In order for this condition to be satisfied either
[math]\displaystyle{ \,\alpha_i= 0 }[/math] or
[math]\displaystyle{ \,y_i(\beta^Tx_i+\beta_0)=1 }[/math]
All points [math]\displaystyle{ \,x_i }[/math] will be either 1 or greater than 1 distance away from the hyperplane.
Case 1: a point [math]\displaystyle{ \displaystyle x_i \gt 1 }[/math] away from the margin
If [math]\displaystyle{ \,y_i(\beta^Tx_i+\beta_0) \gt 1 \Rightarrow \alpha_i = 0 }[/math].
If point [math]\displaystyle{ \, x_i }[/math] is not on the margin, then the corresponding [math]\displaystyle{ \,\alpha_i=0 }[/math].
Case 2: a point [math]\displaystyle{ \displaystyle x_i = 1 }[/math] away from the margin
If [math]\displaystyle{ \,\alpha_i \gt 0 \Rightarrow y_i(\beta^Tx_i+\beta_0) = 1 }[/math] <br\>If point [math]\displaystyle{ \, x_i }[/math] is on the margin, then the corresponding [math]\displaystyle{ \,\alpha_i\gt 0 }[/math].
Points on the margin, with corresponding [math]\displaystyle{ \,\alpha_i \gt 0 }[/math], are called support vectors.
Using support vectors
Support vectors are important because they allow the support vector machine algorithm to be insensitive to outliers. If [math]\displaystyle{ \,\alpha = 0 }[/math], then the cost function is also 0, and won't contribute to the solution of the SVM problem; only points on the margin -- support vectors -- contribute. Hence the model given by SVM in entirely defined by the set of support vectors, a subset of the entire training set. This is interesting because in the NN methods(and can be generalize to classical statistical learning) previous to this the configuration of the network needed to be specified. In this case we have a data-driven or 'nonparametric' model in which is the training set and algorithm will determine the support vectors.
References: Wang, L, 2005. Support Vector Machines: Theory and Applications, Springer, 3
The support vector machine algorithm
- Solve the quadratic programming problem:[math]\displaystyle{ \min_{\alpha} L(\alpha) = \sum_{i=1}^n{\alpha_i} - \frac{1}{2}\sum_{i=1}^n{\sum_{j=1}^n{\alpha_i\alpha_jy_iy_jx_i^Tx_j}} }[/math] such that [math]\displaystyle{ \alpha_i \geq 0 }[/math] and [math]\displaystyle{ \sum_{i=1}^n{\alpha_i y_i} = 0 }[/math]
- Use Matlab's quadprog to find the optimal [math]\displaystyle{ \,\underline{\alpha} }[/math]
- Find [math]\displaystyle{ \beta = \sum_{i=1}^n{\alpha_iy_i\underline{x_i}} }[/math]
- Find [math]\displaystyle{ \,\beta_0 }[/math] by choosing a support vector (a point with [math]\displaystyle{ \,\alpha_i \gt 0 }[/math]) and solving [math]\displaystyle{ \,y_i(\beta^Tx_i+\beta_0) = 1 }[/math]
Example in Matlab
The following code, taken verbatim from the lecture, shows how to use Matlab built-in SVM routines (found in the Bioinformatics toolkit) to do classification through support vector machines.
load 2_3;
[U,Y] = princomp(X');
data = Y(:,1:2);
l = [-ones(1,200) ones(1,200)];
[train,test] = crossvalind('holdOut',400);
% Gives indices of train and test; so, train is a matrix of 0 or 1, 1 where the point should be used as part of the training set
svmStruct = svmtrain(data(train,:), l(train), 'showPlot', true);
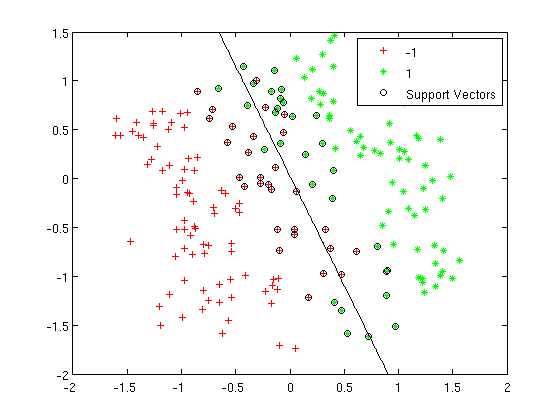
yh = svmclassify(svmStruct, data(test,:), 'showPlot', true);
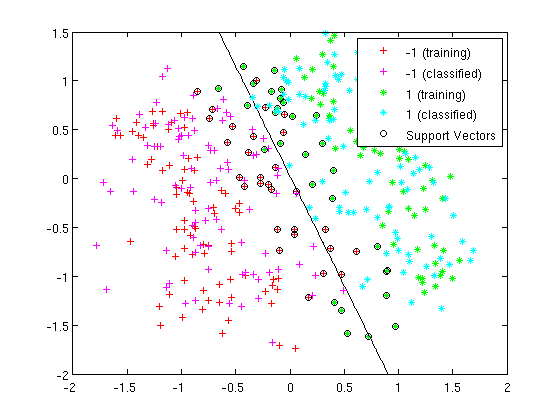
Non-linear hypersurfaces and Non-Separable classes - November 20, 2009
Kernel Trick
We talked about the curse of dimensionality at the beginning of this course, however, we now turn to the power of high dimensions in order to find a linearly separable hyperplane between two classes of data points. To understand this, imagine a two dimensional prison where a two dimensional person is constrained. Suppose magically we give the person a third dimension, then he can escape from the prison. In other words, the prison and the person are linearly separable now with respect to the third dimension. The intuition behind the "kernel trick" is basically to map data to a higher dimension so that they are linearly separable by a hyperplane.
We have seen SVM as a linear classification problem that finds the maximum margin hyperplane in the given input space. However, for many real world problems a more complex decision boundary is required. The following simple method was devised in order to solve the same linear classification problem but in a higher dimensional space, a 'feature space', under which the maximum margin hyperplane is better suited.
Let [math]\displaystyle{ \,\phi }[/math] be a mapping,
[math]\displaystyle{ \phi:\Re^d \rightarrow \Re^D }[/math]
We wish to find a [math]\displaystyle{ \,\phi }[/math] such that our data will be suited for separation by a hyperplane. Given this function, we are lead to solve the previous constrained quadratic optimization on the transformed dataset,
[math]\displaystyle{ \min_{\alpha} L(\alpha) = \sum_{i=1}^n{\alpha_i} - \frac{1}{2}\sum_{i=1}^n{\sum_{j=1}^n{\alpha_i\alpha_jy_iy_j\phi(x_i)^T\phi(x_j)}} }[/math] such that [math]\displaystyle{ \alpha_i \geq 0 }[/math] and [math]\displaystyle{ \sum_{i=1}^n{\alpha_i y_i} = 0 }[/math]
The solution to this optimization problem is now well known; however a workable [math]\displaystyle{ \,\phi }[/math] must be determined. Possibly the largest drawback in this method is that we must compute the inner product of two vectors in the high dimensional space. As the number of dimensions in the initial data set increases, the inner product becomes computationally intensive or impossible.
However, we have a very useful result that says that there exists a class of functions, [math]\displaystyle{ \,\Phi }[/math], which satisfy the above requirements and that for any function [math]\displaystyle{ \,\phi \in \Phi }[/math],
[math]\displaystyle{ \,\phi(x_i)^T\phi(x_j) = K(x_i,x_j) }[/math]
Where K is the kernel function in the input space satisfying Mercer's condition (to guarantee that it indeed corresponds to certain mapping function [math]\displaystyle{ \,\phi }[/math]). As a result, if the objective function depends on inner products but not on coordinates, we can always use the kernel function to implicitly calculate in the feature space without storing the huge data. Not only does this solve the computation problems but it no longer requires us to explicitly determine a specific mapping function in order to use this method. In fact, it is now possible to use an infinite dimensional feature space in SVM without even knowing the function [math]\displaystyle{ \,\phi }[/math].
Three popular kernel choices in the SVM
d-th Degree polynomial: [math]\displaystyle{ \ K(x,x^{'})= (1 + \langle x, x^{'}\rangle)^{d} }[/math],
Radial Basis: [math]\displaystyle{ \ K(x,x^{'})= exp(-\gamma \| x - x^{'}\|^{2}) }[/math],
Neural Network: [math]\displaystyle{ \ K(x,x^{'})= tanh(k_{1} \langle x,x^{'} \rangle +k_{2}) }[/math]
Mercer's Theorem in detail
Let [math]\displaystyle{ \,\phi }[/math] be a mapping to a high dimensional Hibert Space [math]\displaystyle{ \,H }[/math]
[math]\displaystyle{ \phi:x \in \Re^d \rightarrow H }[/math]
The transformed coordinates can be defined as,
[math]\displaystyle{ \phi_1(x)\dots\phi_d(x)\dots }[/math]
By Hilbert - Schmidt theory we can represent an inner product in Hilbert space as,
[math]\displaystyle{ \,\phi(x_i)^T\phi(x_j) = \sum_{r=1}^{\infty}a_k\phi_r(x_i)\phi(x_j) \Leftrightarrow K(x_i,x_j), \ a_r \ge 0 }[/math]
where K is symmetric, then Mercer's theorem gives necessary and sufficient conditions on K for it to satisfy the above relation.
Mercer's Theorem
Let C be a compact subset of [math]\displaystyle{ \Re^d }[/math] and K a function [math]\displaystyle{ \in L^2(C) }[/math], if
[math]\displaystyle{ \, \int_C\int_C K(u,v)g(u)g(v)dudv \ge 0, \ \forall g \in L^2(C) }[/math]
then,
[math]\displaystyle{ \sum_{r=1}^{\infty}a_k\phi_r(u)\phi(v) }[/math] converges absolutely and uniformly to a symmetric function [math]\displaystyle{ \,K(u,v) }[/math]
References: Vapnik, V., 1998. Statistical Learning Theory. John Wiley & Sons, {423}
Kernel Functions
There are various kernel functions, for example:
- Linear kernel: [math]\displaystyle{ \,k(x,y)=x \cdot y }[/math]
- Polynomial kernel: [math]\displaystyle{ \,k(x,y)=(x \cdot y)^d }[/math]
- Gaussian kernel: [math]\displaystyle{ e^{-\frac{|x-y|^2}{2\sigma^2}} }[/math]
If [math]\displaystyle{ \,X }[/math] is a [math]\displaystyle{ \,d \times n }[/math] matrix in the original space, and [math]\displaystyle{ \,\phi(X) }[/math] is a [math]\displaystyle{ \,D \times n }[/math] matrix in the Hilbert space (good explanation video: part 1 part 2), then [math]\displaystyle{ \,\phi^T(X) \cdot \phi(X) }[/math] is an [math]\displaystyle{ \,n \times n }[/math] matrix. The inner product is also illustrated as correlation, which measures the similarity between data points. This gives us some insight in how to choose the kernel. The choice depends on certain prior knowledge of the problem and on how we believe the similarity of our data should be measured. In practice, the Gaussian (RBF) kernel usually works best. Besides the most common kernel functions mentioned above, many novel kernels are also suggested for different problem domains like text classification, gene classification and so on.
These kernel functions can be applied to many algorithms to derive the "kernel version". For example, kernel PCA, kernel LDA, etc.
SVM: non-separable case
We have seen how SVMs are able to find an optimally separating hyperplane of two separable classes of data, in which case the margin contains no data points. However, in the real world, data of different classes are usually mixed together at the boundary and it's hard to find a perfect boundary to totally separate them. To address this problem, we slacken the classification rule to allow data cross the margin. Mathematically the problem becomes,
- [math]\displaystyle{ \min_{\beta, \beta_0} \frac{1}{2}|\beta|^2 }[/math]
- [math]\displaystyle{ \,y_i(\beta^Tx_i+\beta_0) \geq 1-\xi_i }[/math]
- [math]\displaystyle{ \xi_i \geq 0 }[/math]
Now each data point can have some error [math]\displaystyle{ \,\xi_i }[/math]. However, we only want data to cross the boundary when they have to and make the minimum sacrifice; thus, a penalty term is added correspondingly in the objective function to constrain the number of points that cross the margin. The optimization problem now becomes:
- [math]\displaystyle{ \min_{\alpha} \frac{1}{2}|\beta|^2+\gamma\sum_{i=1}^n{\xi_i} }[/math]
- [math]\displaystyle{ \,s.t. }[/math] [math]\displaystyle{ y_i(\beta^Tx+\beta_0) \geq 1-\xi_i }[/math]
- [math]\displaystyle{ \xi_i \geq 0 }[/math]
<br\>Note that [math]\displaystyle{ \,\xi_i }[/math] is not necessarily smaller than one, which means data can not only enter the margin but can also cross the separating hyperplane.
<br\>Note that [math]\displaystyle{ \,\gamma = \infty }[/math] in the separable case.
References:
Mercer, J., 1909. Functions of positive and negative type and their connection with the theory of integral equations. Philos. Trans. Roy. Soc. London, A 209:415{446}
Support Vector Machine algorithm for non-separable cases - November 23, 2009
With the program formulation above, we can form the lagrangian, apply KKT conditions, and come up with a new function to optimize. As we will see, the equation that we will attempt to optimize in the SVM algorithm for non-separable data sets is the same as the optimization for the separable case, with slightly different conditions.
Forming the Lagrangian
In this case we have have two constraints in the Lagrangian and therefore we optimize with respect to two dual variables [math]\displaystyle{ \,\alpha }[/math] and [math]\displaystyle{ \,\lambda }[/math],
- [math]\displaystyle{ L: \frac{1}{2} |\beta|^2 + \gamma \sum_{i=1}^n \xi_i - \sum_{i=1}^n \alpha_i[y_i(\beta^T x_i+\beta_0)-1+\xi_i]-\sum_{i=1}^n \lambda_i \xi_i }[/math]
- [math]\displaystyle{ \alpha_i \geq 0, \lambda_i \geq 0 }[/math]
Applying KKT conditions
- [math]\displaystyle{ \frac{\partial L}{\partial \beta}=\beta - \sum_{i=1}^n \alpha_i y_i x_i = 0 \Rightarrow \beta=\sum_{i=1}^n\alpha_i y_i x_i }[/math] <br\>[math]\displaystyle{ \frac{\partial L}{\partial \beta_0}=-\sum_{i=1}^n \alpha_i y_i =0 \Rightarrow \sum_{i=1}^n \alpha_i y_i =0 }[/math] since the sign does not make a difference
- [math]\displaystyle{ \frac{\partial L}{\partial \xi_i}=\gamma - \alpha_i - \lambda_i \Rightarrow \gamma = \alpha_i+\lambda_i }[/math]
- [math]\displaystyle{ \,\alpha_i[y_i(\beta^T x_i+\beta_0)-1+\xi_i]=0 }[/math] and [math]\displaystyle{ \,\alpha_i \xi_i=0 }[/math]
Putting it all together
With our KKT conditions and the Lagrangian equation, we can now use quadratic programming to find [math]\displaystyle{ \,\alpha }[/math]. <br\> Similar to what we did for the separable case after apply KKT conditions, replace the primal variables in terms of dual variables into the Lagrangian equations and simplify.
In matrix form, we want to solve the following optimization:
- [math]\displaystyle{ L(\alpha) = \underline{\alpha}^T\underline{1} - \frac{1}{2}\underline{\alpha}^TS\underline{\alpha} }[/math]
- [math]\displaystyle{ \,s.t. }[/math] [math]\displaystyle{ \underline{0} \leq \underline{\alpha} \leq \gamma }[/math], [math]\displaystyle{ \underline{\alpha}^T\underline{y} = 0 }[/math]
Solving this gives us [math]\displaystyle{ \,\underline{\alpha} }[/math], which we can use to find [math]\displaystyle{ \,\underline{\beta} }[/math] as before:
- [math]\displaystyle{ \,\underline{\beta} = \sum{\alpha_i y_i \underline{x_i}} }[/math]
However, we cannot find [math]\displaystyle{ \,\beta_0 }[/math] in the same way as before, even if we choose a point with [math]\displaystyle{ \,\alpha_i \gt 0 }[/math], because we do not know the value of [math]\displaystyle{ \,\xi_i }[/math] in the equation
- [math]\displaystyle{ \,y_i(\underline{\beta}^Tx_i + \beta_0) - 1 + \xi_i = 0 }[/math]
From our discussion on the KKT conditions, we know that [math]\displaystyle{ \,\lambda_i \xi_i = 0 }[/math] and [math]\displaystyle{ \,\gamma = \alpha_i + \lambda_i }[/math].
So, if [math]\displaystyle{ \,\alpha_i \lt \gamma }[/math] then [math]\displaystyle{ \,\lambda_i \gt 0 }[/math] and consequently [math]\displaystyle{ \,\xi_i = 0 }[/math].
Therefore, we can solve for [math]\displaystyle{ \,\beta_0 }[/math] if we choose a point where:
- [math]\displaystyle{ \,0 \lt \alpha_i \lt \gamma }[/math]
Note
- When [math]\displaystyle{ \,0 \lt \alpha_i \lt \gamma }[/math], we are considering a point that is on the margin.
- If [math]\displaystyle{ \,0 \lt \alpha_i = \gamma }[/math] then [math]\displaystyle{ \,\lambda_i = 0 \Rightarrow \xi_i \gt 0 }[/math] and we're dealing with a point that has crossed the margin.
The SVM algorithm for non-separable data sets
The algorithm, then, for non-separable data sets is:
- Use
quadprog(or another quadratic programming technique) to solve the above optimization and find [math]\displaystyle{ \,\alpha }[/math] - Find [math]\displaystyle{ \,\underline{\beta} }[/math] by solving [math]\displaystyle{ \,\underline{\beta} = \sum{\alpha_i y_i x_i} }[/math]
- Find [math]\displaystyle{ \,\beta_0 }[/math] by choosing a point where [math]\displaystyle{ \,0 \lt \alpha_i \lt \gamma }[/math] and then solving [math]\displaystyle{ \,y_i(\underline{\beta}^Tx_i + \beta_0) - 1 = 0 }[/math]
Finishing up SVM - November 25, 2009
Does SVM find a global minimum?
When we discussed KKT conditions, we listed the necessary conditions for [math]\displaystyle{ \hat{x} }[/math] to be a local minimum. However, it would be ideal if we could show that SVM finds a global minimum (unlike, say, neural networks that find a local minimum).
Recall that our conditions, for the non-separable case, are [math]\displaystyle{ \,0 \leq \underline{\alpha} \leq \gamma }[/math] and [math]\displaystyle{ \,\underline{\alpha}^T\underline{y} = 0 }[/math]. These are both convex.
Our lagrangian equation is [math]\displaystyle{ L(\alpha) = \underline{\alpha}^T\underline{1} - \frac{1}{2}\underline{\alpha}^TS\underline{\alpha} }[/math]. Since this is quadratic, it might be convex, but it also may not be; it depends on the matrix [math]\displaystyle{ \,S }[/math]. If [math]\displaystyle{ \,S }[/math] is a positive semi-definite matrix, then the lagrangian equation is convex.
Recall that [math]\displaystyle{ \,S }[/math] is the product of [math]\displaystyle{ \,\underline{x}^T\underline{x} }[/math]. Similar to the notion that squaring any number will give us a positive number in the end, a matrix that is the product of a vector transposed times itself will result in a positive semi-definite matrix.
So, we know that [math]\displaystyle{ \,S }[/math] is positive semi-definite. The lagrangian equation is convex, and therefore, the SVM algorithm finds a global minimum.
Naive Bayes, Decision Trees, K Nearest Neighbours, Boosting, and Bagging - November 25, 2009
Now that we've covered a number of more advanced classification algorithms, we can look at some of the simpler classification algorithms that are usually discussed at the beginning of a discussion on classification.
Naive Bayes Classifiers
Recall that one of the major drawbacks of the Bayes classifier was the difficulty in estimating a joint density in a multidimensional space. Naive Bayes classifiers are one possible solution to the problem. They are especially popular for problems with high-dimension feature problems.
A naive Bayes classifier applies a strong independence assumption to the class density [math]\displaystyle{ f_{k}(x) }[/math]. It assumes that inputs within each class are conditionally independent. In other words, it assumes that the value of one feature in a class is unrelated to that of any other feature.
[math]\displaystyle{ \ f_{k}(x) = \prod_{j=1}^d f_{jk}(x_{j}) }[/math]
Each of the d marginal densities can be estimated separately using one-dimensional density estimates. If one of the components [math]\displaystyle{ x_{j} }[/math] is discrete then its density can be estimated using a histogram. We can thus mix discrete and continuous variables in a naive Bayes classifier.
Naive Bayes classifiers often perform extremely well in practice despite these 'naive' and seemingly optimistic assumptions. This is because while individual class density estimates could be biased, the bias does not carry through to the posterior probabilities.
It is also possible to train naive Bayes classifiers using maximum likelihood estimation.
Decision Trees
Decision trees are highly intuitive learning methods that can be thought of as partitioning the feature space into a number of rectangles. Trees can be used for classification, regression, or both. Trees map features of a decision problem onto a conclusion, or label.
We fit a tree model by minimizing some measure of impurity. For a single covariate [math]\displaystyle{ X_{1} }[/math] we choose a point t on the real line that splits the real line into two sets R1 = (-inf,t], R2 = [t,inf) in a way that minimizes impurity.
We denote by [math]\displaystyle{ \hat p_{s}(j) }[/math] the proportion of observations in [math]\displaystyle{ \ R_{s} }[/math] that [math]\displaystyle{ \ Y_{i} = j }[/math].
[math]\displaystyle{ \hat p_{s}(j) = \frac{\sum_{i = 1}^{n} I(Y_{i} = j,X_{i} \in R_{s})}{\sum_{i = 1}^{n} I(X_{i} \in R_{s})} }[/math]
Common Node Impurity Measures
Some common node impurity measures are:
- Misclassification error:
[math]\displaystyle{ 1 - \hat p_{s}(j) }[/math]
- Gini Index:
[math]\displaystyle{ \sum_{j \neq i} \hat p_{s}(j)\hat p_{s}(i) }[/math]
- Cross-entropy:
[math]\displaystyle{ - \sum_{j = 1}^{K} \hat p_{s}(j) log(\hat p_{s}(j)) }[/math]
K-Nearest Neighbours Classification
[math]\displaystyle{ K }[/math]-nearest neighbours is a very simple algorithm that classifies points based on a majority vote of the [math]\displaystyle{ \ k }[/math] nearest points in the feature space, and [math]\displaystyle{ \ k }[/math] is chosen by cross validation.
1. Ties are borken at random.
2. If we assume the features are real, we can use the Euclidean distance in feature space.
3. Since the features are measured in different units, we can standardize the features to have mean zero and variance 1.
Boosting
Boosting algorithms are a class of machine learning meta-algorithms that can improve weak classifiers. If we have a weak classifier which slightly does better than random classification, then by assigning larger weights to points which are misclassified and trying to minimise the new cost function, we probably can get a new classifier which classifies with less error. This procedure can be repeated for a finite number of times and then a new classifier which is a weighed aggregation of the generated classifiers will be used as the boosted classifier. The better each generated classifier is the more its weight is in the final classifier.
AdaBoost Algorithm
- Set all the weights of all points equal [math]\displaystyle{ w_i\leftarrow \frac{1}{n} }[/math] where we have [math]\displaystyle{ n }[/math] points.
- For [math]\displaystyle{ j=1,\dots, J }[/math]
- Find [math]\displaystyle{ h_j:X\rightarrow \{-1,+1\} }[/math] that minimizes the weighted error [math]\displaystyle{ L_j }[/math]
[math]\displaystyle{ h_j=\mbox{argmin}_{h_j} L_j }[/math] where [math]\displaystyle{ L_j=\frac{\sum_{i=1}^n w_i I[y_i\neq h_j(x_i)]}{\sum_{i=1}^n w_i} }[/math] - Let [math]\displaystyle{ \alpha_j\leftarrow\log(\frac{1-L_j}{L_j}) }[/math]
- Update the weights: [math]\displaystyle{ w_i\leftarrow w_i e^{a_j I[y_j\neq h_j(x_i)]} }[/math]
- Find [math]\displaystyle{ h_j:X\rightarrow \{-1,+1\} }[/math] that minimizes the weighted error [math]\displaystyle{ L_j }[/math]
- The final classifier is [math]\displaystyle{ h(x)=\mbox{sign}\left(\sum_{j=1}^J \alpha_j h_j(x)\right) }[/math]
Boosting works very well in practice, and there are a lot of research and published works on why it works this well.
We can see that in AdaBoost if training points are accurately classified, then their weights of being used in the next classifier is reduced, while if points are not accurately classified, their weights of being used again is raised. Thus the AdaBoost focuses on the more informative or difficult points.
Bagging
Bagging, or bootstrap aggregating, is another meta-technique used to reduce the variance of classifiers with high variability. It exploits the fact that a bootstrap mean is approximately equal to the posterior average. It is most effective for highly nonlinear classifiers such as decision trees.
The idea is to train classifiers [math]\displaystyle{ \ h_{1}(x) }[/math] to [math]\displaystyle{ \ h_{B}(x) }[/math] using B bootstrap samples from the data set. The final classifier is obtained using a simple average of the B classifiers as follows:
- [math]\displaystyle{ \, h(x)= \left\{\begin{matrix} 1 & \frac{1}{B} \sum_{i=1}^{B} h_{b}(x) \geq \frac{1}{2} \\ 0 & \mathrm{otherwise} \end{matrix}\right. }[/math]
Many classifiers, such as trees, already have underlying functions that estimate the class probabilities at x. An alternative strategy is to average these class probabilities instead of the final classifiers. This approach can produce bagged estimates with lower variance.