stat441w18/e-gan: Difference between revisions
No edit summary |
No edit summary |
||
| Line 43: | Line 43: | ||
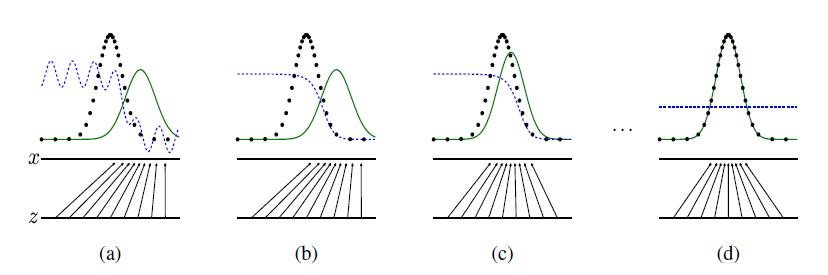
Figure 1: Generative adversarial nets are trained by simultaneously updating the discriminative distribution (D, blue, dashed line) so that it discriminates between samples from the data generating distribution (black, dotted line) px from those of the generative distribution pg (G) (green, solid line). The lower horizontal line is the domain from which z is sampled, in this case uniformly. The horizontal line above is part of the domain of x. The upward arrows show how the mapping x = G(z) imposes the non-uniform distribution pg on transformed samples. G contracts in regions of high density and expands in regions of low density of pg. (a) Consider an adversarial pair near convergence: pg is similar to pdata and D is a partially accurate classifier. (b) In the inner loop of the algorithm D is trained to discriminate samples from data, converging to D ∗ (x) = pdata(x) /(pdata(x)+pg(x) ). (c) After an update to G, gradient of D has guided G(z) to flow to regions that are more likely to be classified as data. (d) After several steps of training, if G and D have enough capacity, they will reach a point at which both cannot improve because pg = pdata. The discriminator is unable to differentiate between the two distributions, i.e. D(x) = 1/2. | Figure 1: Generative adversarial nets are trained by simultaneously updating the discriminative distribution (D, blue, dashed line) so that it discriminates between samples from the data generating distribution (black, dotted line) px from those of the generative distribution pg (G) (green, solid line). The lower horizontal line is the domain from which z is sampled, in this case uniformly. The horizontal line above is part of the domain of x. The upward arrows show how the mapping x = G(z) imposes the non-uniform distribution pg on transformed samples. G contracts in regions of high density and expands in regions of low density of pg. (a) Consider an adversarial pair near convergence: pg is similar to pdata and D is a partially accurate classifier. (b) In the inner loop of the algorithm D is trained to discriminate samples from data, converging to D ∗ (x) = pdata(x) /(pdata(x)+pg(x) ). (c) After an update to G, gradient of D has guided G(z) to flow to regions that are more likely to be classified as data. (d) After several steps of training, if G and D have enough capacity, they will reach a point at which both cannot improve because pg = pdata. The discriminator is unable to differentiate between the two distributions, i.e. D(x) = 1/2. | ||
== Mutations == | == Mutations == | ||
Revision as of 23:41, 13 March 2018
Presented by
1. Yufeng Yue
2. Shanzi Wang
3. Yumeng Li
4. Yuyang Bao
5. Yun Shi
6. Wan Feng Cai
7. Ki Beom Lee
8. Qian Xiang
Introduction
In recent years, Generative Adversarial Networks (GAN) have emerged as a powerful method for learning generative models with real-world data. However, existing GANs (GAN and its variants) is experiencing training problems such as instability and mode collapse.
In this paper, authors proposed a novel GAN framework called Evolutionary Generative Adversarial Networks (E-GAN) for stable GAN training and improved generative performance. Compared with existing GANs, which employ a pre-defined adversarial objective function alternately training a generator and a discriminator, E-GAN uses different adversarial training objectives as mutation operations and evolves a population of generators to adapt to the environment (i.e., the discriminator). E-GAN also uses an evaluation mechanism to measure the quality and diversity of generated samples, such that only well-performing generator(s) are preserved and used for further training so that E-GAN would be able to overcome the limitations of an individual adversarial training objective and always preserves the best offspring, contributing to progress in and the success of GANs.
In a later section of the paper, experiment results on several datasets show that E-GAN achieves convincing generative performance and reduces the training problems inherent in existing GANs.
Method
Generative Adversarial Networks (GAN)
Generative Adversarial Nets (GAN) is a framework for estimating generative models via an adversarial process. A discriminative model is analogous to learn how to determine fake currency. The generative model is analogous to learn how to detect the counterfeit currency.
Taking noisy sample z ~ p(z) as the input. We train two models simultaneously: a generative model G that outputs new data G(z), and a discriminative model D that distinguishes the true data sample x ~ p_data (x) and the generated new data G(z)~p_g (G(z)).
Models D and G play the following two-player minimax game with value function V(G,D):
![]()
Eventually, the models will reach a point at which both cannot improve because p_g= p_data. The discriminator is unable to differentiate between both distributions, that is, D(x)= 1/2.
The process can be seen in Figure 1.
Figure 1: Generative adversarial nets are trained by simultaneously updating the discriminative distribution (D, blue, dashed line) so that it discriminates between samples from the data generating distribution (black, dotted line) px from those of the generative distribution pg (G) (green, solid line). The lower horizontal line is the domain from which z is sampled, in this case uniformly. The horizontal line above is part of the domain of x. The upward arrows show how the mapping x = G(z) imposes the non-uniform distribution pg on transformed samples. G contracts in regions of high density and expands in regions of low density of pg. (a) Consider an adversarial pair near convergence: pg is similar to pdata and D is a partially accurate classifier. (b) In the inner loop of the algorithm D is trained to discriminate samples from data, converging to D ∗ (x) = pdata(x) /(pdata(x)+pg(x) ). (c) After an update to G, gradient of D has guided G(z) to flow to regions that are more likely to be classified as data. (d) After several steps of training, if G and D have enough capacity, they will reach a point at which both cannot improve because pg = pdata. The discriminator is unable to differentiate between the two distributions, i.e. D(x) = 1/2.
Mutations
Many mutation techniques can be used when we are producing the children nodes (or the next generation of data points). These mutation techniques each has their own training objectives, but they all attempt to get the generated distribution as close to the data distribution as possible. In this section, we will introduce 3 mutation techniques that we used inside this paper.
Minimax Mutation
A minimax mutation is defined as the following.
[math]\displaystyle{ M_G = 1/2*E[log(1-D(G(z))] }[/math]
This definition of minimax is identical as the one in the original GAN. Given the optimal discriminator D, the minimax mutation aims to minimize the Jensen-Shannon divergence (JSD) between the data distribution and the generated distribution. Although the minimax mutation is easy to understand and analyze, its practical performance isn't so great due to the generator's vanishing gradient.
If the support of two distributions lies in two manifolds, the JSD will be a constant, leading to the vanishing gradient
However, if the generated distribution overlaps with the data distribution, which means the discriminator cannot completely distinguish the two, the minimax mutation provides effective gradients and continually narrows the JSD between the data distribution and the generated distribution
Heuristic Mutation
The heuristic mutation is defined as the following:
[math]\displaystyle{ M_G = -1/2*E[log(D(G(z))] }[/math]
Notice that this definition looks similar with the minimax mutation formula, this is because they are achieving a similar goal from two different perspective. The minimax mutation aims to minimizes the log probability of the discriminator being correct, and the heuristic mutation aims to maximize the log probability of the discriminator being mistaken
Compared to the minimax mutation, the heuristic mutation will not saturate when the discriminator rejects the generated sample, so it prevented the gradient from vanishing, and provides useful generator updates. However, maximize the heuristic mutation may lead to training instability and generative quality fluctuations
Least-squares Mutation
The least-squares mutation is inspired by Least-squares-GAN and it is defined as the following:
[math]\displaystyle{ M_G = E[(D(G(z))-1)^2] }[/math]
The least-squares mutation is non-saturating when the discriminator can recognize the generated sample, and when the discriminator output grows, the least-squares mutation approaching zero. Therefore, just like the heuristic mutation, this approach can avoid vanishing gradient when the discriminator is performing much better than the generator.
Evaluation
First, we simply feed generator produced images into the discriminator D and observe the average value of the output, which we name the quality fitness score:
Fq = Ez[D(G(z))]
Then, we employ a similar principle to evaluate generator optimization stability and generative diversity as:
Fd = -logr||delta(D) - Ex[logD(x)] - Ez[log(1 - D(G(z)))]||:
Based on the aforementioned two fitness scores, the final evaluation (or fitness) function is:
F = Fq + gamma*Fd
where gamma >= 0. Overall, a relatively high fitness score F, leads to higher training efficiency and better generative performance.
E-GAN
In this section, we are going to focus on the training algorithm of E-GAN. Before introducing the algorithm, let's briefly cover how E-GAN is different from GAN. The core concept of GAN, which is using adversial two-player game to train generator and discrimintor, G and D, still applies here. The only difference is how we update G and D. Ordinary GAN updates G and D alternatively, and for each updates, we are using stochastic gradients. However, as we discussed in the previous sections, alternatively updating G and D requires significant attention. We modify the way we update the generator G to improve stability and generative powers, using the concept of evolutionary algorithms. Below pseudo algorithm will explain what is really happening in the training algorithm.
For each iterations,
1. Train D
- for number of steps you want,
- sample datas and noises with given minibatch size
- calculate sample gradient of total objective function
- use the calculated gredient to update the parameters for D, with Adam
2. Evolve G
- for each parents,
- for number of children you want,
- sample noises
[ Variation ]
- calculate sample gradient of mutation objective funtion
- use the calculated gradient to mutate parameters of G, with Adam
( note that mutated parameters are now the parameters of the child )
[ Evaluation ]
- evaluate fitness
3. Select G
[ Selection ]
- select according to fitness
- use selected children as parents for next iteration
As you can see, the first part ( updating D ) of the iteration is identical to the ordinary GAN. But for the second part, we adapt the evolutionary process. Note that the mutation process is in fact, we generate several identical copies of the previous known generator ( a parent ) and mutate the parameters. Mutation of the parameter is nothing more than calculate the gradient of mutation objective function and apply adam operation to generate new parameters for the child. And you repeat this process until we obtain predetermined number of children ( mutated generators ). Furthermore, we repeat this process for all parents available at each iterations. It is very important to know that the mutation objective function is a function of D(G(z)). Therefore, the evolutionary process takes account of newly updated discriminator D. Now after we generate all mutated G's, we evaluate survival fitness of each mutations. Finally, we sort the generators with their survial fitness values and use top corresponding mutated generators as parents for the next iteration. Here is the rigourous version of the algorithm, which is provided from the paper.
Experiments
To evaluate the proposed E-GAN, in this section, we run and analyze experiments on several generation tasks. We evaluate E-GAN on two synthetic datasets and three image datasets: CIFAR-10, LSUN bedroom, and CelebA. Authors use the default hyper-parameter values in Algorithm 1 for all experiments. They set the number of parents as 1 to reduce E-GAN’s computational cost, thereby accelerating training. Their experiments show that E-GAN already achieves impressive performance and stability even with only one survivor at each step.
Synthetic Datasets and Mode Collapse
The first experiment trains GANs on 2D Gaussian mixture distributions. On these synthetic datasets, the mode collapse issue can be accurately measured. They first compare the proposed evolutionary adversarial training framework with one using an individual adversarial objective (i.e., conventional GANs). The results show that during theevolutionary procedure, the proposed evaluation mechanism can recognize well-performing updatings (i.e.,offspring), and promote the population to a better evolutionary direction.
CIFAR-10 and Inception Score
When evaluating a GAN model, sample quality and convergence speed are two important criteria. Authors train different GANs on CIFAR-10 and plot inception scores over the course of training. The same network architecture based on DCGAN is used in all methods. Utilizing the evolutionary framework shows that E-GAN not only overcomes the limitations of these individual adversarial objectives, but also outperforms other GANs (the WGAN and its improved variation WGAN-GP). Furthermore, E-GAN achieves comparable convergence speed in terms of wall-clock time, although it takes more time for each iteration. During training E-GAN, the minus JSDs of the heuristic mutation may tend to push the generated distribution away from data distribution and lead to training instability. However, in E-GAN, beyond the heuristic mutation, we have other options of mutation, which improves the stability at convergence.
LSUN and Architecture Robustness
To demonstrate the training stability of their method, authors train different network architectures on the LSUN bedroom dataset and compare with several existing works. In addition to the baseline DCGAN architecture, authors choose three additional architectures corresponding to different training challenges. For each architecture, they test five different methods: DCGAN, LSGAN, standard WGAN (with weight clipping),WGAN-GP (with gradient penalty) ,and E-GAN.Result shows that E-GAN generates reasonable results even when other methods are failed. Authors also train E-GAN to generate 128 × 128 bedroom images based on the DCGAN architecture, images shows that E-GAN can be trained to generate diversity and high-quality images from the target data distribution.
CelebA and Space Continuity
Similar to generating bedrooms, authors also employ the same architectures to generate 128 × 128 RGB human face images. In addition, given a well-trained generator, they evaluate the performance of the embedding in the latent space of noisy vectors z. This experiment demonstrates that generator training does not merely memorize training samples but learns a meaningful projection from latent noisy space to face images. Meanwhile, it also shows that the generator trained by E-GAN does not suffer from mode collapse, and shows great space continuity
Conclusions
In this paper, authors present E-GAN for effectively training deep generative models. They invent an evolutionary algorithm to evolve a population of generators to adapt to the dynamic environment. Experiments support that E-GAN improves the training stability of GAN models and achieves convincing performance in several image generation tasks. In the future, it will be interesting to focus on further exploring the relationship between the environment and evolutionary population and further improving generative performance.