stat441w18/Convolutional Neural Networks for Sentence Classification
Presented by
1. Ben Schwarz
2. Cameron Miller
3. Hamza Mirza
4. Pavle Mihajlovic
5. Terry Shi
6. Yitian Wu
7. Zekai Shao
Introduction
Model
Theory of Convolutional Neural Networks
Let [math]\displaystyle{ \boldsymbol{x}_{i:i+j} }[/math] represents the concatenation of words [math]\displaystyle{ \boldsymbol{x}_i, \boldsymbol{x}_{i+1}, \dots, \boldsymbol{x}_{i+j} }[/math] with concatenation operation [math]\displaystyle{ \oplus }[/math], [math]\displaystyle{ \boldsymbol{x}_{i:i+j} = \boldsymbol{x}_i \oplus \boldsymbol{x}_{i+1} \oplus \dots \oplus \boldsymbol{x}_{i+j} }[/math]. Then, a sentence of length [math]\displaystyle{ n }[/math] is a concatenation of [math]\displaystyle{ n }[/math] words, denoted as [math]\displaystyle{ \boldsymbol{x}_{1:n} }[/math], [math]\displaystyle{ \boldsymbol{x}_{1:n} = \boldsymbol{x}_1 \oplus \boldsymbol{x}_2 \oplus \dots \oplus \boldsymbol{x}_n }[/math]. Let [math]\displaystyle{ \boldsymbol{x}_i \in \mathbb{R}^k }[/math] denote the [math]\displaystyle{ i }[/math]-th word in the sentence, [math]\displaystyle{ i \in \{ 1, \dots, n \} }[/math].
A Convolutional Neural Network (CNN) is a nonlinear function [math]\displaystyle{ f: \mathbb{R}^{hk} \to \mathbb{R} }[/math] that computes a series of outputs [math]\displaystyle{ c_i }[/math] from windows of [math]\displaystyle{ h }[/math] words [math]\displaystyle{ \boldsymbol{x}_{i:i+h-1} }[/math] in the sentence. Hence, [math]\displaystyle{ c_i = f \left( \boldsymbol{w} \cdot \boldsymbol{x}_{i:i+h-1} + b \right) }[/math], where [math]\displaystyle{ \boldsymbol{w} \in \mathbb{R}^{hk} }[/math] is call a filter and [math]\displaystyle{ b \in \mathbb{R} }[/math] is a bias term, [math]\displaystyle{ i \in \{ 1, \dots, n-h+1 \} }[/math]. The outputs form a [math]\displaystyle{ (n-h+1) }[/math]-dimensional vector [math]\displaystyle{ \boldsymbol{c} = \left[ c_1, c_2, \dots, c_{n-h+1} \right] }[/math], called a feature map.
To capture the most important feature from a feature map, we take the maximum value [math]\displaystyle{ \hat{c} = max \{ \boldsymbol{c} \} }[/math]. Since each filter corresponds to one feature, we obtain several features from multiple filters the model uses which form a penultimate layer. The penultimate layer then gets passed into a fully connected softmax layer which produces the probability distribution over labels.
Below is a slight variant of CNN with two "channels" of word vectors: static vectors and fine-tuned vectors via backpropagaton. We calculate [math]\displaystyle{ c_i }[/math] by applying each filter to both channels and then adding them together. The rest of the model is equivalent to a single channel CNN architecture as described above.
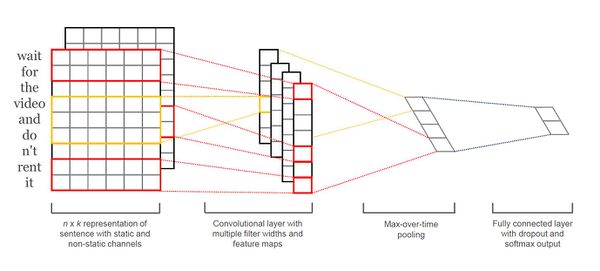
Model Regularization
To prevent co-adaptation and overfitting, we randomly drop out some hidden units on penultimate layer by setting them to zero during forward propagation and restrict the [math]\displaystyle{ l_2 }[/math]-norm of the weight vectors.
For example, consider a penultimate layer [math]\displaystyle{ \boldsymbol{p} }[/math] obtained from [math]\displaystyle{ m }[/math] filters, [math]\displaystyle{ \boldsymbol{p} = \left[ \hat{c}_1, \dots, \hat{c}_m \right] }[/math]. Let [math]\displaystyle{ \boldsymbol{u} \in \mathbb{R}^m }[/math] be a weight vector, [math]\displaystyle{ \boldsymbol{r} \in \mathbb{R}^m }[/math] be a "dropout" vector of Bernoulli random variables with a proportion of [math]\displaystyle{ p }[/math] being 1, and [math]\displaystyle{ \circ }[/math] be an element-wise multiplication operator. In forward propagation, instead of using [math]\displaystyle{ y = \boldsymbol{u} \cdot \boldsymbol{p} + b }[/math], we use [math]\displaystyle{ y = \boldsymbol{u} \cdot \left( \boldsymbol{p} \circ \boldsymbol{r} \right) + b }[/math] to obtain the output [math]\displaystyle{ y }[/math]. Gradients are only backpropagated through "remaining" units. Then at testing, we scale the learned weight vector by [math]\displaystyle{ p }[/math] such that [math]\displaystyle{ \hat{\boldsymbol{u}} = p\boldsymbol{u} }[/math]. We use [math]\displaystyle{ \hat{\boldsymbol{u}} }[/math] to score dropout sentences. Additionally, at each gradient descent step, we restrict [math]\displaystyle{ \| \boldsymbol{u} \|_2 = s }[/math] if [math]\displaystyle{ \| \boldsymbol{u} \|_2 \gt s }[/math].
Datasets and Experimental Setup

There are various benchmark for classification, for example:
MR:
Movie reviews with one sentence per review.
Class: positive/negative (Pang and Lee, 2005).
SST-1:
Standford Sentiment Treebank (An extension of MR) with train/dev*/test splits.
Classes: very positive, positive, neutral, negative, very negative.
dev set *: The set used for selecting the best performing model. (re-labeled by Socher er al. 2013)
SST-2:
Same as SST-1 but with neutral reviews removed and binary labels.
Class: positive/negative
Subj:
To classify a sentence as subjective or objective.
Class: subjective/objective (Pang and Lee, 2004)
TREC:
TREC question dataset, classifying a question into 6 question types
Class: question about person, location, numeric information. etc (Li and Roth, 2002).
CR:
Customer review towards various products (i.e. cameras, MP3 etc.).
Class: positive/negative reviews. (Hu and Liiu, 2004)
MPQA:
Opinion polarity detetion subtask of the MPQA dataset.
(Wiebe et al., 2005).
Hyperparameters and Training
If no dev set is specified, then randomly pick 10 percent of training set as the dev set.
Using grid search, we find out the best combination of hyperparameters. On dev set of SST-2 dev set, we set all the hyperparameters: rectified linear units, filter windows(h) of 3, 4, 5 with 100 feature maps each, dropout rate (p) of 0.5, l2 constraint (s) of 3, and mini-batch size of 50.
Training is done through stochastic gradient descent over mini-batches with the Adadelta update rule(Zeiler, 2012)
Pre-trained Word Vectors
It is a popular method to initialize word vector through an unsupervised neural language model, which improves perfomance in the absense of a large supervised training set (Collobert et al ., 2011; Socher et al., 2011; lyyer et al,. 2014).
We use 'word2vec' vectors that were trained on 100 billion words from Google News. The vectors have dimensionality of 300 and were trained using bag-of-words architecture*( Mikolov et al., 2013). For words not present in the set of pre-trained words, we initialized them randomly.
Model Variations
CNN-rand:
baseline model where all words are randomly initialized and then modified during training
CNN-static:
model with pre-trained vectors from 'word2vec'(publicly available).
All words are randomly initialized and are kept static and the other parameters of the model are learned
CNN-non-static:
same as above but the pre-trained vectors are fine-tuned for each task
CNN-multichannel:
A model with two sets of word vectors.
Each set is a 'channel' and each filter is applied on both channels. One channel is fine-tuned via back-propagation, and the other is static(unchanged).
Both channels are initialized from 'word2vec'.
We keep other sources of randomness uniform within each datasets(such as CV-fold assignment, initialization of unknown word vectors, initialization of CNN parameters) to eliminate the effect of the above variations versus other random factors.
Training and Results
Criticisms
The author has acknowledged that at the time of his original experiments he did not have access to a GPU and thus could not run many differing experiments. Therefore the paper is missing things like ablation studies, which refers to removing/adding some feature of the model/algorithm and seeing how that can affect performance of the CNN (e.g. dropout rate). When a model is assessed it would be vital for the author to replicate the k-fold cross validation procedure and include ranges and variances of the performance. The author only reported the mean of the CV results but this overlooks the randomness of the stochastic processes which were used. This paper did not report variances despite using stochastic gradient descent, random dropout and random weight parameter initialization, which are all highly stochastic learning procedures. For more on an exhaustive analysis of model variants on CNNs Ye Zhang did a sensitivity analysis of CNNs for sentence classification (https://arxiv.org/pdf/1510.03820.pdf).
More Formulations/New Concepts
Adadelta update rule:
continuous bag-of-words architecture:
unsupervised/supervised learning:
Conclusion
Yoon Kim described a series of experiments with CNNs using word2vec for differing types of sentence classifications. With minimal hyperparameter tuning and a simple CNN with 1 layer of convolution the models performed in some cases better than the other established benchmarks. The author was able to beat the provided benchmarks in 4/7 datasets effectively demonstrating the power of CNNs for sentence classification.