stat340s13: Difference between revisions
No edit summary |
m (in class3, I added "because it requires a closed form expression for F(x)", It helped us to understand the limitation of the inverse mothord and why it is difficult to find F(x)) |
||
| Line 1: | Line 1: | ||
== Introduction, Class 1 - Tuesday, May 7 | == Introduction, Class 1 - Tuesday, May 7 == | ||
| Line 62: | Line 62: | ||
(A simple practice might be investigating the hypothesis that higher levels of education cause higher levels of income.) <br /> | (A simple practice might be investigating the hypothesis that higher levels of education cause higher levels of income.) <br /> | ||
3. Clustering: Use common features of objects in same class or group to form clusters.(in this case, x is given, y is unknown) <br /> | 3. Clustering: Use common features of objects in same class or group to form clusters.(in this case, x is given, y is unknown) <br /> | ||
4. Dimensionality Reduction (aka Feature extraction, Manifold learning): Used when we have a variable in high dimension space and we want to reduce the dimension | 4. Dimensionality Reduction (aka Feature extraction, Manifold learning): Used when we have a variable in high dimension space and we want to reduce the dimension <br /> | ||
=== Applications === | === Applications === | ||
| Line 166: | Line 166: | ||
<br>A computer cannot generate truly random numbers because computers can only run algorithms, which are deterministic in nature. They can, however, generate Pseudo Random Numbers<br> | <br>A computer cannot generate truly random numbers because computers can only run algorithms, which are deterministic in nature. They can, however, generate Pseudo Random Numbers<br> | ||
'''Pseudo Random Numbers''' are the numbers that seem random but are actually deterministic. Although the pseudo random numbers are deterministic, these numbers have a sequence of value and all of them have the | '''Pseudo Random Numbers''' are the numbers that seem random but are actually deterministic. Although the pseudo random numbers are deterministic, these numbers have a sequence of value and all of them have the appearances of being independent uniform random variables. Being deterministic, pseudo random numbers are valuable and beneficial due to the ease to generate and manipulate. | ||
When people do the test many times, the results will be the closed express values, which make the trial look deterministic, however for each trial, the result is random. | When people do the test many times, the results will be the closed express values, which make the trial look deterministic, however for each trial, the result is random. | ||
| Line 335: | Line 335: | ||
''The number 31 will never appear. When you perform the operation <math>\mod m</math>, the largest possible answer that you could receive is <math>m-1</math>. Whether or not a particular number in the range from 0 to <math>m - 1</math> appears in the above algorithm will be dependent on the values chosen for <math>a, b</math> and <math>m</math>. '' | ''The number 31 will never appear. When you perform the operation <math>\mod m</math>, the largest possible answer that you could receive is <math>m-1</math>. Whether or not a particular number in the range from 0 to <math>m - 1</math> appears in the above algorithm will be dependent on the values chosen for <math>a, b</math> and <math>m</math>. '' | ||
<hr/> | <hr/> | ||
'''Examples:[From Textbook]'''<br /> | '''Examples:[From Textbook]'''<br /> | ||
| Line 451: | Line 440: | ||
In short, what the theorem tells us is that we can use a random number <math> U from U(0,1) </math> to randomly sample a point on the CDF of X, then apply the inverse of the CDF to map the given probability to its domain, which gives us the random variable X.<br/> | In short, what the theorem tells us is that we can use a random number <math> U from U(0,1) </math> to randomly sample a point on the CDF of X, then apply the inverse of the CDF to map the given probability to its domain, which gives us the random variable X.<br/> | ||
| Line 509: | Line 491: | ||
Step 2: Compute <math>X = F^-1(U)</math> i.e. <math>X = \theta + \frac {1}{\lambda} ln(2U)</math> for U < 0.5 else <math>X = \theta -\frac {1}{\lambda} ln(2(1-U))</math> | Step 2: Compute <math>X = F^-1(U)</math> i.e. <math>X = \theta + \frac {1}{\lambda} ln(2U)</math> for U < 0.5 else <math>X = \theta -\frac {1}{\lambda} ln(2(1-U))</math> | ||
'''Example 3 - <math>F(x) = x^5</math>''':<br/> | '''Example 3 - <math>F(x) = x^5</math>''':<br/> | ||
| Line 532: | Line 503: | ||
Step 1: Draw U ~ rand[0, 1];<br /> | Step 1: Draw U ~ rand[0, 1];<br /> | ||
Step 2: X=U^(1/5);<br /> | Step 2: X=U^(1/5);<br /> | ||
'''Example 4 - BETA(1,β)''':<br/> | '''Example 4 - BETA(1,β)''':<br/> | ||
| Line 549: | Line 514: | ||
<math>x = 1-(1-u)^\frac {1}{\beta}</math><br /> | <math>x = 1-(1-u)^\frac {1}{\beta}</math><br /> | ||
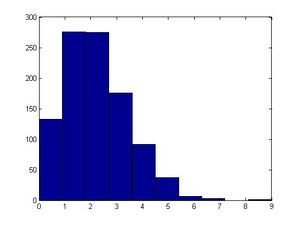
let β=3, use Matlab to construct N=1000 observations from Beta(1,3)<br /> | let β=3, use Matlab to construct N=1000 observations from Beta(1,3)<br /> | ||
Matlab Code:<br /> | |||
>> u = rand(1,1000);<br /> | |||
x = 1-(1-u)^(1/3);<br /> | |||
>> u = rand(1,1000); | >> hist(x,50)<br /> | ||
>> mean(x)<br /> | |||
>> hist(x,50) | |||
>> mean(x) | |||
</ | |||
'''Example 5 - Estimating <math>\pi</math>''':<br/> | '''Example 5 - Estimating <math>\pi</math>''':<br/> | ||
| Line 593: | Line 555: | ||
=== Recall the Inverse Transform Method === | === Recall the Inverse Transform Method === | ||
To sample X with CDF F(x), <br /> | |||
'''1. Draw u~U(0,1) '''<br /> | '''1. Draw u~U(0,1) '''<br /> | ||
| Line 611: | Line 573: | ||
This is the c.d.f. of X. <br /> | This is the c.d.f. of X. <br /> | ||
<br /> | <br /> | ||
'''Note''': that the CDF of a U(a,b) random variable is: | '''Note''': that the CDF of a U(a,b) random variable is: | ||
| Line 622: | Line 582: | ||
\end{cases} | \end{cases} | ||
</math> | </math> | ||
Thus, for <math> U </math> ~ <math>U(0,1) </math>, we have <math>P(U\leq 1) = 1</math> and <math>P(U\leq 1/2) = 1/2</math>.<br /> | Thus, for <math> U </math> ~ <math>U(0,1) </math>, we have <math>P(U\leq 1) = 1</math> and <math>P(U\leq 1/2) = 1/2</math>.<br /> | ||
| Line 639: | Line 597: | ||
Note that on a single point there is no mass probability (i.e. <math>u</math> <= 0.5, is the same as <math> u </math> < 0.5) | Note that on a single point there is no mass probability (i.e. <math>u</math> <= 0.5, is the same as <math> u </math> < 0.5) | ||
More formally, this is saying that <math> P(X = x) = F(x)- \lim_{s \to x^-}F(x)</math> which equals zero for any continuous random variable | More formally, this is saying that <math> P(X = x) = F(x)- \lim_{s \to x^-}F(x)</math> which equals zero for any continuous random variable | ||
====Limitations of the Inverse Transform Method==== | ====Limitations of the Inverse Transform Method==== | ||
Though this method is very easy to use and apply, it does have | Though this method is very easy to use and apply, it does have a major disadvantage/limitation: | ||
* We need to find the inverse cdf <math> F^{-1}(\cdot) </math>. In some cases the inverse function does not exist, or is difficult to find because it requires a closed form expression for F(x). | |||
* We need to find the inverse cdf <math> F^{-1}(\cdot) </math>. In some cases the inverse function does not exist, or is difficult to find. | |||
For example, it is too difficult to find the inverse cdf of the Gaussian distribution, so we must find another method to sample from the Gaussian distribution. | For example, it is too difficult to find the inverse cdf of the Gaussian distribution, so we must find another method to sample from the Gaussian distribution. | ||
=== Discrete Case === | |||
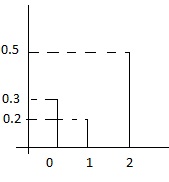
The same technique can be used for discrete case. We want to generate a discrete random variable x, that has probability mass function: <br/> | The same technique can be used for discrete case. We want to generate a discrete random variable x, that has probability mass function: <br/> | ||
| Line 697: | Line 649: | ||
else if U < 0.8 then output 2<br /> | else if U < 0.8 then output 2<br /> | ||
else if U < 0.9 then output -2<br /> | else if U < 0.9 then output -2<br /> | ||
else if U < 0.97 then output 0 | else if U < 0.97 then output 0 else output 1<br /> | ||
else output 1<br / | |||
'''Example 3.1 (from class):''' (Coin Flipping Example)<br /> | '''Example 3.1 (from class):''' (Coin Flipping Example)<br /> | ||
| Line 791: | Line 726: | ||
3. else if 0.3<U<=0.5 deliver x=1<br /> | 3. else if 0.3<U<=0.5 deliver x=1<br /> | ||
4. else 0.5<U<=1 deliver x=2 | 4. else 0.5<U<=1 deliver x=2 | ||
Can you find a faster way to run this algorithm? Consider: | |||
:<math> | |||
x = \begin{cases} | |||
2, & \text{if } U\leq 0.5 \\ | |||
1, & \text{if } 0.5 < U \leq 0.7 \\ | |||
0, & \text{if } 0.7 <U\leq 1 | |||
\end{cases}</math> | |||
The logic for this is that U is most likely to fall into the largest range. Thus by putting the largest range (in this case x >= 0.5) we can improve the run time of this algorithm. Could this algorithm be improved further using the same logic? | |||
* '''Code''' (as shown in class)<br /> | * '''Code''' (as shown in class)<br /> | ||
| Line 812: | Line 758: | ||
[[File:Discrete_example.jpg|300px]] | [[File:Discrete_example.jpg|300px]] | ||
'''Example 3.3''': Generating a random variable from pdf <br> | |||
:<math> | |||
f_{x}(x) = \begin{cases} | |||
2x, & \text{if } 0\leq x \leq 1 \\ | |||
0, & \text{if } otherwise | |||
\end{cases}</math> | |||
:<math> | :<math> | ||
F_{x}(x) = \begin{cases} | |||
F_{x}(x) = \begin{cases} | |||
0, & \text{if } x < 0 \\ | 0, & \text{if } x < 0 \\ | ||
\int_{0}^{x}2sds = x^{2}, & \text{if } 0\leq x \leq 1 \\ | \int_{0}^{x}2sds = x^{2}, & \text{if } 0\leq x \leq 1 \\ | ||
| Line 857: | Line 773: | ||
:<math>\begin{align} U = x^{2}, X = F^{-1}x(U)= U^{\frac{1}{2}}\end{align}</math> | :<math>\begin{align} U = x^{2}, X = F^{-1}x(U)= U^{\frac{1}{2}}\end{align}</math> | ||
'''Example 3.4''': Generating a Bernoulli random variable <br> | '''Example 3.4''': Generating a Bernoulli random variable <br> | ||
| Line 880: | Line 788: | ||
\end{cases}</math> | \end{cases}</math> | ||
'''Example 3.5''': Generating Binomial(n,p) Random Variable<br> | '''Example 3.5''': Generating Binomial(n,p) Random Variable<br> | ||
| Line 901: | Line 799: | ||
*Note: These steps can be found in Simulation 5th Ed. by Sheldon Ross. | *Note: These steps can be found in Simulation 5th Ed. by Sheldon Ross. | ||
*Note: Another method by seeing the Binomial as a sum of n independent Bernoulli random variables.<br> | *Note: Another method by seeing the Binomial as a sum of n independent Bernoulli random variables.<br> | ||
Step 1: Generate n uniform numbers U1 ... Un.<br> | Step 1: Generate n uniform numbers U1 ... Un.<br> | ||
Step 2: X = <math>\sum U_i < = p</math> where P is the probability of success. | Step 2: X = <math>\sum U_i < = p</math> where P is the probability of success. | ||
| Line 958: | Line 854: | ||
... | ... | ||
Else if <math>U \leq P_{0} + ... + P_{k} </math> deliver <math>x = x_{k}</math><br /> | Else if <math>U \leq P_{0} + ... + P_{k} </math> deliver <math>x = x_{k}</math><br /> | ||
<br /'''>===Inverse Transform Algorithm for Generating a Binomial(n,p) Random Variable(from textbook)===''' | <br /'''>===Inverse Transform Algorithm for Generating a Binomial(n,p) Random Variable(from textbook)===''' | ||
| Line 1,014: | Line 908: | ||
</pre> | </pre> | ||
</div> | </div> | ||
===Acceptance-Rejection Method=== | ===Acceptance-Rejection Method=== | ||
Although the inverse transformation method does allow us to change our uniform distribution, it has two limits; | Although the inverse transformation method does allow us to change our uniform distribution, it has two limits; | ||
| Line 1,060: | Line 920: | ||
[[File:AR_Method.png]] | [[File:AR_Method.png]] | ||
{{Cleanup|reason= Do not write <math>c*g(x)</math>. Instead write <math>c \times g(x)</math> or <math>\,c g(x)</math> | |||
}} | |||
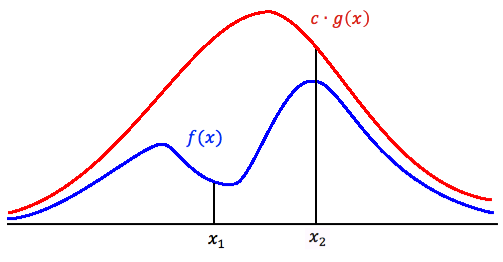
The main logic behind the Acceptance-Rejection Method is that:<br> | The main logic behind the Acceptance-Rejection Method is that:<br> | ||
| Line 1,108: | Line 972: | ||
At X<sub>2</sub>, high probability to accept the point. <math>P(U\leq a)=a</math> in Uniform Distribution. | At X<sub>2</sub>, high probability to accept the point. <math>P(U\leq a)=a</math> in Uniform Distribution. | ||
Note: | Note: Since U is the variable for uniform distribution between 0 and 1. It equals to 1 for all. The condition depends on the constant c. so the condition changes to <math>c\leq \frac{f(y)}{g(y)}</math> | ||
introduce the relationship of cg(x)and f(x),and prove why they have that relationship and where we can use this rule to reject some cases. | |||
and learn how to see the graph to find the accurate point to reject or accept the ragion above the random variable x. | and learn how to see the graph to find the accurate point to reject or accept the ragion above the random variable x. | ||
for the example, x1 is bad point and x2 is good point to estimate the rejection and acceptance | for the example, x1 is bad point and x2 is good point to estimate the rejection and acceptance | ||
'''Some notes on the constant C'''<br> | '''Some notes on the constant C'''<br> | ||
| Line 1,139: | Line 999: | ||
<math>P(y|accepted)=f(y)=\frac{P(accepted|y)P(y)}{P(accepted)}</math><br /> | <math>P(y|accepted)=f(y)=\frac{P(accepted|y)P(y)}{P(accepted)}</math><br /> | ||
<br />based on the concept from '''procedure-step1''':<br /> | <br />based on the concept from '''procedure-step1''':<br /> | ||
<math>P(y)=g(y)</math><br /> | <math>P(y)=g(y)</math><br /> | ||
<math>P(accepted|y)=\frac{f(y)}{cg(y)}</math> <br /> | <math>P(accepted|y)=\frac{f(y)}{cg(y)}</math> <br /> | ||
| Line 1,152: | Line 1,012: | ||
&=\frac{1}{c} | &=\frac{1}{c} | ||
\end{align}</math><br /> | \end{align}</math><br /> | ||
Therefore:<br /> | Therefore:<br /> | ||
| Line 1,160: | Line 1,019: | ||
&=\frac{\frac{f(y)}{c}}{1/c}\\ | &=\frac{\frac{f(y)}{c}}{1/c}\\ | ||
&=f(y)\end{align}</math><br /><br /><br /> | &=f(y)\end{align}</math><br /><br /><br /> | ||
'''''Here is an alternative introduction of Acceptance-Rejection Method''''' | '''''Here is an alternative introduction of Acceptance-Rejection Method''''' | ||
| Line 1,265: | Line 1,123: | ||
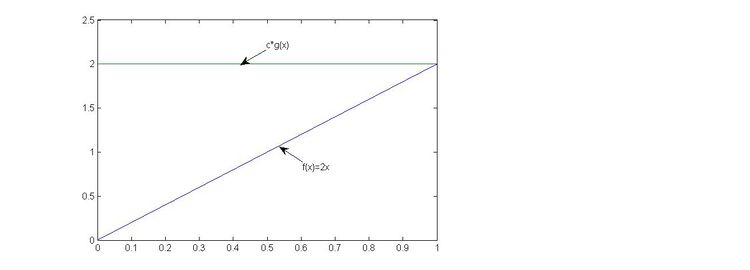
*The relationship between the proposal distribution and target distribution is: <math> c \cdot g(x) \geq f(x) </math>, where c is a constant. This means that the area of f(x) is under the area of <math> c \cdot g(x)</math>. <br> | *The relationship between the proposal distribution and target distribution is: <math> c \cdot g(x) \geq f(x) </math>, where c is a constant. This means that the area of f(x) is under the area of <math> c \cdot g(x)</math>. <br> | ||
*Chance of acceptance is less if the distance between <math>f(x)</math> and <math> c \cdot g(x)</math> is big, and vice-versa, we use <math> c </math> to keep <math> \frac {f(x)}{c \cdot g(x)} </math> below 1 (so <math>f(x) \leq c \cdot g(x)</math>). Therefore, we must find the constant <math> C </math> to achieve this.<br /> | *Chance of acceptance is less if the distance between <math>f(x)</math> and <math> c \cdot g(x)</math> is big, and vice-versa, we use <math> c </math> to keep <math> \frac {f(x)}{c \cdot g(x)} </math> below 1 (so <math>f(x) \leq c \cdot g(x)</math>). Therefore, we must find the constant <math> C </math> to achieve this.<br /> | ||
*In other words, a <math>C</math> is chosen to make sure <math> c \cdot g(x) \geq f(x) </math>. However, it will not make sense if <math>C</math> is simply chosen to be arbitrarily large | *In other words, a <math>C</math> is chosen to make sure <math> c \cdot g(x) \geq f(x) </math>. However, it will not make sense if <math>C</math> is simply chosen to be arbitrarily large. We need to choose <math>C</math> such that <math>c \cdot g(x)</math> fits <math>f(x)</math> as tightly as possible.<br /> | ||
*The constant c cannot be a negative number.<br /> | *The constant c cannot be a negative number.<br /> | ||
'''How to find C''':<br /> | '''How to find C''':<br /> | ||
| Line 1,393: | Line 1,250: | ||
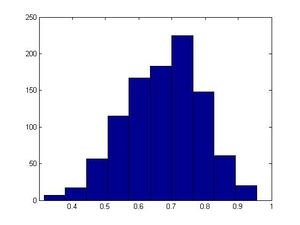
<pre style="font-size:16px"> | <pre style="font-size:16px"> | ||
>>u=rand(1,1000); | >>u=rand(1,1000); | ||
>>x=u.^0.5; | >>x=u.^0.5; | ||
>>hist(x) | >>hist(x) | ||
</pre> | </pre> | ||
| Line 1,399: | Line 1,256: | ||
<span style="font-weight:bold;colour:green;">Matlab Tip:</span> | <span style="font-weight:bold;colour:green;">Matlab Tip:</span> | ||
Periods, ".",meaning "element-wise", are used to describe the operation you want performed on each element of a vector. In the above example, to take the square root of every element in U, the notation U.^0.5 is used | Periods, ".",meaning "element-wise", are used to describe the operation you want performed on each element of a vector. In the above example, to take the square root of every element in U, the notation U.^0.5 is used. However if you want to take the Square root of the entire matrix U the period, "*.*" would be excluded. i.e. Let matrix B=U^0.5, then <math>B^T*B=U</math>. For example if we have a two 1 X 3 matrices and we want to find out their product; using "." in the code will give us their product. However, if we don't use ".", it will just give us an error. For example, a =[1 2 3] b=[2 3 4] are vectors, a.*b=[2 6 12], but a*b does not work since matrix dimensions must agree. | ||
''' | ''' | ||
| Line 1,423: | Line 1,280: | ||
:4: if <math>U2 \leq \frac { \frac{3}{4} * (1-y^2)} { \frac{3}{4}} = {1-y^2}</math>, then x=y, '''note that''' (3/4(1-y^2)/(3/4) is getting from f(y) / (cg(y)) ) | :4: if <math>U2 \leq \frac { \frac{3}{4} * (1-y^2)} { \frac{3}{4}} = {1-y^2}</math>, then x=y, '''note that''' (3/4(1-y^2)/(3/4) is getting from f(y) / (cg(y)) ) | ||
:5: else: return to '''step 1''' | :5: else: return to '''step 1''' | ||
---- | ---- | ||
=====Example of Acceptance-Rejection Method===== | =====Example of Acceptance-Rejection Method===== | ||
| Line 1,481: | Line 1,308: | ||
To obtain a better proposing function g(x), we can first assume a new q(x) and then solve for the normalizing constant by integrating.<br> | To obtain a better proposing function g(x), we can first assume a new q(x) and then solve for the normalizing constant by integrating.<br> | ||
In the previous example, we first assume q(x) = 3x. To find the normalizing constant, we need to solve k * <math>\sum 3x = 1</math> which gives us k = 2/3. So, g(x) = k*q(x) = 2x. | In the previous example, we first assume q(x) = 3x. To find the normalizing constant, we need to solve k * <math>\sum 3x = 1</math> which gives us k = 2/3. So, g(x) = k*q(x) = 2x. | ||
'''Possible Limitations''' | '''Possible Limitations''' | ||
| Line 1,525: | Line 1,342: | ||
3. Now Y follows <math>U(a,b)</math> | 3. Now Y follows <math>U(a,b)</math> | ||
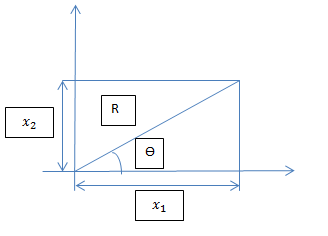
'''Example''': Generate a random variable z from the Semicircular density <math>f(x)= \frac{2}{\pi R^2} \sqrt{R^2-x^2}, -R\leq x\leq R</math>. | '''Example''': Generate a random variable z from the Semicircular density <math>f(x)= \frac{2}{\pi R^2} \sqrt{R^2-x^2}, -R\leq x\leq R</math>. | ||
-> Proposal distribution: | -> Proposal distribution: UNIF(-R, R) | ||
-> We | -> We know how to generate using <math> U \sim UNIF (0,1) </math> Let <math> Y= 2RU-R=R(2U-1)</math>, therefore Y follows <math>U(-R,R)</math> | ||
-> In order to maximize the function we must maximize the top and minimize the bottom. | -> In order to maximize the function we must maximize the top and minimize the bottom. | ||
| Line 1,657: | Line 1,473: | ||
[[File:ARM_cont_example.jpg|300px]] | [[File:ARM_cont_example.jpg|300px]] | ||
a histogram to show variable x, and the bars number is y. | |||
=== Discrete Examples === | === Discrete Examples === | ||
* '''Example 1''' <br> | * '''Example 1''' <br> | ||
| Line 1,676: | Line 1,492: | ||
Step 2. Draw <math>U \sim~ U(0,1)</math>.<br/> | Step 2. Draw <math>U \sim~ U(0,1)</math>.<br/> | ||
Step 3. If <math>U \leq \frac{f(Y)}{c \cdot g(Y)}</math>, then <b> X = Y </b>;<br/> | Step 3. If <math>U \leq \frac{f(Y)}{c \cdot g(Y)}</math>, then <b> X = Y </b>;<br/> | ||
Else return to Step 1.<br/> | |||
C can be found by maximizing the ratio :<math> \frac{f(x)}{g(x)} </math>. To do this, we want to maximize <math> f(x) </math> and minimize <math> g(x) </math>. <br> | C can be found by maximizing the ratio :<math> \frac{f(x)}{g(x)} </math>. To do this, we want to maximize <math> f(x) </math> and minimize <math> g(x) </math>. <br> | ||
| Line 1,683: | Line 1,499: | ||
:<math>\frac{p(x)}{cg(x)} = \frac{p(x)}{1.5*0.2} = \frac{p(x)}{0.3} </math><br> | :<math>\frac{p(x)}{cg(x)} = \frac{p(x)}{1.5*0.2} = \frac{p(x)}{0.3} </math><br> | ||
Note: The U is independent from y in Step 2 and 3 above. | Note: The U is independent from y in Step 2 and 3 above. | ||
The constant c is | ~The constant c is a indicator of rejection rate or efficiency of the algorithm. | ||
the acceptance-rejection method of pmf, the uniform probability is the same for all variables, and there 5 parameters(1,2,3,4,5), so g(x) is 0.2 | |||
Remember that we always want to choose <math> | Remember that we always want to choose <math> cg </math> to be equal to or greater than <math> f </math>, but as close as possible. | ||
<br />limitations: If the form of the proposal | <br />limitations: If the form of the proposal dist g is very different from target dist f, then c is very large and the algorithm is not computatively effect. | ||
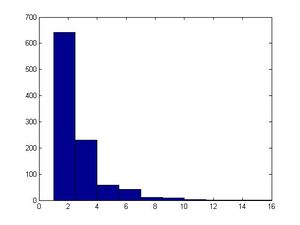
* '''Code for example 1'''<br /> | * '''Code for example 1'''<br /> | ||
| Line 1,712: | Line 1,528: | ||
The acceptance rate is <math>\frac {1}{c}</math>, so the lower the c, the more efficient the algorithm. Theoretically, c equals 1 is the best case because all samples would be accepted; however it would only be true when the proposal and target distributions are exactly the same, which would never happen in practice. | The acceptance rate is <math>\frac {1}{c}</math>, so the lower the c, the more efficient the algorithm. Theoretically, c equals 1 is the best case because all samples would be accepted; however it would only be true when the proposal and target distributions are exactly the same, which would never happen in practice. | ||
For example, if c = 1.5, the acceptance rate would be <math>\frac {1}{1.5}=\frac {2}{3}</math> | For example, if c = 1.5, the acceptance rate would be <math>\frac {1}{1.5}=\frac {2}{3}</math>. Thus, in order to generate 1000 random values, on average, a total of 1500 iterations would be required. | ||
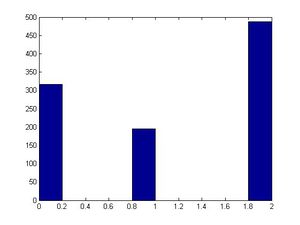
A histogram to show 1000 random values of f(x), more random value make the probability close to the express probability value. | A histogram to show 1000 random values of f(x), more random value make the probability close to the express probability value. | ||
| Line 1,745: | Line 1,561: | ||
</pre> | </pre> | ||
* '''Example 3'''<br> | * '''Example 3'''<br> | ||
| Line 1,759: | Line 1,574: | ||
2. <math>j = \lfloor \frac{ln(U_{1})}{ln(.75)} \rfloor+1;</math><br> | 2. <math>j = \lfloor \frac{ln(U_{1})}{ln(.75)} \rfloor+1;</math><br> | ||
3. if <math>U_{2} < \frac{p_{j}}{cg(j)}</math>, set X = x<sub>j</sub>, else go to step 1. | 3. if <math>U_{2} < \frac{p_{j}}{cg(j)}</math>, set X = x<sub>j</sub>, else go to step 1. | ||
Note: In this case, f(x)/g(x) is extremely difficult to differentiate so we were required to test points. If the function is easily differentiable, we can calculate the max as if it were a continuous function then check the two surrounding points for which is the highest discrete value. | Note: In this case, f(x)/g(x) is extremely difficult to differentiate so we were required to test points. If the function is easily differentiable, we can calculate the max as if it were a continuous function then check the two surrounding points for which is the highest discrete value. | ||
| Line 1,804: | Line 1,600: | ||
Looking for the max f(x) is 0.4945 and the max g(x) is 0.4444, so we can calculate the max c is 1.1127. | Looking for the max f(x) is 0.4945 and the max g(x) is 0.4444, so we can calculate the max c is 1.1127. | ||
But for the graph, this c is not the best because it does not cover all the point of f(x), | But for the graph, this c is not the best because it does not cover all the point of f(x), so we need to move the c*g(x) graph to cover all f(x), and decreasing the rejection ratio. | ||
Limitation: If the shape of the proposed distribution g is very different from the target distribution f, then the rejection rate will be high (High c value). Computationally, the algorithm is always right; however it is inefficient and requires many iterations. <br> | Limitation: If the shape of the proposed distribution g is very different from the target distribution f, then the rejection rate will be high (High c value). Computationally, the algorithm is always right; however it is inefficient and requires many iterations. <br> | ||
| Line 1,940: | Line 1,736: | ||
=== Other Sampling Method: Box Muller === | === Other Sampling Method: Box Muller === | ||
[[File:Unnamed_QQ_Screenshot20130521203625.png]] | [[File:Unnamed_QQ_Screenshot20130521203625.png]] | ||
* From cartesian to polar coordinates <br /> | * From cartesian to polar coordinates <br /> | ||
| Line 1,947: | Line 1,742: | ||
*Box-Muller Transformation:<br> | *Box-Muller Transformation:<br> | ||
It is a transformation that consumes two continuous uniform random variables <math> X \sim U(0,1), Y \sim U(0,1) </math> and outputs a bivariate normal random variable with <math> Z_1\sim N(0,1), Z_2\sim N(0,1). </math> | It is a transformation that consumes two continuous uniform random variables <math> X \sim U(0,1), Y \sim U(0,1) </math> and outputs a bivariate normal random variable with <math> Z_1\sim N(0,1), Z_2\sim N(0,1). </math> | ||
=== '''Matlab''' === | === '''Matlab''' === | ||
| Line 2,088: | Line 1,864: | ||
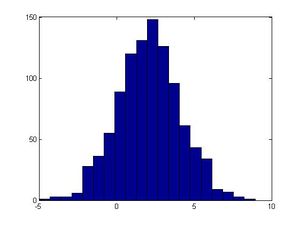
Alternative Method of Generating Standard Normal Random Variables | Alternative Method of Generating Standard Normal Random Variables | ||
Step 1: Generate <math> | Step 1: Generate <math>u1~Unif(0,1)</math> | ||
Step 2: Generate <math> | Step 2: Generate <math>Y1~Exp(1),Y2~Exp(2)</math> | ||
Step 3: If <math>Y2 \geq( | Step 3: If <math>Y2 \geq(Y1-1)^2/2</math>,set <math>V=Y1</math>,otherwise,go to step 1 | ||
Step 4: If <math>u1 \leq 1/2</math>,then <math>X=-V</math> | Step 4: If <math>u1 \leq 1/2</math>,then <math>X=-V</math> | ||
| Line 2,248: | Line 2,024: | ||
where <math> \mu </math> is the mean or expectation of the distribution and <math> \sigma </math> is standard deviation <br /> | where <math> \mu </math> is the mean or expectation of the distribution and <math> \sigma </math> is standard deviation <br /> | ||
The special case of the normal distribution is standard normal distribution, which the variance is 1 and the mean is zero. If X is a general normal deviate, Z = (X − μ)/σ will have a standard normal distribution. | The special case of the normal distribution is standard normal distribution, which the variance is 1 and the mean is zero. If X is a general normal deviate, then Z = (X − μ)/σ will have a standard normal distribution. | ||
If Z ~ N(0,1), and we want <math>X </math>~<math> N(\mu, \sigma^2)</math>, then <math>X = \mu + \sigma * Z</math> Since <math>E(x) = \mu +\sigma*0 = \mu </math> and <math>Var(x) = 0 +\sigma^2*1</math> | If Z ~ N(0,1), and we want <math>X </math>~<math> N(\mu, \sigma^2)</math>, then <math>X = \mu + \sigma * Z</math> Since <math>E(x) = \mu +\sigma*0 = \mu </math> and <math>Var(x) = 0 +\sigma^2*1</math> | ||
| Line 2,259: | Line 2,035: | ||
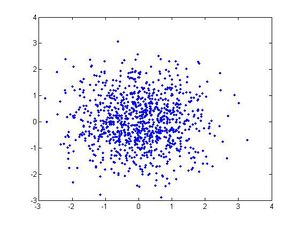
>>clear all | >>clear all | ||
>>z1=randn(1,1000); <-generate variable from standard normal distribution | >>z1=randn(1,1000); <-generate variable from standard normal distribution | ||
>>z2=randn(1,1000); | >>z2=randn(1,1000); | ||
>>z=[z1;z2]; <-produce a vector | >>z=[z1;z2]; <-produce a vector | ||
>>plot(z(1,:),z(2,:),'.') | >>plot(z(1,:),z(2,:),'.') | ||
| Line 2,474: | Line 2,250: | ||
===Universality of the Uniform Distribution/Inverse Method=== | ===Universality of the Uniform Distribution/Inverse Method=== | ||
The inverse method is universal in the sense that we can potentially sample from any distribution where we can find the inverse of the cumulative distribution function | The inverse method is universal in the sense that we can potentially sample from any distribution where we can find the inverse of the cumulative distribution function. | ||
Procedure: | Procedure: | ||
| Line 2,484: | Line 2,260: | ||
'''Remark'''<br> | '''Remark'''<br> | ||
1. The preceding can be written algorithmically as | 1. The preceding can be written algorithmically as | ||
Generate a random number U | Generate a random number U | ||
If U< | If U<<sub>p0</sub> set X=<sub>x0</sub> and stop | ||
If U< | If U<<sub>p0</sub>+<sub>p1</sub> set X=x1 and stop | ||
... | |||
2. If the <sub>xi</sub>, i>=0, are ordered so that <sub>x0</sub><<sub>x1</sub><<sub>x2</sub><... and if we let F denote the distribution function of X, then <math>F(<sub>xk</sub>=<sub>/sum/pi</sub>)</math> and so X will equal <sub>xj</sub> if F(<sub>x(j-1)</sub>)<=U<F(<sub>xj</sub>) | |||
2. If the | |||
'''Example 1'''<br> | '''Example 1'''<br> | ||
| Line 2,568: | Line 2,342: | ||
Similarly if <math> Y = min(X_1,\ldots,X_n)</math> then the cdf of <math>Y</math> is <math>F_Y = 1- </math><math>\prod</math><math>(1- F_{X_i})</math><br> | Similarly if <math> Y = min(X_1,\ldots,X_n)</math> then the cdf of <math>Y</math> is <math>F_Y = 1- </math><math>\prod</math><math>(1- F_{X_i})</math><br> | ||
<br> | <br> | ||
'''Method 1:''' Following the above result we can see that in this example, F<sub>X</sub> = x<sup>n</sup> is the cumulative distribution function of the max of n uniform random variables between 0 and 1 (since for U~Unif(0, 1), F<sub>U</sub>(x) = | '''Method 1:''' Following the above result we can see that in this example, F<sub>X</sub> = x<sup>n</sup> is the cumulative distribution function of the max of n uniform random variables between 0 and 1 (since for U~Unif(0, 1), F<sub>U</sub>(x) = <br> | ||
'''Method 2:''' generate X by having a sample of n independent U~Unif(0, 1) and take the max of the n samples to be x. However, the solution given above using inverse-transform method only requires generating one uniform random number instead of n of them, so it is a more efficient method. | '''Method 2:''' generate X by having a sample of n independent U~Unif(0, 1) and take the max of the n samples to be x. However, the solution given above using inverse-transform method only requires generating one uniform random number instead of n of them, so it is a more efficient method. | ||
<br> | <br> | ||
| Line 2,688: | Line 2,462: | ||
if 0<u<1/3, x = v | if 0<u<1/3, x = v | ||
else if | else if u<2/3, x = v<sup>1/2</sup> | ||
else | else x = v<sup>1/3</sup><br> | ||
'''Matlab Code:''' | '''Matlab Code:''' | ||
<pre style="font-size:16px"> | <pre style="font-size:16px"> | ||
u=rand | u=rand | ||
v=rand | v=rand | ||
if | if u<1/3 | ||
x=v | x=v | ||
elseif | elseif u<2/3 | ||
x=sqrt(v) | x=sqrt(v) | ||
else | else | ||
| Line 2,755: | Line 2,529: | ||
For More Details, please refer to http://www.stanford.edu/class/ee364b/notes/decomposition_notes.pdf | For More Details, please refer to http://www.stanford.edu/class/ee364b/notes/decomposition_notes.pdf | ||
===Fundamental Theorem of Simulation=== | ===Fundamental Theorem of Simulation=== | ||
| Line 2,762: | Line 2,537: | ||
(Basis of the Accept-Reject algorithm) | (Basis of the Accept-Reject algorithm) | ||
The advantage of this method is that we can sample a unknown distribution from a easy distribution. The disadvantage of this method is that it may need to reject many points, which is inefficient. | |||
inverse each part of partial CDF, the partial CDF is divided by the original CDF, partial range is uniform distribution. | |||
===Question 2=== | ===Question 2=== | ||
| Line 2,809: | Line 2,578: | ||
==Class 8 - Thursday, May 30, 2013== | ==Class 8 - Thursday, May 30, 2013== | ||
In this lecture, we will discuss algorithms to generate 3 well-known distributions: Binomial, Geometric | In this lecture, we will discuss algorithms to generate 3 well-known distributions: Binomial, Geometric and Poisson. For each of these distributions, we will first state its general understanding, probability mass function, expectation and variance. Then, we will derive one or more algorithms to sample from each of these distributions, and implement the algorithms on Matlab. <br \> | ||
===The Bernoulli distribution=== | ===The Bernoulli distribution=== | ||
The Bernoulli distribution is a special case of the binomial distribution, where n = 1. X ~ Bin(1, p) has the same meaning as X ~ Ber(p), where p is the probability if the event success, otherwise the probability is 1-p (we usually define a variate q, q= 1-p). Bin(n, p), is the distribution of the sum of n independent Bernoulli trials | The Bernoulli distribution is a special case of the binomial distribution, where n = 1. X ~ Bin(1, p) has the same meaning as X ~ Ber(p), where p is the probability if the event success, otherwise the probability is 1-p (we usually define a variate q, q= 1-p). The mean of Bernoulli is p, variance is p(1-p). Bin(n, p), is the distribution of the sum of n independent Bernoulli trials, Bernoulli(p), each with the same probability p, where 0<p<1. <br> | ||
For example, let X be the event that a coin toss results in a "head" with probability ''p'', then ''X~Bernoulli(p)''. <br> | For example, let X be the event that a coin toss results in a "head" with probability ''p'', then ''X~Bernoulli(p)''. <br> | ||
P(X=1)=p,P(X=0)=1-p, P(x=0)+P(x=1)=p+q=1 | P(X=1)=p,P(X=0)=1-p, P(x=0)+P(x=1)=p+q=1 | ||
| Line 2,845: | Line 2,595: | ||
when U>p, x=0<br> | when U>p, x=0<br> | ||
3.Repeat as necessary | 3.Repeat as necessary | ||
===The Binomial Distribution=== | ===The Binomial Distribution=== | ||
If X~Bin(n,p), then its pmf is of form: | |||
f(x)=(nCx) p<sup>x</sup>(1-p)<sup>(n-x)</sup>, x=0,1,...n<br /> | |||
Or f(x) = <math>(n!/x!(n-x)!)</math> p<sup>x</sup>(1-p)<sup>(n-x)</sup>, x=0,1,...n <br /> | |||
Mean (x) = E(x) = <math> np </math> | |||
Variance = <math> np(1-p) </math><br/> | |||
Generate n uniform random number <math>U_1,...,U_n</math> and let X be the number of <math>U_i</math> that are less than or equal to p. | Generate n uniform random number <math>U_1,...,U_n</math> and let X be the number of <math>U_i</math> that are less than or equal to p. | ||
The logic behind this algorithm is that the Binomial Distribution is simply a | The logic behind this algorithm is that the Binomial Distribution is simply a Bernoulli Trial, with a probability of success of p, repeated n times. Thus, we can sample from the distribution by sampling from n Bernoulli. The sum of these n bernoulli trials will represent one binomial sampling. Thus, in the below example, we are sampling 1000 realizations from 20 Bernoulli random variables. By summing up the rows of the 20 by 1000 matrix that is produced, we are summing up the 20 bernoulli outcomes to produce one binomial sampling. We have 1000 rows, which means we have realizations from 1000 binomial random variables when this sum is done (the output of the sum is a 1 by 1000 sized vector).<br /> | ||
To continue with the previous example, let X be the number of heads in a series of ''n'' independent coin tosses - where for each toss, the probability of coming up with a head is ''p'' - then ''X~Bin(n, p)''. <br /> | To continue with the previous example, let X be the number of heads in a series of ''n'' independent coin tosses - where for each toss, the probability of coming up with a head is ''p'' - then ''X~Bin(n, p)''. <br /> | ||
MATLAB tips: to get a pdf f(x), we can use code binornd(N,P). N means number of trials and p is the probability of success. a=[2 3 4],if set a<3, will produce a=[1 0 0]. If you set "a == 3", it will produce [0 1 0]. If a=[2 6 9 10], if set a<4, will produce a=[1 0 0 0], because only the first element (2) is less than 4, meanwhile the rest are greater. So we can use this to get the number which is less than p.<br /> | |||
MATLAB tips: to get | |||
Algorithm for Bernoulli is given as above | Algorithm for Bernoulli is given as above | ||
| Line 2,903: | Line 2,619: | ||
ans= 1 0 0 | ans= 1 0 0 | ||
>>rand(20,1000) | >>rand(20,1000) | ||
>>rand(20,1000)<0.4 | >>rand(20,1000)<0.4 | ||
>>A = sum(rand(20,1000)<0.4) #sum of raws ~ Bin(20 , 0.3) | >>A = sum(rand(20,1000)<0.4) #sum of raws ~ Bin(20 , 0.3) | ||
| Line 2,918: | Line 2,634: | ||
remark: a=[2 3 4],if set a<3, will produce a=[1 0 0]. If you set "a == 3", it will produce [0 1 0]. | remark: a=[2 3 4],if set a<3, will produce a=[1 0 0]. If you set "a == 3", it will produce [0 1 0]. | ||
using code to find some value what i want to get from the matrix. It`s useful to define some matrixs. | |||
Relation between Bernoulli Distribution and Binomial Distribution: | Relation between Bernoulli Distribution and Binomial Distribution: | ||
| Line 2,923: | Line 2,640: | ||
===The Geometric Distribution=== | ===The Geometric Distribution=== | ||
Geometric distribution is a discrete distribution. There are two types | Geometric distribution is a discrete distribution. There are two types geometric distributions, the first one is the probability distribution of the number of X Bernoulli fail trials, with probability 1-p, needed until the first success situation happened, X come from the set { 1, 2, 3, ...}; the other one is the probability distribution of the number Y = X − 1 of failures, with probability 1-p, before the first success, Y comes from the set { 0, 1, 2, 3, ... }. | ||
For example,<br /> | For example,<br /> | ||
| Line 2,940: | Line 2,655: | ||
. .<br /> | . .<br /> | ||
. .<br /> | . .<br /> | ||
n P(1-P)<sup>(n-1)</sup> | n P(1-P)<sup>(n-1)</sup><br /> | ||
For example, suppose a die is thrown repeatedly until the first time a "6" appears. This is a question of geometric distribution of the number of times on the set { 1, 2, 3, ... } with p = 1/6. | For example, suppose a die is thrown repeatedly until the first time a "6" appears. This is a question of geometric distribution of the number of times on the set { 1, 2, 3, ... } with p = 1/6. | ||
| Line 2,956: | Line 2,671: | ||
The CDF : P(X<n) = 1 - <math>(1-p)^n</math> | The CDF : P(X<n) = 1 - <math>(1-p)^n</math> | ||
| Line 3,114: | Line 2,827: | ||
If <math>\displaystyle X \sim \text{Poi}(\lambda)</math>, its pdf is of the form <math>\displaystyle \, f(x) = \frac{e^{-\lambda}\lambda^x}{x!}</math> , where <math>\displaystyle \lambda </math> is the rate parameter.<br /> | If <math>\displaystyle X \sim \text{Poi}(\lambda)</math>, its pdf is of the form <math>\displaystyle \, f(x) = \frac{e^{-\lambda}\lambda^x}{x!}</math> , where <math>\displaystyle \lambda </math> is the rate parameter.<br /> | ||
definition:In probability theory and statistics, the Poisson distribution (pronounced [pwasɔ̃]) is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time and/or space if these events occur with a known average rate and independently of the time since the last event. The Poisson distribution can also be used for the number of events in other specified intervals such as distance, area or volume. | |||
For instance, suppose someone typically gets 4 pieces of mail per day on average. There will be, however, a certain spread: sometimes a little more, sometimes a little less, once in a while nothing at all.[2] Given only the average rate, for a certain period of observation (pieces of mail per day, phonecalls per hour, etc.), and assuming that the process, or mix of processes, that produces the event flow is essentially random, the Poisson distribution specifies how likely it is that the count will be 3, or 5, or 10, or any other number, during one period of observation. That is, it predicts the degree of spread around a known average rate of occurrence. | |||
The Derivation of the Poisson distribution section shows the relation with a formal definition.(from Wikipedia) | |||
Understanding of Poisson distribution: | Understanding of Poisson distribution: | ||
If customers '''independently''' come to bank over time, all | If customers '''independently''' come to bank over time, all following exponential distributions with rate <math>\lambda</math> per unit of time, then | ||
X(t) = # of customer in [0,t] ~ Poi<math>(\lambda t)</math> | X(t) = # of customer in [0,t] ~ Poi<math>(\lambda t)</math> | ||
| Line 3,197: | Line 2,912: | ||
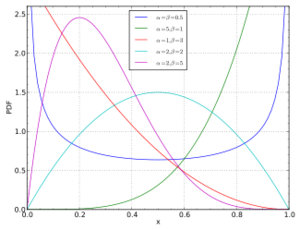
=== Beta Distribution === | === Beta Distribution === | ||
The beta distribution is a continuous probability distribution. There are two positive shape parameters | The beta distribution is a continuous probability distribution. There are two positive shape parameters in this distribution defined as alpha and beta, both parameters greater than 0, and X within the interval [0,1]. The parameter alpha is used as exponents of the random variable. The parameter beta is used to control the shape of the this distribution. We use the beta distribution to build the model of the behavior of random variables, which are limited to intervals of finite length. For example, we can use the beta distribution to analyze the time allocation of sunshine data and variability of soil properties. | ||
If X~Beta(<math>\alpha, \beta</math>) then its p.d.f. is of the form | If X~Beta(<math>\alpha, \beta</math>) then its p.d.f. is of the form | ||
| Line 3,205: | Line 2,920: | ||
<math>f(x;\alpha,\beta)= 0 </math> otherwise | <math>f(x;\alpha,\beta)= 0 </math> otherwise | ||
Note: <math>\Gamma(\alpha)=(\alpha-1)! </math> if <math>\alpha</math> is a positive integer. | Note: <math>\Gamma(\alpha)=(\alpha-1)! </math> if <math>\alpha</math> is a positive integer. | ||
The mean of the beta distribution is <math>\frac{\alpha}{\alpha + \beta}</math>. The variance is <math>\frac{\alpha\beta}{(\alpha+\beta)^2 (\alpha + \beta + 1)}</math> | |||
The variance of the beta distribution decreases monotonically if <math> \alpha = \beta </math> and as <math> \alpha = \beta </math> increases, the variance decreases. | The variance of the beta distribution decreases monotonically if <math> \alpha = \beta </math> and as <math> \alpha = \beta </math> increases, the variance decreases. | ||
The formula for the cumulative distribution function of the beta distribution is also called the incomplete beta function ratio (commonly denoted by Ix) and is defined as F(x) = I(x)(p,q) | The formula for the cumulative distribution function of the beta distribution is also called the incomplete beta function ratio (commonly denoted by Ix) and is defined as F(x) = I(x)(p,q) | ||
| Line 3,229: | Line 2,935: | ||
:<math> = 1 </math><br> | :<math> = 1 </math><br> | ||
Note | Note: 0! = 1. <br> | ||
Hence, the distribution is:<br> | Hence, the distribution is:<br> | ||
:<math>\displaystyle \text{Beta}(1,1) = U (0, 1) </math><br> | :<math>\displaystyle \text{Beta}(1,1) = U (0, 1) </math><br> | ||
| Line 3,303: | Line 3,009: | ||
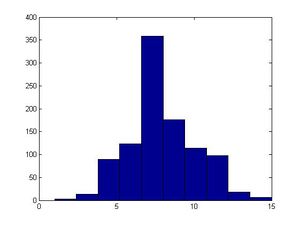
'''MATLAB Code for generating Beta Distribution''' | '''MATLAB Code for generating Beta Distribution''' | ||
<pre style='font-size:16px'> | <pre style='font-size:16px'> | ||
>>Y1 = sum(-log(rand(10,1000))) #Gamma(10,1), sum 10 | >>Y1 = sum(-log(rand(10,1000))) #Gamma(10,1), sum 10 exponentials for each of the 1000 samples | ||
>>Y2 = sum(-log(rand(5,1000))) #Gamma(5,1), sum 5 | >>Y2 = sum(-log(rand(5,1000))) #Gamma(5,1), sum 5 exponentials for each of the 1000 samples | ||
%NOTE: here, lamda is 1, since the scale parameter for Y1 & Y2 are both 1 | %NOTE: here, lamda is 1, since the scale parameter for Y1 & Y2 are both 1 | ||
| Line 3,323: | Line 3,029: | ||
>>hist(Y) #Do this to check that the shape fits beta. ~Beta(10,5). | >>hist(Y) #Do this to check that the shape fits beta. ~Beta(10,5). | ||
>>disttool #Check the beta plot | >>disttool #Check the beta plot. | ||
</pre> | </pre> | ||
| Line 3,335: | Line 3,041: | ||
[[File:325px-Beta_distribution_pdf.png|300px]] | [[File:325px-Beta_distribution_pdf.png|300px]] | ||
[[File:untitled.jpg|300px]]<br /> | |||
MATLAB tips: rand(10,1000) produces one 10*1000 matrix and sum(rand(10,1000)) produces a 10*1000 matrix | MATLAB tips: rand(10,1000) produces one 10*1000 matrix and sum(rand(10,1000)) produces a 10*1000 matrix | ||
and each element in the matrix follows CDF of uniform distribution. | and each element in the matrix follows CDF of uniform distribution. | ||
| Line 3,366: | Line 3,073: | ||
====Case 1==== | ====Case 1==== | ||
if the <math>x_1, x_2 \cdots, x_d</math>'s are independent, then<br/> | |||
<math>f(x) = f(x_1,\cdots, x_d) = f(x_1)\cdots f(x_d)</math><br/> | <math>f(x) = f(x_1,\cdots, x_d) = f(x_1)\cdots f(x_d)</math><br/> | ||
we can sample from each component <math>x_1, x_2,\cdots, x_d</math> individually, and then form a vector.<br/> | |||
based on the property of independence, we can derive the pdf or pmf of <math>x=x_1,x_2,x_3,x_4,x_5,\cdots</math> | |||
====Case 2==== | ====Case 2==== | ||
| Line 3,400: | Line 3,107: | ||
Algorithm: <br/> | Algorithm: <br/> | ||
1) for i = 1 to d <br/> | 1) for i = 1 to d <br/> | ||
2) U<sub>i</sub> ~ U(0,1 | 2) U<sub>i</sub> ~ U(0,1) <br/> | ||
3) x<sub>i</sub> = a<sub>i</sub> + U(b<sub>i</sub>-a<sub>i</sub>) <br/> | 3) x<sub>i</sub> = a<sub>i</sub> + U(b<sub>i</sub>-a<sub>i</sub>) <br/> | ||
4) end <br/> | 4) end <br/> | ||
| Line 3,428: | Line 3,135: | ||
<pre style='font-size:16px'> | <pre style='font-size:16px'> | ||
function x = urectangle (d,n,a,b) | |||
function x = urectangle (d,n,a,b) | |||
for ii = 1:d; | for ii = 1:d; | ||
u(ii,:) = rand(1,n); | u(ii,:) = rand(1,n); | ||
x(ii,:) = a+ u(ii,:)*(b-a); | x(ii,:) = a+ u(ii,:)*(b-a); | ||
%keyboard | %keyboard #makes the function stop at this step so you can evaluate the variables | ||
end | end | ||
>>x=urectangle(2, 100, 2, 5); | >>x=urectangle(2, 100, 2, 5); | ||
>>scatter(x(1,:),x(2,:)) | >>scatter(x(1,:),x(2,:)) | ||
>>x=urectangle(2, 10000, 2, 5); | >>x=urectangle(2, 10000, 2, 5); #generate 10000 numbers (instead of 100) | ||
>>x=urectangle(3, 10000, 2, 5); | >>x=urectangle(3, 10000, 2, 5); #changed to 3-dimensional | ||
>>scatter3(x(1,:), x(2,:), x(3,:)) | >>scatter3(x(1,:), x(2,:), x(3,:)) | ||
>>axis square | >>axis square | ||
| Line 3,473: | Line 3,179: | ||
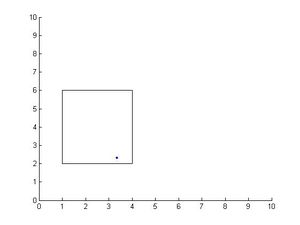
Suppose we sampled from the target area W uniformly, let Aw, Ag indicate the area of W and G, g(x)=1/Aw and f(x)=1/Ag | Suppose we sampled from the target area W uniformly, let Aw, Ag indicate the area of W and G, g(x)=1/Aw and f(x)=1/Ag | ||
This is the picture of the example | This is the picture of the example | ||
[[File: | [[File:Untitled.jpg]] | ||
matlab code: | matlab code: | ||
| Line 3,501: | Line 3,208: | ||
==Class 10 - Thursday June 6th 2013 == | ==Class 10 - Thursday June 6th 2013 == | ||
MATLAB code for using Acceptance | MATLAB code for using Acceptance/Rejection Method to sample from a d-dimensional unit ball. | ||
<pre style='font-size:16px'> | <pre style='font-size:16px'> | ||
| Line 3,515: | Line 3,222: | ||
function output = Unitball(d,n) | function output = Unitball(d,n) | ||
u = rand(d,n); | u = rand(d,n); | ||
z = 1 - 2*u; | z = 1- 2 *u; | ||
R = sum(z.^2); | R = sum(z.^2); | ||
jj=1; | jj=1; | ||
| Line 3,538: | Line 3,245: | ||
>> scatter(data(1,:), data(2,:)) %plot 2d graph | >> scatter(data(1,:), data(2,:)) %plot 2d graph | ||
R(ii) | R(ii) computes the sum of the square of each element of a vector, so if it is less than 1, | ||
then the vector is in the unit ball. | |||
x(:,jj) means all the numbers in the jj column. | x(:,jj) means all the numbers in the jj column. | ||
| Line 3,556: | Line 3,263: | ||
Execution: | Execution: | ||
>>[x]=Unitball(2,10000); | >>[x]=Unitball(2,10000); | ||
>>scatter(x(1,:),x(2,:)); %plot 2D circle | >>scatter(x(1,:),x(2,:)); %plot 2D circle | ||
>>axis square; %make the x-y axis has same size | >>axis square; %make the x-y axis has same size | ||
| Line 3,563: | Line 3,270: | ||
ans = | ans = | ||
2 | 2 7839 | ||
>>scatter(x(1,:),x(2,:)) | >>scatter(x(1,:),x(2,:)) | ||
| Line 3,573: | Line 3,280: | ||
<pre style='font-size:16px'> | <pre style='font-size:16px'> | ||
>>c=7839/10000 % | >>c=7839/10000 %Efficiency = points accepted / total points | ||
c = | c = | ||
0.7839 | 0.7839 | ||
</pre> | </pre> | ||
| Line 3,630: | Line 3,329: | ||
=== Efficiency === | === Efficiency === | ||
In the above example, the efficiency of the vector A/R is equal to the ratio | In the above example, the efficiency of the vector A/R is equal to the ratio | ||
| Line 3,646: | Line 3,343: | ||
<span style="color:red;padding:0 auto;"><br>The end of midterm coverage</span> | <span style="color:red;padding:0 auto;"><br>The end of midterm coverage</span> | ||
==== Stochastic Process ==== | ==== Stochastic Process ==== | ||
The basic idea of Stochastic Process (also called random process) is a collection of some random variables, | The basic idea of Stochastic Process (also called random process) is a collection of some random variables, | ||
| Line 3,663: | Line 3,349: | ||
'''Definition:''' In probability theory, a stochastic process /stoʊˈkæstɪk/, or sometimes random process (widely used) is a collection of random variables; this is often used to represent the evolution of some random value, or system, over time. This is the probabilistic counterpart to a deterministic process (or deterministic system). Instead of describing a process which can only evolve in one way (as in the case, for example, of solutions of an ordinary differential equation), in a stochastic or random process there is some indeterminacy: even if the initial condition (or starting point) is known, there are several (often infinitely many) directions in which the process may evolve. (from Wikipedia) | '''Definition:''' In probability theory, a stochastic process /stoʊˈkæstɪk/, or sometimes random process (widely used) is a collection of random variables; this is often used to represent the evolution of some random value, or system, over time. This is the probabilistic counterpart to a deterministic process (or deterministic system). Instead of describing a process which can only evolve in one way (as in the case, for example, of solutions of an ordinary differential equation), in a stochastic or random process there is some indeterminacy: even if the initial condition (or starting point) is known, there are several (often infinitely many) directions in which the process may evolve. (from Wikipedia) | ||
A stochastic process is non-deterministic. This means that there is some indeterminacy in the final state, even if the initial condition is known. | |||
We can illustrate this with an example of speech: if "I" is the first word in a sentence, the set of words that could follow would be limited (eg. like, want, am), and the same happens for the third word and so on. The words then have some probabilities among them such that each of them is a random variable, and the sentence would be a collection of random variables. <br> | We can illustrate this with an example of speech: if "I" is the first word in a sentence, the set of words that could follow would be limited (eg. like, want, am), and the same happens for the third word and so on. The words then have some probabilities among them such that each of them is a random variable, and the sentence would be a collection of random variables. <br> | ||
Also, | Also, Different Stochastic Process has different properties. | ||
In the course, we study two | In the course, we study two Stochastic Process models. | ||
The two stochastic | The two stochastic Process models we will study are: | ||
1. Poisson Process - This is | 1. Poisson Process-This is continuous time counting process that satisfies a couple of properties that are listed in the next section. The Poisson process is understood to be a good model for events such as incoming phone calls, number of traffic accidents, and goals during a game of hockey or soccer. It is also an example of a birth-death process.<br> | ||
2. Markov Process - This is a stochastic process that satisfies the Markov property which can be understood as the memory-less property. The property states that the jump to a future state only depends on the current state of the process, and not of the process's history. This model is used to model random walks exhibited by particles, the health state of a life insurance policyholder, decision making by a memory-less mouse in a maze, etc. <br> | 2. Markov Process- This is a stochastic process that satisfies the Markov property which can be understood as the memory-less property. The property states that the jump to a future state only depends on the current state of the process, and not of the process's history. This model is used to model random walks exhibited by particles, the health state of a life insurance policyholder, decision making by a memory-less mouse in a maze, etc. <br> | ||
Stochastic | Stochastic Process means even we get some conditions at the beginning, we just can guess some variables followed the first, but at the end the variable would be unpredictable. | ||
=====Example===== | |||
The state space is the set of English words, and <math>x_t</math> are words that are said. Another example involves the stock market: the set of all non-negative numbers is the state space, and <math>x_t</math> are stock prices. | |||
The | |||
stochastic process always has state space and the index set to limit the range. | |||
The state space is the set of cars , while <math>x_t</math> are sport cars. | |||
==== Poisson Process ==== | ==== Poisson Process ==== | ||
| Line 3,702: | Line 3,391: | ||
E[N<sub>t</sub>] = <math>\lambda t</math> and Var[N<sub>t</sub>] = <math>\lambda t</math> | E[N<sub>t</sub>] = <math>\lambda t</math> and Var[N<sub>t</sub>] = <math>\lambda t</math> | ||
==== | ==== ==== | ||
<br /> | <br /> | ||
'''How to generate a multivariate normal with build in function "randn": (example)'''<br /> | '''How to generate a multivariate normal with build in function "randn": (example)'''<br /> | ||
| Line 3,729: | Line 3,418: | ||
X = Z*R + ones(n,1)*mu'; | X = Z*R + ones(n,1)*mu'; | ||
</pre> | </pre> | ||
==== '''Central Limit Theorem''' ==== | ==== '''Central Limit Theorem''' ==== | ||
| Line 3,741: | Line 3,431: | ||
>> X = exprnd (20,20,1000); % 1000 instances of 20 exponential random numbers with mean 20 | >> X = exprnd (20,20,1000); % 1000 instances of 20 exponential random numbers with mean 20 | ||
>> hist(X(1,:)) | >> hist(X(1,:)) | ||
>> hist | >> hist(X(1:2,:)) | ||
... | ... | ||
>>hist | >>hist(X(1:20,:)) -> approaches to normal | ||
</pre> | </pre> | ||
==Class 11 - Tuesday,June 11, 2013== | |||
=== Announcement === | |||
Midterm covers up to the middle of last lecture, which means stochastic process will not be on midterm. There won't be any Matlab syntax questions. And Students can contribute to any previous classes. We might however be asked to write down algorithms. | |||
===Poisson Process=== | ===Poisson Process=== | ||
A discrete stochastic variable ''X'' is said to have a Poisson distribution with parameter ''λ'' > 0 if | A discrete stochastic variable ''X'' is said to have a Poisson distribution with parameter ''λ'' > 0 if | ||
:<math>\!f(n)= \frac{\lambda^n e^{-\lambda}}{n!} \qquad n= 0,1,\ldots,</math>. | :<math>\!f(n)= \frac{\lambda^n e^{-\lambda}}{n!} \qquad n= 0,1,\ldots,</math>. | ||
'''Properties of Homogeneous Poisson Process'''<br> | '''Properties of Homogeneous Poisson Process'''<br> | ||
(a) '''Independence:''' The numbers of arrivals in non-overlapping intervals are independent <br> | (a) '''Independence:''' The numbers of arrivals in non-overlapping intervals are independent <br> | ||
(b) '''Homogeneity or Uniformity:''' The number of arrival in each interval I(a,b] is Poisson distribution with rate <math>\lambda (b-a)</math><br/> | (b) '''Homogeneity or Uniformity:''' The number of arrival in each interval I(a,b] is Poisson distribution with rate <math>\lambda (b-a)</math><br/> | ||
(c) '''Individuality:''' for a sufficiently short time period of length h, the probability of 2 or more events occurring in the interval is close to 0 | (c) '''Individuality:''' for a sufficiently short time period of length h, the probability of 2 or more events occurring in the interval is close to 0, or formally <math>\mathcal{O}(h)</math><br> | ||
'''Notation'''<br> | '''Notation'''<br> | ||
N<sub>t</sub> denotes the number of arrivals up to t, i.e.(0,t] <br> | N<sub>t</sub> denotes the number of arrivals up to t, i.e.(0,t] <br> | ||
N(a,b] = N<sub>b</sub> - N<sub>a</sub> denotes the number of arrivals in I(a, b]. <br> | N(a,b] = N<sub>b</sub> - N<sub>a</sub> denotes the number of arrivals in I(a, b]. <br> | ||
| Line 3,785: | Line 3,464: | ||
Similarly, the probability of not observing an arrival in this interval is 1-<math>\lambda </math> h.<br> | Similarly, the probability of not observing an arrival in this interval is 1-<math>\lambda </math> h.<br> | ||
'''Generate a Poisson Process'''<br /> | |||
<math>U_n \sim U(0,1)</math><br> | |||
<math>T_n-T_{n-1}=-\frac {1}{\lambda} log(U_n)</math><br> | |||
1. set T<sub>0</sub>=0 and n=1<br /> | |||
2. U<sub>n</sub>~ U(0,1)<br /> | |||
3. T<sub>n</sub> = T<sub>n-1</sub> <math> -\frac {1}{\lambda} </math> log (U<sub>n</sub>) (declare an arrival)<br /> | |||
4. if T<sub>n</sub>>T stop<br /> | |||
else<br /> | |||
n=n+1 go to step 2<br /> | |||
Since <math>P(N(t,t+h)=1) = e^{-{\lambda} h}\lambda h</math>, we can regard <math>\lambda </math>h as a exponential distribution, and according to what we learnt, <math>T_n-T_{n-1} = h = -\frac {1}{\lambda} log(U_n)</math>.<br> | |||
*Note : Recall that exponential random variable is the waiting time until one event of interested occurs. | |||
'''Review of Poisson - Example''' | '''Review of Poisson - Example''' | ||
| Line 3,804: | Line 3,498: | ||
when we use the inverse-transfer method, we can assume the poisson process to be exp distribution, and get the h function from the inverse method, and sometimes we assume h is very small. | when we use the inverse-transfer method, we can assume the poisson process to be exp distribution, and get the h function from the inverse method, and sometimes we assume h is very small. | ||
'''Multi-dimensional Poisson Process'''<br> | |||
The poisson distribution arises as the distribution of counts of occurrences of events in (multidimensional) intervals in multidimensional poisson process in a directly equivalent way to the result for unidimensional processes. This,is ''D'' is any region the multidimensional space for which |D|, the area or volume of the region, is finite, and if {{nowrap|''N''(''D'')}} is count of the number of events in ''D'', then | |||
<math> P(N(D)=k)=\frac{(\lambda|D|)^k e^{-\lambda|D|}}{k!} .</math> | |||
=== Generating a Homogeneous Poisson Process === | === Generating a Homogeneous Poisson Process === | ||
| Line 3,819: | Line 3,519: | ||
1) Set T<sub>0</sub> = 0 ,and n = 1 <br> | 1) Set T<sub>0</sub> = 0 ,and n = 1 <br> | ||
2) U<sub>n</sub> follow U(0,1) <br> | 2) U<sub>n</sub> follow U(0,1) <br> | ||
3) T<sub>n</sub> - T<sub>n-1</sub> =<math> -\frac {1}{\lambda} </math> log (U<sub>n</sub>) (Declare an arrival | 3) T<sub>n</sub> - T<sub>n-1</sub> =<math> -\frac {1}{\lambda} </math> log (U<sub>n</sub>) (Declare an arrival)<br> | ||
4) if T<sub>n</sub> >T stop; | 4) if T<sub>n</sub> >T stop; | ||
else n = n + 1, go to step 2 | else n = n + 1, go to step 2 <br> | ||
h is the a range and we assume the probability of every point in this rang is the same by uniform ditribution.(cause h is small) | h is the a range and we assume the probability of every point in this rang is the same by uniform ditribution.(cause h is small) | ||
| Line 3,827: | Line 3,527: | ||
<b>Higher Dimensions:</b><br> | <b>Higher Dimensions:</b><br> | ||
To sample from higher dimensional Poisson process:<br> | To sample from higher dimensional Poisson process:<br> | ||
1. Generate a random number N that is Poisson distributed with parameter <math>{\lambda}</math>*A<sub>d</sub>, where A<sub>d</sub> is the area under the bounded region. (ie A<sub>2</sub> is area of the region, A<sub>3</sub> is the volume of the 3-d space.<br> | 1. Generate a random number N that is Poisson distributed with parameter <math>{\lambda}</math>*A<sub>d</sub>, where A<sub>d</sub> is the area under the bounded region. (ie A<sub>2</sub> is area of the region, A<sub>3</sub> is the volume of the 3-d space.<br> | ||
| Line 3,846: | Line 3,541: | ||
TT=5; | TT=5; | ||
while T(ii)<=TT | while T(ii)<=TT | ||
u=rand; | u=rand; | ||
ii=ii+1; | ii=ii+1; | ||
| Line 3,852: | Line 3,547: | ||
end | end | ||
plot(T) | plot(T, '.') | ||
</pre> | </pre> | ||
| Line 3,896: | Line 3,591: | ||
<math> x_1 \rightarrow x_2\rightarrow...\rightarrow x_n</math> | <math> x_1 \rightarrow x_2\rightarrow...\rightarrow x_n</math> | ||
Formal Definition: | |||
The process <math> \{x_n: n \in T\} </math> is a markov chain if:<br /> | The process <math> \{x_n: n \in T\} </math> is a markov chain if:<br /> | ||
<math> Pr(x_n|x_{n-1},...,x_1) = Pr(x_n|x_{n-1}) \ \ \forall n\in T </math> and <math> \forall x\in X</math> | <math> Pr(x_n|x_{n-1},...,x_1) = Pr(x_n|x_{n-1}) \ \ \forall n\in T </math> and <math> \forall x\in X</math> | ||
<span style="background:#F5F5DC">CONTINUOUS TIME MARKOV PROCESS</span> | <span style="background:#F5F5DC">CONTINUOUS TIME MARKOV PROCESS</span> | ||
| Line 3,910: | Line 3,602: | ||
====Transition Matrix==== | ====Transition Matrix==== | ||
Transition Probability: <math> P_{ij} = P(X_{t+1} =j | X_t =i) </math> is the one-step transition probability from state i to state j. | Transition Probability: <math> P_{ij} = P(X_{t+1} =j | X_t =i) </math> is the one-step transition probability from state i to state j. | ||
| Line 3,950: | Line 3,640: | ||
This means our model can be simulated as a sequence of random variables <math> (X_0, X_1, X_2, \ldots ) </math> with state space <math> \Omega </math> and transition matrix <math> P = [P_{ij}] </math> where <math> \forall t \in \N, 0 \leq s \leq t+1, x_s \in \Omega, </math> <br/> | This means our model can be simulated as a sequence of random variables <math> (X_0, X_1, X_2, \ldots ) </math> with state space <math> \Omega </math> and transition matrix <math> P = [P_{ij}] </math> where <math> \forall t \in \N, 0 \leq s \leq t+1, x_s \in \Omega, </math> <br/> | ||
we have | we have to following property (Markov property): <br/> | ||
<math> P(X_{t+1}= x_{t+1} \vert \cap^{t}_{s=0} X_s = x_s) = P(X_{t+1} =x_{t+1} \vert X_t =x_t) = P(x_t,x_{t+1}) </math> <br> | <math> P(X_{t+1}= x_{t+1} \vert \cap^{t}_{s=0} X_s = x_s) = P(X_{t+1} =x_{t+1} \vert X_t =x_t) = P(x_t,x_{t+1}) </math> <br> | ||
| Line 3,959: | Line 3,649: | ||
Then one might consider the periodicity of the chain and derive a notion of cyclic behavior. <br> | Then one might consider the periodicity of the chain and derive a notion of cyclic behavior. <br> | ||
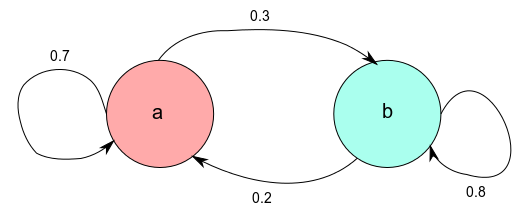
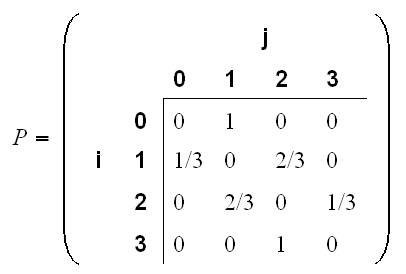
=== Examples of Transition Matrix === | === Examples of Transition Matrix === | ||
[[File:Mark13.png]] | [[File:Mark13.png]] | ||
| Line 4,042: | Line 3,675: | ||
<math> \begin{align} P(X_{1} &=0 &\mid X_{0} &=0) * P(X_{2} &=1 &\mid X_{1} &=0)+P(X_{1} &=1 &\mid X_{0} &=0) * P(X_{2} &=1 &\mid X_{1}&=1) &=1/3*2/3+ 2/3*1/4 &=7/18 \\ | <math> \begin{align} P(X_{1} &=0 &\mid X_{0} &=0) * P(X_{2} &=1 &\mid X_{1} &=0)+P(X_{1} &=1 &\mid X_{0} &=0) * P(X_{2} &=1 &\mid X_{1}&=1) &=1/3*2/3+ 2/3*1/4 &=7/18 \\ | ||
\end{align}</math><br /> | \end{align}</math><br /> | ||
== Class 12 - Thursday,June 13, 2013 == | |||
<b>Time</b> | |||
Jun 17, 2013 2:30 PM - 3:30 PM | |||
===Midterm Review=== | ===Midterm Review=== | ||
| Line 4,085: | Line 3,715: | ||
===Acceptance-Rejection Method=== | ===Acceptance-Rejection Method=== | ||
cg(x)>=f(x) | cg(x)>=f(x) | ||
<math>c=max | <math>c=max\frac{f(x)}{g(x)}</math> | ||
<br><math>\frac{1}{c}</math> is the efficiency of the method/probability of acceptance | <br><math>\frac{1}{c}</math> is the efficiency of the method/probability of acceptance | ||
| Line 4,151: | Line 3,781: | ||
Gamma(t,λ) <br> | Gamma(t,λ) <br> | ||
t: The number of exponentials and the shape parameter<br> | t: The number of exponentials and the shape parameter<br> | ||
λ: The mean of the exponentials and the scale parameter<br> | |||
Also, Gamma(t,λ) can be expressed into a summation of t exp(λ).<br> | Also, Gamma(t,λ) can be expressed into a summation of t exp(λ).<br> | ||
| Line 4,178: | Line 3,808: | ||
<br\> | <br\> | ||
X~ Bin(n,p)<br/> | X~ Bin(n,p)<br/> | ||
1. U1, U2, ... Un ~ U(0,1) | 1. U1, U2, ... Un ~ U(0,1)<br/> | ||
2. <math> X= \sum^{n}_{1} I(U_i \leq p) </math> ,where <math>I(U_i \leq p)</math> is an indicator for a successful trial.<br/> | 2. <math> X= \sum^{n}_{1} I(U_i \leq p) </math> ,where <math>I(U_i \leq p)</math> is an indicator for a successful trial.<br/> | ||
Return to 1<br/> | Return to 1<br/> | ||
| Line 4,206: | Line 3,836: | ||
:<math>\displaystyle \text{Beta}(1,1) = U (0, 1) </math><br> | :<math>\displaystyle \text{Beta}(1,1) = U (0, 1) </math><br> | ||
:<math>\displaystyle \text{Beta}(\alpha,1)={f}(x) = \frac{\Gamma(\alpha+1)}{\Gamma(\alpha)\Gamma(1)}x^{\alpha-1}(1-x)^{1-1}=\alpha x^{\alpha-1}</math><br> | :<math>\displaystyle \text{Beta}(\alpha,1)={f}(x) = \frac{\Gamma(\alpha+1)}{\Gamma(\alpha)\Gamma(1)}x^{\alpha-1}(1-x)^{1-1}=\alpha x^{\alpha-1}</math><br> | ||
'''Gamma Distribution''' | |||
'''Algorithm'''<br\> | '''Algorithm'''<br\> | ||
| Line 4,220: | Line 3,851: | ||
This distribution models the number of failures before the first success. | This distribution models the number of failures before the first success. | ||
X~Geo(p) | X~Geo(p) | ||
| Line 4,261: | Line 3,892: | ||
===Poisson=== | ===Poisson=== | ||
This distribution models the number of times and event occurs in a given time period | |||
X~Poi<math>(\lambda)</math> <br> | X~Poi<math>(\lambda)</math> <br> | ||
X is the maximum number of iid Exp(<math>\lambda</math>) whose sum is less than or equal to 1.<br> | X is the maximum number of iid Exp(<math>\lambda</math>) whose sum is less than or equal to 1.<br> | ||
| Line 4,273: | Line 3,899: | ||
<math> = \max\{n: \sum\limits_{i=1}^n \frac{-1}{\lambda} log(U_i)<=1 , U_i \sim U[0,1]\}</math><br> | <math> = \max\{n: \sum\limits_{i=1}^n \frac{-1}{\lambda} log(U_i)<=1 , U_i \sim U[0,1]\}</math><br> | ||
<math> = \max\{n: \prod\limits_{i=1}^n U_i >= e^{-\lambda}, U_i \sim U[0,1]\}</math><br> | <math> = \max\{n: \prod\limits_{i=1}^n U_i >= e^{-\lambda}, U_i \sim U[0,1]\}</math><br> | ||
'''Algorithm'''<br\> | '''Algorithm'''<br\> | ||
*1. Set n=1, a=1<br\> | *1. Set n=1, a=1<br\> | ||
| Line 4,286: | Line 3,907: | ||
An alternate way to write an algorithm for Poisson is as followings: | An alternate way to write an algorithm for Poisson is as followings: | ||
1) x = 0, F = | 1) x = 0, F = P(X=0) = e^-λ = p | ||
| Line 4,295: | Line 3,916: | ||
4) Else | 4) Else p = (λ/(x+1)) * p | ||
F = F + p | F = F + p | ||
| Line 4,306: | Line 3,927: | ||
== Class 13 - Tuesday June 18th 2013 == | == Class 13 - Tuesday June 18th 2013 == | ||
An n-step transition matrix is a matrix <math> P_n </math> whose elements are the probability of moving to state j from state i in n steps. <br/> | |||
<math>P_n (i,j)=Pr(X_{m+n}=j|X_m=i)</math> <br/> | |||
One-step transition probability:<br/> | |||
The probability of X<sub>n+1</sub> being in state j given that X<sub>n</sub> is in state i is called the | |||
one-step transition probability and is denoted by P<sub>i,j</sub><sup>n,n+1</sup>. That is <br/> | |||
P<sub>i,j</sub><sup>n,n+1</sup> = Pr(X<sub>n+1</sub> =j/X<sub>n</sub> =i) | |||
Example from previous class: <br/> | |||
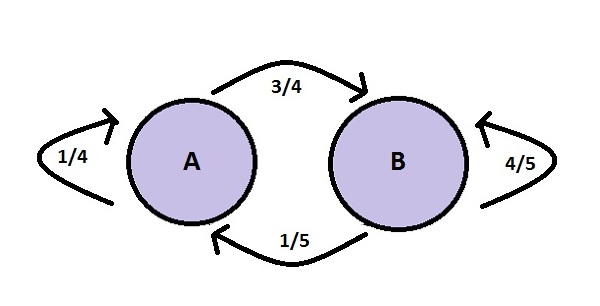
<math> P= \left [ \begin{matrix} | <math> P= \left [ \begin{matrix} | ||
0.7 & 0.3 \\ | 0.7 & 0.3 \\ | ||
0.2 & 0.8 | 0.2 & 0.8 | ||
\end{matrix} \right] </math> | \end{matrix} \right] </math> | ||
| Line 4,352: | Line 3,960: | ||
<math>P_2 = P_1 P_1 </math><br\> | <math>P_2 = P_1 P_1 </math><br\> | ||
<math>P_n = P_1^n </math><br\> | <math>P_n = P_1^n </math><br\> | ||
The two-step transition probability of moving from state a to state a: | |||
<br/> | |||
<math>P_2 (a,a)=Pr (X_{m+2}=a| X_m=a)=Pr(X_{m+1}=a| X_m=a)Pr(X_{m+2}=a|X_{m+1}=a)+ Pr(X_{m+1}=b|X_m=a)Pr(X_{m+2}=a|X_{m+1}=b)</math> <br/> | |||
< | <math> =0.7(0.7)+0.3(0.2)=0.55 </math><br/> | ||
< | === n-step transition matrix === | ||
The elements of matrix P<sub>n</sub> (i.e. the ij<sub>th</sub> entry P<sub>ij</sub>) is the probability of moving to state j from state i in n steps | |||
In general <math>P_n = P^n</math> with <math>P_n(i,j) \geq 0</math> and <math>\sum_{j} P_n(i,j) = 1</math><br /> | |||
Note: <math>P_2 = P_1\times P_1; P_n = P^n</math><br /> | |||
The equation above is a special case of the Chapman-Kolmogorov equations.<br /> | |||
It is true because of the Markov property or<br /> | |||
the memoryless property of Markov chains, where the probabilities of going forward to the next state <br /> | |||
only depends on your current state, not your previous states. By intuition, we can multiply the 1-step transition <br /> | |||
matrix n-times to get a n-step transition matrix.<br /> | |||
<math> P | |||
Example: We can see how <math>P_n = P^n</math> from the following: | |||
<br/> | |||
<math>P_2 = P_1 P_1 </math><br | |||
< | |||
We can see how <math>P_n = P^n</math> from the following:<br/> | |||
<math>\mu_1=\mu_0\cdot P</math> <br/> | <math>\mu_1=\mu_0\cdot P</math> <br/> | ||
<math>\mu_2=\mu_1\cdot P</math> <br/> | <math>\mu_2=\mu_1\cdot P</math> <br/> | ||
<math>\mu_3=\mu_2\cdot P</math> <br/> | <math>\mu_3=\mu_2\cdot P</math> <br/> | ||
Therefore, | Therefore, | ||
<br/> | <br/> | ||
| Line 4,405: | Line 3,990: | ||
</math> <br/> | </math> <br/> | ||
<math>P_n(i,j)</math> is called | <math>P_n(i,j)</math> is called n-steps transition probability. <br> | ||
<math>\mu_0 </math> is called the ''' | <math>\mu_0 </math> is called the '''initial distribution'''. <br> | ||
<math>\mu_n = \mu_0* P^n </math> <br /> | <math>\mu_n = \mu_0* P^n </math> <br /> | ||
Example with Markov Chain: | |||
Consider a two-state Markov chain {<math>X_t; t = 0, 1, 2,...</math>} with states {1,2} and transition probability matrix | Consider a two-state Markov chain {<math>X_t; t = 0, 1, 2,...</math>} with states {1,2} and transition probability matrix | ||
| Line 4,424: | Line 4,008: | ||
b)<math> P(X_2=1, X_1=1 |X_0=1) = P(X_2=1|X_1=1)*P(X_1=1|X_0=1)= 1/2 * 1/2 = 1/4 </math> | b)<math> P(X_2=1, X_1=1 |X_0=1) = P(X_2=1|X_1=1)*P(X_1=1|X_0=1)= 1/2 * 1/2 = 1/4 </math> | ||
c)<math> P(X_2=1|X_0=1)= P_2(1,1) = 5/12 </math> | c)<math> P(X_2=1|X_0=1)= P_2(1,1) = 5/12 </math> | ||
d)<math> P^2=P*P= \left [ \begin{matrix} | d)<math> P^2=P*P= \left [ \begin{matrix} | ||
| Line 4,431: | Line 4,015: | ||
\end{matrix} \right] </math> | \end{matrix} \right] </math> | ||
=== Marginal Distribution of Markov Chain === | |||
We represent the probability of all states at time t with a vector <math>\underline{\mu_t}</math><br/> | |||
<math>\underline{\mu_t}~=(\mu_t(1), \mu_t(2),...\mu_t(n))</math> where <math>\mu_t(1)</math> is the probability of being on state 1 at time t.<br/> | |||
and in general, <math>\mu_t(i)</math> shows the probability of being on state i at time t.<br/> | |||
=== Marginal Distribution of Markov Chain === | |||
<math>\underline{\mu_t}~=(\mu_t(1), \mu_t(2),...\mu_t(n))</math> where <math>\mu_t(1)</math> is the probability of being on state 1 at time t.<br/> | |||
and in general, <math>\mu_t(i)</math> shows the probability of being on state i at time t.<br/> | |||
For example, if there are two states a and b, then <math>\underline{\mu_5}</math>=(0.1, 0.9) means that the chance of being in state a at time 5 is 0.1 and the chance of being on state b at time 5 is 0.9. <br/> | For example, if there are two states a and b, then <math>\underline{\mu_5}</math>=(0.1, 0.9) means that the chance of being in state a at time 5 is 0.1 and the chance of being on state b at time 5 is 0.9. <br/> | ||
If we generate a chain for many times, the frequency of states at each time shows marginal distribution of the chain at that time. <br/> | If we generate a chain for many times, the frequency of states at each time shows marginal distribution of the chain at that time. <br/> | ||
The vector <math>\underline{\mu_0}</math> is called the initial distribution. <br/> | The vector <math>\underline{\mu_0}</math> is called the initial distribution. <br/> | ||
<math> P_2~=P_1 P_1 </math> (as verified above) | <math> P_2~=P_1 P_1 </math> (as verified above) | ||
| Line 4,462: | Line 4,029: | ||
<math>\mu_n~=\mu_0 P_n</math><br/> | <math>\mu_n~=\mu_0 P_n</math><br/> | ||
where <math>\mu_0</math> is the initial distribution, | where <math>\mu_0</math> is the initial distribution, | ||
and <math>\ | and <math>\mu_m+n~=\mu_m P_n</math><br/> | ||
N can be negative, if P is invertible. | N can be negative, if P is invertible. | ||
| Line 4,483: | Line 4,050: | ||
<math>\mu_1~ = \mu_0P</math> <br> | <math>\mu_1~ = \mu_0P</math> <br> | ||
<math>\mu_2~ = \mu_1P = \mu_0PP = \mu_0P^2</math> <br> | <math>\mu_2~ = \mu_1P = \mu_0PP = \mu_0P^2</math> <br> | ||
In general, <math>\mu_n~ = \mu_0P^n</math><br /> | In general, <math>\mu_n~ = \mu_0P^n</math><br /> | ||
Property: If <math>\mu_n~ | Property: If <math>\mu_n~ =/= \mu_t~</math>(for any t less than n), then we say P does not converge. <br /> | ||
| Line 4,493: | Line 4,058: | ||
==== Stationary Distribution ==== | ==== Stationary Distribution ==== | ||
<math>\pi</math> is stationary distribution of the chain if <math>\pi</math>P = <math>\pi</math> | |||
where <math>\pi</math> is a probability vector <math>\pi</math>=(<math>\pi</math><sub>i</sub> | <math>i \in X</math>) such that all the entries are nonnegative and sum to 1. | |||
<math> | In other words, if X''<sub>0</sub>'' is draw from <math>\pi</math>. Then marginally, X''<sub>n</sub>'' is also drawn from the same distribution <math>\pi</math> for every n≥0. | ||
\ | '''Comments:'''<br/> | ||
As n gets bigger and bigger, <math>\mu_n</math> will possibly stop changing, so the quantity <math>\pi</math> <sub>i</sub> can also be interpreted as the limiting probability that the chain is in the state <math>j</math> | |||
< | Comments: <br/> | ||
1. <math>\pi</math> may not exist and even if it exists, it may not always be unique. <br/> | |||
2. If <math>\pi</math> exists and is unique, then <math>\pi</math><sub>i</sub> is called the long-run proportion of the process in state i and the stationary distribution is also the limiting distribution of the process.<br/> | |||
==== MatLab Code ==== | |||
<pre style='font-size:14px'> | <pre style='font-size:14px'> | ||
| Line 4,544: | Line 4,096: | ||
0.3000 0.7000 | 0.3000 0.7000 | ||
>> mu=[.9 .1] | >> mu=[.9 .1] | ||
mu = | mu = | ||
| Line 4,550: | Line 4,102: | ||
0.9000 0.1000 | 0.9000 0.1000 | ||
>> mu*p % | >> mu*p % enter mu=mu*P, repeat multiple times until the value of the vector mu remains unchanged | ||
ans = | ans = | ||
| Line 4,575: | Line 4,127: | ||
0.4000 0.6000 | 0.4000 0.6000 | ||
0.4000 0.6000 | 0.4000 0.6000 | ||
</pre> | </pre> | ||
The definition of stationary distribution is that <math>\pi</math> is the stationary distribution of the chain if <math>\pi=\pi~P</math>, where <math>\pi</math> is a probability vector. For every n<math>>=</math>0. | |||
However, just because X<sub>''n''</sub> ~ <math>\pi</math> for every n<math>>=</math>0 does ''not'' mean every state is independently identically distributed. | |||
''' | '''Limiting distribution''' of the chain refers the transition matrix that reaches the stationary state. If the lim(n-> infinite)P^n -> c, where c is a constant, then, we say this Markov chain is coverage; otherwise, it's not coverage. | ||
Example: Find the stationary distribution of P= <math>\left[ {\begin{array}{ccc} | |||
1/3 & 1/3 & 1/3 \\ | |||
1/4 & 3/4 & 0 \\ | |||
1/2 & 0 & 1/2 \end{array} } \right]</math> | |||
Solution: | |||
<math>\pi=\left[ {\begin{array}{ccc} | |||
\pi_0 & \pi_1 & \pi_2 \end{array} } \right]</math> | |||
the | Using the stationary distribution property <math>\pi=\pi~P</math> we get, <br> | ||
<math>\pi_0=\frac{1}{3}\pi_0+\frac{1}{4}\pi_1+\frac{1}{2}\pi_2 </math><br> | |||
<math>\pi_1=\frac{1}{3}\pi_0+\frac{3}{4}\pi_1+0\pi_2 </math><br> | |||
<math>\pi_2=\frac{1}{3}\pi_0+0\pi_1+\frac{1}{2}\pi_2 </math><br> | |||
And since <math>\pi</math> is a probability vector, <br> | |||
<math> \pi_{0}~ + \pi_{1} + \pi_{2} = 1 </math> | |||
<span style="background:#F5F5DC"> | Solving the 4 equations for the 3 unknowns gets, <br> | ||
Generating Random Initial distribution<br> | <math>\pi_{0}~=1/3</math>, <math>\pi_{1}~=4/9</math>, and <math>\pi_{2}~=2/9</math> <br> | ||
Therefore <math>\pi=\left[ {\begin{array}{ccc} | |||
1/3 & 4/9 & 2/9 \end{array} } \right]</math> | |||
Example 2: Find the stationary distribution of P= <math>\left[ {\begin{array}{ccc} | |||
1/3 & 1/3 & 1/3 \\ | |||
1/4 & 1/2 & 1/4 \\ | |||
1/6 & 1/3 & 1/2 \end{array} } \right]</math> | |||
Solution: | |||
<math>\pi=\left[ {\begin{array}{ccc} | |||
\pi_0 & \pi_1 & \pi_2 \end{array} } \right]</math> | |||
Using the stationary distribution property <math>\pi=\pi~P</math> we get, <br> | |||
<math>\pi_0=\frac{1}{3}\pi_0+\frac{1}{4}\pi_1+\frac{1}{6}\pi_2 </math><br> | |||
<math>\pi_1=\frac{1}{3}\pi_0+\frac{1}{2}\pi_1+\frac{1}{3}\pi_2 </math><br> | |||
<math>\pi_2=\frac{1}{3}\pi_0+\frac{1}{4}\pi_1+\frac{1}{2}\pi_2 </math><br> | |||
And since <math>\pi</math> is a probability vector, <br> | |||
<math> \pi_{0}~ + \pi_{1} + \pi_{2} = 1 </math> | |||
Solving the 4 equations for the 3 unknowns gets, <br> | |||
<math>\pi_{0}=\frac {6}{25}</math>, <math>\pi_{1}~=\frac {2}{5}</math>, and <math>\pi_{2}~=\frac {9}{25}</math> <br> | |||
Therefore <math>\pi=\left[ {\begin{array}{ccc} | |||
\frac {6}{25} & \frac {2}{5} & \frac {9}{25} \end{array} } \right]</math> | |||
The above two examples are designed to solve for the stationary distribution of the matrix P however they also give us the limiting distribution of the matrices as we have mentioned earlier that the stationary distribution is equivalent to the limiting distribution. | |||
'''Alternate Method of Computing the Stationary Distribution''' <br> | |||
Recall that if <math>\lambda v = A v</math>, then <math>\lambda</math> is the eigenvalue of <math>A</math> corresponding to the eigenvector <math>v</math><br> | |||
By definition of stationary distribution, <math>\pi = \pi P</math><br> | |||
Taking the transpose, <math>\pi^T = (\pi P)^T </math><br> | |||
then <math>I \pi^T = P^T \pi^T \Rightarrow (P^T-I) \pi^T = 0 </math><br> | |||
So <math>\pi^T </math> is an eigenvector of <math>P^T</math> with corresponding eigenvalue 1. <br> | |||
the transpose method to calculate the pi matrix probability. | |||
It is thus possible to compute the stationary distribution by taking the eigenvector of the transpose of the transition matrix corresponding to 1, and normalize it such that all elements are non-negative and sum to one so that the elements satisfy the definition of a stationary distribution. The transformed vector is still an eigenvector since a linear transformation of an eigenvector is still within the eigenspace. Taking the transpose of this transformed eigenvector gives the stationary distribution. <br> | |||
<span style="background:#F5F5DC"> | |||
Generating Random Initial distribution<br> | |||
<math>\mu~=rand(1,n)</math><br> | <math>\mu~=rand(1,n)</math><br> | ||
<math>\mu~=\mu/\Sigma(\mu)</math></span> | <math>\mu~=\mu/\Sigma(\mu)</math></span> | ||
| Line 4,607: | Line 4,213: | ||
A Markov chain is a random process usually characterized as '''memoryless''': the next state depends only on the current state and not on the sequence of events that preceded it. This specific kind of "memorylessness" is called the Markov property. Markov chains have many applications as statistical models of real-world processes. | A Markov chain is a random process usually characterized as '''memoryless''': the next state depends only on the current state and not on the sequence of events that preceded it. This specific kind of "memorylessness" is called the Markov property. Markov chains have many applications as statistical models of real-world processes. | ||
1. Reducibility <br> | 1. Reducibility <br> | ||
| Line 4,629: | Line 4,230: | ||
== Class 14 - Thursday June 20th 2013 == | == Class 14 - Thursday June 20th 2013 == | ||
Example: Find the stationary distribution of <math> P= \left[ {\begin{array}{ccc} | |||
\frac{1}{3} & \frac{1}{3} & \frac{1}{3} \\[6pt] | |||
\frac{1}{4} & \frac{3}{4} & 0 \\[6pt] | |||
\frac{1}{2} & 0 & \frac{1}{2} \end{array} } \right]</math> | |||
<math>\pi=\pi p</math> | |||
Solve the system of linear equations to find a stationary distribution | |||
<math>\pi=(\frac{1}{3},\frac{4}{9}, \frac{2}{9})</math> | |||
<math>\pi=(\frac{1}{3},\frac{4}{9}, \frac{2}{9})</math> | |||
<math>\lambda u=A u</math> | <math>\lambda u=A u</math> | ||
<math>\pi</math> can be considered as an eigenvector of P with eigenvalue = 1. | <math>\pi</math> can be considered as an eigenvector of P with eigenvalue = 1. | ||
But the vector u here needs to be a column vector. So we need to transform <math>\pi</math> into a column vector. | But the vector u here needs to be a column vector. So we need to transform <math>\pi</math> into a column vector. | ||
<math>\pi</math><sup>T</sup>= P<sup>T</sup><math>\pi</math><sup>T</sup> | <math>\pi</math><sup>T</sup>= P<sup>T</sup><math>\pi</math><sup>T</sup> | ||
Then <math>\pi</math><sup>T</sup> is an eigenvector of P<sup>T</sup> with eigenvalue = 1. <br /> | Then <math>\pi</math><sup>T</sup> is an eigenvector of P<sup>T</sup> with eigenvalue = 1. <br /> | ||
MatLab tips:[V D]=eig(A), where D is a diagonal matrix of eigenvalues and V is a matrix of eigenvectors of matrix A<br /> | MatLab tips:[V D]=eig(A), where D is a diagonal matrix of eigenvalues and V is a matrix of eigenvectors of matrix A<br /> | ||
==== MatLab Code ==== | |||
==== Limiting distribution ==== | |||
==== Limiting | A Markov chain has limiting distribution <math>\pi</math> if | ||
A Markov chain has | |||
<math>\lim_{n\to \infty} P^n= \left[ {\begin{array}{ccc} | <math>\lim_{n\to \infty} P^n= \left[ {\begin{array}{ccc} | ||
| Line 4,717: | Line 4,262: | ||
That is <math>\pi_j=\lim[P^n]_{ij}</math> exists and is independent of i.<br/> | That is <math>\pi_j=\lim[P^n]_{ij}</math> exists and is independent of i.<br/> | ||
A Markov Chain is convergent if and only if its limiting distribution exists | A Markov Chain is convergent if and only if its limiting distribution exists. <br/> | ||
If the limiting distribution <math>\pi</math> exists, it must be equal to the stationary distribution.<br/> | |||
In general, there are chains with | In general, there are chains with stationery distributions that don't converge, this means that they have stationary distribution but are not limiting.<br/> | ||
| Line 4,734: | Line 4,278: | ||
\end{matrix} \right] </math> | \end{matrix} \right] </math> | ||
This chain converges but is not a | This chain converges but is not a limiting distribution as the rows are not the same and it doesn't converge to the stationary distribution.<br /> | ||
<span style="font-size:20px;color:red">The following contents are problematic. Please correct it if possible.</span><br /> | <span style="font-size:20px;color:red">The following contents are problematic. Please correct it if possible.</span><br /> | ||
Suppose we're given that the | Suppose we're given that the limiting distribution <math> \pi </math> exists for stochastic matrix P, that is, <math> \pi = \pi * P </math> <br> | ||
WLOG assume P is diagonalizable, (if not we can always consider the Jordan form and the computation below is exactly the same. <br> | WLOG assume P is diagonalizable, (if not we can always consider the Jordan form and the computation below is exactly the same. <br> | ||
Let <math> P = U * \Sigma * U^{-1} </math> be the eigenvalue decomposition of <math> P </math>, where <math>\Sigma = diag(\lambda_1,\ldots,\lambda_n) | Let <math> P = U * \Sigma * U^{-1} </math> be the eigenvalue decomposition of <math> P </math>, where <math>\Sigma = diag(\lambda_1,\ldots,\lambda_n) ; |\lambda_i| > |\lambda_j|, \forall i < j </math><br> | ||
Suppose <math> | Suppose <math> \pi^T = \sum a_i u_i </math> where <math> a_i \in \mathcal{R} </math> and <math> u_i </math> are eigenvectors of <math> P </math> for <math> i = 1\ldots n </math> <br> | ||
By definition: <math> \pi^k = \pi*P = \pi*P^k \implies \pi = \pi*(U * \Sigma * U^{-1}) *(U * \Sigma * U^{-1} )*\ldots*(U * \Sigma * U^{-1}) </math> <br> | By definition: <math> \pi^k = \pi*P = \pi*P^k \implies \pi = \pi*(U * \Sigma * U^{-1}) *(U * \Sigma * U^{-1} )*\ldots*(U * \Sigma * U^{-1}) </math> <br> | ||
| Line 4,753: | Line 4,297: | ||
=== MatLab Code === | === MatLab Code === | ||
<pre style='font-size:14px'> | <pre style='font-size:14px'> | ||
>> P=[1/3, 1/3, 1/3; 1/4, 3/4, 0; 1/2, 0, 1/2] % We input a matrix P.This is the same matrix as last class | >> P=[1/3, 1/3, 1/3; 1/4, 3/4, 0; 1/2, 0, 1/2] % We input a matrix P.This is the same matrix as last class. | ||
P = | P = | ||
| Line 4,779: | Line 4,323: | ||
>> P^10 | >> P^10 | ||
the example of code and an example of | the example of code and an example of stand distribution, then the all the pi probability in the matrix are the same. | ||
ans = | ans = | ||
| Line 4,787: | Line 4,331: | ||
0.3360 0.4358 0.2282 | 0.3360 0.4358 0.2282 | ||
>> P^100 % The | >> P^100 % The stationary distribution is [0.3333 0.4444 0.2222] since values keep unchanged. | ||
ans = | ans = | ||
| Line 4,811: | Line 4,355: | ||
0 0 -0.0643 | 0 0 -0.0643 | ||
>> a=-vec(:,1) | >> a=-vec(:,1) % The eigenvectors can be mutiplied by (-1) since λV=AV can be written as λ(-V)=A(-V) | ||
a = | a = | ||
| Line 4,836: | Line 4,380: | ||
This is <math>\pi_j = lim[p^n]_(ij)</math> exist and is independent of i | This is <math>\pi_j = lim[p^n]_(ij)</math> exist and is independent of i | ||
Example: Find the | Example: Find the stationary distribution of P= <math>\left[ {\begin{array}{ccc} | ||
0 & 1 & 0 \\ | 0 & 1 & 0 \\ | ||
0 & 0 & 1 \\ | 0 & 0 & 1 \\ | ||
| Line 4,855: | Line 4,399: | ||
Also, <math>\pi</math><sub>1</sub> = <math>\pi</math><sub>2</sub> = 1/3 <br> | Also, <math>\pi</math><sub>1</sub> = <math>\pi</math><sub>2</sub> = 1/3 <br> | ||
So, <math>\pi</math> = <math>[\frac{1}{3}, \frac{1}{3}, \frac{1}{3}]</math> <br> | So, <math>\pi</math> = <math>[\frac{1}{3}, \frac{1}{3}, \frac{1}{3}]</math> <br> | ||
when the p matrix is a standard matrix, then all the probabilities of pi are the same in the matrix. | when the p matrix is a standard matrix, then all the probabilities of pi are the same in the matrix. | ||
| Line 4,919: | Line 4,463: | ||
</pre> | </pre> | ||
The first condition of | The first condition of limiting distribution is satisfied; however, the second condition where <math>\pi</math><sub>j</sub> has to be independent of i (i.e. all rows of the matrix are the same) is not met.<br> | ||
This example shows the distinction between having a | This example shows the distinction between having a stationary distribution and convergence(having a limiting distribution).Note: <math>\pi=(1/3,1/3,1/3)</math> is the stationary distribution as <math>\pi=\pi*p</math>. However, upon repeatedly multiplying P by itself (repeating the step <math>P^n</math> as n goes to infinite) one will note that the results become a cycle (of period 3) of the same sequence of matrices. The chain has a stationary distribution, but does not converge to it. Thus, there is no limiting distribution.<br> | ||
Another example: | Another example: | ||
| Line 4,946: | Line 4,490: | ||
So, <math>\pi = [\frac{1}{2}, \frac{1}{4}, \frac{1}{4}]</math> <br> | So, <math>\pi = [\frac{1}{2}, \frac{1}{4}, \frac{1}{4}]</math> <br> | ||
=== Ergodic Chain === | |||
A Markov chain is called an ergodic chain if it is possible to go from every state to every state (not necessarily in one move). For instance, note that we can claim a Markov chain is ergodic if it is possible to somehow start at any state i and end at any state j in the matrix. We could have a chain with states 0, 1, 2, 3, 4 where it is not possible to go from state 0 to state 4 in just one step. However, it may be possible to go from 0 to 1, then from 1 to 2, then from 2 to 3, and finally 3 to 4 so we can claim that it is possible to go from 0 to 4 and this would satisfy a requirement of an ergodic chain. The example below will further explain this concept. | |||
''' | '''Note:'''if there's a finite number N then every other state can be reached in N steps. | ||
====Example==== | |||
<math> | <math> P= \left[ \begin{matrix} | ||
\ | \frac{1}{3} \; & \frac{1}{3} \; & \frac{1}{3} \\ \\ | ||
\frac{1}{4} \; & \frac{3}{4} \; & 0 \\ \\ | |||
\frac{1}{2} \; & 0 \; & \frac{1}{2} | |||
\end{matrix} \right] </math><br /> | |||
<math> \pi=\left[ \begin{matrix} | |||
\frac{1}{3} & \frac{4}{9} & \frac{2}{9} | |||
\end{matrix} \right] </math><br /> | |||
There are three states in this example. | |||
[[File:ab.png]] | |||
In this case, state a can go to state a, b, or c; state b can go to state a, b, or c; and state c can go to state a, b, or c so it is possible to go from every state to every state. (Although state b cannot directly go into c in one move, it must go to a, and then to c.). | |||
A k-by-k matrix indicates that the chain has k states. | |||
- Ergodic Markov chains are irreducible. | |||
- A Markov chain is called a '''regular''' chain if some power of the transition matrix has only positive elements.<br /> | |||
*Any transition matrix that has no zeros determines a regular Markov chain | |||
*However, it is possible for a regular Markov chain to have a transition matrix that has zeros. | |||
<br /> | |||
For example, recall the matrix of the Land of Oz | |||
<math>P = \left[ \begin{matrix} | |||
\ | & R & N & S \\ | ||
R & 1/2 & 1/4 & 1/4 \\ | |||
N & 1/2 & 0 & 1/2 \\ | |||
S & 1/4 & 1/4 & 1/2 \\ | |||
\end{matrix} \right]</math><br /> | |||
=== Theorem === | |||
An ergodic Markov chain has a unique stationary distribution <math>\pi</math>. The limiting distribution exists and is equal to <math>\pi</math><br/> | |||
Note: Ergodic Markov Chain is irreducible, aperiodic and positive recurrent. | |||
Example: Consider the markov chain of <math>\left[\begin{matrix}0 & 1 \\ 1 & 0\end{matrix}\right]</math>, the stationary distribution is obtained by solving <math>\pi P = \pi</math>, getting <math>\pi=[0.5, 0.5]</math>, but from the assignment we know that it does not converge, ie. there is no limiting distribution, because the Markov chain is not aperiodic and cycle repeats <math>P^2=\left[\begin{matrix}1 & 0 \\ 0 & 1\end{matrix}\right]</math> and <math>P^3=\left[\begin{matrix}0 & 1 \\ 1 & 0\end{matrix}\right]</math> | |||
'''Another Example''' | |||
<math>P=\left[ {\begin{array}{ccc} | |||
\frac{1}{4} & \frac{3}{4} \\[6pt] | |||
\frac{1}{5} & \frac{4}{5} \end{array} } \right]</math> <br> | |||
[[File:Untitled*.jpg]] | |||
This matrix means that there are two points in the space, let's call them a and b<br/> | |||
< | Starting from a, the probability of staying in a is 1/4 <br/> | ||
< | Starting from a, the probability of going from a to b is 3/4 <br/> | ||
Starting from b, the probability of going from b to a is 1/5 <br/> | |||
Starting from b, the probability of staying in b is 4/5 <br/> | |||
Solve the equation <math> \pi = \pi P </math> <br> | |||
<math> \pi_0 = .25 \pi_0 + .2 \pi_1 </math> <br> | |||
<math> \pi_1 = .75 \pi_0 + .8 \pi_1 </math> <br> | |||
<math> \pi_0 + \pi_1 = 1 </math> <br> | |||
Solving this system of equations we get: <br> | |||
<math> \pi_0 = \frac{4}{15} \pi_1 </math> <br> | |||
<math> \pi_1 = \frac{15}{19} </math> <br> | |||
<math> \pi_0 = \frac{4}{19} </math> <br> | |||
<math> \pi = [\frac{4}{19}, \frac{15}{19}] </math> <br> | |||
<math> \pi </math> is the long run distribution | |||
<math> | We can use the stationary distribution to compute the expected waiting time to return to state 'a' <br/> | ||
\frac{1}{ | given that we start at state 'a' and so on.. Formula for this will be : <math> E[T_{i,i}]=\frac{1}{\pi_i}</math><br/> | ||
In the example above this will mean that that expected waiting time for the markov process to return to<br/> | |||
state 'a' given that we start at state 'a' is 19/4.<br/> | |||
definition of limiting distribution. | |||
remark:satisfied balance of <math>\pi_i P_{ij} = P_{ji} \pi_j</math>, so there is other way to calculate the step probability. | |||
=== MatLab Code === | |||
In the following, P is the transition matrix. eye(n) refers to the n by n Identity matrix. L is the Laplacian matrix, L = (I - P). The Laplacian matrix will have at least 1 zero Eigenvalue. For every 0 in the diagonal, there is a component. If there is exactly 1 zero Eigenvalue, then the matrix is connected and has only 1 component. The number of zeros in the Laplacian matrix is the number of parts in your graph/process. If there is more than one zero on the diagonal of this matrix, this means there is a disconnect in the graph. | |||
<pre style='font-size:14px'> | |||
>> P=[1/3, 1/3, 1/3; 1/4, 3/4, 0; 1/2, 0, 1/2] | |||
P = | |||
0.3333 0.3333 0.3333 | |||
0.2500 0.7500 0 | |||
0.5000 0 0.5000 | |||
>> eye(3) %%returns 3x3 identity matrix | |||
ans = | |||
1 0 0 | |||
0 1 0 | |||
0 0 1 | |||
>> L=(eye(3)-P) | |||
L = | |||
0.6667 -0.3333 -0.3333 | |||
-0.2500 0.2500 0 | |||
-0.5000 0 0.5000 | |||
>> [vec val]=eigs(L) | |||
vec = | |||
-0.7295 0.2329 0.5774 | |||
0.2239 -0.5690 0.5774 | |||
0.6463 0.7887 0.5774 | |||
val = | |||
1.0643 0 0 | |||
0 0.3523 0 | |||
0 0 -0.0000 | |||
%% Only one value of zero on the diagonal means the chain is connected | |||
>> P=[0.8, 0.2, 0, 0;0.2, 0.8, 0, 0; 0, 0, 0.8, 0.2; 0, 0, 0.1, 0.9] | |||
P = | |||
0.8000 0.2000 0 0 | |||
0.2000 0.8000 0 0 | |||
0 0 0.8000 0.2000 | |||
0 0 0.1000 0.9000 | |||
>> eye(4) | |||
ans = | |||
1 0 0 0 | |||
0 1 0 0 | |||
0 0 1 0 | |||
0 0 0 1 | |||
>> L=(eye(4)-P) | |||
L = | |||
0.2000 -0.2000 0 0 | |||
-0.2000 0.2000 0 0 | |||
0 0 0.2000 -0.2000 | |||
0 0 -0.1000 0.1000 | |||
>> [vec val]=eigs(L) | |||
= | vec = | ||
0.7071 0 0.7071 0 | |||
-0.7071 0 0.7071 0 | |||
0 0.8944 0 0.7071 | |||
0 -0.4472 0 0.7071 | |||
val = | |||
0. | 0.4000 0 0 0 | ||
0 0.3000 0 0 | |||
0 0 -0.0000 0 | |||
0 0 0 -0.0000 | |||
%% Two values of zero on the diagonal means there are two 'islands' of chains | |||
</pre> | |||
<math>\Pi</math> satisfies detailed balance if <math>\Pi_i P_{ij}=P_{ij} \Pi_j</math>. Detailed balance guarantees that <math>\Pi</math> is stationary distribution.<br /> | |||
>> | '''Adjacency matrix''' - a matrix <math>A</math> that dictates which states are connected and way of portraying which vertices in the matrix are adjacent. If we compute <math>A^2</math>, we can know which states are connected with paths of length 2.<br /> | ||
A '''Markov chain''' is called an irreducible chain if it is possible to go from every state to every state (not necessary in one more).<br /> | |||
Theorem: An '''ergodic''' Markov chain has a unique stationary distribution <math>\pi</math>. The limiting distribution exists and is equal to <math>\pi</math>. <br /> | |||
Markov process satisfies detailed balance if and only if it is a '''reversible''' Markov process | |||
where P is the matrix of Markov transition.<br /> | |||
>> | Satisfying the detailed balance condition guarantees that <math>\pi</math> is stationary distributed. | ||
<math> \pi </math> satisfies detailed balance if <math> \pi_i P_{ij} = P_{ji} \pi_j </math> <br> | |||
which is the same as the Markov process equation. | |||
Example in the class: | |||
<math>P= \left[ {\begin{array}{ccc} | |||
\frac{1}{3} & \frac{1}{3} & \frac{1}{3} \\[6pt] | |||
\frac{1}{4} & \frac{3}{4} & 0 \\[6pt] | |||
\frac{1}{2} & 0 & \frac{1}{2} \end{array} } \right]</math> | |||
and <math>\pi=(\frac{1}{3},\frac{4}{9}, \frac{2}{9})</math> | |||
<math>\pi_1 P_{1,2} = 1/3 \times 1/3 = 1/9,\, P_{2,1} \pi_2 = 1/4 \times 4/9 = 1/9 \Rightarrow \pi_1 P_{1,2} = P_{2,1} \pi_2 </math><br> | |||
<math>\pi_2 P_{2,3} = 4/9 \times 0 = 0,\, P_{3,2} \pi_3 = 0 \times 2/9 = 0 \Rightarrow \pi_2 P_{2,3} = P_{3,2} \pi_3</math><br> | |||
Remark:Detailed balance of <math> \pi_i * Pij = Pji * \pi_j</math> , so there is other way to calculate the step probability<br /> | |||
<math>\pi</math> is stationary but is not limiting. | |||
== Class 15 - Tuesday June 25th 2013 == | |||
=== Announcement === | |||
Note to all students, the first half of today's lecture will cover the midterm's solution; however please do not post the solution on the Wikicoursenote.<br /> | |||
====Detailed balance==== | |||
P = | Let <math>P</math> be the transition probability matrix of a Markov chain. If there exists a distribution vector <math>\pi</math> such that <math>\pi_i \cdot P_{ij}=P_{ji} \cdot \pi_j, \; \forall i,j</math>, then the Markov chain is said to have '''detailed balance'''. A detailed balanced Markov chain must have <math>\pi</math> given above as a stationary distribution, that is <math>\pi=\pi P</math>, where <math>\pi</math> is a 1 by n matrix and P is a n by n matrix.<br> | ||
'''Proof:''' <br> | |||
<math>\; [\pi P]_j = \sum_i \pi_i P_{ij} =\sum_i P_{ji}\pi_j =\pi_j\sum_i P_{ji} =\pi_j ,\forall j</math> | |||
:Note: Since <math>\pi_j</math> is a sum of coloum j and we can do this proof for every element in matrix P; in general, we can prove <math>\pi=\pi P</math> <br> | |||
>> | Hence <math>\pi</math> is always a stationary distribution of <math>P(X_n+1=j|X_n=i)</math>, for every n. | ||
In other terms, <math> P_{ij} = P(X_n = j| X_{n-1} = i) </math>, where <math>\pi_j</math> is the equilibrium probability of being in state j and <math>\pi_i</math> is the equilibrium probability of being in state i. <math>P(X_{n-1} = i) = \pi_i</math> is equivalent to <math>P(X_{n-1} = i, Xn = j)</math> being symmetric in i and j. | |||
Keep in mind that the detailed balance is a sufficient but not required condition for a distribution to be stationary. | |||
i.e. A distribution satisfying the detailed balance is stationary, but a stationary distribution does not necessarily satisfy the detailed balance. | |||
>> | In the stationary distribution <math>\pi=\pi P</math>, in the proof the sum of the p is equal 1 so the <math>\pi P=\pi</math>. | ||
=== PageRank (http://en.wikipedia.org/wiki/PageRank) === | |||
*PageRank is a link-analysis algorithm developed by Larry Page from Google; used for measuring a website's importance, relevance and popularity. | |||
*PageRank is a graph containing web pages and their links to each other. | |||
*Many social media sites use this (such as Facebook and Twitter) | |||
*It can also be used to find criminals (ie. theives, hackers, terrorists, etc.) by finding out the links. | |||
This is what made Google the search engine of choice over Yahoo, Bing, etc.- What made Google's search engine a huge success is not its search function, but rather the algorithm it used to rank the pages. (Ex. If we come up with 100 million search results, how do you list them by relevance and importance so the users can easily find what they are looking for. Most users will not go past the first 3 or so search pages to find what they are looking for. It is this ability to rank pages that allow Google to remain more popular than Yahoo, Bink, AskJeeves, etc.)<br /> | |||
<br />'''The order of importance'''<br /> | |||
1. A web page is important if it has many other pages linked to it<br /> | |||
2. The more important a web page is, the more weight should be assigned to its outgoing links<br/ > | |||
3. If a webpage has many outgoing links then its links have less value (ex: if a page links to everyone, like 411, it is not as important as pages that have incoming links)<br /> | |||
<br /> | |||
[[File:diagram.jpg]] | |||
<math>L= | |||
\left[ {\begin{matrix} | |||
0 & 0 & 0 & 0 & 0 \\ | |||
1 & 0 & 0 & 0 & 0 \\ | |||
1 & 1 & 0 & 1 & 0 \\ | |||
0 & 1 & 0 & 0 & 1 \\ | |||
0 & 0 & 0 & 0 & 0 \end{matrix} } \right]</math> | |||
ie: According to the above example <br/ > | |||
Page 3 is the most important since it has the most links pointing to it, therefore more weigh should be placed on its outgoing links.<br/ > | |||
Page 4 comes after page 3 since it has the second most links pointing to it<br/ > | |||
Page 2 comes after page 4 since it has the third most links pointing to it<br/> | |||
Page 1 and page 5 are the least important since no links point to them<br/ > | |||
As page 1 and page 2 has the most outgoing links, then their links have less value compared to the other pages. <br/ > | |||
<math>L_{ij} = 1</math> if j has a link to i;<br/ > | |||
<math>L_{ij} = 0</math> otherwise.<br /> | |||
<br /> | |||
C<sub>j</sub> The number of outgoing links of page <math>j</math>: | |||
<math>C_j=\sum_i L_{ij}</math> | |||
(i.e. sum of entries in column j)<br /> | |||
<br /> | |||
<math>P_j</math> is the rank of page <math>j</math>.<br /> | |||
Suppose we have <math>N</math> pages, <math>P</math> is a vector containing ranks of all pages.<br /> | |||
- <math>P</math> is a <math>N \times 1</math> vector. | |||
</ | - <math>P_i</math> counts the number of incoming links of page <math>i</math> | ||
<math>P_i=\sum_j L_{ij}</math> <br />(i.e. sum of entries in row i) | |||
for each row, if there is a 1 in the third column, it means page three point to that page. | |||
A PageRank results from a mathematical algorithm based on the webgraph, created by all World Wide Web pages as nodes and hyperlinks as edges, taking into consideration authority hubs such as cnn.com or usa.gov. The rank value indicates an importance of a particular page. A hyperlink to a page counts as a vote of support. (This would be represented in our diagram as an arrow pointing towards the page. Hence in our example, Page 3 is the most important, since it has the most 'votes of support). The PageRank of a page is defined recursively and depends on the number and PageRank metric of all pages that link to it ("incoming links"). A page that is linked to by many pages with high PageRank receives a high rank itself. If there are no links to a web page, then there is no support for that page (In our example, this would be Page 1 and Page 5). | |||
(source:http://en.wikipedia.org/wiki/PageRank#Description) | |||
For those interested in PageRank, here is the original paper by Google co-founders Brin and Page: http://infolab.stanford.edu/pub/papers/google.pdf | |||
=== Example of Page Rank Application in Real Life === | |||
'''Page Rank checker''' | |||
- This is a free service to check Google™ page rank instantly via online PR checker or by adding a PageRank checking button to the | |||
web pages (http://www.prchecker.info/check_page_rank.php) | |||
GoogleMatrix G = d * [ (Hyperlink Matrix H) + (Dangling Nodes Matrix A) ] + ((1-d)/N) * (NxN Matrix U of all 1's) | |||
[[File:Google matrix.png]] | |||
(source: https://googledrive.com/host/0B2GQktu-wcTiaWw5OFVqT1k3bDA/) | |||
== Class 16 - Thursday June 27th 2013 == | |||
<math> | === Page Rank === | ||
<math>L_{ij}</math> equals 1 if j has a link to i, and equals 0 otherwise. <br> | |||
<math>C_j</math> :The number of outgoing links for page j, where <math>c_j=\sum_i L_{ij}</math> | |||
P is N by 1 vector contains rank of all N pages; for page i, the rank is <math>P_i</math> | |||
<math> | |||
<math>P_i= (1-d) + d\cdot \sum_j \frac {L_{ij}P_j}{c_j}</math> | |||
< | where 0 < d < 1 is constant (in original page rank algorithm d = 0.8). | ||
< | Interpretation of the formula:<br/> | ||
1) sum of L<sub>ij</sub> is the total number of incoming links<br/> | |||
2) the above sum is weighted by page rank of the pages that contain the link to i (P<sub>j</sub>) i.e. if a high-rank page points to page i, then this link carries more weight than links from lower-rank pages.<br/> | |||
3) the sum is then weighted by the inverse of the number of outgoing links from the pages that contain links to i (c<sub>j</sub>). i.e. if a page has more outgoing links than other pages then its links carry less weight.<br/> | |||
4) finally, we take a linear combination of the page rank obtained from above and a constant 1. This ensures that every page has a rank greater than zero.<br/> | |||
Note that this is a system of N equations with N unknowns.<br/> | |||
<math>c_j</math> is the number of outgoing links, less outgoing links means more important.<br/> | |||
Let D be a diagonal N by N matrix such that <math> D_{ii}</math> = <math>c_i</math> | |||
[ | <math>D= | ||
\left[ {\begin{matrix} | |||
c_1 & 0 & ... & 0 \\ | |||
0 & c_2 & ... & 0 \\ | |||
0 & 0 & ... & 0 \\ | |||
0 & 0 & ... & c_N \end{matrix} } \right]</math> | |||
Then P = (1-d) e + dLD<sup>-1</sup>P <br/> where e =[1 1 ....]<sup>T</sup> , i.e. a N by 1 vector.<br/> | |||
< | We assume that rank of all N pages sums to N. The sum of rank of all N pages can be any number, as long as the ranks have certain propotion. <br/> | ||
i.e. e<sup>T</sup> P = N, then <math>~\frac{e^{T}P}{N} = 1</math> | |||
D<sup>-1</sup> will be: | |||
D<sup>-1</sup><math>= | |||
\left[ {\begin{matrix} | |||
\frac {1}{c_1} & 0 & ... & 0 \\ | |||
0 & \frac {1}{c_2} & ... & 0 \\ | |||
0 & 0 & ... & 0 \\ | |||
0 & 0 & ... & \frac {1}{c_N} \end{matrix} } \right]</math> | |||
<math>P=~(1-d)e+dLD^{-1}P</math> where <math>e=\begin{bmatrix} | |||
1\\ | |||
1\\ | |||
...\\ | |||
1 | |||
\end{bmatrix}</math> | |||
<math>P=(1-d)~\frac{ee^{T}P}{N}+dLD^{-1}P</math> | |||
<math>P=[(1-d)~\frac{ee^T}{N}+dLD^{-1}]P</math> | |||
P=AP | |||
N is a N*N matrix, | |||
L is a N*N matrix, | |||
D<sup>-1</sup> is a N*N matrix, | |||
P is a N*1 matrix | |||
d is a constant between 0 and 1 | |||
''' | '''P=AP'''<br /> | ||
P is an eigenvector of A with corresponding eigenvalue equal to 1.<br> | |||
'''P<sup>T</sup>=P<sup>T</sup>A<sup>T</sup><br>''' | |||
Notice that all entries in A are non-negative and each row sums to 1. Hence A satisfies the definition of a transition probability matrix.<br> | |||
P<sup>T</sup> is the stationary distribution of a Markov Chain with transition probability matrix A<sup>T</sup>. | |||
We can consider A to be the matrix describing all possible movements following links on the internet, and P<sup>t</sup> as the probability of being on any given webpage if we were on the internet long enough. | |||
Definition of rank page and proof it steps by steps, it shows with 3 n*n matrix and and one n*1 matrix and a constant d between 0 to 1. | |||
p is the stationary distribution so p=Ap. | |||
=== Damping Factor "d" === | |||
The PageRank assumes that any imaginary user who is randomly clicking on links will eventually stop clicking. The probability, at any step, that the person will keep on clicking is a damping factor, "d". After many studies, the approximation of "d" is 0.85. Other values for "d" have been used in class and may appear on assignments/exams. | |||
=== | ===Examples=== | ||
<span style="background:#F5F5DC"> | |||
==== Example 1 ==== | |||
[[File:eg1.jpg]] | |||
<br /> | <br /> | ||
</span> | |||
<math>L= | <math>L= | ||
\left[ {\begin{matrix} | \left[ {\begin{matrix} | ||
0 & 0 & | 0 & 0 & 1 \\ | ||
1 | 1 & 0 & 0 \\ | ||
0 & 1 & 0 \end{matrix} } \right]</math> | |||
0 & 1 | |||
<math>c= | |||
\left[ {\begin{matrix} | |||
1 & 1 & 1 \end{matrix} } \right]</math> | |||
<math> | <math>D= | ||
\left[ {\begin{matrix} | |||
1 & 0 & 0 \\ | |||
0 & 1 & 0 \\ | |||
0 & 0 & 1 \end{matrix} } \right]</math> | |||
<pre style='font-size:14px'> | |||
MATLAB Code | |||
d=0.8 | |||
N=3 | |||
A=(1-d)*ones(N)/N+d*L*pinv(D) #pinv: Moore-Penrose inverse (pseudoinverse) of symbolic matrix | |||
We use the pinv(D) function [pseudo-inverse] instead of the inv(D) function because in | |||
the case of a non-invertible matrix, it would not crash the program. | |||
[vec val]=eigs(A) (eigen-decomposition) | |||
a=-vec(:,1) (find the eigenvector equals to 1) | |||
a=a/sum(a) (normalize a) | |||
or to show that A transpose is a stationary transition matrix | |||
(transpose(A))^200 will be the same as a=a/sum(a) | |||
</pre> | |||
'''NOTE:''' Changing the value of d, does not change the ranking order of the pages. | |||
By looking at each entry after normalizing a, we can tell the ranking order of each page.<br> | |||
<span style="background:#F5F5DC"> | |||
c = [1 1 1] since there are 3 pages, each page is one way recurrent to each other and there is only one outgoing for each page. Hence, D is a 3x3 standard diagonal matrix. | |||
==== Example 2 ==== | |||
[[File:Screen_shot_2013-07-02_at_3.43.04_AM.png]] | |||
<math>L= | |||
\left[ {\begin{matrix} | |||
0 & 0 & 1 \\ | |||
1 & 0 & 1 \\ | |||
0 & 1 & 0 \end{matrix} } \right]</math> | |||
<math>c= | |||
\left[ {\begin{matrix} | |||
1 & 1 & 2 \end{matrix} } \right]</math> | |||
<math>D= | |||
\left[ {\begin{matrix} | |||
1 & 0 & 0 \\ | |||
0 & 1 & 0 \\ | |||
0 & 0 & 2 \end{matrix} } \right]</math> | |||
<pre style='font-size:14px'> | |||
Matlab code | |||
( | >> L=[0 0 1;1 0 1;0 1 0]; | ||
>> C=sum(L); | |||
== | >> D=diag(C); | ||
>> d=0.8; | |||
>> N=3; | |||
>> A=(1-d)*ones(N)/N+d*L*pinv(D); | |||
>> [vec val]=eigs(A) | |||
= | vec = | ||
-0.3707 -0.3536 + 0.3536i -0.3536 - 0.3536i | |||
-0.6672 -0.3536 - 0.3536i -0.3536 + 0.3536i | |||
-0.6461 0.7071 0.7071 | |||
val = | |||
1.0000 0 0 | |||
0 -0.4000 - 0.4000i 0 | |||
0 0 -0.4000 + 0.4000i | |||
>> a=-vec(:,1) | |||
1) | |||
a = | |||
0.3707 | |||
0.6672 | |||
0.6461 | |||
>> a=a/sum(a) | |||
a = | |||
< | 0.2201 | ||
0.3962 | |||
2 | 0.3836 | ||
3 | </pre> | ||
'''NOTE:''' Page 2 is the most important page because it has 2 incomings. Similarly, page 3 is more important than page 1 because page 3 has the incoming result from page 2. | |||
This example is similar to the first example, but here, page 3 can go back to page 2, so the matrix of the outgoing matrix, the third column of the D matrix is 3 in the third row. And we use the code to calculate the p=Ap. | |||
==== Example 3 ==== | |||
[[File:eg 3.jpg]]<br> | |||
<math>L= | |||
\left[ {\begin{matrix} | |||
0 & 1 & 0 \\ | |||
1 & 0 & 1 \\ | |||
0 & 1 & 0 \end{matrix} } \right]</math> | |||
<math>c= | |||
\left[ {\begin{matrix} | |||
1 & 2 & 1 \end{matrix} } \right]</math> | |||
<math>D= | <math>D= | ||
\left[ {\begin{matrix} | \left[ {\begin{matrix} | ||
1 & 0 & 0 \\ | |||
0 & | 0 & 2 & 0 \\ | ||
0 & 0 & | 0 & 0 & 1 \end{matrix} } \right]</math> | ||
<math>d=0.8</math><br> | |||
<math>N=3</math><br> | |||
</span> | |||
this example is the second page have 2 outgoings. | |||
Another Example: | |||
< | Consider: 1 -> ,<-2 ->3 | ||
L= [0 1 0; 1 0 0; 0 1 0]; c=[1,1,1]; D= [1 0 0; 0 1 0; 0 0 1] | |||
==== Example 4 ==== | |||
< | 1 <-> 2 -> 3 <-> 4 | ||
<math>L= | <math>L= | ||
\left[ {\begin{matrix} | \left[ {\begin{matrix} | ||
0 & 1 & 0 & 0 \\ | |||
1 & 0 & 0 & 0 \\ | |||
0 & 1 & 0 & 1 \\ | |||
0 & 0 & 1 & 0 \end{matrix} } \right]</math> | |||
<math> | <math>c= | ||
\left[ {\begin{matrix} | \left[ {\begin{matrix} | ||
1 | 1 & 2 & 1 & 1 \end{matrix} } \right]</math> | ||
<math> | <math>D= | ||
\left[ {\begin{matrix} | \left[ {\begin{matrix} | ||
1 & 0 & 0 & 0 \\ | |||
0 & 2 & 0 & 0 \\ | |||
0 & 0 & 1 & 0 \\ | |||
0 & 0 & 0 & 1 \end{matrix} } \right]</math><br /> | |||
Matlab code | |||
<pre style='font-size:14px'> | |||
>> L=L= [0 1 0 0;1 0 0 0;0 1 0 1;0 0 1 0]; | |||
>> C=sum(L); | |||
>> D=diag(C); | |||
>> d=0.8; | |||
>> N=4; | |||
>> A=(1-d)*ones(N)/N+d*L*pinv(D) | |||
A = | |||
0.0500 0.4500 0.0500 0.0500 | |||
0.8500 0.0500 0.0500 0.0500 | |||
0.0500 0.4500 0.0500 0.8500 | |||
0.0500 0.0500 0.8500 0.0500 | |||
>> [vec val]=eigs(A) | |||
vec = | |||
0.1817 -0.0000 -0.4082 0.4082 | |||
0.2336 0.0000 0.5774 0.5774 | |||
0.7009 -0.7071 0.4082 -0.4082 | |||
0.6490 0.7071 -0.5774 -0.5774 | |||
val = | |||
1.0000 0 0 0 | |||
0 -0.8000 0 0 | |||
0 0 -0.5657 0 | |||
0 0 0 0.5657 | |||
= | >> a=vec(:,1) | ||
>> a=vec(:,1) | |||
a = | |||
0.1817 | |||
0.2336 | |||
0.7009 | |||
0.6490 | |||
>> a=a/sum(a) | |||
a = | |||
0.1029 | |||
0.1324 | |||
0.3971 | |||
0 | 0.3676 | ||
0 | |||
</pre> | </pre> | ||
'''NOTE:''' The ranking of each page is as follows: Page 3, Page 4, Page 2 and Page 1. Page 3 is the highest since it has the most incoming links. All of the other pages only have one incoming link but since Page 3, highest ranked page, links to Page 4, Page 4 is the second highest ranked. Lastly, since Page 2 links into Page 3 it is the next highest rank. | |||
Page 2 has 2 outgoing links. Pages with the same incoming links can be ranked closest to the highest ranked page. If the highest page P1 is incoming into a page P2, then P2 is ranked second, and so on. | |||
==== Example 5 ==== | |||
<math>L= | <math>L= | ||
\left[ {\begin{matrix} | \left[ {\begin{matrix} | ||
0 & 0 & 1 | 0 & 1 & 0 & 1 \\ | ||
1 & 0 & 1 | 1 & 0 & 1 & 1 \\ | ||
0 & 1 & 0 \end{matrix} } \right]</math> | 1 & 0 & 0 & 1 \\ | ||
1 & 0 & 0 & 0 \end{matrix} } \right]</math> | |||
<math>c= | <math>c= | ||
\left[ {\begin{matrix} | \left[ {\begin{matrix} | ||
1 & 1 & | 3 & 1 & 1 & 3 \end{matrix} } \right]</math> | ||
<math>D= | <math>D= | ||
\left[ {\begin{matrix} | \left[ {\begin{matrix} | ||
1 & 0 & 0 | 3 & 0 & 0 & 0 \\ | ||
0 & 1 & 0 \\ | 0 & 1 & 0 & 0 \\ | ||
0 & 0 & | 0 & 0 & 1 & 0 \\ | ||
0 & 0 & 0 & 3 \end{matrix} } \right]</math> | |||
<pre style='font-size:14px'> | <pre style='font-size:14px'> | ||
| Line 5,595: | Line 5,123: | ||
Matlab code | Matlab code | ||
>> L=[0 0 1;1 0 1;0 1 0]; | >> L= [0 1 0 1; 1 0 1 1; 1 0 0 1;1 0 0 0]; | ||
>> C=sum(L); | >> d = 0.8; | ||
>> D=diag(C) | >> N = 4; | ||
>> C = sum(L); | |||
>> D = diag(C); | |||
>> A=(1-d)*ones(N)/N+d*L*pinv(D); | >> A=(1-d)*ones(N)/N+d*L*pinv(D); | ||
>> [vec val]=eigs(A) | >> [vec val]=eigs(A); | ||
>> a=vec(:,1); | |||
>> a=a/sum(a) | |||
a = | |||
0.3492 | |||
0.3263 | |||
0.1813 | |||
0.1431 | |||
</pre> | |||
==== Example 6 ==== | |||
<math>L= | |||
\left[ {\begin{matrix} | |||
0 & 1 & 0 & 0 & 1\\ | |||
1 & 0 & 0 & 0 & 0\\ | |||
0 & 1 & 0 & 0 & 0\\ | |||
0 & 1 & 1 & 0 & 1\\ | |||
0 & 0 & 0 & 1 & 0 \end{matrix} } \right]</math> | |||
<br /> | |||
Matlab Code<br /> | |||
<pre style="font-size:16px"> | |||
>> d=0.8 | |||
d = | |||
0.8000 | |||
>> L=[0 1 0 0 1;1 0 0 0 0;0 1 0 0 0;0 1 1 0 1;0 0 0 1 0] | |||
L = | |||
0 1 0 0 1 | |||
1 0 0 0 0 | |||
0 1 0 0 0 | |||
0 1 1 0 1 | |||
0 0 0 1 0 | |||
>> c=sum(L) | |||
c = | |||
1 3 1 1 2 | |||
= | >> D=diag(c) | ||
D = | |||
1 0 0 0 0 | |||
0 3 0 0 0 | |||
0 | 0 0 1 0 0 | ||
1 | 0 0 0 1 0 | ||
0 | 0 0 0 0 2 | ||
>> N=5 | |||
N = | |||
5 | |||
>> A=(1-d)*ones(N)/N+d*L*pinv(D) | |||
A = | |||
0.0400 0.3067 0.0400 0.0400 0.4400 | |||
0.8400 0.0400 0.0400 0.0400 0.0400 | |||
0.0400 0.3067 0.0400 0.0400 0.0400 | |||
0.0400 0.3067 0.8400 0.0400 0.4400 | |||
0.0400 0.0400 0.0400 0.8400 0.0400 | |||
>> [vec val]=eigs(A) | |||
vec = | |||
Columns 1 through 4 | |||
-0.4129 0.4845 + 0.1032i 0.4845 - 0.1032i -0.0089 + 0.2973i | |||
-0.4158 -0.6586 -0.6586 -0.5005 + 0.2232i | |||
0 | -0.1963 0.2854 - 0.0608i 0.2854 + 0.0608i -0.2570 - 0.2173i | ||
-0.5700 0.1302 + 0.2612i 0.1302 - 0.2612i 0.1462 - 0.3032i | |||
0 | -0.5415 -0.2416 - 0.3036i -0.2416 + 0.3036i 0.6202 | ||
0 | |||
0 | |||
Column 5 | |||
-0.0089 - 0.2973i | |||
-0.5005 - 0.2232i | |||
-0.2570 + 0.2173i | |||
0.1462 + 0.3032i | |||
0.6202 | |||
val = | |||
Columns 1 through 4 | |||
1 | |||
1.0000 0 0 0 | |||
0 -0.5886 - 0.1253i 0 0 | |||
0 0 -0.5886 + 0.1253i 0 | |||
0 0 0 0.1886 - 0.3911i | |||
0 0 0 0 | |||
Column 5 | |||
0 | |||
0 | |||
0 | |||
0 | |||
0.1886 + 0.3911i | |||
>> a=-vec(:,1) | |||
a = | |||
0.4129 | |||
0.4158 | |||
0.1963 | |||
0.5700 | |||
0.5415 | |||
>> a=a/sum(a) | |||
a = | |||
0.1933 | |||
0.1946 | |||
0.0919 | |||
0.2668 % (the most important) | |||
0.2534 | |||
</pre> | |||
for the matrix , page 1 has 2 outgoing, and page 2 has one from page 1, page 3 has 2 from 2, page 4 has 3 outgoing ,and page 5 has 1 outgoing , 1 and 2, 4 and 5 outgoing to each other. so the c=[2 1 1 3 1], the rank is page 4 , page 5, page 2 and page 1 and page 3.<br /> | |||
== Class 17 - Tuesday July 2nd 2013 == | |||
=== Markov Chain Monte Carlo (MCMC) === | |||
Idea: generate a Markov Chain whose stationary distribution is the target distribution. | |||
>> | Motivation example<br /> | ||
- Suppose we want to generate random variable X according to distribution <math>\pi=(\pi_1, \pi_2, ... , \pi_m)</math> <br/> | |||
X can take m different values from x={1,2,3,....,m}<br /> | |||
- We want to generate {Xt, t=0, 1, ....., n } according to <math>\pi</math><br /> | |||
{X0, X1, ....., Xn}<br /> | |||
example: | |||
M=6, | |||
Pi=[0.1,0.1,0.1,0.2,0.3,0.2] | |||
X=[1,2,3,4,5,6] | |||
- Suppose Xt=j<br /> | |||
consider an arbitrary probability transition matrix Q with entry q<sub>ij</sub>. <br/> | |||
>> | <math> \mathbf{Q} = | ||
\begin{bmatrix} | |||
q_{11} & q_{12} & \cdots & q_{1m} \\ | |||
q_{21} & q_{22} & \cdots & q_{2m} \\ | |||
\vdots & \vdots & \ddots & \vdots \\ | |||
q_{m1} & q_{m2} & \cdots & q_{mm} | |||
\end{bmatrix} | |||
</math> <br/> | |||
q<sub>ij</sub> is the probability of moving to state i from state j. <br/> | |||
Generate Y according to i-th row of matrix Q. | |||
i.e.P(Y=j)=q<sub>ij</sub><br /> | |||
r<sub>ij</sub> is the probabiliy of accepting j. <br/> | |||
<math> | '''Algorithm:''' <br/> | ||
\ | *<math>P(Y=j) = q_{ij} </math>(*) <br/> | ||
*<math> r_{ij} = min (\frac{\pi_j q_{ji}}{\pi_i q_{ij}}, 1) </math> <br/> | |||
* <math> | |||
x_{t+1} = \begin{cases} | |||
Y, & \text{w/p} r_{ij} \\ | |||
x_t, & \text{otherwise} \end{cases} </math> <br/> | |||
*go to (*) <br/> | |||
<math> | This algorithm generates <math> {x_t, t=0,...,n} </math>. In the long run, the marginal distribution of <math> x_t </math> is <math>\underline{\Pi} </math></br> | ||
<math> {x_t, t = 0, 1,...,n}</math> is a Markov chain with probability transition matrix P. | |||
This is a Markov Chain since <math> x_t+1 </math> only depends on <math> x_t | |||
<math> | |||
<math> | \text{Where }P_{ij}= \begin{cases} | ||
\ | q_{ij} r_{ij}& \text {if i != j} \\ | ||
1 - \sum_{j} (q_{ij} r_{ij}), & \text{if i = j} \end{cases} </math> | |||
< | |||
>> | |||
> | |||
end | |||
</ | |||
Detailed Balance: | |||
<math>\pi_i P_{ij} = p_{ji} \pi_j</math> | |||
LHS: | |||
<math>\pi_i P_{ij} = \pi_i q_{ij} r_{ij} = \pi_i q_{ij} \frac{\pi_j q_{ij}}{\pi_i q_{ij}} = \pi_i q_{ji} | |||
Revision as of 21:06, 12 July 2013
Introduction, Class 1 - Tuesday, May 7
Course Instructor: Ali Ghodsi
Lecture:
001: T/Th 8:30-9:50am MC1085
002: T/Th 1:00-2:20pm DC1351
Tutorial:
2:30-3:20pm Mon M3 1006
Office Hours:
Friday at 10am, M3 4208
Midterm
Monday June 17,2013 from 2:30pm-3:20pm
Final
Saturday August 10,2013 from 7:30pm-10:00pm
TA(s):
| TA | Day | Time | Location |
|---|---|---|---|
| Lu Cheng | Monday | 3:30-5:30 pm | M3 3108, space 2 |
| Han ShengSun | Tuesday | 4:00-6:00 pm | M3 3108, space 2 |
| Yizhou Fang | Wednesday | 1:00-3:00 pm | M3 3108, space 1 |
| Huan Cheng | Thursday | 3:00-5:00 pm | M3 3111, space 1 |
| Wu Lin | Friday | 11:00-1:00 pm | M3 3108, space 1 |
Four Fundamental Problems
1. Classification: Given an input object X, we have a function which will take in this input X and identify which 'class (Y)' it belongs to (Discrete Case)
i.e taking value from x, we could predict y.
(For example, if you have 40 images of oranges and 60 images of apples (represented by x), you can estimate a function that takes the images and states what type of fruit it is - note Y is discrete in this case.)
2. Regression: Same as classification but in the continuous case except y is non discrete. (Example of stock prices)
(A simple practice might be investigating the hypothesis that higher levels of education cause higher levels of income.)
3. Clustering: Use common features of objects in same class or group to form clusters.(in this case, x is given, y is unknown)
4. Dimensionality Reduction (aka Feature extraction, Manifold learning): Used when we have a variable in high dimension space and we want to reduce the dimension
Applications
Most useful when structure of the task is not well understood but can be characterized by a dataset with strong statistical regularity
Examples:
- Computer Vision, Computer Graphics, Finance (fraud detection), Machine Learning
- Search and recommendation (eg. Google, Amazon)
- Automatic speech recognition, speaker verification
- Text parsing
- Face identification
- Tracking objects in video
- Financial prediction(e.g. credit cards)
- Fraud detection
- Medical diagnosis
Course Information
Prerequisite: (One of CS 116, 126/124, 134, 136, 138, 145, SYDE 221/322) and (STAT 230 with a grade of at least 60% or STAT 240) and (STAT 231 or 241)
Antirequisite: CM 361/STAT 341, CS 437, 457
General Information
- No required textbook
- Recommended: "Simulation" by Sheldon M. Ross
- Computing parts of the course will be done in Matlab, but prior knowledge of Matlab is not essential (will have a tutorial on it)
- First midterm will be held on Monday, June 17 from 2:30 to 3:30
- Announcements and assignments will be posted on Learn.
- Other course material on: http://wikicoursenote.com/wiki/
- Log on to both Learn and wikicoursenote frequently.
- Email all questions and concerns to UWStat340@gmail.com. Do not use your personal email address! Do not email instructor or TAs about the class directly to their personal accounts!
Wikicourse note (10% of final mark):
When applying for an account in the wikicourse note, please use the quest account as your login name while the uwaterloo email as the registered email. This is important as the quest id will be used to identify the students who make the contributions.
Example:
User: questid
Email: questid@uwaterloo.ca
After the student has made the account request, do wait for several hours before students can login into the account using the passwords stated in the email. During the first login, students will be ask to create a new password for their account.
As a technical/editorial contributor: Make contributions within 1 week and do not copy the notes on the blackboard.
All contributions are now considered general contributions you must contribute to 50% of lectures for full marks
- A general contribution can be correctional (fixing mistakes) or technical (expanding content, adding examples, etc.) but at least half of your contributions should be technical for full marks.
Do not submit copyrighted work without permission, cite original sources. Each time you make a contribution, check mark the table. Marks are calculated on an honour system, although there will be random verifications. If you are caught claiming to contribute but have not, you will not be credited.
Wikicoursenote contribution form : https://docs.google.com/forms/d/1Sgq0uDztDvtcS5JoBMtWziwH96DrBz2JiURvHPNd-xs/viewform
- you can submit your contributions multiple times.
- you will be able to edit the response right after submitting
- send email to make changes to an old response : uwstat340@gmail.com
Tentative Topics
- Random variable and stochastic process generation
- Discrete-Event Systems
- Variance reduction
- Markov Chain Monte Carlo
Tentative Marking Scheme
| Item | Value |
|---|---|
| Assignments (~6) | 30% |
| WikiCourseNote | 10% |
| Midterm | 20% |
| Final | 40% |
The final exam is going to be closed book and only non-programmable calculators are allowed.
A passing mark must be achieved in the final to pass the course
Class 2 - Thursday, May 9
Generating Random Numbers
Introduction
Simulation is the imitation of a process or system over time. Computational power has introduced the possibility of using simulation study to analyze models used to describe a situation.
In order to perform a simulation study, we must first:
<br\> 1. Use a computer to generate (pseudo) random numbers.
2. Use these numbers to generate values of random variable from distributions.
3. Using the concept of discrete events, we show how the random variables can be used to generate the behavior of a stochastic model over time. (Note: A stochastic model is the opposite of deterministic model, where there are several directions the process can evolve to)
4. After continually generating the behavior of the system, we can obtain estimators and other quantities of interest.
The building block of a simulation study is the ability to generate a random number. This random number is a value from a random variable distributed uniformly on (0,1). There are many different methods of generating a random number:
Physical Method: Roulette wheel, lottery balls, dice rolling, card shuffling etc.
Numerically/Arithmetically: Use of a computer to successively generate pseudorandom numbers. The
sequence of numbers can appear to be random; however they are deterministically calculated with an
equation which defines pseudorandom.
(Source: Ross, Sheldon M., and Sheldon M. Ross. Simulation. San Diego: Academic, 1997. Print.)
In general, a deterministic model produces specific results given certain inputs by the model user, contrasting with a stochastic model which encapsulates randomness and probabilistic events.
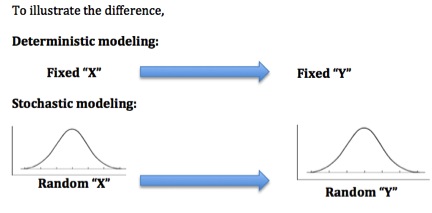
A computer cannot generate truly random numbers because computers can only run algorithms, which are deterministic in nature. They can, however, generate Pseudo Random Numbers
Pseudo Random Numbers are the numbers that seem random but are actually deterministic. Although the pseudo random numbers are deterministic, these numbers have a sequence of value and all of them have the appearances of being independent uniform random variables. Being deterministic, pseudo random numbers are valuable and beneficial due to the ease to generate and manipulate.
When people do the test many times, the results will be the closed express values, which make the trial look deterministic, however for each trial, the result is random. So, it looks like pseudo random numbers.
Mod
Let [math]\displaystyle{ n \in \N }[/math] and [math]\displaystyle{ m \in \N^+ }[/math], then by Division Algorithm,
[math]\displaystyle{ \exists q, \, r \in \N \;\text{with}\; 0\leq r \lt m, \; \text{s.t.}\; n = mq+r }[/math],
where [math]\displaystyle{ q }[/math] is called the quotient and [math]\displaystyle{ r }[/math] the remainder. Hence we can define a binary function
[math]\displaystyle{ \mod : \N \times \N^+ \rightarrow \N }[/math] given by [math]\displaystyle{ r:=n \mod m }[/math] which returns the remainder after division by m.
Generally, mod means taking the reminder after division by m.
We say that n is congruent to r mod m if n = mq + r, where m is an integer.
if y = ax + b, then [math]\displaystyle{ b:=y \mod a }[/math].
For example:
30 = 4 * 7 + 2
2 = 30 mod 7
25 = 8 * 3 + 1
1 = 25 mod 3
Note: [math]\displaystyle{ \mod }[/math] here is different from the modulo congruence relation in [math]\displaystyle{ \Z_m }[/math], which is an equivalence relation instead of a function.
The modulo operation is useful for determining if an integer divided by another integer produces a non-zero remainder. But both integers should satisfy n = mq + r, where m, r, q, and n are all integers, and r is smaller than m.
Mixed Congruential Algorithm
We define the Linear Congruential Method to be [math]\displaystyle{ x_{k+1}=(ax_k + b) \mod m }[/math], where [math]\displaystyle{ x_k, a, b, m \in \N, \;\text{with}\; a, m \neq 0 }[/math]. Given a seed (i.e. an initial value [math]\displaystyle{ x_0 \in \N }[/math]), we can obtain values for [math]\displaystyle{ x_1, \, x_2, \, \cdots, x_n }[/math] inductively. The Multiplicative Congruential Method, invented by Berkeley professor D. H. Lehmer, may also refer to the special case where [math]\displaystyle{ b=0 }[/math] and the Mixed Congruential Method is case where [math]\displaystyle{ b \neq 0 }[/math]
An interesting fact about Linear Congruential Method is that it is one of the oldest and best-known pseudo random number generator algorithms. It is very fast and requires minimal memory to retain state. However, this method should not be used for applications that require high randomness. They should not be used for Monte Carlo simulation and cryptographic applications. (Monte Carlo simulation will consider possibilities for every choice of consideration, and it shows the extreme possibilities. This method is not precise enough.)
First consider the following algorithm
[math]\displaystyle{ x_{k+1}=x_{k} \mod m }[/math]
Example
[math]\displaystyle{ \text{Let }x_{0}=10,\,m=3 }[/math]
- [math]\displaystyle{ \begin{align} x_{1} &{}= 10 &{}\mod{3} = 1 \\ x_{2} &{}= 1 &{}\mod{3} = 1 \\ x_{3} &{}= 1 &{}\mod{3} =1 \\ \end{align} }[/math]
[math]\displaystyle{ \ldots }[/math]
Excluding [math]\displaystyle{ x_{0} }[/math], this example generates a series of ones. In general, excluding [math]\displaystyle{ x_{0} }[/math], the algorithm above will always generate a series of the same number less than M. Hence, it has a period of 1. The period can be described as the length of a sequence before it repeats. We want a large period with a sequence that is random looking. We can modify this algorithm to form the Multiplicative Congruential Algorithm.
[math]\displaystyle{ x_{k+1}=(a \cdot x_{k} + b) \mod m }[/math](a little tip: [math]\displaystyle{ (a \cdot b)\mod c = (a\mod c)\cdot(b\mod c)) }[/math]
Example
[math]\displaystyle{ \text{Let }a=2,\, b=1, \, m=3, \, x_{0} = 10 }[/math]
[math]\displaystyle{ \begin{align}
\text{Step 1: } 0&{}=(2\cdot 10 + 1) &{}\mod 3 \\
\text{Step 2: } 1&{}=(2\cdot 0 + 1) &{}\mod 3 \\
\text{Step 3: } 0&{}=(2\cdot 1 + 1) &{}\mod 3 \\
\end{align} }[/math]
[math]\displaystyle{ \ldots }[/math]
This example generates a sequence with a repeating cycle of two integers.
(If we choose the numbers properly, we could get a sequence of "random" numbers. How do we find the value of [math]\displaystyle{ a,b, }[/math] and [math]\displaystyle{ m }[/math]? At the very least [math]\displaystyle{ m }[/math] should be a very large, preferably prime number. The larger [math]\displaystyle{ m }[/math] is, the higher the possibility to get a sequence of "random" numbers. This is easier to solve in Matlab. In Matlab, the command rand() generates random numbers which are uniformly distributed on the interval (0,1)). Matlab uses [math]\displaystyle{ a=7^5, b=0, m=2^{31}-1 }[/math] – recommended in a 1988 paper, "Random Number Generators: Good Ones Are Hard To Find" by Stephen K. Park and Keith W. Miller (Important part is that [math]\displaystyle{ m }[/math] should be large and prime)
Note: [math]\displaystyle{ \frac {x_{n+1}}{m-1} }[/math] is an approximation to the value of a U(0,1) random variable.
MatLab Instruction for Multiplicative Congruential Algorithm:
Before you start, you need to clear all existing defined variables and operations:
>>clear all >>close all
>>a=17 >>b=3 >>m=31 >>x=5 >>mod(a*x+b,m) ans=26 >>x=mod(a*x+b,m)
(Note:
1. Keep repeating this command over and over again and you will get random numbers – this is how the command rand works in a computer.
2. There is a function in MATLAB called RAND to generate a random number between 0 and 1.
For example, in MATLAB, we can use rand(1,1000) to generate 1000's numbers between 0 and 1. This is essentially a vector with 1 row, 1000 columns, with each entry a random number between 0 and 1.
3. If we would like to generate 1000 or more numbers, we could use a for loop
(Note on MATLAB commands:
1. clear all: clears all variables.
2. close all: closes all figures.
3. who: displays all defined variables.
4. clc: clears screen.
5. ; : prevents the results from printing.
>>a=13 >>b=0 >>m=31 >>x(1)=1 >>for ii=2:1000 x(ii)=mod(a*x(ii-1)+b,m); end >>size(x) ans=1 1000 >>hist(x)
(Note: The semicolon after the x(ii)=mod(a*x(ii-1)+b,m) ensures that Matlab will not print the entire vector of x. It will instead calculate it internally and you will be able to work with it. Adding the semicolon to the end of this line reduces the run time significantly.)
This algorithm involves three integer parameters [math]\displaystyle{ a, b, }[/math] and [math]\displaystyle{ m }[/math] and an initial value, [math]\displaystyle{ x_0 }[/math] called the seed. A sequence of numbers is defined by [math]\displaystyle{ x_{k+1} = ax_k+ b \mod m }[/math].
Note: For some bad [math]\displaystyle{ a }[/math] and [math]\displaystyle{ b }[/math], the histogram may not look uniformly distributed.
Note: In MATLAB, hist(x) will generate a graph representing the distribution. Use this function after you run the code to check the real sample distribution.
Example: [math]\displaystyle{ a=13, b=0, m=31 }[/math]
The first 30 numbers in the sequence are a permutation of integers from 1 to 30, and then the sequence repeats itself so it is important to choose [math]\displaystyle{ m }[/math] large to decrease the probability of each number repeating itself too early. Values are between [math]\displaystyle{ 0 }[/math] and [math]\displaystyle{ m-1 }[/math]. If the values are normalized by dividing by [math]\displaystyle{ m-1 }[/math], then the results are approximately numbers uniformly distributed in the interval [0,1]. There is only a finite number of values (30 possible values in this case). In MATLAB, you can use function "hist(x)" to see if it looks uniformly distributed. We saw that the values between 0-30 had the same frequency in the histogram, so we can conclude that they are uniformly distributed.
If [math]\displaystyle{ x_0=1 }[/math], then
- [math]\displaystyle{ x_{k+1} = 13x_{k}\mod{31} }[/math]
So,
- [math]\displaystyle{ \begin{align} x_{0} &{}= 1 \\ x_{1} &{}= 13 \times 1 + 0 &{}\mod{31} = 13 \\ x_{2} &{}= 13 \times 13 + 0 &{}\mod{31} = 14 \\ x_{3} &{}= 13 \times 14 + 0 &{}\mod{31} =27 \\ \end{align} }[/math]
etc.
For example, with [math]\displaystyle{ a = 3, b = 2, m = 4, x_0 = 1 }[/math], we have:
- [math]\displaystyle{ x_{k+1} = (3x_{k} + 2)\mod{4} }[/math]
So,
- [math]\displaystyle{ \begin{align}
x_{0} &{}= 1 \\
x_{1} &{}= 3 \times 1 + 2 \mod{4} = 1 \\
x_{2} &{}= 3 \times 1 + 2 \mod{4} = 1 \\
\end{align} }[/math]
etc.
FAQ:
1.Why is it 1 to 30 instead of 0 to 30 in the example above?
[math]\displaystyle{ b = 0 }[/math] so in order to have [math]\displaystyle{ x_k }[/math] equal to 0, [math]\displaystyle{ x_{k-1} }[/math] must be 0 (since [math]\displaystyle{ a=13 }[/math] is relatively prime to 31). However, the seed is 1. Hence, we will never observe 0 in the sequence.
Alternatively, {0} and {1,2,...,30} are two orbits of the left multiplication by 13 in the group [math]\displaystyle{ \Z_{31} }[/math].
2.Will the number 31 ever appear?Is there a probability that a number never appears?
The number 31 will never appear. When you perform the operation [math]\displaystyle{ \mod m }[/math], the largest possible answer that you could receive is [math]\displaystyle{ m-1 }[/math]. Whether or not a particular number in the range from 0 to [math]\displaystyle{ m - 1 }[/math] appears in the above algorithm will be dependent on the values chosen for [math]\displaystyle{ a, b }[/math] and [math]\displaystyle{ m }[/math].
Examples:[From Textbook]
If [math]\displaystyle{ x_0=3 }[/math] and [math]\displaystyle{ x_n=(5x_{n-1}+7)\mod 200 }[/math], find [math]\displaystyle{ x_1,\cdots,x_{10} }[/math].
Solution:
[math]\displaystyle{ \begin{align}
x_1 &{}= (5 \times 3+7) &{}\mod{200} &{}= 22 \\
x_2 &{}= 117 &{}\mod{200} &{}= 117 \\
x_3 &{}= 592 &{}\mod{200} &{}= 192 \\
x_4 &{}= 2967 &{}\mod{200} &{}= 167 \\
x_5 &{}= 14842 &{}\mod{200} &{}= 42 \\
x_6 &{}= 74217 &{}\mod{200} &{}= 17 \\
x_7 &{}= 371092 &{}\mod{200} &{}= 92 \\
x_8 &{}= 1855467 &{}\mod{200} &{}= 67 \\
x_9 &{}= 9277342 &{}\mod{200} &{}= 142 \\
x_{10} &{}= 46386717 &{}\mod{200} &{}= 117 \\
\end{align} }[/math]
Comments:
Typically, it is good to choose [math]\displaystyle{ m }[/math] such that [math]\displaystyle{ m }[/math] is large, and [math]\displaystyle{ m }[/math] is prime. Careful selection of parameters '[math]\displaystyle{ a }[/math]' and '[math]\displaystyle{ b }[/math]' also helps generate relatively "random" output values, where it is harder to identify patterns. For example, when we used a composite (non prime) number such as 40 for [math]\displaystyle{ m }[/math], our results were not satisfactory in producing an output resembling a uniform distribution.
The computed values are between 0 and [math]\displaystyle{ m-1 }[/math]. If the values are normalized by dividing by [math]\displaystyle{ m-1 }[/math], their result is numbers uniformly distributed on the interval [math]\displaystyle{ \left[0,1\right] }[/math] (similar to computing from uniform distribution).
From the example shown above, if we want to create a large group of random numbers, it is better to have large, prime [math]\displaystyle{ m }[/math] so that the generated random values will not repeat after several iterations. Note: the period for this example is 8: from '[math]\displaystyle{ x_2 }[/math]' to '[math]\displaystyle{ x_9 }[/math]'.
There has been a research on how to choose uniform sequence. Many programs give you the options to choose the seed. Sometimes the seed is chosen by CPU.
Theorem (extra knowledge)
Let c be a non-zero constant. Then for any seed x0, and LCG will have largest max. period if and only if
(i) m and c are coprime;
(ii) (a-1) is divisible by all prime factor of m;
(iii) if and only if m is divisible by 4, then a-1 is also divisible by 4.
We want our LCG to have a large cycle. We call a cycle with m element the maximal period. We can make it bigger by making m big and prime. Recall:any number you can think of can be broken into a factor of prime Define coprime:Two numbers X and Y, are coprime if they do not share any prime factors.
Example:
Xn=(15Xn-1 + 4) mod 7
(i) m=7 c=4 -> coprime;
(ii) a-1=14 and a-1 is divisible by 7;
(iii) dose not apply.
(The extra knowledge stops here)
In this part, I learned how to use R code to figure out the relationship between two integers division, and their remainder. And when we use R to calculate R with random variables for a range such as(1:1000),the graph of distribution is like uniform distribution.
Summary of Multiplicative Congruential Algorithm
Problem: generate Pseudo Random Numbers.
Plan:
- find integer: a b m(large prime) x0(the seed) .
- [math]\displaystyle{ x_{k+1}=(ax_{k}+b) }[/math]mod m
Matlab Instruction:
>>clear all >>close all >>a=17 >>b=3 >>m=31 >>x=5 >>mod(a*x+b,m) ans=26 >>x=mod(a*x+b,m)
[math]\displaystyle{ \lt math\gt Insert formula here }[/math][math]\displaystyle{ \lt math\gt Insert formula here }[/math]</math></math>=== Inverse Transform Method ===
Now that we know how to generate random numbers, we use these values to sample form distributions such as exponential. However, to easily use this method, the probability distribution consumed must have a cumulative distribution function (cdf) [math]\displaystyle{ F }[/math] with a tractable (that is, easily found) inverse [math]\displaystyle{ F^{-1} }[/math].
Theorem:
If we want to generate the value of a discrete random variable X, we must generate a random number U, uniformly distributed over (0,1).
Let [math]\displaystyle{ F:\R \rightarrow \left[0,1\right] }[/math] be a cdf. If [math]\displaystyle{ U \sim U\left[0,1\right] }[/math], then the random variable given by [math]\displaystyle{ X:=F^{-1}\left(U\right) }[/math]
follows the distribution function [math]\displaystyle{ F\left(\cdot\right) }[/math],
where [math]\displaystyle{ F^{-1}\left(u\right):=\inf F^{-1}\big(\left[u,+\infty\right)\big) = \inf\{x\in\R | F\left(x\right) \geq u\} }[/math] is the generalized inverse.
Note: [math]\displaystyle{ F }[/math] need not be invertible everywhere on the real line, but if it is, then the generalized inverse is the same as the inverse in the usual case. We only need it to be invertible on the range of F(x), [0,1].
Proof of the theorem:
The generalized inverse satisfies the following:
[math]\displaystyle{ \begin{align}
\forall u \in \left[0,1\right], \, x \in \R, \\
&{} F^{-1}\left(u\right) \leq x &{} \\
\Rightarrow &{} F\Big(F^{-1}\left(u\right)\Big) \leq F\left(x\right) &&{} F \text{ is non-decreasing} \\
\Rightarrow &{} F\Big(\inf \{y \in \R | F(y)\geq u \}\Big) \leq F\left(x\right) &&{} \text{by definition of } F^{-1} \\
\Rightarrow &{} \inf \{F(y) \in [0,1] | F(y)\geq u \} \leq F\left(x\right) &&{} F \text{ is right continuous and non-decreasing} \\
\Rightarrow &{} u \leq F\left(x\right) &&{} \text{by definition of } \inf \\
\Rightarrow &{} x \in \{y \in \R | F(y) \geq u\} &&{} \\
\Rightarrow &{} x \geq \inf \{y \in \R | F(y)\geq u \}\Big) &&{} \text{by definition of } \inf \\
\Rightarrow &{} x \geq F^{-1}(u) &&{} \text{by definition of } F^{-1} \\
\end{align} }[/math]
That is [math]\displaystyle{ F^{-1}\left(u\right) \leq x \Leftrightarrow u \leq F\left(x\right) }[/math]
Finally, [math]\displaystyle{ P(X \leq x) = P(F^{-1}(U) \leq x) = P(U \leq F(x)) = F(x) }[/math], since [math]\displaystyle{ U }[/math] is uniform on the unit interval.
This completes the proof.
Therefore, in order to generate a random variable X~F, it can generate U according to U(0,1) and then make the transformation x=[math]\displaystyle{ F^{-1}(U) }[/math]
Note that we can apply the inverse on both sides in the proof of the inverse transform only if the pdf of X is monotonic. A monotonic function is one that is either increasing for all x, or decreasing for all x. Of course, this holds true for all CDFs, since they are monotonic by definition.
In short, what the theorem tells us is that we can use a random number [math]\displaystyle{ U from U(0,1) }[/math] to randomly sample a point on the CDF of X, then apply the inverse of the CDF to map the given probability to its domain, which gives us the random variable X.
Example 1 - Exponential: [math]\displaystyle{ f(x) = \lambda e^{-\lambda x} }[/math]
Calculate the CDF:
[math]\displaystyle{ F(x)= \int_0^x f(t) dt = \int_0^x \lambda e ^{-\lambda t}\ dt }[/math]
[math]\displaystyle{ = \frac{\lambda}{-\lambda}\, e^{-\lambda t}\, | \underset{0}{x} }[/math]
[math]\displaystyle{ = -e^{-\lambda x} + e^0 =1 - e^{- \lambda x} }[/math]
Solve the inverse:
[math]\displaystyle{ y=1-e^{- \lambda x} \Rightarrow 1-y=e^{- \lambda x} \Rightarrow x=-\frac {ln(1-y)}{\lambda} }[/math]
[math]\displaystyle{ y=-\frac {ln(1-x)}{\lambda} \Rightarrow F^{-1}(x)=-\frac {ln(1-x)}{\lambda} }[/math]
Note that 1 − U is also uniform on (0, 1) and thus −log(1 − U) has the same distribution as −logU.
Steps:
Step 1: Draw U ~U[0,1];
Step 2: [math]\displaystyle{ x=\frac{-ln(U)}{\lambda} }[/math]
MatLab Code:
>>u=rand(1,1000); >>hist(u) #will generate a fairly uniform diagram
#let λ=2 in this example; however, you can make another value for λ >>x=(-log(1-u))/2; >>size(x) #1000 in size >>figure >>hist(x) #exponential
Example 2 - Continuous Distribution:
[math]\displaystyle{ f(x) = \dfrac {\lambda } {2}e^{-\lambda \left| x-\theta \right| } for -\infty \lt X \lt \infty , \lambda \gt 0 }[/math]
Calculate the CDF:
[math]\displaystyle{ F(x)= \frac{1}{2} e^{-\lambda (\theta - x)} , for \ x \le \theta }[/math]
[math]\displaystyle{ F(x) = 1 - \frac{1}{2} e^{-\lambda (x - \theta)}, for \ x \gt \theta }[/math]
Solve for the inverse:
[math]\displaystyle{ F^{-1}(x)= \theta + ln(2y)/\lambda, for \ 0 \le y \le 0.5 }[/math]
[math]\displaystyle{ F^{-1}(x)= \theta - ln(2(1-y))/\lambda, for \ 0.5 \lt y \le 1 }[/math]
Algorithm:
Steps:
Step 1: Draw U ~ U[0, 1];
Step 2: Compute [math]\displaystyle{ X = F^-1(U) }[/math] i.e. [math]\displaystyle{ X = \theta + \frac {1}{\lambda} ln(2U) }[/math] for U < 0.5 else [math]\displaystyle{ X = \theta -\frac {1}{\lambda} ln(2(1-U)) }[/math]
Example 3 - [math]\displaystyle{ F(x) = x^5 }[/math]:
Given a CDF of X: [math]\displaystyle{ F(x) = x^5 }[/math], transform U~U[0,1].
Sol:
Let [math]\displaystyle{ y=x^5 }[/math], solve for x: [math]\displaystyle{ x=y^\frac {1}{5} }[/math]. Therefore, [math]\displaystyle{ F^{-1} (x) = x^\frac {1}{5} }[/math]
Hence, to obtain a value of x from F(x), we first set u as an uniform distribution, then obtain the inverse function of F(x), and set
[math]\displaystyle{ x= u^\frac{1}{5} }[/math]
Algorithm:
Steps:
Step 1: Draw U ~ rand[0, 1];
Step 2: X=U^(1/5);
Example 4 - BETA(1,β):
Given u~U[0,1], generate x from BETA(1,β)
Solution:
[math]\displaystyle{ F(x)= 1-(1-x)^\beta }[/math],
[math]\displaystyle{ u= 1-(1-x)^\beta }[/math]
Solve for x:
[math]\displaystyle{ (1-x)^\beta = 1-u }[/math],
[math]\displaystyle{ 1-x = (1-u)^\frac {1}{\beta} }[/math],
[math]\displaystyle{ x = 1-(1-u)^\frac {1}{\beta} }[/math]
let β=3, use Matlab to construct N=1000 observations from Beta(1,3)
Matlab Code:
>> u = rand(1,1000);
x = 1-(1-u)^(1/3);
>> hist(x,50)
>> mean(x)
Example 5 - Estimating [math]\displaystyle{ \pi }[/math]:
Let's use rand() and Monte Carlo Method to estimate [math]\displaystyle{ \pi }[/math]
N= total number of points
Nc = total number of points inside the circle
Prob[(x,y) lies in the circle=[math]\displaystyle{ \frac {Area(circle)}{Area(square)} }[/math]
If we take square of size 2, circle will have area =[math]\displaystyle{ \pi (\frac {2}{2})^2 =\pi }[/math].
Thus [math]\displaystyle{ \pi= 4(\frac {N_c}{N}) }[/math]
For example, UNIF(a,b)
[math]\displaystyle{ y = F(x) = (x - a)/ (b - a) }[/math] [math]\displaystyle{ x = (b - a ) * y + a }[/math] [math]\displaystyle{ X = a + ( b - a) * U }[/math]
where U is UNIF(0,1)
Limitations:
1. This method is flawed since not all functions are invertible or monotonic: generalized inverse is hard to work on.
2. It may be impractical since some CDF's and/or integrals are not easy to compute such as Gaussian distribution.
We learned how to prove the transformation from cdf to inverse cdf,and use the uniform distribution to obtain a value of x from F(x). We can also use uniform distribution in inverse method to determine other distributions. The probability of getting a point for a circle over the triangle is a closed uniform distribution, each point in the circle and over the triangle is almost the same. Then, we can look at the graph to determine what kind of distribution the graph resembles.
Probability Distribution Function Tool in MATLAB
disttool #shows different distributions
This command allows users to explore the effect of changes of parameters on the plot of either a CDF or PDF.
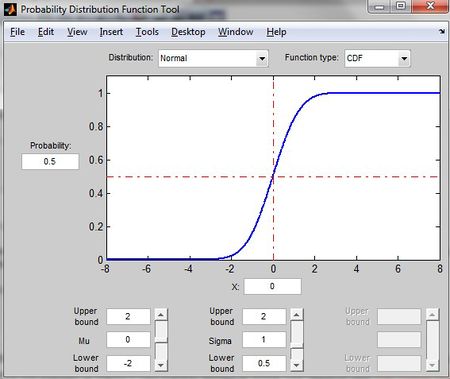 change the value of mu and sigma can change the graph skew side.
change the value of mu and sigma can change the graph skew side.
Class 3 - Tuesday, May 14
Recall the Inverse Transform Method
To sample X with CDF F(x),
1. Draw u~U(0,1)
2. X = F-1(u)
Proof
First note that
[math]\displaystyle{ P(U\leq a)=a, \forall a\in[0,1] }[/math]
- [math]\displaystyle{ P(X\leq x) }[/math]
[math]\displaystyle{ = P(F^{-1}(U)\leq x) }[/math] (since [math]\displaystyle{ X= F^{-1}(U) }[/math] by the inverse method)
[math]\displaystyle{ = P((F(F^{-1}(U))\leq F(x)) }[/math] (since [math]\displaystyle{ F }[/math] is monotonically increasing)
[math]\displaystyle{ = P(U\leq F(x)) }[/math] (since [math]\displaystyle{ P(U\leq a)= a }[/math] for [math]\displaystyle{ U \sim U(0,1), a \in [0,1] }[/math], this is explained further below)
[math]\displaystyle{ = F(x) , \text{ where } 0 \leq F(x) \leq 1 }[/math]
This is the c.d.f. of X.
Note: that the CDF of a U(a,b) random variable is:
- [math]\displaystyle{ F(x)= \begin{cases} 0 & \text{for }x \lt a \\[8pt] \frac{x-a}{b-a} & \text{for }a \le x \lt b \\[8pt] 1 & \text{for }x \ge b \end{cases} }[/math]
Thus, for [math]\displaystyle{ U }[/math] ~ [math]\displaystyle{ U(0,1) }[/math], we have [math]\displaystyle{ P(U\leq 1) = 1 }[/math] and [math]\displaystyle{ P(U\leq 1/2) = 1/2 }[/math].
More generally, we see that [math]\displaystyle{ P(U\leq a) = a }[/math].
For this reason, we had [math]\displaystyle{ P(U\leq F(x)) = F(x) }[/math].
Reminder:
This is only for uniform distribution [math]\displaystyle{ U~ \sim~ Unif [0,1] }[/math]
[math]\displaystyle{ P (U \le 1) = 1 }[/math]
[math]\displaystyle{ P (U \le 0.5) = 0.5 }[/math]
[math]\displaystyle{ P (U \le a) = a }[/math]
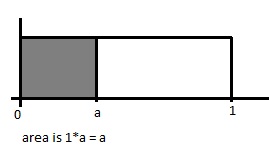 [math]\displaystyle{ P(U\leq a)=a }[/math]
[math]\displaystyle{ P(U\leq a)=a }[/math]
Note that on a single point there is no mass probability (i.e. [math]\displaystyle{ u }[/math] <= 0.5, is the same as [math]\displaystyle{ u }[/math] < 0.5) More formally, this is saying that [math]\displaystyle{ P(X = x) = F(x)- \lim_{s \to x^-}F(x) }[/math] which equals zero for any continuous random variable
Limitations of the Inverse Transform Method
Though this method is very easy to use and apply, it does have a major disadvantage/limitation:
- We need to find the inverse cdf [math]\displaystyle{ F^{-1}(\cdot) }[/math]. In some cases the inverse function does not exist, or is difficult to find because it requires a closed form expression for F(x).
For example, it is too difficult to find the inverse cdf of the Gaussian distribution, so we must find another method to sample from the Gaussian distribution.
Discrete Case
The same technique can be used for discrete case. We want to generate a discrete random variable x, that has probability mass function:
- [math]\displaystyle{ \begin{align}P(X = x_i) &{}= p_i \end{align} }[/math]
- [math]\displaystyle{ x_0 \leq x_1 \leq x_2 \dots \leq x_n }[/math]
- [math]\displaystyle{ \sum p_i = 1 }[/math]
Algorithm for applying Inverse Transformation Method in Discrete Case (Procedure):
1. Define a probability mass function for [math]\displaystyle{ x_{i} }[/math] where i = 1,....,k. Note: k could grow infinitely.
2. Generate a uniform random number U, [math]\displaystyle{ U~ \sim~ Unif [0,1] }[/math]
3. If [math]\displaystyle{ U\leq p_{o} }[/math], deliver [math]\displaystyle{ X = x_{o} }[/math]
4. Else, if [math]\displaystyle{ U\leq p_{o} + p_{1} }[/math], deliver [math]\displaystyle{ X = x_{1} }[/math]
5. Repeat the process again till we reached to [math]\displaystyle{ U\leq p_{o} + p_{1} + ......+ p_{k} }[/math], deliver [math]\displaystyle{ X = x_{k} }[/math]
Note that after generating a random U, the value of X can be determined by finding the interval [math]\displaystyle{ [F(x_{j-1}),F(x_{j})] }[/math] in which U lies.
Example 3.0:
Generate a random variable from the following probability function:
| x | -2 | -1 | 0 | 1 | 2 |
| f(x) | 0.1 | 0.5 | 0.07 | 0.03 | 0.3 |
Answer:
1. Gen U~U(0,1)
2. If U < 0.5 then output -1
else if U < 0.8 then output 2
else if U < 0.9 then output -2
else if U < 0.97 then output 0 else output 1
Example 3.1 (from class): (Coin Flipping Example)
We want to simulate a coin flip. We have U~U(0,1) and X = 0 or X = 1.
We can define the U function so that:
If U <= 0.5, then X = 0
and if 0.5 < U <= 1, then X =1.
This allows the probability of Heads occurring to be 0.5 and is a good generator of a random coin flip.
[math]\displaystyle{ U~ \sim~ Unif [0,1] }[/math]
- [math]\displaystyle{ \begin{align} P(X = 0) &{}= 0.5\\ P(X = 1) &{}= 0.5\\ \end{align} }[/math]
The answer is:
- [math]\displaystyle{ x = \begin{cases} 0, & \text{if } U\leq 0.5 \\ 1, & \text{if } 0.5 \lt U \leq 1 \end{cases} }[/math]
- Code
>>for ii=1:1000
u=rand;
if u<0.5
x(ii)=0;
else
x(ii)=1;
end
end
>>hist(x)
Note: The role of semi-colon in Matlab: Matlab will not print out the results if the line ends in a semi-colon and vice versa.
Example 3.2 (From class):
Suppose we have the following discrete distribution:
- [math]\displaystyle{ \begin{align} P(X = 0) &{}= 0.3 \\ P(X = 1) &{}= 0.2 \\ P(X = 2) &{}= 0.5 \end{align} }[/math]
The cumulative distribution function (cdf) for this distribution is then:
- [math]\displaystyle{ F(x) = \begin{cases} 0, & \text{if } x \lt 0 \\ 0.3, & \text{if } x \lt 1 \\ 0.5, & \text{if } x \lt 2 \\ 1, & \text{if } x \ge 2 \end{cases} }[/math]
Then we can generate numbers from this distribution like this, given [math]\displaystyle{ U \sim~ Unif[0, 1] }[/math]:
- [math]\displaystyle{ x = \begin{cases} 0, & \text{if } U\leq 0.3 \\ 1, & \text{if } 0.3 \lt U \leq 0.5 \\ 2, & \text{if } 0.5 \lt U\leq 1 \end{cases} }[/math]
"Procedure"
1. Draw U~u (0,1)
2. if U<=0.3 deliver x=0
3. else if 0.3<U<=0.5 deliver x=1
4. else 0.5<U<=1 deliver x=2
Can you find a faster way to run this algorithm? Consider:
- [math]\displaystyle{ x = \begin{cases} 2, & \text{if } U\leq 0.5 \\ 1, & \text{if } 0.5 \lt U \leq 0.7 \\ 0, & \text{if } 0.7 \lt U\leq 1 \end{cases} }[/math]
The logic for this is that U is most likely to fall into the largest range. Thus by putting the largest range (in this case x >= 0.5) we can improve the run time of this algorithm. Could this algorithm be improved further using the same logic?
- Code (as shown in class)
Use Editor window to edit the code
>>close all
>>clear all
>>for ii=1:1000
u=rand;
if u<=0.3
x(ii)=0;
elseif u<=0.5
x(ii)=1;
else
x(ii)=2;
end
end
>>size(x)
>>hist(x)
Example 3.3: Generating a random variable from pdf
- [math]\displaystyle{ f_{x}(x) = \begin{cases} 2x, & \text{if } 0\leq x \leq 1 \\ 0, & \text{if } otherwise \end{cases} }[/math]
- [math]\displaystyle{ F_{x}(x) = \begin{cases} 0, & \text{if } x \lt 0 \\ \int_{0}^{x}2sds = x^{2}, & \text{if } 0\leq x \leq 1 \\ 1, & \text{if } x \gt 1 \end{cases} }[/math]
- [math]\displaystyle{ \begin{align} U = x^{2}, X = F^{-1}x(U)= U^{\frac{1}{2}}\end{align} }[/math]
Example 3.4: Generating a Bernoulli random variable
- [math]\displaystyle{ \begin{align} P(X = 1) = p, P(X = 0) = 1 - p\end{align} }[/math]
- [math]\displaystyle{ F(x) = \begin{cases} 1-p, & \text{if } x \lt 1 \\ 1, & \text{if } x \ge 1 \end{cases} }[/math]
1. Draw [math]\displaystyle{ U~ \sim~ Unif [0,1] }[/math]
2. [math]\displaystyle{
X = \begin{cases}
0, & \text{if } 0 \lt U \lt 1-p \\
1, & \text{if } 1-p \le U \lt 1
\end{cases} }[/math]
Example 3.5: Generating Binomial(n,p) Random Variable
[math]\displaystyle{ use p\left( x=i+1\right) =\dfrac {n-i} {i+1}\dfrac {p} {1-p}p\left( x=i\right) }[/math]
Step 1: Generate a random number [math]\displaystyle{ U }[/math].
Step 2: [math]\displaystyle{ c = \frac {p}{(1-p)} }[/math], [math]\displaystyle{ i = 0 }[/math], [math]\displaystyle{ pr = (1-p)^n }[/math], [math]\displaystyle{ F = pr }[/math]
Step 3: If U<F, set X = i and stop,
Step 4: [math]\displaystyle{ pr = \, {\frac {c(n-i)}{(i+1)}} {pr}, F = F +pr, i = i+1 }[/math]
Step 5: Go to step 3
- Note: These steps can be found in Simulation 5th Ed. by Sheldon Ross.
- Note: Another method by seeing the Binomial as a sum of n independent Bernoulli random variables.
Step 1: Generate n uniform numbers U1 ... Un.
Step 2: X = [math]\displaystyle{ \sum U_i \lt = p }[/math] where P is the probability of success.
Example 3.6: Generating a Poisson random variable
Let X ~ Poi(u). Write an algorithm to generate X. The PDF of a poisson is:
- [math]\displaystyle{ \begin{align} f(x) = \frac {\, e^{-u} u^x}{x!} \end{align} }[/math]
We know that
- [math]\displaystyle{ \begin{align} P_{x+1} = \frac {\, e^{-u} u^{x+1}}{(x+1)!} \end{align} }[/math]
The ratio is [math]\displaystyle{ \begin{align} \frac {P_{x+1}}{P_x} = ... = \frac {u}{{x+1}} \end{align} }[/math] Therefore, [math]\displaystyle{ \begin{align} P_{x+1} = \, {\frac {u}{x+1}} P_x\end{align} }[/math]
Algorithm:
1) Generate U ~ U(0,1)
2) [math]\displaystyle{ \begin{align} X = 0 \end{align} }[/math]
[math]\displaystyle{ \begin{align} F = P(X = 0) = e^{-u}*u^0/{0!} = e^{-u} = p \end{align} }[/math]
3) If U<F, output x
Else, [math]\displaystyle{ \begin{align} p = (u/(x+1))^p \end{align} }[/math]
[math]\displaystyle{ \begin{align} F = F + p \end{align} }[/math]
[math]\displaystyle{ \begin{align} x = x + 1 \end{align} }[/math]
4) Go to 1
Acknowledgements: This is from Stat 340 Winter 2013
Example 3.7: Generating Geometric Distribution:
Consider Geo(p) where p is the probability of success, and define random variable X such that X is the total number of trials required to achieve the first success. x=1,2,3..... We have pmf: [math]\displaystyle{ P(X=x_i) = \, p (1-p)^{x_{i}-1} }[/math] We have CDF: [math]\displaystyle{ F(x)=P(X \leq x)=1-P(X\gt x) = 1-(1-p)^x }[/math], P(X>x) means we get at least x failures before observe the first success. Now consider the inverse transform:
- [math]\displaystyle{ x = \begin{cases} 1, & \text{if } U\leq p \\ 2, & \text{if } p \lt U \leq 1-(1-p)^2 \\ 3, & \text{if } 1-(1-p)^2 \lt U\leq 1-(1-p)^3 \\ .... k, & \text{if } 1-(1-p)^{k-1} \lt U\leq 1-(1-p)^k .... \end{cases} }[/math]
Note: Unlike the continuous case, the discrete inverse-transform method can always be used for any discrete distribution (but it may not be the most efficient approach)
General Procedure
1. Draw U ~ U(0,1)
2. If [math]\displaystyle{ U \leq P_{0} }[/math] deliver [math]\displaystyle{ x = x_{0} }[/math]
3. Else if [math]\displaystyle{ U \leq P_{0} + P_{1} }[/math] deliver [math]\displaystyle{ x = x_{1} }[/math]
4. Else if [math]\displaystyle{ U \leq P_{0} + P_{1} + P_{2} }[/math] deliver [math]\displaystyle{ x = x_{2} }[/math]
...
Else if [math]\displaystyle{ U \leq P_{0} + ... + P_{k} }[/math] deliver [math]\displaystyle{ x = x_{k} }[/math]
===Inverse Transform Algorithm for Generating a Binomial(n,p) Random Variable(from textbook)===
step 1: Generate a random number U
step 2: c=p/(1-p),i=0, pr=(1-p)n, F=pr.
step 3: If U<F, set X=i and stop.
step 4: pr =[c(n-i)/(i+1)]pr, F=F+pr, i=i+1.
step 5: Go to step 3.
Problems
1. We have to find [math]\displaystyle{ F^{-1} }[/math]
2. For many distributions, such as Gaussian, it is too difficult to find the inverse of [math]\displaystyle{ F(x) }[/math].
Flipping a coin is a discrete case of uniform distribution, and the code below shows an example of flipping a coin 1000 times; the result is closed to the expected value 0.5.
Example 2, as another discrete distribution, shows that we can sample from parts like 0,1 and 2, and the probability of each part or each trial is the same.
Example 3 uses inverse method to figure out the probability range of each random varible.
Summary of Inverse Transform Method
Problem:generate types of distribution.
Plan:
Continuous case:
- find CDF F
- find the inverse F-1
- Generate a list of uniformly distributed number {x}
- {F-1(x)} is what we want
Matlab Instruction
>>u=rand(1,1000); >>hist(u) >>x=(-log(1-u))/2; >>size(x) >>figure >>hist(x)
Discrete case:
- generate a list of uniformly distributed number {u}
- di=xi if[math]\displaystyle{ X=x_i, }[/math] if [math]\displaystyle{ F(x_{i-1})\lt U\leq F(x_i) }[/math]
- {di=xi} is what we want
Matlab Instruction
>>for ii=1:1000
u=rand;
if u<0.5
x(ii)=0;
else
x(ii)=1;
end
end
>>hist(x)
Acceptance-Rejection Method
Although the inverse transformation method does allow us to change our uniform distribution, it has two limits;
- Not all functions have inverse functions (ie, the range of x and y have limit and do not fix the inverse functions)
- For some distributions, such as Gaussian, it is too difficult to find the inverse
To generate random samples for these functions, we will use different methods, such as the Acceptance-Rejection Method. This method is more efficient than the inverse transform method. The basic idea is to find an alternative probability distribution with density function f(x);
Suppose we want to draw random sample from a target density function f(x), x∈Sx, where Sx is the support of f(x). If we can find some constant c(≥1) (In practice, we prefer c as close to 1 as possible) and a density function g(x) having the same support Sx so that f(x)≤cg(x), ∀x∈Sx, then we can apply the procedure for Acceptance-Rejection Method. Typically we choose a density function that we already know how to sample from for g(x).
{{
Template:namespace detect
| type = style | image = | imageright = | style = | textstyle = | text = This article may require cleanup to meet Wikicoursenote's quality standards. The specific problem is: Do not write [math]\displaystyle{ c*g(x) }[/math]. Instead write [math]\displaystyle{ c \times g(x) }[/math] or [math]\displaystyle{ \,c g(x) }[/math]. Please improve this article if you can. | small = | smallimage = | smallimageright = | smalltext = }}
The main logic behind the Acceptance-Rejection Method is that:
1. We want to generate sample points from an unknown distribution, say f(x).
2. We use [math]\displaystyle{ \,cg(x) }[/math] to generate points so that we have more points than f(x) could ever generate for all x. (where c is a constant, and g(x) is a known distribution)
3. For each value of x, we accept and reject some points based on a probability, which will be discussed below.
Note: If the red line was only g(x) as opposed to [math]\displaystyle{ \,c g(x) }[/math] (i.e. c=1), then [math]\displaystyle{ g(x) \geq f(x) }[/math] for all values of x if and only if g and f are the same functions. This is because the sum of pdf of g(x)=1 and the sum of pdf of f(x)=1, hence, [math]\displaystyle{ g(x) \ngeqq f(x) }[/math] ∀x.
Also remember that [math]\displaystyle{ \,c g(x) }[/math] always generates higher probability than what we need. Thus we need an approach of getting the proper probabilities.
c must be chosen so that [math]\displaystyle{ f(x)\leqslant c g(x) }[/math] for all value of x. c can only equal 1 when f and g have the same distribution. Otherwise:
Either use a software package to test if [math]\displaystyle{ f(x)\leqslant c g(x) }[/math] for an arbitrarily chosen c > 0, or:
1. Find first and second derivatives of f(x) and g(x).
2. Identify and classify all local and absolute maximums and minimums, using the First and Second Derivative Tests, as well as all inflection points.
3. Verify that [math]\displaystyle{ f(x)\leqslant c g(x) }[/math] at all the local maximums as well as the absolute maximums.
4. Verify that [math]\displaystyle{ f(x)\leqslant c g(x) }[/math] at the tail ends by calculating [math]\displaystyle{ \lim_{x \to +\infty} \frac{f(x)}{\, c g(x)} }[/math] and [math]\displaystyle{ \lim_{x \to -\infty} \frac{f(x)}{\, c g(x)} }[/math] and seeing that they are both < 1. Use of L'Hopital's Rule should make this easy, since both f and g are p.d.f's, resulting in both of them approaching 0.
5.Efficiency: the number of times N that steps 1 and 2 need to be called(also the number of iterations needed to successfully generate X) is a random variable and has a geometric distribution with success probability p=P(U<= f(Y)/(cg(Y))) , P(N=n)=(1-p^(n-1))p ,n>=1.Thus on average the number of iterations required is given by E(N)=1/p
c should be close to the maximum of f(x)/g(x), not just some arbitrarily picked large number. Otherwise, the Acceptance-Rejection method will have more rejections (since our probability [math]\displaystyle{ f(x)\leqslant c g(x) }[/math] will be close to zero). This will render our algorithm inefficient.
The expected number of iterations of the algorithm required with an X is c.
Note:
1. Value around x1 will be sampled more often under cg(x) than under f(x).There will be more samples than we actually need, if [math]\displaystyle{ \frac{f(y)}{\, c g(y)} }[/math] is small, the acceptance-rejection technique will need to be done to these points to get the accurate amount.In the region above x1, we should accept less and reject more.
2. Value around x2: number of sample that are drawn and the number we need are much closer. So in the region above x2, we accept more. As a result, g(x) and f(x) are comparable.
3. The constant c is needed because we need to adjust the height of g(x) to ensure that it is above f(x). Besides that, it is best to keep the number of rejected varieties small for maximum efficiency.
Another way to understand why the the acceptance probability is [math]\displaystyle{ \frac{f(y)}{\, c g(y)} }[/math], is by thinking of areas. From the graph above, we see that the target function in under the proposed function c g(y). Therefore, [math]\displaystyle{ \frac{f(y)}{\, c g(y)} }[/math] is the proportion or the area under c g(y) that also contains f(y). Therefore we say we accept sample points for which u is less then [math]\displaystyle{ \frac{f(y)}{\, c g(y)} }[/math] because then the sample points are guaranteed to fall under the area of c g(y) that contains f(y).
There are 2 cases that are possible:
-Sample of points is more than enough, [math]\displaystyle{ c g(x) \geq f(x) }[/math]
-Similar or the same amount of points, [math]\displaystyle{ c g(x) \geq f(x) }[/math]
There is 1 case that is not possible:
-Less than enough points, such that [math]\displaystyle{ g(x) }[/math] is greater than [math]\displaystyle{ f }[/math], [math]\displaystyle{ g(x) \geq f(x) }[/math]
Procedure
- Draw Y~g(.)
- Draw U~u(0,1) (Note: U and Y are independent)
- If [math]\displaystyle{ u\leq \frac{f(y)}{cg(y)} }[/math] (which is [math]\displaystyle{ P(accepted|y) }[/math]) then x=y, else return to Step 1
Note: Recall [math]\displaystyle{ P(U\leq a)=a }[/math]. Thus by comparing u and [math]\displaystyle{ \frac{f(y)}{\, c g(y)} }[/math], we can get a probability of accepting y at these points. For instance, at some points that cg(x) is much larger than f(x), the probability of accepting x=y is quite small.
ie. At X1, low probability to accept the point since f(x) is much smaller than cg(x).
At X2, high probability to accept the point. [math]\displaystyle{ P(U\leq a)=a }[/math] in Uniform Distribution.
Note: Since U is the variable for uniform distribution between 0 and 1. It equals to 1 for all. The condition depends on the constant c. so the condition changes to [math]\displaystyle{ c\leq \frac{f(y)}{g(y)} }[/math]
introduce the relationship of cg(x)and f(x),and prove why they have that relationship and where we can use this rule to reject some cases.
and learn how to see the graph to find the accurate point to reject or accept the ragion above the random variable x.
for the example, x1 is bad point and x2 is good point to estimate the rejection and acceptance
Some notes on the constant C
1. C is chosen such that [math]\displaystyle{ c g(y)\geq f(y) }[/math], that is,[math]\displaystyle{ c g(y) }[/math] will always dominate [math]\displaystyle{ f(y) }[/math]. Because of this,
C will always be greater than or equal to one and will only equal to one if and only if the proposal distribution and the target distribution are the same. It is normally best to choose C such that the absolute maxima of both [math]\displaystyle{ c g(y) }[/math] and [math]\displaystyle{ f(y) }[/math] are the same.
2. [math]\displaystyle{ \frac {1}{C} }[/math] is the area of [math]\displaystyle{ F(y) }[/math] over the area of [math]\displaystyle{ c G(y) }[/math] and is the acceptance rate of the points generated. For example, if [math]\displaystyle{ \frac {1}{C} = 0.7 }[/math] then on average, 70 percent of all points generated are accepted.
3. C is the average number of times Y is generated from g .
Theorem
Let [math]\displaystyle{ f: \R \rightarrow [0,+\infty] }[/math] be a well-defined pdf, and [math]\displaystyle{ \displaystyle Y }[/math] be a random variable with pdf [math]\displaystyle{ g: \R \rightarrow [0,+\infty] }[/math] such that [math]\displaystyle{ \exists c \in \R^+ }[/math] with [math]\displaystyle{ f \leq c \cdot g }[/math]. If [math]\displaystyle{ \displaystyle U \sim~ U(0,1) }[/math] is independent of [math]\displaystyle{ \displaystyle Y }[/math], then the random variable defined as [math]\displaystyle{ X := Y \vert U \leq \frac{f(Y)}{c \cdot g(Y)} }[/math] has pdf [math]\displaystyle{ \displaystyle f }[/math], and the condition [math]\displaystyle{ U \leq \frac{f(Y)}{c \cdot g(Y)} }[/math] is denoted by "Accepted".
Proof
Recall the conditional probability formulas:
[math]\displaystyle{ \begin{align}
P(A|B)=\frac{P(A \cap B)}{P(B)}, \text{ or }P(A|B)=\frac{P(B|A)P(A)}{P(B)} \text{ for pmf}
\end{align} }[/math]
[math]\displaystyle{ P(y|accepted)=f(y)=\frac{P(accepted|y)P(y)}{P(accepted)} }[/math]
based on the concept from procedure-step1:
[math]\displaystyle{ P(y)=g(y) }[/math]
[math]\displaystyle{ P(accepted|y)=\frac{f(y)}{cg(y)} }[/math]
(the larger the value is, the larger the chance it will be selected)
[math]\displaystyle{
\begin{align}
P(accepted)&=\int_y\ P(accepted|y)P(y)\\
&=\int_y\ \frac{f(s)}{cg(s)}g(s)ds\\
&=\frac{1}{c} \int_y\ f(s) ds\\
&=\frac{1}{c}
\end{align} }[/math]
Therefore:
[math]\displaystyle{ \begin{align}
P(x)&=P(y|accepted)\\
&=\frac{\frac{f(y)}{cg(y)}g(y)}{1/c}\\
&=\frac{\frac{f(y)}{c}}{1/c}\\
&=f(y)\end{align} }[/math]
Here is an alternative introduction of Acceptance-Rejection Method
Comments:
-Acceptance-Rejection Method is not good for all cases. The limitation with this method is that sometimes many points will be rejected. One obvious cons is that it could be very hard to pick the [math]\displaystyle{ g(y) }[/math] and the constant [math]\displaystyle{ c }[/math] in some cases. We have to pick the SMALLEST C such that [math]\displaystyle{ cg(x) \leq f(x) }[/math] else the the algorithm will not be efficient. This is because [math]\displaystyle{ f(x)/cg(x) }[/math] will become smaller and probability [math]\displaystyle{ u \leq f(x)/cg(x) }[/math] will go down and many points will be rejected making the algorithm inefficient.
-Note: When [math]\displaystyle{ f(y) }[/math] is very different than [math]\displaystyle{ g(y) }[/math], it is less likely that the point will be accepted as the ratio above would be very small and it will be difficult for [math]\displaystyle{ U }[/math] to be less than this small value.
An example would be when the target function ([math]\displaystyle{ f }[/math]) has a spike or several spikes in its domain - this would force the known distribution ([math]\displaystyle{ g }[/math]) to have density at least as large as the spikes, making the value of [math]\displaystyle{ c }[/math] larger than desired. As a result, the algorithm would be highly inefficient.
Acceptance-Rejection Method
Example 1 (discrete case)
We wish to generate X~Bi(2,0.5), assuming that we cannot generate this directly.
We use a discrete distribution DU[0,2] to approximate this.
[math]\displaystyle{ f(x)=Pr(X=x)=2Cx*(0.5)^2 }[/math]
| [math]\displaystyle{ x }[/math] | 0 | 1 | 2 |
| [math]\displaystyle{ f(x) }[/math] | 1/4 | 1/2 | 1/4 |
| [math]\displaystyle{ g(x) }[/math] | 1/3 | 1/3 | 1/3 |
| [math]\displaystyle{ c=f(x)/g(x) }[/math] | 3/4 | 3/2 | 3/4 |
| [math]\displaystyle{ f(x)/(cg(x)) }[/math] | 1/2 | 1 | 1/2 |
Since we need [math]\displaystyle{ c \geq f(x)/g(x) }[/math]
We need [math]\displaystyle{ c=3/2 }[/math]
Therefore, the algorithm is:
1. Generate [math]\displaystyle{ u,v~U(0,1) }[/math]
2. Set [math]\displaystyle{ y= \lfloor 3*u \rfloor }[/math] (This is using uniform distribution to generate DU[0,2]
3. If [math]\displaystyle{ (y=0) }[/math] and [math]\displaystyle{ (v\lt 1/2), output=0 }[/math]
If [math]\displaystyle{ (y=2) }[/math] and [math]\displaystyle{ (v\lt 1/2), output=2 }[/math]
Else if [math]\displaystyle{ y=1, output=1 }[/math]
An elaboration of “c”
c is the expected number of times the code runs to output 1 random variable. Remember that when [math]\displaystyle{ u \lt f(x)/(cg(x)) }[/math] is not satisfied, we need to go over the code again.
Proof
Let [math]\displaystyle{ f(x) }[/math] be the function we wish to generate from, but we cannot use inverse transform method to generate directly.
Let [math]\displaystyle{ g(x) }[/math] be the helper function
Let [math]\displaystyle{ kg(x)\gt =f(x) }[/math]
Since we need to generate y from [math]\displaystyle{ g(x) }[/math],
[math]\displaystyle{ Pr(select y)=g(y) }[/math]
[math]\displaystyle{ Pr(output y|selected y)=Pr(u\lt f(y)/(cg(y)))= f(y)/(cg(y)) }[/math] (Since u~Unif(0,1))
[math]\displaystyle{ Pr(output y)=Pr(output y1|selected y1)Pr(select y1)+ Pr(output y2|selected y2)Pr(select y2)+…+ Pr(output yn|selected yn)Pr(select yn)=1/c }[/math]
Consider that we are asking for expected time for the first success, it is a geometric distribution with probability of success=1/c
Therefore, [math]\displaystyle{ E(X)=1/(1/c))=c }[/math]
Acknowledgements: Some materials have been borrowed from notes from Stat340 in Winter 2013.
Use the conditional probability to proof if the probability is accepted, then the result is closed pdf of the original one. the example shows how to choose the c for the two function [math]\displaystyle{ g(x) }[/math] and [math]\displaystyle{ f(x) }[/math].
Example of Acceptance-Rejection Method
Generating a random variable having p.d.f.
[math]\displaystyle{ f(x) = 20x(1 - x)^3, 0\lt x \lt 1 }[/math]
Since this random variable (which is beta with parameters 2, 4) is concentrated in the interval (0, 1), let us consider the acceptance-rejection method with
g(x) = 1, 0 < x < 1
To determine the constant c such that f(x)/g(x) <= c, we use calculus to determine the maximum value of
[math]\displaystyle{ f(x)/g(x) = 20x(1 - x)^3 }[/math]
Differentiation of this quantity yields
[math]\displaystyle{ d/dx[f(x)/g(x)]=20*[(1-x)^3-3x(1-x)^2] }[/math]
Setting this equal to 0 shows that the maximal value is attained when x = 1/4, and thus,
[math]\displaystyle{ f(x)/g(x)\lt = 20*(1/4)*(3/4)^3=135/64=c }[/math]
Hence,
[math]\displaystyle{ f(x)/cg(x)=(256/27)*(x*(1-x)^3) }[/math]
and thus the simulation procedure is as follows:
1) Generate two random numbers U1 and U2 .
2) If U2<(256/27)*U1*(1-U1)3, set X=U1, and stop Otherwise return to step 1). The average number of times that step 1) will be performed is c = 135/64.
(The above example is from http://www.cs.bgu.ac.il/~mps042/acceptance.htm, example 2.)
use the derivative to proof the accepetance-rejection method, find the local maximum of f(x)/g(x). and we can calculate the best constant c.
Another Example of Acceptance-Rejection Method
Generate a random variable from:
[math]\displaystyle{ f(x)=3*x^2 }[/math], 0< x <1
Assume g(x) to be uniform over interval (0,1), where 0< x <1
Therefore:
[math]\displaystyle{ c = max(f(x)/(g(x)))= 3 }[/math]
the best constant c is the max(f(x)/(cg(x))) and the c make the area above the f(x) and below the g(x) to be small. because g(.) is uniform so the g(x) is 1. max(g(x)) is 1
[math]\displaystyle{ f(x)/(cg(x))= x^2 }[/math]
Acknowledgement: this is example 1 from http://www.cs.bgu.ac.il/~mps042/acceptance.htm
Class 4 - Thursday, May 16
- When we want to find a target distribution, denoted as [math]\displaystyle{ f(x) }[/math], we need to first find a proposal distribution [math]\displaystyle{ g(x) }[/math] that is easy to sample from.
- The relationship between the proposal distribution and target distribution is: [math]\displaystyle{ c \cdot g(x) \geq f(x) }[/math], where c is a constant. This means that the area of f(x) is under the area of [math]\displaystyle{ c \cdot g(x) }[/math].
- Chance of acceptance is less if the distance between [math]\displaystyle{ f(x) }[/math] and [math]\displaystyle{ c \cdot g(x) }[/math] is big, and vice-versa, we use [math]\displaystyle{ c }[/math] to keep [math]\displaystyle{ \frac {f(x)}{c \cdot g(x)} }[/math] below 1 (so [math]\displaystyle{ f(x) \leq c \cdot g(x) }[/math]). Therefore, we must find the constant [math]\displaystyle{ C }[/math] to achieve this.
- In other words, a [math]\displaystyle{ C }[/math] is chosen to make sure [math]\displaystyle{ c \cdot g(x) \geq f(x) }[/math]. However, it will not make sense if [math]\displaystyle{ C }[/math] is simply chosen to be arbitrarily large. We need to choose [math]\displaystyle{ C }[/math] such that [math]\displaystyle{ c \cdot g(x) }[/math] fits [math]\displaystyle{ f(x) }[/math] as tightly as possible.
- The constant c cannot be a negative number.
How to find C:
[math]\displaystyle{ \begin{align}
&c \cdot g(x) \geq f(x)\\
&c\geq \frac{f(x)}{g(x)} \\
&c= \max \left(\frac{f(x)}{g(x)}\right)
\end{align} }[/math]
If [math]\displaystyle{ f }[/math] and [math]\displaystyle{ g }[/math] are continuous, we can find the extremum by taking the derivative and solve for [math]\displaystyle{ x_0 }[/math] such that:
[math]\displaystyle{ 0=\frac{d}{dx}\frac{f(x)}{g(x)}|_{x=x_0} }[/math]
Thus [math]\displaystyle{ c = \frac{f(x_0)}{g(x_0)} }[/math]
- The logic behind this:
The Acceptance-Rejection method involves finding a distribution that we know how to sample from (g(x)) and multiplying g(x) by a constant c so that [math]\displaystyle{ c \cdot g(x) }[/math] is always greater than or equal to f(x). Mathematically, we want [math]\displaystyle{ c \cdot g(x) \geq f(x) }[/math].
And it means c has to be greater or equal to [math]\displaystyle{ \frac{f(x)}{g(x)} }[/math]. So the smallest possible c that satisfies the condition is the maximum value of [math]\displaystyle{ \frac{f(x)}{g(x)} }[/math]
. If c is too large, the chance of acceptance of generated values will be small, thereby losing efficiency of the algorithm. Therefore, it is best to get the smallest possible c such that [math]\displaystyle{ c g(x) \geq f(x) }[/math].
- For this method to be efficient, the constant c must be selected so that the rejection rate is low. (The efficiency for this method is [math]\displaystyle{ \left ( \frac{1}{c} \right ) }[/math])
- It is easy to show that the expected number of trials for an acceptance is [math]\displaystyle{ \frac{Total Number of Trials} {C} }[/math].
- recall the acceptance rate is 1/c. (Not rejection rate)
- Let [math]\displaystyle{ X }[/math] be the number of trials for an acceptance, [math]\displaystyle{ X \sim~ Geo(\frac{1}{c}) }[/math]
- [math]\displaystyle{ \mathbb{E}[X] = \frac{1}{\frac{1}{c}} = c }[/math]
- The number of trials needed to generate a sample size of [math]\displaystyle{ N }[/math] follows a negative binomial distribution. The expected number of trials needed is then [math]\displaystyle{ cN }[/math].
- So far, the only distribution we know how to sample from is the UNIFORM distribution.
Procedure:
1. Choose [math]\displaystyle{ g(x) }[/math] (simple density function that we know how to sample, i.e. Uniform so far)
The easiest case is UNIF(0,1). However, in other cases we need to generate UNIF(a,b). We may need to perform a linear transformation on the UNIF(0,1) variable.
2. Find a constant c such that :[math]\displaystyle{ c \cdot g(x) \geq f(x) }[/math], otherwise return to step 1.
Recall the general procedure of Acceptance-Rejection Method
- Let [math]\displaystyle{ Y \sim~ g(y) }[/math]
- Let [math]\displaystyle{ U \sim~ Unif [0,1] }[/math]
- If [math]\displaystyle{ U \leq \frac{f(Y)}{c \cdot g(Y)} }[/math] then X=Y; else return to step 1 (This is not the way to find C. This is the general procedure.)
Example: Generate a random variable from the pdf
[math]\displaystyle{ f(x) = \begin{cases} 2x, & \mbox{if }0 \leqslant x \leqslant 1 \\ 0, & \mbox{otherwise} \end{cases} }[/math]
We can note that this is a special case of Beta(2,1), where,
[math]\displaystyle{ beta(a,b)=\frac{\Gamma(a+b)}{\Gamma(a)\Gamma(b)}x^{(a-1)}(1-x)^{(b-1)} }[/math]
Where Γ (n)=(n-1)! if n is positive integer
[math]\displaystyle{ Gamma(z)=\int _{0}^{\infty }t^{z-1}e^{-t}dt }[/math]
Aside: Beta function
In mathematics, the beta function, also called the Euler integral of the first kind, is a special function defined by
[math]\displaystyle{ B(x,y)=\int_0^1 \! {t^{(x-1)}}{(1-t)^{(y-1)}}\,dt }[/math]
[math]\displaystyle{ beta(2,1)= \frac{\Gamma(3)}{(\Gamma(2)\Gamma(1))}x^1 (1-x)^0 = 2x }[/math]
[math]\displaystyle{ g=u(0,1) }[/math]
[math]\displaystyle{ y=g }[/math]
[math]\displaystyle{ f(x)\leq c\cdot g(x) }[/math]
[math]\displaystyle{ c\geq \frac{f(x)}{g(x)} }[/math]
[math]\displaystyle{ c = \max \frac{f(x)}{g(x)} }[/math]
[math]\displaystyle{ c = \max \frac{2x}{1}, 0 \leq x \leq 1 }[/math]
Taking x = 1 gives the highest possible c, which is c=2
Note that c is a scalar greater than 1.
cg(x) is proposal dist, and f(x) is target dist.
Note: g follows uniform distribution, it only covers half of the graph which runs from 0 to 1 on y-axis. Thus we need to multiply by c to ensure that [math]\displaystyle{ c\cdot g }[/math] can cover entire f(x) area. In this case, c=2, so that makes g runs from 0 to 2 on y-axis which covers f(x).
Comment:
From the picture above, we could observe that the area under f(x)=2x is a half of the area under the pdf of UNIF(0,1). This is why in order to sample 1000 points of f(x), we need to sample approximately 2000 points in UNIF(0,1).
And in general, if we want to sample n points from a distritubion with pdf f(x), we need to scan approximately [math]\displaystyle{ n\cdot c }[/math] points from the proposal distribution (g(x)) in total.
Step
- Draw y~U(0,1)
- Draw u~U(0,1)
- if [math]\displaystyle{ u \leq \frac{(2\cdot y)}{(2\cdot 1)}, u \leq y, }[/math] then [math]\displaystyle{ x=y }[/math]
- Else go to Step 1
Note: In the above example, we sample 2 numbers. If second number (u) is less than or equal to first number (y), then accept x=y, if not then start all over.
Matlab Code
>>close all
>>clear all
>>ii=1; # ii:numbers that are accepted
>>jj=1; # jj:numbers that are generated
>>while ii<1000
y=rand;
u=rand;
jj=jj+1;
if u<=y
x(ii)=y;
ii=ii+1;
end
end
>>hist(x)
>>jj
jj = 2024 # should be around 2000
- *Note: The reason that a for loop is not used is that we need to continue the looping until we get 1000 successful samples. We will reject some samples during the process and therefore do not know the number of y we are going to generate.
- *Note2: In this example, we used c=2, which means we accept half of the points we generate on average. Generally speaking, 1/c would be the probability of acceptance, and an indicator of the efficiency of your chosen proposal distribution and algorithm.
- *Note3: We use while instead of for when looping because we do not know how many iterations are required to generate 1000 successful samples. We can view this as a negative binomial distribution so while the expected number of iterations required is n * c, it will likely deviate from this amount. We expect 2000 in this case.
- *Note4: If c=1, we will accept all points, which is the ideal situation. However, this is essentially impossible because if c = 1 then our distributions f(x) and g(x) must be identical, so we will have to be satisfied with as close to 1 as possible.
Use Inverse Method for this Example
- [math]\displaystyle{ F(x)=\int_0^x \! 2s\,ds={x^2}-0={x^2} }[/math]
- [math]\displaystyle{ y=x^2 }[/math]
- [math]\displaystyle{ x=\sqrt y }[/math]
- [math]\displaystyle{ F^{-1}\left (\, x \, \right) =\sqrt x }[/math]
- Procedure
- 1: Draw [math]\displaystyle{ U~ \sim~ Unif [0,1] }[/math]
- 2: [math]\displaystyle{ x=F^{-1}\left (\, u\, \right) =\sqrt u }[/math]
Matlab Code
>>u=rand(1,1000); >>x=u.^0.5; >>hist(x)
Matlab Tip: Periods, ".",meaning "element-wise", are used to describe the operation you want performed on each element of a vector. In the above example, to take the square root of every element in U, the notation U.^0.5 is used. However if you want to take the Square root of the entire matrix U the period, "*.*" would be excluded. i.e. Let matrix B=U^0.5, then [math]\displaystyle{ B^T*B=U }[/math]. For example if we have a two 1 X 3 matrices and we want to find out their product; using "." in the code will give us their product. However, if we don't use ".", it will just give us an error. For example, a =[1 2 3] b=[2 3 4] are vectors, a.*b=[2 6 12], but a*b does not work since matrix dimensions must agree.
Example for A-R method:
Given [math]\displaystyle{ f(x)= \frac{3}{4} (1-x^2), -1 \leq x \leq 1 }[/math], use A-R method to generate random number
Let g=U(-1,1) and g(x)=1/2
let y ~ f, [math]\displaystyle{ cg(x)\geq f(x), c\frac{1}{2} \geq \frac{3}{4} (1-x^2) /1, c=max 2*\frac{3}{4} (1-x^2) = 3/2 }[/math]
The process:
- 1: Draw U1 ~ U(0,1)
- 2: Draw U2 ~ U(0,1)
- 3: let [math]\displaystyle{ y = U1*2 - 1 }[/math]
- 4: if [math]\displaystyle{ U2 \leq \frac { \frac{3}{4} * (1-y^2)} { \frac{3}{4}} = {1-y^2} }[/math], then x=y, note that (3/4(1-y^2)/(3/4) is getting from f(y) / (cg(y)) )
- 5: else: return to step 1
Example of Acceptance-Rejection Method
[math]\displaystyle{ f(x) = 3x^2, 0\lt x\lt 1 }[/math] [math]\displaystyle{ g(x)=1, 0\lt x\lt 1 }[/math]
[math]\displaystyle{ c = \max \frac{f(x)}{g(x)} = \max \frac{3x^2}{1} = 3 }[/math]
[math]\displaystyle{ \frac{f(x)}{c \cdot g(x)} = x^2 }[/math]
1. Generate two uniform numbers in the unit interval [math]\displaystyle{ U_1, U_2 \sim~ U(0,1) }[/math]
2. If [math]\displaystyle{ U_2 \leqslant {U_1}^2 }[/math], accept [math]\displaystyle{ U_1 }[/math] as the random variable with pdf [math]\displaystyle{ f }[/math], if not return to Step 1
We can also use [math]\displaystyle{ g(x)=2x }[/math] for a more efficient algorithm
[math]\displaystyle{ c = \max \frac{f(x)}{g(x)} = \max \frac {3x^2}{2x} = \frac {3x}{2} }[/math]. Use the inverse method to sample from [math]\displaystyle{ g(x) }[/math] [math]\displaystyle{ G(x)=x^2 }[/math]. Generate [math]\displaystyle{ U }[/math] from [math]\displaystyle{ U(0,1) }[/math] and set [math]\displaystyle{ x=sqrt(u) }[/math]
1. Generate two uniform numbers in the unit interval [math]\displaystyle{ U_1, U_2 \sim~ U(0,1) }[/math]
2. If [math]\displaystyle{ U_2 \leq \frac{3\sqrt{U_1}}{2} }[/math], accept [math]\displaystyle{ U_1 }[/math] as the random variable with pdf [math]\displaystyle{ f }[/math], if not return to Step 1
- Note :the function q(x) = c * g(x) is called an envelop or majoring function.
To obtain a better proposing function g(x), we can first assume a new q(x) and then solve for the normalizing constant by integrating.
In the previous example, we first assume q(x) = 3x. To find the normalizing constant, we need to solve k * [math]\displaystyle{ \sum 3x = 1 }[/math] which gives us k = 2/3. So, g(x) = k*q(x) = 2x.
Possible Limitations
-This method could be computationally inefficient depending on the rejection rate. We may have to sample many points before
we get the 1000 accepted points. In the example we did in class relating the [math]\displaystyle{ f(x)=2x }[/math],
we had to sample around 2070 points before we finally accepted 1000 sample points.
-If the form of the proposal distribution, g, is very different from target distribution, f, then c is very large and the algorithm is not computationally efficient.
Acceptance - Rejection Method Application on Normal Distribution
[math]\displaystyle{ X \sim∼ N(\mu,\sigma^2), \text{ or } X = \sigma Z + \mu, Z \sim~ N(0,1) }[/math]
[math]\displaystyle{ \vert Z \vert }[/math] has probability density function of
f(x) = (2/[math]\displaystyle{ \sqrt{2\pi} }[/math]) e-x2/2
g(x) = e-x
Take h(x) = f(x)/g(x) and solve for h'(x) = 0 to find x so that h(x) is maximum.
Hence x=1 maximizes h(x) => c = [math]\displaystyle{ \sqrt{2e/\pi} }[/math]
Thus f(y)/cg(y) = e-(y-1)2/2
learn how to use code to calculate the c between f(x) and g(x).
How to transform [math]\displaystyle{ U(0,1) }[/math] to [math]\displaystyle{ U(a, b) }[/math]
1. Draw U from [math]\displaystyle{ U(0,1) }[/math]
2. Take [math]\displaystyle{ Y=(b-a)U+a }[/math]
3. Now Y follows [math]\displaystyle{ U(a,b) }[/math]
Example: Generate a random variable z from the Semicircular density [math]\displaystyle{ f(x)= \frac{2}{\pi R^2} \sqrt{R^2-x^2}, -R\leq x\leq R }[/math].
-> Proposal distribution: UNIF(-R, R)
-> We know how to generate using [math]\displaystyle{ U \sim UNIF (0,1) }[/math] Let [math]\displaystyle{ Y= 2RU-R=R(2U-1) }[/math], therefore Y follows [math]\displaystyle{ U(-R,R) }[/math]
-> In order to maximize the function we must maximize the top and minimize the bottom.
Now, we need to find c:
Since c=max[f(x)/g(x)], where
[math]\displaystyle{ f(x)= \frac{2}{\pi R^2} \sqrt{R^2-x^2} }[/math], [math]\displaystyle{ g(x)=\frac{1}{2R} }[/math], [math]\displaystyle{ -R\leq x\leq R }[/math]
Thus, we have to maximize R^2-x^2.
=> When x=0, it will be maximized.
Therefore, c=4/pi. * Note: This also means that the probability of accepting a point is [math]\displaystyle{ \pi/4 }[/math].
We will accept the points with limit f(x)/[cg(x)]. Since [math]\displaystyle{ \frac{f(y)}{cg(y)}=\frac{\frac{2}{\pi R^{2}} \sqrt{R^{2}-y^{2}}}{\frac{4}{\pi} \frac{1}{2R}}=\frac{\frac{2}{\pi R^{2}} \sqrt{R^{2}-R^{2}(2U-1)^{2}}}{\frac{2}{\pi R}} }[/math]
- Note: Y= R(2U-1)
We can also get Y= R(2U-1) by using the formula y = a+(b-a)*u, to transform U~(0,1) to U~(a,b). Letting a=-R and b=R, and substituting it in the formula y = a+(b-a)*u, we get Y= R(2U-1).
Thus, [math]\displaystyle{ \frac{f(y)}{cg(y)}=\sqrt{1-(2U-1)^{2}} }[/math] * this also means the probability we can accept points
The algorithm to generate random variable x is then:
1. Draw [math]\displaystyle{ \ U }[/math] from [math]\displaystyle{ \ U(0,1) }[/math]
2. Draw [math]\displaystyle{ \ U_{1} }[/math] from [math]\displaystyle{ \ U(0,1) }[/math]
3. If [math]\displaystyle{ U_{1} \leq \sqrt{1-(2U-1)^2}, set x = U_{1} }[/math]
else return to step 1.
The condition is
[math]\displaystyle{ U_{1} \leq \sqrt{(1-(2U-1)^2)} }[/math]
[math]\displaystyle{ \ U_{1}^2 \leq 1 - (2U -1)^2 }[/math]
[math]\displaystyle{ \ U_{1}^2 - 1 \leq -(2U - 1)^2 }[/math]
[math]\displaystyle{ \ 1 - U_{1}^2 \geq (2U - 1)^2 }[/math]
One more example about AR method
(In this example, we will see how to determine the value of c when c is a function with unknown parameters instead of a value)
Let [math]\displaystyle{ f(x)=x*e^{-x}, x\gt 0 }[/math]
Use [math]\displaystyle{ g(x)=a*e^{-a*x} }[/math]to generate random variable
Solution: First of all, we need to find c
[math]\displaystyle{ cg(x)\gt =f(x) }[/math]
[math]\displaystyle{ c\gt =\frac{f(x)}{g(x)} }[/math]
[math]\displaystyle{ \frac{f(x)}{g(x)}=\frac{x}{a} * e^{-(1-a)x} }[/math]
take derivative with respect to x, and set it to 0 to get the maximum,
[math]\displaystyle{ \frac{1}{a} * e^{-(1-a)x} - \frac{x}{a} * e^{-(1-a)x} * (1-a) = 0 }[/math]
[math]\displaystyle{ x=\frac {1}{1-a} }[/math]
[math]\displaystyle{ \frac {f(x)}{g(x)} = \frac {e^{-1}}{a*(1-a)} }[/math]
[math]\displaystyle{ \frac {f(0)}{g(0)} = 0 }[/math]
[math]\displaystyle{ \frac {f(\infty)}{g(\infty)} = 0 }[/math]
therefore, [math]\displaystyle{ c= \frac {e^{-1}}{a*(1-a)} }[/math]
In order to minimize c, we need to find the appropriate a
Take derivative with respect to a and set it to be zero,
We could get [math]\displaystyle{ a= \frac {1}{2} }[/math]
[math]\displaystyle{ c=\frac{4}{e} }[/math]
Procedure:
1. Generate u v ~unif(0,1)
2. Generate y from g, since g is exponential with rate 2, let y=-0.5*ln(u)
3. If [math]\displaystyle{ v\lt \frac{f(y)}{c\cdot g(y)} }[/math], output y
Else, go to 1
Acknowledgements: The example above is from Stat 340 Winter 2013 notes.
Summary of how to find the value of c
Let [math]\displaystyle{ h(x) = \frac {f(x)}{g(x)} }[/math], and then we have the following:
1. First, take derivative of h(x) with respect to x, get x1;
2. Plug x1 into h(x) and get the value(or a function) of c, denote as c1;
3. Check the endpoints of x and sub the endpoints into h(x);
4. (if c1 is a value, then we can ignore this step) Since we want the smallest value of c such that [math]\displaystyle{ f(x) \leq c\cdot g(x) }[/math] for all x, we want the unknown parameter that minimizes c.
So we take derivative of c1 with respect to the unknown parameter (ie k=unknown parameter) to get the value of k.
Then we submit k to get the value of c1. (Double check that [math]\displaystyle{ c_1 \geq 1 }[/math]
5. Pick the maximum value of h(x) to be the value of c.
For the two examples above, we need to generate the probability function to uniform distribution, and figure out [math]\displaystyle{ c=max\frac {f(y)}{g(y)} }[/math]. If [math]\displaystyle{ v\lt \frac {f(y)}{c\cdot g(y)} }[/math], output y.
Summary of when to use the Accept Rejection Method
1) When the calculation of inverse cdf cannot to be computed or is too difficult to compute.
2) When f(x) can be evaluated to at least one of the normalizing constant.
3) A constant c where [math]\displaystyle{ f(x)\leq c\cdot g(x) }[/math]
4) A uniform draw
Interpretation of 'C'
We can use the value of c to calculate the acceptance rate by '1/c'.
For instance, assume c=1.5, then we can tell that 66.7% of the points will be accepted (1/1.5=0.667). We can also call the efficiency of the method is 66.7%.
Class 5 - Tuesday, May 21
Recall the example in the last lecture. The following code will generate a random variable required by the question.
- Code
>>close all
>>clear all
>>ii=1;
>>R=1; #Note: that R is a constant in which we can change
i.e. if we changed R=4 then we would have a density between -4 and 4
>>while ii<1000
u1 = rand;
u2 = rand;
y = R*(2*u2-1);
if (1-u1^2)>=(2*u2-1)^2
x(ii) = y;
ii = ii + 1; #Note: for beginner programmers that this step increases
the ii value for next time through the while loop
end
end
>>hist(x,20) # 20 is the number of bars
MATLAB tips: hist(x,y) where y is the number of bars in the graph.
a histogram to show variable x, and the bars number is y.
Discrete Examples
- Example 1
Generate random variable [math]\displaystyle{ X }[/math] according to p.m.f
[math]\displaystyle{ \begin{align}
P(x &=1) &&=0.15 \\
P(x &=2) &&=0.25 \\
P(x &=3) &&=0.3 \\
P(x &=4) &&=0.1 \\
P(x &=5) &&=0.2 \\
\end{align} }[/math]
The discrete case is analogous to the continuous case. Suppose we want to generate an X that is a discrete random variable with pmf f(x)=P(X=x). Suppose also that we use the discrete uniform distribution as our target distribution, then [math]\displaystyle{ g(x)= P(X=x) =0.2 }[/math] for all X.
The following algorithm then yields our X:
Step 1. Draw discrete uniform distribution of 1, 2, 3, 4 and 5, [math]\displaystyle{ Y \sim~ g }[/math].
Step 2. Draw [math]\displaystyle{ U \sim~ U(0,1) }[/math].
Step 3. If [math]\displaystyle{ U \leq \frac{f(Y)}{c \cdot g(Y)} }[/math], then X = Y ;
Else return to Step 1.
C can be found by maximizing the ratio :[math]\displaystyle{ \frac{f(x)}{g(x)} }[/math]. To do this, we want to maximize [math]\displaystyle{ f(x) }[/math] and minimize [math]\displaystyle{ g(x) }[/math].
- [math]\displaystyle{ c = max \frac{f(x)}{g(x)} = \frac {0.3}{0.2} = 1.5 }[/math]
Note: In this case [math]\displaystyle{ f(x)=P(X=x)=0.3 }[/math] (highest probability from the discrete probabilities in the question)
- [math]\displaystyle{ \frac{p(x)}{cg(x)} = \frac{p(x)}{1.5*0.2} = \frac{p(x)}{0.3} }[/math]
Note: The U is independent from y in Step 2 and 3 above. ~The constant c is a indicator of rejection rate or efficiency of the algorithm.
the acceptance-rejection method of pmf, the uniform probability is the same for all variables, and there 5 parameters(1,2,3,4,5), so g(x) is 0.2
Remember that we always want to choose [math]\displaystyle{ cg }[/math] to be equal to or greater than [math]\displaystyle{ f }[/math], but as close as possible.
limitations: If the form of the proposal dist g is very different from target dist f, then c is very large and the algorithm is not computatively effect.
- Code for example 1
>>close all
>>clear all
>>p=[.15 .25 .3 .1 .2]; %This a vector holding the values
>>ii=1;
>>while ii < 1000
y=unidrnd(5); %generates random numbers for the discrete uniform
u=rand; distribution with maximum 5.
if u<= p(y)/0.3
x(ii)=y;
ii=ii+1;
end
end
>>hist(x)
unidrnd(k) draws from the discrete uniform distribution of integers [math]\displaystyle{ 1,2,3,...,k }[/math] If this function is not built in to your MATLAB then we can do simple transformation on the rand(k) function to make it work like the unidrnd(k) function.
The acceptance rate is [math]\displaystyle{ \frac {1}{c} }[/math], so the lower the c, the more efficient the algorithm. Theoretically, c equals 1 is the best case because all samples would be accepted; however it would only be true when the proposal and target distributions are exactly the same, which would never happen in practice.
For example, if c = 1.5, the acceptance rate would be [math]\displaystyle{ \frac {1}{1.5}=\frac {2}{3} }[/math]. Thus, in order to generate 1000 random values, on average, a total of 1500 iterations would be required.
A histogram to show 1000 random values of f(x), more random value make the probability close to the express probability value.
- Example 2
p(x=1)=0.1
p(x=2)=0.3
p(x=3)=0.6
Let g be the uniform distribution of 1, 2, or 3
g(x)= 1/3
[math]\displaystyle{ c=max(p_{x}/g(x))=0.6/(1/3)=1.8 }[/math]
Hence p(x)/cg(x) = p(x)/(1.8*1/3)= p(x)/0.6
1,y~g
2,u~U(0,1)
3, If [math]\displaystyle{ U \leq \frac{f(y)}{cg(y)} }[/math], set x = y. Else go to 1.
- Code for example 2
>>close all
>>clear all
>>p=[.1 .3 .6];
>>ii=1;
>>while ii < 1000
y=unidrnd(3);
u=rand;
if u<= p(y)/0.6
x(ii)=y;
ii=ii+1;
end
end
>>hist(x)
- Example 3
[math]\displaystyle{ p_{x}=e^{-3}3^{x}/x! , x\gt =0 }[/math]
(poisson distribution)
Try the first few p_{x}'s: .0498 .149 .224 .224 .168 .101 .0504 .0216 .0081 .0027
Use the geometric distribution for [math]\displaystyle{ g(x) }[/math];
[math]\displaystyle{ g(x)=p(1-p)^{x} }[/math], choose p=0.25
Look at [math]\displaystyle{ p_{x}/g(x) }[/math] for the first few numbers: .199 .797 1.59 2.12 2.12 1.70 1.13 .647 .324 .144
We want [math]\displaystyle{ c=max(p_{x}/g(x)) }[/math] which is approximately 2.12
1. Generate [math]\displaystyle{ U_{1} \sim~ U(0,1); U_{2} \sim~ U(0,1) }[/math]
2. [math]\displaystyle{ j = \lfloor \frac{ln(U_{1})}{ln(.75)} \rfloor+1; }[/math]
3. if [math]\displaystyle{ U_{2} \lt \frac{p_{j}}{cg(j)} }[/math], set X = xj, else go to step 1.
Note: In this case, f(x)/g(x) is extremely difficult to differentiate so we were required to test points. If the function is easily differentiable, we can calculate the max as if it were a continuous function then check the two surrounding points for which is the highest discrete value.
- Example 4 (Hypergeometric & Binomial)
Suppose we are given f(x) such that it is hypergeometically distributed, given 10 white balls, 5 red balls, and select 3 balls, let X be the number of red ball selected, without replacement.
Choose g(x) such that it is binomial distribution, Bin(3, 1/3). Find the rejection constant, c
Solution:
For hypergeometric: [math]\displaystyle{ P(X=0) =\binom{10}{3}/\binom{15}{3} =0.2637, P(x=1)=\binom{10}{2} * \binom{5}{1} /\binom{15}{3}=0.4945, P(X=2)=\binom{10}{1} * \binom{5}{2} /\binom{15}{3}=0.2198, }[/math]
[math]\displaystyle{ P(X=3)=\binom{5}{3}/\binom{15}{3}= 0.02198 }[/math]
For Binomial g(x): P(X=0) = (2/3)^3=0.2963; P(X=1)= 3*(1/3)*(2/3)^2 = 0.4444, P(X=2)=3*(1/3)^2*(2/3)=0.2222, P(X=3)=(1/3)^3=0.03704
Find the value of f/g for each X
X=0: 0.8898; X=1: 1.1127; X=2: 0.9891; X=3: 0.5934
Choose the maximum which is c=1.1127
Looking for the max f(x) is 0.4945 and the max g(x) is 0.4444, so we can calculate the max c is 1.1127. But for the graph, this c is not the best because it does not cover all the point of f(x), so we need to move the c*g(x) graph to cover all f(x), and decreasing the rejection ratio.
Limitation: If the shape of the proposed distribution g is very different from the target distribution f, then the rejection rate will be high (High c value). Computationally, the algorithm is always right; however it is inefficient and requires many iterations.
Here is an example:
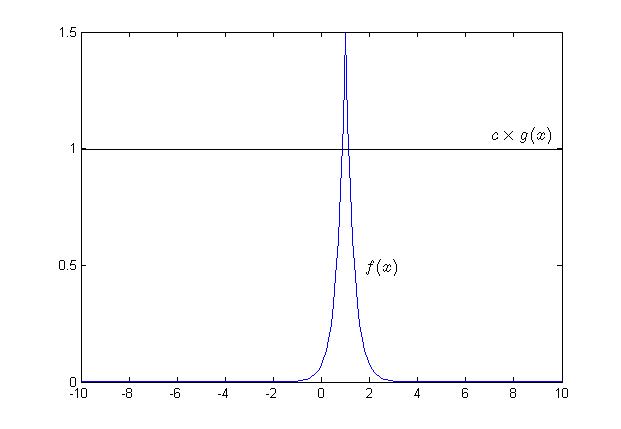
In the above example, we need to move c*g(x) to the peak of f to cover the whole f. Thus c will be very large and 1/c will be small.
The higher the rejection rate, more points will be rejected.
More on rejection/acceptance rate: 1/c is the acceptance rate. As c decreases (note: the minimum value of c is 1), the acceptance rate increases. In our last example, 1/c=1/1.5≈66.67%. Around 67% of points generated will be accepted.
which brings the acceptance rate low which leads to very time consuming sampling
Acceptance-Rejection Method
Problem: The CDF is not invertible or it is difficult to find the inverse.
Plan:
- Draw y~g(.)
- Draw u~Unif(0,1)
- If [math]\displaystyle{ u\leq \frac{f(y)}{cg(y)} }[/math]then set x=y. Else return to Step 1
x will have the desired distribution.
Matlab Example
close all
clear all
ii=1;
R=1;
while ii<1000
u1 = rand;
u2 = rand;
y = R*(2*u2-1);
if (1-u1^2)>=(2*u2-1)^2
x(ii) = y;
ii = ii + 1;
end
end
hist(x,20)
Recall that,
Suppose we have an efficient method for simulating a random variable having probability mass function {q(j),j>=0}. We can use this as the basis for simulating from the distribution having mass function {p(j),j>=0} by first simulating a random variable Y having mass function {q(j)} and then accepting this simulated value with a probability proportional to p(Y)/q(Y).
Specifically, let c be a constant such that
p(j)/q(j)<=c for all j such that p(j)>0
We now have the following technique, called the acceptance-rejection method, for simulating a random variable X having mass function p(j)=P{X=j}.
Sampling from commonly used distributions
Please note that this is not a general technique as is that of acceptance-rejection sampling. Later, we will generalize the distributions for multidimensional purposes.
- Gamma
The CDF of the Gamma distribution [math]\displaystyle{ Gamma(t,\lambda) }[/math] is(t denotes the shape, [math]\displaystyle{ \lambda }[/math] denotes the scale:
[math]\displaystyle{ F(x) = \int_0^{x} \frac{e^{-y}y^{t-1}}{(t-1)!} \mathrm{d}y, \; \forall x \in (0,+\infty) }[/math], where [math]\displaystyle{ t \in \N^+ \text{ and } \lambda \in (0,+\infty) }[/math].
Neither Inverse Transformation nor Acceptance/Rejection Method can be easily applied to Gamma distribution.
However, we can use additive property of Gamma distribution to generate random variables.
- Additive Property
If [math]\displaystyle{ X_1, \dots, X_t }[/math] are independent exponential distributions with hazard rate [math]\displaystyle{ \lambda }[/math] (in other words, [math]\displaystyle{ X_i\sim~ Exp (\lambda) }[/math][math]\displaystyle{ , Exp (\lambda)= Gamma (1, \lambda)), then \Sigma_{i=1}^t X_i \sim~ Gamma (t, \lambda) }[/math]
Side notes: if [math]\displaystyle{ X_i\sim~ Gamma(a,\lambda) }[/math] and [math]\displaystyle{ Y_i\sim~ Gamma(B,\lambda) }[/math] are independent gamma distributions, then [math]\displaystyle{ \frac{X}{X+Y} }[/math] has a distribution of [math]\displaystyle{ Beta(a,B). }[/math]
If we want to sample from the Gamma distribution, we can consider sampling from [math]\displaystyle{ t }[/math] independent exponential distributions using the Inverse Method for each [math]\displaystyle{ X_i }[/math] and add them up. Note that this only works the specific set of gamma distributions where t is a positive integer.
According to this property, a random variable that follows Gamma distribution is the sum of i.i.d (independent and identically distributed) exponential random variables. Now we want to generate 1000 values of [math]\displaystyle{ Gamma(20,10) }[/math] random variables, so we need to obtain the value of each one by adding 20 values of [math]\displaystyle{ X_i \sim~ Exp(10) }[/math]. To achieve this, we generate a 20-by-1000 matrix whose entries follow [math]\displaystyle{ Exp(10) }[/math] and add the rows together. [math]\displaystyle{ x_1 }[/math]~Exp([math]\displaystyle{ \lambda }[/math]) [math]\displaystyle{ x_2 }[/math]~Exp([math]\displaystyle{ \lambda }[/math]) ... [math]\displaystyle{ x_t }[/math]~Exp([math]\displaystyle{ \lambda }[/math]) [math]\displaystyle{ x_1+x_2+...+x_t }[/math]
>>l=1 >>u-rand(1,1000); >>x=-(1/l)*log(u); >>hist(x) >>rand
- Procedure
- Sample independently from a uniform distribution [math]\displaystyle{ t }[/math] times, giving [math]\displaystyle{ U_1,\dots,U_t \sim~ U(0,1) }[/math]
- Use the Inverse Transform Method, [math]\displaystyle{ X_i = -\frac {1}{\lambda}\log(1-U_i) }[/math], giving [math]\displaystyle{ X_1,\dots,X_t \sim~Exp(\lambda) }[/math]
- Use the additive property,[math]\displaystyle{ X = \Sigma_{i=1}^t X_i \sim~ Gamma (t, \lambda) }[/math]
- Note for Procedure
- If [math]\displaystyle{ U\sim~U(0,1) }[/math], then [math]\displaystyle{ U }[/math] and [math]\displaystyle{ 1-U }[/math] will have the same distribution (both follows [math]\displaystyle{ U(0,1) }[/math])
- This is because the range for [math]\displaystyle{ 1-U }[/math] is still [math]\displaystyle{ (0,1) }[/math], and their densities are identical over this range.
- Let [math]\displaystyle{ Y=1-U }[/math], [math]\displaystyle{ Pr(Y\lt =y)=Pr(1-U\lt =y)=Pr(U\gt =1-y)=1-Pr(U\lt =1-y)=1-(1-y)=y }[/math], thus [math]\displaystyle{ 1-U\sim~U(0,1) }[/math]
- Code
>>close all
>>clear all
>>lambda = 1;
>>u = rand(20, 1000); Note: this command generate a 20x1000 matrix
(which means we generate 1000 number for each X_i with t=20);
all the elements are generated by rand
>>x = (-1/lambda)*log(1-u); Note: log(1-u) is essentially the same as log(u) only if u~U(0,1)
>>xx = sum(x) Note: sum(x) will sum all elements in the same column.
size(xx) can help you to verify
>>size(sum(x)) Note: see the size of x if we forget it
(the answer is 20 1000)
>>hist(x(1:)) Note: the graph of the first exponential distribution
>>hist(xx)
size(x) and size(u) are both 20*1000 matrix. Since if u~unif(0, 1), u and 1 - u have the same distribution, we can substitute 1-u with u to simply the equation. Alternatively, the following command will do the same thing with the previous commands.
- Code
>>close all
>>clear all
>>lambda = 1;
>>xx = sum((-1/lambda)*log(rand(20, 1000))); ''This is simple way to put the code in one line.
Here we can use either log(u) or log(1-u) since U~U(0,1);
>>hist(xx)
in the matrix rand(20,1000) means 20 row with 1000 numbers for each. use the code to show the generalize the distributions for multidimensional purposes in different cases, such as sum xi (each xi not equal xj), and they are independent, or matrix. Finally, we can see the conclusion is shown by the histogram.
Other Sampling Method: Box Muller
- From cartesian to polar coordinates
[math]\displaystyle{ R=\sqrt{x_{1}^2+x_{2}^2}= x_{2}/sin(\theta)= x_{1}/cos(\theta) }[/math]
[math]\displaystyle{ tan(\theta)=x_{2}/x_{1} \rightarrow \theta=tan^{-1}(x_{2}/x_{1}) }[/math]
- Box-Muller Transformation:
It is a transformation that consumes two continuous uniform random variables [math]\displaystyle{ X \sim U(0,1), Y \sim U(0,1) }[/math] and outputs a bivariate normal random variable with [math]\displaystyle{ Z_1\sim N(0,1), Z_2\sim N(0,1). }[/math]
Matlab
If X is a matrix,
- X(1,:) returns the first row
- X(:,1) returns the first column
- X(i,j) returns the (i,j)th entry
- sum(X,1) or sum(X) is a summation of the rows of X. The output is a row vector of the sums of each column.
- sum(X,2) is a summation of the columns of X, returning a vector.
- rand(r,c) will generate uniformly distributed random numbers in r rows and c columns.
- The dot operator (.), when placed before a function, such as +,-,^, *, and many others specifies to apply that function to every element of a vector or a matrix. For example, to add a constant c to elements of a matrix A, do A.+c as opposed to simply A+c. The dot operator is not required for functions that can only take a number as their input (such as log).
- Matlab processes loops very slow, while it is fast with matrices and vectors, so it is preferable to use the dot operator to and matrices of random numbers than loops if it is possible.
Class 6 - Thursday, May 23
Announcement
1. On the day of each lecture, students from the morning section can only contribute the first half of the lecture (i.e. 8:30 - 9:10 am), so that the second half can be saved for the ones from the afternoon section. After the day of lecture, students are free to contribute anything.
Standard Normal distribution
If X ~ N(0,1) i.e. Standard Normal Distribution - then its p.d.f. is of the form
- [math]\displaystyle{ f(x) = \frac{1}{\sqrt{2\pi}}\, e^{- \frac{\scriptscriptstyle 1}{\scriptscriptstyle 2} x^2} }[/math]
- Warning : the General Normal distribution is
[math]\displaystyle{ f(x) = \frac{1}{\sigma\sqrt{2\pi}} e^{ -\frac{(x-\mu)^2}{2\sigma^2} } }[/math] |
which is almost useless in this course
|
where [math]\displaystyle{ \mu }[/math] is the mean or expectation of the distribution and [math]\displaystyle{ \sigma }[/math] is standard deviation
- N(0,1) is standard normal. [math]\displaystyle{ \mu }[/math] =0 and [math]\displaystyle{ \sigma }[/math]=1
Let X and Y be independent standard normal.
Let [math]\displaystyle{ \theta }[/math] and R denote the Polar coordinate of the vector (X, Y)
Note: R must satisfy two properties:
- 1. Be a positive number (as it is a length)
- 2. It must be from a distribution that has more data points closer to the origin so that as we go further from the origin, less points are generated (the two options are Chi-squared and Exponential distribution)
The form of the joint distribution of R and [math]\displaystyle{ \theta }[/math] will show that the best choice for distribution of R2 is exponential.
We cannot use the Inverse Transformation Method since F(x) does not have a closed form solution. So we will use joint probability function of two independent standard normal random variables and polar coordinates to simulate the distribution:
We know that
- R2= X2+Y2 and [math]\displaystyle{ \tan(\theta) = \frac{y}{x} }[/math] where X and Y are two independent standard normal
- [math]\displaystyle{ f(x) = \frac{1}{\sqrt{2\pi}}\, e^{- \frac{\scriptscriptstyle 1}{\scriptscriptstyle 2} x^2} }[/math]
- [math]\displaystyle{ f(y) = \frac{1}{\sqrt{2\pi}}\, e^{- \frac{\scriptscriptstyle 1}{\scriptscriptstyle 2} y^2} }[/math]
- [math]\displaystyle{ f(x,y) = \frac{1}{\sqrt{2\pi}}\, e^{- \frac{\scriptscriptstyle 1}{\scriptscriptstyle 2} x^2} * \frac{1}{\sqrt{2\pi}}\, e^{- \frac{\scriptscriptstyle 1}{\scriptscriptstyle 2} y^2}=\frac{1}{2\pi}\, e^{- \frac{\scriptscriptstyle 1}{\scriptscriptstyle 2} (x^2+y^2)} }[/math]
- Since for independent distributions, their joint probability function is the multiplication of two independent probability functions
It can also be shown using 1-1 transformation that the joint distribution of R and θ is given by,
1-1 transformation:
Let [math]\displaystyle{ d=R^2 }[/math]
[math]\displaystyle{ x= \sqrt {d}\cos \theta }[/math] [math]\displaystyle{ y= \sqrt {d}\sin \theta }[/math]
then [math]\displaystyle{ \left| J\right| = \left| \dfrac {1} {2}d^{-\frac {1} {2}}\cos \theta d^{\frac{1}{2}}\cos \theta +\sqrt {d}\sin \theta \dfrac {1} {2}d^{-\frac{1}{2}}\sin \theta \right| = \dfrac {1} {2} }[/math] It can be shown that the pdf of [math]\displaystyle{ d }[/math] and [math]\displaystyle{ \theta }[/math] is:
- [math]\displaystyle{ \begin{matrix} f(d,\theta) = \frac{1}{2}e^{-\frac{d}{2}}*\frac{1}{2\pi},\quad d = R^2 \end{matrix},\quad for\quad 0\leq d\lt \infty\ and\quad 0\leq \theta\leq 2\pi }[/math]
Note that [math]\displaystyle{ \begin{matrix}f(r,\theta)\end{matrix} }[/math] consists of two density functions, Exponential and Uniform, so assuming that r and [math]\displaystyle{ \theta }[/math] are independent [math]\displaystyle{ \begin{matrix} \Rightarrow d \sim~ Exp(1/2), \theta \sim~ Unif[0,2\pi] \end{matrix} }[/math]
- [math]\displaystyle{ \begin{align} R^2 = x^2 + y^2 \end{align} }[/math]
- [math]\displaystyle{ \tan(\theta) = \frac{y}{x} }[/math]
[math]\displaystyle{ \begin{align} f(d) = Exp(1/2)=\frac{1}{2}e^{-\frac{d}{2}}\ \end{align} }[/math]
[math]\displaystyle{ \begin{align} f(\theta) =\frac{1}{2\pi}\ \end{align} }[/math]
To sample from the normal distribution, we can generate a pair of independent standard normal X and Y by:
1) Generating their polar coordinates
2) Transforming back to rectangular (Cartesian) coordinates.
Alternative Method of Generating Standard Normal Random Variables
Step 1: Generate [math]\displaystyle{ u1~Unif(0,1) }[/math] Step 2: Generate [math]\displaystyle{ Y1~Exp(1),Y2~Exp(2) }[/math] Step 3: If [math]\displaystyle{ Y2 \geq(Y1-1)^2/2 }[/math],set [math]\displaystyle{ V=Y1 }[/math],otherwise,go to step 1 Step 4: If [math]\displaystyle{ u1 \leq 1/2 }[/math],then [math]\displaystyle{ X=-V }[/math]
Expectation of a Standard Normal distribution
The expectation of a standard normal distribution is 0
- Below is the proof:
- [math]\displaystyle{ \operatorname{E}[X]= \;\int_{-\infty}^{\infty} x \frac{1}{\sqrt{2\pi}} e^{-x^2/2} \, dx. }[/math]
- [math]\displaystyle{ \phi(x) = \frac{1}{\sqrt{2\pi}}\, e^{- \frac{\scriptscriptstyle 1}{\scriptscriptstyle 2} x^2}. }[/math]
- [math]\displaystyle{ =\;\int_{-\infty}^{\infty} x \phi(x), dx. }[/math]
- Since the first derivative ϕ′(x) is −xϕ(x)
- [math]\displaystyle{ =\;\ - \int_{-\infty}^{\infty} \phi'(x), dx. }[/math]
- [math]\displaystyle{ = - \left[\phi(x)\right]_{-\infty}^{\infty} }[/math]
- [math]\displaystyle{ = 0 }[/math]
More intuitively, because x is an odd function (f(x)+f(-x)=0). Taking integral of x will give [math]\displaystyle{ x^2/2 }[/math] which is an even function (f(x)=f(-x)). If support is from negative infinity to infinity, then the integral will return 0.
- Procedure (Box-Muller Transformation Method):
Pseudorandom approaches to generating normal random variables used to be limited. Inefficient methods such as inverse Gaussian function, sum of uniform random variables, and acceptance-rejection were used. In 1958, a new method was proposed by George Box and Mervin Muller of Princeton University. This new technique was easy to use and also had the accuracy to the inverse transform sampling method that it grew more valuable as computers became more computationally astute.
The Box-Muller method takes a sample from a bivariate independent standard normal distribution, each component of which is thus a univariate standard normal. The algorithm is based on the following two properties of the bivariate independent standard normal distribution:
if [math]\displaystyle{ Z = (Z_{1}, Z_{2} }[/math]) has this distribution, then
1.[math]\displaystyle{ R^2=Z_{1}^2+Z_{2}^2 }[/math] is exponentially distributed with mean 2, i.e.
[math]\displaystyle{ P(R^2 \leq x) = 1-e^{-x/2} }[/math].
2.Given [math]\displaystyle{ R^2 }[/math], the point [math]\displaystyle{ (Z_{1},Z_{2} }[/math]) is uniformly distributed on the circle of radius R centered at the origin.
We can use these properties to build the algorithm:
1) Generate random number [math]\displaystyle{ \begin{align} U_1,U_2 \sim~ \mathrm{Unif}(0, 1) \end{align} }[/math]
2) Generate polar coordinates using the exponential distribution of d and uniform distribution of θ,
[math]\displaystyle{ \begin{align} R^2 = d = -2\log(U_1), & \quad r = \sqrt{d} \\ & \quad \theta = 2\pi U_2 \end{align} }[/math]
[math]\displaystyle{ \begin{matrix} \ R^2 \sim~ Exp(1/2), \theta \sim~ Unif[0,2\pi] \end{matrix} }[/math]
Note: If U~unif(0,1), then ln(1-U)=ln(U)
3) Transform polar coordinates (i.e. R and θ) back to Cartesian coordinates (i.e. X and Y),
[math]\displaystyle{ \begin{align} x = R\cos(\theta) \\ y = R\sin(\theta) \end{align} }[/math]
.
Alternatively,
[math]\displaystyle{ x =\cos(2\pi U_2)\sqrt{-2\ln U_1}\, }[/math] and
[math]\displaystyle{ y =\sin(2\pi U_2)\sqrt{-2\ln U_1}\, }[/math]
Note: In steps 2 and 3, we are using a similar technique as that used in the inverse transform method.
The Box-Muller Transformation Method generates a pair of independent Standard Normal distributions, X and Y (Using the transformation of polar coordinates).
If you want to generate a number of independent standard normal distributed numbers (more than two), you can run the Box-Muller method several times.
For example:
If you want 8 independent standard normal distributed numbers, then run the Box-Muller methods 4 times (8/2 times).
If you want 9 independent standard normal distributed numbers, then run the Box-Muller methods 5 times (10/2 times), and then delete one.
- Code
>>close all >>clear all >>u1=rand(1,1000); >>u2=rand(1,1000); >>d=-2*log(u1); >>tet=2*pi*u2; >>x=d.^0.5.*cos(tet); >>y=d.^0.5.*sin(tet); >>hist(tet) >>hist(d) >>hist(x) >>hist(y)
"Remember: For the above code to work the "." needs to be after the d to ensure that each element of d is raised to the power of 0.5.
Otherwise matlab will raise the entire matrix to the power of 0.5."
Note:
the first graph is hist(tet) and it is a uniform distribution.
The second one is hist(d) and it is a exponential distribution.
The third one is hist(x) and it is a normal distribution.
The last one is hist(y) and it is also a normal distribution.
Attention:There is a "dot" between sqrt(d) and "*". It is because d and tet are vectors.
 File:normal x.jpgFile:normal y.jpg
File:normal x.jpgFile:normal y.jpg
As seen in the histograms above, X and Y generated from this procedure have a standard normal distribution.
- Code
>>close all >>clear all >>x=randn(1,1000); >>hist(x) >>hist(x+2) >>hist(x*2+2)
Note: randn is random sample from a standard normal distribution.
Note: hist(x+2) will be centered at 2 instead of at 0.
hist(x*3+2) is also centered at 2. The mean doesn't change, but the variance of x*3+2 becomes nine times (3^2) the variance of x.
Comment: Box-Muller transformations are not computationally efficient. The reason for this is the need to compute sine and cosine functions. A way to get around this time-consuming difficulty is by an indirect computation of the sine and cosine of a random angle (as opposed to a direct computation which generates U and then computes the sine and cosine of 2πU.
Alternative Methods of generating normal distribution
1. Even though we cannot use inverse transform method, we can approximate this inverse using different functions.One method would be rational approximation.
2.Central limit theorem : If we sum 12 independent U(0,1) distribution and subtract 6 (which is E(ui)*12)we will approximately get a standard normal distribution.
3. Ziggurat algorithm which is known to be faster than Box-Muller transformation and a version of this algorithm is used for the randn function in matlab.
If Z~N(0,1) and X= μ +Zσ then X~[math]\displaystyle{ N(\mu, \sigma^2) }[/math]
If Z1, Z2... Zd are independent identically distributed N(0,1), then Z=(Z1,Z2...Zd)T ~N(0, Id), where 0 is the zero vector and Id is the identity matrix.
For the histogram, the constant is the parameter that affect the center of the graph.
Proof of Box Muller Transformation
Definition: A transformation which transforms from a two-dimensional continuous uniform distribution to a two-dimensional bivariate normal distribution (or complex normal distribution).
Let U1 and U2 be independent uniform (0,1) random variables. Then [math]\displaystyle{ X_{1} = (-2lnU)^0.5_{1}*cos(2\pi U_{2}) }[/math]
[math]\displaystyle{ X_{2} = (-2lnU)^0.5_{1}*sin(2\pi U_{2}) }[/math] are independent N(0,1) random variables.
This is a standard transformation problem. The joint distribution is given by
f(x1 ,x2) = fu1, u2(g1^− 1(x1,x2),g2^− 1(x1,x2)) * | J |
where J is the Jacobian of the transformation,
J = |∂u1/∂x1,∂u1/∂x2|
|∂u2/∂x1,∂u2/∂x2|
where
u1 = g1 ^-1(x1,x2)
u2 = g2 ^-1(x1,x2)
Inverting the above transformations, we have
u1 = exp^{-(x1 ^2+ x2 ^2)/2}
u2 = (1/2pi)*tan^-1 (x2/x1)
Finally we get
f(x1,x2) = {exp^(-(x1^2+x2^2)/2)}/2pi
which factors into two standard normal pdfs.
General Normal distributions
General normal distribution is a special version of the standard normal distribution. The domain of the general normal distribution is affected by the standard deviation and translated by the mean value.
- The pdf of the general normal distribution is
[math]\displaystyle{ f(x) = \frac{1}{\sigma\sqrt{2\pi}} e^{ -\frac{(x-\mu)^2}{2\sigma^2} } }[/math] |
which is almost useless in this course
|
where [math]\displaystyle{ \mu }[/math] is the mean or expectation of the distribution and [math]\displaystyle{ \sigma }[/math] is standard deviation
The special case of the normal distribution is standard normal distribution, which the variance is 1 and the mean is zero. If X is a general normal deviate, then Z = (X − μ)/σ will have a standard normal distribution.
If Z ~ N(0,1), and we want [math]\displaystyle{ X }[/math]~[math]\displaystyle{ N(\mu, \sigma^2) }[/math], then [math]\displaystyle{ X = \mu + \sigma * Z }[/math] Since [math]\displaystyle{ E(x) = \mu +\sigma*0 = \mu }[/math] and [math]\displaystyle{ Var(x) = 0 +\sigma^2*1 }[/math]
If [math]\displaystyle{ Z_1,...Z_d }[/math] ~ N(0,1) and are independent then [math]\displaystyle{ Z = (Z_1,..Z_d)^{T} }[/math]~ [math]\displaystyle{ N(0,I_d) }[/math] ie.
- Code
>>close all >>clear all >>z1=randn(1,1000); <-generate variable from standard normal distribution >>z2=randn(1,1000); >>z=[z1;z2]; <-produce a vector >>plot(z(1,:),z(2,:),'.')
If Z~N(0,Id) and X= [math]\displaystyle{ \underline{\mu} + \Sigma^{\frac{1}{2}} \,Z }[/math] then [math]\displaystyle{ \underline{X} }[/math] ~[math]\displaystyle{ N(\underline{\mu},\Sigma) }[/math]
Non-Standard Normal Distributions
Example 1: Single-variate Normal
If X ~ Norm(0, 1) then (a + bX) has a normal distribution with a mean of [math]\displaystyle{ \displaystyle a }[/math] and a standard deviation of [math]\displaystyle{ \displaystyle b }[/math] (which is equivalent to a variance of [math]\displaystyle{ \displaystyle b^2 }[/math]). Using this information with the Box-Muller transform, we can generate values sampled from some random variable [math]\displaystyle{ \displaystyle Y\sim N(a,b^2) }[/math] for arbitrary values of [math]\displaystyle{ \displaystyle a,b }[/math].
- Generate a sample u from Norm(0, 1) using the Box-Muller transform.
- Set v = a + bu.
The values for v generated in this way will be equivalent to sample from a [math]\displaystyle{ \displaystyle N(a, b^2) }[/math]distribution. We can modify the MatLab code used in the last section to demonstrate this. We just need to add one line before we generate the histogram:
v = a + b * x;
For instance, this is the histogram generated when b = 15, a = 125:
Example 2: Multi-variate Normal
The Box-Muller method can be extended to higher dimensions to generate multivariate normals. The objects generated will be nx1 vectors, and their variance will be described by nxn covariance matrices.
[math]\displaystyle{ \mathbf{z} = N(\mathbf{u}, \Sigma) }[/math] defines the n by 1 vector [math]\displaystyle{ \mathbf{z} }[/math] such that:
- [math]\displaystyle{ \displaystyle u_i }[/math] is the average of [math]\displaystyle{ \displaystyle z_i }[/math]
- [math]\displaystyle{ \!\Sigma_{ii} }[/math] is the variance of [math]\displaystyle{ \displaystyle z_i }[/math]
- [math]\displaystyle{ \!\Sigma_{ij} }[/math] is the co-variance of [math]\displaystyle{ \displaystyle z_i }[/math] and [math]\displaystyle{ \displaystyle z_j }[/math]
If [math]\displaystyle{ \displaystyle z_1, z_2, ..., z_d }[/math] are normal variables with mean 0 and variance 1, then the vector [math]\displaystyle{ \displaystyle (z_1, z_2,..., z_d) }[/math] has mean 0 and variance [math]\displaystyle{ \!I }[/math], where 0 is the zero vector and [math]\displaystyle{ \!I }[/math] is the identity matrix. This fact suggests that the method for generating a multivariate normal is to generate each component individually as single normal variables.
The mean and the covariance matrix of a multivariate normal distribution can be adjusted in ways analogous to the single variable case. If [math]\displaystyle{ \mathbf{z} \sim N(0,I) }[/math], then [math]\displaystyle{ \Sigma^{1/2}\mathbf{z}+\mu \sim N(\mu,\Sigma) }[/math]. Note here that the covariance matrix is symmetric and nonnegative, so its square root should always exist.
We can compute [math]\displaystyle{ \mathbf{z} }[/math] in the following way:
- Generate an n by 1 vector [math]\displaystyle{ \mathbf{x} = \begin{bmatrix}x_{1} & x_{2} & ... & x_{n}\end{bmatrix} }[/math] where [math]\displaystyle{ x_{i} }[/math] ~ Norm(0, 1) using the Box-Muller transform.
- Calculate [math]\displaystyle{ \!\Sigma^{1/2} }[/math] using singular value decomposition.
- Set [math]\displaystyle{ \mathbf{z} = \Sigma^{1/2} \mathbf{x} + \mathbf{u} }[/math].
The following MatLab code provides an example, where a scatter plot of 10000 random points is generated. In this case x and y have a co-variance of 0.9 - a very strong positive correlation.
x = zeros(10000, 1);
y = zeros(10000, 1);
for ii = 1:10000
u1 = rand;
u2 = rand;
R2 = -2 * log(u1);
theta = 2 * pi * u2;
x(ii) = sqrt(R2) * cos(theta);
y(ii) = sqrt(R2) * sin(theta);
end
E = [1, 0.9; 0.9, 1];
[u s v] = svd(E);
root_E = u * (s ^ (1 / 2)) * u';
z = (root_E * [x y]');
z(1,:) = z(1,:) + 0;
z(2,:) = z(2,:) + -3;
scatter(z(1,:), z(2,:))
Note: The svd command computes the matrix singular value decomposition.
[u,s,v] = svd(E) produces a diagonal matrix s of the same dimension as E, with nonnegative diagonal elements in decreasing order, and unitary matrices u and v so that E = u*s*v'.
This code generated the following scatter plot:
In Matlab, we can also use the function "sqrtm()" or "chol()" (Cholesky Decomposition) to calculate square root of a matrix directly. Note that the resulting root matrices may be different but this does materially affect the simulation. Here is an example:
E = [1, 0.9; 0.9, 1]; r1 = sqrtm(E); r2 = chol(E);
R code for a multivariate normal distribution:
n=10000; r2<--2*log(runif(n)); theta<-2*pi*(runif(n)); x<-sqrt(r2)*cos(theta); y<-sqrt(r2)*sin(theta); a<-matrix(c(x,y),nrow=n,byrow=F); e<-matrix(c(1,.9,09,1),nrow=2,byrow=T); svde<-svd(e); root_e<-svde$u %*% diag(svde$d)^1/2; z<-t(root_e %*%t(a)); z[,1]=z[,1]+5; z[,2]=z[,2]+ -8; par(pch=19); plot(z,col=rgb(1,0,0,alpha=0.06))
Bernoulli Distribution
The Bernoulli distribution is a discrete probability distribution, which usually describes an event that only has two possible results, i.e. success or failure (x=0 or 1). If the event succeed, we usually take value 1 with success probability p, and take value 0 with failure probability q = 1 - p.
P ( x = 0) = q = 1 - p
P ( x = 1) = p
P ( x = 0) + P (x = 1) = p + q = 1
If X~Ber(p), its pdf is of the form [math]\displaystyle{ f(x)= p^{x}(1-p)^{(1-x)} }[/math], x=0,1
P is the success probability.
The Bernoulli distribution is a special case of binomial distribution, where the variate x only has two outcomes; so that the Bernoulli also can use the probability density function of the binomial distribution with the variate x taking values 0 and 1.
Let x1,x2 denote the lifetime of 2 independent particles, x1~exp([math]\displaystyle{ \lambda }[/math]), x2~exp([math]\displaystyle{ \lambda }[/math]) we are interested in y=min(x1,x2)
Procedure: To simulate the event of flipping a coin, let P be the probability of flipping head and X = 1 and 0 represent flipping head and tail respectively: 1. Draw U ~ Uniform(0,1) 2. If U <= P X = 1 Else X = 0 3. Repeat as necessary
An intuitive way to think of this is in the coin flip example we discussed in a previous lecture. In this example we set p = 1/2 and this allows for 50% of points to be heads or tails.
- Code to Generate Bernoulli(p = 0.3)
i = 1;
while (i <=1000)
u =rand();
p = 0.3;
if (u <= p)
x(i) = 1;
else
x(i) = 0;
end
i = i + 1;
end
hist(x)
However, we know that if [math]\displaystyle{ \begin{align} X_i \sim Bernoulli(p) \end{align} }[/math] where each [math]\displaystyle{ \begin{align} X_i \end{align} }[/math] is independent,
[math]\displaystyle{ U = \sum_{i=1}^{n} X_i \sim Binomial(n,p) }[/math]
So we can sample from binomial distribution using this property.
Note: We can consider Binomial distribution as the sum of n, independent, Bernoulli distributions
- Code to Generate Binomial(n = 20,p = 0.7)
p = 0.7;
n = 20;
for k=1:5000
i = 1;
while (i <= n)
u=rand();
if (u <= p)
y(i) = 1;
else
y(i) = 0;
end
i = i + 1;
end
x(k) = sum(y==1);
end
hist(x)
Note: We can also regard the Bernoulli Distribution as either a conditional distribution or [math]\displaystyle{ f(x)= p^{x}(1-p)^{(1-x)} }[/math], x=0,1.
Comments on Matlab: When doing operations on vectors, always put a dot before the operator if you want the operation to be done to every element in the vector. example: Let V be a vector with dimension 2*4 and you want each element multiply by 3.
The Matlab code is 3.*V
some examples for using code to generate distribution.
Class 7 - Tuesday, May 28
Universality of the Uniform Distribution/Inverse Method
The inverse method is universal in the sense that we can potentially sample from any distribution where we can find the inverse of the cumulative distribution function.
Procedure:
1.Generate U~Unif [0, 1)
2.set [math]\displaystyle{ x=F^{-1}(u) }[/math]
3.X~f(x)
Remark
1. The preceding can be written algorithmically as
Generate a random number U
If U<p0 set X=x0 and stop
If U<p0+p1 set X=x1 and stop
...
2. If the xi, i>=0, are ordered so that x0<x1<x2<... and if we let F denote the distribution function of X, then [math]\displaystyle{ F(\lt sub\gt xk\lt /sub\gt =\lt sub\gt /sum/pi\lt /sub\gt ) }[/math] and so X will equal xj if F(x(j-1))<=U<F(xj)
Example 1
Let [math]\displaystyle{ X }[/math]1,[math]\displaystyle{ X }[/math]2 denote the lifetime of two independent particles:
[math]\displaystyle{ X }[/math]1~exp([math]\displaystyle{ \lambda }[/math]1)
[math]\displaystyle{ X }[/math]2~exp([math]\displaystyle{ \lambda }[/math]2)
We are interested in [math]\displaystyle{ y=min(X }[/math]1[math]\displaystyle{ ,X }[/math]2[math]\displaystyle{ ) }[/math]
Design an algorithm based on the Inverse-Transform Method to generate samples according to [math]\displaystyle{ f }[/math]y[math]\displaystyle{ (y) }[/math]
Solution:
x1~exp([math]\displaystyle{ \lambda_1 }[/math])
x2~exp([math]\displaystyle{ \lambda_2 }[/math])
[math]\displaystyle{ f_{x(x)}=\lambda e^{-\lambda x},x\geq0 }[/math]
[math]\displaystyle{ F_X(x)=1-e^{-\lambda x}, x\geq 0 }[/math]
[math]\displaystyle{ 1-F_Y(y) = P(Y\gt y) }[/math] = P(min(X1,X2) > y) = [math]\displaystyle{ \, P((X_1)\gt y) P((X_2)\gt y) = e^{\, -(\lambda_1 + \lambda_2) y} }[/math]
[math]\displaystyle{ F_Y(y)=1-e^{\, -(\lambda_1 + \lambda_2) y}, y\geq 0 }[/math]
[math]\displaystyle{ U=1-e^{\, -(\lambda_1 + \lambda_2) y} }[/math] => [math]\displaystyle{ y=\, {-\frac {1}{{\lambda_1 +\lambda_2}}} ln(1-u) }[/math]
Procedure:
Step1: Generate U~ U(0, 1)
Step2: set [math]\displaystyle{ y=\, {-\frac {1}{{\lambda_1 +\lambda_2}}} ln(u) }[/math]
If we generalize this example from two independent particles to n independent particles we will have:
[math]\displaystyle{ X }[/math]1~exp([math]\displaystyle{ \lambda }[/math]1)
[math]\displaystyle{ X }[/math]2~exp([math]\displaystyle{ \lambda }[/math]2)
...
[math]\displaystyle{ X }[/math]n~exp([math]\displaystyle{ \lambda }[/math]n)
.
And the algorithm using the inverse-transform method as follows:
step1: Generate U~U(0,1)
Step2: [math]\displaystyle{ y=\, {-\frac {1}{{ \sum\lambda_i}}} ln(1-u) }[/math]
Example 2
Consider U~Unif[0,1)
[math]\displaystyle{ X=\, a (1-\sqrt{1-u}) }[/math],
where a>0 and a is a real number
What is the distribution of X?
Solution:
We can find a form for the cumulative distribution function of X by isolating U as U~Unif[0,1) will take values from the range of F(X)uniformly. It then remains to differentiate the resulting form by X to obtain the probability density function.
[math]\displaystyle{ X=\, a (1-\sqrt{1-u}) }[/math]
=>[math]\displaystyle{ 1-\frac {x}{a}=\sqrt{1-u} }[/math]
=>[math]\displaystyle{ u=1-(1-\frac {x}{a})^2 }[/math]
=>[math]\displaystyle{ u=\, {\frac {x}{a}} (2-\frac {x}{a}) }[/math]
[math]\displaystyle{ f(x)=\frac {dF(x)}{dx}=\frac {2}{a}-\frac {2x}{a^2}=\, \frac {2}{a} (1-\frac {x}{a}) }[/math]
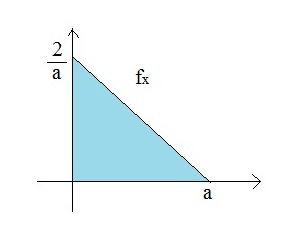
Example 3
Suppose FX(x) = xn, 0 ≤ x ≤ 1, n ∈ N > 0. Generate values from X.
Solution:
1. generate u ~ Unif[0, 1)
2. Set x = U1/n
For example, when n = 20,
u = 0.6 => x = u1/20 = 0.974
u = 0.5 => x = u1/20 = 0.966
u = 0.2 => x = u1/20 = 0.923
Observe from above that the values of X for n = 20 are close to 1, this is because we can view Xn as the maximum of n independent random variables X, X~Unif(0,1) and is much likely to be close to 1 as n increases. This is because when n is large the exponent tends towards 0. This observation is the motivation for method 2 below.
Recall that
If Y = max (X1, X2, ... , Xn), where X1, X2, ... , Xn are independent,
FY(y) = P(Y ≤ y) = P(max (X1, X2, ... , Xn) ≤ y) = P(X1 ≤ y, X2 ≤ y, ... , Xn ≤ y) = Fx1(y) Fx2(y) ... Fxn(y)
Similarly if [math]\displaystyle{ Y = min(X_1,\ldots,X_n) }[/math] then the cdf of [math]\displaystyle{ Y }[/math] is [math]\displaystyle{ F_Y = 1- }[/math][math]\displaystyle{ \prod }[/math][math]\displaystyle{ (1- F_{X_i}) }[/math]
Method 1: Following the above result we can see that in this example, FX = xn is the cumulative distribution function of the max of n uniform random variables between 0 and 1 (since for U~Unif(0, 1), FU(x) =
Method 2: generate X by having a sample of n independent U~Unif(0, 1) and take the max of the n samples to be x. However, the solution given above using inverse-transform method only requires generating one uniform random number instead of n of them, so it is a more efficient method.
Generate the Y = max (X1, X2, ... , Xn), Y = min (X1, X2, ... , Xn), pdf and cdf, but (xi and xj are independent) i,j=1,2,3,4,5.....
Example 4 (New)
Now, we are having an similar example as example 1 just doing the maximum way.
Let X1,X2 denote the lifetime of two independent particles:
[math]\displaystyle{ \, X_1, X_2 \sim exp(\lambda) }[/math]
We are interested in Z=max(X1,X2)
Design an algorithm based on the Inverse-Transform Method to generate samples according to fZ(z)
[math]\displaystyle{ \, F_Z(z)=P[Z\lt =z] = F_{X_1}(z) \cdot F_{X_2}(z) = (1-e^{-\lambda z})^2 }[/math]
[math]\displaystyle{ \text{thus } F^{-1}(z) = -\frac{1}{\lambda}\log(1-\sqrt z) }[/math]
To sample Z:
[math]\displaystyle{ \, \text{Step 1: Generate } U \sim U[0,1) }[/math]
[math]\displaystyle{ \, \text{Step 2: Let } Z = -\frac{1}{\lambda}\log(1-\sqrt U) }[/math], therefore we can generate random variable of Z.
Discrete Case:
u~unif(0,1)
x <- 0, S <- P0
while u < S
x <- x + 1
S <- S + P0
Return x
Decomposition Method
The CDF, F, is a composition if [math]\displaystyle{ F_{X}(x) }[/math] can be written as:
[math]\displaystyle{ F_{X}(x) = \sum_{i=1}^{n}p_{i}F_{X_{i}}(x) }[/math] where
1) pi > 0
2) [math]\displaystyle{ \sum_{i=1}^{n} }[/math]pi = 1.
3) [math]\displaystyle{ F_{X_{i}}(x) }[/math] is a CDF
The general algorithm to generate random variables from a composition CDF is:
1) Generate U, V ~ [math]\displaystyle{ U(0,1) }[/math]
2) If u < p1, v=[math]\displaystyle{ F_{X_{1}}(x) }[/math]-1
3) Else if u < p1+p2, v=[math]\displaystyle{ F_{X_{2}}(x) }[/math]-1
4) ....
Explanation
Each random variable that is a part of X contributes [math]\displaystyle{ p_{i} F_{X_{i}}(x) }[/math] to [math]\displaystyle{ F_{X}(x) }[/math] every time.
From a sampling point of view, that is equivalent to contributing [math]\displaystyle{ F_{X_{i}}(x) }[/math] [math]\displaystyle{ p_{i} }[/math] of the time. The logic of this is similar to that of the Accept-Reject Method, but instead of rejecting a value depending on the value u takes, we instead decide which distribution to sample it from.
Simplified Version
1) Generate [math]\displaystyle{ u \sim Unif(0,1) }[/math]
2) Set [math]\displaystyle{ X=0, s=P_0 }[/math]
3) While [math]\displaystyle{ u \gt s, }[/math]
set [math]\displaystyle{ X = X+1 }[/math] and [math]\displaystyle{ s=s+P_x }[/math]
4) Return [math]\displaystyle{ X }[/math]
Examples of Decomposition Method
Example 1
[math]\displaystyle{ f(x) = \frac{5}{12}(1+(x-1)^4) 0\leq x\leq 2 }[/math]
[math]\displaystyle{ f(x) = \frac{5}{12}+\frac{5}{12}(x-1)^4 = \frac{5}{6} (\frac{1}{2})+\frac {1}{6}(\frac{5}{2})(x-1))^4 }[/math]
Let[math]\displaystyle{ f_{x_1}= \frac{1}{2} }[/math] and [math]\displaystyle{ f_{x_2} = \frac {5}{2}(x-1)^4 }[/math]
Algorithm:
Generate U~Unif(0,1)
If [math]\displaystyle{ 0\lt u\lt \frac {5}{6} }[/math], then we sample from fx1
Else if [math]\displaystyle{ \frac{5}{6}\lt u\lt 1 }[/math], we sample from fx2
We can find the inverse CDF of fx2 and utilize the Inverse Transform Method in order to sample from fx2
Sampling from fx1 is more straightforward since it is uniform over the interval (0,2)
divided f(x) to two pdf of x1 and x2, with uniform distribution, of two range of uniform.
Example 2
[math]\displaystyle{ f(x)=\frac{1}{4}e^{-x}+2x+\frac{1}{12}, \quad 0\leq x \leq 3 }[/math]
We can rewrite f(x) as [math]\displaystyle{ f(x)=(\frac{1}{4}) e^{-x}+(\frac{2}{4}) 4x+(\frac{1}{4}) \frac{1}{3} }[/math]
Let fx1 = [math]\displaystyle{ e^{-x} }[/math], fx2 = 4x, and fx3 = [math]\displaystyle{ \frac{1}{3} }[/math]
Generate U~Unif(0,1)
If [math]\displaystyle{ 0\lt u\lt \frac{1}{4} }[/math], we sample from fx1
If [math]\displaystyle{ \frac{1}{4}\leq u \lt \frac{3}{4} }[/math], we sample from fx2
Else if [math]\displaystyle{ \frac{3}{4} \leq u \lt 1 }[/math], we sample from fx3
We can find the inverse CDFs of fx1 and fx2 and utilize the Inverse Transform Method in order to sample from fx1 and fx2
We find Fx1 = [math]\displaystyle{ 1-e^{-x} }[/math] and Fx2 = [math]\displaystyle{ 2x^{2} }[/math]
We find the inverses are [math]\displaystyle{ X = -ln(1-u) }[/math] for Fx1 and [math]\displaystyle{ X = \sqrt{\frac{U}{2}} }[/math] for Fx2
Sampling from fx3 is more straightforward since it is uniform over the interval (0,3)
In general, to write an efficient algorithm for:
[math]\displaystyle{ F_{X}(x) = p_{1}F_{X_{1}}(x) + p_{2}F_{X_{2}}(x) + ... + p_{n}F_{X_{n}}(x) }[/math]
We would first calculate [math]\displaystyle{ {q_i} = \sum_{j=1}^i p_j, \forall i = 1,\dots, n }[/math]
Then Generate [math]\displaystyle{ U \sim~ Unif(0,1) }[/math]
If [math]\displaystyle{ U \lt q_1 }[/math] sample from [math]\displaystyle{ f_1 }[/math]
else if [math]\displaystyle{ u\lt q_i }[/math] sample from [math]\displaystyle{ f_i }[/math] for [math]\displaystyle{ 1 \lt i \lt n }[/math]
else sample from [math]\displaystyle{ f_n }[/math]
when we divided the pdf of different range of f(x1) f(x2) and f(x3), and generate all of them and inverse, U~U(0,1)
Example of Decomposition Method
Fx(x) = 1/3*x+1/3*x2+1/3*x3, 0<= x<=1
let U =Fx(x) = 1/3*x+1/3*x2+1/3*x3, solve for x.
P1=1/3, Fx1(x)= x, P2=1/3,Fx2(x)= x2, P3=1/3,Fx3(x)= x3
Algorithm:
Generate U ~ Unif [0,1)
Generate V~ Unif [0,1)
if 0<u<1/3, x = v
else if u<2/3, x = v1/2
else x = v1/3
Matlab Code:
u=rand v=rand if u<1/3 x=v elseif u<2/3 x=sqrt(v) else x=v^(1/3) end
=== Example of Decomposition Method(new) ===
Fx(x) = 1/2*x+1/2*x2, 0<= x<=1
let U =Fx(x) = 1/2*x+1/2*x2, solve for x.
P1=1/2, Fx1(x)= x, P2=1/2,Fx2(x)= x2,
Algorithm:
Generate U ~ Unif [0,1)
Generate V~ Unif [0,1)
if 0<u<1/2, x = v
else x = v1/2
Matlab Code:
u=rand v=rand if u<1/2 x=v else x=sqrt(v) end
Extra Knowledge about Decomposition Method
There are different types and applications of Decomposition Method
1. Primal decomposition
2. Dual decomposition
3. Decomposition with constraints
4. More general decomposition structures
5. Rate control
6. Single commodity network flow
For More Details, please refer to http://www.stanford.edu/class/ee364b/notes/decomposition_notes.pdf
Fundamental Theorem of Simulation
Consider two shapes, A and B, where B is a sub-shape (subset) of A. We want to sample uniformly from inside the shape B. Then we can sample uniformly inside of A, and throw away all samples outside of B, and this will leave us with a uniform sample from within B. (Basis of the Accept-Reject algorithm)
The advantage of this method is that we can sample a unknown distribution from a easy distribution. The disadvantage of this method is that it may need to reject many points, which is inefficient.
inverse each part of partial CDF, the partial CDF is divided by the original CDF, partial range is uniform distribution.
Question 2
Use Acceptance and Rejection Method to sample from [math]\displaystyle{ f_X(x)=b*x^n*(1-x)^n }[/math] , [math]\displaystyle{ n\gt 0 }[/math], [math]\displaystyle{ 0\lt x\lt 1 }[/math]
Solution: This is a beta distribution, Beta ~[math]\displaystyle{ \int _{0}^{1}b*x^{n}*(1-x)^{n}dx = 1 }[/math]
U1~Unif[0,1)
U2~Unif[0,1)
fx=[math]\displaystyle{ bx^{1/2}(1-x)^{1/2} \lt = bx^{-1/2}\sqrt2 ,0\lt =x\lt =1/2 }[/math]
The beta distribution maximized at 0.5 with value [math]\displaystyle{ (1/4)^n }[/math]. So, [math]\displaystyle{ c=b*(1/4)^n }[/math] Algorithm: 1.Draw [math]\displaystyle{ U_1 }[/math] from [math]\displaystyle{ U(0, 1) }[/math].[math]\displaystyle{ U_2 }[/math] from [math]\displaystyle{ U(0, 1)\lt math\gt 2.If \lt math\gt U_2\lt =b*(U_1)^n*(1-(U_1))^n/b*(1/4)^n=(4*(U_1)*(1-(U_1)))^n }[/math]
then X=U_1 Else return to step 1.
Discrete Case:
Most discrete random variables do not have a closed form inverse CDF. Also, its CDF [math]\displaystyle{ F:X \rightarrow [0,1] }[/math] is not necessarily onto. This means that not every point in the interval [math]\displaystyle{ [0,1] }[/math] has a preimage in the support set of X through the CDF function.
Let [math]\displaystyle{ X }[/math] be a discrete random variable where [math]\displaystyle{ a \leq X \leq b }[/math] and [math]\displaystyle{ a,b \in \mathbb{Z} }[/math] .
To sample from [math]\displaystyle{ X }[/math], we use the partition method below:
[math]\displaystyle{ \, \text{Step 1: Generate u from } U \sim Unif[0,1] }[/math]
[math]\displaystyle{ \, \text{Step 2: Set } x=a, s=P(X=a) }[/math]
[math]\displaystyle{ \, \text{Step 3: While } u\gt s, x=x+1, s=s+P(X=x) }[/math]
[math]\displaystyle{ \, \text{Step 4: Return } x }[/math]
Class 8 - Thursday, May 30, 2013
In this lecture, we will discuss algorithms to generate 3 well-known distributions: Binomial, Geometric and Poisson. For each of these distributions, we will first state its general understanding, probability mass function, expectation and variance. Then, we will derive one or more algorithms to sample from each of these distributions, and implement the algorithms on Matlab.
The Bernoulli distribution
The Bernoulli distribution is a special case of the binomial distribution, where n = 1. X ~ Bin(1, p) has the same meaning as X ~ Ber(p), where p is the probability if the event success, otherwise the probability is 1-p (we usually define a variate q, q= 1-p). The mean of Bernoulli is p, variance is p(1-p). Bin(n, p), is the distribution of the sum of n independent Bernoulli trials, Bernoulli(p), each with the same probability p, where 0<p<1.
For example, let X be the event that a coin toss results in a "head" with probability p, then X~Bernoulli(p).
P(X=1)=p,P(X=0)=1-p, P(x=0)+P(x=1)=p+q=1
Algorithm:
1. Generate u~Unif(0,1)
2. If u ≤ p, then x = 1
else x = 0
The answer is:
when U≤p, x=1
when U>p, x=0
3.Repeat as necessary
The Binomial Distribution
If X~Bin(n,p), then its pmf is of form:
f(x)=(nCx) px(1-p)(n-x), x=0,1,...n
Or f(x) = [math]\displaystyle{ (n!/x!(n-x)!) }[/math] px(1-p)(n-x), x=0,1,...n
Mean (x) = E(x) = [math]\displaystyle{ np }[/math]
Variance = [math]\displaystyle{ np(1-p) }[/math]
Generate n uniform random number [math]\displaystyle{ U_1,...,U_n }[/math] and let X be the number of [math]\displaystyle{ U_i }[/math] that are less than or equal to p.
The logic behind this algorithm is that the Binomial Distribution is simply a Bernoulli Trial, with a probability of success of p, repeated n times. Thus, we can sample from the distribution by sampling from n Bernoulli. The sum of these n bernoulli trials will represent one binomial sampling. Thus, in the below example, we are sampling 1000 realizations from 20 Bernoulli random variables. By summing up the rows of the 20 by 1000 matrix that is produced, we are summing up the 20 bernoulli outcomes to produce one binomial sampling. We have 1000 rows, which means we have realizations from 1000 binomial random variables when this sum is done (the output of the sum is a 1 by 1000 sized vector).
To continue with the previous example, let X be the number of heads in a series of n independent coin tosses - where for each toss, the probability of coming up with a head is p - then X~Bin(n, p).
MATLAB tips: to get a pdf f(x), we can use code binornd(N,P). N means number of trials and p is the probability of success. a=[2 3 4],if set a<3, will produce a=[1 0 0]. If you set "a == 3", it will produce [0 1 0]. If a=[2 6 9 10], if set a<4, will produce a=[1 0 0 0], because only the first element (2) is less than 4, meanwhile the rest are greater. So we can use this to get the number which is less than p.
Algorithm for Bernoulli is given as above
Code
>>a=[3 5 8]; >>a<5 ans= 1 0 0 >>rand(20,1000) >>rand(20,1000)<0.4 >>A = sum(rand(20,1000)<0.4) #sum of raws ~ Bin(20 , 0.3) >>hist(A) >>mean(A) Note: `1` in the above code means sum the matrix by column >>sum(sum(rand(20,1000)<0.4)>8)/1000 This is an estimate of Pr[A>8].
remark: a=[2 3 4],if set a<3, will produce a=[1 0 0]. If you set "a == 3", it will produce [0 1 0]. using code to find some value what i want to get from the matrix. It`s useful to define some matrixs.
Relation between Bernoulli Distribution and Binomial Distribution: For instance, we want to find numbers ≤0.3. Uniform collects which is ≤0.3, and Binomial calculates how many numbers are there ≤0.3.
The Geometric Distribution
Geometric distribution is a discrete distribution. There are two types geometric distributions, the first one is the probability distribution of the number of X Bernoulli fail trials, with probability 1-p, needed until the first success situation happened, X come from the set { 1, 2, 3, ...}; the other one is the probability distribution of the number Y = X − 1 of failures, with probability 1-p, before the first success, Y comes from the set { 0, 1, 2, 3, ... }.
For example,
If the success event showed at the first time, which x=1, then f(x)=p.
If the success event showed at the second time and failed at the first time, which x=2, then f(x)=p(1-p).
If the success event showed at the third time and failed at the first and second time, which x=3, then f(x)= p(1-p)(k-1). etc.
If the success event showed at the x time and all failed before time x, which x=x, then f(x)= p(1-p)(k-1)
which is,
x Pr
1 P
2 P(1-P)
3 P(1-P)2
. .
. .
. .
n P(1-P)(n-1)
For example, suppose a die is thrown repeatedly until the first time a "6" appears. This is a question of geometric distribution of the number of times on the set { 1, 2, 3, ... } with p = 1/6.
Generally speaking, if X~G(p) then its pdf is of the form f(x)=(1-p)(x-1)*p, x=1,2,...
The random variable X is the number of trials required until the first success in a series of independent Bernoulli trials.
Other properties
Probability mass function : P(X=k) = p(1-p)(k-1)
Tail probability : P(X>n) = [math]\displaystyle{ (1-p)^n }[/math]
The CDF : P(X<n) = 1 - [math]\displaystyle{ (1-p)^n }[/math]
Mean of x = 1/p Var(x) = (1-p)/p^2
There are two ways to look at a geometric distribution.
1st Method
We look at the number of trials before the first success. This includes the last trial in which you succeeded. This will be used in our course.
pdf is of form f(x)=>(1-p)(x-1)*(p), x = 1, 2, 3, ...
2nd Method
This involves modeling the failure before the first success. This does not include the last trial in which we succeeded.
pdf is of form f(x)=> ((1-p)^x)*p , x = 0, 1, 2, ....
If Y~Exp([math]\displaystyle{ \lambda }[/math]) then X=floor(Y)+1 is geometric.
Choose e^(-[math]\displaystyle{ \lambda }[/math])=1-p. Then X ~ geo (p)
P (X > x) = (1-p)x(because first x trials are not successful)
Proof
P(X>x) = P( floor(Y) + 1 > X) = P(floor (Y) > x- 1) = P(Y>= x) = e(-[math]\displaystyle{ \lambda }[/math] * x)
SInce p = 1- e-[math]\displaystyle{ \lambda }[/math] or [math]\displaystyle{ \lambda }[/math]= [math]\displaystyle{ -log(1-p) }[/math](compare the pdf of exponential distribution and Geometric distribution,we can look at e-[math]\displaystyle{ \lambda }[/math] the probability of the fail trial), then
P(X>x) = e(-[math]\displaystyle{ \lambda }[/math] * x) = elog(1-p)*x = (1-p)x
Note that floor(Y)>X -> Y >= X+1 (X is an integer)
proof how to use EXP distribution to find P(X>x)=(1-p)^x
Suppose X has the exponential distribution with rate parameter [math]\displaystyle{ \lambda \gt 0 }[/math]
the [math]\displaystyle{ \left \lfloor X \right \rfloor }[/math] and [math]\displaystyle{ \left \lceil X \right \rceil }[/math] have geometric distribution on [math]\displaystyle{ \mathcal{N} }[/math] and [math]\displaystyle{ \mathcal{N}_{+} }[/math] respectively each with success probability [math]\displaystyle{ 1-e^ {- \lambda} }[/math]
Proof:
[math]\displaystyle{ \text{For } n \in \mathcal{N} }[/math]
[math]\displaystyle{ \begin{align}
P(\left \lfloor X \right \rfloor = n)&{}= P( n \leq X \lt n+1) \\
&{}= F( n+1) - F(n) \\
\text{By algebra and simplification:} \\
P(\left \lfloor X \right \rfloor = n)&{}= (e^ {-\lambda})^n \cdot (1 - e^ {-\lambda}) \\
&{}= Geo (1 - e^ {-\lambda}) \\
\text{Proof of ceiling part follows immediately.} \\
\end{align} }[/math]
Algorithm:
1) Let [math]\displaystyle{ \lambda = -\log (1-p) }[/math]
2) Generate a [math]\displaystyle{ Y \sim Exp(\lambda ) }[/math]
3) We can then let [math]\displaystyle{ X = \left \lfloor Y \right \rfloor + 1, where X\sim Geo(p) }[/math]
note: [math]\displaystyle{ \left \lfloor Y \right \rfloor \gt 2 -\gt Y\gt =3 }[/math]
[math]\displaystyle{ \left \lfloor Y \right \rfloor \gt 5 -\gt Y\gt =6 }[/math]
[math]\displaystyle{ \left \lfloor Y \right \rfloor\gt x }[/math] -> Y>= X+1
[math]\displaystyle{ P(Y\gt =X) }[/math]
Y ~ Exp ([math]\displaystyle{ \lambda }[/math])
pdf of Y : [math]\displaystyle{ \lambda e^{-\lambda} }[/math]
cdf of Y : [math]\displaystyle{ 1- e^{-\lambda} }[/math]
cdf [math]\displaystyle{ P(Y\lt x)=1-e^{-\lambda x} }[/math]
[math]\displaystyle{ P(Y\gt =x)=1-(1- e^{-\lambda x})=e^{-\lambda x} }[/math]
[math]\displaystyle{ e^{-\lambda}=1-p -\gt -log(1-p)=\lambda }[/math]
[math]\displaystyle{ P(Y\gt =x)=e^{-\lambda x}=e^{log(1-p)x}=(1-p)^x }[/math]
[math]\displaystyle{ E[x]=1/P }[/math]
[math]\displaystyle{ Var= (1-P)/(P^2) }[/math]
P(X>x)
=P(floor(y)+1>x)
=P(floor(y)>x-1)
=P(y>=x)
use [math]\displaystyle{ e^{-\lambda}=1-p }[/math] to figure out the mean and variance.
Code
>>p=0.4;
>>l=-log(1-p);
>>u=rand(1,1000);
>>y=(-1/l)*log(u);
>>x=floor(y)+1;
>>hist(x)
===Note:===
mean(x)~E[X]=> 1/p
Var(x)~V[X]=> (1-p)/p^2
A specific Example:
Consider x=5
>> sum(x==5)/1000 -> chance that will succeed at fifth trial;
>> ans =
0.0780
>> sum(x>10)/1000 -> chance that will succeed after 10 trials
>> ans =
0.0320
Note that the above mean is the average amount of times you should try until you get a successful case.
EXAMPLE for geometric distribution: Consider the case of rolling a die:
X=the number of rolls that it takes for the number 5 to appear.
We have X ~Geo(1/6), [math]\displaystyle{ f(x)=(1/6)*(5/6)^{x-1} }[/math], x=1,2,3....
Now, let [math]\displaystyle{ Y=e^{\lambda} }[/math] => x=floor(Y) +1
Let [math]\displaystyle{ e^{-\lambda}=5/6 }[/math]
[math]\displaystyle{ P(X\gt x) = P(Y\gt =x) }[/math] (from the class notes)
We have [math]\displaystyle{ e^{-\lambda *x} = (5/6)^x }[/math]
Algorithm: let [math]\displaystyle{ \lambda = -\log(5/6) }[/math]
1) Let Y be [math]\displaystyle{ e^{\lambda} }[/math], exponentially distributed
2) Set X= floor(Y)+1, to generate X
[math]\displaystyle{ E[x]=6, Var[X]=5/6 /(1/6^2) = 30 }[/math]
GENERATING NEGATIVE BINOMIAL RV USING GEOMETRIC RV'S
Property of negative binomial Random Variable:
The negative binomial random variable is a sum of r independent geometric random variables.
Using this property we can formulate the following algorithm:
Step 1: Generate r geometric rv's each with probability p using the procedure presented above.
Step 2: Take the sum of these r geometric rv's. This RV follows NB(r,p)
remark the step 1 and step 2. Looking for the floor Y, and e^(-mu)=1-p=5/6, and then generate x.
Poisson Distribution
If [math]\displaystyle{ \displaystyle X \sim \text{Poi}(\lambda) }[/math], its pdf is of the form [math]\displaystyle{ \displaystyle \, f(x) = \frac{e^{-\lambda}\lambda^x}{x!} }[/math] , where [math]\displaystyle{ \displaystyle \lambda }[/math] is the rate parameter.
definition:In probability theory and statistics, the Poisson distribution (pronounced [pwasɔ̃]) is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time and/or space if these events occur with a known average rate and independently of the time since the last event. The Poisson distribution can also be used for the number of events in other specified intervals such as distance, area or volume. For instance, suppose someone typically gets 4 pieces of mail per day on average. There will be, however, a certain spread: sometimes a little more, sometimes a little less, once in a while nothing at all.[2] Given only the average rate, for a certain period of observation (pieces of mail per day, phonecalls per hour, etc.), and assuming that the process, or mix of processes, that produces the event flow is essentially random, the Poisson distribution specifies how likely it is that the count will be 3, or 5, or 10, or any other number, during one period of observation. That is, it predicts the degree of spread around a known average rate of occurrence. The Derivation of the Poisson distribution section shows the relation with a formal definition.(from Wikipedia)
Understanding of Poisson distribution:
If customers independently come to bank over time, all following exponential distributions with rate [math]\displaystyle{ \lambda }[/math] per unit of time, then X(t) = # of customer in [0,t] ~ Poi[math]\displaystyle{ (\lambda t) }[/math]
Its mean and variance are
[math]\displaystyle{ \displaystyle E[X]=\lambda }[/math]
[math]\displaystyle{ \displaystyle Var[X]=\lambda }[/math]
An useful property: If [math]\displaystyle{ X_i \sim \mathrm{Pois}(\lambda_i)\, i=1,\dots,n }[/math] are independent and [math]\displaystyle{ \lambda=\sum_{i=1}^n \lambda_i }[/math], then [math]\displaystyle{ Y = \left( \sum_{i=1}^n X_i \right) \sim \mathrm{Pois}(\lambda) }[/math]
A Poisson random variable X can be interpreted as the maximal number of i.i.d. (Independent and Identically Distributed) exponential variables(with parameter [math]\displaystyle{ \lambda }[/math]) whose sum does not exceed 1.
The traditional understanding of the Poisson distribution as the total number of events in a specific interval can be understood here since the above definition simply describes the Poisson as the sum of waiting times for n events in an interval of length 1.
[math]\displaystyle{ \displaystyle\text{Let } Y_j \sim \text{Exp}(\lambda), U_j \sim \text{Unif}(0,1) }[/math]
[math]\displaystyle{ Y_j = -\frac{1}{\lambda}\log(U_j) \text{ from Inverse Transform Method} }[/math]
[math]\displaystyle{ \begin{align}
X &= \max \{ n: \sum_{j=1}^{n} Y_j \leq 1 \} \\
&= \max \{ n: \sum_{j=1}^{n} - \frac{1}{\lambda}\log(U_j) \leq 1 \} \\
&= \max \{ n: \sum_{j=1}^{n} \log(U_j) \gt = -\lambda \} \\
&= \max \{ n: \log(\prod_{j=1}^{n} U_j) \gt = -\lambda \} \\
&= \max \{ n: \prod_{j=1}^{n} U_j \gt = e^{-\lambda} \} \\
&= \min \{ n: \prod_{j=1}^{n} U_j \gt = e^{-\lambda} \} - 1 \\
\end{align} }[/math]
Note: From above, we can use Logarithm Rules [math]\displaystyle{ \log(a)+\log(b)=\log(ab) }[/math] to generate the result.
Algorithm:
1) Set n=1, a=1
2) Generate [math]\displaystyle{ U_n \sim U(0,1), a=aU_n }[/math]
3) If [math]\displaystyle{ a \gt = e^{-\lambda} }[/math] , then n=n+1, and go to Step 2. Else, x=n-1
using inverse-method to proof mean and variance of poisson distribution.
MATLAB Code for generating Poisson Distribution
>>l=2; N=1000
>>for ii=1:N
n=1;
a=1;
u=rand;
a=a*u;
while a>exp(-l)
n=n+1;
u=rand;
a=a*u;
end
x(ii)=n-1;
end
>>hist(x)
>>Sum(x==1)/N # Probability of x=1
>>Sum(x>3)/N # Probability of x > 3
Another way to generate random variable from poisson distribution
Note: [math]\displaystyle{ P(X=x)=\frac {e^{-\lambda}\lambda^x}{x!}, \forall x \in \N }[/math]
Let [math]\displaystyle{ \displaystyle p(x) = P(X=x) }[/math] denote the pmf of [math]\displaystyle{ \displaystyle X }[/math].
Then ratio is [math]\displaystyle{ \frac{p(x+1)}{p(x)}=\frac{\lambda}{x+1}, \forall x \in \N }[/math]
Therefore, [math]\displaystyle{ p(x+1)=\frac{\lambda}{x+1}p(x) }[/math]
Algorithm:
1. Set [math]\displaystyle{ \displaystyle x=0 }[/math]
2. Set [math]\displaystyle{ \displaystyle F=p=e^{-\lambda} }[/math]
3. Generate [math]\displaystyle{ \displaystyle U \sim~ \text{Unif}(0,1) }[/math]
4. If [math]\displaystyle{ \displaystyle U\lt F }[/math], output [math]\displaystyle{ \displaystyle x }[/math]
Else
[math]\displaystyle{ \displaystyle p=\frac{\lambda}{x+1} p }[/math]
[math]\displaystyle{ \displaystyle F=F+p }[/math]
[math]\displaystyle{ \displaystyle x = x+1 }[/math]
Go to 4.
This is indeed the inverse-transform method, with a clever way to calculate the CDF on the fly.
u=rand(0.1000) hist(x)
Class 9 - Tuesday, June 4, 2013
Beta Distribution
The beta distribution is a continuous probability distribution. There are two positive shape parameters in this distribution defined as alpha and beta, both parameters greater than 0, and X within the interval [0,1]. The parameter alpha is used as exponents of the random variable. The parameter beta is used to control the shape of the this distribution. We use the beta distribution to build the model of the behavior of random variables, which are limited to intervals of finite length. For example, we can use the beta distribution to analyze the time allocation of sunshine data and variability of soil properties.
If X~Beta([math]\displaystyle{ \alpha, \beta }[/math]) then its p.d.f. is of the form
- [math]\displaystyle{ \displaystyle \text{ } f(x) = \frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha)\Gamma(\beta)}x^{\alpha-1}(1-x)^{\beta-1} }[/math] where [math]\displaystyle{ 0 \leq x \leq 1 }[/math] and [math]\displaystyle{ \alpha }[/math]>0, [math]\displaystyle{ \beta }[/math]>0
and [math]\displaystyle{ f(x;\alpha,\beta)= 0 }[/math] otherwise Note: [math]\displaystyle{ \Gamma(\alpha)=(\alpha-1)! }[/math] if [math]\displaystyle{ \alpha }[/math] is a positive integer.
The mean of the beta distribution is [math]\displaystyle{ \frac{\alpha}{\alpha + \beta} }[/math]. The variance is [math]\displaystyle{ \frac{\alpha\beta}{(\alpha+\beta)^2 (\alpha + \beta + 1)} }[/math]
The variance of the beta distribution decreases monotonically if [math]\displaystyle{ \alpha = \beta }[/math] and as [math]\displaystyle{ \alpha = \beta }[/math] increases, the variance decreases.
The formula for the cumulative distribution function of the beta distribution is also called the incomplete beta function ratio (commonly denoted by Ix) and is defined as F(x) = I(x)(p,q)
To generate random variables of a Beta distribution, there are multiple cases depending on the value of [math]\displaystyle{ \alpha }[/math] and [math]\displaystyle{ \beta }[/math]:
Case 1: If [math]\displaystyle{ \alpha=1 }[/math] and [math]\displaystyle{ \beta=1 }[/math]
- [math]\displaystyle{ \displaystyle \text{Beta}(1,1) = \frac{\Gamma(1+1)}{\Gamma(1)\Gamma(1)}x^{1-1}(1-x)^{1-1} }[/math]
- [math]\displaystyle{ = \frac{1!}{0!0!}x^{0}(1-x)^{0} }[/math]
- [math]\displaystyle{ = 1 }[/math]
Note: 0! = 1.
Hence, the distribution is:
- [math]\displaystyle{ \displaystyle \text{Beta}(1,1) = U (0, 1) }[/math]
If the Question asks for sampling Beta Distribution, we can sample from Uniform Distribution which we already know how to sample from
Algorithm:
Generate U~Unif(0,1)
Case 2: Either [math]\displaystyle{ \alpha=1 }[/math] or [math]\displaystyle{ \beta=1 }[/math]
e.g. [math]\displaystyle{ \alpha=1 }[/math]
We don't make any assumption about [math]\displaystyle{ \beta }[/math] except that it is a positive integer. <br\>
- [math]\displaystyle{ \displaystyle \text{f}(x) = \frac{\Gamma(1+\beta)}{\Gamma(1)\Gamma(\beta)}x^{1-1}(1-x)^{\beta-1}=\beta(1-x)^{\beta-1} }[/math]
- [math]\displaystyle{ \beta=1 }[/math]
- [math]\displaystyle{ \displaystyle \text{f}(x) = \frac{\Gamma(\alpha+1)}{\Gamma(\alpha)\Gamma(1)}x^{\alpha-1}(1-x)^{1-1}=\alpha x^{\alpha-1} }[/math]
The CDF is [math]\displaystyle{ F(x) = x^{\alpha} }[/math] (using integration of [math]\displaystyle{ f(x) }[/math]) WIth CDF F(x) = x^α, if U have CDF, it is very easy to sample: y=x^α --> x=y^α --> inverseF(x)= x^(1/α) U~U(0,1) --> x=u^(1/α) Applying the inverse transform method with [math]\displaystyle{ y = x^\alpha \Rightarrow x = y^\frac {1}{\alpha} }[/math]
[math]\displaystyle{ F(x)^{-1} = y^\frac {1}{\alpha} }[/math]
between case 1 and case 2, when alpha and beta be different value, the beta distribution can simplify to other distribution.
Algorithm
- 1. Generate U~Unif(0,1)<br\>
- 2. Assign [math]\displaystyle{ x = u^\frac {1}{\alpha} }[/math]
After we have simplified this example, we can use other distribution methods to solve the problem.
MATLAB Code to generate random n variables using the above algorithm
x = rand(1,n).^(1/alpha)
Case 3:<br\> To sample from beta in general. we use the property that <br\>
- if [math]\displaystyle{ Y_1 }[/math] follows gamma [math]\displaystyle{ (\alpha,1) }[/math]<br\>
- [math]\displaystyle{ Y_2 }[/math] follows gamma [math]\displaystyle{ (\beta,1) }[/math]<br\>
Note: 1. [math]\displaystyle{ \alpha }[/math] and [math]\displaystyle{ \beta }[/math] are shape parameters here and 1 is the scale parameter.<br\>
- then [math]\displaystyle{ Y=\frac {Y_1}{Y_1+Y_2} }[/math] follows Beta [math]\displaystyle{ (\alpha,\beta) }[/math]<br\>
2.Exponential: [math]\displaystyle{ -\frac{1}{\lambda} \log(u) }[/math] <br\> 3.Gamma: [math]\displaystyle{ -\frac{1}{\lambda} \log(u_1 * \cdots * u_t) }[/math]<br\>
Algorithm<br\>
- 1. Sample from Y1 ~ Gamma ([math]\displaystyle{ \alpha }[/math],1) #[math]\displaystyle{ \alpha }[/math] is the shape, and 1 is the scale. <br\>
- 2. Sample from Y2 ~ Gamma ([math]\displaystyle{ \beta }[/math],1) <br\>
- 3. Set
- [math]\displaystyle{ Y = \frac{Y_1}{Y_1+Y_2} }[/math]
Please see the following example for Matlab code.
Case 4:<br\> Use The Acceptance-Rejection Method <br\>
The beta density is
[math]\displaystyle{ \displaystyle \text{Beta}(\alpha,\beta) = \frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha)\Gamma(\beta)}x^{\alpha-1}(1-x)^{\beta-1} }[/math] where [math]\displaystyle{ 0 \leq x \leq 1 }[/math]
Assume [math]\displaystyle{ \alpha,\beta \geq 1 }[/math]. Then [math]\displaystyle{ \displaystyle f(x) }[/math] has the maximum at [math]\displaystyle{ \frac{\alpha-1}{\alpha+\beta-2} }[/math].
(Please note that we could find the maximum by taking the derivative of f(x), let f'(x)=0 and then use maximum likelihood estimate to find what the maximum value is)
Define
[math]\displaystyle{ c=f(\frac{\alpha-1}{\alpha+\beta-2} }[/math]) and choose [math]\displaystyle{ \displaystyle g(x)=1 }[/math].
The A-R method becomes
1.Generate independent [math]\displaystyle{ \displaystyle U_1 }[/math] and [math]\displaystyle{ \displaystyle U_2 }[/math] from [math]\displaystyle{ \displaystyle UNIF[0,1] }[/math] until [math]\displaystyle{ \displaystyle cU_2 \leq f(U_1) }[/math];
2.Return [math]\displaystyle{ \displaystyle U_1 }[/math].
MATLAB Code for generating Beta Distribution
>>Y1 = sum(-log(rand(10,1000))) #Gamma(10,1), sum 10 exponentials for each of the 1000 samples >>Y2 = sum(-log(rand(5,1000))) #Gamma(5,1), sum 5 exponentials for each of the 1000 samples %NOTE: here, lamda is 1, since the scale parameter for Y1 & Y2 are both 1 >>Y=Y1./(Y1+Y2) #Don't forget to divide elements using "." Where Y follows Beta(10,5) >>figure >>hist(Y1) #Gamma curve >>figure >>hist(Y2) #Gamma curve >>figure >>hist(Y) #Do this to check that the shape fits beta. ~Beta(10,5). >>disttool #Check the beta plot.
This is the histogram of Y, precisely simulated version of Beta (10,5)
This is the pdf of various beta distributions
File:untitled.jpg
MATLAB tips: rand(10,1000) produces one 10*1000 matrix and sum(rand(10,1000)) produces a 10*1000 matrix
and each element in the matrix follows CDF of uniform distribution.
Example for the code to explain the beta distribution.
Another MATLAB Code for generating Beta Distribution using AR method
>>alpha = 3 >>beta = 2 >> a = sum (-log(rand(alpha,1000))) >> b = sum (-log(rand(beta,1000))) >> aandb=sum(-log(rand(alpha+beta,1000))) >> t = (alpha - 1)/(alpha + beta -2) >> c = (andb/(a*b))*t^(alpha-1)*(1-t)^(beta-1) >> u1 = rand >> u2 = rand >> x = (andb/(a*b))*u1^(alpha-1)*(1-u1)^(beta-1) >> while c*u2>x >> u1 = rand >> u2 = rand >> x = (andb/(a*b))*u1^(alpha-1)*(1-u1)^(beta-1) >> end >> u1
Random Vector Generation
We want to sample from [math]\displaystyle{ X = (X_1, X_2, }[/math]…,[math]\displaystyle{ X_d) }[/math], a d-dimensional vector from a known pdf [math]\displaystyle{ f(x) }[/math] and cdf [math]\displaystyle{ F(x) }[/math]. We need to take into account the following two cases:
Case 1
if the [math]\displaystyle{ x_1, x_2 \cdots, x_d }[/math]'s are independent, then
[math]\displaystyle{ f(x) = f(x_1,\cdots, x_d) = f(x_1)\cdots f(x_d) }[/math]
we can sample from each component [math]\displaystyle{ x_1, x_2,\cdots, x_d }[/math] individually, and then form a vector.
based on the property of independence, we can derive the pdf or pmf of [math]\displaystyle{ x=x_1,x_2,x_3,x_4,x_5,\cdots }[/math]
Case 2
If [math]\displaystyle{ X_1, X_2, \cdots , X_d }[/math] are not independent
[math]\displaystyle{ f(x) = f(x_1, \cdots , x_d) = f(x_1) f(x_2|x_1) \cdots f(x_d|x_{d-1},\cdots ,x_1) }[/math]
we need to know the conditional distributions of [math]\displaystyle{ f(x_2|x_1), f(x_3|x_2, x_1),\cdots, f(x_d|x_{d-1}, \cdots, x_1) }[/math]
This is generally a hard problem. Conditional probabilities are not easy to compute, then sampling from these would be based on your statistics knowledge.
In each case, we have to consider the previous cases.
[math]\displaystyle{ f(x_1) }[/math] is one-dimensional, some as [math]\displaystyle{ f(x_2|x_1) }[/math] and all others.
In general, one could consider the covariance matrix [math]\displaystyle{ C }[/math] of random variables [math]\displaystyle{ X_1 }[/math],…,[math]\displaystyle{ X_d }[/math].
Suppose we now have the Cholesky factor [math]\displaystyle{ G }[/math] of [math]\displaystyle{ C }[/math] (i.e. [math]\displaystyle{ C = GG^T }[/math]). In matlab, we use Chol(C)
For any d-tuple [math]\displaystyle{ X := (X_1 ,\ldots , X_d) }[/math] (i.e random variable generated by [math]\displaystyle{ X_1,\ldots , X_d }[/math] respectively)
[math]\displaystyle{ GX }[/math] would yield the desired distribution.
Note (Product Rule)
1.) All cases can use this (independent or dependent): [math]\displaystyle{ f(x) = f(x_1, x_2)= f(x_1) f(x_2|x_1) }[/math]
2.) If we determine that [math]\displaystyle{ x_1 }[/math] and [math]\displaystyle{ x_2 }[/math] are independent, then we can use [math]\displaystyle{ f(x) = f(x_1, x_2)= f(x_1)f(x_2) }[/math]
- ie. If late for class=[math]\displaystyle{ x_1 }[/math] and sick=[math]\displaystyle{ x_2 }[/math], then these are dependent variables so can only use equation 1 ([math]\displaystyle{ f(x) = f(x_1, x_2)= f(x_1) f(x_2|x_1) }[/math])
- ie. If late for class=[math]\displaystyle{ x_1 }[/math] and milk is white=[math]\displaystyle{ x_2 }[/math], then these are independent variables so can use both equations 1 and 2.
the case show the formula of the X = (X1,X2,…,Xd), a d-dimensional vector, when they are not independent of each x. we use conditional function to define the probability function of x with d-dimensional.
Example
Generate uniform random vectors
1) x = (x1, …, xd) from the d-dimensional rectangle
2) D = { (x1, …, xd) : ai <= xi <= bi , i = 1, …, d}
Algorithm:
1) for i = 1 to d
2) Ui ~ U(0,1)
3) xi = ai + U(bi-ai)
4) end
- Note: xi = ai + U(bi-ai) denotes Xi ~U(ai,bi)
An example of the 2-D case is given below:
>>a=[1 2];
>>b=[4 6];
>>for i=1:2
u(i) = rand();
x(i) = a(i) + (b(i) - a(i))*u(i);
end
>>hold on => this is to retain current graph when adding new graphs
>>rectangle('Position',[1 2 3 4]) => draw the boundary of the rectangle
>>axis([0 10 0 10]) => change the size of axes
>>plot(x(1),x(2),'.')
Code:
function x = urectangle (d,n,a,b)
for ii = 1:d;
u(ii,:) = rand(1,n);
x(ii,:) = a+ u(ii,:)*(b-a);
%keyboard #makes the function stop at this step so you can evaluate the variables
end
>>x=urectangle(2, 100, 2, 5);
>>scatter(x(1,:),x(2,:))
>>x=urectangle(2, 10000, 2, 5); #generate 10000 numbers (instead of 100)
>>x=urectangle(3, 10000, 2, 5); #changed to 3-dimensional
>>scatter3(x(1,:), x(2,:), x(3,:))
>>axis square
Vector Acceptance-Rejection Method
The acceptance-rejection method can be extended to n-dimensional cases, with the same concept:
If a random vector is to be generated uniformly from G, an irregular shape in the nth dimension, and W is a regular shape arbitrarily close to G in the nth dimension, then acceptance-rejection method can be applied as follows:
1. Sample from the regular shape W
2. Accept sample points if they are inside G
Example:
Generate a random vector Z that is uniformly distributed over region G
G: d-dimensional unit ball, [math]\displaystyle{ G = \big\{{x: \sum_{i}{x_i}^2 \leq 1}\big\} }[/math]
w: d-dimensional hypercube, [math]\displaystyle{ W = \big\{{-1 \leq x_i \leq 1}\big\}_{i=1}^d }[/math]
Procedure:
Step 1: [math]\displaystyle{ U_1 \sim~ U(0,1),\cdots, U_d \sim~ U(0,1) }[/math]
Step 2: [math]\displaystyle{ X_1 = 1 - 2U_1, \cdots, X_d = 1 - 2U_d, R = \sum_i X_i^2 }[/math]
Step 3: If [math]\displaystyle{ R \leq 1, Z=(X_1, ..... , X_d) }[/math]
Else go to step 1
it is an example of the vector A/R, regular shape is W likes the proposal distribution g(x), G is the target distribution g(x) <br\>
Suppose we sampled from the target area W uniformly, let Aw, Ag indicate the area of W and G, g(x)=1/Aw and f(x)=1/Ag
This is the picture of the example

matlab code:
u = rand(d,n);
z = 1- 2 *u;
R = sum(z.^2);
jj=1;
for ii=1:n
if R(ii)<=1
x(:,jj)=z(:,ii);
jj=jj+1;
end
end
output = x;
end
Class 10 - Thursday June 6th 2013
MATLAB code for using Acceptance/Rejection Method to sample from a d-dimensional unit ball.
1. U1~UNIF(0, 1)
U2~UNIF(0, 1)
...
Ud~UNIF(0, 1)
Code:
function output = Unitball(d,n)
u = rand(d,n);
z = 1- 2 *u;
R = sum(z.^2);
jj=1;
for ii=1:n
if R(ii)<=1
x(:,jj)=z(:,ii);
jj=jj+1;
end
end
output = x;
end
>> data = Unitball(d, n)
>> scatter(data(1,:), data(2,:)) %plot 2d graph
R(ii) computes the sum of the square of each element of a vector, so if it is less than 1,
then the vector is in the unit ball.
x(:,jj) means all the numbers in the jj column.
z(:,ii) means all the numbers in the ii column starting from 1st column until the nth
column, which is the last one.
Save it with the name of the pattern.
Execution:
>>[x]=Unitball(2,10000);
>>scatter(x(1,:),x(2,:)); %plot 2D circle
>>axis square; %make the x-y axis has same size
>>size(x)
ans =
2 7839
>>scatter(x(1,:),x(2,:))
scatter(x(1,:),x(2,:)) the (x(1,:) means all the numbers in the first row are parameter.
Calculate the efficiency:
>>c=7839/10000 %Efficiency = points accepted / total points
c =
0.7839
We can use the above program to calculate how many points in the circle condition are in the square.
Estimate [math]\displaystyle{ \displaystyle \pi }[/math]
- We know the radius is 1
- Then the area of the square is [math]\displaystyle{ (1-(-1))^2=4 }[/math]<br\>
- Then the area of the circle is [math]\displaystyle{ \pi }[/math]<br\>
- [math]\displaystyle{ \pi }[/math] is approximated to be [math]\displaystyle{ 4\times c=4 \times 0.7839=3.1356 }[/math] in the above example <br\>
>> 4*size(x,2)/10000
ans =
3.1356
>> [x]=Unitball(3,10000);
>> scatter3(x(1,:),x(2,:),x(3,:)) %plot 3d ball
>> axis square
>> size(x,2)/10000 %returns the size of the dimension of X specified by scalar 2
ans =
0.5231
>> [x]=Unitball(5,10000);
>> size(x,2)/10000
ans =
0.1648
3d unit ball
Note that c increases exponentially as d increases, which will result in rejections of more points. So this method is not efficient for large values of d.
In practice, when we need to vectorlize a high quality image or genes then d would have to be very large. So AR method is not an efficient way to solve the problem.
Efficiency
In the above example, the efficiency of the vector A/R is equal to the ratio
[math]\displaystyle{ \frac{1}{C}=\frac{\text{volume of hyperball}}{\text{volume of hybercube}}= \max \frac{g(x)}{f(x)} }[/math]
In general, the efficiency can be thought of as the total number of points accepted divided by the total number of points generated.
As the dimension increase, the efficiency of the algorithm will decrease exponentially.
For example, for approximating value of [math]\displaystyle{ \pi }[/math], when [math]\displaystyle{ d \text{(dimension)} =2 }[/math], the efficiency is around 0.7869; when [math]\displaystyle{ d=3 }[/math], the efficiency is around 0.5244; when [math]\displaystyle{ d=10 }[/math], the efficiency is around 0.0026: it is getting close to 0.
Thus, when we want to generate high dimension vectors, Acceptance-Rejection Method is not efficient to be used.
The end of midterm coverage
Stochastic Process
The basic idea of Stochastic Process (also called random process) is a collection of some random variables, [math]\displaystyle{ \big\{X_t:t\in T\big\} }[/math], where the set X is called the state space that each variable is in it and T is called the index set.
Definition: In probability theory, a stochastic process /stoʊˈkæstɪk/, or sometimes random process (widely used) is a collection of random variables; this is often used to represent the evolution of some random value, or system, over time. This is the probabilistic counterpart to a deterministic process (or deterministic system). Instead of describing a process which can only evolve in one way (as in the case, for example, of solutions of an ordinary differential equation), in a stochastic or random process there is some indeterminacy: even if the initial condition (or starting point) is known, there are several (often infinitely many) directions in which the process may evolve. (from Wikipedia)
A stochastic process is non-deterministic. This means that there is some indeterminacy in the final state, even if the initial condition is known.
We can illustrate this with an example of speech: if "I" is the first word in a sentence, the set of words that could follow would be limited (eg. like, want, am), and the same happens for the third word and so on. The words then have some probabilities among them such that each of them is a random variable, and the sentence would be a collection of random variables.
Also, Different Stochastic Process has different properties.
In the course, we study two Stochastic Process models.
The two stochastic Process models we will study are:
1. Poisson Process-This is continuous time counting process that satisfies a couple of properties that are listed in the next section. The Poisson process is understood to be a good model for events such as incoming phone calls, number of traffic accidents, and goals during a game of hockey or soccer. It is also an example of a birth-death process.
2. Markov Process- This is a stochastic process that satisfies the Markov property which can be understood as the memory-less property. The property states that the jump to a future state only depends on the current state of the process, and not of the process's history. This model is used to model random walks exhibited by particles, the health state of a life insurance policyholder, decision making by a memory-less mouse in a maze, etc.
Stochastic Process means even we get some conditions at the beginning, we just can guess some variables followed the first, but at the end the variable would be unpredictable.
Example
The state space is the set of English words, and [math]\displaystyle{ x_t }[/math] are words that are said. Another example involves the stock market: the set of all non-negative numbers is the state space, and [math]\displaystyle{ x_t }[/math] are stock prices.
stochastic process always has state space and the index set to limit the range.
The state space is the set of cars , while [math]\displaystyle{ x_t }[/math] are sport cars.
Poisson Process
The Poisson process, which is discrete, arises when we count the number of occurrences of events over time.
e.g traffic accidents , arrival of emails. Emails arrive at random time [math]\displaystyle{ T_1, T_2 }[/math] ...
-Let [math]\displaystyle{ N_t }[/math] denote the number of arrivals in the time interval [math]\displaystyle{ (0,t] }[/math]<br\> -Let [math]\displaystyle{ N(a,b] }[/math] denote the number of arrivals in the time interval (a,b]<br\> -By definition, [math]\displaystyle{ N(a,b]=N_b-N_a }[/math]<br\> -The two random variables [math]\displaystyle{ N(a,b] }[/math] and [math]\displaystyle{ N(c,d] }[/math] are independent if [math]\displaystyle{ (a,b] }[/math] and [math]\displaystyle{ (c,d] }[/math] do not intersect.<br\>
Definition: An arrival counting process [math]\displaystyle{ N=(N_t) }[/math] is called (Homogeneous) Poisson Process (PP) with rate [math]\displaystyle{ \lambda \gt 0 }[/math] if
A. The numbers of points in non-overlapping intervals are independent.
B. The number of points in interval [math]\displaystyle{ I(a,b] }[/math] has a poisson distribution with mean [math]\displaystyle{ \lambda (b-a) }[/math] ,where (b-a) represents the length of I.
In particular, observe that if [math]\displaystyle{ N=(N_t) }[/math] is a Poisson process of rate [math]\displaystyle{ \lambda\gt 0 }[/math], then the moments are E[Nt] = [math]\displaystyle{ \lambda t }[/math] and Var[Nt] = [math]\displaystyle{ \lambda t }[/math]
How to generate a multivariate normal with build in function "randn": (example)
(please check the general idea at the end of lecture 6 course note.)
z=randn(length(mu),n); %Here length(mu)=2 since s is a 2*2 matrix;
s=[1 0.7;0.7 1]
A=chol(s)% This only works for a positive definite A, otherwise we need to consider some other form of decomposition
x=mu'*ones(1,n) + A*z; %ones(1,n) is a function expand the size of mu from 1*1
%matrix to 1*n matrix;
and if we want to use box-muller to generate a multivariate normal, we could use the code in lecture 6:
d = length(mu);
R = chol(Sigma);
U1=rand(n,d)
U2=rand(d,d)
D=-2*log(U1)
tet=2*pi*U2
Z=(D.^0.5)*cos(tet)' %since in lecture 6, we set up x and y are independent normal
%distribution, so in here we can choose either cos and sin
X = Z*R + ones(n,1)*mu';
Central Limit Theorem
We can use simulation to test results in probability and statistics. For example, with the central limit theorem, if we sample from a sufficiently large number of independently distributed random variables, the mean will be approximately normally distributed. We illustrate with an example using 1000 observations each of 20 independent exponential random variables.
Definition:
Given certain conditions, the mean of a sufficiently large number of independent random variables, each with a well defined mean and variance, will be approximately normal distributed.
>> X = exprnd (20,20,1000); % 1000 instances of 20 exponential random numbers with mean 20 >> hist(X(1,:)) >> hist(X(1:2,:)) ... >>hist(X(1:20,:)) -> approaches to normal
Class 11 - Tuesday,June 11, 2013
Announcement
Midterm covers up to the middle of last lecture, which means stochastic process will not be on midterm. There won't be any Matlab syntax questions. And Students can contribute to any previous classes. We might however be asked to write down algorithms.
Poisson Process
A discrete stochastic variable X is said to have a Poisson distribution with parameter λ > 0 if
- [math]\displaystyle{ \!f(n)= \frac{\lambda^n e^{-\lambda}}{n!} \qquad n= 0,1,\ldots, }[/math].
Properties of Homogeneous Poisson Process
(a) Independence: The numbers of arrivals in non-overlapping intervals are independent
(b) Homogeneity or Uniformity: The number of arrival in each interval I(a,b] is Poisson distribution with rate [math]\displaystyle{ \lambda (b-a) }[/math]
(c) Individuality: for a sufficiently short time period of length h, the probability of 2 or more events occurring in the interval is close to 0, or formally [math]\displaystyle{ \mathcal{O}(h) }[/math]
Notation
Nt denotes the number of arrivals up to t, i.e.(0,t]
N(a,b] = Nb - Na denotes the number of arrivals in I(a, b].
For a small interval (t,t+h], where h is small
1. The number of arrivals in this interval is independent of the number of arrivals up to t(Nt)
2. [math]\displaystyle{ P (N(t,t+h)=1|N_{t} ) = P (N(t,t+h)=1) =\frac{e^{-\lambda h} (\lambda h)^1}{1!} =e^{-\lambda h} {\lambda h} \approx \lambda h }[/math] since [math]\displaystyle{ e^{-\lambda h} \approx 1 }[/math] when h is small.
[math]\displaystyle{ \lambda h }[/math] can be thought of as the probability of observing an arrival in the interval t to t+h.
Similarly, the probability of not observing an arrival in this interval is 1-[math]\displaystyle{ \lambda }[/math] h.
Generate a Poisson Process
[math]\displaystyle{ U_n \sim U(0,1) }[/math]
[math]\displaystyle{ T_n-T_{n-1}=-\frac {1}{\lambda} log(U_n) }[/math]
1. set T0=0 and n=1
2. Un~ U(0,1)
3. Tn = Tn-1 [math]\displaystyle{ -\frac {1}{\lambda} }[/math] log (Un) (declare an arrival)
4. if Tn>T stop
else
n=n+1 go to step 2
Since [math]\displaystyle{ P(N(t,t+h)=1) = e^{-{\lambda} h}\lambda h }[/math], we can regard [math]\displaystyle{ \lambda }[/math]h as a exponential distribution, and according to what we learnt, [math]\displaystyle{ T_n-T_{n-1} = h = -\frac {1}{\lambda} log(U_n) }[/math].
- Note : Recall that exponential random variable is the waiting time until one event of interested occurs.
Review of Poisson - Example
Let X be the r.v of the number of accidents in an hour, following the Poisson distribution with mean 1.8.
[math]\displaystyle{ P(X=0)=e^{-1.8} }[/math]
[math]\displaystyle{ P(X=4)=\frac {e^{-1.8}(1.8)^4}{4!} }[/math]
[math]\displaystyle{ P(X\geq1) = 1 - P(x=0) = 1- e^{-1.8} }[/math]
P(N3>3|N2)=P(N1>2)
when we use the inverse-transfer method, we can assume the poisson process to be exp distribution, and get the h function from the inverse method, and sometimes we assume h is very small.
Multi-dimensional Poisson Process
The poisson distribution arises as the distribution of counts of occurrences of events in (multidimensional) intervals in multidimensional poisson process in a directly equivalent way to the result for unidimensional processes. This,is D is any region the multidimensional space for which |D|, the area or volume of the region, is finite, and if Template:nowrap is count of the number of events in D, then
[math]\displaystyle{ P(N(D)=k)=\frac{(\lambda|D|)^k e^{-\lambda|D|}}{k!} . }[/math]
Generating a Homogeneous Poisson Process
Suppose we want to generate the first n events of a Poisson process with rate [math]\displaystyle{ {\lambda} }[/math]. We showed that the times between successive events are independent exponential random variables, each with rate [math]\displaystyle{ {\lambda} }[/math]. Therefore, we can first generate n random numbers U1, U2,...,Un and use the inverse transform method to find the corresponding exponential variable X1, X2,...,Xn. Then Xi can be interpreted as the time between the (i-1)st and the ith event of the process.
The actual time of the jth event is the sum of the first j interarrival times. Therefore, the generated values of the first n event times are [math]\displaystyle{ \sum_{i=1}^{j} X_i }[/math], j = 1...n.
Homogeneous poisson process refers to the rate of occurrences remaining constant for all periods of time.
Un~U(0,1)
[math]\displaystyle{ T_n-T_{n-1}=-\frac {1}{\lambda} log(U_n) }[/math]
The waiting time between each occurrence follows the exponential distribution with parameter [math]\displaystyle{ \lambda }[/math]. [math]\displaystyle{ T_n }[/math] represents the time elapsed at the nth occurence.
1) Set T0 = 0 ,and n = 1
2) Un follow U(0,1)
3) Tn - Tn-1 =[math]\displaystyle{ -\frac {1}{\lambda} }[/math] log (Un) (Declare an arrival)
4) if Tn >T stop;
else n = n + 1, go to step 2
h is the a range and we assume the probability of every point in this rang is the same by uniform ditribution.(cause h is small) and we test the rang is Tn smaller than T. And [math]\displaystyle{ -\frac {1}{\lambda} }[/math] log (Un)represents that chance that one arrival arrives.
Higher Dimensions:
To sample from higher dimensional Poisson process:
1. Generate a random number N that is Poisson distributed with parameter [math]\displaystyle{ {\lambda} }[/math]*Ad, where Ad is the area under the bounded region. (ie A2 is area of the region, A3 is the volume of the 3-d space.
2. Given N=n, generate n random (uniform) points in the region.
At the end, it generates n (cumulative) arrival times, up to time TT.
MatLab Code
T(1)=0; % Matlab does not allow 0 as an index, so we start with T(1). ii=1; l=2; TT=5; while T(ii)<=TT u=rand; ii=ii+1; T(ii)=T(ii-1) - (1/l)*log(u); end plot(T, '.')
The following plot is using TT = 50.
The number of points generated every time on average should be [math]\displaystyle{ \lambda }[/math] * TT.
The maximum value of the points should be TT.
 when TT be big, the plot of the graph will be linear, when we set the TT be 5 or small number, the plot graph looks like discrete distribution.
when TT be big, the plot of the graph will be linear, when we set the TT be 5 or small number, the plot graph looks like discrete distribution.
Markov chain
A Markov Chain is a stochastic process where:
1) Each stage has a fixed number of states,
2) the (conditional) probabilities at each stage only depend on the previous state.
Source: "http://math.scu.edu/~cirving/m6_chapter8_notes.pdf"
A Markov Chain is said to be irreducible if for each pair of states i and j there is a positive probability, starting in state i, that the process will ever enter state j.
Markov Chain is the simplification of assumption, for instance, the result of GPA in university depend on the GPA's in high school, middle school, elementary school, etc., but during a job interview after university graduation, the interviewer would most likely to ask about the GPA in university of the interviewee but not the GPA from early years because they assume what happened before are summarized and adequately represented by the information of the GPA earned during university. Therefore, it's not necessary to look back to elementary school. A Markov Chain works the same way, we assume that everything that has occurred earlier in the process is only important for finding out where we are now, the future only depends on the present of where we are now, not the past of how we got here. So the nthrandom variable would only depend on the n-1thterm but not all the previous ones. A Markov process exhibits the memoryless property.
Examples of Markov Chain applications in various fields:
- Physics: The movement of a particle (memory-less random walk)
- Finance: The volatility of prices of financial securities or commodities
- Actuarial Science: The pricing and valuation of multiple-state and multiple-lives insurance and annuity contracts
- Technology: The Google link analysis algorithm "PageRank"
Product Rule (Stochastic Process):
[math]\displaystyle{ f(x_1,x_2,...,x_n)=f(x_1)f(x_2\mid x_1)f(x_3\mid x_2,x_1)...f(x_n\mid x_{n-1},x_{n-2},....) }[/math]
In Markov Chain
[math]\displaystyle{ f(x_1,x_2,...,x_n)=f(x_1)f(x_2\mid x_1)f(x_3\mid x_2)...f(x_n\mid x_{n-1}) }[/math]
Concept: The current status of a subject must be relative to the past.However, it will only depend on the previous result only. In other words, if an event occurring tomorrow follows a Markov process it will depend on today and yesterday (the past) is negligible. The past (not including the current state of course) is negligible since its information is believed to have been captured and reflected in the current state.
A Markov Chain is a Stochastic Process for which the distribution of [math]\displaystyle{ x_t }[/math] depends only on [math]\displaystyle{ x_{t-1} }[/math].
Given [math]\displaystyle{ x_t }[/math], [math]\displaystyle{ x_{t-1} }[/math] and [math]\displaystyle{ x_{t+1} }[/math] are independent. The process of getting [math]\displaystyle{ x_n }[/math] is drawn as follows. The distribution of [math]\displaystyle{ x_n }[/math] only depends on the value of [math]\displaystyle{ x_{n-1} }[/math].
[math]\displaystyle{ x_1 \rightarrow x_2\rightarrow...\rightarrow x_n }[/math]
Formal Definition:
The process [math]\displaystyle{ \{x_n: n \in T\} }[/math] is a markov chain if:
[math]\displaystyle{ Pr(x_n|x_{n-1},...,x_1) = Pr(x_n|x_{n-1}) \ \ \forall n\in T }[/math] and [math]\displaystyle{ \forall x\in X }[/math]
CONTINUOUS TIME MARKOV PROCESS
A continuous time markov process would be one where the time spent in each state is not discrete, but can take
on positive real values. In other words, the index set is the positive real numbers. If the process is homogeneous, then the time spent will have an exponential distribution. In this case we will have a transition rate matrix that captures the rate at which we move between two states. An example will be the homogeneous Poisson process.
Transition Matrix
Transition Probability: [math]\displaystyle{ P_{ij} = P(X_{t+1} =j | X_t =i) }[/math] is the one-step transition probability from state i to state j.
Transition Probability: [math]\displaystyle{ P_{ij}(k) = P(X_{t+1}(k) =j | X_t(k) =i) }[/math] is the k-step transition probability from state i to state j.
The matrix P whose elements are transition Probabilities [math]\displaystyle{ P_{ij} }[/math] is a one-step transition matrix.
Example:
[math]\displaystyle{ \begin{align}
P_{ab} &=P(X_{t+1} &=b &\mid X_{t} &=a) &= 0.3 \\
P_{aa} &=P(X_{t+1} &=a &\mid X_{t} &=a) &= 0.7 \\
P_{ba} &=P(X_{t+1} &=a &\mid X_{t} &=b) &= 0.2 \\
P_{bb} &=P(X_{t+1} &=b &\mid X_{t} &=b) &= 0.8 \\
\end{align} }[/math]
[math]\displaystyle{ P= \left [ \begin{matrix} 0.7 & 0.3 \\ 0.2 & 0.8 \end{matrix} \right] }[/math]
The above matrix can be drawn into a state transition diagram
Properties of Transition Matrix:
1. [math]\displaystyle{ 1 \geq P_{ij} \geq 0 }[/math]
2. [math]\displaystyle{ \sum_{j}^{}{P_{ij}=1} }[/math] which means the rows of P should sum to 1.
In general, one would consider a (finite) set of elements [math]\displaystyle{ \Omega }[/math] such that:
[math]\displaystyle{ \forall x \in \Omega }[/math], the probability of the next state is given according to the distribution [math]\displaystyle{ P(x,\cdot) }[/math]
This means our model can be simulated as a sequence of random variables [math]\displaystyle{ (X_0, X_1, X_2, \ldots ) }[/math] with state space [math]\displaystyle{ \Omega }[/math] and transition matrix [math]\displaystyle{ P = [P_{ij}] }[/math] where [math]\displaystyle{ \forall t \in \N, 0 \leq s \leq t+1, x_s \in \Omega, }[/math]
we have to following property (Markov property):
[math]\displaystyle{ P(X_{t+1}= x_{t+1} \vert \cap^{t}_{s=0} X_s = x_s) = P(X_{t+1} =x_{t+1} \vert X_t =x_t) = P(x_t,x_{t+1}) }[/math]
And [math]\displaystyle{ \forall x \in \Omega, \sum_{y\in\Omega} P(x,y) =1; \; \forall x,y\in\Omega, P_{xy} = P(x,y) \geq 0 }[/math]
Moreover if [math]\displaystyle{ \forall x,y \in \Omega, \exists k, P^k (x,y) \gt 0 }[/math]
[math]\displaystyle{ |\Omega| \lt \infty }[/math] (i.e Any two states can be translated somehow)
Then one might consider the periodicity of the chain and derive a notion of cyclic behavior.
Examples of Transition Matrix
1.There are four states: 0,1,2, and 3.
Each row adds up to 1, and all the entries are between 0 and 1(since the transition probability is always between 0 and 1).
This matrix means that
- at state 0, can only go to state 1, since probability is 1.
- at state 1, can go to state 0 with a probability of 1/3 and state 2 with a probability of 2/3
- at state 2, can go to state 1 with a probability of 2/3 and state 3 with a probability of 1/3
- at state 3, can only go to state 2, since probability is 1.
2. Consider a Markov chain with state space {0, 1} and transition matrix [math]\displaystyle{ P= \left [ \begin{matrix} 1/3 & 2/3 \\ 3/4 & 1/4 \end{matrix} \right] }[/math]. Assuming that the chain starts in state 0 at time n = 0, what is the probability that it is in state 1 at time n = 2?
[math]\displaystyle{ \begin{align}
P(X_{2} &=1 &\mid X_{0} &=0) & =P(X_{1} &=0,X_{2} &=1 &\mid X_{0} &=0)+P(X_{1} &=1,X_{2} &=1 &\mid X_{0} &=0)\end{align} }[/math]
[math]\displaystyle{ \begin{align} P(X_{1} &=0 &\mid X_{0} &=0) * P(X_{2} &=1 &\mid X_{1} &=0)+P(X_{1} &=1 &\mid X_{0} &=0) * P(X_{2} &=1 &\mid X_{1}&=1) &=1/3*2/3+ 2/3*1/4 &=7/18 \\
\end{align} }[/math]
Class 12 - Thursday,June 13, 2013
Time Jun 17, 2013 2:30 PM - 3:30 PM
Midterm Review
Multiplicative Congruential Algorithm
xk+1= (axk+c) mod m
Where a, c, m and x1 (the seed) are values we must chose before running the algorithm. While there is no set value for each, it is best for m to be large and prime.
Examples:
X0 = 10 ,a = 2 , c = 1 , m = 13
X1 = 2 * 10 + 1 mod 13 = 8
X2 = 2 * 8 + 1 mod 13 = 4
... and so on
X0 = 44 ,a = 13 , c = 17 , m = 211
X1 = 13 * 44 + 17 mod 211 = 167
X2 = 13 * 167 + 17 mod 211 = 78
X3 = 13 * 78 + 17 mod 211 = 187
... and so on
Inverse Transformation Method
For continuous cases:
1. U~U(0,1)
2. X=F-1(u)
Note:
In Uniform Distribution [math]\displaystyle{ P(X\lt =a)=a }[/math]
proof:[math]\displaystyle{ P(X\lt =x) = P(F^{-1}(u)\lt =x)=P(u\lt =F(x)) = F(x) }[/math]
For discrete cases:
1. U~U(0,1)
2. x=xi if F(xi-1)[math]\displaystyle{ \lt }[/math]u[math]\displaystyle{ \leq }[/math]F(xi)
Acceptance-Rejection Method
cg(x)>=f(x)
[math]\displaystyle{ c=max\frac{f(x)}{g(x)} }[/math]
[math]\displaystyle{ \frac{1}{c} }[/math] is the efficiency of the method/probability of acceptance
1. Y~g(x)
2. U~U(0,1)
3. If [math]\displaystyle{ U\lt =\frac{f(y)}{c*g(y)} }[/math] then X=Y
else go to step 1
Proof that this method generates the desired distribution: [math]\displaystyle{ P(Y|accepted)=\frac{P(accepted|Y)P(Y)}{P(accepted)}=\frac{\frac{f(y)}{cg(y)} g(y)}{\int_{y}^{ } \frac{f(y)}{cg(y)} g(y) dy}=\frac{\frac{f(y)}{c}}{\frac{1}{c}\cdot 1}=f(y) }[/math]
Multivariate
f(x1,....,xn)=f(x1)f(x2|x1)...f(xn|xn-1,...x1) in general we need knowledge of conditional distribution if x1....xn are independent i.e. f(x1...xn)=f(x1)f(x2)...f(xn)
Vector A/R Method
This method is not efficient for high dimensional vectors
- Sample uniformly from a space W that contains the sample space G of interest
-Accept if the point is inside G
Sample uniformly from W
g(x)=[math]\displaystyle{ \frac{1}{A_W} }[/math], where AW is the area of W.
f(x)=[math]\displaystyle{ \frac{1}{A_G} }[/math], where AG is the area of G.
-[math]\displaystyle{ \frac{A_G}{A_W} }[/math] = [math]\displaystyle{ \frac{1}{c} }[/math] is the efficiency of the algorithm. That is the amount of points accepted over the amount of points rejected. This acceptance rate drops greatly for each dimension added.
Note that [math]\displaystyle{ \frac{A_G}{A_W} }[/math] decreases exponentially as the dimensional goes up, thus its not efficient for for high dimensional.
Common distribution
Exponential
Models the waiting until the first success.
X~Exp[math]\displaystyle{ (\lambda) }[/math]
[math]\displaystyle{ f (x) = \lambda e^{-\lambda x} }[/math] , [math]\displaystyle{ x\gt 0 }[/math]
1. U~Unif(0,1)
2. The inverse of exponential function is x = [math]\displaystyle{ \frac{-1}{\lambda} log(U) }[/math]
Normal
Box-Muller method
1.[math]\displaystyle{ U_{1},U_{2}\sim~ U(0,1) }[/math]
2.[math]\displaystyle{ R^{2}=-2log(U_{1}), R^{2}\sim~ Exp(1/2) }[/math]
[math]\displaystyle{ \theta = 2\pi U_{2},\theta\sim~ U(0,2\pi) }[/math]
3.[math]\displaystyle{ X=Rcos(\theta), Y=Rsin(\theta), X,Y\sim~ N(0,1) }[/math]
To obtain any normal distribution X once a set of standard normal samples Z is generated, apply the following transformations:
[math]\displaystyle{ Z\sim N(0,1)\rightarrow X \sim N(\mu,\sigma ^{2}) }[/math]
[math]\displaystyle{ X=\mu+\sigma~Z }[/math]
In the multivariate case,
[math]\displaystyle{ \underline{Z}\sim N(\underline{0},I)\rightarrow \underline{X} \sim N(\underline{\mu},\Sigma) }[/math]
[math]\displaystyle{ \underline{X} = \underline{\mu} +\Sigma ^{1/2} \underline{Z} }[/math]
Gamma
Gamma(t,λ)
t: The number of exponentials and the shape parameter
λ: The mean of the exponentials and the scale parameter
Also, Gamma(t,λ) can be expressed into a summation of t exp(λ).
[math]\displaystyle{ x=\frac {-1}{\lambda}\log(u_1)-\frac {1}{\lambda}\log(u_2)-.......-\frac {1}{\lambda}\log(u_t) }[/math]
[math]\displaystyle{ =\frac {-1}{\lambda}[\log(u_1)+\log(u_2)+.....+\log(u_t)] }[/math]
[math]\displaystyle{ =\frac {-1}{\lambda}\log(\prod_{j=1}^{t} U_j) }[/math]
Bernoulli
A Bernoulli random variable can only take two possible values: 0 and 1. 1 represents "success" and 0 represents "failure." If p is the probability of success, we have pdf
[math]\displaystyle{ f(x)= p^x (1-p)^{1-x}, x=0,1 }[/math]
To generate a Bernoulli random variable we use the following procedure:
sample u~U(0,1)
if u <= p, then x=1
else x=0
where 1 stands for success and 0 stands for failure.
Binomial
The sum of n independent Bernoulli trials
<br\>
X~ Bin(n,p)
1. U1, U2, ... Un ~ U(0,1)
2. [math]\displaystyle{ X= \sum^{n}_{1} I(U_i \leq p) }[/math] ,where [math]\displaystyle{ I(U_i \leq p) }[/math] is an indicator for a successful trial.
Return to 1
I is an indicator variable if for U <= P, then I(U<=P)=1; else I(U>P)=0.
Repeat this N times if you need N samples.
The theory behind the algorithm is the fact that the sum of n independent and identically distributed Bernoulli trials, Ber(p), follows a binomial Bin(n,p) distribution.
Example:
Suppose rolling a die, success= lands on 5, fail ow
p=1/6, 1-p=5/6, rolling for 10 times, n=10
simulate this binomial distribution.
1) Generate [math]\displaystyle{ U_1....U_{10} }[/math] ~ [math]\displaystyle{ U(0,1) }[/math]
2) [math]\displaystyle{ X= \sum^{10}_{1} I(U_i \leq \frac{1}{6}) }[/math]
3)Return to one.
Beta Distribution
[math]\displaystyle{ \displaystyle \text{Beta}(\alpha,\beta) = \frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha)\Gamma(\beta)}x^{\alpha-1}(1-x)^{\beta-1} }[/math] where [math]\displaystyle{ 0 \leq x \leq 1 }[/math] and [math]\displaystyle{ \alpha }[/math]>0, [math]\displaystyle{ \beta }[/math]>0
and
[math]\displaystyle{ f(x;\alpha,\beta)= 0 }[/math] otherwise
- [math]\displaystyle{ \displaystyle \text{Beta}(1,1) = U (0, 1) }[/math]
- [math]\displaystyle{ \displaystyle \text{Beta}(\alpha,1)={f}(x) = \frac{\Gamma(\alpha+1)}{\Gamma(\alpha)\Gamma(1)}x^{\alpha-1}(1-x)^{1-1}=\alpha x^{\alpha-1} }[/math]
Gamma Distribution
Algorithm<br\>
- 1. Sample from Y1 ~ Gamma ([math]\displaystyle{ \alpha }[/math],1) where [math]\displaystyle{ \alpha }[/math] is the shape, and 1 is the scale.<br\>
- 2. Sample from Y2 ~ Gamma ([math]\displaystyle{ \beta }[/math],1) where [math]\displaystyle{ \alpha }[/math] is the shape, and 1 is the scale.<br\>
- 3. Set [math]\displaystyle{ Y = \frac{Y_1}{Y_1+Y_2}, }[/math] Then Y ~ [math]\displaystyle{ \beta ( \alpha , \beta ) }[/math], where we suppose [math]\displaystyle{ \alpha , \beta }[/math] are integers.
Geometric
This distribution models the number of failures before the first success.
X~Geo(p)
[math]\displaystyle{ f(x)=p*(1-p)^{x-1}, x=1, 2, ........ }[/math]
If Y~Exp[math]\displaystyle{ (\lambda) }[/math] where [math]\displaystyle{ \lambda=-log(1-p) }[/math]
then [math]\displaystyle{ X=floor[Y]+1 }[/math] is Geo(p)
Proof:
[math]\displaystyle{ F(x)=P(X\lt =x) }[/math]
[math]\displaystyle{ =1-P(X\gt x) }[/math]
[math]\displaystyle{ =1-P(floor [Y]+1\gt x) }[/math] as [math]\displaystyle{ floor [Y]+1\gt x }[/math] implies [math]\displaystyle{ Y\leq x }[/math] for all real-valued Y
[math]\displaystyle{ =1-P(Y\gt =x) }[/math]
[math]\displaystyle{ =1-(1-P(Y\lt x)) }[/math]
[math]\displaystyle{ =1-e^{-\lambda*x} }[/math]
[math]\displaystyle{ =1-(1-p)^x }[/math], which is the CDF of Geo(p)
The above method can also be viewed with the inverse method since it is not rejecting any points. The following uses inverse method to generate Geo(p).
[math]\displaystyle{ F(x)=P(X \leq x) }[/math]
[math]\displaystyle{ F(x)=1- P(X\gt x) }[/math]
[math]\displaystyle{ P(X \leq x)=1-(1-p)^x }[/math] since [math]\displaystyle{ P(X\gt x)=(1-p)^x }[/math]
[math]\displaystyle{ y=1-(1-p)^x }[/math]
[math]\displaystyle{ y-1=-(1-p)^x }[/math]
[math]\displaystyle{ 1-y=(1-p)^x }[/math]
[math]\displaystyle{ 1-y=(e^(-\lambda))^x=e^(-\lambda*x) }[/math] since [math]\displaystyle{ 1-p=e^-\lambda }[/math]
[math]\displaystyle{ log(1-y)=-\lambda*x }[/math]
[math]\displaystyle{ x=-1/(\lambda)*log(1-y) }[/math]
[math]\displaystyle{ F^(-1)(x)=-1/(\lambda)*log(1-x) }[/math]
Algorithm:
1. Generate U ~ U(0,1)
2. Generate [math]\displaystyle{ Y=-1/(\lambda)*log(1-u) }[/math] where [math]\displaystyle{ Y ~ \sim Exp(\lambda) }[/math]
3. Set [math]\displaystyle{ X=[Y]+1 }[/math]
Note:
If X~Unif (0,1), Y= floor(3X) = [3X]-> Y ~ DU[0,2] (DU means discrete uniform)
If X~Unif (0,1), Y= floor(5U)-2 = [5U]-2 -> Y~ DU[-2,2]
Poisson
This distribution models the number of times and event occurs in a given time period
X~Poi[math]\displaystyle{ (\lambda) }[/math]
X is the maximum number of iid Exp([math]\displaystyle{ \lambda }[/math]) whose sum is less than or equal to 1.
[math]\displaystyle{ X = \max\{n: \sum\limits_{i=1}^n Y_i \leq 1, Y_i \sim Exp(\lambda)\} }[/math]
[math]\displaystyle{ = \max\{n: \sum\limits_{i=1}^n \frac{-1}{\lambda} log(U_i)\lt =1 , U_i \sim U[0,1]\} }[/math]
[math]\displaystyle{ = \max\{n: \prod\limits_{i=1}^n U_i \gt = e^{-\lambda}, U_i \sim U[0,1]\} }[/math]
Algorithm<br\>
- 1. Set n=1, a=1<br\>
- 2. [math]\displaystyle{ U_n }[/math] ~ [math]\displaystyle{ U[0,1] }[/math] and set [math]\displaystyle{ a=aU_n }[/math]<br\>
- 3. If [math]\displaystyle{ a \geq e^{-\lambda} }[/math] then: n=n+1 and go to Step 2. Else set X=n-1.
An alternate way to write an algorithm for Poisson is as followings:
1) x = 0, F = P(X=0) = e^-λ = p
2) Generate U ~ U(0,1)
3) If U < F, then output x
4) Else p = (λ/(x+1)) * p
F = F + p
x = x+1
5) else go to step 2
Acknowledgments: from Spring 2012 stat 340 coursenotes
Class 13 - Tuesday June 18th 2013
An n-step transition matrix is a matrix [math]\displaystyle{ P_n }[/math] whose elements are the probability of moving to state j from state i in n steps.
[math]\displaystyle{ P_n (i,j)=Pr(X_{m+n}=j|X_m=i) }[/math]
One-step transition probability:
The probability of Xn+1 being in state j given that Xn is in state i is called the
one-step transition probability and is denoted by Pi,jn,n+1. That is
Pi,jn,n+1 = Pr(Xn+1 =j/Xn =i)
Example from previous class:
[math]\displaystyle{ P= \left [ \begin{matrix} 0.7 & 0.3 \\ 0.2 & 0.8 \end{matrix} \right] }[/math]
The two step transition probability matrix is:
[math]\displaystyle{ P P= \left [ \begin{matrix} 0.7 & 0.3 \\ 0.2 & 0.8 \end{matrix} \right] \left [ \begin{matrix} 0.7 & 0.3 \\ 0.2 & 0.8 \end{matrix} \right] }[/math]=[math]\displaystyle{ \left [ \begin{matrix} 0.7(0.7)+0.3(0.2) & 0.7(0.3)+0.3(0.8) \\ 0.2(0.7)+0.8(0.2) & 0.2(0.3)+0.8(0.8) \end{matrix} \right] }[/math]=[math]\displaystyle{ \left [ \begin{matrix} 0.55 & 0.45 \\ 0.3 & 0.7 \end{matrix} \right] }[/math]<br\>
[math]\displaystyle{ P_2 = P_1 P_1 }[/math]<br\>
[math]\displaystyle{ P_n = P_1^n }[/math]<br\>
The two-step transition probability of moving from state a to state a:
[math]\displaystyle{ P_2 (a,a)=Pr (X_{m+2}=a| X_m=a)=Pr(X_{m+1}=a| X_m=a)Pr(X_{m+2}=a|X_{m+1}=a)+ Pr(X_{m+1}=b|X_m=a)Pr(X_{m+2}=a|X_{m+1}=b) }[/math]
[math]\displaystyle{ =0.7(0.7)+0.3(0.2)=0.55 }[/math]
n-step transition matrix
The elements of matrix Pn (i.e. the ijth entry Pij) is the probability of moving to state j from state i in n steps
In general [math]\displaystyle{ P_n = P^n }[/math] with [math]\displaystyle{ P_n(i,j) \geq 0 }[/math] and [math]\displaystyle{ \sum_{j} P_n(i,j) = 1 }[/math]
Note: [math]\displaystyle{ P_2 = P_1\times P_1; P_n = P^n }[/math]
The equation above is a special case of the Chapman-Kolmogorov equations.
It is true because of the Markov property or
the memoryless property of Markov chains, where the probabilities of going forward to the next state
only depends on your current state, not your previous states. By intuition, we can multiply the 1-step transition
matrix n-times to get a n-step transition matrix.
Example: We can see how [math]\displaystyle{ P_n = P^n }[/math] from the following:
[math]\displaystyle{ \mu_1=\mu_0\cdot P }[/math]
[math]\displaystyle{ \mu_2=\mu_1\cdot P }[/math]
[math]\displaystyle{ \mu_3=\mu_2\cdot P }[/math]
Therefore,
[math]\displaystyle{ \mu_3=\mu_0\cdot P^3
}[/math]
[math]\displaystyle{ P_n(i,j) }[/math] is called n-steps transition probability.
[math]\displaystyle{ \mu_0 }[/math] is called the initial distribution.
[math]\displaystyle{ \mu_n = \mu_0* P^n }[/math]
Example with Markov Chain: Consider a two-state Markov chain {[math]\displaystyle{ X_t; t = 0, 1, 2,... }[/math]} with states {1,2} and transition probability matrix
[math]\displaystyle{ P= \left [ \begin{matrix} 1/2 & 1/2 \\ 1/3 & 2/3 \end{matrix} \right] }[/math]
Given [math]\displaystyle{ X_0 = 1 }[/math]. Compute the following:
a)[math]\displaystyle{ P(X_1=1 | X_0=1) = P(1,1) = 1/2 }[/math]
b)[math]\displaystyle{ P(X_2=1, X_1=1 |X_0=1) = P(X_2=1|X_1=1)*P(X_1=1|X_0=1)= 1/2 * 1/2 = 1/4 }[/math]
c)[math]\displaystyle{ P(X_2=1|X_0=1)= P_2(1,1) = 5/12 }[/math]
d)[math]\displaystyle{ P^2=P*P= \left [ \begin{matrix} 5/12 & 7/12 \\ 7/18 & 11/18 \end{matrix} \right] }[/math]
Marginal Distribution of Markov Chain
We represent the probability of all states at time t with a vector [math]\displaystyle{ \underline{\mu_t} }[/math]
[math]\displaystyle{ \underline{\mu_t}~=(\mu_t(1), \mu_t(2),...\mu_t(n)) }[/math] where [math]\displaystyle{ \mu_t(1) }[/math] is the probability of being on state 1 at time t.
and in general, [math]\displaystyle{ \mu_t(i) }[/math] shows the probability of being on state i at time t.
For example, if there are two states a and b, then [math]\displaystyle{ \underline{\mu_5} }[/math]=(0.1, 0.9) means that the chance of being in state a at time 5 is 0.1 and the chance of being on state b at time 5 is 0.9.
If we generate a chain for many times, the frequency of states at each time shows marginal distribution of the chain at that time.
The vector [math]\displaystyle{ \underline{\mu_0} }[/math] is called the initial distribution.
[math]\displaystyle{ P_2~=P_1 P_1 }[/math] (as verified above)
In general,
[math]\displaystyle{ P_n~=(P_1)^n }[/math] **Note that [math]\displaystyle{ P_1 }[/math] is equal to the matrix P
[math]\displaystyle{ \mu_n~=\mu_0 P_n }[/math]
where [math]\displaystyle{ \mu_0 }[/math] is the initial distribution,
and [math]\displaystyle{ \mu_m+n~=\mu_m P_n }[/math]
N can be negative, if P is invertible.
0 a a b a
1 a b a a
2 b a a b
3 b a b b
4 a a a b
5 a b b a
[math]\displaystyle{ \mu_4~=(3/4, 1/4) }[/math]
if we simulate a chain many times, frequency of states at time t show the marginal distribution at time t
Marginal Distribution
[math]\displaystyle{ \mu_1~ = \mu_0P }[/math]
[math]\displaystyle{ \mu_2~ = \mu_1P = \mu_0PP = \mu_0P^2 }[/math]
In general, [math]\displaystyle{ \mu_n~ = \mu_0P^n }[/math]
Property: If [math]\displaystyle{ \mu_n~ =/= \mu_t~ }[/math](for any t less than n), then we say P does not converge.
Stationary Distribution
[math]\displaystyle{ \pi }[/math] is stationary distribution of the chain if [math]\displaystyle{ \pi }[/math]P = [math]\displaystyle{ \pi }[/math]
where [math]\displaystyle{ \pi }[/math] is a probability vector [math]\displaystyle{ \pi }[/math]=([math]\displaystyle{ \pi }[/math]i | [math]\displaystyle{ i \in X }[/math]) such that all the entries are nonnegative and sum to 1.
In other words, if X0 is draw from [math]\displaystyle{ \pi }[/math]. Then marginally, Xn is also drawn from the same distribution [math]\displaystyle{ \pi }[/math] for every n≥0.
Comments:
As n gets bigger and bigger, [math]\displaystyle{ \mu_n }[/math] will possibly stop changing, so the quantity [math]\displaystyle{ \pi }[/math] i can also be interpreted as the limiting probability that the chain is in the state [math]\displaystyle{ j }[/math]
Comments:
1. [math]\displaystyle{ \pi }[/math] may not exist and even if it exists, it may not always be unique.
2. If [math]\displaystyle{ \pi }[/math] exists and is unique, then [math]\displaystyle{ \pi }[/math]i is called the long-run proportion of the process in state i and the stationary distribution is also the limiting distribution of the process.
MatLab Code
In Matlab, you can find the stationary distribution by:
>> p=[.7 .3;.2 .8] % Input the matrix P
p =
0.7000 0.3000
0.2000 0.8000
>> p^2 % one state to another state by 2 steps transition
ans =
0.5500 0.4500
0.3000 0.7000
>> mu=[.9 .1]
mu =
0.9000 0.1000
>> mu*p % enter mu=mu*P, repeat multiple times until the value of the vector mu remains unchanged
ans =
0.6500 0.3500
>> mu=mu*p
mu =
0.4002 0.5998
>> mu=mu*p %The vector mu will be your stationary distribution
mu =
0.4000 0.6000
>> p^100 % it is limiting distribution of chain which finally gives a stable matrix
ans =
0.4000 0.6000
0.4000 0.6000
The definition of stationary distribution is that [math]\displaystyle{ \pi }[/math] is the stationary distribution of the chain if [math]\displaystyle{ \pi=\pi~P }[/math], where [math]\displaystyle{ \pi }[/math] is a probability vector. For every n[math]\displaystyle{ \gt = }[/math]0.
However, just because Xn ~ [math]\displaystyle{ \pi }[/math] for every n[math]\displaystyle{ \gt = }[/math]0 does not mean every state is independently identically distributed.
Limiting distribution of the chain refers the transition matrix that reaches the stationary state. If the lim(n-> infinite)P^n -> c, where c is a constant, then, we say this Markov chain is coverage; otherwise, it's not coverage.
Example: Find the stationary distribution of P= [math]\displaystyle{ \left[ {\begin{array}{ccc} 1/3 & 1/3 & 1/3 \\ 1/4 & 3/4 & 0 \\ 1/2 & 0 & 1/2 \end{array} } \right] }[/math]
Solution: [math]\displaystyle{ \pi=\left[ {\begin{array}{ccc} \pi_0 & \pi_1 & \pi_2 \end{array} } \right] }[/math]
Using the stationary distribution property [math]\displaystyle{ \pi=\pi~P }[/math] we get,
[math]\displaystyle{ \pi_0=\frac{1}{3}\pi_0+\frac{1}{4}\pi_1+\frac{1}{2}\pi_2 }[/math]
[math]\displaystyle{ \pi_1=\frac{1}{3}\pi_0+\frac{3}{4}\pi_1+0\pi_2 }[/math]
[math]\displaystyle{ \pi_2=\frac{1}{3}\pi_0+0\pi_1+\frac{1}{2}\pi_2 }[/math]
And since [math]\displaystyle{ \pi }[/math] is a probability vector,
[math]\displaystyle{ \pi_{0}~ + \pi_{1} + \pi_{2} = 1 }[/math]
Solving the 4 equations for the 3 unknowns gets,
[math]\displaystyle{ \pi_{0}~=1/3 }[/math], [math]\displaystyle{ \pi_{1}~=4/9 }[/math], and [math]\displaystyle{ \pi_{2}~=2/9 }[/math]
Therefore [math]\displaystyle{ \pi=\left[ {\begin{array}{ccc}
1/3 & 4/9 & 2/9 \end{array} } \right] }[/math]
Example 2: Find the stationary distribution of P= [math]\displaystyle{ \left[ {\begin{array}{ccc} 1/3 & 1/3 & 1/3 \\ 1/4 & 1/2 & 1/4 \\ 1/6 & 1/3 & 1/2 \end{array} } \right] }[/math]
Solution: [math]\displaystyle{ \pi=\left[ {\begin{array}{ccc} \pi_0 & \pi_1 & \pi_2 \end{array} } \right] }[/math]
Using the stationary distribution property [math]\displaystyle{ \pi=\pi~P }[/math] we get,
[math]\displaystyle{ \pi_0=\frac{1}{3}\pi_0+\frac{1}{4}\pi_1+\frac{1}{6}\pi_2 }[/math]
[math]\displaystyle{ \pi_1=\frac{1}{3}\pi_0+\frac{1}{2}\pi_1+\frac{1}{3}\pi_2 }[/math]
[math]\displaystyle{ \pi_2=\frac{1}{3}\pi_0+\frac{1}{4}\pi_1+\frac{1}{2}\pi_2 }[/math]
And since [math]\displaystyle{ \pi }[/math] is a probability vector,
[math]\displaystyle{ \pi_{0}~ + \pi_{1} + \pi_{2} = 1 }[/math]
Solving the 4 equations for the 3 unknowns gets,
[math]\displaystyle{ \pi_{0}=\frac {6}{25} }[/math], [math]\displaystyle{ \pi_{1}~=\frac {2}{5} }[/math], and [math]\displaystyle{ \pi_{2}~=\frac {9}{25} }[/math]
Therefore [math]\displaystyle{ \pi=\left[ {\begin{array}{ccc}
\frac {6}{25} & \frac {2}{5} & \frac {9}{25} \end{array} } \right] }[/math]
The above two examples are designed to solve for the stationary distribution of the matrix P however they also give us the limiting distribution of the matrices as we have mentioned earlier that the stationary distribution is equivalent to the limiting distribution.
Alternate Method of Computing the Stationary Distribution
Recall that if [math]\displaystyle{ \lambda v = A v }[/math], then [math]\displaystyle{ \lambda }[/math] is the eigenvalue of [math]\displaystyle{ A }[/math] corresponding to the eigenvector [math]\displaystyle{ v }[/math]
By definition of stationary distribution, [math]\displaystyle{ \pi = \pi P }[/math]
Taking the transpose, [math]\displaystyle{ \pi^T = (\pi P)^T }[/math]
then [math]\displaystyle{ I \pi^T = P^T \pi^T \Rightarrow (P^T-I) \pi^T = 0 }[/math]
So [math]\displaystyle{ \pi^T }[/math] is an eigenvector of [math]\displaystyle{ P^T }[/math] with corresponding eigenvalue 1.
the transpose method to calculate the pi matrix probability.
It is thus possible to compute the stationary distribution by taking the eigenvector of the transpose of the transition matrix corresponding to 1, and normalize it such that all elements are non-negative and sum to one so that the elements satisfy the definition of a stationary distribution. The transformed vector is still an eigenvector since a linear transformation of an eigenvector is still within the eigenspace. Taking the transpose of this transformed eigenvector gives the stationary distribution.
Generating Random Initial distribution
[math]\displaystyle{ \mu~=rand(1,n) }[/math]
[math]\displaystyle{ \mu~=\mu/\Sigma(\mu) }[/math]
Doubly Stochastic Matrices
We say that the transition matrix [math]\displaystyle{ \, P=(p_{ij}) }[/math] is doubly stochastic if both rows and columns sum to 1, i.e.,
[math]\displaystyle{ \, \sum_{i} p_{ij} = \sum_{j} p_{ij} = 1 }[/math]
It is easy to show that the stationary distribution of an nxn doubly stochastic matrix P is:
[math]\displaystyle{ (\frac{1}{n}, \ldots , \frac{1}{n}) }[/math]
Properties of Markov Chain
A Markov chain is a random process usually characterized as memoryless: the next state depends only on the current state and not on the sequence of events that preceded it. This specific kind of "memorylessness" is called the Markov property. Markov chains have many applications as statistical models of real-world processes.
1. Reducibility
State [math]\displaystyle{ j }[/math] is said to be accessible from State [math]\displaystyle{ i }[/math] (written [math]\displaystyle{ i \rightarrow j }[/math]) if a system started in State [math]\displaystyle{ i }[/math] has a non-zero probability of transitioning into State [math]\displaystyle{ j }[/math] at some point. Formally, State [math]\displaystyle{ j }[/math] is accessible from State [math]\displaystyle{ i }[/math] if there exists an integer [math]\displaystyle{ n_{ij} \geq 0 }[/math] such that
[math]\displaystyle{ P(X_{n_{ij}} =j \vert X_0 =i) \gt 0 }[/math]
This integer is allowed to be different for each pair of states, hence the subscripts in [math]\displaystyle{ n_{ij} }[/math]. By allowing n to be zero, every state is defined to be accessible from itself.
2. Periodicity
State [math]\displaystyle{ i }[/math] has period [math]\displaystyle{ k }[/math] if any return to State [math]\displaystyle{ i }[/math] must occur in multiples of [math]\displaystyle{ k }[/math] time steps. Formally, the period of a state is defined as
[math]\displaystyle{ k= \gcd\{n:P(X_n =j \vert X_0 =i)\gt 0\} }[/math]
3. Recurrence
State [math]\displaystyle{ i }[/math] is said to be transient if, given that we start in State [math]\displaystyle{ i }[/math], there is a non-zero probability that we will never return to [math]\displaystyle{ i }[/math]. Formally, let the random variable [math]\displaystyle{ T_i }[/math] be the first return time to State [math]\displaystyle{ i }[/math] (the "hitting time"):
[math]\displaystyle{ T_i = \min\{n \geq 1:X_n=i \vert X_0=i\} }[/math]
Class 14 - Thursday June 20th 2013
Example: Find the stationary distribution of [math]\displaystyle{ P= \left[ {\begin{array}{ccc} \frac{1}{3} & \frac{1}{3} & \frac{1}{3} \\[6pt] \frac{1}{4} & \frac{3}{4} & 0 \\[6pt] \frac{1}{2} & 0 & \frac{1}{2} \end{array} } \right] }[/math]
[math]\displaystyle{ \pi=\pi p }[/math]
Solve the system of linear equations to find a stationary distribution
[math]\displaystyle{ \pi=(\frac{1}{3},\frac{4}{9}, \frac{2}{9}) }[/math]
[math]\displaystyle{ \lambda u=A u }[/math]
[math]\displaystyle{ \pi }[/math] can be considered as an eigenvector of P with eigenvalue = 1. But the vector u here needs to be a column vector. So we need to transform [math]\displaystyle{ \pi }[/math] into a column vector.
[math]\displaystyle{ \pi }[/math]T= PT[math]\displaystyle{ \pi }[/math]T
Then [math]\displaystyle{ \pi }[/math]T is an eigenvector of PT with eigenvalue = 1.
MatLab tips:[V D]=eig(A), where D is a diagonal matrix of eigenvalues and V is a matrix of eigenvectors of matrix A
MatLab Code
Limiting distribution
A Markov chain has limiting distribution [math]\displaystyle{ \pi }[/math] if
[math]\displaystyle{ \lim_{n\to \infty} P^n= \left[ {\begin{array}{ccc} \pi \\ \vdots \\ \pi \\ \end{array} } \right] }[/math]
That is [math]\displaystyle{ \pi_j=\lim[P^n]_{ij} }[/math] exists and is independent of i.
A Markov Chain is convergent if and only if its limiting distribution exists.
If the limiting distribution [math]\displaystyle{ \pi }[/math] exists, it must be equal to the stationary distribution.
In general, there are chains with stationery distributions that don't converge, this means that they have stationary distribution but are not limiting.
Example:
[math]\displaystyle{ P= \left [ \begin{matrix} \frac{4}{5} & \frac{1}{5} & 0 & 0 \\[6pt] \frac{1}{5} & \frac{4}{5} & 0 & 0 \\[6pt] 0 & 0 & \frac{4}{5} & \frac{1}{5} \\[6pt] 0 & 0 & \frac{1}{10} & \frac{9}{10} \\[6pt] \end{matrix} \right] }[/math]
This chain converges but is not a limiting distribution as the rows are not the same and it doesn't converge to the stationary distribution.
The following contents are problematic. Please correct it if possible.
Suppose we're given that the limiting distribution [math]\displaystyle{ \pi }[/math] exists for stochastic matrix P, that is, [math]\displaystyle{ \pi = \pi * P }[/math]
WLOG assume P is diagonalizable, (if not we can always consider the Jordan form and the computation below is exactly the same.
Let [math]\displaystyle{ P = U * \Sigma * U^{-1} }[/math] be the eigenvalue decomposition of [math]\displaystyle{ P }[/math], where [math]\displaystyle{ \Sigma = diag(\lambda_1,\ldots,\lambda_n) ; |\lambda_i| \gt |\lambda_j|, \forall i \lt j }[/math]
Suppose [math]\displaystyle{ \pi^T = \sum a_i u_i }[/math] where [math]\displaystyle{ a_i \in \mathcal{R} }[/math] and [math]\displaystyle{ u_i }[/math] are eigenvectors of [math]\displaystyle{ P }[/math] for [math]\displaystyle{ i = 1\ldots n }[/math]
By definition: [math]\displaystyle{ \pi^k = \pi*P = \pi*P^k \implies \pi = \pi*(U * \Sigma * U^{-1}) *(U * \Sigma * U^{-1} )*\ldots*(U * \Sigma * U^{-1}) }[/math]
Therefore [math]\displaystyle{ \pi^k = \sum a_i * \lambda_i^k u_i }[/math] since [math]\displaystyle{ \lt u_i , u_j\gt = 0, \forall i\neq j }[/math].
Therefore [math]\displaystyle{ \lim_{k \rightarrow \infty} \pi^k = \lim_{k \rightarrow \infty} \lambda_i^k * a_1 * u_1 = u_1 }[/math]
MatLab Code
>> P=[1/3, 1/3, 1/3; 1/4, 3/4, 0; 1/2, 0, 1/2] % We input a matrix P.This is the same matrix as last class.
P =
0.3333 0.3333 0.3333
0.2500 0.7500 0
0.5000 0 0.5000
>> P^2
ans =
0.3611 0.3611 0.2778
0.2708 0.6458 0.0833
0.4167 0.1667 0.4167
>> P^3
ans =
0.3495 0.3912 0.2593
0.2934 0.5747 0.1319
0.3889 0.2639 0.3472
>> P^10
the example of code and an example of stand distribution, then the all the pi probability in the matrix are the same.
ans =
0.3341 0.4419 0.2240
0.3314 0.4507 0.2179
0.3360 0.4358 0.2282
>> P^100 % The stationary distribution is [0.3333 0.4444 0.2222] since values keep unchanged.
ans =
0.3333 0.4444 0.2222
0.3333 0.4444 0.2222
0.3333 0.4444 0.2222
>> [vec val]=eigs(P') % We can find the eigenvalues and eigenvectors from the transpose of matrix P.
vec =
-0.5571 0.2447 0.8121
-0.7428 -0.7969 -0.3324
-0.3714 0.5523 -0.4797
val =
1.0000 0 0
0 0.6477 0
0 0 -0.0643
>> a=-vec(:,1) % The eigenvectors can be mutiplied by (-1) since λV=AV can be written as λ(-V)=A(-V)
a =
0.5571
0.7428
0.3714
>> sum(a)
ans =
1.6713
>> a/sum(a)
ans =
0.3333
0.4444
0.2222
This is [math]\displaystyle{ \pi_j = lim[p^n]_(ij) }[/math] exist and is independent of i
Example: Find the stationary distribution of P= [math]\displaystyle{ \left[ {\begin{array}{ccc} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 1 & 0 & 0 \end{array} } \right] }[/math]
[math]\displaystyle{ \pi=\pi~P }[/math]
[math]\displaystyle{ \pi= }[/math] [[math]\displaystyle{ \pi }[/math]0, [math]\displaystyle{ \pi }[/math]1, [math]\displaystyle{ \pi }[/math]2]
The system of equations is:
0*[math]\displaystyle{ \pi }[/math]0+0*[math]\displaystyle{ \pi }[/math]1+1*[math]\displaystyle{ \pi }[/math]2 = [math]\displaystyle{ \pi }[/math]0 => [math]\displaystyle{ \pi }[/math]2 = [math]\displaystyle{ \pi }[/math]0
1*[math]\displaystyle{ \pi }[/math]0+0*[math]\displaystyle{ \pi }[/math]1+0*[math]\displaystyle{ \pi }[/math]2 = [math]\displaystyle{ \pi }[/math]1 => [math]\displaystyle{ \pi }[/math]1 = [math]\displaystyle{ \pi }[/math]0
0*[math]\displaystyle{ \pi }[/math]0+1*[math]\displaystyle{ \pi }[/math]1+0*[math]\displaystyle{ \pi }[/math]2 = [math]\displaystyle{ \pi }[/math]2
[math]\displaystyle{ \pi }[/math]0+[math]\displaystyle{ \pi }[/math]1+[math]\displaystyle{ \pi }[/math]2 = 1
[math]\displaystyle{ \pi }[/math]0+[math]\displaystyle{ \pi }[/math]0+[math]\displaystyle{ \pi }[/math]0 = 3[math]\displaystyle{ \pi }[/math]0 = 1, which gives [math]\displaystyle{ \pi }[/math]0 = 1/3
Also, [math]\displaystyle{ \pi }[/math]1 = [math]\displaystyle{ \pi }[/math]2 = 1/3
So, [math]\displaystyle{ \pi }[/math] = [math]\displaystyle{ [\frac{1}{3}, \frac{1}{3}, \frac{1}{3}] }[/math]
when the p matrix is a standard matrix, then all the probabilities of pi are the same in the matrix.
MatLab Code
MATLAB
>> P=[0, 1, 0;0, 0, 1; 1, 0, 0]
P =
0 1 0
0 0 1
1 0 0
>> pii=[1/3, 1/3, 1/3]
pii =
0.3333 0.3333 0.3333
>> pii*P
ans =
0.3333 0.3333 0.3333
>> P^1000
ans =
0 1 0
0 0 1
1 0 0
>> P^10000
ans =
0 1 0
0 0 1
1 0 0
>> P^10002
ans =
1 0 0
0 1 0
0 0 1
>> P^10003
ans =
0 1 0
0 0 1
1 0 0
>> %P^10000 = P^10003
>> % This chain does not have limiting distribution, it has a stationary distribution.
This chain does not converge, it has a cycle.
The first condition of limiting distribution is satisfied; however, the second condition where [math]\displaystyle{ \pi }[/math]j has to be independent of i (i.e. all rows of the matrix are the same) is not met.
This example shows the distinction between having a stationary distribution and convergence(having a limiting distribution).Note: [math]\displaystyle{ \pi=(1/3,1/3,1/3) }[/math] is the stationary distribution as [math]\displaystyle{ \pi=\pi*p }[/math]. However, upon repeatedly multiplying P by itself (repeating the step [math]\displaystyle{ P^n }[/math] as n goes to infinite) one will note that the results become a cycle (of period 3) of the same sequence of matrices. The chain has a stationary distribution, but does not converge to it. Thus, there is no limiting distribution.
Another example:
Find the stationary distribution of P= [math]\displaystyle{ \left[ {\begin{array}{ccc}
0.5 & 0 & 0 \\
1 & 0 & 0.5 \\
0 & 1 & 0.5 \end{array} } \right] }[/math]
[math]\displaystyle{ \pi=\pi~P }[/math]
[math]\displaystyle{ \pi= }[/math] [[math]\displaystyle{ \pi }[/math]0, [math]\displaystyle{ \pi }[/math]1, [math]\displaystyle{ \pi }[/math]2]
The system of equations is:
[math]\displaystyle{ 0.5\pi_0+1\pi_1+0\pi_2= \pi_0=\gt 2\pi_1 = \pi_0 }[/math]
[math]\displaystyle{ 0\pi_0+0\pi_1+1\pi_2= \pi_1 =\gt \pi_1=\pi_2 }[/math]
[math]\displaystyle{ 0\pi_0+0.5\pi_1+0.5\pi_2 = \pi_2 =\gt \pi_1 = \pi_2 }[/math]
[math]\displaystyle{ \pi_0+\pi_1+\pi_2 = 1 }[/math]
[math]\displaystyle{ 2\pi_1+\pi_1+\pi_1 = 4\pi_1 = 1 }[/math], which gives [math]\displaystyle{ \pi_1=\frac {1}{4} }[/math]
Also, [math]\displaystyle{ \pi_1 = \pi_2 = \frac {1}{4} }[/math]
So, [math]\displaystyle{ \pi = [\frac{1}{2}, \frac{1}{4}, \frac{1}{4}] }[/math]
Ergodic Chain
A Markov chain is called an ergodic chain if it is possible to go from every state to every state (not necessarily in one move). For instance, note that we can claim a Markov chain is ergodic if it is possible to somehow start at any state i and end at any state j in the matrix. We could have a chain with states 0, 1, 2, 3, 4 where it is not possible to go from state 0 to state 4 in just one step. However, it may be possible to go from 0 to 1, then from 1 to 2, then from 2 to 3, and finally 3 to 4 so we can claim that it is possible to go from 0 to 4 and this would satisfy a requirement of an ergodic chain. The example below will further explain this concept.
Note:if there's a finite number N then every other state can be reached in N steps.
Example
[math]\displaystyle{ P= \left[ \begin{matrix}
\frac{1}{3} \; & \frac{1}{3} \; & \frac{1}{3} \\ \\
\frac{1}{4} \; & \frac{3}{4} \; & 0 \\ \\
\frac{1}{2} \; & 0 \; & \frac{1}{2}
\end{matrix} \right] }[/math]
[math]\displaystyle{ \pi=\left[ \begin{matrix}
\frac{1}{3} & \frac{4}{9} & \frac{2}{9}
\end{matrix} \right] }[/math]
There are three states in this example.
In this case, state a can go to state a, b, or c; state b can go to state a, b, or c; and state c can go to state a, b, or c so it is possible to go from every state to every state. (Although state b cannot directly go into c in one move, it must go to a, and then to c.).
A k-by-k matrix indicates that the chain has k states.
- Ergodic Markov chains are irreducible.
- A Markov chain is called a regular chain if some power of the transition matrix has only positive elements.
- Any transition matrix that has no zeros determines a regular Markov chain
- However, it is possible for a regular Markov chain to have a transition matrix that has zeros.
For example, recall the matrix of the Land of Oz
[math]\displaystyle{ P = \left[ \begin{matrix}
& R & N & S \\
R & 1/2 & 1/4 & 1/4 \\
N & 1/2 & 0 & 1/2 \\
S & 1/4 & 1/4 & 1/2 \\
\end{matrix} \right] }[/math]
Theorem
An ergodic Markov chain has a unique stationary distribution [math]\displaystyle{ \pi }[/math]. The limiting distribution exists and is equal to [math]\displaystyle{ \pi }[/math]
Note: Ergodic Markov Chain is irreducible, aperiodic and positive recurrent.
Example: Consider the markov chain of [math]\displaystyle{ \left[\begin{matrix}0 & 1 \\ 1 & 0\end{matrix}\right] }[/math], the stationary distribution is obtained by solving [math]\displaystyle{ \pi P = \pi }[/math], getting [math]\displaystyle{ \pi=[0.5, 0.5] }[/math], but from the assignment we know that it does not converge, ie. there is no limiting distribution, because the Markov chain is not aperiodic and cycle repeats [math]\displaystyle{ P^2=\left[\begin{matrix}1 & 0 \\ 0 & 1\end{matrix}\right] }[/math] and [math]\displaystyle{ P^3=\left[\begin{matrix}0 & 1 \\ 1 & 0\end{matrix}\right] }[/math]
Another Example
[math]\displaystyle{ P=\left[ {\begin{array}{ccc}
\frac{1}{4} & \frac{3}{4} \\[6pt]
\frac{1}{5} & \frac{4}{5} \end{array} } \right] }[/math]
This matrix means that there are two points in the space, let's call them a and b
Starting from a, the probability of staying in a is 1/4
Starting from a, the probability of going from a to b is 3/4
Starting from b, the probability of going from b to a is 1/5
Starting from b, the probability of staying in b is 4/5
Solve the equation [math]\displaystyle{ \pi = \pi P }[/math]
[math]\displaystyle{ \pi_0 = .25 \pi_0 + .2 \pi_1 }[/math]
[math]\displaystyle{ \pi_1 = .75 \pi_0 + .8 \pi_1 }[/math]
[math]\displaystyle{ \pi_0 + \pi_1 = 1 }[/math]
Solving this system of equations we get:
[math]\displaystyle{ \pi_0 = \frac{4}{15} \pi_1 }[/math]
[math]\displaystyle{ \pi_1 = \frac{15}{19} }[/math]
[math]\displaystyle{ \pi_0 = \frac{4}{19} }[/math]
[math]\displaystyle{ \pi = [\frac{4}{19}, \frac{15}{19}] }[/math]
[math]\displaystyle{ \pi }[/math] is the long run distribution
We can use the stationary distribution to compute the expected waiting time to return to state 'a'
given that we start at state 'a' and so on.. Formula for this will be : [math]\displaystyle{ E[T_{i,i}]=\frac{1}{\pi_i} }[/math]
In the example above this will mean that that expected waiting time for the markov process to return to
state 'a' given that we start at state 'a' is 19/4.
definition of limiting distribution.
remark:satisfied balance of [math]\displaystyle{ \pi_i P_{ij} = P_{ji} \pi_j }[/math], so there is other way to calculate the step probability.
MatLab Code
In the following, P is the transition matrix. eye(n) refers to the n by n Identity matrix. L is the Laplacian matrix, L = (I - P). The Laplacian matrix will have at least 1 zero Eigenvalue. For every 0 in the diagonal, there is a component. If there is exactly 1 zero Eigenvalue, then the matrix is connected and has only 1 component. The number of zeros in the Laplacian matrix is the number of parts in your graph/process. If there is more than one zero on the diagonal of this matrix, this means there is a disconnect in the graph.
>> P=[1/3, 1/3, 1/3; 1/4, 3/4, 0; 1/2, 0, 1/2]
P =
0.3333 0.3333 0.3333
0.2500 0.7500 0
0.5000 0 0.5000
>> eye(3) %%returns 3x3 identity matrix
ans =
1 0 0
0 1 0
0 0 1
>> L=(eye(3)-P)
L =
0.6667 -0.3333 -0.3333
-0.2500 0.2500 0
-0.5000 0 0.5000
>> [vec val]=eigs(L)
vec =
-0.7295 0.2329 0.5774
0.2239 -0.5690 0.5774
0.6463 0.7887 0.5774
val =
1.0643 0 0
0 0.3523 0
0 0 -0.0000
%% Only one value of zero on the diagonal means the chain is connected
>> P=[0.8, 0.2, 0, 0;0.2, 0.8, 0, 0; 0, 0, 0.8, 0.2; 0, 0, 0.1, 0.9]
P =
0.8000 0.2000 0 0
0.2000 0.8000 0 0
0 0 0.8000 0.2000
0 0 0.1000 0.9000
>> eye(4)
ans =
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1
>> L=(eye(4)-P)
L =
0.2000 -0.2000 0 0
-0.2000 0.2000 0 0
0 0 0.2000 -0.2000
0 0 -0.1000 0.1000
>> [vec val]=eigs(L)
vec =
0.7071 0 0.7071 0
-0.7071 0 0.7071 0
0 0.8944 0 0.7071
0 -0.4472 0 0.7071
val =
0.4000 0 0 0
0 0.3000 0 0
0 0 -0.0000 0
0 0 0 -0.0000
%% Two values of zero on the diagonal means there are two 'islands' of chains
[math]\displaystyle{ \Pi }[/math] satisfies detailed balance if [math]\displaystyle{ \Pi_i P_{ij}=P_{ij} \Pi_j }[/math]. Detailed balance guarantees that [math]\displaystyle{ \Pi }[/math] is stationary distribution.
Adjacency matrix - a matrix [math]\displaystyle{ A }[/math] that dictates which states are connected and way of portraying which vertices in the matrix are adjacent. If we compute [math]\displaystyle{ A^2 }[/math], we can know which states are connected with paths of length 2.
A Markov chain is called an irreducible chain if it is possible to go from every state to every state (not necessary in one more).
Theorem: An ergodic Markov chain has a unique stationary distribution [math]\displaystyle{ \pi }[/math]. The limiting distribution exists and is equal to [math]\displaystyle{ \pi }[/math].
Markov process satisfies detailed balance if and only if it is a reversible Markov process
where P is the matrix of Markov transition.
Satisfying the detailed balance condition guarantees that [math]\displaystyle{ \pi }[/math] is stationary distributed.
[math]\displaystyle{ \pi }[/math] satisfies detailed balance if [math]\displaystyle{ \pi_i P_{ij} = P_{ji} \pi_j }[/math]
which is the same as the Markov process equation.
Example in the class: [math]\displaystyle{ P= \left[ {\begin{array}{ccc} \frac{1}{3} & \frac{1}{3} & \frac{1}{3} \\[6pt] \frac{1}{4} & \frac{3}{4} & 0 \\[6pt] \frac{1}{2} & 0 & \frac{1}{2} \end{array} } \right] }[/math]
and [math]\displaystyle{ \pi=(\frac{1}{3},\frac{4}{9}, \frac{2}{9}) }[/math]
[math]\displaystyle{ \pi_1 P_{1,2} = 1/3 \times 1/3 = 1/9,\, P_{2,1} \pi_2 = 1/4 \times 4/9 = 1/9 \Rightarrow \pi_1 P_{1,2} = P_{2,1} \pi_2 }[/math]
[math]\displaystyle{ \pi_2 P_{2,3} = 4/9 \times 0 = 0,\, P_{3,2} \pi_3 = 0 \times 2/9 = 0 \Rightarrow \pi_2 P_{2,3} = P_{3,2} \pi_3 }[/math]
Remark:Detailed balance of [math]\displaystyle{ \pi_i * Pij = Pji * \pi_j }[/math] , so there is other way to calculate the step probability
[math]\displaystyle{ \pi }[/math] is stationary but is not limiting.
Class 15 - Tuesday June 25th 2013
Announcement
Note to all students, the first half of today's lecture will cover the midterm's solution; however please do not post the solution on the Wikicoursenote.
Detailed balance
Let [math]\displaystyle{ P }[/math] be the transition probability matrix of a Markov chain. If there exists a distribution vector [math]\displaystyle{ \pi }[/math] such that [math]\displaystyle{ \pi_i \cdot P_{ij}=P_{ji} \cdot \pi_j, \; \forall i,j }[/math], then the Markov chain is said to have detailed balance. A detailed balanced Markov chain must have [math]\displaystyle{ \pi }[/math] given above as a stationary distribution, that is [math]\displaystyle{ \pi=\pi P }[/math], where [math]\displaystyle{ \pi }[/math] is a 1 by n matrix and P is a n by n matrix.
Proof:
[math]\displaystyle{ \; [\pi P]_j = \sum_i \pi_i P_{ij} =\sum_i P_{ji}\pi_j =\pi_j\sum_i P_{ji} =\pi_j ,\forall j }[/math]
- Note: Since [math]\displaystyle{ \pi_j }[/math] is a sum of coloum j and we can do this proof for every element in matrix P; in general, we can prove [math]\displaystyle{ \pi=\pi P }[/math]
Hence [math]\displaystyle{ \pi }[/math] is always a stationary distribution of [math]\displaystyle{ P(X_n+1=j|X_n=i) }[/math], for every n.
In other terms, [math]\displaystyle{ P_{ij} = P(X_n = j| X_{n-1} = i) }[/math], where [math]\displaystyle{ \pi_j }[/math] is the equilibrium probability of being in state j and [math]\displaystyle{ \pi_i }[/math] is the equilibrium probability of being in state i. [math]\displaystyle{ P(X_{n-1} = i) = \pi_i }[/math] is equivalent to [math]\displaystyle{ P(X_{n-1} = i, Xn = j) }[/math] being symmetric in i and j.
Keep in mind that the detailed balance is a sufficient but not required condition for a distribution to be stationary. i.e. A distribution satisfying the detailed balance is stationary, but a stationary distribution does not necessarily satisfy the detailed balance.
In the stationary distribution [math]\displaystyle{ \pi=\pi P }[/math], in the proof the sum of the p is equal 1 so the [math]\displaystyle{ \pi P=\pi }[/math].
PageRank (http://en.wikipedia.org/wiki/PageRank)
- PageRank is a link-analysis algorithm developed by Larry Page from Google; used for measuring a website's importance, relevance and popularity.
- PageRank is a graph containing web pages and their links to each other.
- Many social media sites use this (such as Facebook and Twitter)
- It can also be used to find criminals (ie. theives, hackers, terrorists, etc.) by finding out the links.
This is what made Google the search engine of choice over Yahoo, Bing, etc.- What made Google's search engine a huge success is not its search function, but rather the algorithm it used to rank the pages. (Ex. If we come up with 100 million search results, how do you list them by relevance and importance so the users can easily find what they are looking for. Most users will not go past the first 3 or so search pages to find what they are looking for. It is this ability to rank pages that allow Google to remain more popular than Yahoo, Bink, AskJeeves, etc.)
The order of importance
1. A web page is important if it has many other pages linked to it
2. The more important a web page is, the more weight should be assigned to its outgoing links
3. If a webpage has many outgoing links then its links have less value (ex: if a page links to everyone, like 411, it is not as important as pages that have incoming links)
File:diagram.jpg
[math]\displaystyle{ L=
\left[ {\begin{matrix}
0 & 0 & 0 & 0 & 0 \\
1 & 0 & 0 & 0 & 0 \\
1 & 1 & 0 & 1 & 0 \\
0 & 1 & 0 & 0 & 1 \\
0 & 0 & 0 & 0 & 0 \end{matrix} } \right] }[/math]
ie: According to the above example
Page 3 is the most important since it has the most links pointing to it, therefore more weigh should be placed on its outgoing links.
Page 4 comes after page 3 since it has the second most links pointing to it
Page 2 comes after page 4 since it has the third most links pointing to it
Page 1 and page 5 are the least important since no links point to them
As page 1 and page 2 has the most outgoing links, then their links have less value compared to the other pages.
[math]\displaystyle{ L_{ij} = 1 }[/math] if j has a link to i;
[math]\displaystyle{ L_{ij} = 0 }[/math] otherwise.
Cj The number of outgoing links of page [math]\displaystyle{ j }[/math]:
[math]\displaystyle{ C_j=\sum_i L_{ij} }[/math]
(i.e. sum of entries in column j)
[math]\displaystyle{ P_j }[/math] is the rank of page [math]\displaystyle{ j }[/math].
Suppose we have [math]\displaystyle{ N }[/math] pages, [math]\displaystyle{ P }[/math] is a vector containing ranks of all pages.
- [math]\displaystyle{ P }[/math] is a [math]\displaystyle{ N \times 1 }[/math] vector.
- [math]\displaystyle{ P_i }[/math] counts the number of incoming links of page [math]\displaystyle{ i }[/math]
[math]\displaystyle{ P_i=\sum_j L_{ij} }[/math]
(i.e. sum of entries in row i)
for each row, if there is a 1 in the third column, it means page three point to that page.
A PageRank results from a mathematical algorithm based on the webgraph, created by all World Wide Web pages as nodes and hyperlinks as edges, taking into consideration authority hubs such as cnn.com or usa.gov. The rank value indicates an importance of a particular page. A hyperlink to a page counts as a vote of support. (This would be represented in our diagram as an arrow pointing towards the page. Hence in our example, Page 3 is the most important, since it has the most 'votes of support). The PageRank of a page is defined recursively and depends on the number and PageRank metric of all pages that link to it ("incoming links"). A page that is linked to by many pages with high PageRank receives a high rank itself. If there are no links to a web page, then there is no support for that page (In our example, this would be Page 1 and Page 5). (source:http://en.wikipedia.org/wiki/PageRank#Description)
For those interested in PageRank, here is the original paper by Google co-founders Brin and Page: http://infolab.stanford.edu/pub/papers/google.pdf
Example of Page Rank Application in Real Life
Page Rank checker - This is a free service to check Google™ page rank instantly via online PR checker or by adding a PageRank checking button to the
web pages (http://www.prchecker.info/check_page_rank.php)
GoogleMatrix G = d * [ (Hyperlink Matrix H) + (Dangling Nodes Matrix A) ] + ((1-d)/N) * (NxN Matrix U of all 1's)
(source: https://googledrive.com/host/0B2GQktu-wcTiaWw5OFVqT1k3bDA/)
Class 16 - Thursday June 27th 2013
Page Rank
[math]\displaystyle{ L_{ij} }[/math] equals 1 if j has a link to i, and equals 0 otherwise.
[math]\displaystyle{ C_j }[/math] :The number of outgoing links for page j, where [math]\displaystyle{ c_j=\sum_i L_{ij} }[/math]
P is N by 1 vector contains rank of all N pages; for page i, the rank is [math]\displaystyle{ P_i }[/math]
[math]\displaystyle{ P_i= (1-d) + d\cdot \sum_j \frac {L_{ij}P_j}{c_j} }[/math]
where 0 < d < 1 is constant (in original page rank algorithm d = 0.8).
Interpretation of the formula:
1) sum of Lij is the total number of incoming links
2) the above sum is weighted by page rank of the pages that contain the link to i (Pj) i.e. if a high-rank page points to page i, then this link carries more weight than links from lower-rank pages.
3) the sum is then weighted by the inverse of the number of outgoing links from the pages that contain links to i (cj). i.e. if a page has more outgoing links than other pages then its links carry less weight.
4) finally, we take a linear combination of the page rank obtained from above and a constant 1. This ensures that every page has a rank greater than zero.
Note that this is a system of N equations with N unknowns.
[math]\displaystyle{ c_j }[/math] is the number of outgoing links, less outgoing links means more important.
Let D be a diagonal N by N matrix such that [math]\displaystyle{ D_{ii} }[/math] = [math]\displaystyle{ c_i }[/math]
[math]\displaystyle{ D= \left[ {\begin{matrix} c_1 & 0 & ... & 0 \\ 0 & c_2 & ... & 0 \\ 0 & 0 & ... & 0 \\ 0 & 0 & ... & c_N \end{matrix} } \right] }[/math]
Then P = (1-d) e + dLD-1P
where e =[1 1 ....]T , i.e. a N by 1 vector.
We assume that rank of all N pages sums to N. The sum of rank of all N pages can be any number, as long as the ranks have certain propotion.
i.e. eT P = N, then [math]\displaystyle{ ~\frac{e^{T}P}{N} = 1 }[/math]
D-1 will be:
D-1[math]\displaystyle{ = \left[ {\begin{matrix} \frac {1}{c_1} & 0 & ... & 0 \\ 0 & \frac {1}{c_2} & ... & 0 \\ 0 & 0 & ... & 0 \\ 0 & 0 & ... & \frac {1}{c_N} \end{matrix} } \right] }[/math]
[math]\displaystyle{ P=~(1-d)e+dLD^{-1}P }[/math] where [math]\displaystyle{ e=\begin{bmatrix} 1\\ 1\\ ...\\ 1 \end{bmatrix} }[/math]
[math]\displaystyle{ P=(1-d)~\frac{ee^{T}P}{N}+dLD^{-1}P }[/math]
[math]\displaystyle{ P=[(1-d)~\frac{ee^T}{N}+dLD^{-1}]P }[/math]
P=AP
N is a N*N matrix,
L is a N*N matrix,
D-1 is a N*N matrix,
P is a N*1 matrix
d is a constant between 0 and 1
P=AP
P is an eigenvector of A with corresponding eigenvalue equal to 1.
PT=PTAT
Notice that all entries in A are non-negative and each row sums to 1. Hence A satisfies the definition of a transition probability matrix.
PT is the stationary distribution of a Markov Chain with transition probability matrix AT.
We can consider A to be the matrix describing all possible movements following links on the internet, and Pt as the probability of being on any given webpage if we were on the internet long enough.
Definition of rank page and proof it steps by steps, it shows with 3 n*n matrix and and one n*1 matrix and a constant d between 0 to 1. p is the stationary distribution so p=Ap.
Damping Factor "d"
The PageRank assumes that any imaginary user who is randomly clicking on links will eventually stop clicking. The probability, at any step, that the person will keep on clicking is a damping factor, "d". After many studies, the approximation of "d" is 0.85. Other values for "d" have been used in class and may appear on assignments/exams.
Examples
Example 1
File:eg1.jpg
[math]\displaystyle{ L=
\left[ {\begin{matrix}
0 & 0 & 1 \\
1 & 0 & 0 \\
0 & 1 & 0 \end{matrix} } \right] }[/math]
[math]\displaystyle{ c= \left[ {\begin{matrix} 1 & 1 & 1 \end{matrix} } \right] }[/math]
[math]\displaystyle{ D= \left[ {\begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{matrix} } \right] }[/math]
MATLAB Code d=0.8 N=3 A=(1-d)*ones(N)/N+d*L*pinv(D) #pinv: Moore-Penrose inverse (pseudoinverse) of symbolic matrix We use the pinv(D) function [pseudo-inverse] instead of the inv(D) function because in the case of a non-invertible matrix, it would not crash the program. [vec val]=eigs(A) (eigen-decomposition) a=-vec(:,1) (find the eigenvector equals to 1) a=a/sum(a) (normalize a) or to show that A transpose is a stationary transition matrix (transpose(A))^200 will be the same as a=a/sum(a)
NOTE: Changing the value of d, does not change the ranking order of the pages.
By looking at each entry after normalizing a, we can tell the ranking order of each page.
c = [1 1 1] since there are 3 pages, each page is one way recurrent to each other and there is only one outgoing for each page. Hence, D is a 3x3 standard diagonal matrix.
Example 2
[math]\displaystyle{ L=
\left[ {\begin{matrix}
0 & 0 & 1 \\
1 & 0 & 1 \\
0 & 1 & 0 \end{matrix} } \right] }[/math]
[math]\displaystyle{ c= \left[ {\begin{matrix} 1 & 1 & 2 \end{matrix} } \right] }[/math]
[math]\displaystyle{ D= \left[ {\begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 2 \end{matrix} } \right] }[/math]
Matlab code
>> L=[0 0 1;1 0 1;0 1 0];
>> C=sum(L);
>> D=diag(C);
>> d=0.8;
>> N=3;
>> A=(1-d)*ones(N)/N+d*L*pinv(D);
>> [vec val]=eigs(A)
vec =
-0.3707 -0.3536 + 0.3536i -0.3536 - 0.3536i
-0.6672 -0.3536 - 0.3536i -0.3536 + 0.3536i
-0.6461 0.7071 0.7071
val =
1.0000 0 0
0 -0.4000 - 0.4000i 0
0 0 -0.4000 + 0.4000i
>> a=-vec(:,1)
a =
0.3707
0.6672
0.6461
>> a=a/sum(a)
a =
0.2201
0.3962
0.3836
NOTE: Page 2 is the most important page because it has 2 incomings. Similarly, page 3 is more important than page 1 because page 3 has the incoming result from page 2.
This example is similar to the first example, but here, page 3 can go back to page 2, so the matrix of the outgoing matrix, the third column of the D matrix is 3 in the third row. And we use the code to calculate the p=Ap.
Example 3
[math]\displaystyle{ L= \left[ {\begin{matrix} 0 & 1 & 0 \\ 1 & 0 & 1 \\ 0 & 1 & 0 \end{matrix} } \right] }[/math]
[math]\displaystyle{ c= \left[ {\begin{matrix} 1 & 2 & 1 \end{matrix} } \right] }[/math]
[math]\displaystyle{ D= \left[ {\begin{matrix} 1 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 1 \end{matrix} } \right] }[/math]
[math]\displaystyle{ d=0.8 }[/math]
[math]\displaystyle{ N=3 }[/math]
this example is the second page have 2 outgoings.
Another Example:
Consider: 1 -> ,<-2 ->3
L= [0 1 0; 1 0 0; 0 1 0]; c=[1,1,1]; D= [1 0 0; 0 1 0; 0 0 1]
Example 4
1 <-> 2 -> 3 <-> 4
[math]\displaystyle{ L= \left[ {\begin{matrix} 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{matrix} } \right] }[/math]
[math]\displaystyle{ c= \left[ {\begin{matrix} 1 & 2 & 1 & 1 \end{matrix} } \right] }[/math]
[math]\displaystyle{ D=
\left[ {\begin{matrix}
1 & 0 & 0 & 0 \\
0 & 2 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1 \end{matrix} } \right] }[/math]
Matlab code
>> L=L= [0 1 0 0;1 0 0 0;0 1 0 1;0 0 1 0];
>> C=sum(L);
>> D=diag(C);
>> d=0.8;
>> N=4;
>> A=(1-d)*ones(N)/N+d*L*pinv(D)
A =
0.0500 0.4500 0.0500 0.0500
0.8500 0.0500 0.0500 0.0500
0.0500 0.4500 0.0500 0.8500
0.0500 0.0500 0.8500 0.0500
>> [vec val]=eigs(A)
vec =
0.1817 -0.0000 -0.4082 0.4082
0.2336 0.0000 0.5774 0.5774
0.7009 -0.7071 0.4082 -0.4082
0.6490 0.7071 -0.5774 -0.5774
val =
1.0000 0 0 0
0 -0.8000 0 0
0 0 -0.5657 0
0 0 0 0.5657
>> a=vec(:,1)
>> a=vec(:,1)
a =
0.1817
0.2336
0.7009
0.6490
>> a=a/sum(a)
a =
0.1029
0.1324
0.3971
0.3676
NOTE: The ranking of each page is as follows: Page 3, Page 4, Page 2 and Page 1. Page 3 is the highest since it has the most incoming links. All of the other pages only have one incoming link but since Page 3, highest ranked page, links to Page 4, Page 4 is the second highest ranked. Lastly, since Page 2 links into Page 3 it is the next highest rank.
Page 2 has 2 outgoing links. Pages with the same incoming links can be ranked closest to the highest ranked page. If the highest page P1 is incoming into a page P2, then P2 is ranked second, and so on.
Example 5
[math]\displaystyle{ L= \left[ {\begin{matrix} 0 & 1 & 0 & 1 \\ 1 & 0 & 1 & 1 \\ 1 & 0 & 0 & 1 \\ 1 & 0 & 0 & 0 \end{matrix} } \right] }[/math]
[math]\displaystyle{ c= \left[ {\begin{matrix} 3 & 1 & 1 & 3 \end{matrix} } \right] }[/math]
[math]\displaystyle{ D= \left[ {\begin{matrix} 3 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 3 \end{matrix} } \right] }[/math]
Matlab code
>> L= [0 1 0 1; 1 0 1 1; 1 0 0 1;1 0 0 0];
>> d = 0.8;
>> N = 4;
>> C = sum(L);
>> D = diag(C);
>> A=(1-d)*ones(N)/N+d*L*pinv(D);
>> [vec val]=eigs(A);
>> a=vec(:,1);
>> a=a/sum(a)
a =
0.3492
0.3263
0.1813
0.1431
Example 6
[math]\displaystyle{ L=
\left[ {\begin{matrix}
0 & 1 & 0 & 0 & 1\\
1 & 0 & 0 & 0 & 0\\
0 & 1 & 0 & 0 & 0\\
0 & 1 & 1 & 0 & 1\\
0 & 0 & 0 & 1 & 0 \end{matrix} } \right] }[/math]
Matlab Code
>> d=0.8
d =
0.8000
>> L=[0 1 0 0 1;1 0 0 0 0;0 1 0 0 0;0 1 1 0 1;0 0 0 1 0]
L =
0 1 0 0 1
1 0 0 0 0
0 1 0 0 0
0 1 1 0 1
0 0 0 1 0
>> c=sum(L)
c =
1 3 1 1 2
>> D=diag(c)
D =
1 0 0 0 0
0 3 0 0 0
0 0 1 0 0
0 0 0 1 0
0 0 0 0 2
>> N=5
N =
5
>> A=(1-d)*ones(N)/N+d*L*pinv(D)
A =
0.0400 0.3067 0.0400 0.0400 0.4400
0.8400 0.0400 0.0400 0.0400 0.0400
0.0400 0.3067 0.0400 0.0400 0.0400
0.0400 0.3067 0.8400 0.0400 0.4400
0.0400 0.0400 0.0400 0.8400 0.0400
>> [vec val]=eigs(A)
vec =
Columns 1 through 4
-0.4129 0.4845 + 0.1032i 0.4845 - 0.1032i -0.0089 + 0.2973i
-0.4158 -0.6586 -0.6586 -0.5005 + 0.2232i
-0.1963 0.2854 - 0.0608i 0.2854 + 0.0608i -0.2570 - 0.2173i
-0.5700 0.1302 + 0.2612i 0.1302 - 0.2612i 0.1462 - 0.3032i
-0.5415 -0.2416 - 0.3036i -0.2416 + 0.3036i 0.6202
Column 5
-0.0089 - 0.2973i
-0.5005 - 0.2232i
-0.2570 + 0.2173i
0.1462 + 0.3032i
0.6202
val =
Columns 1 through 4
1.0000 0 0 0
0 -0.5886 - 0.1253i 0 0
0 0 -0.5886 + 0.1253i 0
0 0 0 0.1886 - 0.3911i
0 0 0 0
Column 5
0
0
0
0
0.1886 + 0.3911i
>> a=-vec(:,1)
a =
0.4129
0.4158
0.1963
0.5700
0.5415
>> a=a/sum(a)
a =
0.1933
0.1946
0.0919
0.2668 % (the most important)
0.2534
for the matrix , page 1 has 2 outgoing, and page 2 has one from page 1, page 3 has 2 from 2, page 4 has 3 outgoing ,and page 5 has 1 outgoing , 1 and 2, 4 and 5 outgoing to each other. so the c=[2 1 1 3 1], the rank is page 4 , page 5, page 2 and page 1 and page 3.
Class 17 - Tuesday July 2nd 2013
Markov Chain Monte Carlo (MCMC)
Idea: generate a Markov Chain whose stationary distribution is the target distribution.
Motivation example
- Suppose we want to generate random variable X according to distribution [math]\displaystyle{ \pi=(\pi_1, \pi_2, ... , \pi_m) }[/math]
X can take m different values from x={1,2,3,....,m}
- We want to generate {Xt, t=0, 1, ....., n } according to [math]\displaystyle{ \pi }[/math]
{X0, X1, ....., Xn}
example:
M=6,
Pi=[0.1,0.1,0.1,0.2,0.3,0.2]
X=[1,2,3,4,5,6]
- Suppose Xt=j
consider an arbitrary probability transition matrix Q with entry qij.
[math]\displaystyle{ \mathbf{Q} =
\begin{bmatrix}
q_{11} & q_{12} & \cdots & q_{1m} \\
q_{21} & q_{22} & \cdots & q_{2m} \\
\vdots & \vdots & \ddots & \vdots \\
q_{m1} & q_{m2} & \cdots & q_{mm}
\end{bmatrix}
}[/math]
qij is the probability of moving to state i from state j.
Generate Y according to i-th row of matrix Q.
i.e.P(Y=j)=qij
rij is the probabiliy of accepting j.
Algorithm:
- [math]\displaystyle{ P(Y=j) = q_{ij} }[/math](*)
- [math]\displaystyle{ r_{ij} = min (\frac{\pi_j q_{ji}}{\pi_i q_{ij}}, 1) }[/math]
- [math]\displaystyle{
x_{t+1} = \begin{cases}
Y, & \text{w/p} r_{ij} \\
x_t, & \text{otherwise} \end{cases} }[/math]
- go to (*)
This algorithm generates [math]\displaystyle{ {x_t, t=0,...,n} }[/math]. In the long run, the marginal distribution of [math]\displaystyle{ x_t }[/math] is [math]\displaystyle{ \underline{\Pi} }[/math]
[math]\displaystyle{ {x_t, t = 0, 1,...,n} }[/math] is a Markov chain with probability transition matrix P.
This is a Markov Chain since [math]\displaystyle{ x_t+1 }[/math] only depends on [math]\displaystyle{ x_t
\lt math\gt
\text{Where }P_{ij}= \begin{cases}
q_{ij} r_{ij}& \text {if i != j} \\
1 - \sum_{j} (q_{ij} r_{ij}), & \text{if i = j} \end{cases} }[/math]
Detailed Balance:
[math]\displaystyle{ \pi_i P_{ij} = p_{ji} \pi_j }[/math]
LHS: <math>\pi_i P_{ij} = \pi_i q_{ij} r_{ij} = \pi_i q_{ij} \frac{\pi_j q_{ij}}{\pi_i q_{ij}} = \pi_i q_{ji}