residual Component Analysis: Generalizing PCA for more flexible inference in linear-Gaussian models
Introduction
Probabilistic principle component analysis (PPCA) is a method based on an isotropic error model to estimate the principal axes when any data vector has one or more missing values. It assumes that the values are missing at random through the data set. This means that whether a data value is missing or not does not depend on the latent variable given the observed data values. PPCA decomposes the covariance of a data vector [math]\displaystyle{ y }[/math] in [math]\displaystyle{ \mathbb{R}^p }[/math], into a low-rank term and a spherical noise term.
[math]\displaystyle{ W \in \mathbb{R}^{p \times q} }[/math] such that [math]\displaystyle{ q \lt p-1 }[/math] imposes a reduced rank structure on the covariance. The log-likelihood of the centered dataset [math]\displaystyle{ Y }[/math] in [math]\displaystyle{ \mathbb{R}^{n \times p} }[/math] with n data points and p features
can be maximized<ref name="tipping1999">
Tipping, M. E. and Bishop, C.M. Probabilistic principle component analysis. Journal of the Royal Statistical Society. Series B(Statistical Methodology), 61(3):611-622,1999
</ref> with the result
where [math]\displaystyle{ U_q }[/math] are [math]\displaystyle{ q }[/math] principle eigenvectors of the sample covariance [math]\displaystyle{ \tilde S }[/math], with [math]\displaystyle{ \tilde S = n^{-1}Y^TY }[/math] and [math]\displaystyle{ L^q }[/math] is a diagonal matrix with elements [math]\displaystyle{ l_{i,i} = (\lambda_i - \sigma^2)^{1/2} }[/math], where [math]\displaystyle{ \lambda_i }[/math] is the ith eigenvalue of the sample covariance and [math]\displaystyle{ \sigma^2 }[/math] is the noise variance. This max-likelihood solution is rotation invariant; [math]\displaystyle{ R }[/math] is an arbitrary rotation matrix. The matrix [math]\displaystyle{ W }[/math] spans the principle subspace of the data and the model is known as probabilistic PCA. In face, we can get the traditional MLE by using Expectation Maximization algorithm when [math]\displaystyle{ \sigma }[/math] goes into 0.
The underlying assumption of the model is that the data set can be represented by [math]\displaystyle{ Y = XW^T+E }[/math] where [math]\displaystyle{ X }[/math] in [math]\displaystyle{ \mathbb{R}^{n \times p} }[/math] is a matrix of [math]\displaystyle{ q }[/math] dimensional latent variables and [math]\displaystyle{ E }[/math] is a matrix of noise variables [math]\displaystyle{ e_{ij} \sim \mathcal{N} (0,\sigma^2) }[/math]. The marginal log-likelihood above is obtained by placing an isotropic prior independently on the elements of [math]\displaystyle{ X }[/math] with [math]\displaystyle{ x_{ij} \sim \mathcal{N}(0,1) }[/math].
It is shown<ref name="lawerence2005"> Lawrence N.D. Probabilistic non-linear principle component analysis with Gaussian process latent variable models. Journal of Machine Learning . MIT Press, Cambridge, MA, 2006.
</ref> that the PCA solution is also obtained for log-likelihoods of the form
This is recovered when we marginalize the loadings [math]\displaystyle{ W }[/math], instead of latent variable [math]\displaystyle{ X }[/math], with a Gaussian isotropic prior. This is the dual form of probabilistic PCA. This is analogous to the Dual form of PCA and similarly to the primal form, the max likelihood solution solves for the latent coordinates [math]\displaystyle{ X_{ML} = U^'_q L_qR^T }[/math], instead of the principle subspace basis. Here, [math]\displaystyle{ U^'_q }[/math] are the first [math]\displaystyle{ q }[/math] principle eigenvectors of the inner product matrix [math]\displaystyle{ p^{-1}YY^T }[/math] with [math]\displaystyle{ Lq }[/math] define as before. Both primal and dual scenarios involve maximizing likelihoods of a similar covariance structure, namely when the covariance of the Gaussians is given by a low-rank term plus a spherical term. This paper considers a more general form
Where [math]\displaystyle{ \Sigma }[/math] is a general positive definite matrix. The log-likelihood of this general problem is given by
where [math]\displaystyle{ \Sigma = ZZ^T+ \sigma^2I }[/math]. The underlying model of this log-liklihood function can be considered as a linear mixed effect model with two factors and noise,
where [math]\displaystyle{ Z }[/math] is a matrix of known covariates and [math]\displaystyle{ X }[/math] is a matrix of latent variables.
The question this papers attempts to answer is that given [math]\displaystyle{ \Sigma }[/math] how can we solve for [math]\displaystyle{ X }[/math]( respectively [math]\displaystyle{ W }[/math]), and for what values of [math]\displaystyle{ \Sigma }[/math] we can formulate useful new algorithm for machine learning? This paper shows that the maximum likelihood solution for [math]\displaystyle{ X }[/math] is simply based on generalized eigenvalue problem (GEP) on the sample-covariance matrix. Hence the low-rank term [math]\displaystyle{ XX^T }[/math] can be optimized for general [math]\displaystyle{ \Sigma }[/math]. The authors call this approach residual component analysis (RCA).
Maximum likelihood RCA
Theorem: The maximum likelihood estimate of the parameter [math]\displaystyle{ X }[/math] in the likelihood model in equation (*), for positive-definite and invertible [math]\displaystyle{ \Sigma }[/math], is [math]\displaystyle{ X_{ML} = \Sigma S(D-I)^{1/2} }[/math] where [math]\displaystyle{ S }[/math] is the solution to the generalized eigenvalue problem [math]\displaystyle{ \frac{1}{p}YY^TS=\Sigma SD }[/math], with its columns as the generalised eigenvectors and [math]\displaystyle{ D }[/math] is diagonal with the corresponding generalized eigenvalues.
<proof>
The RCA log-likelihood is given by
Where [math]\displaystyle{ K=XX^T+\Sigma }[/math].
Since [math]\displaystyle{ \Sigma }[/math] is positive-deifinite we can consider the eigen-decompostion on [math]\displaystyle{ \Sigma }[/math]
[math]\displaystyle{ \Sigma = U \Lambda U^T }[/math]
where [math]\displaystyle{ U U^T = U^T U=I }[/math] and [math]\displaystyle{ \Lambda }[/math] is diagonal.
The projection of the covariance on to this eigen-basis, scaled by the eigenvalues gives
[math]\displaystyle{ \hat K = \Lambda^{-1/2}U^T K U \Lambda^{-1/2} =\Lambda^{-1/2}U^T (XX^T+\Sigma) U \Lambda^{-1/2} }[/math].
Note that
[math]\displaystyle{ \Lambda^{-1/2}U^T \Sigma U \Lambda^{-1/2} = \Lambda^{-1/2}U^T U \Lambda U^T U \Lambda^{-1/2} = \Lambda^{-1/2} \Lambda \Lambda^{-1/2}=I }[/math]
Hence
[math]\displaystyle{ \hat K=\Lambda^{-1/2}U^TXX^TU\Lambda^{-1/2} +I }[/math]
The maximum likelihood of the RCA can be re-written as
Then solve the maximum likelihood solution of for [math]\displaystyle{ \hat X }[/math]. Relating the stationary point of[math]\displaystyle{ \hat X }[/math] to the solution for [math]\displaystyle{ X }[/math]and then we proceed by expressing this eigenvalue problem in terms of [math]\displaystyle{ YY^T }[/math]. Eventually we can recover X up to an arbitrary rotation (R, which for convenience is normally set to I), via the first q generalised eigenvectors of[math]\displaystyle{ (1/q)YY^T }[/math],
</proof>
Aside from [math]\displaystyle{ \Sigma }[/math], we note a subtle difference from the PPCA solution for [math]\displaystyle{ W }[/math]: Whereas PPCA explicitly subtracts the noise variance from the [math]\displaystyle{ q }[/math] retained principal eigenvalues, RCA implicitly incorporates any noise terms into [math]\displaystyle{ \Sigma }[/math] and standardises them when it projects the total covariance onto the eigen-basis of [math]\displaystyle{ \Sigma }[/math]. Thus we get a reduction of unity from the retained generalised eigenvalues from the theorem. For [math]\displaystyle{ \Sigma=I }[/math] the two solutions are identical.
The posterior density for the RCA probabilistic model (primal case) and [math]\displaystyle{ \mu_y=0 }[/math].
where [math]\displaystyle{ \Sigma_{x|y} = (W^T_{ML} \Sigma^{-1}W_{ML} + I)^{-1} }[/math].
Low Rank Plus Sparse Inverse
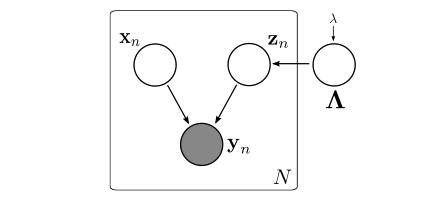
The graphical model optimised by the EM/RCA hybrid algorithm.
where [math]\displaystyle{ \Lambda }[/math] is sampled from a Laplace prior density,
Marginalizing [math]\displaystyle{ X }[/math], yields
Where [math]\displaystyle{ q(Z) }[/math] is the variational distribution and [math]\displaystyle{ \Sigma = \Lambda^{-1}+ \sigma^2I }[/math], which we wish to optimise for some known [math]\displaystyle{ W }[/math]. This is an intractable problem, so instead we optimized the lower bound in an EM fashion.
E-step: Replacing [math]\displaystyle{ q(Z) }[/math] with the posterior [math]\displaystyle{ p(Z|Y,\Lambda ') }[/math] for a current estimate [math]\displaystyle{ \Lambda ' }[/math], amounts to the E-step for updating the posterior density of [math]\displaystyle{ \,z_n|y_n }[/math] with
M-step: Then for fixed [math]\displaystyle{ Z' }[/math], the only free parameter in the expected complete data log likelihood [math]\displaystyle{ Q = {\mathbb{E}}_{Z|Y} (log p(Z', \Lambda)) }[/math] is [math]\displaystyle{ \Lambda }[/math].
Therefore,
.
This amounts to standard GLASSO optimization with covariance matrix.
RCA-step: After one interation of EM, we update [math]\displaystyle{ W }[/math] via RCA based on the newly estimated [math]\displaystyle{ \Lambda }[/math],
for the generalized eigen-value problem. [math]\displaystyle{ \frac{1}{n}Y^TYS = \Sigma SD }[/math] and [math]\displaystyle{ \, \Lambda = \Lambda^{-1}+\sigma^2I }[/math]
Iterate until the lower-bound converge.
Experiments
We describe three experiments with EM/RCA and one purely with RCA analysing the residual left from a Gaussian process (GP) in a time-series.
The four experiments with EM/RCA are as following:
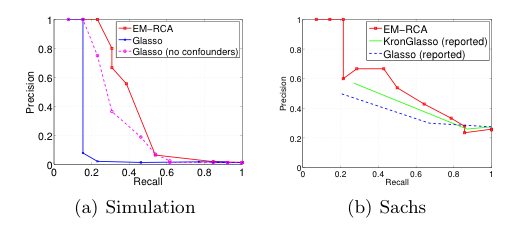
Experiment (1), simulation: the authors consider an artificial dataset sampled from the generative model to illustrate the effects of confounders on the estimation of the sparse-inverse covariance.
Figure (a) shows the precision-recall curve for GLASSO and EM/RCA. The EM/RCA curve shows significantly better performance than GLASSO on the confounded data, while the dashed line shows the performance of GLASSO on similarly generated data without the confounding effects [math]\displaystyle{ (W = 0) }[/math]. We note that EM/RCA performs better on confounded data than GLASSO on non-confounded data, because of the lower signal-to-noise ratio in the non-confounded data.
Experiment (2), reconstruction of a biological network, we applied EM/RCA on the protein-signaling data of <ref name="Sachs2008"> Sachs, K., Perez, O., Pe’er, D., Lauffenburger, D. A., and Nolan, G. P. Causal protein-signaling networks derived from multiparameter single-cell data. Science, 308:523– 529, April 2008. </ref>. Figure (b), EM/RCA performs slightly better than all other methods. Figure 4 shows the reconstructed networks for recall 0.4. We note that EM/RCA is more conservative in calling edges.
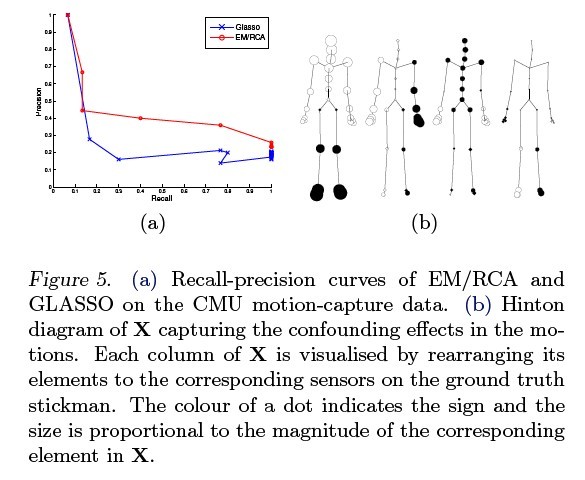
Experiment (3), reconstruction of human form, the objective here is to reconstruct the underlying connectivity of a human being, given only the 3 dimensional locations of 31 sensors placed about the figures body. The aim is to construct a model which recovers connectivity between these points. EM/RCA method also showed promising result.
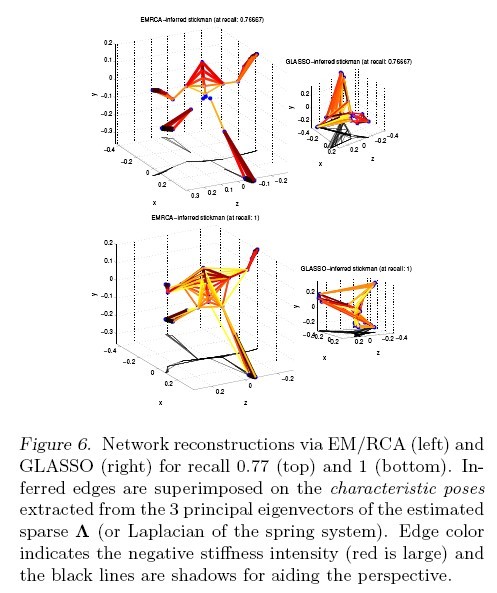
Figure 5 shows the comparison in the form of recall/precision curves between GLASSO and the EM/RCA implementation of a sparse-inverse plus lowrank model. As can be seen, the EM/RCA algorithm outperforms the GLASSO. The recovered stickmen of EM/RCA and GLASSO are shown in figure 6.
Experiment (4), differences in gene-expression profiles, the authors applied the RCA method to address the common challenge in data analysis is to summarize the difference between treatment and control samples. Assuming that both time-series are identical, implies [math]\displaystyle{ y^T = (y_1^T y_2^T) }[/math] can be modeled by a Gaussian process (GP) with a temporal covariance function, y is distributed as N(0, K), where [math]\displaystyle{ K \in R^{n\times n} }[/math] for [math]\displaystyle{ n=n_1+n_2 }[/math]is structured such that both y1 and y2 are generated from the same function. A RBF kernel is used.
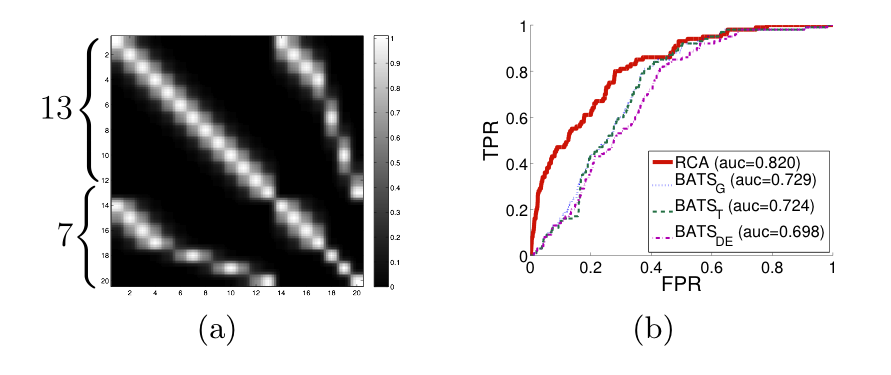
For the figure above, (a)RBF kernel computed on augmented time- input vectors of gene-expression. The kernel is computed across times [math]\displaystyle{ (0 : 20 : 240, 0, 20, 40, 60, 120, 180, 240) }[/math], jointly for control and treatment. (b) shows the ROC curves of RCA and BATS variants with different noise models. We note that RCA outperforms BATS in terms the area under the ROC curve for all of its noise models.
Discussion
RCA is an algorithm for describing a low-dimensional representation of the residuals of a data set, given partial explanation by a covariance matrix [math]\displaystyle{ \Sigma }[/math].The low-rank component of the model can be determined through a generalized eigenvalue problem. The paper illustrated how a treatment and a control time series could have their differences highlighted through appropriate selection of [math]\displaystyle{ \Sigma }[/math](in this case we used an RBF kernel). The paper also introduced an algorithm for fitting a variant of CCA where the private spaces are explained through low dimensional latent variables.
Full covariance matrix model is often run into problem as their parameterization scales with [math]\displaystyle{ D^2 }[/math]. This technique combined sparse-inverse covariance (as in GLASSO) with low rank (as in probabilistic PCA) approaches, and have good effect in the experiment. It was demonstrated to good effect in a motion capture and protein network example.
Another way to impose sparsity is to put a prior such as Laplace prior or Jeffrey prior on the covariance matrix in probabilistic PCA, which is closely related to Bayesian PCA.
References
<references />