parsing natural scenes and natural language with recursive neural networks: Difference between revisions
m (→Input Representation: Adjusted some of the math formatting to make it easier to read.) |
(→Recursive Neural Networks for Structure Prediction: Improved readability of math expressions by inserting "\,") |
||
| Line 75: | Line 75: | ||
and their activations added to a set of potential child node pairs: | and their activations added to a set of potential child node pairs: | ||
::::<math>C = \{ [a_i, a_j]: A(i, j) = 1 \}</math> | ::::<math>\,C = \{ [a_i, a_j]: A(i, j) = 1 \}</math> | ||
So for example, from the image in Fig 2. we would have the following pairs: | So for example, from the image in Fig 2. we would have the following pairs: | ||
::::<math>C = \{[a_1, a_2], [a_1, a_3], [a_2, a_1], [a_2, a_4], [a_3, a_1], [a_3, a_4], [a_4, a_2], [a_4, a_3], [a_4, a_5], [a_5, a_4]\}</math> | ::::<math>\,C = \{[a_1, a_2], [a_1, a_3], [a_2, a_1], [a_2, a_4], [a_3, a_1], [a_3, a_4], [a_4, a_2], [a_4, a_3], [a_4, a_5], [a_5, a_4]\}</math> | ||
Where these are concatenated and given as inputs into the neural network. Potential parent representations for possible child nodes are calculated with: | Where these are concatenated and given as inputs into the neural network. Potential parent representations for possible child nodes are calculated with: | ||
::::<math>p(i, j) = f(W[c_i: c_j] + b)</math> | ::::<math>\,p(i, j) = f(W[c_i: c_j] + b)</math> | ||
And the local score with: | And the local score with: | ||
::::<math>s(i, j) = W^{score} p(i, j) </math> | ::::<math>\,s(i, j) = W^{score} p(i, j) </math> | ||
Once the scores for all pairs are calculated, three steps are performed: | Once the scores for all pairs are calculated, three steps are performed: | ||
1. The highest scoring pair ''<math>[a_i, a_j]</math>'' will be removed from the set of potential child node pairs ''<math>C</math>''. As well as any other pair containing either ''<math>a_i</math>'' or ''<math>a_j</math>''. | 1. The highest scoring pair ''<math>\,[a_i, a_j]</math>'' will be removed from the set of potential child node pairs ''<math>\,C</math>''. As well as any other pair containing either ''<math>\,a_i</math>'' or ''<math>\,a_j</math>''. | ||
2. Adjacency Matrix ''<math>A</math>'' is updated with a new row and column that reflects new segment along with its child segments. | 2. Adjacency Matrix ''<math>\,A</math>'' is updated with a new row and column that reflects new segment along with its child segments. | ||
3. Potential new child pairs are added to ''<math>C</math>''. | 3. Potential new child pairs are added to ''<math>\,C</math>''. | ||
Steps 1-3 are repeated until all pairs are merged and only one parent activation is left in the set ''<math>C</math>''. The last remaining activation is at the root of the Recursive Neural Network that represents the whole image. | Steps 1-3 are repeated until all pairs are merged and only one parent activation is left in the set ''<math>\,C</math>''. The last remaining activation is at the root of the Recursive Neural Network that represents the whole image. | ||
The equation that determines the quality of the structure amongst other variants is simply the sum of all the local decisions: | The equation that determines the quality of the structure amongst other variants is simply the sum of all the local decisions: | ||
| Line 109: | Line 109: | ||
How do we find reconstruction error? | How do we find reconstruction error? | ||
1. p is the parent representation for children <math>[c_1;c_2]</math> (same as before) | 1. p is the parent representation for children <math>\,[c_1;c_2]</math> (same as before) | ||
<math> p=f(W^{(1)}[c_1;c_2]+b^{(1)}) </math> | <math>\, p=f(W^{(1)}[c_1;c_2]+b^{(1)}) </math> | ||
2. one way of assessing how well this p represents its children is to reconstruct the children in a reconstruction layer. | 2. one way of assessing how well this p represents its children is to reconstruct the children in a reconstruction layer. | ||
<math>[c_1^';c_2^']=W^{(2)}p+b^{(2)} </math> | <math>[c_1^';c_2^']=W^{(2)}p+b^{(2)} </math> | ||
3. Then, the reconstruction is defined below. The goal is to minimize <math>E_{rec}([c_1];c_2)</math>. | 3. Then, the reconstruction is defined below. The goal is to minimize <math>\,E_{rec}([c_1];c_2)</math>. | ||
<math>E_{rec}([c_1;c_2])=\frac{1}{2}||[c_1;c_2]-[c_1^';c_2^']||^2 </math> | <math>E_{rec}([c_1;c_2])=\frac{1}{2}||[c_1;c_2]-[c_1^';c_2^']||^2 </math> | ||
How to construct the tree? | How to construct the tree? | ||
* It first takes the first pair of neighboring vecotrs <math> (c_1;c_2)=(x_1;x_2) </math>. We save the parent node and the resulting reconstruction error. The network shifted by one position and takes as input vectors <math> (c_1;c_2)=(x_2;x_3) </math> and obtains <math> p , E_{rec}</math>. Repeat the process until it hits the last pair. | * It first takes the first pair of neighboring vecotrs <math>\, (c_1;c_2)=(x_1;x_2) </math>. We save the parent node and the resulting reconstruction error. The network shifted by one position and takes as input vectors <math> \,(c_1;c_2)=(x_2;x_3) </math> and obtains <math> \,p,\, E_{rec}</math>. Repeat the process until it hits the last pair. | ||
* Select the pair with lowest <math>E_{rec}</math>. | * Select the pair with lowest <math>\,E_{rec}</math>. | ||
eg. Given sequence <math>(x_1,x_2,x_3,x_4)</math>, we get lowest <math>E_{rec}</math> by the pair <math>(x_3, x_4)</math>. The new sequence then consists of <math>(x_1, x_2 , p(3,4))</math>. | eg. Given sequence <math>\,(x_1,x_2,x_3,x_4)</math>, we get lowest <math>\,E_{rec}</math> by the pair <math>\,(x_3, x_4)</math>. The new sequence then consists of <math>\,(x_1, x_2 , p(3,4))</math>. | ||
* The process repeats and treats the new vector <math>p(3,4)</math> like any other vector. | * The process repeats and treats the new vector <math>\,p(3,4)</math> like any other vector. | ||
* The process stops until it reaches a deterministic choice of collapsing the remaining two states into one parent. The tree is then recovered. | * The process stops until it reaches a deterministic choice of collapsing the remaining two states into one parent. The tree is then recovered. | ||
Revision as of 12:15, 23 October 2015
Introduction
This paper uses Recursive Neural Networks (RNN) to find a recursive structure that is commonly found in the inputs of different modalities such as natural scene images or natural language sentences. This is the first deep learning work which learns full scene segmentation, annotation and classification. The same algorithm can be used both to provide a competitive syntactic parser for natural language sentences from the Penn Treebank and to outperform alternative approaches for semantic scene segmentation, annotation and classification.
For vision applications, the approach differs from any previous works in that it uses off-the-shelf vision features of segments obtained from oversegmented images instead of learning feature from raw images. In addition, the same network can be used recursively to achieve classification instead of building a hierarchy by a convolutional neural network.
Also, this particular approach for NLP is different in that it handles variable sized sentences in a natural way and captures the recursive nature of natural language. Furthermore, it jointly learns parsing decisions, categories for each phrase and phrase feature embeddings which capture the semantics of their constituents.
Core Idea
The following figure describes the recursive structure that is present in the images and the sentences.
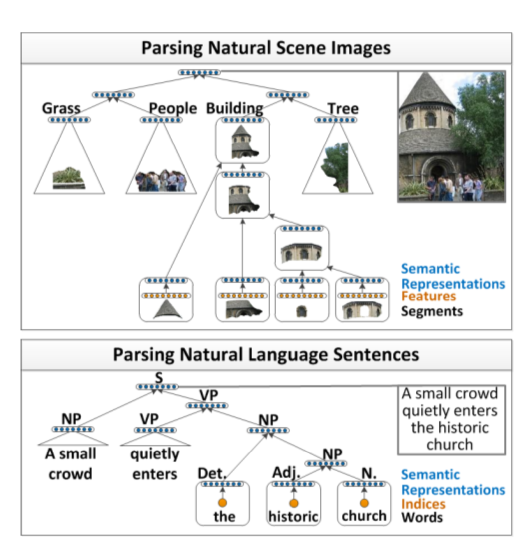
Images are first over segmented into regions which are later mapped to semantic feature vector using a neural network. These features are then used as an input to the RNN, which decides whether or not to merge the neighbouring images. This is decided based on a score which is higher if the neighbouring images share the same class label.
In total the RNN computed 3 outputs :
- Score, indicating whether the neighboring regions should be merged or not
- A new semantic feature representation for this larger region
- Class label
The same procedure is applied to parsing of words too. The semantic features are given as an input to the RNN, then they are merged into phrases in a syntactically and semantically meaningful order.
Input Representation
Each image is divided into 78 segments, and 119 Features(described by Gould et al.<ref> Gould, Stephen, Richard Fulton, and Daphne Koller. "Decomposing a scene into geometric and semantically consistent regions." Computer Vision, 2009 IEEE 12th International Conference on. IEEE, 2009. </ref>) from each segment are extracted. These features include color and texture features , boosted pixel classifier scores (trained on the labelled training data), as well as appearance and shape features.
Each of these images are then transformed semantically by applying it to a neural network layer using a logistic function as the activation unit as follows:
[math]\displaystyle{ \,a_i=f(W^{sem}F_i + b^{sem}) }[/math]
where W is the weight that we want to learn, F is the Feature Vector, b is the bias and f is the activation function. In this version of experiments, the original sigmoid function [math]\displaystyle{ f(x)=\tfrac{1}{1 + e^{-x}} }[/math] was used.
For the sentences each word is represented by an [math]\displaystyle{ n }[/math]-dimensional vector (n=100 in the paper). The values of these vectors are learned to capture co-occurrence statistics and they are stored as columns in a matrix [math]\displaystyle{ L \in \mathbb{R}^{n \times |V|} }[/math] where [math]\displaystyle{ |V|\, }[/math] is the size of the vocabulary (i.e., the total number of unique words that might occur). To extract the features or semantic representation of a word a binary vector [math]\displaystyle{ \,e_k }[/math] with all zeros except for the [math]\displaystyle{ \,k^{th} }[/math] index can be used, where [math]\displaystyle{ \,k }[/math] corresponds to the word's column index in [math]\displaystyle{ \,L }[/math]. Given this vector, the semantic representation of the word is obtained by
[math]\displaystyle{ a_i=Le_k\, }[/math].
Recursive Neural Networks for Structure Prediction
In our discriminative parsing architecture, the goal is to learn a function f : X → Y, where Y is the set of all possible binary parse trees. An input x consists of two parts: (i) A set of activation vectors [math]\displaystyle{ \{a_1 , . . . , a_{N_{segs}}\} }[/math], which represent input elements such as image segments or words of a sentence. (ii) A symmetric adjacency matrix A, where A(i, j) = 1, if segment i neighbors j. This matrix defines which elements can be merged. For sentences, this matrix has a special form with 1’s only on the first diagonal below and above the main diagonal.
The following figure illustrates how the inputs to RNN look like and what the correct label is. For images, there will be more than one correct binary parse tree, but for sentences there will only have one correct tree. A correct tree means that segments belong to the same class are merged together into one superclass before they get merged with other segments from different superclasses.
The structural loss margin for RNN to predict the tree is defined as follows
[math]\displaystyle{ \Delta(x,l,y^{\mathrm{proposed}})=\kappa \sum_{d \in N(y^{\mathrm{proposed}})} 1\{subTree(d) \notin Y (x, l)\} }[/math]
where the summation is over all non terminal nodes and [math]\displaystyle{ \Kappa }[/math] is a parameter. Y(x,l) is the set of correct trees corresponding to input x and label l. [math]\displaystyle{ 1\{\dots\} }[/math] will be one for a non-empty set and zero for an empty set. To express this in somewhat more natural terms, any subtree that does not occur in any of the ground truth trees will increase the loss by one.
Given the training set, the algorithm will search for a function f with small expected loss on unseen inputs, i.e. File:pic3.png where θ are all the parameters needed to compute a score s with an RNN. The score of a tree y is high if the algorithm is confident that the structure of the tree is correct.
An additional constraint imposed is that the score of the highest scoring tree should be greater than margin defined y the structural loss function so that the model output's as high score as possible on the correct tree and as low score as possible on the wrong tree. This constraint can be expressed as File:pic4.png
With these constraints minimizing the following objective function maximizes the correct tree’s score and minimizes (up to a margin) the score of the highest scoring but incorrect tree. File:pic5.png
For learning the RNN structure, the authors used activation vectors and adjacency matrix as inputs, as well as a greedy approximation since there is no efficient dynamic programming algorithms for their RNN setting.
With an adjacency matrix A, neighboring segments are found with the algorithm and their activations added to a set of potential child node pairs:
- [math]\displaystyle{ \,C = \{ [a_i, a_j]: A(i, j) = 1 \} }[/math]
So for example, from the image in Fig 2. we would have the following pairs:
- [math]\displaystyle{ \,C = \{[a_1, a_2], [a_1, a_3], [a_2, a_1], [a_2, a_4], [a_3, a_1], [a_3, a_4], [a_4, a_2], [a_4, a_3], [a_4, a_5], [a_5, a_4]\} }[/math]
Where these are concatenated and given as inputs into the neural network. Potential parent representations for possible child nodes are calculated with:
- [math]\displaystyle{ \,p(i, j) = f(W[c_i: c_j] + b) }[/math]
And the local score with:
- [math]\displaystyle{ \,s(i, j) = W^{score} p(i, j) }[/math]
Once the scores for all pairs are calculated, three steps are performed:
1. The highest scoring pair [math]\displaystyle{ \,[a_i, a_j] }[/math] will be removed from the set of potential child node pairs [math]\displaystyle{ \,C }[/math]. As well as any other pair containing either [math]\displaystyle{ \,a_i }[/math] or [math]\displaystyle{ \,a_j }[/math].
2. Adjacency Matrix [math]\displaystyle{ \,A }[/math] is updated with a new row and column that reflects new segment along with its child segments.
3. Potential new child pairs are added to [math]\displaystyle{ \,C }[/math].
Steps 1-3 are repeated until all pairs are merged and only one parent activation is left in the set [math]\displaystyle{ \,C }[/math]. The last remaining activation is at the root of the Recursive Neural Network that represents the whole image.
The equation that determines the quality of the structure amongst other variants is simply the sum of all the local decisions:
- [math]\displaystyle{ s(RNN(\theta,x_i,\widehat y))=\sum_{d\in N(\widehat y)}s_d }[/math]
Unsupervised Recursive Autoencoer for structure Prediction<ref>http://nlp.stanford.edu/pubs/SocherPenningtonHuangNgManning_EMNLP2011.pdf</ref>.
Instead of using scores (as described above) to predict the tree structure, we can also use the reconstruction error to predict the structure.
How do we find reconstruction error?
1. p is the parent representation for children [math]\displaystyle{ \,[c_1;c_2] }[/math] (same as before)
[math]\displaystyle{ \, p=f(W^{(1)}[c_1;c_2]+b^{(1)}) }[/math]
2. one way of assessing how well this p represents its children is to reconstruct the children in a reconstruction layer.
[math]\displaystyle{ [c_1^';c_2^']=W^{(2)}p+b^{(2)} }[/math]
3. Then, the reconstruction is defined below. The goal is to minimize [math]\displaystyle{ \,E_{rec}([c_1];c_2) }[/math].
[math]\displaystyle{ E_{rec}([c_1;c_2])=\frac{1}{2}||[c_1;c_2]-[c_1^';c_2^']||^2 }[/math]
How to construct the tree?
- It first takes the first pair of neighboring vecotrs [math]\displaystyle{ \, (c_1;c_2)=(x_1;x_2) }[/math]. We save the parent node and the resulting reconstruction error. The network shifted by one position and takes as input vectors [math]\displaystyle{ \,(c_1;c_2)=(x_2;x_3) }[/math] and obtains [math]\displaystyle{ \,p,\, E_{rec} }[/math]. Repeat the process until it hits the last pair.
- Select the pair with lowest [math]\displaystyle{ \,E_{rec} }[/math].
eg. Given sequence [math]\displaystyle{ \,(x_1,x_2,x_3,x_4) }[/math], we get lowest [math]\displaystyle{ \,E_{rec} }[/math] by the pair [math]\displaystyle{ \,(x_3, x_4) }[/math]. The new sequence then consists of [math]\displaystyle{ \,(x_1, x_2 , p(3,4)) }[/math].
- The process repeats and treats the new vector [math]\displaystyle{ \,p(3,4) }[/math] like any other vector.
- The process stops until it reaches a deterministic choice of collapsing the remaining two states into one parent. The tree is then recovered.
Learning
The objective function J is not differentiable due to hinge loss. Therefore, we must opt for the subgradient method (Ratliff et al., 2007) which computes a gradient-like method called the subgradient. Let [math]\displaystyle{ \theta = (W^{sem},W,W^{score},W^{label}) }[/math], then the gradient becomes:
- [math]\displaystyle{ \frac{\partial J}{\partial \theta} = \frac{1}{x} \sum_{i}\frac{\partial s(\hat{y}_i)}{\partial \theta} - \frac{\partial s(\hat{y}_i)}{\partial \theta} + \lambda\theta, }[/math]
where [math]\displaystyle{ s(\hat{y}_i) = s(RNN(\theta,x_i,\hat{y}_{max(\tau(x_i))})) }[/math] and [math]\displaystyle{ s(\hat{y}_i) = s(RNN(\theta,x_i,\hat{y}_{max(Y(x_i,l_i))})) }[/math]. In order to compute this gradient, we calculate the derivative by using backpropagation through structure (Goller & Küchler, 1996). L-BFGS was used over the complete training data to minimize the objective. This may cause problems in non-differentiable functions, but none was observed in practice.
L-BFGS is short for Limited-memory BFGS, which is an iterative method for solving unconstrained nonlinear optimization problems that using a limited amount of computer memory. Thus it is particularly suited to problems with very large numbers of variables (e.g., >1000)<ref> https://en.wikipedia.org/wiki/Broyden%E2%80%93Fletcher%E2%80%93Goldfarb%E2%80%93Shanno_algorithm </ref>.
Results
The parameters to tune in this algorithm are n, the size of the hidden layer; κ, the penalization term for incorrect parsing decisions and λ, the regularization parameter. It was found that the method was quite robust, varying in performance by only a few percent for some perameter combinations. The parameter values used were n = 100, κ = 0.05 and λ = 0.001.
Additional resources that are helpful for replicating and extending this work can be found here on the first author's personal website. This includes the source code for the project, as well as download links for the datasets used.
Scene understanding
For training and testing the researchers opted for the Stanford Background dataset—a dataset that can roughly be categorized into three types: city, countryside and sea-side. The team labelled the images with these three labels and a SVM was trained using the average over all nodes' activations in the tree as features. With an accuracy of 88.1%, this algorithm outperforms the state-of-the art features for scene categorization, Gist descriptors, which obtained only 84.0%. The results are summarized in the following figure. File:pic6.png
A single neural network layer followed by a softmax layer is also tested in this paper, which performed about 2% worse than the full RNN model.
In order to show the learned feature representations captured import appearance and label information, the researchers visualized nearest neighbour super segments. The team computed nearest neighbours across all images and all such subtrees. The figure below shows the results. The first image in each row is a random subtree's top node and the remaining nodes are the closest subtrees in the dataset in terms of Euclidean distance between the vector representations.
Natural language processing
The method was also tested on natural language processing with the Wall Street Journal section of the Penn Treebank and was evaluated with the F-measure (Manning & Schütz, 1999). While the widely used Berkeley parser was not outperformed, the scores are close (91.63% vs 90.29%). Interestingly, no syntactic information of the child nodes is provided by the parser to the parent nodes. All syntatic information used is encoded in the learned continuous representations.
Similar to the nearest neighbour scene subtrees, nearest neighbours for multiword phrases were collected. For example, "All the figures are adjusted for seasonal variatons" is a close neighbour to "All the numbers are adjusted for seasonal fluctuations".
Related work
Based on this work, the author published another paper to improve semantic representations, using Long Short-Term Memory (LSTM) networks which is a recurrent neural network with a more complex computational unit. It outperforms the existing systems on aspects of semantic relatedness and sentiment classification.<ref> Tai K S, Socher R, Manning C D. Improved semantic representations from tree-structured long short-term memory networks[J]. arXiv preprint arXiv:1503.00075, 2015. </ref>
Reference
<references />