paper 13: Difference between revisions
| (45 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
==Random mapping (Random Projection)== | ==Random mapping (Random Projection)== | ||
For vector <math>x \in R^{N}</math> and | The following passage contains a short review and brief introduction about Random Mapping <ref> Samuel Kaski; Dimensionality Reduction by Random Mapping:Fast Similarity Computation for Clustering, 1998 IEEE </ref>. We later explain some important results for estimating the Intrinsic Dimensionality (ID) of the manifold embedding in high dimensional space using <math> n </math> sample points, as well as, some interesting results about the upper an lower bounds for Intrinsic Dimensionality of projected manifold and Minimum Number of Random Projections needed for an efficient mapping. <ref> Chinmay Hedg and Colleagues: Random Projection for Manifold Learning (2007)</ref> | ||
<math> y= \sum_{i}x_{i}r_{i} </math> | ===Introduction=== | ||
where <math>r_{i}'s</math> are the columns of <math>R</math>. | For vector <math>x \in R^{N}</math> and an <math> N\times M </math> Random matrix <math> R </math>, <math> y=Rx </math> is called Random map (projection) of <math> x </math>.<br> note that <math> y\in R^{M}</math> and can be expressed as:<br> | ||
In Random mapping orthogonal directions are replaced by random directions | |||
By definition the number of columns of matrix <math>R</math> called the Number of Random projections (<math>M</math>) required to project a K-dimensional manifold from <math>R^{N}</math> into <math>R^{M}</math><br> | <math> y= \sum_{i}x_{i}r_{i} </math> | ||
For Large <math>N</math> applying adaptive (data dependent) algorithms like Isomap, LLE, etc | |||
For example if Cosine of the angle made by two vectors is the measure | where <math>r_{i}'s</math> are the columns of <math>R</math>.<br> | ||
In Random mapping orthogonal directions are replaced by random directions. | |||
By definition the number of columns of matrix <math>R</math> is called the Number of Random projections (<math>M</math>) required to project a K-dimensional manifold from <math>R^{N}</math> into <math>R^{M}</math><br> | |||
For Large <math>N</math> applying adaptive (data dependent) algorithms like Isomap, LLE, etc. is too costly and it is not feasible at times; Since Random Mapping almost preserves the metric structure, it is reasonable to use random projection (non-adaptive method) to map data into lower dimension (<math>M</math>) and then apply clustering algorithms or other dimensionality reduction algorithms. As an special case, If <math>R</math> is orthonormal then similarity under random mapping is exactly preserved.<br> | |||
For example if Cosine of the angle made by two vectors is the measure of their similarity, we can assume <math>y_{1}</math> and <math>y_{2}</math> are the random maps of <math>x_{1}</math> and <math>x_{2}</math>; Hence we will have<br> | |||
<math> y^{T}_{1}y_{2}=x^{T}_{1}R^{T}Rx_{2} </math> <br> | <math> y^{T}_{1}y_{2}=x^{T}_{1}R^{T}Rx_{2} </math> <br> | ||
where <math>R</math> can be written as<br> | where <math>R</math> can be written as<br> | ||
| Line 20: | Line 24: | ||
so <br> <math>y^{T}_{1}y_{2}=x^{T}_{1}x_{2}</math> | so <br> <math>y^{T}_{1}y_{2}=x^{T}_{1}x_{2}</math> | ||
An interesting result about random matrix <math>R</math> is that we can show when matrix <math>M</math> (reduced dimension) is large, | |||
then <math>\epsilon_{ij}</math> are independently distributed as Normal distribution | then <math>\epsilon_{ij}</math>'s are independently distributed as Normal distribution with mean <math>0</math> and variance <math>1/M</math><br> | ||
===The GP algorithm=== | |||
An important preprocessing step in manifold learning is the issue of estimating <math>K</math>, the intrinsic dimension (ID) of <math>M</math>. | |||
A common geometric approach for ID estimation is the Grassberger-Procaccia (GP) algorithm, which involves calculation and processing of pairwise distances between the data points. A sketch of the algorithm is as follows: given a set of points <math>X = {x_{1}; x_{2};...}</math> sampled from <math>M</math>, define <math>Q_{j}(r)</math> as the number of points that lie within a ball of radius <math>r</math> centered around <math>x_{j}</math> . Let <math>Q(r)</math> be the average of <math>Q_{j}(r)</math> over all <math>j = 1; 2;...;n</math>. Then, the estimated scale-dependent correlation dimension is the slope obtained by linearly regressing <math>ln(Q(r))</math> over <math>ln(r)</math> over the best possible linear part. It has been shown that with increasing cardinality of the sample set <math>X</math> and decreasing scales, the estimated correlation dimension well approximates the intrinsic dimension of the underlying manifold. | |||
===Estimating The Intrinsic Dimension=== | ===Estimating The Intrinsic Dimension=== | ||
Intrinsic Dimension (<math>K</math>) is an important input for almost all metric learning algorithms. Grossberger-Proccacia (GP) algorithm can help us to estimate <math>K</math> using <math>n</math> sample points selected from <math>K</math>-dimensional manifold embedded in <math>R^{N}</math>. Define <br> | Intrinsic Dimension (<math>K</math>) is an important input for almost all metric learning algorithms. Grossberger-Proccacia (GP) algorithm can help us to estimate <math>K</math> using <math>n</math> sample points selected from <math>K</math>-dimensional manifold embedded in <math>R^{N}</math>. Define <br> | ||
<math> C_{n}(r)=\frac{1}{n(n-1)} \sum_{i\neq j}I \left\|x_{i}-x_{j}\right\|<r </math><br> | <math> C_{n}(r)=\frac{1}{n(n-1)} \sum_{i\neq j}I \left\|x_{i}-x_{j}\right\|<r </math><br> | ||
which basically measures the probability of a random pairs of points havinng distances less than <math>r</math>. Then estimate of <math>K</math> is obtained the following formula (known as the Scale-dependent Correlation Dimension of <math>X=(x_{1},x_{2},...,x_{n})</math>): | which basically measures the probability of a random pairs of points havinng distances less than <math>r</math>. Then the estimate of <math>K</math> is obtained by using the following formula (known as the Scale-dependent Correlation Dimension of <math>X=(x_{1},x_{2},...,x_{n})</math>): | ||
<math> \hat{D}_{corr}(r_{1},r_{2})=\frac{log(C_{n}(r_{1}))-log(C_{n}(r_{2}))}{log(r_{1})-log(r_{2})} </math><br> | <math> \hat{D}_{corr}(r_{1},r_{2})=\frac{log(C_{n}(r_{1}))-log(C_{n}(r_{2}))}{log(r_{1})-log(r_{2})} </math><br> | ||
When <math>r_{1}</math> and <math>r_{2}</math> are selected such that they cover the biggest range of graph at which <math>C_{n}(r)</math> is linear, GP gives the best estimate. Another important point to consider is that <math>\widehat{K}</math> the obtained GP algorithm based on finite sample points is a Biased estimate.<br> | |||
The reason why the above formula works | The reason why the above formula works can be explained as follows: if the intrinsic dimensionality is 1, the number of points within a (1-dim) sphere around a given point would be proportional to <math>r</math>. If the intrinsic dimensionality is 2 and the points are (at least locally) distributed on a plane, then the number of points within a (2-dim) sphere around a given point would be proportional to <math>\pi r^2</math>, i.e., the area of the corresponding circle. Similarly in the case of a 3-dim sphere, we will have proportionality to <math>4/3 \pi r^3</math>, and so on. So if we take logarithm of this function, we expect the number of intrinsic dimensionality to be reflected in the ''slope'' of the resulting function, as implied by the the formula above. | ||
===Upper and Lower Bound for estimator <math>K</math>=== | ===Upper and Lower Bound for estimator of <math>K</math>=== | ||
Baraniuk and Wakin (2007) showed that if the number of random projection <math>(M)</math> is large we can be sure that the projection of a smooth manifold into lower dimensional space will be a near-isometric embedding. | Baraniuk and Wakin (2007) showed that if the number of random projection <math>(M)</math> is large, we can be sure that the projection of a smooth manifold into lower dimensional space will be a near-isometric embedding. <math>M</math> should have linear relation with <math>K</math> and Logarithmic relationship with <math>N</math> described by<br> | ||
<math> M=c K log(N) </math> <br> | |||
<math> M=c K log\left( N \right)</math> <br> | |||
Chinmay Hedg and colleagues (2007) showed that under some conditions, for random orthoprojector <math>R</math> (consists of <math>M</math> orthogonalized vectors of length <math>N</math>) and sequence of sample <math>X=\left\{x_{1},x_{2},...\right\}</math> | |||
Remember that, since random mapping almost preserves metric structure, we need to estimate the ID of the projected data.<br> | |||
Chinmay Hedg and his colleagues (2007) showed that under some conditions, for random orthoprojector <math>R</math> (consists of <math>M</math> orthogonalized vectors of length <math>N</math>) and sequence of sample <math>X=\left\{x_{1},x_{2},...\right\}</math>, with probability <math>1-\rho</math><br> | |||
<math> (1-\delta)\hat{K}\leq \hat{K}_{R}\leq (1+\delta)\hat{K} </math> | <math> (1-\delta)\hat{K}\leq \hat{K}_{R}\leq (1+\delta)\hat{K} </math> | ||
| Line 47: | Line 60: | ||
===Lower Bound for the number of Random Projections=== | ===Lower Bound for the number of Random Projections=== | ||
We can also find the minimum number of | We can also find the minimum number of projections needed such that, the difference between residuals obtained from applying Isomap on projected data and original data does not exceed an arbitary value.<br> | ||
Let <math> \Gamma=max_{1\leq i,j\leq n}d_{iso}(x_{i},x_{j})</math> and call it Diameter of data set <math>X=\left\{x_{1},x_{2},...,x_{n}\right\}</math> where <math>d_{iso}(x_{i},x_{j})</math> is the Isomap estimate of geodesic distance | Let <math> \Gamma=max_{1\leq i,j\leq n}d_{iso}(x_{i},x_{j})</math> and call it Diameter of data set <math>X=\left\{x_{1},x_{2},...,x_{n}\right\}</math> where <math>d_{iso} \left(x_{i},x_{j}\right)</math> is the Isomap estimate of geodesic distance; also let <math>L</math> and <math>L_{R}</math> be the residuals obtained from Isomap generated <math>K</math>-dimentional embeding of <math>X</math> and its progection <math>RX</math>, respectively. then we have,<br> | ||
<math> L_{R}<L+C(n)\Gamma^{2}\epsilon</math> <br> | <math> L_{R}<L+C \left(n\right) \Gamma^{2}\epsilon</math> <br> | ||
in which <math>C(n)</math> is a function of the number of sample points.<br> | in which <math>C(n)</math> is a function of the number of sample points.<br> | ||
| Line 57: | Line 70: | ||
===practical algorithm to determine <math>K</math> and <math>M</math>=== | ===practical algorithm to determine <math>K</math> and <math>M</math>=== | ||
The above theorems are not able to give us the estimates without some prior information ( | The above theorems are not able to give us the estimates without some prior information ( about the volume and condition of manifold), hence they are called Theoretical Theorems, But with the help of ML-RP algorithm we can make achieve this goal. | ||
let <math>M=1</math> and select a random vector for <math>R</math> <br> | let <math>M=1</math> and select a random vector for <math>R</math> <br> | ||
| Line 68: | Line 81: | ||
EndWhile <br> | EndWhile <br> | ||
Print <math>M</math> and <math>\hat{K}</math><br> | Print <math>M</math> and <math>\hat{K}</math><br> | ||
=== Where ML-RP is applicable? === | |||
Compressive Sensing (CS) has come to focus in recent years. Think of a situation in which a huge number of low-power devices which are not expensive and capture, store, and transmit very small number of measurements of high-dimensional data. We can apply ML-RP in this scenario. | |||
ML-RP also provides a simple solution to the manifold learning problem in situations where the bottleneck lies in the transmission of the data to the central processing node. The algorithm ensures that with minimum transmitted amount of information, we can perform effective manifold learning. Since with high probability the metric structure of the projected dataset upon termination of MLRP closely resembles that of the original dataset, ML-RP can be regarded as a new adaptive algorithm for finding an efficient, reduced representation of data of very large | |||
dimension. | |||
===Applications=== | ===Applications=== | ||
While the main goal of dimensionality reduction methods is to preserve as much information as possible from the higher dimension to lower dimensional space, it is also important to consider the computational complexity of the algorithm. Random projections preserves the similarity between the data vectors when the data is projected in fewer dimensions and the projections can also be computed faster.<br> | |||
In <ref> Ella Bingham and Heikki Mannila:Random projection in dimensionality reduction: Applications to image and text data</ref>, | In [1] <ref> Ella Bingham and Heikki Mannila:Random projection in dimensionality reduction: Applications to image and text data. </ref> , authors applied random projections technique of dimensonality reduction to image (both, noisy and noiseless) and text data and concluded that the random lower dimension subspace yields results comparable to conventional dimensionality reduction method like PCA, but the computation time is significantly reduced. They also demonstarted that using a sparse random matrix leads to a further savings in computational complexity. The benefit of random projections is applicable only in applications where the distance between the points in the higher dimension have some meaning but if the distances are themselves suspect, then there is no point in preserving them in lower dimensional space. They provide an example: "In a Euclidean space, every dimension is equally important and independent of the others, whereas e.g. in a process monitoring application, some measured quantities (that is, dimensions) might be closely related to others, and the interpoint distances do not necessarily bear a clear meaning."<br> | ||
Random projections do not suffer from the curse of dimensionality.<br> | Random projections do not suffer from the curse of dimensionality.<br> | ||
Random projections also have application in the area of signal processing, where the device can perform tasks directly on random projections and thereby save storage and processing costs. | Random projections also have application in the area of signal processing, where the device can perform tasks directly on random projections and thereby save storage and processing costs. | ||
==Experimental Results== | |||
===Convergence of Random Projections GP to conventional GP=== | |||
Given a data set, the conventional GP algorithm gives an estimation of its intrinsic dimension (ID), which we denote by '''<math>EID</math>'''. In Random Projections GP, ID estimations, which we denote by '''<math>EID_M</math>''', are obtained by running the GP algorithm on '''<math>M</math>''' random projections of the original data set. Theorem 3.1 in the paper essentially shows that '''<math>EID_M</math>''' converges to '''<math>EID</math>''' when '''<math>M</math>''' is sufficiently large. Section 5 of the paper illustrates the convergence using a synthesized data set. | |||
The data set is obtained from drawing <math>n=1000</math> samples from uniform distributions supported on K-dimensional hyper-spheres embedded in an ambient space of dimension <math>N=150</math>, where <math>K<<N</math>. The paper shows the result for values of K between 2 and 7. | |||
[[File:GPEID.jpg]] | |||
In the figure on the left, the solid lines correspond to the '''<math>EID</math>''' for different K and the dashed lines correspond to '''<math>EID_M</math>'''. As is obvious from the figure, '''<math>EID_M</math>''' converges to '''<math>EID</math>''' as M gets larger. | |||
In the figure on the right, the minimum number of projections M required to obtain a 90% accurate '''<math>EID_M</math>''' approximation of '''<math>EID</math>''' is plotted against K, the real intrinsic dimension. Note the linear relationship, which is predicted by Theorem 3.1. | |||
==References== | |||
<references/> | |||
Latest revision as of 09:45, 30 August 2017
Random mapping (Random Projection)
The following passage contains a short review and brief introduction about Random Mapping <ref> Samuel Kaski; Dimensionality Reduction by Random Mapping:Fast Similarity Computation for Clustering, 1998 IEEE </ref>. We later explain some important results for estimating the Intrinsic Dimensionality (ID) of the manifold embedding in high dimensional space using [math]\displaystyle{ n }[/math] sample points, as well as, some interesting results about the upper an lower bounds for Intrinsic Dimensionality of projected manifold and Minimum Number of Random Projections needed for an efficient mapping. <ref> Chinmay Hedg and Colleagues: Random Projection for Manifold Learning (2007)</ref>
Introduction
For vector [math]\displaystyle{ x \in R^{N} }[/math] and an [math]\displaystyle{ N\times M }[/math] Random matrix [math]\displaystyle{ R }[/math], [math]\displaystyle{ y=Rx }[/math] is called Random map (projection) of [math]\displaystyle{ x }[/math].
note that [math]\displaystyle{ y\in R^{M} }[/math] and can be expressed as:
[math]\displaystyle{ y= \sum_{i}x_{i}r_{i} }[/math]
where [math]\displaystyle{ r_{i}'s }[/math] are the columns of [math]\displaystyle{ R }[/math].
In Random mapping orthogonal directions are replaced by random directions.
By definition the number of columns of matrix [math]\displaystyle{ R }[/math] is called the Number of Random projections ([math]\displaystyle{ M }[/math]) required to project a K-dimensional manifold from [math]\displaystyle{ R^{N} }[/math] into [math]\displaystyle{ R^{M} }[/math]
For Large [math]\displaystyle{ N }[/math] applying adaptive (data dependent) algorithms like Isomap, LLE, etc. is too costly and it is not feasible at times; Since Random Mapping almost preserves the metric structure, it is reasonable to use random projection (non-adaptive method) to map data into lower dimension ([math]\displaystyle{ M }[/math]) and then apply clustering algorithms or other dimensionality reduction algorithms. As an special case, If [math]\displaystyle{ R }[/math] is orthonormal then similarity under random mapping is exactly preserved.
For example if Cosine of the angle made by two vectors is the measure of their similarity, we can assume [math]\displaystyle{ y_{1} }[/math] and [math]\displaystyle{ y_{2} }[/math] are the random maps of [math]\displaystyle{ x_{1} }[/math] and [math]\displaystyle{ x_{2} }[/math]; Hence we will have
[math]\displaystyle{ y^{T}_{1}y_{2}=x^{T}_{1}R^{T}Rx_{2} }[/math]
where [math]\displaystyle{ R }[/math] can be written as
[math]\displaystyle{ R^{T}R=I+\epsilon }[/math] in which
[math]\displaystyle{ \epsilon_{ij}= \left\{\begin{matrix}
r^{T}_{i}r_{j} & \text{if } j \neq i \\
0 & \text{if} i=j \end{matrix}\right. }[/math]
now for special case where [math]\displaystyle{ R }[/math] is orthonormal,
[math]\displaystyle{ R^{T}R=I }[/math]
since
[math]\displaystyle{ \epsilon_{ij}=r^{T}_{i}r_{j}=0 }[/math]
so
[math]\displaystyle{ y^{T}_{1}y_{2}=x^{T}_{1}x_{2} }[/math]
An interesting result about random matrix [math]\displaystyle{ R }[/math] is that we can show when matrix [math]\displaystyle{ M }[/math] (reduced dimension) is large,
then [math]\displaystyle{ \epsilon_{ij} }[/math]'s are independently distributed as Normal distribution with mean [math]\displaystyle{ 0 }[/math] and variance [math]\displaystyle{ 1/M }[/math]
The GP algorithm
An important preprocessing step in manifold learning is the issue of estimating [math]\displaystyle{ K }[/math], the intrinsic dimension (ID) of [math]\displaystyle{ M }[/math].
A common geometric approach for ID estimation is the Grassberger-Procaccia (GP) algorithm, which involves calculation and processing of pairwise distances between the data points. A sketch of the algorithm is as follows: given a set of points [math]\displaystyle{ X = {x_{1}; x_{2};...} }[/math] sampled from [math]\displaystyle{ M }[/math], define [math]\displaystyle{ Q_{j}(r) }[/math] as the number of points that lie within a ball of radius [math]\displaystyle{ r }[/math] centered around [math]\displaystyle{ x_{j} }[/math] . Let [math]\displaystyle{ Q(r) }[/math] be the average of [math]\displaystyle{ Q_{j}(r) }[/math] over all [math]\displaystyle{ j = 1; 2;...;n }[/math]. Then, the estimated scale-dependent correlation dimension is the slope obtained by linearly regressing [math]\displaystyle{ ln(Q(r)) }[/math] over [math]\displaystyle{ ln(r) }[/math] over the best possible linear part. It has been shown that with increasing cardinality of the sample set [math]\displaystyle{ X }[/math] and decreasing scales, the estimated correlation dimension well approximates the intrinsic dimension of the underlying manifold.
Estimating The Intrinsic Dimension
Intrinsic Dimension ([math]\displaystyle{ K }[/math]) is an important input for almost all metric learning algorithms. Grossberger-Proccacia (GP) algorithm can help us to estimate [math]\displaystyle{ K }[/math] using [math]\displaystyle{ n }[/math] sample points selected from [math]\displaystyle{ K }[/math]-dimensional manifold embedded in [math]\displaystyle{ R^{N} }[/math]. Define
[math]\displaystyle{ C_{n}(r)=\frac{1}{n(n-1)} \sum_{i\neq j}I \left\|x_{i}-x_{j}\right\|\lt r }[/math]
which basically measures the probability of a random pairs of points havinng distances less than [math]\displaystyle{ r }[/math]. Then the estimate of [math]\displaystyle{ K }[/math] is obtained by using the following formula (known as the Scale-dependent Correlation Dimension of [math]\displaystyle{ X=(x_{1},x_{2},...,x_{n}) }[/math]):
[math]\displaystyle{ \hat{D}_{corr}(r_{1},r_{2})=\frac{log(C_{n}(r_{1}))-log(C_{n}(r_{2}))}{log(r_{1})-log(r_{2})} }[/math]
When [math]\displaystyle{ r_{1} }[/math] and [math]\displaystyle{ r_{2} }[/math] are selected such that they cover the biggest range of graph at which [math]\displaystyle{ C_{n}(r) }[/math] is linear, GP gives the best estimate. Another important point to consider is that [math]\displaystyle{ \widehat{K} }[/math] the obtained GP algorithm based on finite sample points is a Biased estimate.
The reason why the above formula works can be explained as follows: if the intrinsic dimensionality is 1, the number of points within a (1-dim) sphere around a given point would be proportional to [math]\displaystyle{ r }[/math]. If the intrinsic dimensionality is 2 and the points are (at least locally) distributed on a plane, then the number of points within a (2-dim) sphere around a given point would be proportional to [math]\displaystyle{ \pi r^2 }[/math], i.e., the area of the corresponding circle. Similarly in the case of a 3-dim sphere, we will have proportionality to [math]\displaystyle{ 4/3 \pi r^3 }[/math], and so on. So if we take logarithm of this function, we expect the number of intrinsic dimensionality to be reflected in the slope of the resulting function, as implied by the the formula above.
Upper and Lower Bound for estimator of [math]\displaystyle{ K }[/math]
Baraniuk and Wakin (2007) showed that if the number of random projection [math]\displaystyle{ (M) }[/math] is large, we can be sure that the projection of a smooth manifold into lower dimensional space will be a near-isometric embedding. [math]\displaystyle{ M }[/math] should have linear relation with [math]\displaystyle{ K }[/math] and Logarithmic relationship with [math]\displaystyle{ N }[/math] described by
[math]\displaystyle{ M=c K log\left( N \right) }[/math]
Remember that, since random mapping almost preserves metric structure, we need to estimate the ID of the projected data.
Chinmay Hedg and his colleagues (2007) showed that under some conditions, for random orthoprojector [math]\displaystyle{ R }[/math] (consists of [math]\displaystyle{ M }[/math] orthogonalized vectors of length [math]\displaystyle{ N }[/math]) and sequence of sample [math]\displaystyle{ X=\left\{x_{1},x_{2},...\right\} }[/math], with probability [math]\displaystyle{ 1-\rho }[/math]
[math]\displaystyle{ (1-\delta)\hat{K}\leq \hat{K}_{R}\leq (1+\delta)\hat{K} }[/math]
for fix [math]\displaystyle{ 0 \lt \delta \lt 1 }[/math] and [math]\displaystyle{ 0 \lt \rho \lt 1 }[/math]
Lower Bound for the number of Random Projections
We can also find the minimum number of projections needed such that, the difference between residuals obtained from applying Isomap on projected data and original data does not exceed an arbitary value.
Let [math]\displaystyle{ \Gamma=max_{1\leq i,j\leq n}d_{iso}(x_{i},x_{j}) }[/math] and call it Diameter of data set [math]\displaystyle{ X=\left\{x_{1},x_{2},...,x_{n}\right\} }[/math] where [math]\displaystyle{ d_{iso} \left(x_{i},x_{j}\right) }[/math] is the Isomap estimate of geodesic distance; also let [math]\displaystyle{ L }[/math] and [math]\displaystyle{ L_{R} }[/math] be the residuals obtained from Isomap generated [math]\displaystyle{ K }[/math]-dimentional embeding of [math]\displaystyle{ X }[/math] and its progection [math]\displaystyle{ RX }[/math], respectively. then we have,
[math]\displaystyle{ L_{R}\lt L+C \left(n\right) \Gamma^{2}\epsilon }[/math]
in which [math]\displaystyle{ C(n) }[/math] is a function of the number of sample points.
practical algorithm to determine [math]\displaystyle{ K }[/math] and [math]\displaystyle{ M }[/math]
The above theorems are not able to give us the estimates without some prior information ( about the volume and condition of manifold), hence they are called Theoretical Theorems, But with the help of ML-RP algorithm we can make achieve this goal.
let [math]\displaystyle{ M=1 }[/math] and select a random vector for [math]\displaystyle{ R }[/math]
While residual variance [math]\displaystyle{ \gt \delta }[/math] do
[math]\displaystyle{ (i) }[/math] for [math]\displaystyle{ X=\left\{x_{1},x_{2},...,x_{n}\right\} }[/math] estimate [math]\displaystyle{ K }[/math] using GP algorithm.
[math]\displaystyle{ (ii) }[/math] Use Isomap to produce an embedding in to [math]\displaystyle{ \hat{K} }[/math]-dimensional space.
[math]\displaystyle{ (iii) }[/math] let [math]\displaystyle{ M=M+1 }[/math] and add one row to [math]\displaystyle{ R }[/math].
EndWhile
Print [math]\displaystyle{ M }[/math] and [math]\displaystyle{ \hat{K} }[/math]
Where ML-RP is applicable?
Compressive Sensing (CS) has come to focus in recent years. Think of a situation in which a huge number of low-power devices which are not expensive and capture, store, and transmit very small number of measurements of high-dimensional data. We can apply ML-RP in this scenario.
ML-RP also provides a simple solution to the manifold learning problem in situations where the bottleneck lies in the transmission of the data to the central processing node. The algorithm ensures that with minimum transmitted amount of information, we can perform effective manifold learning. Since with high probability the metric structure of the projected dataset upon termination of MLRP closely resembles that of the original dataset, ML-RP can be regarded as a new adaptive algorithm for finding an efficient, reduced representation of data of very large dimension.
Applications
While the main goal of dimensionality reduction methods is to preserve as much information as possible from the higher dimension to lower dimensional space, it is also important to consider the computational complexity of the algorithm. Random projections preserves the similarity between the data vectors when the data is projected in fewer dimensions and the projections can also be computed faster.
In [1] <ref> Ella Bingham and Heikki Mannila:Random projection in dimensionality reduction: Applications to image and text data. </ref> , authors applied random projections technique of dimensonality reduction to image (both, noisy and noiseless) and text data and concluded that the random lower dimension subspace yields results comparable to conventional dimensionality reduction method like PCA, but the computation time is significantly reduced. They also demonstarted that using a sparse random matrix leads to a further savings in computational complexity. The benefit of random projections is applicable only in applications where the distance between the points in the higher dimension have some meaning but if the distances are themselves suspect, then there is no point in preserving them in lower dimensional space. They provide an example: "In a Euclidean space, every dimension is equally important and independent of the others, whereas e.g. in a process monitoring application, some measured quantities (that is, dimensions) might be closely related to others, and the interpoint distances do not necessarily bear a clear meaning."
Random projections do not suffer from the curse of dimensionality.
Random projections also have application in the area of signal processing, where the device can perform tasks directly on random projections and thereby save storage and processing costs.
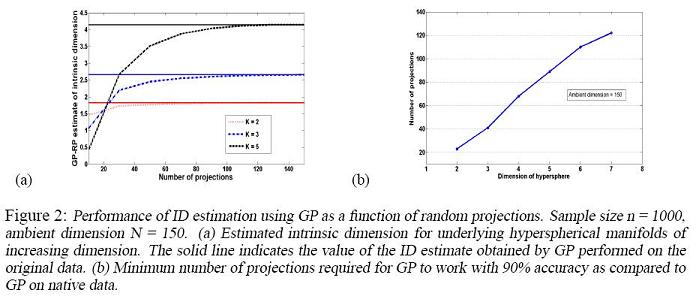
Experimental Results
Convergence of Random Projections GP to conventional GP
Given a data set, the conventional GP algorithm gives an estimation of its intrinsic dimension (ID), which we denote by [math]\displaystyle{ EID }[/math]. In Random Projections GP, ID estimations, which we denote by [math]\displaystyle{ EID_M }[/math], are obtained by running the GP algorithm on [math]\displaystyle{ M }[/math] random projections of the original data set. Theorem 3.1 in the paper essentially shows that [math]\displaystyle{ EID_M }[/math] converges to [math]\displaystyle{ EID }[/math] when [math]\displaystyle{ M }[/math] is sufficiently large. Section 5 of the paper illustrates the convergence using a synthesized data set.
The data set is obtained from drawing [math]\displaystyle{ n=1000 }[/math] samples from uniform distributions supported on K-dimensional hyper-spheres embedded in an ambient space of dimension [math]\displaystyle{ N=150 }[/math], where [math]\displaystyle{ K\lt \lt N }[/math]. The paper shows the result for values of K between 2 and 7.
In the figure on the left, the solid lines correspond to the [math]\displaystyle{ EID }[/math] for different K and the dashed lines correspond to [math]\displaystyle{ EID_M }[/math]. As is obvious from the figure, [math]\displaystyle{ EID_M }[/math] converges to [math]\displaystyle{ EID }[/math] as M gets larger.
In the figure on the right, the minimum number of projections M required to obtain a 90% accurate [math]\displaystyle{ EID_M }[/math] approximation of [math]\displaystyle{ EID }[/math] is plotted against K, the real intrinsic dimension. Note the linear relationship, which is predicted by Theorem 3.1.
References
<references/>