overfeat: integrated recognition, localization and detection using convolutional networks
Introduction
Recognizing the category of the dominant object in an image is a task to which Convolutional Networks (ConvNets) have been applied for many years. ConvNets have advanced the state of the art on large datasets such as 1000-category ImageNet <ref name=DeJ> Deng, Jia, et al "ImageNet: A Large-Scale Hierarchical Image Database." in CVPR09, (2009). </ref>.
Many image datasets include images with a roughly centered object that fills much of the image. Yet, objects of interest sometimes vary significantly in size and position within the image.
The first idea in addressing this is to apply a ConvNet at multiple locations in the image, in a sliding window fashion, and over multiple scales <ref name=MaO> Matan, Ofer, et al "IReading handwritten digits: A zip code recognition system." in IEEE Computer, (1992). </ref> <ref name=NoS> Nowlan, Steven, et al "A convolutional neural network hand tracker." in IEEE Computer, (1995). </ref>. Even with this, however, many viewing windows may contain a perfectly identifiable portion of the object (say, the head of a dog), but not the entire object, nor even the center of the object. This leads to decent classification but poor localization and detection.
The second idea is to train the system to not only produce a distribution over categories for each window, but also to produce a prediction of the location and size of the bounding box containing the object relative to the window.
The third idea is to accumulate the evidence for each category at each location and size.
This research shows that training a convolutional network that simultaneously classifies, locates and detects objects in images can boost the classification, detection and localization accuracy of all tasks. The paper proposes a new integrated approach to object detection, recognition, and localization with a single ConvNet. A novel method for localization and detection by accumulating predicted bounding boxes is also introduced. We suggest that by combining many localization predictions, detection can be performed without training on background samples and that it is possible to avoid the time-consuming and complicated bootstrapping training passes. Not training on background also lets the network focus solely on positive classes for higher accuracy.
Vision Tasks
This research explores three computer vision tasks in increasing order of difficulty:
(i) classification, (ii) localization, and (iii) detection.
Each image is assigned a single label corresponding to the main object in the image. Five guesses are allowed to find the correct answer (because images can also contain multiple unlabeled objects). After classifying five objects in the image, a bounding box for each classified object is returned. The predicted box must match the groundtruth by at least 50% (using the PASCAL criterion of union over intersection), as well as be labeled with the correct class.
Images from 2013 ImageNet Large Scale Visual Recognition Challenge (ILSVRC2013) is used for this research. The detection task differs from localization in that there can be any number of objects in each image (including zero), and false positives are penalized by the mean average precision measure. Figure 1 illustrates the higher difficulty of the detection process.

Classification
During the train phase, this model uses the same fixed input size approach proposed by Krizhevsky et al <ref name=KrA> Krizhevsky, Alex, et al "ImageNet Classification with Deep Convolutional Neural Networks." in NIPS (2012). </ref>. This model maximizes the multinomial logistic regression objective, which is equivalent to maximizing the average across training cases of the log-probability of the correct label under the prediction distribution.As depicted in Figure 2, this network contains eight layers with weights; the first five are convolutional and the remaining three are fully-connected. The output of the last fully-connected layer is fed to a 1000-way softmax which produces a distribution over the 1000 class labels. This network maximizes the multinomial logistic regression objective, which is equivalent to maximizing the average across training cases of the log-probability of the correct label under the prediction distribution.
Each image is downsampled so that the smallest dimension is 256 pixels. Then five random crops (and their horizontal flips) of size 221x221 pixels are extracted and presented to the network in mini-batches of size 128. The weights in the network are initialized randomly. They are then updated by stochastic gradient descent. Overfitting can be reduced by using “DropOut” <ref name=HiG> Hinton, Geoffrey, et al "Improving neural networks by preventing co-adaptation of feature detectors." arXiv:1207.0580, (2012). </ref> to prevent complex co-adaptations on the training data. On each presentation of each training case, each hidden unit is randomly omitted from the network with a probability of 0.5, so a hidden unit cannot rely on other hidden units being present. DropOut is employed on the fully connected layers (6th and 7th) in the classifier. For training phase, multiple GPUs are used to increase the computation speed.

For test phase, the entire image is explored by densely running the network at each location and at multiple scales. This approach yields significantly more views for voting, which increases robustness while remaining efficient. For resolution augmentation, 6 scales of input are used which result in unpooled layer 5 maps of varying resolution. These are then pooled and presented to the classifier using the following procedure,
(a). For a single image, at a given scale, we start with the unpooled layer 5 feature maps.
(b). Each of unpooled maps undergoes a 3x3 max pooling operation (non-overlapping regions), repeated 3x3 times for [math]\displaystyle{ (\Delta x,\Delta y) }[/math] pixel offsets of {0, 1, 2}.
(c). This produces a set of pooled feature maps, replicated (3x3) times for different [math]\displaystyle{ (\Delta x,\Delta y) }[/math] combinations.
(d). The classifier (layers 6,7,8) has a fixed input size of 5x5 and produces a C-dimensional output vector for each location within the pooled maps. The classifier is applied in sliding window fashion to the pooled maps, yielding C-dimensional output maps (for a given [math]\displaystyle{ (\Delta x,\Delta y) }[/math] combination).
(e). The output maps for different [math]\displaystyle{ (\Delta x,\Delta y) }[/math] combinations are reshaped into a single 3D output map (two spatial dimensions x C classes).
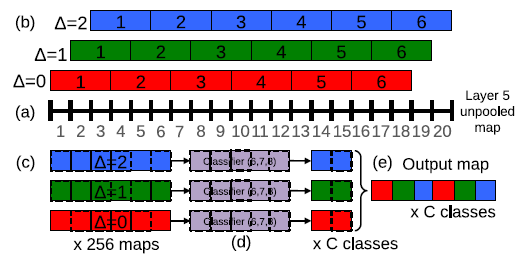
These operations can be viewed as shifting the classifier’s viewing window by 1 pixel through pooling layers without subsampling and using skip-kernels in the following layer (where values in the neighborhood are non-adjacent).
The procedure above is repeated for the horizontally flipped version of each image. The final classification is produced by (I) Taking the spatial max for each class, at each scale and flip. (II) Averaging the resulting C-dimensional vectors from different scales and flip. (III) Taking the top-1 or top-5 elements (depending on the evaluation criterion) from the mean class vector.
The approach described above, with 6 scales, achieves a top-5 error rate of 13.6%. As might be expected, using fewer scales hurts performance: the singlescale model is worse with 16.97% top-5 error. The fine stride technique illustrated in Figure 3 brings a relatively small improvement in the single-scale method, but is also of importance for the multi-scale gains shown here.
Localization
For localization, the classification-trained network is modified. to do so, classifier layers are replaced by a regression network and then trained to predict object bounding boxes at each spatial location and scale. Then regression predictions are combined together, along with the classification results at each location.
Classifier and regressor networks are simultaneously run together across all locations and scales. The output of the final softmax layer for a class c at each location provides a score of confidence that an object of class c is present in the corresponding field of view. So, a confidence can be assigned to each bounding box.
The regression network takes the pooled feature maps from layer 5 as input and the final output layer has 4 units which specify the coordinates for the bounding box edges. The regression network is trained using an l2 loss between the predicted and true bounding box for each example. The final regressor layer is class-specific, having 1000 different versions, one for each class.
The individual predictions are combined via a greedy merge strategy applied to the regressor bounding boxes, using the following algorithm:
(a) Assign to Cs the set of classes in the top k for each scale s [math]\displaystyle{ \in }[/math] 1 . . . 6, found by taking the maximum detection class outputs across spatial locations for that scale.
(b) Assign to Bs the set of bounding boxes predicted by the regressor network for each class in Cs, across all spatial locations at scale s.
(c) Assign [math]\displaystyle{ B \leftarrow \cup _{s} B_{s} }[/math]
(d) Repeat merging until done.
(e) [math]\displaystyle{ (b_{1}^*,b_{2}^*) = argmin_{b_{1} \neq b_{2} \in B} MatchScore (b_{1},b_{2}) }[/math]
(f) If [math]\displaystyle{ MatchScore (b_{1}^*,b_{2}^*)\gt t }[/math] , stop.
(g) Otherwise, set [math]\displaystyle{ B \leftarrow B \backslash (b_{1}^*,b_{2}^*) \cup BoxMerge (b_{1}^*,b_{2}^*) }[/math]
In the above, we compute [math]\displaystyle{ MatchScore }[/math] using the sum of the distance between centers of the two bounding boxes and the intersection area of the boxes. [math]\displaystyle{ BoxMerge }[/math] computes the average of the bounding boxes’ coordinates. The final prediction is given by taking the merged bounding boxes with maximum class scores. This is computed by cumulatively adding the detection class outputs associated with the input windows from which each bounding box was predicted.
This network was applied to the Imagenet 2012 validation set and 2013 localization competition. Localization criterion specified for these competitions was applied to the method. This method is the winner of the 2013 competition with 29.9%.error.
Detection
Detection training is similar to classification training but in a spatial manner. Multiple locations of an image may be trained simultaneously. Since the model is convolutional, all weights are shared among all locations. The main difference with the localization is the necessity to predict a background class when no object is present. Traditionally, negative examples are initially taken at random for training. Then the most offending negative errors are added to the training set in bootstrapping passes. Independent bootstrapping passes render training complicated and risk potential mismatches between the negative examples collection and training times. Additionally, the size of bootstrapping passes needs to be tuned to make sure training does not overfit on a small set. To circumvent all these problems, we perform negative training on the fly, by selecting a few interesting negative examples per image such as random ones or most offending ones. This approach is more computationally expensive but renders the procedure much simpler. And since the feature extraction is initially trained with the classification task, the detection fine-tuning is not as long anyway.
This detection system ranked 3rd with 19.4% mean average precision (mAP) at ILSVRC 2013. In post competition work, with a few modifications, this method achieved a new state of the art with 24.3% mAP. This technique speeds up inference and substantially reduces the number of potential false positives.
Conclusion
This researched presented a multi-scale, sliding window approach that can be used for classification, localization, and detection. This method currently ranks 4th in classification, 1st in localization and 1st in detection at 2013 ILSVRC competition, which proves that ConvNets can be effectively used for detection and localization tasks. The scheme proved here involves substantial modifications to networks designed for classification, but clearly demonstrate that ConvNets are capable of these more challenging tasks. This localization approach won the 2013 ILSVRC competition and significantly outperformed all 2012 and 2013 approaches. The detection model was among the top performers during the competition and ranks first in post-competition results. This research presented an integrated pipeline that can perform different tasks while sharing a common feature extraction base, entirely learned directly from the pixels.
Discussion
This approach might still be improved in several ways:
(I) For localization, back-propping is not used through the whole network; doing so is likely to improve performance.
(II) l2 loss is used, rather than directly optimizing the intersection-over-union (IOU) criterion on which performance is measured. Swapping the loss to this should be possible since IOU is still differentiable, provided there is some overlap.
(III) Alternate parameterizations of the bounding box may help to decorrelate the outputs, which will aid network training.
References
<references />