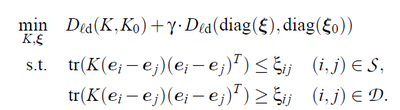metric and Kernel Learning Using a Linear Transformation: Difference between revisions
m (Conversion script moved page Metric and Kernel Learning Using a Linear Transformation to metric and Kernel Learning Using a Linear Transformation: Converting page titles to lowercase) |
|
(No difference)
| |
Latest revision as of 09:46, 30 August 2017
Previous work
Metric Learning: Mahalanbobis distance learning paradigm has been utilized in most of existing work in metric learning. Mahalanbobis distance learning can deal with out-of-sample points and avoid overfitting. However, it is computationally expensive since its number of parameters grows quadratically with the dimensionality and it requires eigenvalue decomposition or semi-definite programming, which is at least cubit time in dimensionality of the data.
Kernel Learning: Parametric approaches of kernel learning restrict the kernel function as specific form and learn the parameters of these specific formed kernel functions. However, they lack flexibility, require non-convex optimization and are limited in supervised learning. Non-parametric kernel learning methods model geometric structure in the data explicityly but most of them are unable to generalize to new added data points as only implicit non-linear transformation is given.
Introduction
The motivation of the papers is to combine the advantages of Mahalanobis distance learning and kernel learning. The paper shows metric learning with linear transformations is equivalent to learning a linear transformation kernel. They use LogDet divergence to formulate a metric learning problem. The LogDet divergence can make the optimization simpler and have a precedence in optimization and statistics. They claim that their algorithm is scalable to large data sets and allow learning of a linear transformation in the kernel space so that it can handle out-of-sample extensions. Also, even though the matrix to be learned may be infinite-dimensional, it can be fully represented in terms of the constrained data points.
LogDet Divergence Based Metric Learning
The original Mahalanobis distance metric is as follows:
[math]\displaystyle{ \,d_W(x_i,x_j)=(x_i-x_j)^TW(x_i-x_j) }[/math] which can be viewed as a Euclidean distance of the linear transformation of the input data. However, in order to deal with the nonlinear case, we use a nonlinear mapping of the data points:
[math]\displaystyle{ \,d_W(\phi(x_i),\phi(x_j))=(\phi(x_i)-\phi(x_j))^TW(\phi(x_i)-\phi(x_j)) }[/math]
then the problem is equivalent to learning a parameterized kernel function [math]\displaystyle{ \,\kappa(x,y)=\phi(x)^{T}W\phi(y) }[/math]
The main challenge is the computation of W. The paper uses the LogDet divergence. The LogDet divergence between two PSD matrices W and [math]\displaystyle{ W_0\in\Re^{d \times d} }[/math] is defined as:
[math]\displaystyle{ D_ld(W,W_0)=tr(WW_0^{-1})-logdet(WW_0^{-1})-d }[/math]
Given the similarity constrains S and dissimilarity constrains D, the following problem is proposed in [1]:
A kernel learning problem which is very similar to the above metric learning problem can be formulated as follows [2]:
The paper proves that there are connections between the optimal solutions of the above two problems. Suppose the optimal learned kernel is K* and the optimal learned Mahalanobis matrix is W*, they are related as follows:
The identical matrix I can be generalized to any arbitrary matrix W0 and the theory holds. To compute the out-of-sample extension, we can represent the inner product of the points after linear transformation by the inner product of the points before transformation:
Thus solving a metric learning problem in kernel space can be transferred to solving a kernel learning problem. Also the slack variables are introduced to deal with the infeasible case:
The Bregman projections technique is used to solve the above problem as discussed in [2]. An iterative method with rank-one update in each iteration is proposed:
[math]\displaystyle{ K \leftarrow K + \beta K(e_i-e_j)(e_i-e_j)^TK }[/math]
The algorithm is as follows:
File:alg metric kernel learning.png
The paper also proposes a heuristic to deal with large data sets. instead of learning Mahalanobis distance or kernel as a full [math]\displaystyle{ d \times d }[/math] (or [math]\displaystyle{ n \times n }[/math]) matrix with [math]\displaystyle{ O(min(n,d)^2) }[/math] parameters, they use compressed representations and parameterize matrices by only [math]\displaystyle{ O(min(n,d)) }[/math] values.
Kernel Learning with Other Convex Loss Functions and Special cases
The authors show that their kernel matrix learning problem is equivalent to learning a linear transformation kernel function with a specific loss function. Considering the size of kernel matrices and parameter matrices will grow quadratically with the number of data points, they reduce the parameters to learn by introducing an additional constraint, similar to the special case of the LogDet divergence.
The authors also considered several cases which are of general interst, including, the von Neumann divergence, the squared Frobenius norm and semidefinite programming. And for each case the authors derived the required optimization problem and provided the algorithms.
Experiments
The proposed method is compared as other metric learning algorithms such as MCML and LMNN on benchmark data, high-dimensional vision, and text classification problems as well as a semi-supervised kernel dimensionality reduction problems (Figure 1-3).
The results show their method outperforms other state-of-the-art methods.
Conclusions
1. LogDet divergence is useful for learning a linear transformation over high-dimensional data because it can be generalized easily in kernel space;
2. The learned metric can be restricted to small dimensional basis efficiently to enable scalability to large data sets with high-dimensional feature space;
3. It can be proved that many loss functions can lead to kernel function learning even though solving them is much difficult than solving the LogDet function;
4. Many existing Mahalanobis metric learning methods can be kernelized by using the proposed kernel learning formulation.
5. Possible future works include proposing an online version of the algorithm; or finding multiple local metrics similar to the large margin metric learning methods.
Reference
[1] Davis, Jason V., et al. "Information-theoretic metric learning." Proceedings of the 24th international conference on Machine learning. ACM, 2007.
[2] Kulis, Brian, M¨¢ty¨¢s A. Sustik, and Inderjit S. Dhillon. "Low-rank kernel learning with Bregman matrix divergences." The Journal of Machine Learning Research 10 (2009): 341-376.