meProp: Sparsified Back Propagation for Accelerated Deep Learning with Reduced Overfitting: Difference between revisions

From statwiki
Jump to navigation Jump to search
No edit summary
 
(233 intermediate revisions by 23 users not shown)
Line 1: Line 1:
==Introduction==
=Introduction=


A simple and effective technique for learning in neural networks has been introduced. Forward computation has been computed as it is typically computed. However. in back-propagation step only the top k elements (in magnitude) are retained for the computation of model parameters. Since only a small subset of the weight matrix is modified so it leads to a linear reduction in the computational cost. The results of the experiments suggest that accuracy is improved rather than being degraded. The name given to the proposed technique is minimal effort back propagation method (meProp).
The backpropagation step in neural network training entails high computational cost since each iteration requires calculation of full gradient vectors and matrices and subsequent update of all model parameters.
The main idea of the paper is to find only a small but critical subset of the gradient information and in each learning step, update only this minimal subset of the parameters. This leads to sparsified gradients because only highly relevant parameters are updated and rest remain untouched.
[[File:20.png|right|650px]]


In the process of neural network training, back propagation step entails the high computational cost because for each iteration it needs to compute full gradients and update all model parameters.
The main idea of the paper is to find only the most critical and small subset of the gradient information and in each learning step update only this minimal subset of the parameters. This leads to sparsified gradients because only highly relevant parameters are updated and rest remain untouched.


Two important questions:
A simple and effective technique for neural networks learning is introduced in the current paper. The main technique entails a modification to the vanilla backpropagation algorithm. The idea is that after a forward pass has been carried out in the usual fashion, we retain only a subset of the full gradient for computation of model parameters. More precisely, a simple quantization technique is employed to sparsify the gradient vectors, viz., the entries of the first gradient in a backpropagation step are set to zero unless they reach a specified size threshold. The rest of the gradients (the ones with respect to the weights and biases of the neural network) are computed using the chain rule in the typical way using the sparsified gradient obtained from the top layer. Since only a small subset of the weight matrix is modified, we obtain a linear reduction in the computational cost. The experimental results presented in the paper suggest that accuracy is improved rather than being degraded. The name given to the proposed technique is minimal effort back propagation method (meProp).
Fig. 1 shows an abstract view of the proposed approach.


1) In the process of stochastic learning how to find that highly relevant subset of parameters from the current sample.


Solution to this question is given by Top-k search method to identify the most imp. parameters. After experiments with this solution the results demonstrate that we only update 1–4% of the weights at each back propagation pass which does not result in a larger number of training iterations.
'''Two important questions:'''


2) Whether this selection of small subset of model parameters hurt the accuracy?
1) In the process of stochastic learning, how do we find a highly relevant subset of parameters from the current sample?


The results demonstrate that rather than reduction, this sparsification actually improves the accuracy.
One solution to this question is given by Top-$k$ search method to identify the most important parameters. Experimental results suggest that if we use this technique, then we can only update 1–4% of the weights at each back propagation pass and this does not result in a larger number of training iterations.  
The inferred reason is that it is probably because the minimal effort update does not modify weakly relevant para-meters in each update, which makes the overfitting less likely, similar to the dropout effect.  


The authors demonstrate the proposed approach using deep learning approaches (like LSTM, MLP), optimization approaches (like Adam and Adagrad) and tasks like NLP and Image Recognition.  
Another likely solution I can think of is the method in the paper: [http://papers.nips.cc/paper/6372-learning-the-number-of-neurons-in-deep-networks.pdf Learning the Number of Neurons in Deep Networks]. We can use the group sparsity regularizer to identify the neurons that have many nonzero parameters, which are considered highly relevant parameters.


==Black-box Variational Inference==
2) Does this process of selecting a small subset of model parameters hurt accuracy?


The basic premise we start from is that we have a latent variable model $p_{\theta}(x, h)$, often called the $\textbf{generative model}$ in the literature, with $x$ the observed variables and $h$ the hidden variables, and we wish to learn the parameters $\theta$. Hence, in variational inference, we are approximating the posterior $p_{\theta}(x, h)$ which has a variational distribution $q_{\phi}(h\mid x)$ with a motive to minimize the Kullback-Leibler divergence. Hence, we assume we are in a situation where the usual strategy of inference by maximum likelihood estimation is infeasible due to intractability of marginalization of the hidden variables. This assumption often holds in real-world applications since generative models for real phenomena are extremely difficult or impossible to integrate. Additionally, we would like to be able to compute the posterior $p(h\mid x)$ over hidden variables and, by Bayes' rule, this requires computation of the marginal distribution $p_{\theta}(x)$.  
The results demonstrate that rather than reduce, this sparsification actually improves the accuracy in most settings.
This result, while somewhat surprising, is attributed to a dropout-like effect which works to prevent overfitting. Because the minimal effort update does not modify any parameters which are weakly relevant, it seems sensible that this would help avoid overfitting the data.


The variational inference approach entails positing a parametric family $q_{\phi}(h\mid x)$, also called the $\textbf{inference model}$, of distributions and introducing new learning parameters $\phi$ which obtain as solutions to an optimization problem. More precisely,  we minimize the KL divergence between the true posterior and the approximate posterior. However, we can think of a slightly indirect approach. We can find a generic lower bound for the log-likelihood $\log p_{\theta}(x)$ and optimize for this lower bound. Observe that, for any parametrized distribution $q_{\phi}(h\mid x)$, we have
The authors demonstrate the proposed approach using deep learning approaches (like LSTM, MLP), optimization approaches (like Adam and Adagrad) and tasks like NLP and Image Recognition.
\begin{align*}
\log p_{\theta}(x) &= \log\int_{h}p_{\theta}(x,h) \\
&= \log\int_{h}p_{\theta}(x,h)\frac{q_{\phi}(h\mid x)}{q_{\phi}(h\mid x)} \\
&= \log\int_{h}\frac{p_{\theta}(x,h)}{q_{\phi}(h\mid x)}q_{\phi}(h\mid x) \\
&= \log\mathbb{E}_{q}\left[\frac{p_{\theta}(x,h)}{q_{\phi}(h\mid x)}\right] \\
&\geq \mathbb{E}_{q}\left[\log\frac{p_{\theta}(x,h)}{q_{\phi}(h\mid x)}\right]
\end{align*}
 
Here we are trying to minimize the Kullback-Leibler which is achieved by maximizing the evidence lower bound:
 
\begin{align*}
\log p_{\theta}(x) &= \mathbb{E}_{q}\left[\log p_{\theta}(x,h) - \log q_{\phi}(h\mid x)\right] \\
&:= \mathcal{L}(x, \theta, \phi),
\end{align*}


where the inequality is an application of Jensen's inequality for the logarithm function and $\mathcal{L}(x,\theta,\phi)$ is known as the $\textbf{evidence lower bound (ELBO)}$. Clearly, if we iteratively choose values for $\theta$ and $\phi$ such that $\mathcal{L}(x,\theta,\phi)$ increases, then we will have found values for $\theta$ such that the log-likelihood $\log p_{\theta}(x)$ is non-decreasing (that is, there is no guarantee that a value for $\theta$ which increases $\mathcal{L}(x,\theta,\phi)$ will also increase $\log p_{\theta}(x)$ but there \textit{is} a guarantee that $\log p_{\theta}(x)$ will not decrease). The natural search strategy now is to use stochastic gradient ascent on $\mathcal{L}(x,\theta,\phi)$. This requires the derivatives $\nabla_{\theta}\mathcal{L}(x,\theta,\phi)$ and $\nabla_{\phi}\mathcal{L}(x,\theta,\phi)$.
=Related Work=


Before moving on, we note that there are alternative ways of expressing the ELBO which can either provide insights or aid us in further calculations. For one alternative form, note that we can massage the ELBO like so.
Some of the notable related work to this paper are as follows:
\begin{align*}
\mathcal{L}(x, \theta, \phi) = & \mathbb{E}_{q} \left[ \log p_{\theta}(x, h) - \log q_{\phi}(h \mid x) \right] \\
= & \mathbb{E}_{q} \left[ \log p_{\theta}(h \mid x) p(x) - \log q_{\phi}(h \mid x) \right] \\
= & \mathbb{E}_{q} \left[ \log p_{\theta}(h \mid x) + \log p(x) - \log q_{\phi}(h \mid x) \right] \\
= & \mathbb{E}_{q} \left[ \log p(x) - \log q_{\phi}(h \mid x) + \log p_{\theta}(h \mid x) \right] \\
= & \mathbb{E}_{q} \left[ \log p(x) \right] - \mathbb{E}_{q} \left[ \log q_{\phi}(h \mid x) - \log p_{\theta}(h \mid x) \right] \\
= & \log p(x) - \mathrm{KL}\left[ q_{\phi}(h \mid x) || p(h \mid x) \right].
\end{align*}
The last expression has a very simple interpretation: maximizing $\mathcal{L}(x, \theta, \phi)$ is equivalent to minimizing the KL divergence between the approximate posterior $q_{\phi}$ and the actual posterior $p_{\theta}(h \mid x)$. In fact, we can rewrite the above equation as a ``conservation law"
\[
\mathcal{L}(x, \theta, \phi) + \mathrm{KL} \left[ q_{\phi}(h \mid x) || p(h \mid x) \right] = \log p(x).
\]
On the other hand, we can also do
\begin{align*}
\mathcal{L}(x, \theta, \phi) = & \mathbb{E}_{q} \left[ \log p_{\theta}(x, h) - \log q_{\phi}(h \mid x) \right] \\
= & \mathbb{E}_{q} \left[ \log p_{\theta}(x \mid h) p_{\theta}(h) - \log q_{\phi}(h \mid x) \right] \\
= & \mathbb{E}_{q} \left[ \log p_{\theta}(x \mid h) + \log p_{\theta}(h) - \log q_{\phi}(h \mid x) \right] \\
= & \mathbb{E}_{q} \left[ \log p_{\theta}(x \mid h) - \log q_{\phi}(h \mid x) + \log p_{\theta}(h) \right] \\
= & \mathbb{E}_{q} \left[ \log p_{\theta}(x \mid h) \right] - \mathrm{KL}\left[ q_{\phi}(h \mid x) || p_{\theta}(h) \right].
\end{align*}
and the hermeneutics here is a bit more interesting. Recall that $q_{\phi}(h \mid x)$ is a distribution we get to choose and choosing a ``good" distribution means choosing something which we believe is faithful to the way observations get encoded or ``compressed" into ``hidden representations". Conversely, $p_{\theta}(x \mid h)$ may be thought as a decoder which unpacks latent ``codes" into observations. Thus, we can think of $\mathbb{E}_{q} \left[ \log p_{\theta}(x \mid h) \right]$ as the expected reconstruction error when we use $q_{\phi}$ as an encoder. The KL term is now interpreted as a regularizer which restricts divergence of the encoder from the prior distribution over latent codes. Note that these remarks simply provide an intuition and even though we use descriptors such as encoder and decoder, there is no \textit{a priori} reason to implement the distributions involved as encoder and decoder networks as in an autoencoder. Indeed, there is nothing preventing us from even letting $q_{\phi}$ compute an overcomplete feature representation $h$ of $x$ (i.e., dimensionality of $h$ is greater than that of $x$).
 
Regardless of which ELBO we use, inference requires the gradients of $\mathcal{L}(x, \theta, \phi)$. Notice that, no matter what, there are expectations with respect to $q_{\phi}$ involved and the presence of these expectations persists into the gradients. As an example, let us compute the gradients with the ELBO written as  
\[
\mathcal{L}(x, \theta, \phi) = \mathbb{E}_{q}\left[\log p_{\theta}(x,h) - \log q_{\phi}(h\mid x)\right].
\]
The gradient with respect to $\theta$ is easy.
\begin{align*}
\nabla_{\theta}\mathcal{L}(x,\theta,\phi) &= \nabla_{\theta}\mathbb{E}_{q}\left[\log p_{\theta}(x,h) - \log q_{\phi}(h\mid x)\right] \\
&= \nabla_{\theta}\mathbb{E}_{q}\left[\log p_{\theta}(x,h)\right] - \nabla_{\theta}\mathbb{E}_{q}\left[\log q_{\phi}(h\mid x)\right] \\
&= \nabla_{\theta}\int_{h}\left[q_{\phi}(h\mid x)\log p_{\theta}(x,h)\right] \\
&= \int_{h}q_{\phi}(h\mid x)\nabla_{\theta}\log p_{\theta}(x,h) \\
&= \mathbb{E}_{q}\left[\nabla_{\theta}\log p_{\theta}(x,h)\right].
\end{align*}
For the derivative with respect to the variational parameters $\phi$, we are going to exploit the identities $$\int_{h}\nabla_{\phi} q_{\phi}(h\mid x)=\nabla_{\phi}\int_{h}q_{\phi}(h\mid x)=\nabla_{\phi}1=0$$ and $$q_{\phi}(h\mid x)\nabla_{\phi}\log q_{\phi}(h\mid x)=\nabla_{\phi}q_{\phi}(h\mid x).$$ Note that the second identity will be used in a ``backwards" direction toward the end of the derivation below. We now have
\begin{align*}
\nabla_{\phi}\mathcal{L}(x, \theta, \phi) &= \nabla_{\phi}\mathbb{E}_{q}\left[\log p_{\theta}(x,h) -\log q_{\phi}(h\mid x)\right] \\
&= \nabla_{\phi}\mathbb{E}_{q}\left[\log p_{\theta}(x,h)\right] - \nabla_{\phi}\mathbb{E}_{q}\left[\log q_{\phi}(h\mid x)\right] \\
&= \nabla_{\phi}\int_{h}q_{\phi}(h\mid x)\log p_{\theta}(x,h) - \nabla_{\phi}\int_{h}q_{\phi}(h\mid x)\log q_{\phi}(h\mid x) \\
&= \int_{h}\log p_{\theta}(x,h)\nabla_{\phi}q_{\phi}(h\mid x) - \int_{h}\nabla_{\phi}q_{\phi}(h\mid x)\log q_{\phi}(h\mid x) \\
&= \int_{h}\log p_{\theta}(x,h)\nabla_{\phi}q_{\phi}(h\mid x) - \int_{h}\left(q_{\phi}(h\mid x)\frac{\nabla_{\phi}q_{\phi}(h\mid x)}{q_{\phi}(h\mid x)} + \log q_{\phi}(h\mid x)\nabla_{\phi}q_{\phi}(h\mid x) \right) \\
&= \int_{h}\log p_{\theta}(x,h)\nabla_{\phi}q_{\phi}(h\mid x) - \int_{h}\left(\nabla_{\phi}q_{\phi}(h\mid x) + \log q_{\phi}(h\mid x)\nabla_{\phi}q_{\phi}(h\mid x) \right) \\
&= \int_{h}\log p_{\theta}(x,h)\nabla_{\phi}q_{\phi}(h\mid x) - \int_{h}\nabla_{\phi}q_{\phi}(h\mid x) - \int_{h}\log q_{\phi}(h\mid x)\nabla_{\phi}q_{\phi}(h\mid x) \\
&= \int_{h}\log p_{\theta}(x,h)\nabla_{\phi}q_{\phi}(h\mid x) - 0 - \int_{h}\log q_{\phi}(h\mid x)\nabla_{\phi}q_{\phi}(h\mid x) \\
&= \int_{h}\left(\log p_{\theta}(x,h)\nabla_{\phi}q_{\phi}(h\mid x) - \log q_{\phi}(h\mid x)\nabla_{\phi}q_{\phi}(h\mid x) \right) \\
&= \int_{h}\left(\log p_{\theta}(x,h) - \log q_{\phi}(h\mid x)\right)\nabla_{\phi}q_{\phi}(h\mid x) \\
&= \int_{h}\left(\log p_{\theta}(x,h) - \log q_{\phi}(h\mid x)\right)q_{\phi}(h\mid x)\nabla_{\phi}\log q_{\phi}(h\mid x) \\
&= \mathbb{E}_{q}\left[\left(\log p_{\theta}(x,h) - \log q_{\phi}(h\mid x)\right)\nabla_{\phi}\log q_{\phi}(h\mid x)\right].
\end{align*}


Observe that everything we have done so far is completely general and independent of any specific modelling assumptions we may have had to make. Indeed, it is the model independence of this approach which led Ranganath et al. <ref name="bbvi"> Rajesh Ranganath, Sean Gerrish and David M. Blei. Black Box Variational Inference. Proceedings of the Seventeenth International Conference on Artificial Intelligence and Statistics, {AISTATS} 2014, Reykjavik, Iceland, April 22-25, 2014</ref> \cite{bbvi} to christen it $\textbf{black-box variational inference}$. The price we pay for such generality is that we have to calculate expectations against the distribution $q_{\phi}$. Broadly speaking, such expectations are intractable integrals for any approximate posterior approaching verisimilitude. However, the notion of $\textbf{normalizing flow}$ represents a technical innovation which allows use of flexible posteriors while maintaining tractability through calculation of expectations against simple distributions (e.g., Gaussians) only.
In 1990, Tollenaere et al.[1] proposed SuperSAB: an adaptive acceleration strategy for error back propagation learning. It is an improvement on SAB (self-adapting back propogation) strategy [7]. SuperSAB avoids taking a step when a change of sign in the weight derivative is discovered. Instead, it decreases the step size until a safe step is discovered (one without a sign change of the weight). They proved that it may converge orders of magnitude faster than the original back propagation algorithm, and is only slightly unstable. In addition, the algorithm is very insensitive to the choice of parameter values and has excellent scaling properties.


The Black-box Variational Inference framework actually can imply the expectation maximization algorithm, which is an iterative method to find maximum likelihood and maximum a posteriori in the statistical model with latent variables. It has been successful implementation on the problems like Gaussian mixture models.  
In 1993, Riedmilller et al.[2] and Braun proposed an algorithm called RPROP, to overcome the inherent disadvantages of pure gradient-descent, it performed a local adaptation of the weight-updates according to the behavior of the error function. To be more specific, the authors defined an individual update-value for each weight. When the update of a weight is too large (mathematically, the partial derivative of a weight changes its sign), such update-value of this weight will decrease. Otherwise, it'll increase. After the process of adapting update-values is finished, the weight-update process is carried out as follows: when the partial derivative of the error function with respect to a specific weight is positive, the original weight decreases by its corresponding update-value, otherwise it increases.


Recalling the maximum likelihood is expressed as below.
In 2014, Srivastava et al.[3] proposed dropout. Large networks are also slow to use, making it difficult to deal with overfitting by combining the predictions of many different large neural nets at test time. The key idea is to randomly drop units (along with their connections) from the neural network during training. This prevents units from co-adapting too much.
\[
\mathcal{L}(x,\theta,\phi) = \mathbb{E}_q [\log p_\theta(x \mid h)] - \mathrm{KL}[q_{\phi}(h \mid x) || p(h \mid x)]
\]
As mentioned before, we need to set $q_{\phi_k}(h\mid x) = p_{\theta_k}(h)$ to minimize the KL divergence with a given estimation of $\theta_k$. Then the maximization step is to calculate that
\[
\mathcal{L}(x, \theta,\phi_k) = \mathbb{E}_{q_{\phi_k}} [\log p_{\theta}(x \mid h)]
\]


And $\theta_{k+1}$ is updated in the maximization step as
The work proposed by the authors of meProp method is quite different from the three related works discussed above.
\[
\theta_{k+1} = argmax_{\theta} \mathbb{E}_{q_{\phi_k}}[\log p_{\theta}(x \mid h)]
\]


==Variational Inference using Normalizing Flows==
In 2017, Shazeer et al.[4] presented a Sparsely-Gated Mixture-of-Experts layer (MoE), consisting of up to thousands of feed-forward sub-networks. A trainable gating network determines a sparse combination of these experts to use for each example. They used this approach for the machine translation task and concluded that it gave significantly better results. Their method is limited to a specific set of a mixture of experts however, the meProp method does not have these sort of limitations.


While our main goal is to describe \cite{946paper}, the paper \cite{normalizing_flow} provides the necessary conceptual backdrop for \cite{946paper} and we will now take a detour through some of the points presented in the latter. The main contribution of \cite{normalizing_flow} lies in a novel technique for creating a rich class of approximate posteriors starting from relatively simple ones. This is important since one of the main drawbacks to the variational approach is that it requires assumptions on the form of the approximate posterior $q_{\phi}(h\mid x)$ and practicality often forces us to stick to simple distributions which fail to capture rich, multimodal properties of the true posterior $p(h \mid x)$. The primary technical tool used in \cite{normalizing_flow} to achieve complexity in the approximate posterior is what we earlier referred to as normalizing flow, which entails using a series of invertible functions to transform simple probability densities into more complex densities.  
=Proposed Approach=
[[File:7.png|center|600px]]
The original back propagation computes the "full gradient" for the input vector and the weight matrix. However, in me-Prop, back propagation computes an "approximate gradient" by keeping top-k values of the backward flowed gradient and masking the remaining values to 0. That is, only the top-k elements with the largest absolute values are kept and rest are made 0.


Suppose we have a random variable $h$ with probability density $q(h)$ and that $f:\mathbb{R}^{d}\to\mathbb{R}^{d}$ is an invertible function with inverse $g:\mathbb{R}^{d}\to\mathbb{R}^{d}$. A basic result in probability states that the random variable $h'\colon = f(h)$ has distribution $$q'(h') = q(h)\Bigg\lvert\det\frac{\partial f}{\partial h}\Bigg\rvert^{-1}.$$ Chaining together a (finite) sequence of invertible maps $f_{1},\ldots,f_{K}$ and applying it to the distribution $q_{0}$ of a random variable $h_{0}$ leads to the formula $$q_{K}(h_{K}) = q_{0}(h_{0})\prod\limits^{K}_{k=1}\Bigg\lvert\det\frac{\partial f_{k}}{\partial h_{k-1}}\Bigg\rvert^{-1},$$ where $h_{k}\colon = f_{k}(h_{k-1})$ and $q_{k}$ is the distribution associated to $h_{k}$. We can equivalently rewrite the above equation as $$\log q_{K}(h_{K}) = \log q_{0}(h_{0}) - \sum\limits^{K}_{k=1}\log\Bigg\lvert\det\frac{\partial f_{k}}{\partial h_{k-1}}\Bigg\rvert.$$ So, if we were to start from a simple distribution $q_{0}(h_{0})$, choose a sequence of functions $f_{1},\ldots,f_{K}$ and then \textit{define} $$q_{\phi}(h \mid x)\colon = q_{K}(h_{K}),$$ we can manipulate the ELBO as follows:
Authors describe conversion of the traditional back-propagation to the back-propagation used in meProp with a computation unit with one linear transformation and one non-linear transformation as an example as given by eq. (1) and (2):
\begin{align*}
\begin{align*}
\mathcal{L}(x,\theta,\phi) &= \mathbb{E}_{q}\left[\log p_{\theta}(x,h) - \log q_{\phi}(h\mid x)\right] \\
y &= W x \quad \quad \quad (1)
&= \mathbb{E}_{q_{K}}\left[\log p_{\theta}(x,h) - \log q_{K}(z_{K})\right] \\
\end{align*}
&= \mathbb{E}_{q_{K}}\left[\log p_{\theta}(x,h)\right] - \mathbb{E}_{q_{K}}\left[\log q_{K}(z_{K})\right].
\end{align*}
The reason this is an useful thing to do is the $\textbf{law of the unconscious statistician (LOTUS)}$ as applied to $q_{K} = f_{K}\circ\cdots\circ f_{1}(q_{0})$: $$\mathbb{E}_{q_{K}}\left[s(h_{K})\right] = \mathbb{E}_{q_{0}}\left[s(f_{K}\circ\cdots\circ f_{1}(h_{0}))\right]$$ assuming that $s$ does not depend on $q_{K}$. Hence,
\begin{align*}
\begin{align*}
\mathcal{L}(x,\theta,\phi) &= \mathbb{E}_{q_{K}}\left[\log p_{\theta}(x,h)\right] - \mathbb{E}_{q_{K}}\left[\log q_{K}(z_{K})\right] \\
z &= \sigma (y) \quad \quad \quad (2)
&= \mathbb{E}_{q_{K}}\left[\log p_{\theta}(x,h)\right] - \mathbb{E}_{q_{K}}\left[\log q_{0}(h_{0}) - \sum\limits^{K}_{k=1}\log\Bigg\lvert\det\frac{\partial f_{k}}{\partial h_{k-1}}\Bigg\rvert\right] \\
&= \mathbb{E}_{q_{K}}\left[\log p_{\theta}(x,h)\right] - \mathbb{E}_{q_{K}}\left[\log q_{0}(h_{0})\right] - \mathbb{E}_{q_{K}}\left[\sum\limits^{K}_{k=1}\log\Bigg\lvert\det\frac{\partial f_{k}}{\partial h_{k-1}}\Bigg\rvert\right] \\
&= \mathbb{E}_{q_{0}}\left[\log p_{\theta}(x,h)\right] - \mathbb{E}_{q_{0}}\left[\log q_{0}(h_{0})\right] - \mathbb{E}_{q_{0}}\left[\sum\limits^{K}_{k=1}\log\Bigg\lvert\det\frac{\partial f_{k}}{\partial h_{k-1}}\Bigg\rvert\right]
\end{align*}
\end{align*}
and we are only computing expectations with respect to the simple distribution $q_{0}$. The latter expression for ELBO is called the $\textbf{flow-based free energy bound}$ in \cite{normalizing_flow}. Note that $\theta$ has apparently disappeared in the final expression even though it is still present in $\mathcal{L}(x,\theta,\phi)$. This is an illusion: the parameters $\phi$ are associated to $q_{\phi}(h\mid x) = q_{K}(h_{K})$ and $q_{K}(h_{K})$ depends on the quantities $q_{0}(h_{0})$ and $\frac{\partial f_{k}}{\partial h_{k-1}}$. Thus, $\phi$ now encapsulates the defining parameters of $q_{0}$ and the $f_{k}$.  
where $W \in R_{n \times m}$, $x \in R_m$, $y \in R_n$, $z \in R_n$, $m$ is the dimension of the input vector, $n$ is the dimension of the output vector, and $\sigma$ is a non-linear function (e.g., ReLU, tanh,
 
and sigmoid). During back propagation, we need to compute the gradient of the parameter matrix $W$ and the input vector $x$:
To summarize, we can start with a very simple distribution $q_{0}$ against which expectations are easy to calculate and if we can cleverly choose a series of invertible functions $\{f_{k}\}^{K}_{k=1}$ for which it is easy to compute determinants of the Jacobians, we can get a relatively rich approximate posterior $q_{K}$ such that the ELBO and its gradients are tractable. We should now ask: what is a suitable family of functions which can serve as a normalizing flow?
 
==Inverse Autoregressive Flow==


The answer presented by \cite{946paper} to the last question is
\[
\[
f_{k}(h_{k-1}) := \mu_{k} + \sigma_{k} \odot h_{k-1},
\frac{\partial z}{\partial W_{ij}} = \sigma^{'}_{i}x^{T}_{j},\quad i \quad \epsilon \quad [1,n], \quad j \quad \epsilon \quad [1,m] \quad \quad \quad (3)
\]
\]
where $\odot$ means element-wise multiplication, $\mu_{k}$, $\sigma_{k}$ are outputs from an autoregressive neural network with inputs $h_{k-1}$ and an extra constant vector $c$ and we initialize with
 
\[
\[
h_{0} := \mu_{0} + \sigma_{0} \odot \epsilon
\frac{\partial z}{\partial x_{i}} = \sum\limits_j W^{T}_{ij} \sigma^{'}_{j},\quad i \quad \epsilon \quad [1,n], \quad j \quad \epsilon \quad [1,m] \quad \quad \quad (4)
\]
\]
such that $\epsilon \!\sim \mathcal{N}(0, I)$. The authors of \cite{946paper} call this series of functions the \textbf{inverse autoregressive flow}. We will solve the mystery of where this definition comes from later. The important point is that the functional form of $f_{k}$ is parametrized by the outputs of an autoregressive neural network and this implies that the Jacobians
 
Since the proposed meProp keeps only top-k elements based on the magnitude values so eq. (3) and (4) get transformed to (5) and (6), respectively:
 
\[
\[
\frac{\partial \mu_{k}}{\partial h_{k-1}}, \frac{\partial \sigma_{k}}{\partial h_{k-1}}
\frac{\partial z}{\partial W_{ij}} \leftarrow \sigma^{'}_{i}x^{T}_{j}, \quad if \quad i \quad \epsilon \quad \{ t_{1}, t_{2},....., t_{k} \} \quad else \quad 0 \quad \quad (5)
\]
\]
are lower triangular with zeroes on the diagonal (this is not a trivial fact since $\mu_{k}$ and $\sigma_{k}$ are some complicated functions of $h_{k-1}$ -- they are outputs of a neural network which takes $h_{k-1}$ as an input).  Hence, the derivative
 
\[
\[
\frac{\partial f_{k}}{\partial h_{k-1}}
\frac{\partial z}{\partial x_{i}} \leftarrow \sum\limits_j W^{T}_{ij} \sigma^{'}_{j}, \quad if \quad j \quad \epsilon \quad \{ t_{1}, t_{2},....., t_{k} \} \quad else \quad 0 \quad \quad (6)
\]
\]
is a triangular matrix with the entries of $\sigma_{k}$ occupying the diagonal. The determinant of this is obviously just
 
 
 
The original back-propagation computes the gradient of the matrix W and the gradient of the input vector x as shown in eq. (7) and (8), respectively:
 
\[
\[
\prod\limits^{D}_{i=1} \sigma_{k, i},
\frac{\partial L}{\partial W} = \frac{\partial L}{\partial y} . \frac{\partial y}{\partial W} \quad \quad (7)
\]
\]
and it is very cheap to compute. Note also that the approximate posterior that comes out of this normalizing flow is
 
\[
\[
\log q_{K}(h_{K}) = - \sum\limits^{D}_{i=1} \left[ \frac{1}{2} \epsilon_{i}^{2} + \frac{1}{2} \log 2\pi + \sum\limits^{K}_{k=1} \log \sigma_{k,i} \right].
\frac{\partial L}{\partial x} = \frac{\partial y}{\partial x} . \frac{\partial L}{\partial y} \quad \quad (8)
\]
\]
In conclusion, we have a nice expression for the ELBO. To round out the parsimony of the ELBO, we need an inference model which is computationally cheap to evaluate. Additionally, we typically do not calculate the ELBO gradients analytically but instead perform Monte Carlo estimation by sampling from the inference model. This requires inexpensive sampling from the inference model. Since expectations are calculated only with respect to the simple initial distribution $q_{0}$, both of these requirements are easily satisfied. 


==Inverse Autoregressive Transformations or, Whence Inverse Autoregressive Flow?==
Since, the proposed meProp selects top-k elements of the traditional gradient to approximate it, hence the gradient of loss function with respect to W and x transform to the one shown in eq. (9) and (10):


Once we have the inverse autoregressive flow, the main result of \cite{946paper} falls out. Let us consider how we could have come up with the idea of the inverse autoregressive flow. It will be helpful to start with a discussion of $\textbf{autoregressive neural networks}$, which we briefly alluded to when defining the flow. As the Latin prefix suggests, autoregression means that we deduce components of a random vector $h$ based on its \textit{own} components. More precisely, the $d^{th}$ element of $h$ depends on the preceding components $h_{1:d-1}$.


To elucidate this further, we shall follow the introductory exposition presented in \cite{MADE}. Let us consider a very simple autoencoder with just one hidden layer. That is, we have a feedforward neural network defined by
\begin{align*}
r(h) &:= g(b + Wh) \\
\hat{h} & := \mathrm{sigm}(c + Vr(h)),
\end{align*}  
where $W$, $V$ are matrices of weights, $b$, $c$ are biases, $g$ is some non-linearity and $\mathrm{sigm}$ is element-wise sigmoid. Here, $r(h)$ is thought of as a hidden representation of the input $h$ and $\hat{h}$ is a reconstructed version of $h$. For simplicity, suppose that $h$ is a $D$-ary binary vector. Then we can measure the quality of our reconstruction using cross-entropy
\[
\[
l(h) := - \sum\limits h_{d} \log \hat{h}_{d} + (1 - h_{d}) \log (1 - \hat{h}_{d}).
\frac{\partial L}{\partial W} \leftarrow top_{k}(\frac{\partial L}{\partial y}) . \frac{\partial y}{\partial W} \quad \quad (9)
\]
\]
It is tempting to interpret $l(h)$ as a negative log-likelihood induced by the distribution
 
\[
\[
\prod\limits^{D}_{d=1} \hat{h}_{d}^{h_{d}} (1 - \hat{h}_{d})^{1 - h_{d}}.
\frac{\partial L}{\partial x} \leftarrow \frac{\partial y}{\partial x} . top_{k}(\frac{\partial L}{\partial y}) \quad \quad (10)
\]
\]
However, absent restrictions on the above expression, this is in general \textit{not} the case. As an example, suppose our hidden layer has as many units as the input layer. Then it is possible to drive the cross-entropy loss to $0$ by copying the input into the hidden layer. In this situation, $q(h) = 1$ for every possible $h$ and $q(h)$ is seen to actually not define a probability distribution.


If $l(h)$ is indeed to be a negative log-likelihood, i.e.,
The intuition behind the discussed conversions is depicted in Fig. 2.
\[
 
l(h) = - \log p(h)
'''Where to apply meProp:'''
\]
In general, the authors leave the process of back propagation largely unchanged. Noting that, in the learning task Matrix-to-Matrix and Matrix-to-Vector multiplications consume more than 90% of the computation time, meProp is designed to improve the efficiencies there. The authors apply meProp only to the back propagation from the output of the multiplication to its inputs. Any operation which is applied elementwise (i.e. non-linear activation), the original back propagation algorithm remains unchanged. This means that for every hidden layer meProp is applied since between each hidden layer the gradient will remain dense.
for a genuine probability distribution $p(h)$, it must satisfy
 
\begin{align*}
The authors note that the choice of $k$ could, and likely should, vary between the hidden layers and the output. Intuitively, if a network outputs with dimensionality 10, (say MNIST), and has a hidden layer with 500 nodes, taking $k$ close to 10 may be reasonable for the output, but is likely too small for the hidden layer. Despite this, the authors note that $k$ was kept constant for the paper.
l(h) = & - \sum\limits^{D}_{d=1} \log p(h_{d} \mid h_{1:d-1}) \\
 
= & - \sum\limits^{D}_{d=1} h_{d} \log p(h_{d} = 1 \mid h_{1:d-1}) + (1 - h_{d}) \log p(h_{d} = 0 \mid h_{1:d-1}) \\
 
= & - \sum\limits^{D}_{d=1} h_{d} \log p(h_{d} = 1 \mid h_{1:d-1}) + (1 - h_{d})(1 - \log p(h_{d} = 1 \mid h_{1:d-1})).
'''Choice of top-k algorithms:''' A variant (focusing on memory reuse) of min heap-based top-k selection method is used. The time complexity is: O(n log k) and space complexity is O(k). This is done to save time on sorting the entire vector. A min-heap is a binary tree such that the data contained in each node is less than (or equal to) the data in that node’s children.
\end{align*}
 
The first equation is just the chain rule of probability
=Experiments and Configurations=
\[
 
p(h) = \prod\limits^{D}_{d=1} p(h_{d} \mid h_{1:d-1}),
To establish that the approach is general purpose, authors performed experiments on different deep learning algorithms(i.e. LSTM, MLP) with different optimizers (i.e. Adam, Adagrad) and different problem sets (i.e. Part of Speech Tagging, Transition based dependency parsing, MNIST Image Recognition).
\]
 
the second equation is true because of our assumption that each entry of $h$ is either $0$ or $1$ and the third equation holds due to the fact that $p(h)$ is a probability distribution. Comparing the naive cross-entropy loss
'''POS-Tag:'''
\[
Part-of-speech tagging is the process of identifying and assigning the parts of speech such as noun, verb, adjectice etc. in a corpus
- \sum\limits h_{d} \log \hat{h}_{d} + (1 - h_{d}) \log (1 - \hat{h}_{d})
Baseline model: LSTM. Benchmark dataset: Penn Treebank Corpus. For training and testing: Wall Street Journal.
\]
 
with the term
'''Parsing:''' Baseline model: MLP. Benchmark dataset: Penn Treebank Corpus. For training, development, and testing: Wall Street Journal. The most common method for evaluating parsers are labeled and unlabeled attachment scores. In this work, the authors use the unlabeled attachment score. Labeled attachment refers to the correct matching of a word to its head along with the correct dependency relation. Unlabeled attachment ignores the dependency relation and focuses on the correctness of the assigned head.  
\[
- \sum\limits^{D}_{d=1} h_{d} \log p(h_{d} = 1 \mid h_{1:d-1}) + (1 - h_{d})(1 - \log p(h_{d} = 1 \mid h_{1:d-1})),
\]
we see that a correct reconstruction (``correct" in the sense that the loss function is a negative log-likelihood) needs to satisfy
\[
\hat{h}_{d} = \log p(h_{d} = 1 \mid h_{1:d-1}).
\]


More generally, for a (deep) autoencoder we can require the reconstructed vector to have components satisfying
'''MNIST:'''
\[
The MNIST dataset consists of hand-written digits and the solution involves classifying the images among 10 digit classes.
\hat{h}_{d} = p(h_{d} \mid h_{1:d-1}).
Baseline model: MLP. For training, development, and testing: MNIST dataset.
\]
In other words, the $d^{th}$ component is the probability of observing $h_{d}$ given the preceding components $h_{1:d-1}$. This latter property is known as the $\textbf{autoregressive property}$ since we can think of it as sequentially performing regression on the components of $h$. Unsurprisingly, an autoencoder satisfying the autoregressive property is called an $\textbf{autoregressive autoencoder}$.


Suppose now that we have an autoregressive autoencoder which takes an input vector $\mathbf{y} \in \mathbb{R}^{D}$ and we interpret the outputs of this network as parameters for a normal distribution. Write $[\mathbf{\mu}(\mathbf{y}),\mathbf{\sigma}(\mathbf{y})]$ for such output. The autoregressive structure implies that, for $j \in \{1, \ldots, D\}$, $\mathbf{y}_{j}$ depends only on the components $\mathbf{y}_{1:j-1}$. Therefore, if we take the vector $[\mathbf{\mu}_{i}, \mathbf{\sigma}_{i}]$ and compute the derivative with respect to $\mathbf{y}$, we will obtain a lower triangular matrix since
In the configuration for Parsing and MNIST authors use the same k for the output and hidden layers. For POS-Tag authors use different k for the output and hidden layers. Due to low dimensionality of output layer in POS-Tag meProp isn't applied to it.
\[
\frac{\partial [\mathbf{\mu}_{i}, \mathbf{\sigma}_{i}]}{\partial \mathbf{y}_{j}} = [0, 0]
\]
whenever $j \geq i$. We interpret the vector $[\mathbf{\mu}_{i}(\mathbf{y}_{1:j-1}), \mathbf{\sigma}_{i}(\mathbf{y}_{1:j-1})]$ as being the predicted mean and standard deviation of the $i^{th}$ element of (the reconstruction of) $\mathbf{y}$. In slightly more detail, the components of $\mathbf{y}$ are successively generated via
\begin{align*}
& \mathbf{y}_{0} = \mathbf{\mu}_{0} + \mathbf{\sigma}_{0} \cdot \mathbf{\epsilon}_{0}, \\
& \mathbf{y}_{i} = \mathbf{\mu}_{i}(\mathbf{y}_{1:i-1}) + \mathbf{\sigma}_{i}(\mathbf{y}_{1:i-1}) \cdot \mathbf{\epsilon}_{i},
\end{align*}
where $\mathbf{\epsilon} \!\sim \mathcal{N}(\mathbf{0}, \mathbf{I})$.  


To relate this back to the normalizing flow chosen by the authors of \cite{946paper}, replace $\mathbf{y}$ with $h_{k}$ as input to the autoregressive autoencoder and replace the outputs $\mathbf{\mu}$, $\mathbf{\sigma}$ with $\mu_{k}$, $\sigma_{k}$.
The code for the paper can be found on Github : https://github.com/jklj077/meProp


== Implementation ==
=Results=
[[File:implementation.PNG]]


The authors have open sourced the code for this paper on Github : https://github.com/openai/iaf
[[File:13.png|right|750px]]


== Experiments==
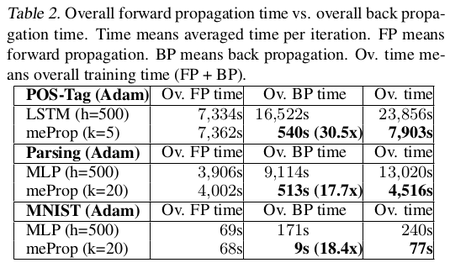
meProp is applied to the linear transformations which actually entail the major computational cost. Authors call linear transformation related backprop time as Backprop Time. It does not include the time required for non-linear activations which usually entail less than 2% of the computational cost. The total time of back propagation including non-linear activations is reported as Overall Backprop Time.
The authors showcase the potential for improvement of variational autoencoders afforded by the novel IAF methodology they proposed by providing empirical evidence in the context of two key benchmark datasets: MNIST and CIFAR 10.


'''MNIST DATASET:'''
Through results, it was observed that meProp substantially speeds up the backpropagation and provides a linear reduction in computational cost. Authors state the main reason for this reduction to be that meProp does not modify weakly relevant parameters, which makes overfitting less likely similar to the dropout effect. Also, the results depict that the proposed approach is independent of specific optimization methods.
The results of the experiment authors conducted are displayed in the figure below. [[File:IAF MINST.PNG]]


They provide some evidence as to the improvement of the variational inference via IAF when compared with other state of the art techniques.
The graphs shown in Fig. 4 depict that meProp addresses the problem of overfitting and it provides better accuracy if the top-k weights are selected instead of random weights. The term backprop ratio in the figure is the ratio of k to the total number of parameters. It suggests that top-k elements contain
the most important information of the gradients. This makes us think, instead of using dropout which randomly turns off few neurons, can it be done more deterministically based on the contribution of a neuron to the final prediction or output. Also, it was inferred that meProp can achieve further improvements over dropout for reducing overfitting and a model should take advantage of both meProp and dropout to reduce overfitting. Adding hidden layers does not hurt the performance of the model. Although this may be the case for the current set of test cases, a better understanding of the variation of hidden layer size and choice-of-k can be obtained by varying k with different hidden unit sizes <math>h</math> by keeping <math>k*h</math> or a similarly related term constant. This is better studied in [5] where the authors kept <math>p*n</math> constant to obtain greater reductions in training error for smaller p values ( p being the dropout coefficient. Low p, more units dropped).  The relevant numerical results have been shown in table 1-5.  


'''CIFAR 10:'''
'''Further speed up:'''
For further speeding up the backpropagation on GPUs authors presented a simple unified top-k approach (implementation in PyTorch). The main idea is to treat the entire mini-batch as a "big training example" where the top-k operation is based on the averaged values of all examples in the mini-batch so that the large consistent sparse matrix of the mini-batch can be converted into a dense small matrix by simply removing the zero values. The authors refer to this method as the simplified unified top-$k$ method. The results are presented in Table 6. This GPU acceleration works much more outstandingly for heavy models, with the relevant numerical results shown in table 7 and 8.


The results for the CIFAR 10 data set is displayed in the figure below. [[File:CIFAR 10.PNG]]
=List of Tables=


==Concluding Remarks==
[[File:11.png|thumb|center|750px]]
[[File:12.png|thumb|center|450px]]
[[File:14.png|thumb|center|350px]]
[[File:15.png|thumb|center|400px]]
[[File:16.png|thumb|center|500px]]
[[File:meProp.PNG|thumb|center|750px]]
[[File:56.png|thumb|center|500px]]
[[File:57.png|thumb|center|400px]]


In wrapping up, we note that there is something interesting about how the normalizing flow is derived. Essentially, the authors of \cite{946paper} took a neural network model with nice properties (fast sampling, simple Jacobian, etc.), looked at the function it implemented and basically dropped in this function in the recursive definition of the normalizing flow. This is not an isolated case. The authors of \cite{normalizing_flow} do much the same thing in coming up with the flow
=Critiques=
The main idea behind meProp is to wipe out the backprop mechanism of (n-k) nodes where "n" is the number of nodes in the current layer and "k" is the number of nodes contributing to the maximum of the loss in that layer. Intuitively, meProp in backpropagation process is actually a threshold w.r.t. k, or an activation function in the gradient backpropagation: only if the gradients are big enough in magnitude that will be passed to the previous layer. Referring to equation 10,
\[
\[
f_{k}(h_{k}) = h_{k} + u_{k}s(w_{k}^{T}h_{k} + b_{k}).
\frac{\partial L}{\partial x} \leftarrow \frac{\partial y}{\partial x} . top_{k}(\frac{\partial L}{\partial y}) \quad \quad
\]
\]
We believe that this flow is implicitly justified by the fact that functions of the above form are implemented by deep latent Gaussian models (see \cite{autoencoderRezende}). These flows, while interesting and useful, probably do not exhaust the possibilities for tractable and practical normalizing flows. It may be an interesting project to try and come up with novel normalizing flows by taking a favorite neural network architecture and using the function implemented by it as a flow. Additionally, it may be worth exploring boutique normalizing flows to improve variational inference in domain-specific settings (e.g., use a normalizing flow induced by a parsimonious convolutional neural network architecture for training an image-processing model using variational inference).
#The authors have not proposed any method on how k should be selected, hence it is left to the reader's discretion to possibly take it as a hyperparameter. If so, in a deeply layered architecture, where the weights between each layer are randomly initialized during each execution, "k" might change for each layer since the features learned at each layer may not be the same from the previous layers. However, under the assumption that we only perform top-$k$ selection for the gradient vector associated to the top layer, we do not choose $k$ for each subsequent layer through which we backpropagate. The concern as to whether we may lose valuable feature selection due to hidden layers is a valuable one. Moreover, further study should be carried out to see whether this is, in fact, the case and if not, whether we can directly sparsify weight matrices of hidden layers.
#If the sum of losses caused by the (n-k) nodes in the current layer exceed any of the losses incurred due to "k" nodes, then it would not be correct to drop the (n-k) nodes as we can assume the aggregate (n-k) nodes as a single opaque node with a composite weight which will incur an aggregated loss greater than any of the "k" nodes.
 
In essence, the idea of selecting "k" nodes to drop-out prove to be effective as shown by the authors, but the lack of information on the conditions on selecting "k" for each layer given the current state of the layer might lead to lack of consistency in the results.
 
In addition to this, the authors did not include convolutional neural networks in their experiments. It would have been interesting to see whether similar results were observed on that architecture. Theoretically, the method presented in this paper should only update kernels in parts of an image that contribute the most to the loss.
 
As the experiment settings, all networks are using Adam and AdaGrad, it is an interesting guess that whether the choice of the optimizer will influence the accuracy. The authors did not include the results with SGD(momentum). Since Adam and AdaGrad are using adaptive learning rate for each weight.
 
There has been no mention by the authors on the loss ( significant loss or the insignificance) of using meProp on tasks where preservation of temporal information and contextual data is important. For example, in tasks like using RNNs for Question-Answering tasks, the memory of details of earlier regions of the paragraph could be garbled due to not updating the weights which do not belong to the top-k set in backpropagation. Indeed, the lack of principled methods for sparsification is a major issue in this case since tasks such as machine translation often entail data where certain parts of an input are much more predictive than other parts in a systematic way. There could be a trade-off between knowledge preservation and choice of the hyperparameter k which can be verified by further analysis like correlation/covariance studies.


== List of Figures ==
The approach can be thought of as a deterministic Dropout giving priority to higher gradient contributing connections during backpropagation. However, unlike dropout (which is random in nature), selecting k-top may permanently exclude some parts of NN from training at all, which has not been mentioned in the paper at all. Authors have also failed to test their approach on bigger datasets such as Imagenet, therefore it might be possible that dataset (MNIST) used by the authors is too simple for the given NN architecture, therefore, meProp approach helped to generalize the model better. It is generally a bad habit to use MNIST results in 2017's research works, as they shed no light on the real world AI problems. The idea is really simple, basically applying only k strongest gradients during backprop which should work for different architectures as well (LSTM, RNNs). This paper has shown the advantage of their method empirically, but only in a simple dataset.It is lacking its results in a real world and more complex dataset. Lastly, the approximate gradient introduced here can be interpreted as a projection of the actual gradient on some lower dimensional subspace. This observation suggests that this method might have some connections with the projected gradient optimization algorithm.
[[File:fig1.PNG]]
[[File:fig2.PNG]]
[[File:fig3.PNG]]


==References==
=References=
Blei, David M., Alp Kucukelbir, and Jon D. McAuliffe. "Variational inference: A review for statisticians." Journal of the American Statistical Association just-accepted (2017).
# Tollenaere, Tom. "SuperSAB: fast adaptive back propagation with good scaling properties." Neural networks 3.5 (1990): 561-573.
# Riedmiller, Martin, and Heinrich Braun. "A direct adaptive method for faster backpropagation learning: The RPROP algorithm." Neural Networks, 1993., IEEE International Conference on. IEEE, 1993.
# Srivastava, Nitish, et al. "Dropout: a simple way to prevent neural networks from overfitting." Journal of machine learning research 15.1 (2014): 1929-1958.
# Shazeer, Noam, et al. "Outrageously large neural networks: The sparsely-gated mixture-of-experts layer." arXiv preprint arXiv:1701.06538 (2017).
# Nitish Srivastava, Geoffrey Hinton, Alex Krizhevsky, Ilya Sutskever, Ruslan Salakhutdinov. "Dropout: A Simple Way to Prevent Neural Networks from Overfitting", Journal of Machine Learning Research 15 (2014) 1929-1958
# Speech and Language Processing. Daniel Jurafsky & James H. Martin. 2017. Draft of August 28, 2017.
# Devos. M. R., Orban. G. A. "Self adaptive backpropagation." Proceedings NeuroNimes 1988.

Latest revision as of 20:40, 28 November 2017

Introduction

The backpropagation step in neural network training entails high computational cost since each iteration requires calculation of full gradient vectors and matrices and subsequent update of all model parameters. The main idea of the paper is to find only a small but critical subset of the gradient information and in each learning step, update only this minimal subset of the parameters. This leads to sparsified gradients because only highly relevant parameters are updated and rest remain untouched.


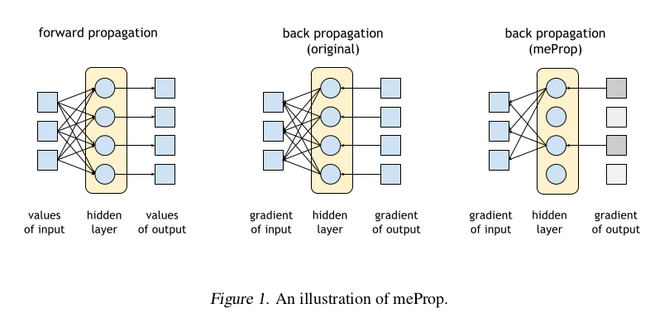
A simple and effective technique for neural networks learning is introduced in the current paper. The main technique entails a modification to the vanilla backpropagation algorithm. The idea is that after a forward pass has been carried out in the usual fashion, we retain only a subset of the full gradient for computation of model parameters. More precisely, a simple quantization technique is employed to sparsify the gradient vectors, viz., the entries of the first gradient in a backpropagation step are set to zero unless they reach a specified size threshold. The rest of the gradients (the ones with respect to the weights and biases of the neural network) are computed using the chain rule in the typical way using the sparsified gradient obtained from the top layer. Since only a small subset of the weight matrix is modified, we obtain a linear reduction in the computational cost. The experimental results presented in the paper suggest that accuracy is improved rather than being degraded. The name given to the proposed technique is minimal effort back propagation method (meProp). Fig. 1 shows an abstract view of the proposed approach.


Two important questions:

1) In the process of stochastic learning, how do we find a highly relevant subset of parameters from the current sample?

One solution to this question is given by Top-$k$ search method to identify the most important parameters. Experimental results suggest that if we use this technique, then we can only update 1–4% of the weights at each back propagation pass and this does not result in a larger number of training iterations.

Another likely solution I can think of is the method in the paper: Learning the Number of Neurons in Deep Networks. We can use the group sparsity regularizer to identify the neurons that have many nonzero parameters, which are considered highly relevant parameters.

2) Does this process of selecting a small subset of model parameters hurt accuracy?

The results demonstrate that rather than reduce, this sparsification actually improves the accuracy in most settings. This result, while somewhat surprising, is attributed to a dropout-like effect which works to prevent overfitting. Because the minimal effort update does not modify any parameters which are weakly relevant, it seems sensible that this would help avoid overfitting the data.

The authors demonstrate the proposed approach using deep learning approaches (like LSTM, MLP), optimization approaches (like Adam and Adagrad) and tasks like NLP and Image Recognition.

Related Work

Some of the notable related work to this paper are as follows:

In 1990, Tollenaere et al.[1] proposed SuperSAB: an adaptive acceleration strategy for error back propagation learning. It is an improvement on SAB (self-adapting back propogation) strategy [7]. SuperSAB avoids taking a step when a change of sign in the weight derivative is discovered. Instead, it decreases the step size until a safe step is discovered (one without a sign change of the weight). They proved that it may converge orders of magnitude faster than the original back propagation algorithm, and is only slightly unstable. In addition, the algorithm is very insensitive to the choice of parameter values and has excellent scaling properties.

In 1993, Riedmilller et al.[2] and Braun proposed an algorithm called RPROP, to overcome the inherent disadvantages of pure gradient-descent, it performed a local adaptation of the weight-updates according to the behavior of the error function. To be more specific, the authors defined an individual update-value for each weight. When the update of a weight is too large (mathematically, the partial derivative of a weight changes its sign), such update-value of this weight will decrease. Otherwise, it'll increase. After the process of adapting update-values is finished, the weight-update process is carried out as follows: when the partial derivative of the error function with respect to a specific weight is positive, the original weight decreases by its corresponding update-value, otherwise it increases.

In 2014, Srivastava et al.[3] proposed dropout. Large networks are also slow to use, making it difficult to deal with overfitting by combining the predictions of many different large neural nets at test time. The key idea is to randomly drop units (along with their connections) from the neural network during training. This prevents units from co-adapting too much.

The work proposed by the authors of meProp method is quite different from the three related works discussed above.

In 2017, Shazeer et al.[4] presented a Sparsely-Gated Mixture-of-Experts layer (MoE), consisting of up to thousands of feed-forward sub-networks. A trainable gating network determines a sparse combination of these experts to use for each example. They used this approach for the machine translation task and concluded that it gave significantly better results. Their method is limited to a specific set of a mixture of experts however, the meProp method does not have these sort of limitations.

Proposed Approach

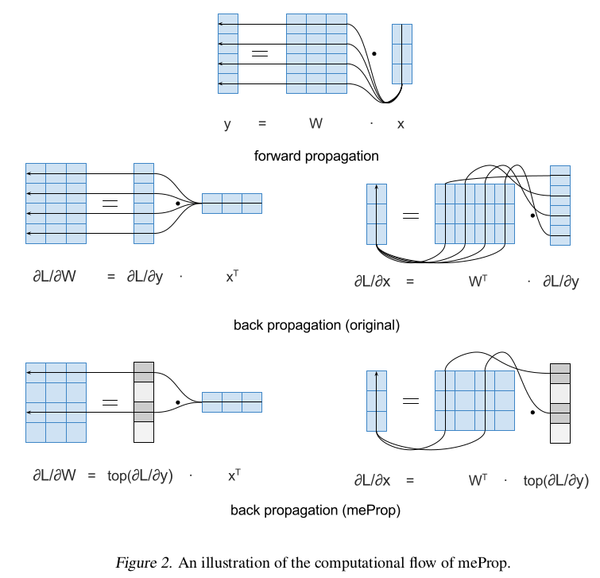
The original back propagation computes the "full gradient" for the input vector and the weight matrix. However, in me-Prop, back propagation computes an "approximate gradient" by keeping top-k values of the backward flowed gradient and masking the remaining values to 0. That is, only the top-k elements with the largest absolute values are kept and rest are made 0.

Authors describe conversion of the traditional back-propagation to the back-propagation used in meProp with a computation unit with one linear transformation and one non-linear transformation as an example as given by eq. (1) and (2): \begin{align*} y &= W x \quad \quad \quad (1) \end{align*} \begin{align*} z &= \sigma (y) \quad \quad \quad (2) \end{align*} where $W \in R_{n \times m}$, $x \in R_m$, $y \in R_n$, $z \in R_n$, $m$ is the dimension of the input vector, $n$ is the dimension of the output vector, and $\sigma$ is a non-linear function (e.g., ReLU, tanh, and sigmoid). During back propagation, we need to compute the gradient of the parameter matrix $W$ and the input vector $x$:

\[ \frac{\partial z}{\partial W_{ij}} = \sigma^{'}_{i}x^{T}_{j},\quad i \quad \epsilon \quad [1,n], \quad j \quad \epsilon \quad [1,m] \quad \quad \quad (3) \]

\[ \frac{\partial z}{\partial x_{i}} = \sum\limits_j W^{T}_{ij} \sigma^{'}_{j},\quad i \quad \epsilon \quad [1,n], \quad j \quad \epsilon \quad [1,m] \quad \quad \quad (4) \]

Since the proposed meProp keeps only top-k elements based on the magnitude values so eq. (3) and (4) get transformed to (5) and (6), respectively:

\[ \frac{\partial z}{\partial W_{ij}} \leftarrow \sigma^{'}_{i}x^{T}_{j}, \quad if \quad i \quad \epsilon \quad \{ t_{1}, t_{2},....., t_{k} \} \quad else \quad 0 \quad \quad (5) \]

\[ \frac{\partial z}{\partial x_{i}} \leftarrow \sum\limits_j W^{T}_{ij} \sigma^{'}_{j}, \quad if \quad j \quad \epsilon \quad \{ t_{1}, t_{2},....., t_{k} \} \quad else \quad 0 \quad \quad (6) \]


The original back-propagation computes the gradient of the matrix W and the gradient of the input vector x as shown in eq. (7) and (8), respectively:

\[ \frac{\partial L}{\partial W} = \frac{\partial L}{\partial y} . \frac{\partial y}{\partial W} \quad \quad (7) \]

\[ \frac{\partial L}{\partial x} = \frac{\partial y}{\partial x} . \frac{\partial L}{\partial y} \quad \quad (8) \]

Since, the proposed meProp selects top-k elements of the traditional gradient to approximate it, hence the gradient of loss function with respect to W and x transform to the one shown in eq. (9) and (10):


\[ \frac{\partial L}{\partial W} \leftarrow top_{k}(\frac{\partial L}{\partial y}) . \frac{\partial y}{\partial W} \quad \quad (9) \]

\[ \frac{\partial L}{\partial x} \leftarrow \frac{\partial y}{\partial x} . top_{k}(\frac{\partial L}{\partial y}) \quad \quad (10) \]

The intuition behind the discussed conversions is depicted in Fig. 2.

Where to apply meProp: In general, the authors leave the process of back propagation largely unchanged. Noting that, in the learning task Matrix-to-Matrix and Matrix-to-Vector multiplications consume more than 90% of the computation time, meProp is designed to improve the efficiencies there. The authors apply meProp only to the back propagation from the output of the multiplication to its inputs. Any operation which is applied elementwise (i.e. non-linear activation), the original back propagation algorithm remains unchanged. This means that for every hidden layer meProp is applied since between each hidden layer the gradient will remain dense.

The authors note that the choice of $k$ could, and likely should, vary between the hidden layers and the output. Intuitively, if a network outputs with dimensionality 10, (say MNIST), and has a hidden layer with 500 nodes, taking $k$ close to 10 may be reasonable for the output, but is likely too small for the hidden layer. Despite this, the authors note that $k$ was kept constant for the paper.


Choice of top-k algorithms: A variant (focusing on memory reuse) of min heap-based top-k selection method is used. The time complexity is: O(n log k) and space complexity is O(k). This is done to save time on sorting the entire vector. A min-heap is a binary tree such that the data contained in each node is less than (or equal to) the data in that node’s children.

Experiments and Configurations

To establish that the approach is general purpose, authors performed experiments on different deep learning algorithms(i.e. LSTM, MLP) with different optimizers (i.e. Adam, Adagrad) and different problem sets (i.e. Part of Speech Tagging, Transition based dependency parsing, MNIST Image Recognition).

POS-Tag: Part-of-speech tagging is the process of identifying and assigning the parts of speech such as noun, verb, adjectice etc. in a corpus Baseline model: LSTM. Benchmark dataset: Penn Treebank Corpus. For training and testing: Wall Street Journal.

Parsing: Baseline model: MLP. Benchmark dataset: Penn Treebank Corpus. For training, development, and testing: Wall Street Journal. The most common method for evaluating parsers are labeled and unlabeled attachment scores. In this work, the authors use the unlabeled attachment score. Labeled attachment refers to the correct matching of a word to its head along with the correct dependency relation. Unlabeled attachment ignores the dependency relation and focuses on the correctness of the assigned head.

MNIST: The MNIST dataset consists of hand-written digits and the solution involves classifying the images among 10 digit classes. Baseline model: MLP. For training, development, and testing: MNIST dataset.

In the configuration for Parsing and MNIST authors use the same k for the output and hidden layers. For POS-Tag authors use different k for the output and hidden layers. Due to low dimensionality of output layer in POS-Tag meProp isn't applied to it.

The code for the paper can be found on Github : https://github.com/jklj077/meProp

Results

meProp is applied to the linear transformations which actually entail the major computational cost. Authors call linear transformation related backprop time as Backprop Time. It does not include the time required for non-linear activations which usually entail less than 2% of the computational cost. The total time of back propagation including non-linear activations is reported as Overall Backprop Time.

Through results, it was observed that meProp substantially speeds up the backpropagation and provides a linear reduction in computational cost. Authors state the main reason for this reduction to be that meProp does not modify weakly relevant parameters, which makes overfitting less likely similar to the dropout effect. Also, the results depict that the proposed approach is independent of specific optimization methods.

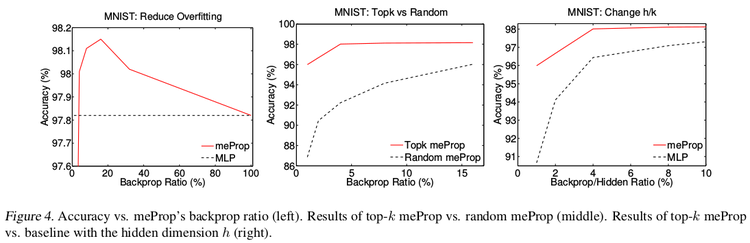
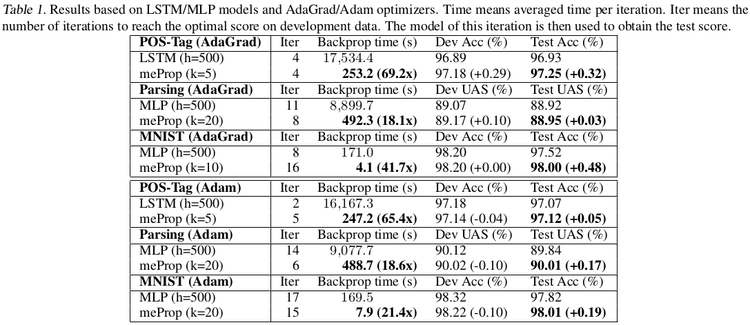
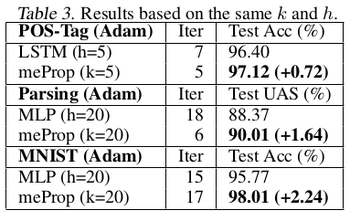
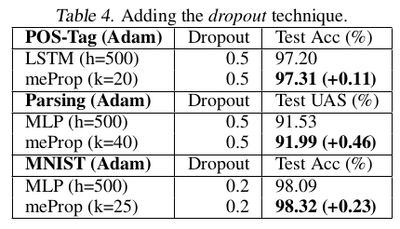
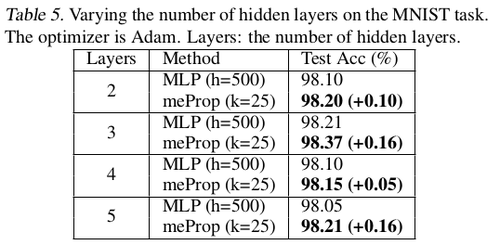
The graphs shown in Fig. 4 depict that meProp addresses the problem of overfitting and it provides better accuracy if the top-k weights are selected instead of random weights. The term backprop ratio in the figure is the ratio of k to the total number of parameters. It suggests that top-k elements contain the most important information of the gradients. This makes us think, instead of using dropout which randomly turns off few neurons, can it be done more deterministically based on the contribution of a neuron to the final prediction or output. Also, it was inferred that meProp can achieve further improvements over dropout for reducing overfitting and a model should take advantage of both meProp and dropout to reduce overfitting. Adding hidden layers does not hurt the performance of the model. Although this may be the case for the current set of test cases, a better understanding of the variation of hidden layer size and choice-of-k can be obtained by varying k with different hidden unit sizes [math]\displaystyle{ h }[/math] by keeping [math]\displaystyle{ k*h }[/math] or a similarly related term constant. This is better studied in [5] where the authors kept [math]\displaystyle{ p*n }[/math] constant to obtain greater reductions in training error for smaller p values ( p being the dropout coefficient. Low p, more units dropped). The relevant numerical results have been shown in table 1-5.

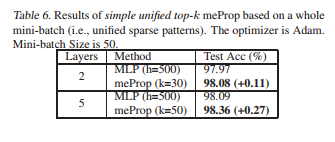
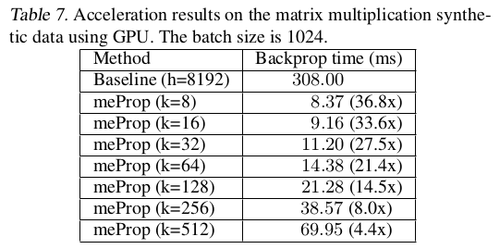
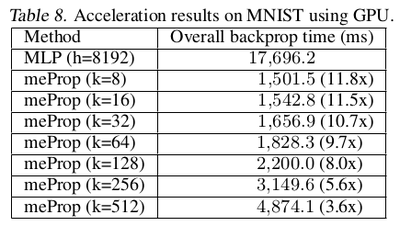
Further speed up: For further speeding up the backpropagation on GPUs authors presented a simple unified top-k approach (implementation in PyTorch). The main idea is to treat the entire mini-batch as a "big training example" where the top-k operation is based on the averaged values of all examples in the mini-batch so that the large consistent sparse matrix of the mini-batch can be converted into a dense small matrix by simply removing the zero values. The authors refer to this method as the simplified unified top-$k$ method. The results are presented in Table 6. This GPU acceleration works much more outstandingly for heavy models, with the relevant numerical results shown in table 7 and 8.

List of Tables

Critiques

The main idea behind meProp is to wipe out the backprop mechanism of (n-k) nodes where "n" is the number of nodes in the current layer and "k" is the number of nodes contributing to the maximum of the loss in that layer. Intuitively, meProp in backpropagation process is actually a threshold w.r.t. k, or an activation function in the gradient backpropagation: only if the gradients are big enough in magnitude that will be passed to the previous layer. Referring to equation 10, \[ \frac{\partial L}{\partial x} \leftarrow \frac{\partial y}{\partial x} . top_{k}(\frac{\partial L}{\partial y}) \quad \quad \]

  1. The authors have not proposed any method on how k should be selected, hence it is left to the reader's discretion to possibly take it as a hyperparameter. If so, in a deeply layered architecture, where the weights between each layer are randomly initialized during each execution, "k" might change for each layer since the features learned at each layer may not be the same from the previous layers. However, under the assumption that we only perform top-$k$ selection for the gradient vector associated to the top layer, we do not choose $k$ for each subsequent layer through which we backpropagate. The concern as to whether we may lose valuable feature selection due to hidden layers is a valuable one. Moreover, further study should be carried out to see whether this is, in fact, the case and if not, whether we can directly sparsify weight matrices of hidden layers.
  2. If the sum of losses caused by the (n-k) nodes in the current layer exceed any of the losses incurred due to "k" nodes, then it would not be correct to drop the (n-k) nodes as we can assume the aggregate (n-k) nodes as a single opaque node with a composite weight which will incur an aggregated loss greater than any of the "k" nodes.

In essence, the idea of selecting "k" nodes to drop-out prove to be effective as shown by the authors, but the lack of information on the conditions on selecting "k" for each layer given the current state of the layer might lead to lack of consistency in the results.

In addition to this, the authors did not include convolutional neural networks in their experiments. It would have been interesting to see whether similar results were observed on that architecture. Theoretically, the method presented in this paper should only update kernels in parts of an image that contribute the most to the loss.

As the experiment settings, all networks are using Adam and AdaGrad, it is an interesting guess that whether the choice of the optimizer will influence the accuracy. The authors did not include the results with SGD(momentum). Since Adam and AdaGrad are using adaptive learning rate for each weight.

There has been no mention by the authors on the loss ( significant loss or the insignificance) of using meProp on tasks where preservation of temporal information and contextual data is important. For example, in tasks like using RNNs for Question-Answering tasks, the memory of details of earlier regions of the paragraph could be garbled due to not updating the weights which do not belong to the top-k set in backpropagation. Indeed, the lack of principled methods for sparsification is a major issue in this case since tasks such as machine translation often entail data where certain parts of an input are much more predictive than other parts in a systematic way. There could be a trade-off between knowledge preservation and choice of the hyperparameter k which can be verified by further analysis like correlation/covariance studies.

The approach can be thought of as a deterministic Dropout giving priority to higher gradient contributing connections during backpropagation. However, unlike dropout (which is random in nature), selecting k-top may permanently exclude some parts of NN from training at all, which has not been mentioned in the paper at all. Authors have also failed to test their approach on bigger datasets such as Imagenet, therefore it might be possible that dataset (MNIST) used by the authors is too simple for the given NN architecture, therefore, meProp approach helped to generalize the model better. It is generally a bad habit to use MNIST results in 2017's research works, as they shed no light on the real world AI problems. The idea is really simple, basically applying only k strongest gradients during backprop which should work for different architectures as well (LSTM, RNNs). This paper has shown the advantage of their method empirically, but only in a simple dataset.It is lacking its results in a real world and more complex dataset. Lastly, the approximate gradient introduced here can be interpreted as a projection of the actual gradient on some lower dimensional subspace. This observation suggests that this method might have some connections with the projected gradient optimization algorithm.

References

  1. Tollenaere, Tom. "SuperSAB: fast adaptive back propagation with good scaling properties." Neural networks 3.5 (1990): 561-573.
  2. Riedmiller, Martin, and Heinrich Braun. "A direct adaptive method for faster backpropagation learning: The RPROP algorithm." Neural Networks, 1993., IEEE International Conference on. IEEE, 1993.
  3. Srivastava, Nitish, et al. "Dropout: a simple way to prevent neural networks from overfitting." Journal of machine learning research 15.1 (2014): 1929-1958.
  4. Shazeer, Noam, et al. "Outrageously large neural networks: The sparsely-gated mixture-of-experts layer." arXiv preprint arXiv:1701.06538 (2017).
  5. Nitish Srivastava, Geoffrey Hinton, Alex Krizhevsky, Ilya Sutskever, Ruslan Salakhutdinov. "Dropout: A Simple Way to Prevent Neural Networks from Overfitting", Journal of Machine Learning Research 15 (2014) 1929-1958
  6. Speech and Language Processing. Daniel Jurafsky & James H. Martin. 2017. Draft of August 28, 2017.
  7. Devos. M. R., Orban. G. A. "Self adaptive backpropagation." Proceedings NeuroNimes 1988.
Retrieved from "http://wiki.math.uwaterloo.ca/statwiki/index.php?title=meProp:_Sparsified_Back_Propagation_for_Accelerated_Deep_Learning_with_Reduced_Overfitting&oldid=31684"