learning Spectral Clustering, With Application To Speech Separation
Introduction
The paper <ref>Francis R. Bach and Michael I. Jordan, Learning Spectral Clustering,With Application To Speech Separation, Journal of Machine Learning Research 7 (2006) 1963-2001.</ref> presented here is about spectral clustering which makes use of dimension reduction and learning a similarity matrix that generalizes to the unseen datasets when spectral clustering is applied to them.
Clustering
Clustering refers to partition a given dataset into clusters such that data points in the same cluster are similar and data points in different clusters are dissimilar. Similarity is usually measured over distance between data points.
Formally stated, given a set of data points [math]\displaystyle{ X=\{{{\mathbf x}}_1,{{\mathbf x}}_2,\dots ,{{\mathbf x}}_P\} }[/math], we would like to find [math]\displaystyle{ K }[/math] disjoint clusters [math]\displaystyle{ {C{\mathbf =}\{C_k\}}_{k\in \{1,\dots ,K\}} }[/math] such that [math]\displaystyle{ \bigcup{C_k}=X }[/math], that optimizes a certain objective function. The dimensionality of data points is [math]\displaystyle{ D }[/math], and [math]\displaystyle{ X }[/math] can be represented as a matrix [math]\displaystyle{ {{\mathbf X}}_{D\times P} }[/math].The similarity matrix that measures the similarity between each pair of points is denoted by [math]\displaystyle{ {{\mathbf W}}_{P\times P} }[/math]. A classical similarity matrix for clustering is the diagonally-scaled Gaussian similarity, defined as
[math]\displaystyle{ \mathbf W(i,j)= \rm exp (-(\mathbf{x}_i-\mathbf{x}_j)^{\rm T}Diag(\boldsymbol{\alpha})(\mathbf{x}_i-\mathbf{x}_j) ) }[/math]
where [math]\displaystyle{ {\mathbf \boldsymbol{\alpha} }\in {{\mathbb R}}^D }[/math] is a vector of positive parameters, and [math]\displaystyle{ \rm Diag(\boldsymbol{\alpha} ) }[/math] denotes the [math]\displaystyle{ D\times D }[/math] diagonal matrix with diagonal [math]\displaystyle{ {\boldsymbol{\alpha} } }[/math].
Objective functions
Objective function for K-means clustering
Given the number of clusters [math]\displaystyle{ K }[/math], it aims to minimize an objective function (sum of within-cluster distance) over all clustering scheme [math]\displaystyle{ C }[/math].
[math]\displaystyle{ \mathop{\min_C} J=\sum^K_{k=1}\sum_{\mathbf x \in C_k}\|\mathbf x - \boldsymbol{\mu}_k\|^2 }[/math]
[math]\displaystyle{ {\boldsymbol{\mu}}_k{\mathbf =}\frac{{\mathbf 1}}{\left|C_k\right|}\sum_{{\mathbf x}\in C_k}{{\mathbf x}} }[/math] is the mean of the cluster [math]\displaystyle{ C_k }[/math]
Min cut
For two subsets of [math]\displaystyle{ A,B\subset X }[/math], we define
[math]\displaystyle{ cut(A,B)=\sum_{{\mathbf x}_i \in A}\sum_{{\mathbf x}_j \in B}\mathbf W (i,j) }[/math]
Mincut is the sum of inter-cluster weights.
[math]\displaystyle{ Mincut(C)=\sum^K_{k=1} cut(C_k,X \backslash C_k) }[/math]
Normalized cut
The normalized cut in the paper is defined as
[math]\displaystyle{ Ncut(C)=\sum^K_{k=1}\frac{cut(C_k,X\backslash C_k)}{cut(C_k,X)}=\sum^K_{k=1}\frac{cut(C_k,X)-cut(C_k,C_k)}{cut(C_k,X)}=K-\sum^K_{k=1}{\frac{cut(C_k,C_k)}{cut(C_k,X)}} }[/math]
Normalized cut takes a small value if the clusters [math]\displaystyle{ C_k }[/math] are not too small <ref> Ulrike von Luxburg, A Tutorial on Spectral Clustering, Technical Report No. TR-149, Max Planck Institute for Biological Cybernetics.</ref> as measured by the intra-cluster weights. So it tries to achieve balanced clusters. There is unlikely that we will have clusters containing one data point.
The matrix representation of Normalized cut
Let [math]\displaystyle{ {{\mathbf e}}_k\in {\{0,1\}}^P }[/math] be the indicator vector for cluster [math]\displaystyle{ C_k }[/math], where the non-zero elements indicate the data points in cluster [math]\displaystyle{ C_k }[/math]. Therefore, knowing [math]\displaystyle{ {\mathbf E}{\mathbf =}({{\mathbf e}}_1,\dots ,{{\mathbf e}}_K) }[/math] is equivalent to know clustering scheme [math]\displaystyle{ C }[/math]. Further let [math]\displaystyle{ {\mathbf D} }[/math] denotes the diagonal matrix whose [math]\displaystyle{ i }[/math]-th diagonal element is the sum of the elements in the [math]\displaystyle{ i }[/math]-th row of [math]\displaystyle{ {\mathbf W} }[/math], that is, [math]\displaystyle{ {\mathbf D}{\mathbf =}{\rm Diag(}{\mathbf W}\cdot {\mathbf 1}{\rm )} }[/math], where [math]\displaystyle{ {\mathbf 1} }[/math] is defined as the vector in [math]\displaystyle{ {\{1\}}^P }[/math].
So the normalized cut can be written as
[math]\displaystyle{ Ncut(C)=C(\mathbf{W,E})=\sum^K_{k=1}\frac{{\mathbf e}^{\rm T}_k (\mathbf{D-W}){\mathbf e}_k}{{\mathbf e}^{\rm T}_k (\mathbf{D}){\mathbf e}_k}=K-tr(\mathbf {E^{\rm T} W E}(\mathbf {E^{\rm T} D E})^{-1}) }[/math]
Spectral Clustering
Solving the problem of Normalized cut is NP-hard, so we turn to the relaxed version of it.
Theorem 1
Minimizing normalized cut over all [math]\displaystyle{ C }[/math] is equivalent to the following optimization problem (refer as original optimization problem).
[math]\displaystyle{ \mathop{\min_{\mathbf Y}}K-tr(\mathbf{Y^{\rm T}(D^{\rm{1/2}}WD^{\rm{1/2}})Y}) }[/math]
subject to
[math]\displaystyle{ {\mathbf Y}{\mathbf =}{{\mathbf D}}^{{{\rm 1}}/{{\rm 2}}}{\mathbf E}{\mathbf \Lambda } }[/math] (1a)
and
[math]\displaystyle{ {{\mathbf Y}}^{{\rm T}}{\mathbf Y}{\mathbf =}{\mathbf I} }[/math] (1b)
Where [math]\displaystyle{ {\mathbf \Lambda }\in {{\mathbb R}}^{K\times K},{\mathbf Y}\in {{\mathbb R}}^{P\times K} }[/math]
In other words, given [math]\displaystyle{ {\mathbf E} }[/math] and let[math]\displaystyle{ \mathbf{\Lambda =(E^{\rm T} D E)^{\rm{1/2}}} }[/math], we can form a candidate solution [math]\displaystyle{ {\mathbf Y}{\mathbf =}{{\mathbf D}}^{{{\rm 1}}/{{\rm 2}}}{\mathbf E}{\left({{\mathbf E}}^{{\rm T\ }}{\mathbf {D E}}\right)}^{{\mathbf -}{{\rm 1}}/{{\rm 2}}} }[/math] for the above optimization problem.
Relaxed optimization problem
Since minimizing normalized cut is NP-hard problem, its equivalent optimization problem is NP-hard too. However, by removing the constraint (1a) in Theorem 1, a relaxed problem is obtained.
[math]\displaystyle{ \mathop{\min_{\mathbf Y}}K-tr(\mathbf{Y^{\rm T}(D^{\rm{-1/2}}WD^{\rm{-1/2}})Y}) }[/math]
subject to
[math]\displaystyle{ {{\mathbf Y}}^{{\rm T}}{\mathbf Y}{\mathbf =}{\mathbf I} }[/math]
Where [math]\displaystyle{ {\mathbf Y}\in {{\mathbb R}}^{P\times K} }[/math]
Theorem 2
The maximum of [math]\displaystyle{ tr\left({{\mathbf Y}}^{{\rm T}}\left({{\mathbf D}}^{{\mathbf -}{{\rm 1}}/{{\rm 2}}}{\mathbf W}{{\mathbf D}}^{{\mathbf -}{{\rm 1}}/{{\rm 2}}}\right){\mathbf Y}\right) }[/math] over matrices [math]\displaystyle{ {\mathbf Y}\in {{\mathbb R}}^{P\times K} }[/math] such that [math]\displaystyle{ {{\mathbf Y}}^{{\rm T}}{\mathbf Y}{\mathbf =}{\mathbf I} }[/math] is the sum of the [math]\displaystyle{ K }[/math] largest eigenvalues of [math]\displaystyle{ \tilde{{\mathbf W}}={{\mathbf D}}^{{\mathbf -}{{\rm 1}}/{{\rm 2}}}{\mathbf W}{{\mathbf D}}^{{\mathbf -}{{\rm 1}}/{{\rm 2}}} }[/math]. It is attained at all [math]\displaystyle{ {\mathbf Y} }[/math] of the form [math]\displaystyle{ {\mathbf Y}{\rm =}{\mathbf U}{{\mathbf B}}_{{\rm 1}} }[/math] where [math]\displaystyle{ {\mathbf U}\in {{\mathbb R}}^{P\times K} }[/math] is any orthonormal basis of the [math]\displaystyle{ K }[/math]-th principal subspace of [math]\displaystyle{ {{\tilde{\mathbf {W}}}} }[/math] and [math]\displaystyle{ {{\mathbf B}}_{{\rm 1}} }[/math] is an arbitrary orthogonal matrix in [math]\displaystyle{ {{\mathbb R}}^{K\times K} }[/math].
Since [math]\displaystyle{ {{\mathbf B}}_{{\mathbf 1}} }[/math] is an arbitrary orthogonal matrix, let it be an identity matrix, so we have [math]\displaystyle{ {{\mathbf Y}}_{{\mathbf {opt}}}{\rm =}{\mathbf U} }[/math]
The optimal solution[math]\displaystyle{ {\mathbf \ }{{\mathbf Y}}_{{\mathbf {opt}}} }[/math] for the relaxed problem in general does not satisfy the constraint (1a), therefore we would like to find a candidate solution of the original optimization problem which is close to the optimal solution [math]\displaystyle{ {{\mathbf Y}}_{{\mathbf {opt}}} }[/math]. This is called rounding.
Rounding
As we know that given a partition [math]\displaystyle{ {\mathbf E} }[/math], the candidate solution of the original optimization problem can be [math]\displaystyle{ {{\mathbf Y}}_{{\mathbf {part}}}{\mathbf =}{{\mathbf D}}^{{{\rm 1}}/{{\rm 2}}}{\mathbf E}{\left({{\mathbf E}}^{{\rm T\ }}{\mathbf DE}\right)}^{{\mathbf -}{{\rm 1}}/{{\rm 2}}} }[/math]. Therefore we want to compare [math]\displaystyle{ {{\mathbf Y}}_{{\mathbf {opt}}} }[/math] with [math]\displaystyle{ {{\mathbf Y}}_{{\mathbf {part}}} }[/math]. Since both [math]\displaystyle{ {{\mathbf Y}}_{{\mathbf {opt}}} }[/math] and [math]\displaystyle{ {{\mathbf Y}}_{{\mathbf {part}}} }[/math] are orthogonal matrices and their column vectors span the [math]\displaystyle{ K }[/math] dimension subspaces, it makes sense to compare [math]\displaystyle{ {{\mathbf Y}}_{{\mathbf {opt}}} }[/math] and [math]\displaystyle{ {{\mathbf Y}}_{{\mathbf {part}}} }[/math] by comparing the subspaces spanned by their column vectors. One of the common way is to compare the subspaces is to compare the orthogonal projections on those subspaces. That is, to compute the Frobenius norm between [math]\displaystyle{ {{\mathbf Y}}_{{\mathbf {opt}}}{{\mathbf Y}}^{{\rm T}}_{{\mathbf {opt}}} }[/math] and [math]\displaystyle{ {{\mathbf Y}}_{{\mathbf {part}}}{{\mathbf Y}}^{{\rm T}}_{{\mathbf {part}}} }[/math].
The cost function or the difference between [math]\displaystyle{ {{\mathbf Y}}_{{\mathbf {opt}}} }[/math] and [math]\displaystyle{ {{\mathbf Y}}_{{\mathbf {part}}} }[/math] is defined as
[math]\displaystyle{ J_1(\mathbf{W,E})=\frac {1} {2} \|\mathbf{Y^{\rm T}_{opt} Y_{opt}-Y^{\rm T}_{part} Y_{part}} \|^2_F=\frac {1} {2} \|\mathbf{U^{\rm T} U-D^{\rm {-1/2}}E(E^{\rm T}DE)^{\rm -1}E^{\rm T}D^{\rm {-1/2}}}\|^2_F }[/math]
We want to minimize [math]\displaystyle{ J_1\left({\mathbf W},{\mathbf E}\right) }[/math], the difference between [math]\displaystyle{ {{\mathbf Y}}_{{\mathbf {opt}}} }[/math] and [math]\displaystyle{ {{\mathbf Y}}_{{\mathbf {part}}} }[/math].
After Expansion, we have [math]\displaystyle{ J_1\left({\mathbf W},{\mathbf E}\right)=K-tr\left({{{\mathbf E}}^{{\rm T\ }}{{\mathbf D}}^{{{\rm 1}}/{{\rm 2}}}{\mathbf U}{{\mathbf U}}^{{\rm T}}{{\mathbf D}}^{{{\rm 1}}/{{\rm 2}}}{\mathbf E}\left({{\mathbf E}}^{{\rm T\ }}{\mathbf {DE}}\right)}^{{\mathbf -}{\rm 1}}\right) }[/math].
Compared to the normalized cut [math]\displaystyle{ C\left({\mathbf W},{\mathbf E}\right)=K-tr\left({{\mathbf E}}^{{\rm T}}{\mathbf {WE}}{\left({{\mathbf E}}^{{\rm T}}{\mathbf {DE}}\right)}^{{\mathbf -}{\rm 1}}\right) }[/math],
We notice that [math]\displaystyle{ J_1\left({\mathbf W},{\mathbf E}\right)=C\left({\mathbf W},{\mathbf E}\right) }[/math] if [math]\displaystyle{ {{\mathbf D}}^{{{\rm 1}}/{{\rm 2}}}{\mathbf U}{{\mathbf U}}^{{\rm T}}{{\mathbf D}}^{{{\rm 1}}/{{\rm 2}}}={\mathbf W} }[/math], that is, [math]\displaystyle{ {\mathbf U}{{\mathbf U}}^{{\rm T}}={{\mathbf D}}^{{\mathbf -}{{\rm 1}}/{{\rm 2}}}{\mathbf \ }{\mathbf W}{{\mathbf D}}^{{\mathbf -}{{\rm 1}}/{{\rm 2}}}=\tilde{{\mathbf W}} }[/math]
In the paper, it says if [math]\displaystyle{ {\mathbf W} }[/math] has rank equal to [math]\displaystyle{ K }[/math], then [math]\displaystyle{ J_1\left({\mathbf W},{\mathbf E}\right) }[/math] is exactly the normalized cut [math]\displaystyle{ C\left({\mathbf W},{\mathbf E}\right) }[/math]. Here I doubt its assertion. Instead, it can be asserted that if [math]\displaystyle{ \tilde{{\mathbf W}} }[/math] can be decomposed into [math]\displaystyle{ {\mathbf U}{{\mathbf U}}^{{\rm T}} }[/math], where [math]\displaystyle{ {\mathbf U}\in {{\mathbb R}}^{P\times K} }[/math] is any orthonormal basis of the [math]\displaystyle{ K }[/math]-th principal subspace of [math]\displaystyle{ \tilde{{\mathbf W}} }[/math], then [math]\displaystyle{ {\mathbf W} }[/math] has rank equal to [math]\displaystyle{ K }[/math] and [math]\displaystyle{ J_1\left({\mathbf W},{\mathbf E}\right) }[/math] is exactly the normalized cut [math]\displaystyle{ C\left({\mathbf W},{\mathbf E}\right) }[/math].
In general, [math]\displaystyle{ {\mathbf U}{{\mathbf U}}^{{\rm T}} }[/math] could be a bad approximation of [math]\displaystyle{ \tilde{{\mathbf W}} }[/math], and hence [math]\displaystyle{ J_1\left({\mathbf W},{\mathbf E}\right) }[/math] could be a bad approximation of [math]\displaystyle{ C\left({\mathbf W},{\mathbf E}\right) }[/math]. That is, the rounding error could be not close to the normalized cut. So what justify this rounding scheme? The optimal partition [math]\displaystyle{ \mathbf E }[/math] for [math]\displaystyle{ J_1(\mathbf{W,E}) }[/math] is not a close optimal solution for minimizing normalized cut. It is interesting to know its relationship with normalized cut, e.g. are they having close performance in clustering, however the paper does not mention it.
Theorem 3
[math]\displaystyle{ J_1(\mathbf{W,E})=\sum^K_{k=1}\sum_{\mathbf {x}_j \in C_k}\|\mathbf{u}_j-d^{\rm {1/2}}_j \boldsymbol{\mu}_k\|^2 }[/math]
Where [math]\displaystyle{ {{\mathbf u}}_j }[/math] is the [math]\displaystyle{ j }[/math]-th row of [math]\displaystyle{ {\mathbf U} }[/math] and hence a low dimension representation of data point [math]\displaystyle{ {{\mathbf x}}_j }[/math], [math]\displaystyle{ d_j={\mathbf \ }{{\mathbf D}}_{jj} }[/math] and [math]\displaystyle{ {{\boldsymbol{\mu} }}_k{\mathbf =}{\sum_{{{\mathbf x}}_j\in C_k}{d^{{1}/{2}}_j}{{\mathbf u}}_j}/{\sum_{{{\mathbf x}}_j\in C_k}{d_j}} }[/math]
Compared to the objective function of K-means clustering
[math]\displaystyle{ J=\sum^K_{k=1}{\sum_{{\mathbf x}\in C_k}{{\|{\mathbf x}{\mathbf -}{{\boldsymbol{\mu} }}_k\|}^2}} }[/math].
It is quite similar, except that now [math]\displaystyle{ {{\mathbf u}}_j }[/math] the low dimension representation of data point [math]\displaystyle{ {{\mathbf x}}_j }[/math] is the input and the mean of the cluster [math]\displaystyle{ {{\boldsymbol{\mu} }}_k }[/math] is a weighted one.
Spectral Clustering using weighted K-means
So a spectral clustering algorithm that minimizes [math]\displaystyle{ J_1\left({\mathbf W},{\mathbf E}\right) }[/math] with respect to [math]\displaystyle{ {\mathbf E} }[/math] with weighted K-means is proposed. Using K-means will find a local minima solution for [math]\displaystyle{ J_1\left({\mathbf W},{\mathbf E}\right) }[/math].
Input: Similarity matrix [math]\displaystyle{ {\mathbf W}\in {{\mathbb R}}^{P\times P} }[/math]
Algorithm:
1. Compute first [math]\displaystyle{ K }[/math] eigenvectors [math]\displaystyle{ {\mathbf U}\in {{\mathbb R}}^{P\times K} }[/math] of [math]\displaystyle{ {{\mathbf D}}^{{\mathbf -}{{\rm 1}}/{{\rm 2}}}{\mathbf W}{{\mathbf D}}^{{\mathbf -}{{\rm 1}}/{{\rm 2}}} }[/math] where [math]\displaystyle{ {\mathbf D}{\mathbf =}{\rm Diag(}{\mathbf W}\cdot {\mathbf 1}{\rm )} }[/math].
2. Let [math]\displaystyle{ {{\mathbf u}}_i }[/math] be the [math]\displaystyle{ i }[/math]-th row of [math]\displaystyle{ {\mathbf U} }[/math] and [math]\displaystyle{ d_i={\mathbf \ }{{\mathbf D}}_{ii} }[/math].
3. Initialize partition [math]\displaystyle{ C }[/math].
4. Weighted K-means: While partition [math]\displaystyle{ C }[/math] is not stationary,
a. For [math]\displaystyle{ k=1,\dots ,K }[/math], [math]\displaystyle{ {{\boldsymbol{ \mu} }}_k{\mathbf =}{\sum_{{{\mathbf x}}_j\in C_k}{d^{{1}/{2}}_j}{{\mathbf u}}_j}/{\sum_{{{\mathbf x}}_j\in C_k}{d_j}} }[/math]
b. For [math]\displaystyle{ i=1,\dots ,P }[/math], assign [math]\displaystyle{ {{\mathbf x}}_i }[/math] to [math]\displaystyle{ C_k }[/math] where [math]\displaystyle{ k={\arg {\mathop{\min }_{k^'} \|{{\mathbf u}}_j{\mathbf -}d^{{1}/{2}}_j{{\boldsymbol{ \mu} }}_{k^'}\|\ } } }[/math]
Output: partition [math]\displaystyle{ C }[/math], distortion measure [math]\displaystyle{ \sum^K_{k=1}\sum_{\mathbf {x}_j \in C_k}\|\mathbf{u}_j-d^{\rm {1/2}}_j \boldsymbol{\mu}_k\|^2 }[/math].
Relationship among minimizing normalized cut, minimizing [math]\displaystyle{ J_1\left({\mathbf W},{\mathbf E}\right) }[/math] and Spectral clustering using weighted K-means is shown below.

Alternative cost function [math]\displaystyle{ J_2\left({\mathbf W},{\mathbf E}\right) }[/math]
Remember that the cost function [math]\displaystyle{ J_1\left({\mathbf W},{\mathbf E}\right){\mathbf =}\frac{{\rm 1}}{{\rm 2}}{\|{\mathbf U}{{\mathbf U}}^{{\rm T}}{\rm -}{{\mathbf Y}}_{{\mathbf {part}}}{{\mathbf Y}}^{{\rm T}}_{{\mathbf {part}}}\|}^{{\rm 2}}_F }[/math]
Let [math]\displaystyle{ {\mathbf V} }[/math] come from multiplying [math]\displaystyle{ {\mathbf U} }[/math] by [math]\displaystyle{ {{\mathbf D}}^{{\mathbf -}{{\rm 1}}/{{\rm 2}}} }[/math] and re-orthogonalizing, that is, [math]\displaystyle{ {\mathbf V}{\mathbf =}{{\mathbf D}}^{{\mathbf -}{{\rm 1}}/{{\rm 2}}}{\mathbf U}{\left({{\mathbf U}}^{{\rm T}}{{\mathbf D}}^{{\mathbf -}1}{\mathbf U}\right)}^{{{\rm -}{\rm 1}}/{{\rm 2}}} }[/math], and [math]\displaystyle{ {{\mathbf Y}{\mathbf '}}_{{\mathbf {part}}} }[/math] comes from multiplying [math]\displaystyle{ {{\mathbf Y}}_{{\mathbf {part}}} }[/math] by [math]\displaystyle{ {{\mathbf D}}^{{\mathbf -}{{\rm 1}}/{{\rm 2}}} }[/math] and re-orthogonalizing, that is, [math]\displaystyle{ {{\mathbf Y}{\mathbf '}}_{{\mathbf {part}}}{\rm =}{\mathbf E}{\left({{\mathbf E}}^{{\rm T\ }}{\mathbf E}\right)}^{{\mathbf -}{\rm 1}}{{\mathbf E}}^{{\rm T}} }[/math]
Replacing [math]\displaystyle{ {\mathbf U} }[/math] and [math]\displaystyle{ {{\mathbf Y}}_{{\mathbf {part}}} }[/math] by [math]\displaystyle{ {\mathbf V} }[/math] and [math]\displaystyle{ {{\mathbf Y}{\mathbf '}}_{{\mathbf {part}}} }[/math] respectively in [math]\displaystyle{ J_1\left({\mathbf W},{\mathbf E}\right) }[/math], we obtain a new cost function
[math]\displaystyle{ J_2\left({\mathbf W},{\mathbf E}\right){\mathbf =}\frac{{\rm 1}}{{\rm 2}}{\|{\mathbf V}{{\mathbf V}}^{{\rm T}}{\rm -}{\mathbf E}{\left({{\mathbf E}}^{{\rm T\ }}{\mathbf E}\right)}^{{\mathbf -}{\rm 1}}{{\mathbf E}}^{{\rm T}}\|}^{{\rm 2}}_F }[/math]
In the paper, two versions of [math]\displaystyle{ {\mathbf V} }[/math]is used, which I think is not correct. One is [math]\displaystyle{ {\mathbf V}{\mathbf =}{{\mathbf D}}^{{{\rm 1}}/{{\rm 2}}}{\mathbf U}{\left({{\mathbf U}}^{{\rm T}}{{\mathbf D}}^{{\mathbf -}1}{\mathbf U}\right)}^{{{\rm -}{\rm 1}}/{{\rm 2}}} }[/math] and the other is [math]\displaystyle{ {\mathbf V}{\mathbf =}{{\mathbf D}}^{{{\rm 1}}/{{\rm 2}}}{\mathbf U}{\left({{\mathbf U}}^{{\rm T}}{\mathbf DU}\right)}^{{{\rm -}{\rm 1}}/{{\rm 2}}} }[/math]. For [math]\displaystyle{ J_2\left({\mathbf W},{\mathbf E}\right) }[/math], I think it is not good formulated compared to [math]\displaystyle{ J_1\left({\mathbf W},{\mathbf E}\right) }[/math]. I can't figure out which relaxation problem it comes from and what is the relationship between [math]\displaystyle{ J_2\left({\mathbf W},{\mathbf E}\right) }[/math] and the normalized cut.
Theorem 4
[math]\displaystyle{ J_2\left({\mathbf W},{\mathbf E}\right)=\sum^K_{k=1}{\sum_{{{\mathbf x}}_j\in C_k}{{\|{{\mathbf v}}_j{\mathbf -}{{\boldsymbol{\mu} }}_k\|}^2}} }[/math]
Where [math]\displaystyle{ {{\mathbf v}}_j }[/math] is the [math]\displaystyle{ j }[/math]-th row of [math]\displaystyle{ {\mathbf V} }[/math] and hence a low dimension representation of data point [math]\displaystyle{ {{\mathbf x}}_j }[/math] and [math]\displaystyle{ {{\boldsymbol{\mu} }}_k{\mathbf =}\frac{{\rm 1}}{\left|C_k\right|}\sum_{{{\mathbf x}}_j\in C_k}{{{\mathbf v}}_j} }[/math]
It is the same with the objective function of K-means expect that [math]\displaystyle{ {{\mathbf v}}_j }[/math] the low dimension representation of data point [math]\displaystyle{ {{\mathbf x}}_j }[/math]is the input.
Spectral clustering using K-means algorithm
Input: Similarity matrix [math]\displaystyle{ {\mathbf W}\in {{\mathbb R}}^{P\times P} }[/math].
Algorithm:
1. Compute first [math]\displaystyle{ K }[/math] eigenvectors [math]\displaystyle{ {\mathbf U}\in {{\mathbb R}}^{P\times K} }[/math] of [math]\displaystyle{ {{\mathbf D}}^{{\rm -}{{\rm 1}}/{{\rm 2}}}{\mathbf W}{{\mathbf D}}^{{\rm -}{{\rm 1}}/{{\rm 2}}} }[/math] where [math]\displaystyle{ {\mathbf D}{\rm =Diag(}{\mathbf W}\cdot {\mathbf 1}{\rm )} }[/math].
2. Let [math]\displaystyle{ {\mathbf V}{\rm =}{{\mathbf D}}^{{{\rm -1}}/{{\rm 2}}}{\mathbf U}{\left({{\mathbf U}}^{{\rm T}}{{\mathbf D}}^{{\rm -}{\rm 1}}{\mathbf U}\right)}^{{{\rm -}{\rm 1}}/{{\rm 2}}} }[/math]
3. Let [math]\displaystyle{ {{\mathbf v}}_i }[/math] be the [math]\displaystyle{ i }[/math]-th row of [math]\displaystyle{ {\mathbf V} }[/math].
4. Initialize partition [math]\displaystyle{ C }[/math].
5. K-means: While partition [math]\displaystyle{ C }[/math] is not stationary,
a. For [math]\displaystyle{ {\rm k=1,}\dots {\rm ,}K }[/math], [math]\displaystyle{ {{\boldsymbol{\mu} }}_k{\mathbf =}\frac{{\rm 1}}{\left|C_k\right|}\sum_{{{\mathbf x}}_j\in C_k}{{{\mathbf v}}_j} }[/math]
b. For [math]\displaystyle{ {\rm i=1,}\dots {\rm ,}P }[/math], assign [math]\displaystyle{ {{\mathbf x}}_i }[/math] to [math]\displaystyle{ C_k }[/math] where [math]\displaystyle{ k{\rm =}{\arg {\mathop{\min }_{k^{{\rm '}}} \|{{\mathbf v}}_j{\rm -}{{\boldsymbol{\mu} }}_{k^{{\rm '}}}\|\ }\ } }[/math]
Output: partition [math]\displaystyle{ C }[/math], distortion measure [math]\displaystyle{ \sum^K_{k=1}{\sum_{{{\mathbf x}}_j\in C_k}{{\|{{\mathbf v}}_j{\mathbf -}{{\boldsymbol{\mu} }}_k\|}^2}} }[/math].
Learning the Similarity Matrix
In clustering, the similarity matrix [math]\displaystyle{ {\mathbf W} }[/math] is given, and the goal is to find a partition [math]\displaystyle{ {\mathbf E} }[/math] minimizing the objective function. In this section, the partition [math]\displaystyle{ {\mathbf E} }[/math] is assumed to be given and our goal is to learn the similarity matrix [math]\displaystyle{ {\mathbf W} }[/math].
Trivial solution
If no constraint is put on [math]\displaystyle{ {\mathbf W} }[/math], given a dataset with partition [math]\displaystyle{ {\mathbf E} }[/math], the trivial solution would be any matrix that is block-constant with the appropriate blocks, that is, the matrix that sets the similarity between points in the same cluster large and the similarity between points in different clusters 0.
The meaningful formulation
We have a parametric form for [math]\displaystyle{ {\mathbf W} }[/math], which is a function of a vector variable [math]\displaystyle{ {\boldsymbol{\alpha} }\in {{\mathbb R}}^F }[/math], denote it as [math]\displaystyle{ {\mathbf W}\left({\boldsymbol{\alpha} }\right) }[/math]. Given datasets with known partition [math]\displaystyle{ {\mathbf E} }[/math], we would like to learn [math]\displaystyle{ {\boldsymbol{\alpha} } }[/math] such that the distance between the true partition and the partition we obtained from clustering algorithm using [math]\displaystyle{ {\mathbf W}\left({\boldsymbol{\alpha} }\right) }[/math] is minimized and hopefully it generalizes to the unseen dataset with similar structure. In the paper, diagonally-scaled Gaussian kernel matrices are considered.
[math]\displaystyle{ \mathbf W(\boldsymbol{\alpha})(i,j)= \rm exp (-(\mathbf{x}_i-\mathbf{x}_j)^{\rm T}Diag(\boldsymbol{\alpha})(\mathbf{x}_i-\mathbf{x}_j) ) }[/math]
Moreover, the elements in [math]\displaystyle{ {\boldsymbol{\alpha} } }[/math] are in one-to-one correspondence with the features; setting one of these parameters to zero is equivalent to ignoring the corresponding feature. Labeled data sets are available for the speech separation and image segmentation.
Relationship with distance metric learning
this formulation is similar with the distance metric learning we learned in class. Although here it does not emphasize to learn a metric such that similar points are close and dissimilar points are far apart, it is interesting to know if we use the distance metric learning to learn [math]\displaystyle{ {\boldsymbol{\alpha} } }[/math], apply it to obtain the similarity matrix for unseen data and do clustering, how is the performance? Would it be overfitting?
Distance between partitions
Let [math]\displaystyle{ {\mathbf E}{\mathbf =}({{\mathbf e}}_1,\dots ,{{\mathbf e}}_R) }[/math] and [math]\displaystyle{ {\mathbf F}{\mathbf =}({{\mathbf f}}_1,\dots ,{{\mathbf f}}_S) }[/math] be two partitions of [math]\displaystyle{ P }[/math] data points, the distance between these partitions is defined as
[math]\displaystyle{ D\left({\mathbf E},{\mathbf F}\right)=\frac{1}{\sqrt{2}}{\|{{\mathbf E}\left({{\mathbf E}}^{{\rm T\ }}{\mathbf E}\right)}^{{\mathbf -}{\rm 1}}{{\mathbf E}}^{{\rm T\ }}-{{\mathbf F}\left({{\mathbf F}}^{{\rm T\ }}{\mathbf F}\right)}^{{\mathbf -}{\rm 1}}{{\mathbf F}}^{{\rm T\ }}\|}_F }[/math]
Naive approach
Minimizing the distance between true partition [math]\displaystyle{ {\mathbf E} }[/math] and the partition [math]\displaystyle{ {\mathbf E}\left({\mathbf W}\right) }[/math] we obtain from spectral clustering. However, it is hard to optimize since K-means algorithm is a non-continuous map and makes the cost function non-continuous.
Theorem 5
Let [math]\displaystyle{ \eta ={{\mathop{\max }_{{{\mathbf x}}_i} {{\mathbf D}}_{ii}\ }}/{{\mathop{\min }_{{{\mathbf x}}_i} {{\mathbf D}}_{ii}\ }}\ge 1 }[/math], [math]\displaystyle{ {{\mathbf E}}_{{\mathbf 1}}\left({\mathbf W}\right){\mathbf =}{\arg {\mathop{\min }_{{\mathbf E}} J_1\left({\mathbf W},{\mathbf E}\right)\ }\ } }[/math] and [math]\displaystyle{ {{\mathbf E}}_{{\mathbf 2}}\left({\mathbf W}\right){\mathbf =}{\arg {\mathop{\min }_{{\mathbf E}} J_2\left({\mathbf W},{\mathbf E}\right)\ }\ } }[/math], we have
[math]\displaystyle{ {D\left({\mathbf E},{{\mathbf E}}_{{\mathbf 1}}\left({\mathbf W}\right)\right)}^2\le 4\eta J_1\left({\mathbf W},{\mathbf E}\right) }[/math]
and
[math]\displaystyle{ {D\left({\mathbf E},{{\mathbf E}}_{{\mathbf 2}}\left({\mathbf W}\right)\right)}^2\le 4J_2\left({\mathbf W},{\mathbf E}\right) }[/math]
This theorem shows that instead of minimizing [math]\displaystyle{ D\left({\mathbf E},{\mathbf E}\left({\mathbf W}\right)\right) }[/math], we can minimize its upper bound [math]\displaystyle{ J\left({\mathbf W},{\mathbf E}\right) }[/math], if we can obtain [math]\displaystyle{ {\mathbf W} }[/math] which produces small [math]\displaystyle{ J\left({\mathbf W},{\mathbf E}\right) }[/math], [math]\displaystyle{ {\mathbf E}\left({\mathbf W}\right) }[/math] will be close to [math]\displaystyle{ {\mathbf E} }[/math]
Approximation of eigensubspace
Given a matrix [math]\displaystyle{ {\mathbf M}\in {{\mathbb R}}^{P\times P} }[/math], let [math]\displaystyle{ {\mathbf U}\in {{\mathbb R}}^{P\times K} }[/math] denote any orthonormal basis of the [math]\displaystyle{ K }[/math]-th principal subspace of [math]\displaystyle{ {\mathbf M} }[/math]. Eigensubspace of [math]\displaystyle{ {\mathbf M} }[/math] can be approximated as [math]\displaystyle{ {{\mathbf M}}^q{\mathbf V} }[/math] where [math]\displaystyle{ {\mathbf V}\in {{\mathbb R}}^{P\times K} }[/math], [math]\displaystyle{ q }[/math] is the power we used. [math]\displaystyle{ {\mathbf U} }[/math] can be approximated as [math]\displaystyle{ {{\mathbf M}}^q{\mathbf V}{\left({\left({{\mathbf M}}^q{\mathbf V}\right)}^{{\rm T}}{{\mathbf M}}^q{\mathbf V}\right)}^{{\mathbf -}{{\rm 1}}/{{\rm 2}}} }[/math] by orthonormalizing. The approximation of orthogonal projection [math]\displaystyle{ {\mathbf U}{{\mathbf U}}^{{\rm T}} }[/math] is [math]\displaystyle{ {{\mathbf M}}^q{\mathbf V}{\left({\left({{\mathbf M}}^q{\mathbf V}\right)}^{{\rm T}}{{\mathbf M}}^q{\mathbf V}\right)}^{{\mathbf -}{\rm 1}}{{\mathbf V}}^{{\rm T}}{{\mathbf M}}^q }[/math]
Derivative of orthogonal projection [math]\displaystyle{ {\mathbf \Pi }={\mathbf U}{{\mathbf U}}^{{\rm T}} }[/math]
[math]\displaystyle{ d{\mathbf \Pi }{\mathbf =}{\mathbf U}{{\mathbf N}}^{{\rm T}}{\rm +}{\mathbf N}{{\mathbf U}}^{{\rm T}} }[/math] can be obtained by solving the following linear system:
[math]\displaystyle{ {\mathbf {MN}}{\mathbf -}{\mathbf N}{{\mathbf U}}^{{\rm T}}{\mathbf {MU}}{\mathbf =-}\left({\mathbf I}{\mathbf -}{\mathbf U}{{\mathbf U}}^{{\rm T}}\right)d{\mathbf {MU}} }[/math] and [math]\displaystyle{ {{\mathbf U}}^{{\rm T}}{\mathbf N}{\mathbf =}{\mathbf 0} }[/math]
Approximation of the cost function [math]\displaystyle{ J\left({\mathbf W},{\mathbf E}\right) }[/math]
Let [math]\displaystyle{ {\mathbf F} }[/math] be a random partition of the dataset, [math]\displaystyle{ {\mathbf V}\in {{\mathbb R}}^{{ P}\times { K}} }[/math] be [math]\displaystyle{ {{\mathbf D}}^{{{\rm 1}}/{{\rm 2}}}{\mathbf F} }[/math], the approximated orthonormal basis of the [math]\displaystyle{ {K} }[/math]-th principal subspace of [math]\displaystyle{ \tilde{{\mathbf W}} }[/math] is [math]\displaystyle{ {{\mathbf U}{\mathbf '=}\tilde{{\mathbf W}}}^q{\mathbf V}{\left({\left({\tilde{{\mathbf W}}}^q{\mathbf V}\right)}^{{\rm T}}{\tilde{{\mathbf W}}}^q{\mathbf V}\right)}^{{\mathbf -}{{\rm 1}}/{{\rm 2}}} }[/math]
The approximated function for [math]\displaystyle{ J_1\left({\mathbf W},{\mathbf E}\right) }[/math] is
[math]\displaystyle{ F_1\left({\mathbf W},{\mathbf E}\right){\mathbf =}\frac{{\rm 1}}{{\rm 2}}{\|{\mathbf U}{\mathbf '}{{\mathbf U}{\mathbf '}}^{{\rm T}}{\rm -}{{\mathbf D}}^{{{\rm 1}}/{{\rm 2}}}{\mathbf E}{\left({{\mathbf E}}^{{\rm T\ }}{\mathbf {DE}}\right)}^{{\mathbf -}{\rm 1}}{{\mathbf E}}^{{\rm T}}{{\mathbf D}}^{{{\rm 1}}/{{\rm 2}}}\|}^{{\rm 2}}_F }[/math]
and
The approximated function for [math]\displaystyle{ J_2\left({\mathbf W},{\mathbf E}\right) }[/math] is
[math]\displaystyle{ F_2\left({\mathbf W},{\mathbf E}\right)=\frac{{\rm 1}}{{\rm 2}}{\|{\mathbf V}{\mathbf '}{{\mathbf V}{\mathbf '}}^{{\rm T}}{\rm -}{\mathbf E}{\left({{\mathbf E}}^{{\rm T\ }}{\mathbf E}\right)}^{{\mathbf -}{\rm 1}}{{\mathbf E}}^{{\rm T}}\|}^{{\rm 2}}_F }[/math]
Where [math]\displaystyle{ {{\mathbf V}}^{{\mathbf '}}{\mathbf =}{{\mathbf D}}^{{\mathbf -}{{\rm 1}}/{{\rm 2}}}{\mathbf U}{\mathbf '}{\left({{\mathbf U}{\mathbf '}}^{{\rm T}}{{\mathbf D}}^{{\mathbf -}{\mathbf 1}}{\mathbf U}{\mathbf '}\right)}^{{\mathbf -}{{\rm 1}}/{{\rm 2}}} }[/math]
Learning Algorithm
Given [math]\displaystyle{ N }[/math] datasets [math]\displaystyle{ X_n }[/math] [math]\displaystyle{ n=1,2,\dots ,N }[/math], with known partition [math]\displaystyle{ {{\mathbf E}}_n }[/math], the similarity matrix for each dataset is denoted as [math]\displaystyle{ {{\mathbf W}}_n\left({\boldsymbol{\alpha} }\right) }[/math]. The cost function used for learning [math]\displaystyle{ {\boldsymbol{\alpha} } }[/math]is
[math]\displaystyle{ H\left({\boldsymbol{\alpha} }\right)=\frac{1}{N}\sum^N_{n=1}{F\left({{\mathbf W}}_n\left({\boldsymbol{\alpha} }\right),{{\mathbf E}}_n\right)}+\gamma {\|{\boldsymbol{\alpha}}\|}_1 }[/math]
Where [math]\displaystyle{ \gamma }[/math] is some constant, and the [math]\displaystyle{ L_1 }[/math] norm of [math]\displaystyle{ {\boldsymbol{\alpha} } }[/math] serves as a feature selection term, tending to make the solution sparse. The learning algorithm is to minimize [math]\displaystyle{ H\left({\boldsymbol{\alpha} }\right) }[/math] with respect to [math]\displaystyle{ {\boldsymbol{\alpha} } }[/math], using the method of gradient descent.
Experiment
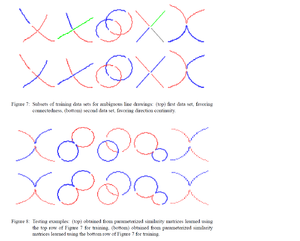
After learning [math]\displaystyle{ {\boldsymbol{\alpha} } }[/math] from the training data set, spectral clustering algorithm is applied to the testing dataset with the similarity matrix generated by [math]\displaystyle{ {\boldsymbol{\alpha} } }[/math]. The figures are from the paper, obviously the authors have some error in the description. The top row and the bottom row of the figure 8 should be switched.
The speech signal is mixed from two English spearkers. After learning the parameters, spetral clustering is able to sperate the mixed signals.

Appendix
Proof for Theorem 1
Substitute [math]\displaystyle{ {\mathbf Y} }[/math] in (1b) using (1a), we have
[math]\displaystyle{ {{{\mathbf \Lambda }}^{{\rm T}}{{\mathbf E}}^{{\rm T\ }}{\mathbf D}}^{{{\rm 1}}/{{\rm 2}}}{{\mathbf D}}^{{{\rm 1}}/{{\rm 2}}}{\mathbf E}{\mathbf \Lambda }{\mathbf =}{\mathbf I} }[/math]
so
[math]\displaystyle{ {{{{\mathbf \Lambda }}^{{\rm T}}\left({{\mathbf E}}^{{\rm T\ }}{\mathbf {DE}}\right)}^{{{\rm 1}}/{{\rm 2}}}{\mathbf \ }\left({{\mathbf E}}^{{\rm T\ }}{\mathbf {DE}}\right)}^{{{\rm 1}}/{{\rm 2}}}{\mathbf \Lambda }{\mathbf =}{\left({{\mathbf E}}^{{\rm T\ }}{\mathbf {DE}}\right)}^{{{\rm 1}}/{{\rm 2}}}{\mathbf \Lambda }{{{\mathbf \Lambda }}^{{\rm T}}\left({{\mathbf E}}^{{\rm T\ }}{\mathbf {DE}}\right)}^{{{\rm 1}}/{{\rm 2}}}{\mathbf =}{\mathbf I} }[/math]
So we finally have [math]\displaystyle{ {\mathbf \Lambda }{{\mathbf \Lambda }}^{{\rm T}}{\mathbf =}{\left({{\mathbf E}}^{{\rm T\ }}{\mathbf {DE}}\right)}^{{\mathbf -}{\rm 1}} }[/math]
For all [math]\displaystyle{ {\mathbf Y} }[/math] satisfies the constraints, we can find corresponding [math]\displaystyle{ {\mathbf E} }[/math] and [math]\displaystyle{ {\mathbf \Lambda } }[/math]such that
[math]\displaystyle{ K-tr\left({{\mathbf Y}}^{{\rm T}}\left({{\mathbf D}}^{{\mathbf -}{{\rm 1}}/{{\rm 2}}}{\mathbf W}{{\mathbf D}}^{{\mathbf -}{{\rm 1}}/{{\rm 2}}}\right){\mathbf Y}\right) }[/math]
[math]\displaystyle{ =K-tr\left({{{{{{\mathbf \Lambda }}^{{\rm T}}{\mathbf E}}^{{\rm T\ }}{\mathbf D}^{{{\rm 1}}/{{\rm 2}}}}{\mathbf D}^{{\mathbf -}{{\rm 1}}/{{\rm 2}}}}{\mathbf W}{{\mathbf D}}^{{\mathbf -}{{\rm 1}}/{{\rm 2}}}{\mathbf D}^{\rm{1/2}}}{\mathbf E}{\mathbf \Lambda }\right) }[/math]
[math]\displaystyle{ =K-tr\left({{\mathbf E}}^{{\rm T\ }}{\mathbf {WE}}{\mathbf \Lambda }{{\mathbf \Lambda }}^{{\rm T}}\right) }[/math]
[math]\displaystyle{ =K-tr\left({{\mathbf E}}^{{\rm T\ }}{\mathbf {WE}}{\left({{\mathbf E}}^{{\rm T\ }}{\mathbf {DE}}\right)}^{{\mathbf -}{\rm 1}}\right) }[/math]
[math]\displaystyle{ =C\left({\mathbf W},{\mathbf E}\right) }[/math]
[math]\displaystyle{ =Ncut\left(C\right) }[/math]
[math]\displaystyle{ J_1\left({\mathbf W},{\mathbf E}\right) }[/math] Expansion
[math]\displaystyle{ J_1\left({\mathbf W},{\mathbf E}\right){\mathbf =}\frac{{\rm 1}}{{\rm 2}}{\|{{\mathbf Y}}_{{\mathbf {opt}}}{{\mathbf Y}}^{{\rm T}}_{{\mathbf {opt}}}{\rm -}{{\mathbf Y}}_{{\mathbf {part}}}{{\mathbf Y}}^{{\rm T}}_{{\mathbf {part}}}\|}^{{\rm 2}}_F }[/math]
[math]\displaystyle{ =\frac{{\rm 1}}{{\rm 2}}tr\left({\mathbf U}{{\mathbf U}}^{{\rm T}}{\rm +}{{\mathbf Y}}_{{\mathbf {part}}}{{\mathbf Y}}^{{\rm T}}_{{\mathbf {part}}}{\rm -}{\rm 2}{\mathbf U}{{\mathbf U}}^{{\rm T}}{{\mathbf Y}}_{{\mathbf {part}}}{{\mathbf Y}}^{{\rm T}}_{{\mathbf {part}}}\right) }[/math]
[math]\displaystyle{ =\frac{{\rm 1}}{{\rm 2}}K+\frac{{\rm 1}}{{\rm 2}}K-tr\left({\mathbf U}{{\mathbf U}}^{{\rm T}}{{\mathbf Y}}_{{\mathbf {part}}}{{\mathbf Y}}^{{\rm T}}_{{\mathbf {part}}}\right) }[/math]
[math]\displaystyle{ =K-tr\left({{{\mathbf E}}^{{\rm T\ }}{{\mathbf D}}^{{{\rm 1}}/{{\rm 2}}}{\mathbf U}{{\mathbf U}}^{{\rm T}}{{\mathbf D}}^{{{\rm 1}}/{{\rm 2}}}{\mathbf E}\left({{\mathbf E}}^{{\rm T\ }}{\mathbf {DE}}\right)}^{{\mathbf -}{\rm 1}}\right) }[/math]
Proof for Theorem 3
[math]\displaystyle{ \sum^K_{k=1}{\sum_{{{\mathbf x}}_j\in C_k}{{\|{{\mathbf u}}_j{\mathbf -}{d^{{1}/{2}}_j{\boldsymbol{\mu} }}_k\|}^2}} }[/math]
[math]\displaystyle{ =\sum^K_{k=1}{\sum_{{{\mathbf x}}_j\in C_k}{{\left({{\mathbf u}}_j{\mathbf -}{d^{{1}/{2}}_j{\boldsymbol{\mu} }}_k\right)}^{{\rm T}}\left({{\mathbf u}}_j{\mathbf -}{d^{{1}/{2}}_j{\boldsymbol{\mu} }}_k\right)}} }[/math]
[math]\displaystyle{ =\sum^K_{k=1}{\sum_{{{\mathbf x}}_j\in C_k}{{{\mathbf u}}^{{\rm T}}_j{{\mathbf u}}_j}}-2\sum^K_{k=1}{\sum_{{{\mathbf x}}_j\in C_k}{{d^{{1}/{2}}_j{\mathbf u}}^{{\rm T}}_j}}{{\boldsymbol{\mu} }}_k{\mathbf +}\sum^K_{k=1}{\sum_{{{\mathbf x}}_j\in C_k}{d_j{{\boldsymbol{\mu} }}^{{\rm T}}_k{{\boldsymbol{\mu} }}_k}} }[/math]
[math]\displaystyle{ =\sum^P_{j=1}{{{\mathbf u}}^{{\rm T}}_j{{\mathbf u}}_j}-\sum^K_{k=1}{\sum_{{{\mathbf x}}_j\in C_k}{{d^{{1}/{2}}_j{\mathbf u}}^{{\rm T}}_j}}\left(\sum_{{{\mathbf x}}_i\in C_k}{d^{{1}/{2}}_i}{{\mathbf u}}_i\right)\frac{1}{\sum_{{{\mathbf x}}_j\in C_k}{d_j}} }[/math]
[math]\displaystyle{ =\sum^P_{j=1}{\sum^K_{i=1}{{{ u}}_{ji}{{ u}}_{ji}}}-\sum^K_{k=1}{\frac{1}{\sum_{{{\mathbf x}}_j\in C_k}{d_j}}\sum_{{{\mathbf x}}_i,{{\mathbf x}}_j\in C_k}{{d^{{1}/{2}}_id^{{1}/{2}}_j{\mathbf u}}^{{\rm T}}_i}{{\mathbf u}}_j} }[/math]
[math]\displaystyle{ =K-\sum^K_{k=1}{\frac{1}{{{\mathbf e}}^{{\rm T}}_k{\mathbf D}{{\mathbf e}}_k}{{{\mathbf e}}^{{\rm T}}_k{\mathbf D}}^{{{\rm 1}}/{{\rm 2}}}{\mathbf U}{{\mathbf U}}^{{\rm T}}{{\mathbf D}}^{{{\rm 1}}/{{\rm 2}}}{{\mathbf e}}_k} }[/math]
[math]\displaystyle{ =K-tr\left({{{\mathbf E}}^{{\rm T\ }}{{\mathbf D}}^{{{\rm 1}}/{{\rm 2}}}{\mathbf U}{{\mathbf U}}^{{\rm T}}{{\mathbf D}}^{{{\rm 1}}/{{\rm 2}}}{\mathbf E}\left({{\mathbf E}}^{{\rm T\ }}{\mathbf {DE}}\right)}^{{\mathbf -}{\rm 1}}\right) }[/math]
[math]\displaystyle{ =J_1\left({\mathbf W},{\mathbf E}\right) }[/math]
Proof for Theorem 5
Remember [math]\displaystyle{ J_2\left({\mathbf W},{\mathbf E}\right){\mathbf =}\frac{{\rm 1}}{{\rm 2}}{\|{\mathbf V}{{\mathbf V}}^{{\rm T}}{\rm -}{\mathbf E}{\left({{\mathbf E}}^{{\rm T\ }}{\mathbf E}\right)}^{{\mathbf -}{\rm 1}}{{\mathbf E}}^{{\rm T}}\|}^{{\rm 2}}_F }[/math]
Using the triangle inequality,
[math]\displaystyle{ D\left({\mathbf E},{{\mathbf E}}_{{\mathbf 2}}\left({\mathbf W}\right)\right)=\frac{1}{\sqrt{2}}{\|{{\mathbf E}\left({{\mathbf E}}^{{\rm T\ }}{\mathbf E}\right)}^{{\mathbf -}{\rm 1}}{{\mathbf E}}^{{\rm T\ }}-{{{\mathbf E}}_{{\mathbf 2}}\left({\mathbf W}\right)\left({{{\mathbf E}}_{{\mathbf 2}}\left({\mathbf W}\right)}^{{\rm T\ }}{{\mathbf E}}_{{\mathbf 2}}\left({\mathbf W}\right)\right)}^{{\mathbf -}{\rm 1}}{{{\mathbf E}}_{{\mathbf 2}}\left({\mathbf W}\right)}^{{\rm T\ }}\|}_F }[/math]
[math]\displaystyle{ \le \frac{1}{\sqrt{2}}{\|{{\mathbf E}\left({{\mathbf E}}^{{\rm T\ }}{\mathbf E}\right)}^{{\mathbf -}{\rm 1}}{{\mathbf E}}^{{\rm T\ }}-{\mathbf V}{{\mathbf V}}^{{\rm T}}\|}_F+\frac{1}{\sqrt{2}}{\|{\mathbf V}{{\mathbf V}}^{{\rm T}}{\rm -}{{{\mathbf E}}_{{\mathbf 2}}\left({\mathbf W}\right)\left({{{\mathbf E}}_{{\mathbf 2}}\left({\mathbf W}\right)}^{{\rm T\ }}{{\mathbf E}}_{{\mathbf 2}}\left({\mathbf W}\right)\right)}^{{\mathbf -}{\rm 1}}{{{\mathbf E}}_{{\mathbf 2}}\left({\mathbf W}\right)}^{{\rm T\ }}\|}_F }[/math]
[math]\displaystyle{ ={J_2\left({\mathbf W},{\mathbf E}\right)}^{{1}/{2}}+{\mathop{\min }_{{\mathbf E}{\mathbf '}} {J_2\left({\mathbf W},{\mathbf E}{\mathbf '}\right)}^{{1}/{2}}\ } }[/math]
[math]\displaystyle{ \le 2{J_2\left({\mathbf W},{\mathbf E}\right)}^{{1}/{2}} }[/math]
So, [math]\displaystyle{ {D\left({\mathbf E},{{\mathbf E}}_{{\mathbf 2}}\left({\mathbf W}\right)\right)}^2\le 4J_2\left({\mathbf W},{\mathbf E}\right) }[/math]
Similarly, we can have [math]\displaystyle{ {D\left({\mathbf E},{{\mathbf E}}_{{\mathbf 1}}\left({\mathbf W}\right)\right)}^2\le 4\eta J_1\left({\mathbf W},{\mathbf E}\right) }[/math]
Reference
<references/>