learning Phrase Representations: Difference between revisions
m (→Experiments: - Added some specifics to the experimental results) |
|||
| Line 11: | Line 11: | ||
</center> | </center> | ||
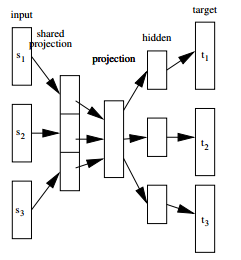
The encoder is an RNN that reads each symbol of an input sequence x sequentially. As it reads each symbol, the hidden state of the RNN changes. | The encoder is an RNN that reads each symbol of an input sequence x sequentially. As it reads each symbol, the hidden state of the RNN changes. At each time step t, the hidden state <math>h_{t}</math> of the RNN is updated by: | ||
::<math> h_t=f(h_{t-1},x_t) </math> <br/> | ::<math> h_t=f(h_{t-1},x_t) </math> <br/> | ||
After reading the end of the sequence (marked by an end-of-sequence symbol), the hidden state of the RNN is a summary <math>\mathbf{c}</math> of the whole input sequence. | where ''f'' is a non-linear activation function. ''f'' may be as simple as an element-wise logistic sigmoid function and as complex as a long short-term memory (LSTM) unit. After reading the end of the sequence (marked by an end-of-sequence symbol), the hidden state of the RNN is a summary <math>\mathbf{c}</math> of the whole input sequence. | ||
The decoder of the proposed model is another RNN which is trained to generate the output sequence by predicting the next symbol <math>y_t</math> given the hidden state<math> h_t</math> . However, as shown in figure 1, both <math>y_t</math> and <math>h_t</math> are also conditioned on <math>y_{t-1}</math> and on the summary <math>\mathbf{c}</math> of the input sequence. Hence, the hidden state of the decoder at time <math>t</math> is computed by, | The decoder of the proposed model is another RNN which is trained to generate the output sequence by predicting the next symbol <math>y_t</math> given the hidden state<math> h_t</math> . However, as shown in figure 1, both <math>y_t</math> and <math>h_t</math> are also conditioned on <math>y_{t-1}</math> and on the summary <math>\mathbf{c}</math> of the input sequence. Hence, the hidden state of the decoder at time <math>t</math> is computed by, | ||
Revision as of 17:24, 16 December 2015
Introduction
In this paper, Cho et al. propose a novel neural network model called RNN Encoder–Decoder that consists of two recurrent neural networks (RNN). One RNN encodes a sequence of symbols into a fixed length vector representation, and the other decodes the representation into another sequence of symbols. The encoder and decoder of the proposed model are jointly trained to maximize the conditional probability of a target sequence given a source sequence. The performance of a statistical machine translation system is empirically found to improve by using the conditional probabilities of phrase pairs computed by the RNN Encoder–Decoder as an additional feature in the existing log-linear model.
RNN Encoder–Decoder
In this paper, researchers propose a novel neural network architecture that learns to encode a variable-length sequence into a fixed-length vector representation and to decode a given fixed-length vector representation back into a variable-length sequence. From a probabilistic perspective, this new model is a general method to learn the conditional distribution over a variable-length sequence conditioned on yet another variable-length sequence, e.g. [math]\displaystyle{ p(y_1, . . . , y_{T'} | x_1, . . . , x_T ) }[/math], where one should note that the input and output sequence lengths [math]\displaystyle{ T }[/math] and [math]\displaystyle{ T' }[/math] may differ.
The encoder is an RNN that reads each symbol of an input sequence x sequentially. As it reads each symbol, the hidden state of the RNN changes. At each time step t, the hidden state [math]\displaystyle{ h_{t} }[/math] of the RNN is updated by:
- [math]\displaystyle{ h_t=f(h_{t-1},x_t) }[/math]
- [math]\displaystyle{ h_t=f(h_{t-1},x_t) }[/math]
where f is a non-linear activation function. f may be as simple as an element-wise logistic sigmoid function and as complex as a long short-term memory (LSTM) unit. After reading the end of the sequence (marked by an end-of-sequence symbol), the hidden state of the RNN is a summary [math]\displaystyle{ \mathbf{c} }[/math] of the whole input sequence.
The decoder of the proposed model is another RNN which is trained to generate the output sequence by predicting the next symbol [math]\displaystyle{ y_t }[/math] given the hidden state[math]\displaystyle{ h_t }[/math] . However, as shown in figure 1, both [math]\displaystyle{ y_t }[/math] and [math]\displaystyle{ h_t }[/math] are also conditioned on [math]\displaystyle{ y_{t-1} }[/math] and on the summary [math]\displaystyle{ \mathbf{c} }[/math] of the input sequence. Hence, the hidden state of the decoder at time [math]\displaystyle{ t }[/math] is computed by,
- [math]\displaystyle{ h_t=f(h_{t-1},y_{t-1},\mathbf{c}) }[/math]
- [math]\displaystyle{ h_t=f(h_{t-1},y_{t-1},\mathbf{c}) }[/math]
and similarly, the conditional distribution of the next symbol is
- [math]\displaystyle{ P(y_t|y_{t-1},y_{t-2},\cdots,y_1,\mathbf{c})=g(h_t,,y_{t-1},\mathbf{c}) }[/math]
- [math]\displaystyle{ P(y_t|y_{t-1},y_{t-2},\cdots,y_1,\mathbf{c})=g(h_t,,y_{t-1},\mathbf{c}) }[/math]
The two components of the proposed RNN Encoder–Decoder are jointly trained to maximize the conditional log-likelihood
- [math]\displaystyle{ \max_{\mathbf{\theta}}\frac{1}{N}\sum_{n=1}^{N}\log p_\mathbf{\theta}(\mathbf{y}_n|\mathbf{x}_n) }[/math]
- [math]\displaystyle{ \max_{\mathbf{\theta}}\frac{1}{N}\sum_{n=1}^{N}\log p_\mathbf{\theta}(\mathbf{y}_n|\mathbf{x}_n) }[/math]
where [math]\displaystyle{ \mathbf{\theta} }[/math] is the set of the model parameters and each [math]\displaystyle{ (\mathbf{y}_n,\mathbf{x}_n) }[/math] is an (input sequence, output sequence) pair from the training set. In our case, as the output of the decoder, starting from the input, is differentiable, the model parameters can be estimated by a gradient-based algorithm. Once the RNN Encoder–Decoder is trained, the model can be used in two ways. One way is to use the model to generate a target sequence given an input sequence. On the other hand, the model can be used to score a given pair of input and output sequences.
Hidden Unit that Adaptively Remembers and Forgets
This paper also propose a new type of hidden node that has been inspired by LSTM but is much simpler to compute and implement. Fig. 2 shows the graphical depiction of the proposed hidden unit.
Mathematically it can be shown as([math]\displaystyle{ \sigma }[/math] is the logistic sigmoid function, [math]\displaystyle{ [.]_j }[/math] denotes the j-th element of a vector and [math]\displaystyle{ \odot }[/math] means elementwise multiply):
- [math]\displaystyle{ r_j=\sigma([\mathbf{W}_r\mathbf{x}]_j+[\mathbf{U}_r\mathbf{h}_{t-1}]_j ) }[/math]
- [math]\displaystyle{ z_j=\sigma([\mathbf{W}_z\mathbf{x}]_j+[\mathbf{U}_z\mathbf{h}_{t-1}]_j ) }[/math]
- [math]\displaystyle{ h_j^{(t)}=z_jh_j^{(t-1)}+(1-z_j)\tilde{h}_j^{(t)} }[/math]
- [math]\displaystyle{ r_j=\sigma([\mathbf{W}_r\mathbf{x}]_j+[\mathbf{U}_r\mathbf{h}_{t-1}]_j ) }[/math]
where
- [math]\displaystyle{ \tilde{h}_j^{(t)}=\phi([\mathbf{W}\mathbf{x}]_j+[\mathbf{U}(\mathbf{r}\odot\mathbf{h}_{t-1})]_j ) }[/math]
- [math]\displaystyle{ \tilde{h}_j^{(t)}=\phi([\mathbf{W}\mathbf{x}]_j+[\mathbf{U}(\mathbf{r}\odot\mathbf{h}_{t-1})]_j ) }[/math]
In this formulation, when the reset gate is close to 0, the hidden state is forced to ignore the previous hidden state and reset with the current input only. This effectively allows the hidden state to drop any information that is found to be irrelevant later in the future, thus, allowing a more compact representation. On the other hand, the update gate controls how much information from the previous hidden state will carry over to the current hidden state. This acts similarly to the memory cell in the LSTM network and helps the RNN to remember longterm information. Furthermore, this may be considered an adaptive variant of a leaky-integration unit.<ref> Bengio Y, Boulanger-Lewandowski N, Pascanu R. Advances in optimizing recurrent networks[C]//Acoustics, Speech and Signal Processing (ICASSP), 2013 IEEE International Conference on. IEEE, 2013: 8624-8628. </ref>
Because each hidden unit has separate gates, it is possible for each hidden to unit to learn to capture dependencies over different lengths of time (determined by the frequency at which its reset and updates gates are active).
Scoring Phrase Pairs with RNN Encoder–Decoder
In a commonly used statistical machine translation system (SMT), the goal of the system (decoder, specifically) is to find a translation f given a source sentence e, which maximizes
[math]\displaystyle{ p(\mathbf{f} | \mathbf{e})\propto p(\mathbf{e} | \mathbf{f})p(\mathbf{f}) }[/math]
where the first term at the right hand side is called translation model and the latter language model (see, e.g., (Koehn, 2005)). In practice, however, most SMT systems model [math]\displaystyle{ \log p(\mathbf{f} | \mathbf{e}) }[/math] as a loglinear model with additional features and corresponding weights:
[math]\displaystyle{ \log p(\mathbf{f} | \mathbf{e})=\sum_{n=1}^Nw_nf_n(\mathbf{f},\mathbf{e})+\log Z(\mathbf{e}) }[/math]
where [math]\displaystyle{ f_n }[/math] and [math]\displaystyle{ w_n }[/math] are the n-th feature and weight, respectively. [math]\displaystyle{ Z(\mathbf{e}) }[/math] is a normalization constant that does not depend on the weights. The weights are often optimized to maximize the BLEU score on a development set.
Cho et al. propose to train the RNN Encoder–Decoder on a table of phrase pairs and use its scores as additional features in the loglinear model showed above when tuning the SMT decoder. For training the RNN-Encoder-Decoder, phrase frequency is ignored for several reasons: to reduce computation time, to ensure the model does not simply rank phrases by frequency, and because frequency information is already encoded in the features for the SMT (so it's better to not use the capacity of the RNN-Encoder-Decoder redundantly).
Alternative Models
The researchers noted a number of other potential translation models and their usability.
The first model is by Schwenk and it is an application of a variant of the continuous space language model to the task of machine translation. The model is essentially a feedforward neural network with a common projection for input words encoded as bag of words vectors. Schwenk fixed the input and output sentence length and for a fixed length, the neural network attempts to estimate the probability of the output sequence of words and score potential translations. However, a major disadvantage is that the input and output length are fixed and cannot handle variable length inputs or outputs.
The model figure<ref> [Schwenk2012] Holger Schwenk. 2012. Continuous space translation models for phrase-based statistical machine translation. In Martin Kay and Christian Boitet, editors, Proceedings of the 24th International Conference on Computational Linguistics (COLIN), pages 1071–1080. </ref>:
Another model, similar to Schwenk's, is by Devlin and a feedforward neural network is also used. Rather than estimating the probability of the entire output sequence of words in Schwenk's model, Devlin only estimates the probability of the next word and uses both a portion of the input sentence and a portion of the output sentence. It reported impressive improvements but similar to Schwenk, it fixes the length of input prior to training.
Chandar et al. trained a feedforward neural network to learn a mapping from a bag-of-words representation of an input phrase to an output phrase.<ref> Lauly, Stanislas, et al. "An autoencoder approach to learning bilingual word representations." Advances in Neural Information Processing Systems. 2014. </ref> This is closely related to both the proposed RNN Encoder–Decoder and the model proposed by Schwenk, except that their input representation of a phrase is a bag-of-words. A similar approach of using bag-of-words representations was proposed by Gao<ref> Gao, Jianfeng, et al. "Learning semantic representations for the phrase translation model." arXiv preprint arXiv:1312.0482 (2013). </ref> as well. One important difference between the proposed RNN Encoder–Decoder and the above approaches is that the order of the words in source and target phrases is taken into account. The RNN Encoder–Decoder naturally distinguishes between sequences that have the same words but in a different order, whereas the aforementioned approaches effectively ignore order information.
Experiments
The model is evaluated on the English/French translation task of the WMT’14 workshop. In building the model Cho et al. used baseline phrase-based SMT system and a Neural Language Model(CSLM)<ref> Schwenk H, Costa-Jussa M R, Fonollosa J A R. Continuous space language models for the IWSLT 2006 task[C]//IWSLT. 2006: 166-173. </ref>
The following model combinations were tested:
- Baseline configuration
- Baseline + RNN
- Baseline + CSLM + RNN
- Baseline + CSLM + RNN + Word penalty
The results are shown in Figure 3. The RNN encoder-decoder consisted of 1000 hidden units. Rank-100 matrices were used to connect the input to the hidden unit. The "word penalty" attempts to penalize the words unknown to the neural network, which is accomplished by using the number of unknown words as a feature in the log-linear model above.
The best performance was achieved when we used both CSLM and the phrase scores from the RNN Encoder–Decoder. This suggests that the contributions of the CSLM and the RNN Encoder– Decoder are not too correlated and that one can expect better results by improving each method independently
Word and Phrase Representations
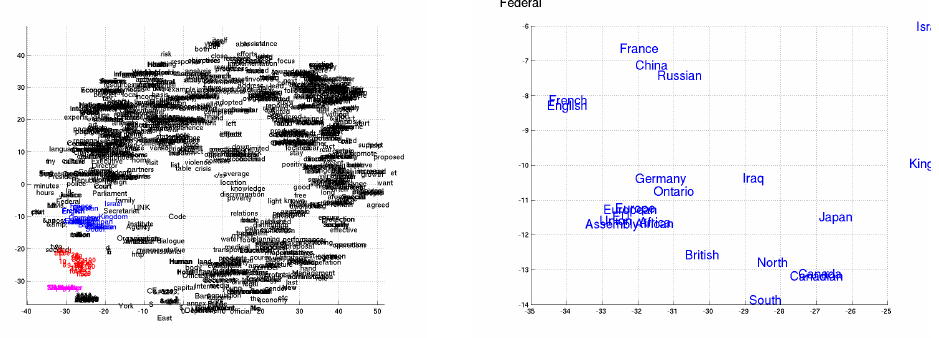
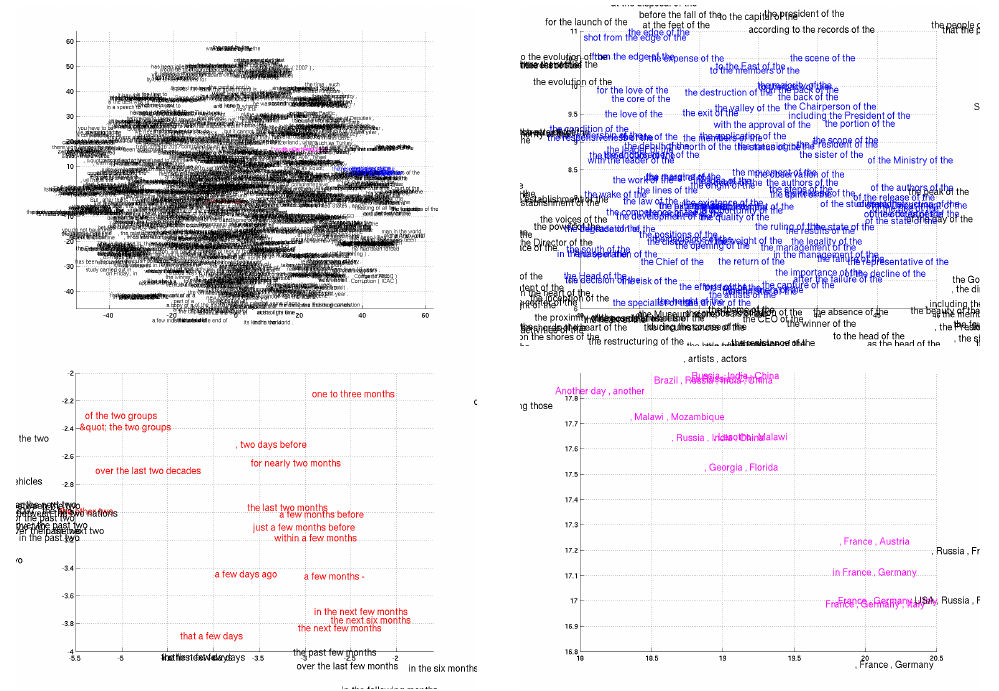
As the presented model maps sentences into a continuous space vector and prior continuous space language models have been known to learn semantically meaningful embeddings, one could expect this to happen for the presented model, too. This is indeed the case. When projecting to a 2D space (with Barnes-Hut-SNE), semantically similar words are clearly clustered.
Phrases are also clustered capturing both semantic and syntactic structures.
References
<references />