incremental Learning, Clustering and Hierarchy Formation of Whole Body Motion Patterns using Adaptive Hidden Markov Chains(Summary)
This paper present a novel approach for incremental learning of motion primitives by observation of human motion. This algorithm aims at online incremental learning of human motion patterns with application to humanoids and other robotic agents. The algorithm automatically abstracts the human motions into a dynamic stochastic model, which is used for subsequent recognition as well as motion generation. The motion modeling is performed as the motions are perceived from a human demonstrator. The size and structure of the HMM models are also learned by the algorithm. This incremental learning of the motion primitives will construct a tree structure representing a hierarchy of known motions. The resulting tree structure is dependent on the history of observations of the robot, with the most specialized (leaf) nodes occurring in those regions of the motion space where the most examples have been observed. The motion primitives are learned using HMM or factorial HMM and the generative hierarchical model is built based on a similarity measure between the learned HMM models for the observed motions. Each node in the resulting tree represents a motion primitive and can be used for motion recognition as well as generation. The algorithm can be used for activity recognition during human-robot interaction, activity monitoring in rehabilitation and sport training, and motion generation on different autonomous structures.
Factorial HMM
In the case of HMM, the dynamic of motion is modeled with a single discrete state variable, which varies according to a transition matrix A[N,N] ( N is the number of hidden states). Each state is associated with a continous output distribution model. The probability of observing an output O at a hidden state Q is modeled by B[N,K], where K is the number of outputs. Mixture of Gaussians are commonly used to model the output distribution. HMMs are commonly used for encoding sequential observations that exhibit some phase and amplitude variations between different exemplars of the observations. HMMs are attractive as they can be used for both recognition and generation. Efficient algorithms exist for estimating the model parameters (e.g., the Baum-Welch algorithm, an expectation-maximization algorithm), evaluating the likelihood that a new observation sequence was generated from an HMM model (e.g., forward algorithm), and estimating the most probable state sequence given an observation sequence(Viterbi algorithm).
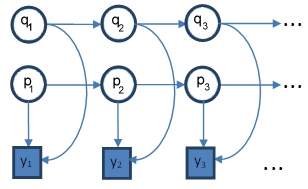
FHMM is an extension of HMM in which multiple independent dynamic processes are coupled to gather to generate an observation sequence. Each layer is a separate HMM model with transition matrix [math]\displaystyle{ A_m[N_m,N_m] }[/math] and observation matrix [math]\displaystyle{ B_m[N_m,K] }[/math], where subscript m represents the HMM model in layer m. Each state in the individual HMM models have [math]\displaystyle{ K }[/math] associated outputs. Observation at each time instance depends on the current state in each layer and is estimated by combining the observations of the individual HMM models through an expectation function for generating the output of the system. The expectation function is a multivariate Gaussian function with the chain output as the means, and a covariance matrix representing the signal noise. Figure 1 shows schematics of a factorial HMM model with two layers of left-to-right HMMs in which {q1, q2, …, qn} and {p1, p2, …, pn} represent hidden states of the HMMs in layer 1 and layer 2, respectively, each with a total number of n states. FHMM observation sequence is represented by {y1, y2, …, yn}.
In human motion analysis, it is shown that FHMM improves recognition abilities between similar motions and also it is found better in generating exemplars of the encoded movements when compared with movement generation using conventional HMM. Baum-Welch EM algorithm has been extended to estimate the parameters of FHMM <ref>Ghahramani, Z., Jordan, M.I.: Factorial hidden markov models. Machine Learning 29, 245–273 (1997)</ref>. However, the resulting EM algorithm is computationally expensive [math]\displaystyle{ O(TmN^{m+1}) }[/math]. As can be seen, the time complexity increases exponentially with increase in number of chains and hence, the E-step of the algorithm becomes intractable. Approximate approaches are proposed with quadratic time complexity in number of chains. These alternative algorithms implement an approximation of the E-step in FHMM training <ref>Jacobs, R.A., Jiang, W., Tanner, M.A.: Factorial hidden markov models and the generalized backfitting algorithm. Neural Computation 14, 2415–2437 (2002)</ref>, <ref>Ghahramani, Z., Jordan, M.I.: Factorial hidden markov models. Machine Learning 29, 245–273 (1997)</ref>. Although these approximate approaches reduce the time complexity of FHMM training, they are still not suitable for online leanirng of motion primitives as they train all the chains simultaneously. This complexity also results in inefficient recognition using trained FHMMs as compared to single HMMs. In this paper a novel approach for sequential trialing of FHMMs is proposed. The new approach is developed based on the idea that a single HMM would be sufficient when the movement is the knowledge space are very dissimilar and hence easy to discriminate and a more complex model in the form of additional chains are added only when movements are very similar and hard to distinguish.
The proposed sequential training starts with training a single HMM first and then adds extra chains as needed. The subsequent HMMs are trained on the error between the training data and the output of the trained HMMs.