generating text with recurrent neural networks
Introduction
The goal of this paper is to introduce a new type of recurrent neural network for character-level language modelling that allows the input character at a given timestep to multiplicatively gate the connections that make up the hidden-to-hidden layer weight matrix. The paper also introduces a solution to the problem of vanishing and exploding gradients by applying a technique called Hessian-Free optimization to effectively train a recurrent network that, when unrolled in time, has approximately 500 layers. At the date of publication, this network was arguably the deepest neural network ever trained successfully.
Strictly speaking, a language model is a probability distribution over sequences of words or characters, and such models are typically used to predict the next character or word in a sequence given some number of preceding characters or words. Recurrent neural networks are naturally applicable to this task, since they make predictions based on a current input and a hidden state whose value is determined by some number of previous inputs. Alternative methods that the authors compare their results to include a hierarchical Bayesian model called a 'sequence memoizer' <ref> Wood, F., C. Archambeau, J. Gasthaus, L. James, and Y.W. The. "A Stochastic Memoizer for Sequence Data" ICML, (2009) </ref> and a mixture of context models referred to as PAQ <ref> Mahoney, M. "Adaptive Weighing of Context Models for Lossless Data Compression", Florida Institute of Technology Technical Report, (2005) </ref>, which actually includes word-level information (rather strictly character-level information). The multiplicative RNN introduced in this paper improves on the state-of-the-art for solely character-level language modelling, but is somewhat worse than the state-of-the-art for text compression.
To give a brief review, an ordinary recurrent neural network is parameterized by three weight matrices, [math]\displaystyle{ \ W_{hi} }[/math], [math]\displaystyle{ \ W_{hh} }[/math], and [math]\displaystyle{ \ W_{oh} }[/math], and functions to map a sequence of [math]\displaystyle{ N }[/math] input states [math]\displaystyle{ \ [i_1, ... , i_N] }[/math] to a sequence of hidden states [math]\displaystyle{ \ [h_1, ... , h_N] }[/math] and a sequence of output states [math]\displaystyle{ \ [o_1, ... , o_N] }[/math]. The matrix [math]\displaystyle{ \ W_{hi} }[/math] parameterizes the mapping from the current input state to the current hidden state, while the matrix [math]\displaystyle{ \ W_{hh} }[/math] parameterizes the mapping from the previous hidden state to current hidden state, such that the current hidden state is function of the previous hidden state and the current input state. Finally, the matrix [math]\displaystyle{ \ W_{oh} }[/math] parameterizes the mapping from the current hidden state to the current output state. So, at a given timestep [math]\displaystyle{ \ t }[/math], the values of the hidden state and output state are as follows:
- [math]\displaystyle{ \ h_t = tanh(W_{hi}i_t + W_{hh}h_{t-1} + b_h) }[/math]
- [math]\displaystyle{ \ o_t = W_{oh}h_t + b_o }[/math]
where [math]\displaystyle{ \ b_o }[/math] and [math]\displaystyle{ \ b_h }[/math] are bias vectors. Typically, the output state is converted into a probability distribution over characters or words using the softmax function. The network can then be treated as a generative model of text by sampling from this distribution and providing the sampled output as the input to the network at the next timestep.
Recurrent networks are known to be very difficult to train due to the existence a highly unstable relationship between a network's parameters and the gradient of its cost function. Intuitively, the surface of the cost function is intermittently punctuated by abrupt changes (giving rise to exploding gradients) and nearly flat plateaus (giving rise to vanishing gradients) that can effectively become poor local minima when a network is trained through gradient descent. Techniques for improving training include the use of Long Short-Term Memory networks <ref> Hochreiter, Sepp, and Jürgen Schmidhuber. "Long short-term memory." Neural computation 9.8 (1997): 1735-1780. </ref>, in which memory units are used to selectively preserve information from previous states, and the use of Echo State networks, <ref> Jaeger, H. and H. Haas. "Harnassing Nonlinearity: Predicting Chaotic Systems and Saving Energy in Wireless Communication." Science, 204.5667 (2004): 78-80. </ref> which learn only the output weights on a network with recurrent connections that implement a wide range of time-varying patterns. In this paper, the method of Hessian free optimization is used instead of these alternatives.
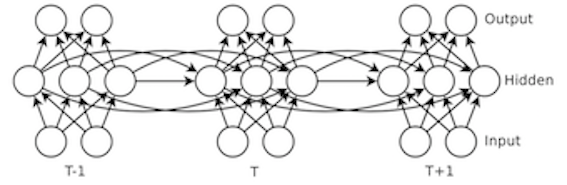
Hessian-Free Optimization
While this optimization technique is described elsewhere in Martens (2010) <ref> Martens, J. "Deep learning via Hessian-free optimization." ICML, (2010) </ref> , its use is essential to obtaining the successful results reported in this paper. In brief, the technique involves uses information about the 2nd derivatives of the cost function to perform more intelligent parameter updates. This information is helpful because in cases where the gradient is changing very slowly on a particular dimension, it is more efficient to take larger steps in the direction of descent along this dimension. Alternatively, if the the gradient is changing very rapidly on a particular dimension, then it makes sense to take smaller steps to avoid 'bouncing' off of a step incline in the cost function and moving to a less desirable location in parameter space. The relevant 2nd order information is computed using the method of finite differences to avoid computing the Hessian of the cost function.
What is important about this technique is that it provides a solution to problem of vanishing and exploding gradients during the training of recurrent neural networks. Vanishing gradients are accommodated by descending much more rapidly along the cost function in areas where it has relatively low curvature (e.g., when the cost function is nearly flat), while exploding gradients are accommodated by descending much more slowly along the cost function in areas where it has relatively high curvature (e.g., when there is a steep cliff). The figure below illustrates how hessian free optimization improves the training of neural networks in general.
Multiplicative Recurrent Neural Networks
The authors report that using a standard neural network trained via Hessian-free optimization produces only mediocre results. As such, they introduce a new architecture called a multiplicative recurrent neural network (MRNN). The motivating intuition behind this architecture is that the input at a given time step should both additively contribute to the hidden state (though the mapping performed by the input-to-hidden weights) and additionally determine the weights on the recurrent connections to the hidden state. In other words, the idea is to define a unique weight matrix [math]\displaystyle{ \ W_{hh} }[/math] for each possible input. The reason this design is hypothesized to the improve the predictive adequacy of the model is due to the idea that the conjunction of the input at one time step and the hidden state at the previous time step is important. Capturing this conjunction requires the input to influence the contribution of the previous hidden state to the current hidden state. Otherwise, the previous hidden state and the current input will make entirely independent contributions to the calculation of the current hidden state. Formally, this changes the calculation of the hidden state at a given time step as follows:
- [math]\displaystyle{ \ h_t = tanh(W_{hi}i_t + W^{i_t}_{hh}h_{t-1} + b_h) }[/math]
where [math]\displaystyle{ \ W^{i_t}_{hh} }[/math] is an input-specific hidden-to-hidden weight matrix. As a first approach to implementing this MRNN, the authors suggest using a tensor of rank 3 to store the hidden-to-hidden weights. The idea is that the tensor stores one weight matrix per possible input; when the input is provided as a one-hot vector, tensor contraction (i.e. a generalization of matrix multiplication) can be used to extract the 'slice' of the tensor that contains the appropriate set of weights. One problem with this approach is that it quickly becomes impractical to store the hidden-to-hidden weights as a tensor if the dimensionality of the hidden state has a large number of dimensions. For instance, if a network's hidden layer encodes a vector with 1000 dimensions, then the number of parameters in the tensor that need to be learned will be equal to [math]\displaystyle{ \ 1000^2 * N }[/math], where [math]\displaystyle{ \ N }[/math] is the vocabulary size. In short, this method will add many millions of parameters to a model for a non-trivially sized vocabulary.
To fix this problem, the tensor is factored using a technique described in Taylor & Hinton (2009) <ref>Taylor, G. and G. Hinton. "Factored Conditional Restricted Boltzmann Machines for Modeling Motion Style" ICML (2009) </ref>. The idea is to define three matrices [math]\displaystyle{ \ W_{fh} }[/math], [math]\displaystyle{ \ W_{fi} }[/math], and [math]\displaystyle{ \ W_{hf} }[/math] that approximate the use of a tensor in determining the value of [math]\displaystyle{ \ W^{i_t}_{hh} }[/math] as follows:
- [math]\displaystyle{ \ W^{i_t}_{hh} = W_{hf} \cdot diag(W_{fi}i_t) \cdot W_{fh} }[/math]
Intuitively, this factorization produces two vectors from the current input state and the previous hidden state, takes their element-wise product, and applies a linear transformation to produce the input to the hidden layer at the current timestep. The triangle units in the figure below indicate where the element-wise product occurs, and the connections into and out of these units are parameterized by the matrices [math]\displaystyle{ \ W_{fh} }[/math], [math]\displaystyle{ \ W_{fi} }[/math], and [math]\displaystyle{ \ W_{hf} }[/math]. The element-wise multiplication is implemented by diagonalizing the matrix-vector product [math]\displaystyle{ \ W_{fi}i_t }[/math], and if the dimensionality of this matrix-vector product (i.e. the dimensionality of the layer of multiplicative units) is allowed to be arbitrarily large, then this factorization is just as expressive as using a tensor to store the hidden-to-hidden weights.
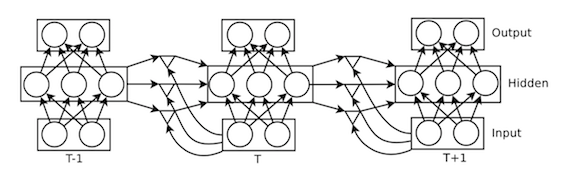
In the experiments described below, an MRNN is trained via Hessian Free optimization on sequences of 250 characters. The first 50 characters used to condition the hidden state, so only 200 predictions are generated per sequence. 1500 hidden units were used, along with 1500 factors (i.e. multiplicative gates, or the triangles in the figure above), yielding an unrolled network of 500 layers if the multiplicative units are treated as forming a layer. Training was performed with a parallelized system consisting of 8 GPUs. A vocabulary of 86 characters was used in all cases.
Quantitative Experiments
To compare the performance of the MRNN to that of the sequence memorizer and PAQ, three 100mb datasets were used: a selection of wikipedia articles, a selection of New York Times articles, and a corpus of all available articles published in NIPS and JMLR. The last 10 million characters in each dataset were held out for testing. Additionally, the MRNN was trained on the larger corpora from which the wikipedia text and NYT articles were drawn (i.e. all of wikipedia, and the entire set of NYT articles).
The models were evaluated by calculating the number of bits per character achieved by each model on the 3 test sets. This metric is essentially a measure of model perplexity, which defines how well a given model predicts the data it is being tested on. If the number of bits per character is high, this means that the model is, on average, highly uncertain about the value of each character in the test set. If the number of bits per character is low, then the model is less uncertain about the value of each character in the test set. One way to think about this quantity is as the average amount of additional information (in bits) needed by the model to exactly identify the value of each character in the test set. So, a lower measure is better, indicating that the model achieves a good representation of the underlying data. (it is sometimes helpful to think of a language model as a compressed representation of a text corpus).
As illustrated in the table below, the MRNN achieves a lower number of bits per character than the hierarchical bayesian model, but a higher number of bits per character than the PAQ model (which recall, is not a strictly character level model). The numbers in brackets indicate the bits per character achieved on the training data, and the column labelled 'Full Set' reports the results of training the MRNN on the full wikipedia and NYT corpora.
These results indicate that the MRNN beat the existing state-of-the-art for pure character-level language modelling at the time of publication.
Qualitative Experiments
By examining the output of the MRNN, it is possible to see what kinds of linguistic patterns it is able to learn. Most striking is the fact that the model consistently produces correct words from a fairly sophisticated vocabulary. The model is also able to balance parentheses and quotation marks over many time steps, and it occasionally produces plausible non-words such as 'cryptoliation' and 'homosomalist'. The text in the figure below was produced by running the model in generative mode less than 10 times using the phrase 'The meaning of life is' as an initial input, and then selecting the most interesting output sequence. The model was trained on wikipedia to produce the results in the figure below. The character '?' indicates an unknown item, and some of the spacing and punctuation oddities are due to preprocessing and are apparently common in the dataset.
Another interesting qualitative demonstration of the model's abilities involves initializing the model with a more complicated sequence and seeing what sort of continuations it produces. In the figure below, a number of sampled continuations of the phrase 'England, Spain, France, Germany' are shown. Generally, the model is able to provide continuations that preserve the list-like structure of the phrase. Moreover, the model is also able to recognize that the list is a list of locations, and typically offers additional locations as its predicted continuation of the sequence.
What is particularly impressive about these results is the fact that the model is learning a distribution over sequences of characters only. From this distribution, a broad range of syntactic and lexical knowledge emerges. It is also worth noting that it is much more efficient to train a model with a small character-level vocabulary than it is to train a model with a word-level vocabulary (which can have tens of thousands of items). As such, the character-level MRNN is able to scale to large datasets quite well.
Moreover, they find that the MRNN is sensitive to some notations like the initial bracket if such string doesn't occur in the training set. They claim that any method which is based on precise context matches is fundamentally incapable of utilizing long contexts, because the probability that a long context occurs more than once is very small.
Discussion
One aspect of this work that is worth considering concerns the degree to which the use of input-dependent gating of the information being passed from hidden state to hidden state actually improves the results over and above the use of a standard recurrent neural network. Presumably, the use of hessian free optimization allows one to successfully train such a network, so it would be helpful to see a comparison to the results obtained using an MRNN. Otherwise, it is hard to discern the relative importance of the optimization technique and the network architecture in achieving the good language modelling results reported in this paper.
Bibliography
<references />