consistency of Trace Norm Minimization
Introduction
In many applications, including collaborative filtering and multi-task learning, the main objective is to estimate a low-rank rectangular matrix. More formally, this problem can be written as follows:
where [math]\displaystyle{ \,(z_i,M_i), }[/math] [math]\displaystyle{ i = 1, \ldots, n, }[/math] are given observations. Unfortunately, this is a difficult problem to solve because of the rank constraint. If the rank function can be replaced by a convex function then the optimization problem becomes much easier to solve. However, this convex function must still generate low rank solutions. Given these two objectives, many authors have proposed using the trace norm as an alternative to the rank function, i.e. instead of solving the above problem, they proposed solving the following equivalent and much more tractable problem instead:
File:c4f1.jpg , where [math]\displaystyle{ \,\|W\|_* }[/math] denotes the trace norm of [math]\displaystyle{ \,W }[/math].
The trace norm, or nuclear norm, of a matrix, is the sum of its singular values and it is the convex envelope (the largest lower bounding convex function) of the rank function over the unit ball of the spectral norm. Since the trace norm is the convex envelope of the rank function, adding the trace norm as a regularization term to the matrix approximation problem should still give low rank solutions. It is then natural to explore what happens when the data is actually generated by a low rank matrix. Under what conditions will the trace norm regularization problem accurately approximate the underlying matrix and under what conditions will the rank be accurately approximated? The author of this paper<ref name="B2008a">F. Bach. Consistency of Trace Norm Minimization. Journal of Machine Learning Research, 8:1019-1048, 2008.</ref> explores these questions and provides necessary and sufficient conditions for rank consistency.
The use of the trace norm regularization term in place of the rank function in approximating low-rank matrices is similar to the use of the [math]\displaystyle{ \,l_1 }[/math]-norm (more details here) regularization term in place of the [math]\displaystyle{ \,l_0 }[/math]-norm (more details here) in approximating sparse vectors. In this case, the main objective is to estimate vectors with low cardinality. However, optimization problems with [math]\displaystyle{ \,l_0 }[/math]-norm constraints are hard to solve. Instead the [math]\displaystyle{ \,l_1 }[/math]-norm is often used as a regularization term to induce sparse loadings (vector coefficients), since the [math]\displaystyle{ \,l_1 }[/math]-norm is the convex envelope of the [math]\displaystyle{ \,l_0 }[/math]-norm on the unit ball. For least squares regression, this regularization scheme is known as the LASSO<ref name="T1994">R. Tibshirani. Regression shrinkage and selection via the lasso. Journal Royal Statistics, 58(1): 267-299, 1994.</ref>. Once again we are interested in whether this procedure can consistently estimate sparse vectors and their sparsity patterns. Recent work by Yuan and Lin<ref name="YL2007">M. Yuan and Y. Lin. On the non-negative garrotte estimator. Journal of The Royal Statistical Society Series B, 69(2): 143-161, 2007.</ref>, Zhao and You<ref name="ZY2006">P. Zhao and B. Yu. On model selection consistency of lasso. Journal of Machine Learning Research, 7:2541-2563, 2006.</ref> and Zou<ref name="Z2006">H. Zou. The adaptive lasso and its oracle properties. Journal of the American Statistical Association, 101:1418-1429, December 2006.</ref> looked at this question for the LASSO procedure. Similar work by Bach<ref name="B2008b">F.R. Bach. Consistency of the group lasso and multiple kernel learning. Journal of Machine Learning Research, 9:1179-1225, 2009.</ref> looked at this question for the group Lasso procedure (more details regarding it can be found in Friedman et al.
's paper). Given the similarities between the low rank matrix approximation problem and the sparse vector approximation problem (one such similarity is detailed in Shen et al.'s paper titled Sparse principal component analysis via regularized low rank matrix approximation), the author compared the consistency results that he obtained with the corresponding results for the LASSO and the group LASSO. In fact, he showed that the LASSO and the group LASSO procedures are in fact embedded in the trace norm regularization procedure itself, and he found that the consistency conditions are merely extensions of the results obtained for the LASSO and the group LASSO. The author also considered simulated data to test the consistency results.
Notation
Before outlining the major results of this paper, we must first introduce some notation. Throughout the remainder of this summary, all vectors will be denoted by lowercase letters can all matrices by uppercase letters. For vectors [math]\displaystyle{ x \in \mathbb{R}^d }[/math], let [math]\displaystyle{ \|\cdot\| }[/math] denote the Euclidean norm, that is [math]\displaystyle{ \|x\| = \|x\|_2 = (x^Tx)^{1/2} }[/math]. On rectangular matrices [math]\displaystyle{ M \in \mathbb{R}^{p \times q} }[/math], consider the following three norms, where [math]\displaystyle{ \sigma }[/math] is the vector of singular values.
- The spectral norm: The largest singular value, [math]\displaystyle{ \| M \|_2 = \|\mathbf{\sigma}\|_\infty }[/math].
- The Frobenius norm: The [math]\displaystyle{ l_2 }[/math]-norm of singular values, [math]\displaystyle{ \| M \|_F = \|\mathbf{\sigma}\|_2 = (\textrm{tr}(M^TM))^{1/2} }[/math].
- The trace norm: The sum of singular values, [math]\displaystyle{ \| M \|_* = \|\mathbf{\sigma}\|_1 }[/math].
Next, we define several other operators on the matrix [math]\displaystyle{ \,M }[/math]. Given a matrix [math]\displaystyle{ M \in \mathbb{R}^{p \times q} }[/math], let [math]\displaystyle{ \,\textrm{vec}(M) }[/math] denote the vector in [math]\displaystyle{ \mathbb{R}^{pq} }[/math] obtained by stacking its columns into a single vector; and [math]\displaystyle{ A \otimes B }[/math] denote the Kronecker product between matrices [math]\displaystyle{ A \in \mathbb{R}^{p_1 \times q_1} }[/math] and [math]\displaystyle{ B \in \mathbb{R}^{p_2 \times q_2} }[/math] where the Kronecker product is defined as
Finally, we introduce the following standard asymptotic notation. A random variable [math]\displaystyle{ \,Z_n }[/math] is said to be of order [math]\displaystyle{ \,O_p(a_n) }[/math] if for any [math]\displaystyle{ \,\eta \gt 0 }[/math], there exists a [math]\displaystyle{ \,M \gt 0 }[/math] such that [math]\displaystyle{ \sup_nP(|Z_n| \gt Ma_n) \lt \eta }[/math]. [math]\displaystyle{ \,Z_n }[/math] is said to be or order [math]\displaystyle{ \,o_p(a_n) }[/math] if [math]\displaystyle{ Z_n/a_n }[/math] converges to zero in probability. In other words, [math]\displaystyle{ Z_n }[/math] is of order [math]\displaystyle{ o_p(a_n) }[/math], if [math]\displaystyle{ P(|Z_n| \geq \eta a_n) \rightarrow 0 }[/math] as [math]\displaystyle{ n \rightarrow \infty }[/math] for any [math]\displaystyle{ \,\eta \gt 0 }[/math].
Problem Formulation
Suppose we are given [math]\displaystyle{ \,n }[/math] observations [math]\displaystyle{ \,(M_i,z_i) }[/math], [math]\displaystyle{ i = 1,\ldots, n }[/math] and we want to predict each [math]\displaystyle{ \,z_i }[/math] as a linear function of [math]\displaystyle{ M_i \in \mathbb{R}^{p \times q} }[/math] using as few entries of [math]\displaystyle{ \,M_i }[/math] as possible. This optimization problem, which we will refer to as the trace norm matrix approximation problem, can be written formally as
where the trace norm regularization term is used as a heuristic to minimize the rank of [math]\displaystyle{ \,W }[/math]. Note that, if [math]\displaystyle{ M_i = \textrm{Diag}(x_i) \in \mathbb{R}^{m \times m} }[/math] then the solution, [math]\displaystyle{ \,\hat{W} }[/math], will be a diagonal matrix and in this case [math]\displaystyle{ \,\|W\|_* }[/math] reduces to the [math]\displaystyle{ l_1 }[/math] norm of the diagonal. The optimization can be rewritten as
which is the Lasso formulation. So the consistency results for the trace norm estimate should be extensions of the Lasso consistency results. In fact, the author shows that the trace norm consistency results are the same as the Lasso consistency results when the [math]\displaystyle{ M_i }[/math] are diagonal. The group Lasso is another special case embedded in the trace norm matrix approximation problem. If [math]\displaystyle{ x_{ij} \in \mathbb{R}^{d_j} }[/math] for [math]\displaystyle{ j = 1,\ldots,m,i = 1, \ldots, n }[/math] and the [math]\displaystyle{ M_{i} \in \mathbb{R}^{\sum_{j=1}^md_j \times m} }[/math] are block diagonal matrices then the solution will have the same structure. The resulting simplification of the trace norm matrix approximation problem is the group Lasso formulation. Once again, the author is able to show how his consistency results match the previous group Lasso consistency results.
Assumptions
Before we can derive the consistency results for [math]\displaystyle{ \hat{W} }[/math], the solution to the matrix approximation problem, we must first make several assumptions about the sampling distributions of [math]\displaystyle{ M_i \in \mathbb{R}^{p \times q} }[/math]. Let [math]\displaystyle{ \hat\Sigma_{mm} = \frac{1}{n}\textrm{vec}(M_i)\textrm{vec}({M_i})^T \in \mathbb{R}^{pq \times pq} }[/math] then
- Suppose the [math]\displaystyle{ n }[/math] values of [math]\displaystyle{ z_i }[/math] are [math]\displaystyle{ i.i.d. }[/math], the [math]\displaystyle{ \,M_i }[/math], [math]\displaystyle{ i = 1,\ldots,n }[/math] are given and there exists a [math]\displaystyle{ \textbf{W} \in \mathbb{R}^{p \times q} }[/math] such that for all [math]\displaystyle{ \,i }[/math], [math]\displaystyle{ \mathbb{E}(z_i | M_1,\ldots, M_n) = \textrm{tr}\textbf{W}^TM_i }[/math] and [math]\displaystyle{ \textrm{var}(z_i | M_1, \ldots, M_n) = \sigma^2 }[/math] where [math]\displaystyle{ \,\sigma^2 }[/math] is a strictly positive constant. [math]\displaystyle{ \textbf{W} }[/math] is not equal to zero and does not have full rank. So, rank[math]\displaystyle{ (\textbf{W}) = \textbf{r} \lt \min\{p,q\} }[/math].
- There exists an invertible matrix [math]\displaystyle{ \Sigma_{mm} \in \mathbb{R}^{pq \times pq} }[/math] such that [math]\displaystyle{ \mathbb{E}\|\hat{\Sigma}_{mm}-\Sigma_{mm}\|_F^2 = O(\xi_n^2) }[/math] for a certain sequence [math]\displaystyle{ \,\xi_n }[/math] that tends to zero. In other words, the expected difference between [math]\displaystyle{ \hat{\Sigma}_{mm} }[/math] and [math]\displaystyle{ \,\Sigma_{mm} }[/math] should go to zero as [math]\displaystyle{ n \rightarrow \infty }[/math].
- The random variable [math]\displaystyle{ n^{-1/2}\sum_{i=1}^n\epsilon_i \textrm{vec}(M_i) }[/math] is converging in distribution to a normal distribution with mean zero and covariance matrix [math]\displaystyle{ \,\sigma^2\Sigma_{mm} }[/math], where [math]\displaystyle{ \epsilon_i = z_i - \textrm{tr}\textbf{W}^TM_i }[/math].
If the first assumption holds then, given the input matrices [math]\displaystyle{ M_i }[/math], [math]\displaystyle{ i = 1,\ldots, n, }[/math] we have a linear prediction model, where the loading matrix [math]\displaystyle{ \textbf{W} }[/math] is non trivial and rank-deficient. This is the matrix we are interested in estimating. Although the second and third conditions seem restrictive there are two cases where they are naturally satisfied. Assume the first condition holds in both cases.
- Case 1: If the matrices [math]\displaystyle{ M_i }[/math] are sampled i.i.d., [math]\displaystyle{ z }[/math] and [math]\displaystyle{ M }[/math] have finite fourth order moments, and [math]\displaystyle{ \Sigma_{mm}^{-1} }[/math] exists then conditions 2 and 3 will be satisfied with [math]\displaystyle{ \xi_n = n^{-1/2} }[/math].
- Case 2: This situation is representative of collaborative filtering. Suppose for each [math]\displaystyle{ i }[/math], [math]\displaystyle{ M_i = x_iy_i^T }[/math] where [math]\displaystyle{ x_i }[/math] and [math]\displaystyle{ y_i }[/math] are independent. If the values of [math]\displaystyle{ x_i }[/math] and [math]\displaystyle{ y_i }[/math] are both sampled [math]\displaystyle{ i.i.d }[/math] from distributions with finite fourth order moments and invertible second order moment matrices, [math]\displaystyle{ \Sigma_{xx} }[/math] and [math]\displaystyle{ \Sigma_{yy} }[/math] and if the [math]\displaystyle{ n }[/math] values of [math]\displaystyle{ M_i }[/math] are chosen uniformly from the [math]\displaystyle{ n_xn_y }[/math] possible pairs of [math]\displaystyle{ x_i }[/math] and [math]\displaystyle{ y_i }[/math], then conditions 2 and 3 are also satisfied with [math]\displaystyle{ \xi_n = n^{-1/2}+n_x^{-1/2}+n_y^{-1/2} }[/math].
Consistency Results
The author considers two types of consistency for [math]\displaystyle{ \hat{W} }[/math] defined as:
- Regular consistency: The estimate [math]\displaystyle{ \hat{W} }[/math] is consistent if [math]\displaystyle{ P(\|\hat{W}-\textbf{W}\| \geq \epsilon) \rightarrow 0 }[/math] as [math]\displaystyle{ n \rightarrow \infty }[/math] for all [math]\displaystyle{ \,\epsilon \gt 0 }[/math].
- Rank consistency: The estimate [math]\displaystyle{ \hat{W} }[/math] is rank consistent if [math]\displaystyle{ P(\textrm{rank}(\hat{W})\neq \textrm{rank}(\textbf{W})) \rightarrow 0 }[/math] as [math]\displaystyle{ n \rightarrow \infty }[/math].
Assuming all three conditions from the previous section hold the author obtains the following results for the consistency of [math]\displaystyle{ \hat{W} }[/math].
- If [math]\displaystyle{ \lambda_n }[/math] does not tend to zero, then the trace norm estimate [math]\displaystyle{ \hat{W} }[/math] is not consistent.
- [math]\displaystyle{ P(\|\hat{W}-\textbf{W}\| \geq \epsilon) \rightarrow l \neq 0 }[/math] as [math]\displaystyle{ n \rightarrow \infty }[/math].
- If [math]\displaystyle{ \lambda_n }[/math] tends to zero faster than [math]\displaystyle{ n^{-1/2} }[/math], then the estimate is consistent and its error is [math]\displaystyle{ O_p(n^{-1/2}) }[/math] while it is not rank-consistent with probability tending to one.
- [math]\displaystyle{ P(\|\hat{W}-\textbf{W}\| \geq \epsilon) \rightarrow 0 }[/math] as [math]\displaystyle{ n \rightarrow \infty }[/math].
- [math]\displaystyle{ P(\textrm{rank}(\hat{W})\neq \textrm{rank}(\textbf{W})) \rightarrow 1 }[/math] as [math]\displaystyle{ n \rightarrow \infty }[/math]
- If [math]\displaystyle{ \lambda_n }[/math] tends to zero exactly at rate [math]\displaystyle{ n^{-1/2} }[/math], then the estimate is consistent and its error is [math]\displaystyle{ O_p(n^{-1/2}) }[/math] but the probability of estimating the correct rank is converging to a limit in (0,1).
- [math]\displaystyle{ P(\|\hat{W}-\textbf{W}\| \geq \epsilon) \rightarrow 0 }[/math] as [math]\displaystyle{ n \rightarrow \infty }[/math].
- [math]\displaystyle{ P(\textrm{rank}(\hat{W})\neq \textrm{rank}(\textbf{W})) \rightarrow l \in (0,1) }[/math] as [math]\displaystyle{ n \rightarrow \infty }[/math]
- If [math]\displaystyle{ \lambda_n }[/math] tends to zero more slowly than [math]\displaystyle{ n^{-1/2} }[/math], then the estimate is consistent and its rank-consistency depends on specific consistency conditions.
- [math]\displaystyle{ P(\|\hat{W}-\textbf{W}\| \geq \epsilon) \rightarrow 0 }[/math] as [math]\displaystyle{ n \rightarrow \infty }[/math].
- [math]\displaystyle{ P(\textrm{rank}(\hat{W})\neq \textrm{rank}(\textbf{W})) \rightarrow \; 0 }[/math] as [math]\displaystyle{ n \rightarrow \infty }[/math] if certain conditions hold.
So, if [math]\displaystyle{ \lambda_n }[/math] tends to zero more slowly than [math]\displaystyle{ n^{-1/2} }[/math] there are certain conditions under which [math]\displaystyle{ \hat{W} }[/math] will be rank consistent. We can take a closer look at what these conditions are. First we must introduce some new notation. Let [math]\displaystyle{ \textbf{W} = \textbf{U}\textrm{Diag}(\textbf{s})\textbf{V}^T }[/math] be the singular value decomposition of [math]\displaystyle{ \textbf{W} }[/math] where [math]\displaystyle{ \textbf{U} \in \mathbb{R}^{p \times \textbf{r}} }[/math], [math]\displaystyle{ \textbf{V} \in \mathbb{R}^{q \times \textbf{r}} }[/math] and [math]\displaystyle{ \textbf{r} \lt \min\{p,q\} }[/math] is the rank of [math]\displaystyle{ \textbf{W} }[/math]. Also, let [math]\displaystyle{ \textbf{U}_\perp \in \mathbb{R}^{p \times (p-\textbf{r})} }[/math], and [math]\displaystyle{ \textbf{V}_\perp \in \mathbb{R}^{q \times (q-\textbf{r})} }[/math] be the orthogonal complements of [math]\displaystyle{ \textbf{U} }[/math] and [math]\displaystyle{ \textbf{V} }[/math]. Finally, define the matrix [math]\displaystyle{ \Lambda \in \mathbb{R}^{(p-r) \times (q-r)} }[/math] as
then we have the following necessary and sufficient conditions for the rank consistency of [math]\displaystyle{ \hat{W}: }[/math]
- Necessary condition: [math]\displaystyle{ \|\Lambda\|_2 \leq 1 }[/math].
- Sufficient condition: [math]\displaystyle{ \|\Lambda\|_2 \lt 1 }[/math].
Adaptive Version
Suppose we would like a rank consistent estimator, [math]\displaystyle{ \hat{W} }[/math], without any conditions such as those derived in the previous section (i.e. [math]\displaystyle{ \|\Lambda\|_2 \leq 1 }[/math]). We can get such an estimator by modifying the trace norm matrix approximation problem. We begin by considering the least-squares estimate [math]\displaystyle{ \textrm{vec}(\hat{W}_{LS}) = \hat{\Sigma}_{mm}^{-1}\textrm{vec}(\hat{\Sigma}_{Mz}) }[/math] where [math]\displaystyle{ \hat{\Sigma}_{Mz} = \frac{1}{n}\sum_iz_iM_i }[/math]. Consider the full singular value decomposition of [math]\displaystyle{ \hat{W}_{LS} = U_{LS}\textrm{Diag}(s_{LS})V_{LS}^T }[/math], where [math]\displaystyle{ U_{LS} }[/math] and [math]\displaystyle{ V_{LS} }[/math] are orthogonal square matrices and the matrix [math]\displaystyle{ \textrm{Diag}(s_{LS}) }[/math] is completed by setting the [math]\displaystyle{ r - \min\{p,q\} }[/math] singular values in [math]\displaystyle{ s_{LS} \in \mathbb{R}^{\min\{p,q\}} }[/math] to [math]\displaystyle{ n^{-1/2} }[/math]. For [math]\displaystyle{ \gamma \in (0,1] }[/math], define
and
Then we can replace [math]\displaystyle{ \| W \|_* }[/math] by [math]\displaystyle{ \|AWB\|_* }[/math] in the trace norm matrix approximation problem to get the adaptive trace norm matrix approximation problem. This same methodology is applied in Zou<ref name="Z2006"/> to derive an adaptive version of the Lasso. Our new optimization problem is
and the global minimizer, [math]\displaystyle{ \hat{W} }[/math], of this problem is both consistent and rank consistent provided [math]\displaystyle{ \gamma \in (0,1] }[/math], [math]\displaystyle{ n^{1/2}\lambda_n \rightarrow 0 }[/math] and [math]\displaystyle{ \lambda_nn^{1/2+\gamma/2} \rightarrow \infty }[/math] and there is no longer any dependency on the matrix [math]\displaystyle{ \,\Lambda_2 }[/math] for rank consistency.
Simulations
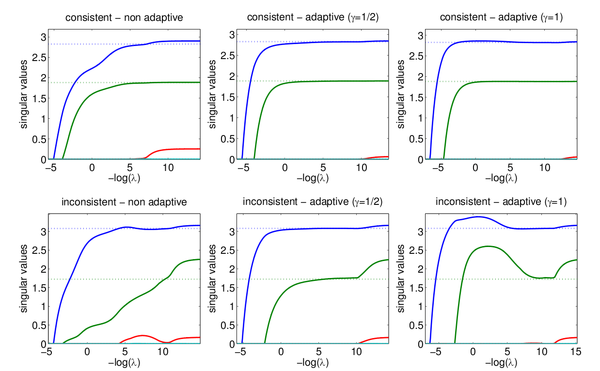
The author performs some simple experiments to demonstrate the consistency results. In these experiments, he lets [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math] be i.i.d data from a normal distribution and lets [math]\displaystyle{ \textbf{W} }[/math] be a low rank matrix selected at random. He then generates [math]\displaystyle{ Z = \textrm{diag}(X^T\textbf{W}Y) + \epsilon }[/math] where [math]\displaystyle{ \,\epsilon \sim N(0, \sigma) }[/math]. For all of the experiments [math]\displaystyle{ \textbf{r} = 2 }[/math], [math]\displaystyle{ p = q = 4 }[/math], while the sample size [math]\displaystyle{ \,n }[/math] varies. The following figure from the paper shows the singular values for [math]\displaystyle{ \hat{W} }[/math] plotted against the true singular values indicated by the dotted lines. Both the consistent ([math]\displaystyle{ \|\Lambda\|_2 = 0.49 \lt 1 }[/math]) and inconsistent case ([math]\displaystyle{ \|\Lambda\|_2 = 4.78 \gt 1 }[/math]) are considered and both the regular and adaptive trace norm penalization terms are used where [math]\displaystyle{ \gamma = 1/2 }[/math] and [math]\displaystyle{ \gamma = 1 }[/math] are considered for the adaptive version. The value of [math]\displaystyle{ n }[/math] is [math]\displaystyle{ 10^3 }[/math]. The estimate is consistent if it can correctly estimate the singular values and it is rank consistent if the rank is correct which is determined by the cardinality of the singular values. In the consistent case, in all three versions, the singular values and the rank are correctly estimated for a range of [math]\displaystyle{ \lambda }[/math] values, as is expected from the consistency results. From the diagram we can see that the range of [math]\displaystyle{ \lambda }[/math] values for which the rank is correctly estimated is much narrower for the regularized version versus the adaptive versions. The results from the inconsistent case are also reflective of the consistency results.
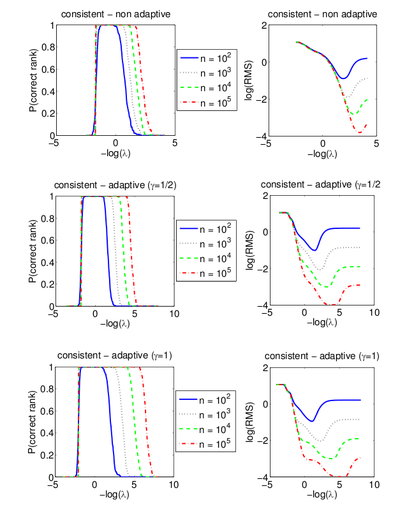
As another test to illustrate the consistency results, the author uses the rank-consistent case from the first experiment and for [math]\displaystyle{ n = 10^2, 10^3, 10^4 }[/math] and [math]\displaystyle{ 10^5 }[/math] computes the paths from 200 replications. The following figure, also from the paper, shows the results, where the plots on the left are the proportion of estimates that correctly estimate the rank while the plots on the right plot are the logarithm of the average root mean squared estimation error.
The simulations can be reproduced with MATLAB code available from http://www.di.ens.fr/~fbach/tracenorm.
References
<references />