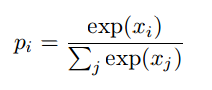a fast learning algorithm for deep belief nets: Difference between revisions
m (Conversion script moved page A fast learning algorithm for deep belief nets to a fast learning algorithm for deep belief nets: Converting page titles to lowercase) |
|
(No difference)
| |
Latest revision as of 09:46, 30 August 2017
Introduction
The authors (Geoffrey Hinton, Simon Osindero, and Yee-Whye Teh) present a method for using complementary priors to simplify the computation of posterior distributions in deep belief networks. Based on this, they are able to construct a fast greedy algorithm to learn weights in deep belief networks, one layer at a time. These weights may be improved using a contrastive version of the wake-sleep algorithm. The result is an efficient way to train a deep belief network with substantial accuracy, as is shown by top-notch scores in standard classification tasks such as MNIST digit recognition.
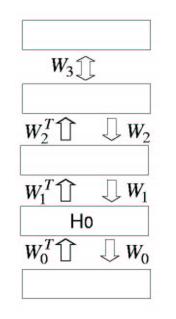
The following figure shows the network used to model the joint distribution of digit images and digit labels
In this paper, each training case consists of an image and an explicit class label, but work in progress has shown that the same learning algorithm can be used if the labels are replaced by a multilayer pathway whose inputs are spectrograms from multiple different speakers saying isolated digits. The network then learns to generate pairs that consist of an image and a spectrogram of the same digit class.
Complementary priors
One obstacle that has hindered the ability to make inference in directed belief nets is the "explaining away" phenomenon: it is extremely difficult, in general, to compute the posterior distribution over hidden variables in a dense directed belief network.
The authors describe a way to cancel out the explaining away phenomenon in a hidden layer by using additional hidden layers to create what they refer to as "complementary priors". The idea behind this is that in a logistic belief net (a network where the probability of turning on a unit is a logistic function of the weighted states of its immediate ancestors), if there is only one hidden layer, then the posterior distribution is independent because it is created by the likelihood term coming from the data. Thus the complementary priors can be set so that they precisely make the posterior distribution factorial, and simplify the computation of posterior distributions.
A fast, greedy learning algorithm
The main contribution of this paper is a fast greedy algorithm that can learn weights for a deep belief network. The idea of the algorithm is to construct multi-layer directed networks, one layer at a time. As each new layer is added, the overall generative model improves. The essence of the algorithm is similar to the concept of boosting, where the same weak learner is repeatedly used, but with different weighting on th   Cancel | Editing help (opens in new window)e data vector each time; however, in this case, it is the representation of the data vector that changes each time the weak learner is used. Here, the weak learner is an undirected graphical model.
The figure below shows a hybrid network where the top two layers have undirected connections and the layers below have directed connections in both directions. h_0^T\,
In the above diagram, the weight matrix [math]\displaystyle{ W_0\, }[/math] can be learned, to some level of accuracy, by assuming that all weight matrices are equal and treating the entire network as a Restricted Boltzmann Machine (RBM). Once [math]\displaystyle{ W_0\, }[/math] is learned, [math]\displaystyle{ W_0^T\, }[/math] can be used to map the data to a higher level in the first hidden layer, and a similar process can be repeated.
In each stage, the higher level weight matrices would have to be modified. The following greedy algorithm is proposed:
- Learn [math]\displaystyle{ W_0\, }[/math] assuming all the weight matrices are tied.
- Freeze [math]\displaystyle{ W_0\, }[/math] and use [math]\displaystyle{ W_0^T\, }[/math] to infer factorial approximate posterior distributions over the states of the variables in the first hidden layer. Do this even though subsequent changes in the higher level weights mean that the inference is no longer always correct.
- Keep all higher weight matrices tied to each other, but untie them from [math]\displaystyle{ W_0\, }[/math]. In this setting, learn an RBM for the higher level states, using results of the data having [math]\displaystyle{ W_0\,^T }[/math] applied as a transformation.
The authors of the paper are able to show that if this greedy algorithm is used to change higher-level weight matrices, then the generative model is guaranteed to improve. , the negative log probability of a single data-vector, [math]\displaystyle{ v_0^T\, }[/math] , under the multilayer generative model is bounded by a variational free energy which is the expected energy under the approximating distribution, [math]\displaystyle{ Q(h_0^T\,|v_0^T\,) }[/math] , minus the entropy of that distribution The only standard machine learning technique that comes close to the 1.25% error rate of our generative model on the basic task is a support vector machine which gives an error rate of 1.4%The only standard machine learning technique that comes close to the 1.25% error rate of our generative model on the basic task is a support vector machine which gives an error rate of 1.4%The only standard machine learning technique that comes close to the 1.25% error rate of our generative model on the basic task is a support vector machine which gives an error rate of 1.4%
The up-down algorithm
The greedy learning algorithm is an effective and (relatively) rapid way to learn the weights in the deep belief network, but will not necessarily guarantee high quality weights. In order to obtain better weights, the "up-down" method has been suggested; this is a contrastive version the "wake-sleep" method proposed in a previous paper of 1995, although without some of the drawbacks.
The idea is that, after weights have been learned in such a way that the posterior in each layer must be approximated with a factorial distribution given the values of the preceding layer, the upward "recognition" weights are untied from the downward "generative" weights. Then, higher-level weights can be used to influence lower-level ones.
Each "up-pass" consists of using the recognition weights to stochastically pick states for each hidden variable, and then adjusting the generative weights using the following maximum likelihood learning rule:
- [math]\displaystyle{ \frac{\partial \log p(v^0)}{\partial w_{ij}^{00}} = \langle h_j^0(v_i^0 - \hat{v_i^0})\rangle }[/math]
The "down-pass" is similar, in that it iterates through layers and adjusts weight matrices, although the iteration begins at the top layers and propagates along the top-down generative connections, and it is the bottom-up recognition weights that are modified. There is some discussion on how the performance may be superior to the similar "wake-sleep" process, if the implementation carries a particular "contrastive" quality.
Performance on MNIST
The training method was applied on a deep belief net consisting of three hidden layers and approximately 1.7 million weights in an experiment to classify MNIST data on handwritten digits. On a basic version of the standard classification task, in which no geometric information is considered and no background knowledge or understanding is taken into account, the generalized performance of the network was approximately 1.25% error on the standard test set.
The network was trained on 44,000 of the training images that were divided into 440 balanced mini-batches each containing 10 examples of each digit class. The weights were updated after each mini-batch. In the initial phase of training, the greedy algorithm was used to train each layer of weights separately, starting at the bottom. Each layer was trained for 30 sweeps through the training set (called “epochs”). During training, the units in the “visible” layer of each RBM hadThe only standard machine learning technique that comes close to the 1.25% error rate of our generative model on the basic task is a support vector machine which gives an error rate of 1.4% real-valued activities between 0 and 1. These were the normalized pixel intensities when learning the bottom layer of weights. For training higher layers of weights, the real-valued activities of the visible units in the RBM were the activation probabilities of the hidden units in the lower-level RBM. The hidden layer of each RBM used stochastic binary values when that RBM was being trained. The greedy training took a few hours per layer in Matlab on a 3GHz Xeon processor and when it was done, the error-rate on the test set was 2.49%.
When training the top layer of weights (the ones in the associative memory) the labels were provided as part of the input. The labels were represented by turning on one unit in a “softmax” group of 10 units. When the activities in this group were reconstructed from the activities in the layer above, exactly one unit was allowed to be active and the probability of picking unit i was given by:
After the greedy layer-by-layer training, the network was trained, with a different learning rate and weight-decay, for 300 epochs using the up-down algorithm described in section 5. The learning rate, momentum, and weight-decay were chosen by training the network several times and observing its performance on a separate validation set of 10,000 images that were taken from the remainder of the full training set. For the first 100 epochs of the up-down algorithm, the up-pass was followed by three full iterations of alternating Gibbs sampling in the associative memory before performing the down-pass. For the second 100 epochs, six iterations were performed, and for the last 100 epochs, ten iterations were performed. Each time the number of iterations of Gibbs sampling was raised, the error on the validation set decreased noticeably. The network that performed best on the validation set was then tested and had an error rate of 1.39%. This network was then trained on all 60,000 training images until its error-rate on the full training set was as low as its final error-rate had been on the initial training set of 44,000 images. This took a further 59 epochs making the total learning time about a week. The final network had an error-rate of 1.25%.
Conclusion
This paper has shown that it is possible to learn a deep, densely connected, belief network one layer at a time. The obvious way to do this is to assume that the higher layers do not exist when learning the lower layers, but this is not compatible with the use of simple factorial approximations to replace the intractable posterior distribution.
This technique can also be viewed as constrained variational learning because a penalty term – the divergence between the approximate and true posteriors – has been replaced by the constraint that the prior must make the variational approximation exact. After each layer has been learned, its weights are untied from the weights in higher layers. As these higher-level weights change, the priors for lower layers cease to be com- plementary, so the true posterior distributions in lower layers are no longer factorial and the use of the transpose of the generative weights for inference is no longer correct.
Some of the major advantages of generative models as compared to discriminative ones are:
1. Generative models can learn low-level features without requiring feedback from the label and they can learn many more parameters than discriminative models without overfitting. In discriminative learning, each training case only constrains the parameters by as many bits of information as are required to specify the label. For a generative model, each training case constrains the parameters by the number of bits required to specify the input. 2. It is easy to see what the network has learned by generating from its model. 3. It is possible to interpret the non-linear, distributed representations in the deep hidden layers by generating images from them. 4. The superior classification performance of discriminative learning methods only holds for domains in which it is not possible to learn a good generative model. This set of domains is being eroded by Moore’s law