a Rank Minimization Heuristic with Application to Minimum Order System Approximation: Difference between revisions
| Line 38: | Line 38: | ||
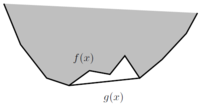
''' Definition:''' Let <math>f:C \rightarrow\real</math> where <math>C\subseteq \real^n</math>. The convex envelope of <math>f</math> (on <math>C</math>) is defined as the largest convex function <math>g</math> such | ''' Definition:''' Let <math>f:C \rightarrow\real</math> where <math>C\subseteq \real^n</math>. The convex envelope of <math>f</math> (on <math>C</math>) is defined as the largest convex function <math>g</math> such | ||
that <math>g(x)\leq f(x)</math> for all <math>x\in X</math> | that <math>g(x)\leq f(x)</math> for all <math>x\in X</math> | ||
[[Image:Convex Envelope.png|thumb|200px|right|convex envelope of a function | [[Image:Convex Envelope.png|thumb|200px|right|convex envelope of a function, borrowed from <ref>Rank Minimization and Applications in System Theory, M. Fazel, H. Hindi, and S. Body</ref>]] | ||
===References=== | ===References=== | ||
<references /> | <references /> | ||
Revision as of 23:00, 23 November 2010
Rank Minimization Problem (RMP) has application in a variety of areas such as control, system identification, statistics and signal processing. Except in some special cases RMP is known to be computationaly hard. [math]\displaystyle{ \begin{array}{ l l } \mbox{minimize} & \mbox{Rank } X \\ \mbox{subject to: } & X \in C \end{array} }[/math]
If the matrix is symmetric and positive semidifinite, trace minimization is a very effective heuristic for rank minimization problem. The trace minimization results in a semidefinite problem which can be easily solved. [math]\displaystyle{ \begin{array}{ l l } \mbox{minimize} & \mbox{Tr } X \\ \mbox{subject to: } & X \in C \end{array} }[/math]
This paper focuses on the following problems:
- Describing a generalization of the trace heuristic for genaral non-square matrices.
- Showing that the new heuristic can be reduced to an SDP, and hence effictively solved.
- Applying the mothod on the minimum order system approximation.
A Generalization Of The Trace Heuristic
This heurisitic minimizes the sum of the singular values of the matrix [math]\displaystyle{ X\in \real^{m\times n} }[/math], which is the nuclear norm of [math]\displaystyle{ X }[/math] denoted by [math]\displaystyle{ |X|_* }[/math].
[math]\displaystyle{ \begin{array}{ l l } \mbox{minimize} & |X|_* \\ \mbox{subject to: } & X \in C \end{array} }[/math]
According to the definition of the nuclear norm we have [math]\displaystyle{ |X|_*=\sum_{i=1}^{\min\{m,n\} }\sigma_i(X) }[/math] where [math]\displaystyle{ \sigma_i(X) = \sqrt{\lambda_i (X^TX)} }[/math].
When the matrix variable [math]\displaystyle{ X }[/math] is symmetric and positive semidefinite, then its singular values are the same as its eigenvalues, and therefore the nuclear norm reduces to [math]\displaystyle{ \mbox{Tr } X }[/math], and that means the heuristic reduces to the trace minimization heuristic.
Nuclear Norm Minimization vs. Rank Minimization
Definition: Let [math]\displaystyle{ f:C \rightarrow\real }[/math] where [math]\displaystyle{ C\subseteq \real^n }[/math]. The convex envelope of [math]\displaystyle{ f }[/math] (on [math]\displaystyle{ C }[/math]) is defined as the largest convex function [math]\displaystyle{ g }[/math] such that [math]\displaystyle{ g(x)\leq f(x) }[/math] for all [math]\displaystyle{ x\in X }[/math]
References
<references />