a Rank Minimization Heuristic with Application to Minimum Order System Approximation: Difference between revisions
| Line 103: | Line 103: | ||
</math> | </math> | ||
is minimized. | is minimized. | ||
The transfer matrix is measured for a few frequencies, <math>\omega_1,\dots,\omega_K\in \real</math> with athe accuracy of <math>\epsilon</math>. | |||
So the <math>G_k</math> are given as the measured approximation of <math>H(j\omega_k)</math>. | |||
Therefore we have the following minimization problem: | |||
===References=== | ===References=== | ||
<references /> | <references /> | ||
Revision as of 00:23, 24 November 2010
Introduction
Rank Minimization Problem (RMP) has application in a variety of areas such as control, system identification, statistics and signal processing. Except in some special cases RMP is known to be computationaly hard. [math]\displaystyle{ \begin{array}{ l l } \mbox{minimize} & \mbox{Rank } X \\ \mbox{subject to: } & X \in C \end{array} }[/math]
If the matrix is symmetric and positive semidifinite, trace minimization is a very effective heuristic for rank minimization problem. The trace minimization results in a semidefinite problem which can be easily solved. [math]\displaystyle{ \begin{array}{ l l } \mbox{minimize} & \mbox{Tr } X \\ \mbox{subject to: } & X \in C \end{array} }[/math]
This paper focuses on the following problems:
- Describing a generalization of the trace heuristic for genaral non-square matrices.
- Showing that the new heuristic can be reduced to an SDP, and hence effictively solved.
- Applying the mothod on the minimum order system approximation.
Nuclear Norm Heuristic A Generalization Of The Trace Heuristic
This heurisitic minimizes the sum of the singular values of the matrix [math]\displaystyle{ X\in \real^{m\times n} }[/math], which is the nuclear norm of [math]\displaystyle{ X }[/math] denoted by [math]\displaystyle{ \|X\|_* }[/math].
[math]\displaystyle{ \begin{array}{ l l } \mbox{minimize} & \|X\|_* \\ \mbox{subject to: } & X \in C \end{array} }[/math]
According to the definition of the nuclear norm we have [math]\displaystyle{ \|X\|_*=\sum_{i=1}^{\min\{m,n\} }\sigma_i(X) }[/math] where [math]\displaystyle{ \sigma_i(X) = \sqrt{\lambda_i (X^TX)} }[/math].
The nuclear norm is dual of the spectrial norm [math]\displaystyle{ \|X\|_* =\sup \{ \mbox{Tr } Y^T X | \|Y\| \leq 1 \} }[/math]. So the relaxed version of the rank minimization problem is a convex optimization problem.
When the matrix variable [math]\displaystyle{ X }[/math] is symmetric and positive semidefinite, then its singular values are the same as its eigenvalues, and therefore the nuclear norm reduces to [math]\displaystyle{ \mbox{Tr } X }[/math], and that means the heuristic reduces to the trace minimization heuristic.
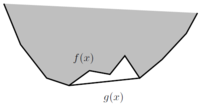
Definition: Let [math]\displaystyle{ f:C \rightarrow\real }[/math] where [math]\displaystyle{ C\subseteq \real^n }[/math]. The convex envelope of [math]\displaystyle{ f }[/math] (on [math]\displaystyle{ C }[/math]) is defined as the largest convex function [math]\displaystyle{ g }[/math] such that [math]\displaystyle{ g(x)\leq f(x) }[/math] for all [math]\displaystyle{ x\in X }[/math].
Theorem 1 The convex envelope of the function [math]\displaystyle{ \phi(X)=\mbox{Rank }(X) }[/math], on [math]\displaystyle{ C=\{X\in \real^{m\times n} | \|X\|\leq 1\} }[/math] is [math]\displaystyle{ \phi_{\mbox{env}}(X) = \|X\|_* }[/math].
Suppose [math]\displaystyle{ X\in C }[/math] is bounded by [math]\displaystyle{ M }[/math] that is [math]\displaystyle{ \|X\|\leq M }[/math], then the convex envelope of [math]\displaystyle{ \mbox{Rank }X }[/math] on [math]\displaystyle{ \{X | \|X\|\leq M\} }[/math] is given by [math]\displaystyle{ \frac{1}{M}\|X\|_* }[/math].
[math]\displaystyle{ \mbox{Rank } X \geq \frac{1}{M} \|X\|_* }[/math] That means if [math]\displaystyle{ p_{\mbox{rank}} }[/math] and [math]\displaystyle{ p_{*} }[/math] are the optimal values of the rank minimization problem and dual spectrial norm minimization problem then we have [math]\displaystyle{ p_{\mbox{rank}}\geq \frac{1}{M} p_{*} }[/math]
Expressing as an SDP
To express the relaxed version as a SDP we need to express the constraints by linear matrix inequalityes (LMIs).
Lemma 1 For [math]\displaystyle{ X\in \real^{m\times n} }[/math] and [math]\displaystyle{ t\in \real }[/math], we have [math]\displaystyle{ R^{m\times m} }[/math] and [math]\displaystyle{ Z\in \real^{n\times n} }[/math] such that
[math]\displaystyle{ \left[\begin{array}{cc} Y & X\\ X^T & Z \end{array}\right]\geq 0, \quad \mbox{Tr}(Y) + \mbox{Tr}(Z) \leq 2t }[/math]
Using this lemma the nuclear norm minimization problem
[math]\displaystyle{ \begin{array}{ l l } \mbox{minimize} & t \\ \mbox{subject to: } & \|X\|_*\leq t\\ & X \in C \end{array} }[/math]
can be expressed as
[math]\displaystyle{ \begin{array}{ l l } \mbox{minimize} & \mbox{Tr}(Y) + \mbox{Tr}(Z) \\ \mbox{subject to: } & \left[\begin{array}{cc} Y & X\\ X^T & Z \end{array}\right] \leq 0 \\ & X \in C \end{array} }[/math]
where [math]\displaystyle{ Y=Y^T, Z=Z^T }[/math] are new variables. If the constraint set [math]\displaystyle{ C }[/math] can be expressed as linear matrix inequalityes then the problem is an SDP, and can be solved using available SDP solvers.
Minimum Order System Approximation
The rank minimization heuristic can be used in the minimum order system approximation problem. In system theory, the effect of a system can be modeled using a ratioanl matrix [math]\displaystyle{ H(s) }[/math]: [math]\displaystyle{ H(s) = R_0 +\sum_{i=1}^N \frac{R_i}{s-p_i} }[/math] where [math]\displaystyle{ R_i \in C^{m\times n} }[/math] and [math]\displaystyle{ p_i }[/math] are the complex poles of the system with the property that for each complex [math]\displaystyle{ p_i }[/math] its compelx conjucate is also a pole, and whenever [math]\displaystyle{ p_i = p_j^* }[/math] we have [math]\displaystyle{ R_i=R_j^* }[/math].
We want the simpler description for the system. That is to say we are looking for [math]\displaystyle{ H }[/math] such that [math]\displaystyle{ \deg(H) = \sum_{i=1}^N \mbox{Rank}(R_i) }[/math] is minimized.
The transfer matrix is measured for a few frequencies, [math]\displaystyle{ \omega_1,\dots,\omega_K\in \real }[/math] with athe accuracy of [math]\displaystyle{ \epsilon }[/math]. So the [math]\displaystyle{ G_k }[/math] are given as the measured approximation of [math]\displaystyle{ H(j\omega_k) }[/math]. Therefore we have the following minimization problem:
References
<references />