a New Approach to Collaborative Filtering: Operator Estimation with Spectral Regularization
Introduction
Collaborative filtering (CF) aims to predict preferences of a set of users for objects such as movies, music, or any object based on previously purchased or rated objects by these users. The goal is to offer new objects to the users based on the predicted preferences. A good example of an application of collaborative filtering in the market place is the use of CF by the popular online shopping website Amazon.com for recommending related products to users of Amazon.com based on what these users have recently purchased from this website. Details of the use of CF by Amazon.com for this purpose is available here.
Regularization-based CF methods have been proposed <ref name="srebro03">N. Srebro and T. Jaakkola. Weighted low-rank approximations. In T. Fawcett and N.Mishra, editors, Proceedings of the Twentieth International Conference on Machine Learning, pages 720–727. AAAI Press, 2003. </ref>, which view the data recorded about a user's preferences as a partially observed matrix of the user's preferences of all items available. Our goal, then, is to predict or infer the other preferences---in a sense, completing the matrix. To do this, we assume that preferences are related in some way, and search for the hidden variables which explain users' preferences.
However, a major drawback of the currently-used regularization-based CF methods is that they do not take advantage of additional information, such as known attributes of each user, such as the users' gender and age, as well as the attributes of the object that are associated with the users, such as the authors and genres of books recently purchased by users. These methods only incorporate the users preferences which can be given as a preference matrix in which the rows and columns represent users and objects, respectively. These additional information are often directly available at no extra cost and, from an intuitive standpoint, they might be very useful for guiding the inferencing of user preferences, in particular for users and their associated objects that have very few known ratings.
In order to solve the problem, a low-rank matrix should be found that approximates the partially observed given preference matrix. This rank constraint is a regularization. Heuristics <ref name="srebro03"> </ref> and penalizing the predicted matrix by its trace norm <ref name="srebro05">N. Srebro, J. D. M. Rennie, and T. S. Jaakkola. Maximum-margin matrix factorization. In L. K. Saul, Y. Weiss, and L. Bottou, editors, Adv. Neural. Inform. Process Syst. 17, pages 1329–1336, Cambridge, MA, 2005. MIT Press. </ref> (Jason D. M. Rennie provides the different equivalent ways of expressing the trace norm of a matrix here) are two approaches for solving the resulting optimization problem.
Abernethy et al.<ref name="self"> J. Abernethy, F. Bach, T. Evgeniou, J. P. Vert. A New Approach to Collaborative Filtering: Operator Estimation with Spectral Regularization. Journal of Machine Learning Research, Vol. 10(Mar):803--826, 2009</ref> present a generalized regularization-based approach for CF which learns the linear operators mapping users space to their desired objects space.
The novelty of this approach is the ability to incorporate additional information, such as different attributes of users/objects by means of kernel methods (details regarding them are available in Sargur Srihari's lecture slides). These attributes can help through predicting the unkown entries of the preference matrix. They also show that some multi-tasking learning methods are special cases of their general framework.
Learning Compact Operators with Spectral Regularization
In this section a mathematical formulation for a general CF problem with spectral regularization (Lorenzo Rosasco provides details regarding it in his lecture slides) is proposed. Given [math]\displaystyle{ \,N }[/math] observations [math]\displaystyle{ ( \mathbf{x}_i, \mathbf{y}_i, t_i)_{i=1,..,N} }[/math] in ([math]\displaystyle{ \mathcal{X}\times \mathcal{Y}\times \mathbb{R} }[/math]), where [math]\displaystyle{ \,t_i }[/math] is the rating of user [math]\displaystyle{ \,x_i }[/math] for object [math]\displaystyle{ \,y_i }[/math], we intend to find a function [math]\displaystyle{ f: \mathcal{X} \times \mathcal{Y} \to \mathbb{R} }[/math] that can be used in prediction of any user [math]\displaystyle{ \,x }[/math]'s rating for any object [math]\displaystyle{ \,y }[/math]. [math]\displaystyle{ \,x_i }[/math] and [math]\displaystyle{ \,y_i }[/math] correspond to [math]\displaystyle{ \,i }[/math]-th available rating.
In this paper, learning preference functions [math]\displaystyle{ \,f(.,.) }[/math], or bilinear of the form [math]\displaystyle{ f(\mathbf{x},\mathbf{y}) = \langle \mathbf{x}, F \mathbf{y} \rangle_{\mathcal{X}} }[/math] for some compact operator [math]\displaystyle{ \,F }[/math], on [math]\displaystyle{ \mathcal{X} \times \mathcal{Y} }[/math], is considered. The set of compact operators from [math]\displaystyle{ \mathcal{X} }[/math] to [math]\displaystyle{ \mathcal{Y} }[/math] is denoted by [math]\displaystyle{ \mathcal{B}_0(\mathcal{Y},\mathcal{X}) }[/math].
So, our problem is to answer this question: "Given a training set of ratings, how may we estimate a good compact operator [math]\displaystyle{ \,F }[/math] to predict future ratings?"<ref name="self"> </ref>.
The operator is defined as the solution to an optimization problem over [math]\displaystyle{ \mathcal{B}_0(\mathcal{Y,X}) }[/math]. The loss function [math]\displaystyle{ \,l(t',t) }[/math] quantifies how good a prediction [math]\displaystyle{ \,t′ \in R }[/math] is, provided that the true value is [math]\displaystyle{ \,t \in R }[/math]. The choice of the loss function depends on the nature of the variable to be predicted and the problem. The data fitting term that is considered is equal to the [http://en.wikipedia.org/wiki/Empirical_risk_minimization empirical risk)(i.e. the mean loss incurred on the training set). This fitting term is:
The regularization term [math]\displaystyle{ \,\Omega(F) }[/math] controls the complexity of the desired operator, and it is defined as the following spectral penalty function:
, where [math]\displaystyle{ \,s_i }[/math] is a non-decreasing penalty function and [math]\displaystyle{ \,s(0)= 0 }[/math], and [math]\displaystyle{ (\,\sigma_i(F))_{i=1,...,d} }[/math] are the [math]\displaystyle{ \,d }[/math] singular values of [math]\displaystyle{ \,F }[/math] in decreasing order. It should be noted that the value of this [math]\displaystyle{ \,d }[/math] has no upper bound.
The objective function of this optimization problem balances the data fitting term [math]\displaystyle{ \,R_N(F) }[/math] with a regularization term [math]\displaystyle{ \,\Omega(F) }[/math].
So, an operator [math]\displaystyle{ \hat{F} }[/math] should be found that solves this optimization problem:
where the parameter [math]\displaystyle{ \lambda \in \mathbb{R}_{+} }[/math] controls the trade-off between fitting and regularization.
The authors show that the above general problem can result in a desired algorithm by selecting an appropriate loss function, kernels or spectral penalty term. For instance, the choice of the loss function ([math]\displaystyle{ \,l }[/math]) defines the empirical risk, and it depends on the type of data and the final objective of the algorithm. The choice of [math]\displaystyle{ \,\Omega(F) }[/math] defines the imposed constraint on the operator, e.g. the rank or the trace norm constraint. Also, this choice affects the efficiency or the feasibility of the learning algorithm. The kernel choice determines the embedding of the users and the objects in their spaces. It should be noted that, interestingly, the choice of the kernel does not affect the algorithm, though it could easily affect the running time of the algorithm. The kernel should be selected based on the available data and the problem to be solved. The authors use Dirac kernels and attribute kernels, and these two kernels are applied to users (with respect to objects) and to attributes, respectively. They also state that choice of kernel can lead to new methods for problem such as matrix completion, multi-task learning, and pairwise learning.
If we assume that each pair of user/object is observed at most once, then the data can be considered as a [math]\displaystyle{ n_{\mathcal{X}} \times n_{\mathcal{Y}} }[/math] incomplete matrix. In addition, when the Dirac kernel is used for both users and objects, the users [math]\displaystyle{ \,{x_i} }[/math]'s and the objects [math]\displaystyle{ \,{y_i} }[/math]'s can be organized into [math]\displaystyle{ n_{\mathcal{X}} }[/math] and [math]\displaystyle{ n_{\mathcal{Y}} }[/math] groups of identical data points, respectively. In the case of completing an incomplete matrix (matrix completion), finding a low-rank approximation of the available entries of the matrix is a popular strategy, for which, the loss function of square loss error can be combined to rank penalty constraint. To overcome the non-convexity of the problem, a convex spectral function can be considered. For instance, in the case of binary preferences, hinge loss function with trace norm penalty can be selected. This can be written as a semi-definite program. (maximum margin matrix factorization (MMMF) by <ref name="srebro05"></ref>).
If we access attributes only for objects [math]\displaystyle{ \mathbf{y} }[/math]. For a finite number of users, the goal is to estimate separate function [math]\displaystyle{ f_{i}(\mathbf{y}) }[/math] for each user [math]\displaystyle{ \,i }[/math]. Each estimation is a learning task. Therefore, this problem will be a multi-task learning problem, i.e. we will learn all of the tasks, the [math]\displaystyle{ f_{i} }[/math]'s, simultaneously. In this case, attribute kernel is used for objects and Dirac kernel for the users, and the choice of loss function depends on what task exactly is solved. selecting a rank penalty function and replace it with trace norm penalty function to achieve convexity results in a similar approach proposed by <ref name="argy08">A. Argyriou, T. Evgeniou, and M. Pontil. Convex multi-task feature learning. Mach. Learn., 73(3):243–272, 2008.</ref> for multi-task learning. In addition, one can also use a multi-task kernel, i.e. a kernel [math]\displaystyle{ \,k_{multi-task} }[/math] over the entire product space [math]\displaystyle{ \,X \times Y }[/math] and defined between any two user/object pairs [math]\displaystyle{ \,(x,y) }[/math] and [math]\displaystyle{ \,(x',y') }[/math] by:
File:c5p2.jpg, where [math]\displaystyle{ \,c \gt 0 }[/math] controls how the variances of the classifiers are constrained in comparison to the norm of each classifier.
If we access attributes for both users and objects, we can apply the attributes kernels to each. Using the Hilbert-Schmidt norm as the spectral penalty and an appropriate loss function (e.g. hinge loss function) results in classical machine learning algorithms (e.g. SVM if the hinge loss is used as the loss function) that is applied to the tensor product of [math]\displaystyle{ \,\mathcal{X} }[/math] and [math]\displaystyle{ \,\mathcal{Y} }[/math]. An interesting point to note is that, as explained by Evgeniou et al. (2005), when [math]\displaystyle{ \,c = 0 }[/math], i.e. when we take a Dirac kernel for the users and an attribute kernel for the objects, then penalizing the Hilbert-Schmidt norm is equivalent to estimating independent models for the users.
There are cases in which we access attributes of users and objects, and want to use them to guide us through better predictions, but the attributes are not informative enough. For instance, we access gender and age of users, but want to infer predictions based on different preferences of users with the same age and gender. So, we may use attribute kernel to apply the attributes of users in inference, but we also should apply Dirac kernel to perform inference for the different users with same attributes. The authors use the following convex combination of Dirac and attributes kernel <ref name="aber06"> J. Abernethy, F. Bach, T. Evgeniou, and J.-P. Vert. Low-rank matrix factorization with attributes. Technical Report N24/06/MM, Ecole des Mines de Paris, 2006.</ref>:
where [math]\displaystyle{ 0 \leq \eta \leq 1 }[/math] and [math]\displaystyle{ 0 \leq \zeta \leq 1 }[/math]. These kernels combine the Dirac kernels [math]\displaystyle{ \,(\eta = 0 and \zeta = 0) }[/math] and the attributes kernels [math]\displaystyle{ \,(\eta = 1 and \zeta = 1) }[/math] by interpolating between them. In addition, combining this choice of kernels with, for example, the trace norm penalty function would enable us to continuously interpolate between the different settings that correspond to the different 'corners' in the [math]\displaystyle{ \,(\eta , \zeta) }[/math] square, which consist of standard CF with matrix completion at the [math]\displaystyle{ \,(0,0) }[/math] corner, multi-task learning at both the [math]\displaystyle{ \,(0,1) }[/math] and the [math]\displaystyle{ \,(1,0) }[/math] corners, and last but not the least learning over pairs at the [math]\displaystyle{ \,(1,1) }[/math] corner. This extra degree of freedom resulting from allowing both [math]\displaystyle{ \,\eta }[/math] and [math]\displaystyle{ \,\zeta }[/math] to vary continuously between [math]\displaystyle{ \,0 }[/math] and [math]\displaystyle{ \,1 }[/math] provides a way that optimally balances the influence of the attributes in the function estimation process.
Optimization Problem
Now the question is how to solve the general optimization problem proposed by the authors. The biggest problem is that the search space of the optimization problem, which is File:c5p3.jpg, can be of infinite-dimensional space. So, they showed that the proposed optimization problem can be modified to a finite-dimensional equivalent, and there are algorithms to solve it. Note that for optimization, we have two strategies, following the same two strategies in regular kernel methods: using the primal problem of the actual dimension of the underlying data or using the dual problem of dimension N (the number of ratings). The choice between those two formulations is problem-dependent.
The authors first showed that in the case of using a Hilbert-Schmidt norm as the penalty function ([math]\displaystyle{ \,\Omega(F) }[/math]), the set of [math]\displaystyle{ \{F\in \mathcal{B}_{0}(\mathcal{Y,X}): \Omega(F) \lt \infty \} }[/math] is the set of Hilbert-Schmidt operators, and the optimization problem can be written as:
It can be shown by the representer theorem (details regarding it are available in Peter Bartlett's lecture notes) that the solution to this problem lives in the linear span of the training data. <ref name="arons1950">N. Aronszajn. Theory of reproducing kernels. Trans. Am. Math. Soc., 68:337 – 404, 1950.</ref> <ref name="schol01">B. Scholkopf, R. Herbrich, and A. J. Smola. A generalized representer theorem. In Proceedings of the 14th Annual Conference on Computational Learning Theory, volume 2011 of Lecture Notes in Computer Science, pages 416–426, Berlin/Heidelberg, 2001. Springer.</ref> A concise proof of this property is on slide number 30 of Abernethy et al.'s slides titled Collaborative filtering in Hilbert spaces with spectral regularization.
The authors stated a generalized representer theorem (details regarding it are available in Scholkopf et al.'s paper titled A Generalized Representer Theorem) which shows the reformulation of the problem to a finite-dimensional problem is valid in the case of using a general spectral function [math]\displaystyle{ \,\Omega(F) }[/math]. This theorem shows that when a spectral penalty function controls the complexity of the compact operators, a solution to the problem can be found in the space of [math]\displaystyle{ \mathcal{X}_N \otimes \mathcal{Y}_N }[/math] which is finite-dimensional (set of [math]\displaystyle{ m_{\mathcal{X}} \times m_{\mathcal{Y}} }[/math] matrices). In other words, this results in finding [math]\displaystyle{ \,F }[/math] such that: [math]\displaystyle{ F=\sum^{m_{\mathcal{X}}}_{i=1}{\sum^{m_{\mathcal{Y}}}_{j=1}{{\alpha}_{ij}\mathbf{u}_{i}\otimes\mathbf{v}_{j}}} }[/math], and the [math]\displaystyle{ \mathbf{u}_i }[/math]s and the [math]\displaystyle{ \mathbf{v}_i }[/math]s are orthonormal bases of [math]\displaystyle{ \mathcal{X}_N }[/math] and [math]\displaystyle{ \mathcal{Y}_N }[/math], respectively. The coefficients [math]\displaystyle{ \,\alpha }[/math] can be found by solving the following finite-dimensional optimization problem:
.
The dimension of the space in this problem, however, might be prohibitively large for real-world applications where, for example, it is not uncommon to have tens of thousands of users and thousands of objects. Thus, to decrease the complexity at the expense of possibly losing convexity, it is convenient to constrain the rank of the operator by using a well-chosen spectral penalty. Indeed, if we add a rank constraint [math]\displaystyle{ \,rank(F) \le r }[/math] to this optimization problem, then the representer theorem still holds whilst we obtain the benefit that the dimension of the parameter [math]\displaystyle{ \,\alpha }[/math] becomes significantly reduced from [math]\displaystyle{ {m_{\mathcal{X}}\times m_{\mathcal{Y}}} }[/math] to [math]\displaystyle{ \,r \times ({m_{\mathcal{X}} + m_{\mathcal{Y}}}) }[/math]. However, some problems do in fact result from adding a rank constraint to the Hilbert-Schmidt norm penalty; one problem is that the classical representer theorem no longer holds, and a more important problem is that doing so will likely lead to algorithmic / efficiency consequences.
Assuming the loss function is convex which is usually held in practice, the authors derived the convex dual problem to solve the optimization problem. [math]\displaystyle{ \,\psi_{i}(v_{i}) = l(v_i,t_i) }[/math] is the loss of predicting [math]\displaystyle{ \,v_i }[/math] for the [math]\displaystyle{ \,i }[/math]-th data point. By applying the representer theorem, the primal form of the optimization problem will look like:
.
The dual problem can be obtained as maximizing the following expression:
where [math]\displaystyle{ \beta \in \mathbb{R}^N }[/math] is the Lagrangian multiplier, and [math]\displaystyle{ \,\psi^{*}_i }[/math] and [math]\displaystyle{ \,\Omega^{*} }[/math] are the Fenchel conjugates of [math]\displaystyle{ \,\psi_i }[/math] and [math]\displaystyle{ \,\Omega }[/math], respectively. For finding [math]\displaystyle{ \,\alpha }[/math], first the optimal dual variable [math]\displaystyle{ \,\beta }[/math] is found and then [math]\displaystyle{ \,\alpha }[/math] is among the Fenchel duals of [math]\displaystyle{ -\frac{1}{\lambda}X^{T}\textrm{Diag}(\beta)Y }[/math].
Choosing either the primal or the dual formulation depends on the problem. For instance, in CF problem, the number of variables of the primal and dual formulation is equal to [math]\displaystyle{ m_{\mathcal{X}} m_{\mathcal{Y}} }[/math] and [math]\displaystyle{ \,N }[/math], respectively, and based on the available ratings [math]\displaystyle{ \,N }[/math] compared to [math]\displaystyle{ m_{\mathcal{X}} m_{\mathcal{Y}} }[/math], one of the primal or dual programs will be chosen.
Experiments
Experiments have been performed to show that incorporating the extra information from users or objects to the CF approach can lead to more accurate predictions. The first series of experiments were done on synthetic data which was created by first sampling i.i.d. multivariate features for [math]\displaystyle{ \,x }[/math] and [math]\displaystyle{ \,y }[/math] (both having 6 dimensions). Next, they sampled [math]\displaystyle{ \,z }[/math] from a bilinear form in [math]\displaystyle{ \,x }[/math] and [math]\displaystyle{ \,y }[/math] plus noise, and finally, restricting the observed features to only [math]\displaystyle{ \,3 }[/math] for both [math]\displaystyle{ \,x }[/math] and [math]\displaystyle{ \,y }[/math]. The comparison results between two cases of applying the trace norm and the Frobenius norm spectral penalties (in the same rank-constrained problem) showed that the trace norm penalty performed slightly better. Also, the best performance in both cases was achieved when there has been a balance between using the Dirac and the attribute kernels, where the pair of values for [math]\displaystyle{ \,\eta }[/math] and [math]\displaystyle{ \,\zeta }[/math] that define this combined usage of the Dirac and the attributes kernels would be in the middle of the square for which the corners are [math]\displaystyle{ (\,\eta=0,\,\zeta=0) }[/math], [math]\displaystyle{ (\,\eta=0,\,\,\zeta=1) }[/math],[math]\displaystyle{ (\,\eta=1,\,\zeta=0) }[/math] , and [math]\displaystyle{ (\,\eta=1,\,\zeta=1) }[/math]. This is shown in the figure below taken from Abernathy et al.'s paper.
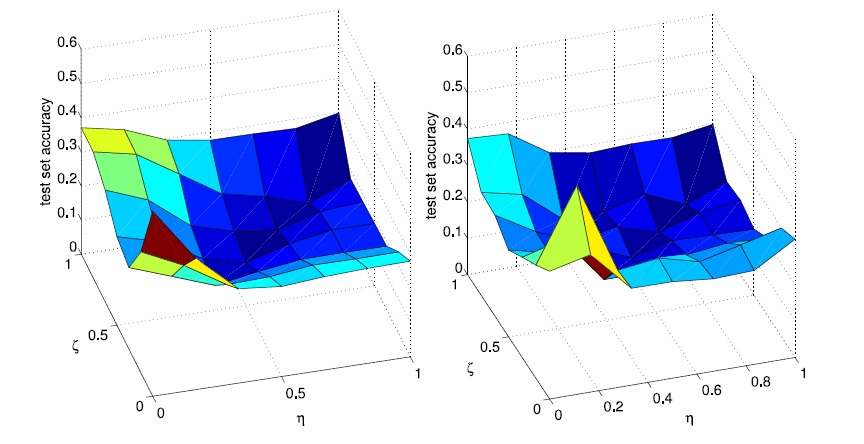
The second series of experiments were performed on the MovieLens data-set which includes rating of [math]\displaystyle{ \,1,682 }[/math] movies by [math]\displaystyle{ \,943 }[/math] users. Movie Rating have been selected from the set of numbers [math]\displaystyle{ \,1 }[/math] to [math]\displaystyle{ \,5 }[/math]. The data-set also includes attribute of genre for movies and attributes of age, gender, and occupation for users. Root mean squared error (RMSE) has been measured in 10-fold cross-validation for the experiments on this data-set. Again, the best balance between the attribute and the Dirac kernels was obtainable inside the mentioned square.
Discussion
One particularly interesting application of collaborative filtering was in the Netflix contest. Netflix, an online movie rental company, proposed a prize of $1,000,000 to any team who could significantly best their own preference prediction algorithm. Interestingly, the best-performing algorithms were those that were finely-tuned ensemble approaches. So, while techniques for including side-information such as those described in this paper <ref name="self" /> are important, particularly when few or no observations have been made of users preferences, developing highly accurate prediction engines requires a lot of tuning for a specific dataset.
Conclusion
The authors presented a generalized formulation for the matrix completion problem. This formulation aims to find a linear compact operator between two Hilbert-Schmidt spaces. Also, they showed that their generalized notion includes different approaches as its special cases. The experiments focused on the CF application and indicated that incorporating attribute information improves the accuracy of the predictions.
A future research could be to further explore the multi-task learning algorithms, such as to study the possibility to derive real-time implementations that may better fit the need for large-scale applications where training data is growing larger and larger. On the theoretical side, a better understanding of the effects of the norm and the rank regularizations and their interaction would be of an interesting topic.
References
<references />