a Dynamic Bayesian Network Click Model for Web Search Ranking
One of the most common click models in Web search, known as the position model, is based on the position bias on the displayed ranked results. Under this model, it is assumed that the chance of click decreases towards the lower ranks on result pages due to the reduced visual attention from the user. A more recent click model, referred to as the cascade model of user behaviour, assumes that the user scans search results from top to bottom and eventually stops because either their information need is satisfied or their patience is exhausted.
The benefit of the cascade model over the position model is its ability to explain click with respect to the relevance of the previous documents; therefore, the later model has shown state-of-the-art performance over the former one. However, the cascade model makes a strong assumption that there is only one click per search; hence, it can not explain the abandoned search or search with multiple clicks. Moreover, none of these models distinguish the perceived relevance and the actual relevance. The perceived relevance is the relevance of a document judged by the user based on their examination of the document as it is shown on a result page. The actual relevance is the relevance of the document judged by the user once she/he clicks on it and sees its content.
A Dynamic Bayesian Network (DBN) model is proposed in this paper in order to study the user's browsing and click behaviour, and eventually to infer the relevance of the documents. The proposed model addresses the issues with the above models through the following assumptions about the user's click and browsing behaviour:
- The user makes a linear traversal through the results and decides whether to click based on the perceived relevance of the document.
- The user chooses to examine the next document if she/he is unsatisfied with the clicked document (based on the actual relevance).
- A click does not necessarily mean that the user is satisfied with the clicked document. With respect to this, the proposed model attempts to distinguish the perceived relevance and the actual relevance.
- There is no limit on the number of clicks that a user can make during a search.
The documents ranked on a result list of a given query are presented through a sequence in DBN. The variables inside the box are defined at the session level, while those out of the box are defined at the query level.
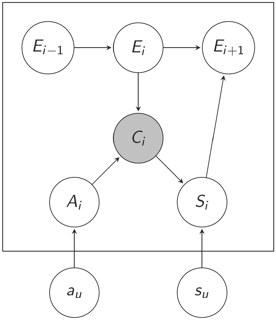
For a given position i, there is an observed variable [math]\displaystyle{ \ C_i }[/math] indicating whether there was a click at position [math]\displaystyle{ \ i }[/math]. There are three hidden binary variables defined for each position [math]\displaystyle{ \ i }[/math] in order to model examination, perceived relevance, and actual relevance:
- [math]\displaystyle{ \ E_i }[/math]: whether the user examined the document at position [math]\displaystyle{ \ i }[/math].
- [math]\displaystyle{ \ A_i }[/math]: whether the user was attracted by the document at position [math]\displaystyle{ \ i }[/math] (i.e. perceived relevance).
- [math]\displaystyle{ \ S_i }[/math]: whether the user was satisfied by the document at position [math]\displaystyle{ \ i }[/math] (i.e. actual relevance).
The variables [math]\displaystyle{ \ a_u }[/math] and [math]\displaystyle{ \ s_u }[/math] are related to the relevance of the document. [math]\displaystyle{ \ a_u }[/math] represents the perceived relevance, and [math]\displaystyle{ \ s_u }[/math] represents the ratio between the actual relevance (denoted by [math]\displaystyle{ \ r_u }[/math]) and the perceived relevance:
The rest of the assumptions about the user click and browsing behaviour are modeled in DBN as follows:
- The user always examines the first result (i.e. document at position 1).
- If the user does not examine the position [math]\displaystyle{ \ i }[/math] she/he will not examine the subsequent positions.
- There is a click if and only if the user looked at the document and was attracted by it.
- The probability of being attracted depends only on the document.
- The user scans the results list linearly from top to bottom until she/he decides to stop. Once the user clicks and visits the document, there is a certain probability that she/he will be satisfied by the document.
- No click from the user indicates no user's satisfaction on the document.
- Once the user is satisfied by the visited document that, she/he stops the search.
- If the user is not satisfied by the current result, there is a probability [math]\displaystyle{ \ 1 − \gamma }[/math] that the user stops the search (a.k.a. search abandonment), and a probability [math]\displaystyle{ \ \gamma }[/math] that the user examines the next document.
The model is trained using the Expectation Maximization:
- E-Step: Given [math]\displaystyle{ \ a_u }[/math] and [math]\displaystyle{ \ s_u }[/math], the posterior probabilities on [math]\displaystyle{ \ A_i }[/math], [math]\displaystyle{ \ E_i }[/math], and [math]\displaystyle{ \ S_i }[/math] are computed.
- M-Step: Given the posterior probabilities, values of [math]\displaystyle{ \ a_u }[/math], [math]\displaystyle{ \ s_u }[/math], and [math]\displaystyle{ \ \gamma }[/math] are updated.
Three types of experiments are conducted in the paper to validate DBN and to compare it with the existing models. First, they evaluate the click model in terms of the predicted click rate at position 1. Then they use the predicted relevance as a feature in a ranking function. In the last set of experiments, they use the predicted relevance as a supplementary information to train a ranking function.
The empirical results from the experiments on the logs of a commercial search engine indicate that DBN can accurately explain the observed clicks. They show that the function learned with the predicted relevance is not far from being as good as a function trained with a large amount of editorial data. They further show that combining both types of information can lead to an even more accurate ranking function.