a Dynamic Bayesian Network Click Model for Web Search Ranking: Difference between revisions
No edit summary |
m (Conversion script moved page A Dynamic Bayesian Network Click Model for Web Search Ranking to a Dynamic Bayesian Network Click Model for Web Search Ranking: Converting page titles to lowercase) |
||
| (36 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
One of the most common click models in Web search, known as the ''position model'', is based on the position bias on the displayed ranked results. Under this model, it is assumed that the chance of click decreases towards the lower ranks on result pages due to the reduced visual attention from the user. A more recent click model, referred to as the ''cascade model'' of user | ===Background: Click Models=== | ||
Nowadays search engines play an important role even in everyday life. A search engine must be able to rank the search results by relevance. This can be considered very hard learning problem. One important data that can be used for training stage is what users chose after using the engine for searching. But as we know most users click on what appears as the first search results and it is unlikely to click on results that do not appear at the beginning, even though relevant. So if we use the results chosen by users for training it is biased since a lot of results are not considered this way. One important thing which can help us is model the click properly and use the model in training stage. | |||
One of the most common click models in Web search, known as the ''position model'', is based on the position bias on the displayed ranked results. Under this model, it is assumed that the chance of click decreases towards the lower ranks on result pages due to the reduced visual attention from the user. A more recent click model, referred to as the ''cascade model'' of user behavior, assumes that the user scans search results from top to bottom and eventually stops because either their information need is satisfied or their patience is exhausted. | |||
The benefit of the cascade model over the position model is its ability to explain click with respect to the relevance of the previous documents; therefore, the later model has shown state-of-the-art performance over the former one. However, the cascade model makes a strong assumption that there is only one click per search; hence, it can not explain the abandoned search or search with multiple clicks. Moreover, none of these models distinguish the perceived relevance and the actual relevance. The perceived relevance is the relevance of a document judged by the user based on their examination of the document as it is shown on a result page. The actual relevance is the relevance of the document judged by the user once she/he clicks on it and sees its content. | The benefit of the cascade model over the position model is its ability to explain click with respect to the relevance of the previous documents; therefore, the later model has shown state-of-the-art performance over the former one. However, the cascade model makes a strong assumption that there is only one click per search; hence, it can not explain the abandoned search or search with multiple clicks. Moreover, none of these models distinguish the perceived relevance and the actual relevance. The perceived relevance is the relevance of a document judged by the user based on their examination of the document as it is shown on a result page. The actual relevance is the relevance of the document judged by the user once she/he clicks on it and sees its content. | ||
A Dynamic Bayesian Network (DBN) model is proposed in this paper in order to study the user's browsing and click | ===The Proposed Model=== | ||
A Dynamic Bayesian Network (DBN) model is proposed in this paper in order to study the user's browsing and click behavior, and eventually to infer the relevance of the documents. The proposed model addresses the issues with the above models through the following assumptions about the user's click and browsing behavior: | |||
* The user makes a linear traversal through the results and decides whether to click based on the perceived relevance of the document. | * The user makes a linear traversal through the results and decides whether to click based on the perceived relevance of the document. | ||
| Line 10: | Line 14: | ||
* There is no limit on the number of clicks that a user can make during a search. | * There is no limit on the number of clicks that a user can make during a search. | ||
The documents ranked on a result list of a given query are presented through a sequence in DBN. The variables inside the box are defined at the session level, while those out of the box are defined at the | The documents ranked on a result list of a given query are presented through a sequence in DBN. The variables inside the box are defined at the session level, while those out of the box are defined at the document level. | ||
<center> [[File:Dbn.png]] </center> | <center> [[File:Dbn.png]] </center> | ||
For a given position i, there is an observed variable <math>\ C_i</math> indicating whether there was a click at position <math>\ i</math>. There are three hidden binary variables defined for each position <math>\ i</math> in order to model examination, perceived relevance, and actual relevance: | For a given position <math>\ i </math>, there is an observed variable <math>\ C_i</math> indicating whether there was a click at position <math>\ i</math>. There are three hidden binary variables defined for each position <math>\ i</math> in order to model examination, perceived relevance, and actual relevance: | ||
* <math>\ E_i</math>: whether the user examined the document at position <math>\ i</math>. | * <math>\ E_i</math>: whether the user examined the document at position <math>\ i</math>. | ||
| Line 20: | Line 24: | ||
* <math>\ S_i</math>: whether the user was satisfied by the document at position <math>\ i</math> (i.e. actual relevance). | * <math>\ S_i</math>: whether the user was satisfied by the document at position <math>\ i</math> (i.e. actual relevance). | ||
The variables <math>\ a_u</math> and <math>\ s_u</math> are related to the relevance of the document. <math>\ a_u</math> represents the perceived relevance, and <math>\ s_u</math> represents the ratio between the actual relevance (denoted by <math>\ r_u</math>) and the perceived relevance: | The variables <math>\ a_u</math> and <math>\ s_u</math> are related to the relevance of the document. <math>\ a_u</math> represents the perceived relevance, and <math>\ s_u</math> represents the ratio between the actual relevance (denoted by <math>\ r_u</math>) and the perceived relevance. The objective of the paper is to estimate the actual relevance of the document <math>\ u</math>: | ||
<center><math>\ r_u | <center><math>\ r_u = P(S_i=1 | E_i=1) = P(S_i=1|C_i=1) P(C_i=1 | E_i=1) = s_u a_u</math></center> | ||
The rest of the assumptions about the user click and browsing | The rest of the assumptions about the user click and browsing behavior are modeled in DBN as follows: | ||
* The user always examines the first result (i.e. document at position 1) | * The user always examines the first result (i.e. document at position 1); | ||
: <math>\ E_1 = 1</math> | |||
* If the user | * If the user does not examine the position <math>\ i </math> she/he will not examine the subsequent positions; | ||
: <math>\ E_i = 0 \Rightarrow E_{i+1} = 0</math> | |||
* There is a click if and only if the user looked at the document and was attracted by it | * There is a click if and only if the user looked at the document and was attracted by it; | ||
: <math>\ A_i = 1, E_i = 1 \Leftrightarrow C_i = 1</math> | |||
* The probability of being attracted depends only on the document | * The probability of being attracted depends only on the document; | ||
: <math>\ P(A_i=1) = a_u</math> | |||
* The user scans the results list linearly from top to bottom until she/he decides to stop. Once the user clicks and visits the document, there is a certain probability that she/he will be satisfied by the document | * The user scans the results list linearly from top to bottom until she/he decides to stop. Once the user clicks and visits the document, there is a certain probability that she/he will be satisfied by the document; | ||
: <math>\ P(S_i = 1 | C_i = 1) = s_u</math> | |||
* No click from the user indicates no user's satisfaction on the document | * No click from the user indicates no user's satisfaction on the document; | ||
: <math>\ C_i = 0 \Rightarrow S_i = 0</math> | |||
* Once the user is satisfied by the visited document | * Once the user is satisfied by the visited document, she/he stops the search; | ||
: <math>\ S_i = 1 \Rightarrow E_{i+1} = 0</math> | |||
* If the user is not satisfied by the current result, she/he will examine the next document with the probability<math>\ \gamma </math> (or will abandon the search with the probability <math>\ 1 - \gamma </math> ); | |||
: <math>\ P(E_{i+1}=1 | E_i = 1, S_i = 0) = \gamma </math> | |||
The model is trained using the Expectation Maximization: | The model is trained using the Expectation Maximization: | ||
* E-Step: Given <math>\ a_u </math> and <math>\ s_u </math>, the posterior probabilities on <math>\ A_i </math>, <math>\ E_i </math>, and <math>\ S_i </math> are computed. | * E-Step: Given <math>\ a_u </math> and <math>\ s_u </math>, the posterior probabilities on <math>\ A_i </math>, <math>\ E_i </math>, and <math>\ S_i </math> are computed. | ||
* M-Step: Given the posterior probabilities, values of <math>\ a_u </math>, <math>\ s_u </ | * M-Step: Given the posterior probabilities, values of <math>\ a_u </math>, <math>\ s_u </math>, and <math>\ \gamma </math> are updated. | ||
Three types of experiments are conducted in the paper to validate DBN and to compare it with the existing models. First, they evaluate the click model in terms of the predicted click rate at position 1. Then they use the predicted relevance as a feature in a ranking function. In the last set of experiments, they use the predicted relevance as a supplementary information to train a ranking function. | ===Evaluation=== | ||
Three types of experiments are conducted in the paper to validate DBN and to compare it with the existing models. First, they evaluate the click model in terms of the predicted click rate at position 1. Then they use the predicted relevance as a feature in a ranking function. In the last set of experiments, they use the predicted relevance as a supplementary information to train a ranking function. The following figure (from source paper) depicts the results (click for larger view): | |||
[[File:aaa.png|thumb|right|Fig.1 Experimental Results.]] | |||
The empirical results from the experiments on the logs of a commercial search engine indicate that DBN can accurately explain the observed clicks. They show that the function learned with the predicted relevance is not far from being as good as a function trained with a large amount of editorial data. They further show that combining both types of information can lead to an even more accurate ranking function. | The empirical results from the experiments on the logs of a commercial search engine indicate that DBN can accurately explain the observed clicks. They show that the function learned with the predicted relevance is not far from being as good as a function trained with a large amount of editorial data. They further show that combining both types of information can lead to an even more accurate ranking function. | ||
===Conclusions=== | |||
A novel model for dynamic click model based on Bayesian networks was proposed. The major contribution is to incorporate satisfaction in click model. Experiments confirms this method to be useful. A next step to improve the model further is to consider the time that the user spends on each page after click. | |||
== A review of the study== | |||
One of the important techniques in web-search ranking is Click modelling, which aims to estimate the probability of click to benefit a wide range of search–related application. Click modeling is a challenging task as it affected by different factors including position bias and hidden variables. Four hypotheses are common in the click modeling which are examination hypothesis, cascade hypothesis, rationality hypothesis and positional rationality hypothesis. Based on these hypotheses many models have proposed to understand user click behaviour, but, the most common models in click modeling are cascade model and examination model. In this paper, the author proposed Dynamic Bayesian Network (DBN) model to compute the value of the perceived relevance ai and user satisfaction si assuming that users scan the links top to bottom and if they satisfy with a document they will not examine the next document. This model is similar to hidden Markov model in that there is a conditional dependency between the probability of examining a URL and the probability of examining the next URL, but it differs in that the probability of examining the next URL depends on the observation and hidden variables of the current documents. | |||
==Another models :== | |||
==Examination Hypothesis:== | |||
This hypothesis assumes that if a URL clicked by a user that means it’s both examined and relevant to the query . In another word , given a query q , position i and URL u the probability of examining a URL is : | |||
<math>P(C=1|u, p)=P(C=1|u,E=1)P(E=1|p)</math> | |||
Many models have proposed based on the examination hypothesis including the Clicks Over | |||
Expected Clicks (COEC) model [http://www2007.org/workshops/paper_63.pdf], the Examination model[http://olivier.chapelle.cc/pub/DBN_www2009.pdf], and the Logistic model[http://research.microsoft.com/apps/pubs/default.aspx?id=78789]. | |||
==The cascade model:== | |||
This model[http://dl.acm.org/citation.cfm?id=1341545] is based on the assumption that the user scans the results top to bottom, and the click depends on the relevance of all the results of a query. This model simply aggregate the click and skip of each documents in the results. | |||
<math>P(C_i=1)=r_i\prod_{j=1}^i-1(1-r_j)</math> where <math>r_i</math> the probability of click in position i and <math>(1-r_j)</math> is the probability of a document being skipped | |||
==Click chain model (CCM):== | |||
This model [http://www2009.eprints.org/2/1/p11.pdf]is similar to the cascade model as it assume that user scan the documents top to bottoms, but it added the transition probability from the ith url to next url i+1, which is similar to DBN approach as the probability of examining the document <math>d_i+1</math> is based on the action in the current document <math>d_i</math>. The conditional probability defined by CCM are : | |||
<math>P(C_i = 1|E_i = 0) = 0</math> | |||
<math>P(C_1 = 1|E_i = 1,R_i) = R_i</math> | |||
<math>P(E_i+1 = 1|Ei = 0) = 0 </math> | |||
<math>P(E_i+1 = 1|E_i = 1, C_i = 0) = \alpha1</math> if the user skipped a url in a potion i the probability of examining the next url is <math>\alpha 1</math> | |||
<math>P(E_i+1 = 1|E_i = 1, C_i = 1, R_i) = \alpha2(1 − R_i) + \alpha3R_i</math> if the user clicked the url in position i the probability of examining the next depends on the relevance of document <math>d_i</math> range between <math>\alpha2</math> and <math>\alpha3</math> (<math>\alpha1</math> , <math>\alpha2</math>,<math>\alpha3</math> are fixed constants that independent of the user and query) | |||
Latest revision as of 09:45, 30 August 2017
Background: Click Models
Nowadays search engines play an important role even in everyday life. A search engine must be able to rank the search results by relevance. This can be considered very hard learning problem. One important data that can be used for training stage is what users chose after using the engine for searching. But as we know most users click on what appears as the first search results and it is unlikely to click on results that do not appear at the beginning, even though relevant. So if we use the results chosen by users for training it is biased since a lot of results are not considered this way. One important thing which can help us is model the click properly and use the model in training stage.
One of the most common click models in Web search, known as the position model, is based on the position bias on the displayed ranked results. Under this model, it is assumed that the chance of click decreases towards the lower ranks on result pages due to the reduced visual attention from the user. A more recent click model, referred to as the cascade model of user behavior, assumes that the user scans search results from top to bottom and eventually stops because either their information need is satisfied or their patience is exhausted.
The benefit of the cascade model over the position model is its ability to explain click with respect to the relevance of the previous documents; therefore, the later model has shown state-of-the-art performance over the former one. However, the cascade model makes a strong assumption that there is only one click per search; hence, it can not explain the abandoned search or search with multiple clicks. Moreover, none of these models distinguish the perceived relevance and the actual relevance. The perceived relevance is the relevance of a document judged by the user based on their examination of the document as it is shown on a result page. The actual relevance is the relevance of the document judged by the user once she/he clicks on it and sees its content.
The Proposed Model
A Dynamic Bayesian Network (DBN) model is proposed in this paper in order to study the user's browsing and click behavior, and eventually to infer the relevance of the documents. The proposed model addresses the issues with the above models through the following assumptions about the user's click and browsing behavior:
- The user makes a linear traversal through the results and decides whether to click based on the perceived relevance of the document.
- The user chooses to examine the next document if she/he is unsatisfied with the clicked document (based on the actual relevance).
- A click does not necessarily mean that the user is satisfied with the clicked document. With respect to this, the proposed model attempts to distinguish the perceived relevance and the actual relevance.
- There is no limit on the number of clicks that a user can make during a search.
The documents ranked on a result list of a given query are presented through a sequence in DBN. The variables inside the box are defined at the session level, while those out of the box are defined at the document level.
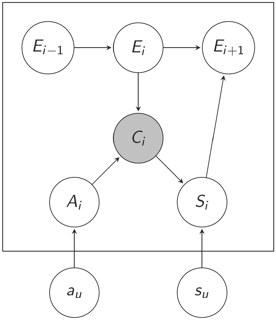
For a given position [math]\displaystyle{ \ i }[/math], there is an observed variable [math]\displaystyle{ \ C_i }[/math] indicating whether there was a click at position [math]\displaystyle{ \ i }[/math]. There are three hidden binary variables defined for each position [math]\displaystyle{ \ i }[/math] in order to model examination, perceived relevance, and actual relevance:
- [math]\displaystyle{ \ E_i }[/math]: whether the user examined the document at position [math]\displaystyle{ \ i }[/math].
- [math]\displaystyle{ \ A_i }[/math]: whether the user was attracted by the document at position [math]\displaystyle{ \ i }[/math] (i.e. perceived relevance).
- [math]\displaystyle{ \ S_i }[/math]: whether the user was satisfied by the document at position [math]\displaystyle{ \ i }[/math] (i.e. actual relevance).
The variables [math]\displaystyle{ \ a_u }[/math] and [math]\displaystyle{ \ s_u }[/math] are related to the relevance of the document. [math]\displaystyle{ \ a_u }[/math] represents the perceived relevance, and [math]\displaystyle{ \ s_u }[/math] represents the ratio between the actual relevance (denoted by [math]\displaystyle{ \ r_u }[/math]) and the perceived relevance. The objective of the paper is to estimate the actual relevance of the document [math]\displaystyle{ \ u }[/math]:
The rest of the assumptions about the user click and browsing behavior are modeled in DBN as follows:
- The user always examines the first result (i.e. document at position 1);
- [math]\displaystyle{ \ E_1 = 1 }[/math]
- If the user does not examine the position [math]\displaystyle{ \ i }[/math] she/he will not examine the subsequent positions;
- [math]\displaystyle{ \ E_i = 0 \Rightarrow E_{i+1} = 0 }[/math]
- There is a click if and only if the user looked at the document and was attracted by it;
- [math]\displaystyle{ \ A_i = 1, E_i = 1 \Leftrightarrow C_i = 1 }[/math]
- The probability of being attracted depends only on the document;
- [math]\displaystyle{ \ P(A_i=1) = a_u }[/math]
- The user scans the results list linearly from top to bottom until she/he decides to stop. Once the user clicks and visits the document, there is a certain probability that she/he will be satisfied by the document;
- [math]\displaystyle{ \ P(S_i = 1 | C_i = 1) = s_u }[/math]
- No click from the user indicates no user's satisfaction on the document;
- [math]\displaystyle{ \ C_i = 0 \Rightarrow S_i = 0 }[/math]
- Once the user is satisfied by the visited document, she/he stops the search;
- [math]\displaystyle{ \ S_i = 1 \Rightarrow E_{i+1} = 0 }[/math]
- If the user is not satisfied by the current result, she/he will examine the next document with the probability[math]\displaystyle{ \ \gamma }[/math] (or will abandon the search with the probability [math]\displaystyle{ \ 1 - \gamma }[/math] );
- [math]\displaystyle{ \ P(E_{i+1}=1 | E_i = 1, S_i = 0) = \gamma }[/math]
The model is trained using the Expectation Maximization:
- E-Step: Given [math]\displaystyle{ \ a_u }[/math] and [math]\displaystyle{ \ s_u }[/math], the posterior probabilities on [math]\displaystyle{ \ A_i }[/math], [math]\displaystyle{ \ E_i }[/math], and [math]\displaystyle{ \ S_i }[/math] are computed.
- M-Step: Given the posterior probabilities, values of [math]\displaystyle{ \ a_u }[/math], [math]\displaystyle{ \ s_u }[/math], and [math]\displaystyle{ \ \gamma }[/math] are updated.
Evaluation
Three types of experiments are conducted in the paper to validate DBN and to compare it with the existing models. First, they evaluate the click model in terms of the predicted click rate at position 1. Then they use the predicted relevance as a feature in a ranking function. In the last set of experiments, they use the predicted relevance as a supplementary information to train a ranking function. The following figure (from source paper) depicts the results (click for larger view):
The empirical results from the experiments on the logs of a commercial search engine indicate that DBN can accurately explain the observed clicks. They show that the function learned with the predicted relevance is not far from being as good as a function trained with a large amount of editorial data. They further show that combining both types of information can lead to an even more accurate ranking function.
Conclusions
A novel model for dynamic click model based on Bayesian networks was proposed. The major contribution is to incorporate satisfaction in click model. Experiments confirms this method to be useful. A next step to improve the model further is to consider the time that the user spends on each page after click.
A review of the study
One of the important techniques in web-search ranking is Click modelling, which aims to estimate the probability of click to benefit a wide range of search–related application. Click modeling is a challenging task as it affected by different factors including position bias and hidden variables. Four hypotheses are common in the click modeling which are examination hypothesis, cascade hypothesis, rationality hypothesis and positional rationality hypothesis. Based on these hypotheses many models have proposed to understand user click behaviour, but, the most common models in click modeling are cascade model and examination model. In this paper, the author proposed Dynamic Bayesian Network (DBN) model to compute the value of the perceived relevance ai and user satisfaction si assuming that users scan the links top to bottom and if they satisfy with a document they will not examine the next document. This model is similar to hidden Markov model in that there is a conditional dependency between the probability of examining a URL and the probability of examining the next URL, but it differs in that the probability of examining the next URL depends on the observation and hidden variables of the current documents.
Another models :
Examination Hypothesis:
This hypothesis assumes that if a URL clicked by a user that means it’s both examined and relevant to the query . In another word , given a query q , position i and URL u the probability of examining a URL is :
[math]\displaystyle{ P(C=1|u, p)=P(C=1|u,E=1)P(E=1|p) }[/math]
Many models have proposed based on the examination hypothesis including the Clicks Over Expected Clicks (COEC) model [1], the Examination model[2], and the Logistic model[3].
The cascade model:
This model[4] is based on the assumption that the user scans the results top to bottom, and the click depends on the relevance of all the results of a query. This model simply aggregate the click and skip of each documents in the results.
[math]\displaystyle{ P(C_i=1)=r_i\prod_{j=1}^i-1(1-r_j) }[/math] where [math]\displaystyle{ r_i }[/math] the probability of click in position i and [math]\displaystyle{ (1-r_j) }[/math] is the probability of a document being skipped
Click chain model (CCM):
This model [5]is similar to the cascade model as it assume that user scan the documents top to bottoms, but it added the transition probability from the ith url to next url i+1, which is similar to DBN approach as the probability of examining the document [math]\displaystyle{ d_i+1 }[/math] is based on the action in the current document [math]\displaystyle{ d_i }[/math]. The conditional probability defined by CCM are :
[math]\displaystyle{ P(C_i = 1|E_i = 0) = 0 }[/math]
[math]\displaystyle{ P(C_1 = 1|E_i = 1,R_i) = R_i }[/math]
[math]\displaystyle{ P(E_i+1 = 1|Ei = 0) = 0 }[/math]
[math]\displaystyle{ P(E_i+1 = 1|E_i = 1, C_i = 0) = \alpha1 }[/math] if the user skipped a url in a potion i the probability of examining the next url is [math]\displaystyle{ \alpha 1 }[/math]
[math]\displaystyle{ P(E_i+1 = 1|E_i = 1, C_i = 1, R_i) = \alpha2(1 − R_i) + \alpha3R_i }[/math] if the user clicked the url in position i the probability of examining the next depends on the relevance of document [math]\displaystyle{ d_i }[/math] range between [math]\displaystyle{ \alpha2 }[/math] and [math]\displaystyle{ \alpha3 }[/math] ([math]\displaystyle{ \alpha1 }[/math] , [math]\displaystyle{ \alpha2 }[/math],[math]\displaystyle{ \alpha3 }[/math] are fixed constants that independent of the user and query)