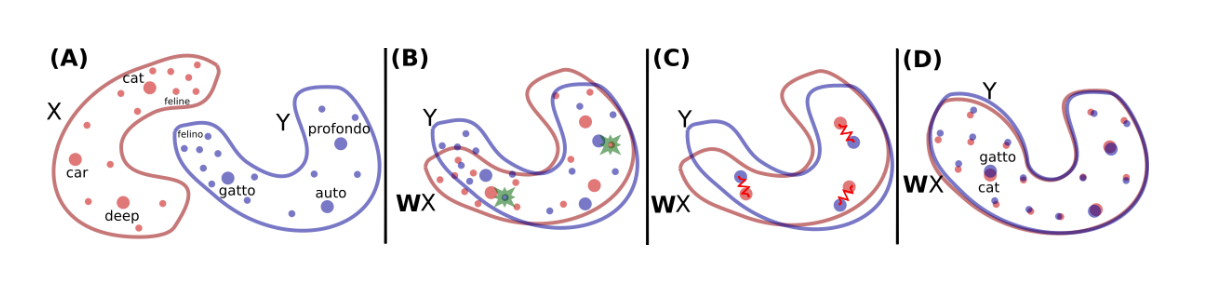
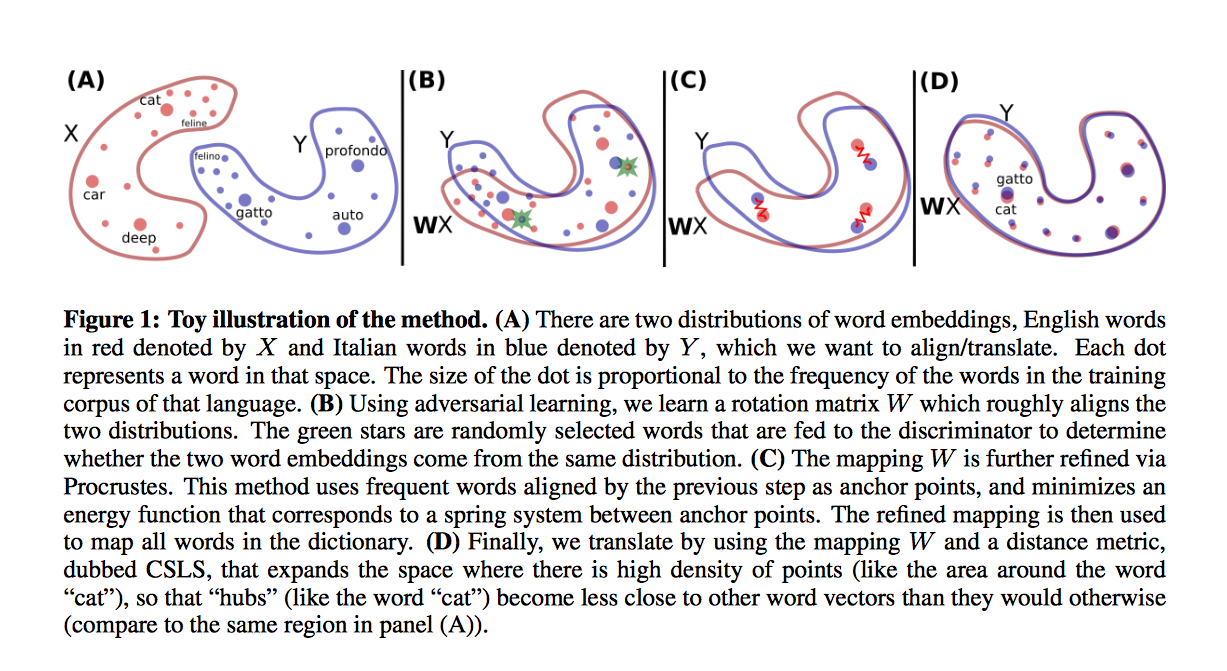
Word translation without parallel data
Presented by
Xia Fan
Introduction
This paper introduce a model that either is on par, or outperforms supervised state-of-the-art methods, without employing any cross-lingual annotated data. This method use a similar idea with GAN: it leverages adversarial training to learn a linear mapping from a source to a distinguish between the mapped source embeddings and the target embeddings, while the mapping is jointly trained to fool the discriminator. Second, this paper extract a synthetic dictionary from the resulting shared embedding space and fine-tune the mapping with the closed-form Procrustes solution from Schonemann (1966). Third, this paper also introduce an unsupervised selection metric that is highly correlated with the mapping quality and that we use both as a stopping criterion and to select the best hyper-parameters.
Model
Estimation of Word Representations in Vector Space
This model focuses on learning a mapping between the two sets such that translations are close in the shared space. Before talking about the model it used, a model which can exploit the similarities of monolingual embedding spaces should be introduced. Mikolov et al.(2013) use a known dictionary of n=5000 pairs of words [math]\displaystyle{ \{x_i,y_i\}_{i\in{1,n}} }[/math]. and learn a linear mapping W between the source and the target space such that
\begin{align} W^*=argmin_{W{\in}M_d(R)}||WX-Y||_F \hspace{1cm} (1) \end{align}
where d is the dimension of the embeddings, [math]\displaystyle{ M_d(R) }[/math] is the space of d*d matrices of real numbers, and X and Y are two aligned matrices of size d*n containing the embeddings of the words in the parallel vocabulary.
Xing et al. (2015) showed that these results are improved by enforcing orthogonality constraint on W. In that case, the equation (1) boils down to the Procrustes problem, which advantageously offers a closed form solution obtained from the singular value decomposition (SVD) of [math]\displaystyle{ YX^T }[/math] :
\begin{align} W^*=argmin_{W{\in}M_d(R)}||WX-Y||_F=UV^T, with U\Sigma V^T=SVD(YX^T) \end{align}
Domain-adversarial setting
This paper shows how to learn this mapping W without cross-lingual supervision. An illustration of the approach is given in Fig. 1. First, this model learn an initial proxy of W by using an adversarial criterion. Then, it use the words that match the best as anchor points for Procrustes. Finally, it improve performance over less frequent words by changing the metric of the space, which leads to spread more of those points in dense region.
Let [math]\displaystyle{ X={x_1,...,x_n} }[/math] and [math]\displaystyle{ Y={y_1,...,y_m} }[/math] be two sets of n and m word embeddings coming from a source and a target language respectively. A model is trained is trained to discriminate between elements randomly sampled from [math]\displaystyle{ WX={Wx_1,...,Wx_n} }[/math] and Y, We call this model the discriminator. W is trained to prevent the discriminator from making accurate predictions. As a result, this is a two-player game, where the discriminator aims at maximizing its ability to identify the origin of an embedding, and W aims at preventing the discriminator from doing so by making WX and Y as similar as possible. This approach is in line with the work of Ganin et al.(2016), who proposed to learn latent representations invariant to the input domain, where in our case, a domain is represented by a language(source or target).
1. Discriminator objective
Refer to the discriminator parameters as [math]\displaystyle{ \theta_D }[/math]. Consider the probability [math]\displaystyle{ P_{\theta_D}(source = 1|z) }[/math] that a vector z is the mapping of a source embedding (as opposed to a target embedding) according to the discriminator. The discriminator loss can be written as:
\begin{align} L_D(\theta_D|W)=-\frac{1}{n} \sum_{i=1}^n log P_{\theta_D}(source=1|Wx_i)-\frac{1}{m} \sum_{i=1}^m log P_{\theta_D}(source=0|Wx_i) \end{align}
2. Mapping objective
In the unsupervised setting, W is now trained so that the discriminator is unable to accurately predict the embedding origins:
\begin{align} L_W(W|\theta_D)=-\frac{1}{n} \sum_{i=1}^n log P_{\theta_D}(source=0|Wx_i)-\frac{1}{m} \sum_{i=1}^m log P_{\theta_D}(source=1|Wx_i) \end{align}
3. Learning algorithm To train our model, we follow the standard training procedure of deep adversarial networks of Goodfellow et al. (2014). For every input sample, the discriminator and the mapping matrix W are trained successively with stochastic gradient updates to respectively minimize [math]\displaystyle{ L_D }[/math] and [math]\displaystyle{ L_W }[/math]
Refinement procedre
The matrix W obtained with adversarial training gives good performance (see Table 1), but the results are still not on par with the supervised approach. In fact, the adversarial approach tries to align all words irrespective of their frequencies. However, rare words have embeddings that are less updated and are more likely to appear in different contexts in each corpus, which makes them harder to align. Under the assumption that the mapping is linear, it is then better to infer the global mapping using only the most frequent words as anchors. Besides, the accuracy on the most frequent word pairs is high after adversarial training. To refine our mapping, this paper build a synthetic parallel vocabulary using the W just learned with ad- versarial training. Specifically, this paper consider the most frequent words and retain only mutual nearest neighbors to ensure a high-quality dictionary. Subsequently, this paper apply the Procrustes solution in (2) on this generated dictionary. Considering the improved solution generated with the Procrustes al- gorithm, it is possible to generate a more accurate dictionary and apply this method iteratively, similarly to Artetxe et al. (2017). However, given that the synthetic dictionary obtained using ad- versarial training is already strong, this paper only observe small improvements when doing more than one iteration, i.e., the improvements on the word translation task are usually below 1%.
Cross-Domain similarity local scaling
In this paper, it considers a bi-partite neighborhood graph, in which each word of a given dictionary is connected to its K nearest neighbors in the other language. [math]\displaystyle{ N_T(Wx_s) }[/math] is used to denote the neighborhood, on this bi-partite graph, associated with a mapped source word embedding [math]\displaystyle{ Wx_s }[/math]. All K elements of [math]\displaystyle{ N_T(Wx_s) }[/math] are words from the target language. Similarly we denote by [math]\displaystyle{ N_S(y_t) }[/math] the neighborhood associated with a word t of the target language. Consider the mean similarity of a source embedding [math]\displaystyle{ x_s }[/math] to its target neighborhood as
\begin{align} r_T(Wx_s)=\frac{1}{K}\sum_{y\in N_T(Wx_s)}cos(Wx_s,y_t) \end{align}
where cos(,) is the cosine similarity. This is used to define similarity measure CSLS(.,.) between mapped source words and target words,as
\begin{align} CSLS(Wx_s,y_t)=2cos(Wx_s,y_t)-r_T(Wx_s)-r_S(y_t) \end{align}
Training and architectural choices
Architecture
This paper use unsupervised word vectors that were trained using fastText2. These correspond to monolin- gual embeddings of dimension 300 trained on Wikipedia corpora; therefore, the mapping W has size 300 × 300. Words are lower-cased, and those that appear less than 5 times are discarded for training. As a post-processing step, only the first 200k most frequent words were selected in the experiments. For the discriminator, it use a multilayer perceptron with two hidden layers of size 2048, and Leaky-ReLU activation functions. The input to the discriminator is corrupted with dropout noise with a rate of 0.1. As suggested by Goodfellow (2016), a smoothing coefficient s = 0.2 is included in the discriminator predictions. This paper use stochastic gradient descent with a batch size of 32, a learning rate of 0.1 and a decay of 0.95 both for the discriminator and W .
Discriminator inputs
Results
The resulting LSTM neural networks outperformed standard Statistical Machine Translation (SMT) with a BLEU score of 34.8 against 33.3 and with certain heuristics or modification, was very close to matching the best performing system. Additionally, it could recognize sentences in both active and passive voice as being similar.
Active Voice: I ate an apple.
Passive Voice: The apple was eaten by me.
An interesting result is the fact that reversing the source sentences (not test sentences) improved the long sentence decoding, which in turn increased the BLEU score from 25.9 to 30.6. While the authors do not have a complete explanation, they theorize the improvement in performance is due to the introduction of many short term dependencies to the data-set, by reversing the source sentences they minimize the time lag between the end of the source and the start of the target sentence. This reduction in the time lag is what the authors believe help the LSTM architecture establish a link between source and target and utilize the memory feature of the network better. Note, that the mean time lag does not change. Given the input sequence [math]\displaystyle{ (x_1, \dots, x_T) }[/math] and the target sequence [math]\displaystyle{ (y_1, \dots, y_T) }[/math], the sequence of time lags is [math]\displaystyle{ \Delta t = (T, \dots, T) }[/math] and [math]\displaystyle{ \frac{1}{T} \sum_{\Delta t_i} T = T }[/math]. If, however, the input is reversed, the sequence of time lags of corresponding inputs is [math]\displaystyle{ \Delta t = (1, 3, \dots, 2T - 1) }[/math] which still has a mean time lag of [math]\displaystyle{ \frac{1}{T} \sum_{\Delta t_i} (2i - 1) = \frac{1}{T} \sum_{i = 1}^{T/2} (2i + 2(T-i)) = T }[/math] (assuming even T, but odd T can be shown similarly). Thus, half of the time lags are shorter with the reversed input sequence.
For example, let "I saw the man" be the source sentence, "with the binoculars" be the target sentence, if we concatenate both source and target sentences we have "I saw the man with the binoculars". By reversing the source sentence ("man the saw I") the subject "man" is now closer to the context target "binoculars", compared to if the source sentence is not reversed. Reversing the input sentences leads to more confident predictions in the early parts of the target sentence and to less confident predictions in the later parts. Also, it results in LSTMs with better memory utilization.
In summary the LSTM method has proven to be quite capable of translating long sentences despite potentially long delay between input time steps. However, it still falls short of [Edinburgh's specialised statistical model http://www.statmt.org/OSMOSES/sysdesc.pdf].
Some developments of LSTM
Dealing with the very rare words are a challenge for the LSTM. A weakness of LSTM is its inability to (correctly) translate the very rare words that comes up with out-of-vocabulary words, i.e. no translation. The long short-term dependencies that are induced in this method can lead to less likelihood for a long sequence words come after the unknown words. In the other hand, these untranslated words impose a longer temporal memory that decrease the overall efficiency of network. Sutskever I ([1]) suggested a method to address the rare word problem. They assumed that if the origin of any undefined word is known then the word can be look up by introducing a post-processing step. This step would replace each unknown word in the system’s output with a translation of its source word. They proposed three strategies to track the source and translate it using either a dictionary or the identity translation.
Open questions
The results of the paper pose some interesting questions which are not discussed in the paper itself:
- Instead of reversing the input sequence the target sequence could be reversed. This would change the time lags between corresponding words in a similar way, but instead of reducing the time lag between the first half of corresponding words, it is reduced between the last half of the words. This might allow conclusions about whether the improved performance is purely due to the reduced minimal time lag or whether structure in natural language is also important (e.g. when a short time lag between the first few words is better than a short time lag between the last few words of sentence).
- For half of the words the time lag increases to more than the average. Thus, they might have only a minor contribution to the model performance. It could be interesting to see how much the performance is affected by leaving those words out of the input sequence. Or more generally, one could ask, how does the performance related to the number of used input words?
More Formulations of Recurrent Neural Networks
The standard RNN is formalized as follows
- [math]\displaystyle{ \,h_t=\tanh(W_{hx}x_t+W_{hh}h_{t-1}+b_h) }[/math]
- [math]\displaystyle{ \,o_t=W_{oh}h_t+b_o }[/math]
Given sequence of input vectors [math]\displaystyle{ \,(x_1,\cdots,x_{T}) }[/math], the RNN computes a sequence of hidden states [math]\displaystyle{ \,(h_1,\cdots,h_{T}) }[/math] and a sequence of output [math]\displaystyle{ \,(o_1,\cdots,o_{T}) }[/math] by iterating the above equations. [math]\displaystyle{ \,W_{hx} }[/math] is the input to hidden weight matrix, [math]\displaystyle{ \,W_{hh} }[/math] is the hidden to hidden weight matrix, [math]\displaystyle{ \,W_{oh} }[/math] is the hidden to output weight matrix. Vector [math]\displaystyle{ \,b_{h} }[/math] and [math]\displaystyle{ \,b_{o} }[/math] are the biases. When t=1, the undefined [math]\displaystyle{ \,W_{hh}h_{t-1} }[/math] is replace with a special initial bias vector, [math]\displaystyle{ \,h_{init} }[/math].
It may seem to train RNNs with gradient descent, but in reality, gradient decays exponentially as it is backpropagated through time. The relation between parameter and dynamics of the RNN is highly unstable, which makes gradient descent ineffective. Thus, it argues that RNN can not learn long-range temporal dependencies when gradient descent is used for training. A good way to deal with inability of gradient descent to learn long-range temporal structure in RNN is known as "Long-Short Term memory". (http://www.cs.utoronto.ca/~ilya/pubs/2011/LANG-RNN.pdf)
There are different variants of LSTM<ref name=grave> </ref><ref> Gers, Felix, and Jürgen Schmidhuber. "Recurrent nets that time and count." Neural Networks, 2000. IJCNN 2000, Proceedings of the IEEE-INNS-ENNS International Joint Conference on. Vol. 3. IEEE, 2000. </ref><ref> Cho, Kyunghyun, et al. "Learning phrase representations using rnn encoder-decoder for statistical machine translation." arXiv preprint arXiv:1406.1078 (2014). </ref> other than the original one proposed by Hochreiter et al.<ref name=lstm> </ref> Greff et al. compare the performance of some different popular variants in their work<ref> Greff, Klaus, et al. "LSTM: A Search Space Odyssey." arXiv preprint arXiv:1503.04069 (2015). </ref> and draw the conclusion that they are about the same. While Jozefowicz, et al. suggest that some architecture can perform better than LSTM on certain tasks<ref> Jozefowicz, Rafal, Wojciech Zaremba, and Ilya Sutskever. "An Empirical Exploration of Recurrent Network Architectures." Proceedings of the 32nd International Conference on Machine Learning (ICML-15). 2015. </ref>.
Criticisms
There is some concern regarding whether this model will be able to provide a truly scalable solution to MT. In particular, it is not obvious that this model will be able to sufficiently scale to long sentences as is evident in the reported results. The model is severely limited, in general, by working only in the absence of infrequent words. These theoretical limitations alongside sparse experimental results give rise to skepticism about the overarching validity of the model.
Source
Sutskever, I. Vinyals, O. & Le. Q. V. Sequence to sequence learning with neural networks. In Proc. Advances in Neural Information Processing Systems 27 3104–3112 (2014). <references />