Word translation without parallel data: Difference between revisions
| (97 intermediate revisions by 20 users not shown) | |||
| Line 7: | Line 7: | ||
= Introduction = | = Introduction = | ||
This paper | Many successful methods for learning relationships between languages stem from the hypothesis that there is a relationship between the context of words and their meanings. This means that if an adequate representation of a language is found in a high dimensional space (this is called an embedding), then words similar to a given word are close to one another in this space (ex. some norm can be minimized to find a word with similar context). Historically, another significant hypothesis is that these embedding spaces show similar structures over different languages. That is to say that given an embedding space for English and one for Spanish, a mapping could be found that aligns the two spaces and such a mapping could be used as a tool for translation. Many papers exploit these hypotheses, but use large parallel datasets for training. Recently, to remove the need for supervised training, methods have been implemented that utilize identical character strings (ex. letters or digits) in order to try to align the embeddings. The downside of this approach is that the two languages need to be similar to begin with as they need to have some shared basic building block. The method proposed in this paper uses an adversarial method to find this mapping between the embedding spaces of two languages without the use of large parallel datasets. | ||
The contributions of this paper can be listed as follows: | |||
1. This paper introduces a model that either is on par, or outperforms supervised state-of-the-art methods, without employing any cross-lingual annotated data such as bilingual dictionaries or parallel corpora (large and structured sets of texts). This method uses an idea similar to GANs: it leverages adversarial training to learn a linear mapping from a source to distinguish between the mapped source embeddings and the target embeddings, while the mapping is jointly trained to fool the discriminator. | |||
2. Second, this paper extracts a synthetic dictionary from the resulting shared embedding space and fine-tunes the mapping with the closed-form Procrustes solution from Schonemann (1966). | |||
3. Third, this paper also introduces an unsupervised selection metric that is highly correlated with the mapping quality and that the authors use both as a stopping criterion and to select the best hyper-parameters. | |||
4. Fourth, they introduce a cross-domain similarity adaptation to mitigate the so-called hubness problem (points tending to be nearest neighbors of many points in high-dimensional spaces). | |||
5. They demonstrate the effectiveness of our method using an example of a low-resource language pair where parallel corpora are not available (English-Esperanto) for which their method is particularly suited. | |||
This paper is published in ICLR 2018. | |||
= Related Work = | |||
'''Bilingual Lexicon Induction''' | |||
Many papers have addressed this subject by using discrete word representations. Regularly however these methods need to have an initialization of prior knowledge, such as the editing distance between the input and output ground truth. This unfortunately only works for closely related languages. | |||
= Model = | = Model = | ||
| Line 20: | Line 40: | ||
\end{align} | \end{align} | ||
where d is the dimension of the embeddings, <math> M_d(R) </math> is the space of d*d matrices of real numbers, and X and Y are two aligned matrices of size d*n containing the embeddings of the words in the parallel vocabulary. | where d is the dimension of the embeddings, <math> M_d(R) </math> is the space of d*d matrices of real numbers, and X and Y are two aligned matrices of size d*n containing the embeddings of the words in the parallel vocabulary. Here <math>||\cdot||_F</math> is the Frobenius matrix norm which is the square root of the sum of the squared components. | ||
Xing et al. (2015) showed that these results are improved by enforcing orthogonality constraint on W. In that case, equation (1) boils down to the Procrustes problem, a matrix approximation problem for which the goal is to find an orthogonal matrix that best maps two given matrices on the measure of the Frobenius norm. It advantageously offers a closed form solution obtained from the singular value decomposition (SVD) of <math> YX^T </math> : | |||
\begin{align} | |||
W^*=argmin_{W{\in}M_d(R)}||WX-Y||_F=UV^T\textrm{, with }U\Sigma V^T=SVD(YX^T). | |||
\end{align} | |||
This can be proven as follows. First note that | |||
\begin{align} | |||
&||WX-Y||_F\\ | |||
&= \langle WX-Y, WX-Y\rangle_F\\ | |||
&= \langle WX, WX \rangle_F -2 \langle W X, Y \rangle_F + \langle Y, Y \rangle_F \\ | |||
&= ||X||_F^2 -2 \langle W X, Y \rangle_F + || Y||_F^2, | |||
\end{align} | |||
where <math display="inline"> \langle \cdot, \cdot \rangle_F </math> denotes the Frobenius inner-product and we have used the orthogonality of <math display="inline"> W </math>. It follows that we need only maximize the inner-product above. Let <math display="inline"> u_1, \ldots, u_d </math> denote the columns of <math display="inline"> U </math>. Let <math display="inline"> v_1, \ldots , v_d </math> denote the columns of <math display="inline"> V </math>. Let <math display="inline"> \sigma_1, \ldots, \sigma_d </math> denote the diagonal entries of <math display="inline"> \Sigma </math>. We have | |||
\begin{align} | |||
&\langle W X, Y \rangle_F \\ | |||
&= \text{Tr} (W^T Y X^T)\\ | |||
& =\text{Tr}(W^T \sum_i \sigma_i u_i v_i^T)\\ | |||
&=\sum_i \sigma_i \text{Tr}(W^T u_i v_i^T)\\ | |||
&=\sum_i \sigma_i ((Wv_i)^T u_i )\text{ invariance of trace under cyclic permutations}\\ | |||
&\le \sum_i \sigma_i ||Wv_i|| ||u_i||\text{ Cauchy-Swarz inequality}\\ | |||
&= \sum_i \sigma_i | |||
\end{align} | |||
where we have used the invariance of trace under cyclic permutations, Cauchy-Schwarz, and the orthogonality of the columns of U and V. Note that choosing | |||
\begin{align} | \begin{align} | ||
W | W=UV^T | ||
\end{align} | \end{align} | ||
achieves the bound. This completes the proof. | |||
=== Domain-adversarial setting === | === Domain-adversarial setting === | ||
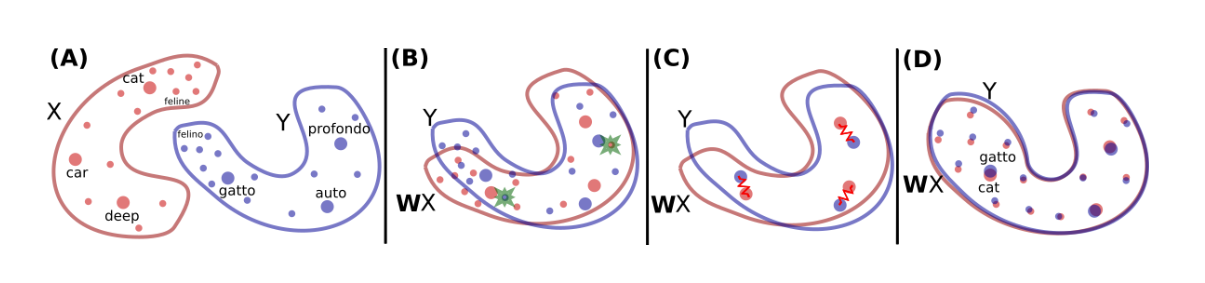
This paper shows how to learn this mapping W without cross-lingual supervision. An illustration of the approach is given in Fig. 1. First, this model | This paper shows how to learn this mapping W without cross-lingual supervision. An illustration of the approach is given in Fig. 1. First, this model learns an initial proxy of W by using an adversarial criterion. Then, it uses the words that match the best as anchor points for Procrustes. Finally, it improves performance over less frequent words by changing the metric of the space, which leads to spread more of those points in dense region. | ||
[[File: | [[File:Toy_example.png |frame|none|alt=Alt text|Figure 1: Toy illustration of the method. (A) There are two distributions of word embeddings, English words in red denoted by X and Italian words in blue denoted by Y , which we want to align/translate. Each dot represents a word in that space. The size of the dot is proportional to the frequency of the words in the training corpus of that language. (B) Using adversarial learning, we learn a rotation matrix W which roughly aligns the two distributions. The green stars are randomly selected words that are fed to the discriminator to determine whether the two word embeddings come from the same distribution. (C) The mapping W is further refined via Procrustes. This method uses frequent words aligned by the previous step as anchor points, and minimizes an energy function that corresponds to a spring system between anchor points. The refined mapping is then used to map all words in the dictionary. (D) Finally, we translate by using the mapping W and a distance metric, dubbed CSLS, that expands the space where there is high density of points (like the area around the word “cat”), so that “hubs” (like the word “cat”) become less close to other word vectors than they would otherwise (compare to the same region in panel (A)).]] | ||
Let <math> X={x_1,...,x_n} </math> and <math> Y={y_1,...,y_m} </math> be two sets of n and m word embeddings coming from a source and a target language respectively. A model is trained is trained to discriminate between elements randomly sampled from <math> WX={Wx_1,...,Wx_n} </math> and Y, We call this model the discriminator. W is trained to prevent the discriminator from making accurate predictions. As a result, this is a two-player game, where the discriminator aims at maximizing its ability to identify the origin of an embedding, and W aims at preventing the discriminator from doing so by making WX and Y as similar as possible. This approach is in line with the work of Ganin et al.(2016), who proposed to learn latent representations invariant to the input domain, where in | Let <math> X={x_1,...,x_n} </math> and <math> Y={y_1,...,y_m} </math> be two sets of n and m word embeddings coming from a source and a target language respectively. A model is trained is trained to discriminate between elements randomly sampled from <math> WX={Wx_1,...,Wx_n} </math> and Y, We call this model the discriminator. W is trained to prevent the discriminator from making accurate predictions. As a result, this is a two-player adversarial game, where the discriminator aims at maximizing its ability to identify the origin of an embedding, and W aims at preventing the discriminator from doing so by making WX and Y as similar as possible. This approach is in line with the work of Ganin et al.(2016), who proposed to learn latent representations invariant to the input domain, where in this case, a domain is represented by a language(source or target). | ||
1.Discriminator objective | 1. Discriminator objective | ||
Refer to the discriminator parameters as <math> \theta_D </math>. Consider the probability <math> P_{\theta_D}(source = 1|z) </math> that a vector z is the mapping of a source embedding (as opposed to a target embedding) according to the discriminator. The discriminator loss can be written as: | Refer to the discriminator parameters as <math> \theta_D </math>. Consider the probability <math> P_{\theta_D}(source = 1|z) </math> that a vector z is the mapping of a source embedding (as opposed to a target embedding) according to the discriminator. The discriminator loss can be written as: | ||
\begin{align} | \begin{align} | ||
L_D(\theta_D|W)=-frac{1}{n}\sum_{i=1}^n log P_{\theta_D}(source=1|Wx_i)-1 | L_D(\theta_D|W)=-\frac{1}{n} \sum_{i=1}^n log P_{\theta_D}(source=1|Wx_i)-\frac{1}{m} \sum_{i=1}^m log P_{\theta_D}(source=0|y_i) | ||
\end{align} | |||
2. Mapping objective | |||
In the unsupervised setting, W is now trained so that the discriminator is unable to accurately predict the embedding origins: | |||
\begin{align} | |||
L_W(W|\theta_D)=-\frac{1}{n} \sum_{i=1}^n log P_{\theta_D}(source=0|Wx_i)-\frac{1}{m} \sum_{i=1}^m log P_{\theta_D}(source=1|y_i) | |||
\end{align} | |||
3. Learning algorithm | |||
To train the model, the authors follow the standard training procedure of deep adversarial networks of Goodfellow et al. (2014). For every input sample, the discriminator and the mapping matrix W are trained successively with stochastic gradient updates to respectively minimize <math> L_D </math> and <math> L_W </math> | |||
=== Refinement procedure === | |||
The matrix W obtained with adversarial training gives good performance (see Table 1), but the results are still not on par with the supervised approach. In fact, the adversarial approach tries to align all words irrespective of their frequencies. However, rare words have embeddings that are less updated and are more likely to appear in different contexts in each corpus, which makes them harder to align. Under the assumption that the mapping is linear, it is then better to infer the global mapping using only the most frequent words as anchors. Besides, the accuracy on the most frequent word pairs is high after adversarial training. | |||
To refine the mapping, this paper build a synthetic parallel vocabulary using the W just learned with adversarial training. Specifically, this paper consider the most frequent words and retain only mutual nearest neighbors to ensure a high-quality dictionary. Subsequently, this paper apply the Procrustes solution in (2) on this generated dictionary. Considering the improved solution generated with the Procrustes algorithm, it is possible to generate a more accurate dictionary and apply this method iteratively, similarly to Artetxe et al. (2017). However, given that the synthetic dictionary obtained using adversarial training is already strong, this paper only observe small improvements when doing more than one iteration, i.e., the improvements on the word translation task are usually below 1%. | |||
=== Cross-Domain Similarity Local Scaling (CSLS) === | |||
This paper considers a bi-partite neighborhood graph, in which each word of a given dictionary is connected to its K nearest neighbors in the other language. a bipartite graph (or bigraph) is a graph whose vertices can be divided into two disjoint and independent sets U and V such that every edge connects a vertex in U to one in V. | |||
<math> N_T(Wx_s) </math> is used to denote the neighborhood, on this bi-partite graph, associated with a mapped source word embedding <math> Wx_s </math>. All K elements of <math> N_T(Wx_s) </math> are words from the target language. Similarly we denote by <math> N_S(y_t) </math> the neighborhood associated with a word t of the target language. Consider the mean similarity of a source embedding <math> x_s </math> to its target neighborhood as | |||
\begin{align} | |||
r_T(Wx_s)=\frac{1}{K}\sum_{y\in N_T(Wx_s)}cos(Wx_s,y_t) | |||
\end{align} | |||
where cos(.,.) is the cosine similarity which is the cosine of the angle between two vectors. Likewise, the mean similarity of a target word <math> y_t </math> to its neighborhood is denoted as <math> r_S(y_t) </math>. This is used to define similarity measure CSLS(.,.) between mapped source words and target words as | |||
\begin{align} | |||
CSLS(Wx_s,y_t)=2cos(Wx_s,y_t)-r_T(Wx_s)-r_S(y_t) | |||
\end{align} | \end{align} | ||
This process increases the similarity associated with isolated word vectors, but decreases the similarity of vectors lying in dense areas. | |||
CSLS represents an improved measure for producing reliable matching words between two languages (i.e. neighbors of a word in one language should ideally correspond to the same words in the second language). The nearest neighbors algorithm is asymmetric, and in high-dimensional spaces, it suffers from the problem of hubness, in which some points are nearest neighbors to exceptionally many points, while others are not nearest neighbors to any points. Existing approaches for combating the effect of hubness on word translation retrieval involve performing similarity updates one language at a time without consideration for the other language in the pair (Dinu et al., 2015, Smith et al., 2017). Consequently, they yielded less accurate results when compared to CSLS in experiments conducted in this paper (Table 1). | |||
= Training and architectural choices = | |||
=== Architecture === | |||
This | This paper use unsupervised word vectors that were trained using fastText2. These correspond to monolingual embeddings of dimension 300 trained on Wikipedia corpora; therefore, the mapping W has size 300 × 300. Words are lower-cased, and those that appear less than 5 times are discarded for training. As a post-processing step, only the first 200k most frequent words were selected in the experiments. | ||
For the discriminator, it use a multilayer perceptron with two hidden layers of size 2048, and Leaky-ReLU activation functions. The input to the discriminator is corrupted with dropout noise with a rate of 0.1. As suggested by Goodfellow (2016), a smoothing coefficient s = 0.2 is included in the discriminator predictions. This paper use stochastic gradient descent with a batch size of 32, a learning rate of 0.1 and a decay of 0.95 both for the discriminator and W . | |||
=== Discriminator inputs === | |||
The embedding quality of rare words is generally not as good as the one of frequent words (Luong et al., 2013), and it is observed that feeding the discriminator with rare words had a small, but not negligible negative impact. As a result, this paper only feed the discriminator with the 50,000 most frequent words. At each training step, the word embeddings given to the discriminator are sampled uniformly. Sampling them according to the word frequency did not have any noticeable impact on the results. | |||
=== Orthogonality=== | |||
In this work, the authors propose to use a simple update step to ensure that the matrix W stays close to an orthogonal matrix during training (Cisse et al. (2017)). Specifically, the following update rule on the matrix W is used: | |||
\begin{align} | |||
W \leftarrow (1+\beta)W-\beta(WW^T)W | |||
\end{align} | |||
where β = 0.01 is usually found to perform well. This method ensures that the matrix stays close to the manifold of orthogonal matrices after each update. | |||
: | This update rule can be justified as follows. Consider the function | ||
\begin{align} | |||
g: \mathbb{R}^{d\times d} \to \mathbb{R}^{d \times d} | |||
\end{align} | |||
defined by | |||
\begin{align} | |||
g(W)= W^T W -I. | |||
\end{align} | |||
The derivative of g at W is is the linear map | |||
\begin{align} | |||
Dg[W]: \mathbb{R}^{d \times d} \to \mathbb{R}^{d \times d} | |||
\end{align} | |||
defined by | |||
\begin{align} | |||
Dg[W](H)= H^T W + W^T H. | |||
\end{align} | |||
The adjoint of this linear map is | |||
\begin{align} | |||
D^\ast g[W](H)= WH^T +WH. | |||
\end{align} | |||
Now consider the function f | |||
\begin{align} | |||
f: \mathbb{R}^{d \times d} \to \mathbb{R} | |||
\end{align} | |||
defined by | |||
\begin{align} | |||
f(W)=||g(W) ||_F^2=||W^TW -I ||_F^2. | |||
\end{align} | |||
f has gradient: | |||
\begin{align} | |||
\nabla f (W) = 2D^\ast g[W] (g(W ) ) =2W(W^TW-I) +2W(W^TW-I)=4W W^TW-4W. | |||
\end{align} | |||
or | |||
\begin{align} | |||
\nabla f (W) = \nabla||W^TW-I||_F = \nabla\text{Tr}(W^TW-I)(W^TW-I)=4(\nabla(W^TW-I))(W^TW-I)=4W(W^TW-I)\text{ (check derivative of trace function)} | |||
\end{align} | |||
Thus the update | |||
\begin{align} | |||
W \leftarrow (1+\beta)W-\beta(WW^T)W | |||
\end{align} | |||
amounts to a step in the direction opposite the gradient of f. That is, a step toward the set of orthogonal matrices. | |||
=== Dictionary generation === | |||
The refinement step requires the generation of a new dictionary at each iteration. In order for the Procrustes solution to work well, it is best to apply it on correct word pairs. As a result, the CSLS method is used to select more accurate translation pairs in the dictionary. To further increase the quality of the dictionary, and ensure that W is learned from correct translation pairs, only mutual nearest neighbors were considered, i.e. pairs of words that are mutually nearest neighbors of each other according to CSLS. This significantly decreases the size of the generated dictionary, but improves its accuracy, as well as the overall performance. | |||
=== | === Validation criterion for unsupervised model selection === | ||
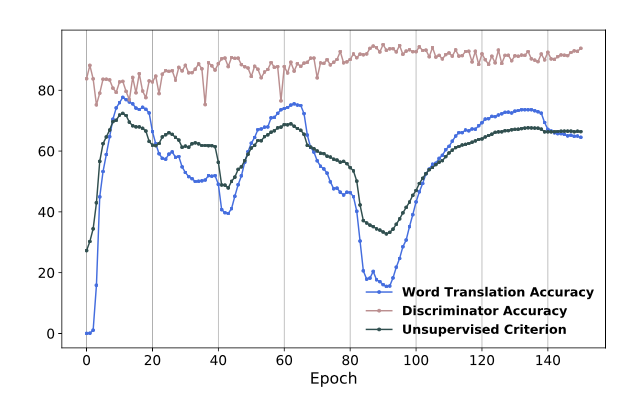
This paper consider the 10k most frequent source words, and use CSLS to generate a translation for each of them, then compute the average cosine similarity between these deemed translations, and use this average as a validation metric. The choice of using the 10 thousand most frequent source words is requires more justification since we would expect those to be the best trained words and may not accurately represent the entire data set. Perhaps a k-fold cross validation approach should be used instead. Figure 2 below shows the correlation between the evaluation score and this unsupervised criterion (without stabilization by learning rate shrinkage) | |||
= | [[File:fig2_fan.png |frame|none|alt=Alt text|Figure 2: Unsupervised model selection. | ||
Correlation between the unsupervised validation criterion (black line) and actual word translation accuracy (blue line). In this particular experiment, the selected model is at epoch 10. Observe how the criterion is well correlated with translation accuracy.]] | |||
== | = Performance Analysis = | ||
== Experiments == | |||
To illustrate the effectiveness of the methodology, the author demonstrated the unsupervised approach on several benchmarks, and compared it with state-of-the-art supervised methods to see if unsupervised model could do better job in terms of learning. The author firstly presented the cross-lingual evaluation tasks that are consider to evaluate the quality of our cross-lingual word embeddings. Then, presented the baseline model. Lastly, by comparing the unsupervised approach to baseline and to previous methods, tried to conclude with complementary analysis on the alignment of several sets of English embeddings trained with different methods and corpora. | |||
== Results == | |||
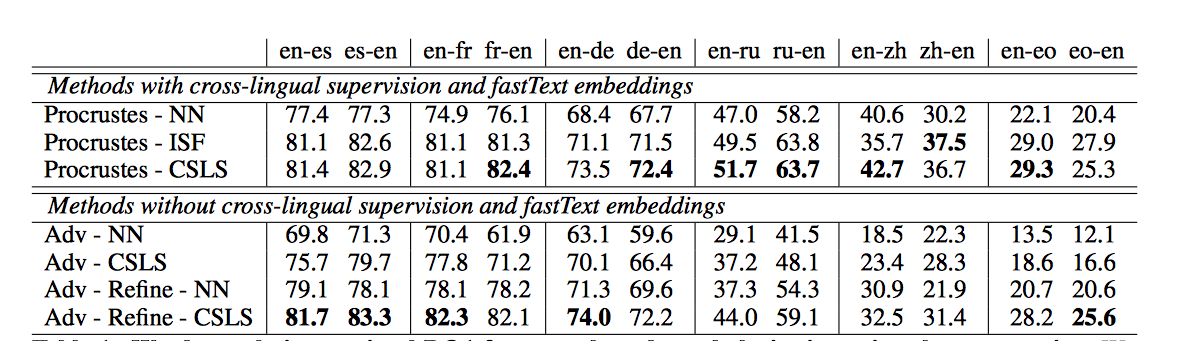
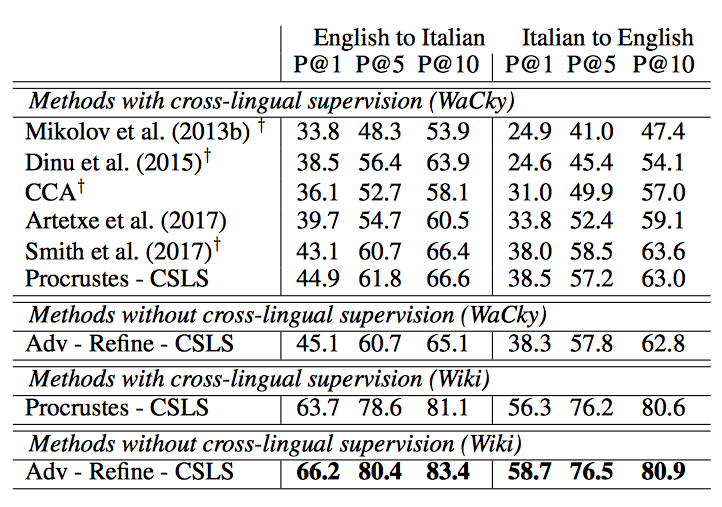
The results on word translation retrieval using the bilingual dictionaries are presented in Table 1, and a comparison to previous work in shown in Table 2 where the unsupervised model significantly outperforms previous approaches. The results on the sentence translation retrieval task are presented in Table 3, and the cross-lingual word similarity task in Table 4. Finally, the results on word-by-word translation for English-Esperanto are presented in Table 5. The bilingual dictionary used here does not account for words with multiple meanings. | |||
= | [[File:table1_fan.png |frame|none|alt=Alt text|Table 1: Word translation retrieval P@1 for the released vocabularies in various language pairs. The authors consider 1,500 source test queries, and 200k target words for each language pair. The authors use fastText embeddings trained on Wikipedia. NN: nearest neighbors. ISF: inverted softmax. (’en’ is English, ’fr’ is French, ’de’ is German, ’ru’ is Russian, ’zh’ is classical Chinese and ’eo’ is Esperanto)]] | ||
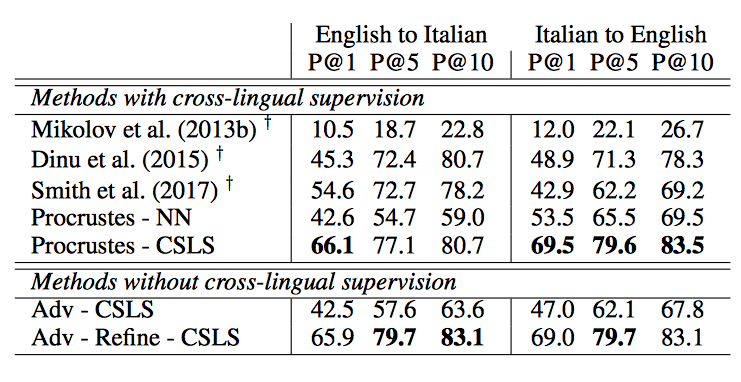
[[File:table2_fan.png |frame|none|alt=Alt text|English-Italian word translation average precisions (@1, @5, @10) from 1.5k source word queries using 200k target words. Results marked with the symbol † are from Smith et al. (2017). Wiki means the embeddings were trained on Wikipedia using fastText. Note that the method used by Artetxe et al. (2017) does not use the same supervision as other supervised methods, as they only use numbers in their ini- tial parallel dictionary.]] | |||
= | [[File:table3_fan.png |frame|none|alt=Alt text|Table 3: English-Italian sentence translation retrieval. The authors report the average P@k from 2,000 source queries using 200,000 target sentences. The authors use the same embeddings as in Smith et al. (2017). Their results are marked with the symbol †.]] | ||
The | |||
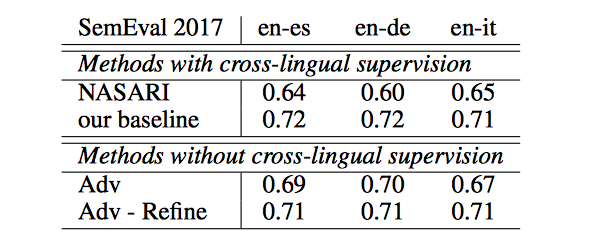
: | [[File:table4_fan.png |frame|none|alt=Alt text|Table 4: Cross-lingual wordsim task. NASARI | ||
(Camacho-Collados et al. (2016)) refers to the official SemEval2017 baseline. The authors report Pearson correlation.]] | |||
[[File:table5_fan.png |frame|none|alt=Alt text|Table 5: BLEU score on English-Esperanto. | |||
Although being a naive approach, word-by- word translation is enough to get a rough idea of the input sentence. The quality of the gener- ated dictionary has a significant impact on the BLEU score.]] | |||
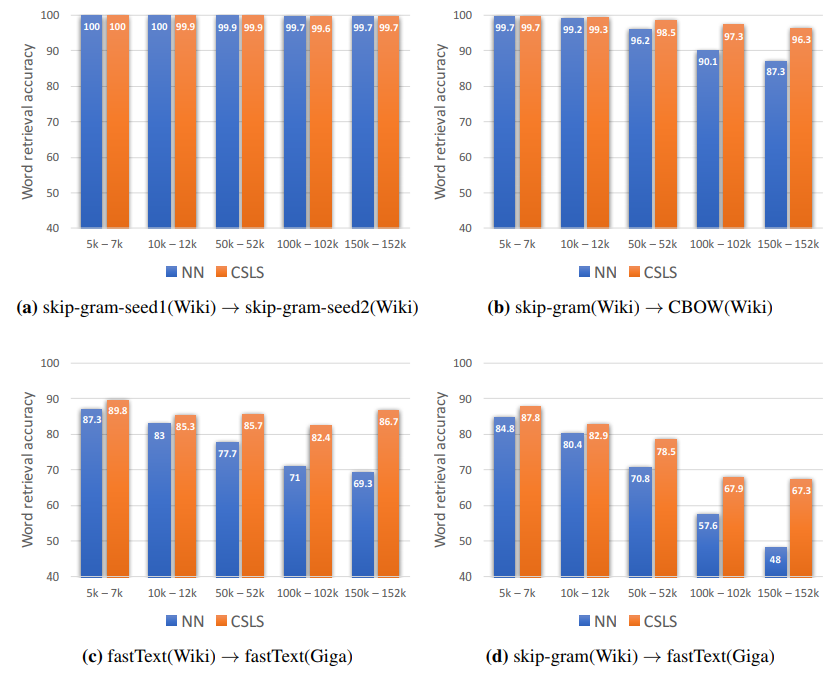
[[File:paper9_fig3.png |frame|none|alt=Alt text|Figure 3: The paper also investigated the impact of monolingual embeddings. It was found that model from this paper can align embeddings obtained through different methods, but not embeddings obtained from different corpora, which explains the large performance increase in Table 2 due to the corpus change from WaCky to Wiki using CBOW embedding. This is conveyed in this figure which displays English to English world alignment accuracies with regard to word frequency. Perfect alignment is achieved using the same model and corpora (a). Also good alignment using different model and corpora, although CSLS consistently has better results (b). Worse results due to use of different corpora (c). Even worse results when both embedding model and corpora are different.]] | |||
= Conclusion = | |||
It is clear that one major downfall of this method when it actually comes to translation is the restriction that the two languages must have similar intrinsic structures to allow for the embeddings to align. However, given this assumption, this paper shows for the first time that one can align word embedding spaces without any cross-lingual supervision, i.e., solely based on unaligned datasets of each language, while reaching or outperforming the quality of previous supervised approaches in several cases. Using adversarial training, the model is able to initialize a linear mapping between a source and a target space, which is also used to produce a synthetic parallel dictionary. It is then possible to apply the same techniques proposed for supervised techniques, namely a Procrustean optimization. | |||
= | = Open source code = | ||
The source code for the paper is provided at the following Github link: https://github.com/facebookresearch/MUSE. The repository provides the source code as written in PyTorch by the authors of this paper. | |||
= Source = | = Source = | ||
Dinu, Georgiana; Lazaridou, Angeliki; Baroni, Marco | |||
| Improving zero-shot learning by mitigating the hubness problem | |||
| arXiv:1412.6568 | |||
Lample, Guillaume; Denoyer, Ludovic; Ranzato, Marc'Aurelio | |||
| Unsupervised Machine Translation Using Monolingual Corpora Only | |||
| arXiv: 1701.04087 | |||
Smith, Samuel L; Turban, David HP; Hamblin, Steven; Hammerla, Nils Y | |||
| Offline bilingual word vectors, orthogonal transformations and the inverted softmax | |||
| arXiv:1702.03859 | |||
Lample, G. (n.d.). Facebookresearch/MUSE. Retrieved March 25, 2018, from https://github.com/facebookresearch/MUSE | |||
Tomas Mikolov, Kai Chen, Greg Corrado, Jeffrey Dean | |||
| Efficient Estimation of Word Representations in Vector Space, 2013 | |||
| arXiv:1301.3781 | |||
Xing, C., Wang, D., Liu, C., & Lin, Y. (2015). Normalized Word Embedding and Orthogonal Transform for Bilingual Word Translation. HLT-NAACL. | |||
Latest revision as of 17:24, 18 April 2018
Presented by
Xia Fan
Introduction
Many successful methods for learning relationships between languages stem from the hypothesis that there is a relationship between the context of words and their meanings. This means that if an adequate representation of a language is found in a high dimensional space (this is called an embedding), then words similar to a given word are close to one another in this space (ex. some norm can be minimized to find a word with similar context). Historically, another significant hypothesis is that these embedding spaces show similar structures over different languages. That is to say that given an embedding space for English and one for Spanish, a mapping could be found that aligns the two spaces and such a mapping could be used as a tool for translation. Many papers exploit these hypotheses, but use large parallel datasets for training. Recently, to remove the need for supervised training, methods have been implemented that utilize identical character strings (ex. letters or digits) in order to try to align the embeddings. The downside of this approach is that the two languages need to be similar to begin with as they need to have some shared basic building block. The method proposed in this paper uses an adversarial method to find this mapping between the embedding spaces of two languages without the use of large parallel datasets.
The contributions of this paper can be listed as follows:
1. This paper introduces a model that either is on par, or outperforms supervised state-of-the-art methods, without employing any cross-lingual annotated data such as bilingual dictionaries or parallel corpora (large and structured sets of texts). This method uses an idea similar to GANs: it leverages adversarial training to learn a linear mapping from a source to distinguish between the mapped source embeddings and the target embeddings, while the mapping is jointly trained to fool the discriminator.
2. Second, this paper extracts a synthetic dictionary from the resulting shared embedding space and fine-tunes the mapping with the closed-form Procrustes solution from Schonemann (1966).
3. Third, this paper also introduces an unsupervised selection metric that is highly correlated with the mapping quality and that the authors use both as a stopping criterion and to select the best hyper-parameters.
4. Fourth, they introduce a cross-domain similarity adaptation to mitigate the so-called hubness problem (points tending to be nearest neighbors of many points in high-dimensional spaces).
5. They demonstrate the effectiveness of our method using an example of a low-resource language pair where parallel corpora are not available (English-Esperanto) for which their method is particularly suited.
This paper is published in ICLR 2018.
Related Work
Bilingual Lexicon Induction
Many papers have addressed this subject by using discrete word representations. Regularly however these methods need to have an initialization of prior knowledge, such as the editing distance between the input and output ground truth. This unfortunately only works for closely related languages.
Model
Estimation of Word Representations in Vector Space
This model focuses on learning a mapping between the two sets such that translations are close in the shared space. Before talking about the model it used, a model which can exploit the similarities of monolingual embedding spaces should be introduced. Mikolov et al.(2013) use a known dictionary of n=5000 pairs of words [math]\displaystyle{ \{x_i,y_i\}_{i\in{1,n}} }[/math]. and learn a linear mapping W between the source and the target space such that
\begin{align} W^*=argmin_{W{\in}M_d(R)}||WX-Y||_F \hspace{1cm} (1) \end{align}
where d is the dimension of the embeddings, [math]\displaystyle{ M_d(R) }[/math] is the space of d*d matrices of real numbers, and X and Y are two aligned matrices of size d*n containing the embeddings of the words in the parallel vocabulary. Here [math]\displaystyle{ ||\cdot||_F }[/math] is the Frobenius matrix norm which is the square root of the sum of the squared components.
Xing et al. (2015) showed that these results are improved by enforcing orthogonality constraint on W. In that case, equation (1) boils down to the Procrustes problem, a matrix approximation problem for which the goal is to find an orthogonal matrix that best maps two given matrices on the measure of the Frobenius norm. It advantageously offers a closed form solution obtained from the singular value decomposition (SVD) of [math]\displaystyle{ YX^T }[/math] :
\begin{align} W^*=argmin_{W{\in}M_d(R)}||WX-Y||_F=UV^T\textrm{, with }U\Sigma V^T=SVD(YX^T). \end{align}
This can be proven as follows. First note that
\begin{align}
&||WX-Y||_F\\
&= \langle WX-Y, WX-Y\rangle_F\\
&= \langle WX, WX \rangle_F -2 \langle W X, Y \rangle_F + \langle Y, Y \rangle_F \\
&= ||X||_F^2 -2 \langle W X, Y \rangle_F + || Y||_F^2,
\end{align}
where [math]\displaystyle{ \langle \cdot, \cdot \rangle_F }[/math] denotes the Frobenius inner-product and we have used the orthogonality of [math]\displaystyle{ W }[/math]. It follows that we need only maximize the inner-product above. Let [math]\displaystyle{ u_1, \ldots, u_d }[/math] denote the columns of [math]\displaystyle{ U }[/math]. Let [math]\displaystyle{ v_1, \ldots , v_d }[/math] denote the columns of [math]\displaystyle{ V }[/math]. Let [math]\displaystyle{ \sigma_1, \ldots, \sigma_d }[/math] denote the diagonal entries of [math]\displaystyle{ \Sigma }[/math]. We have \begin{align} &\langle W X, Y \rangle_F \\ &= \text{Tr} (W^T Y X^T)\\ & =\text{Tr}(W^T \sum_i \sigma_i u_i v_i^T)\\ &=\sum_i \sigma_i \text{Tr}(W^T u_i v_i^T)\\ &=\sum_i \sigma_i ((Wv_i)^T u_i )\text{ invariance of trace under cyclic permutations}\\ &\le \sum_i \sigma_i ||Wv_i|| ||u_i||\text{ Cauchy-Swarz inequality}\\ &= \sum_i \sigma_i \end{align} where we have used the invariance of trace under cyclic permutations, Cauchy-Schwarz, and the orthogonality of the columns of U and V. Note that choosing \begin{align} W=UV^T \end{align} achieves the bound. This completes the proof.
Domain-adversarial setting
This paper shows how to learn this mapping W without cross-lingual supervision. An illustration of the approach is given in Fig. 1. First, this model learns an initial proxy of W by using an adversarial criterion. Then, it uses the words that match the best as anchor points for Procrustes. Finally, it improves performance over less frequent words by changing the metric of the space, which leads to spread more of those points in dense region.
Let [math]\displaystyle{ X={x_1,...,x_n} }[/math] and [math]\displaystyle{ Y={y_1,...,y_m} }[/math] be two sets of n and m word embeddings coming from a source and a target language respectively. A model is trained is trained to discriminate between elements randomly sampled from [math]\displaystyle{ WX={Wx_1,...,Wx_n} }[/math] and Y, We call this model the discriminator. W is trained to prevent the discriminator from making accurate predictions. As a result, this is a two-player adversarial game, where the discriminator aims at maximizing its ability to identify the origin of an embedding, and W aims at preventing the discriminator from doing so by making WX and Y as similar as possible. This approach is in line with the work of Ganin et al.(2016), who proposed to learn latent representations invariant to the input domain, where in this case, a domain is represented by a language(source or target).
1. Discriminator objective
Refer to the discriminator parameters as [math]\displaystyle{ \theta_D }[/math]. Consider the probability [math]\displaystyle{ P_{\theta_D}(source = 1|z) }[/math] that a vector z is the mapping of a source embedding (as opposed to a target embedding) according to the discriminator. The discriminator loss can be written as:
\begin{align} L_D(\theta_D|W)=-\frac{1}{n} \sum_{i=1}^n log P_{\theta_D}(source=1|Wx_i)-\frac{1}{m} \sum_{i=1}^m log P_{\theta_D}(source=0|y_i) \end{align}
2. Mapping objective
In the unsupervised setting, W is now trained so that the discriminator is unable to accurately predict the embedding origins:
\begin{align} L_W(W|\theta_D)=-\frac{1}{n} \sum_{i=1}^n log P_{\theta_D}(source=0|Wx_i)-\frac{1}{m} \sum_{i=1}^m log P_{\theta_D}(source=1|y_i) \end{align}
3. Learning algorithm To train the model, the authors follow the standard training procedure of deep adversarial networks of Goodfellow et al. (2014). For every input sample, the discriminator and the mapping matrix W are trained successively with stochastic gradient updates to respectively minimize [math]\displaystyle{ L_D }[/math] and [math]\displaystyle{ L_W }[/math]
Refinement procedure
The matrix W obtained with adversarial training gives good performance (see Table 1), but the results are still not on par with the supervised approach. In fact, the adversarial approach tries to align all words irrespective of their frequencies. However, rare words have embeddings that are less updated and are more likely to appear in different contexts in each corpus, which makes them harder to align. Under the assumption that the mapping is linear, it is then better to infer the global mapping using only the most frequent words as anchors. Besides, the accuracy on the most frequent word pairs is high after adversarial training. To refine the mapping, this paper build a synthetic parallel vocabulary using the W just learned with adversarial training. Specifically, this paper consider the most frequent words and retain only mutual nearest neighbors to ensure a high-quality dictionary. Subsequently, this paper apply the Procrustes solution in (2) on this generated dictionary. Considering the improved solution generated with the Procrustes algorithm, it is possible to generate a more accurate dictionary and apply this method iteratively, similarly to Artetxe et al. (2017). However, given that the synthetic dictionary obtained using adversarial training is already strong, this paper only observe small improvements when doing more than one iteration, i.e., the improvements on the word translation task are usually below 1%.
Cross-Domain Similarity Local Scaling (CSLS)
This paper considers a bi-partite neighborhood graph, in which each word of a given dictionary is connected to its K nearest neighbors in the other language. a bipartite graph (or bigraph) is a graph whose vertices can be divided into two disjoint and independent sets U and V such that every edge connects a vertex in U to one in V.
[math]\displaystyle{ N_T(Wx_s) }[/math] is used to denote the neighborhood, on this bi-partite graph, associated with a mapped source word embedding [math]\displaystyle{ Wx_s }[/math]. All K elements of [math]\displaystyle{ N_T(Wx_s) }[/math] are words from the target language. Similarly we denote by [math]\displaystyle{ N_S(y_t) }[/math] the neighborhood associated with a word t of the target language. Consider the mean similarity of a source embedding [math]\displaystyle{ x_s }[/math] to its target neighborhood as
\begin{align} r_T(Wx_s)=\frac{1}{K}\sum_{y\in N_T(Wx_s)}cos(Wx_s,y_t) \end{align}
where cos(.,.) is the cosine similarity which is the cosine of the angle between two vectors. Likewise, the mean similarity of a target word [math]\displaystyle{ y_t }[/math] to its neighborhood is denoted as [math]\displaystyle{ r_S(y_t) }[/math]. This is used to define similarity measure CSLS(.,.) between mapped source words and target words as
\begin{align} CSLS(Wx_s,y_t)=2cos(Wx_s,y_t)-r_T(Wx_s)-r_S(y_t) \end{align}
This process increases the similarity associated with isolated word vectors, but decreases the similarity of vectors lying in dense areas.
CSLS represents an improved measure for producing reliable matching words between two languages (i.e. neighbors of a word in one language should ideally correspond to the same words in the second language). The nearest neighbors algorithm is asymmetric, and in high-dimensional spaces, it suffers from the problem of hubness, in which some points are nearest neighbors to exceptionally many points, while others are not nearest neighbors to any points. Existing approaches for combating the effect of hubness on word translation retrieval involve performing similarity updates one language at a time without consideration for the other language in the pair (Dinu et al., 2015, Smith et al., 2017). Consequently, they yielded less accurate results when compared to CSLS in experiments conducted in this paper (Table 1).
Training and architectural choices
Architecture
This paper use unsupervised word vectors that were trained using fastText2. These correspond to monolingual embeddings of dimension 300 trained on Wikipedia corpora; therefore, the mapping W has size 300 × 300. Words are lower-cased, and those that appear less than 5 times are discarded for training. As a post-processing step, only the first 200k most frequent words were selected in the experiments. For the discriminator, it use a multilayer perceptron with two hidden layers of size 2048, and Leaky-ReLU activation functions. The input to the discriminator is corrupted with dropout noise with a rate of 0.1. As suggested by Goodfellow (2016), a smoothing coefficient s = 0.2 is included in the discriminator predictions. This paper use stochastic gradient descent with a batch size of 32, a learning rate of 0.1 and a decay of 0.95 both for the discriminator and W .
Discriminator inputs
The embedding quality of rare words is generally not as good as the one of frequent words (Luong et al., 2013), and it is observed that feeding the discriminator with rare words had a small, but not negligible negative impact. As a result, this paper only feed the discriminator with the 50,000 most frequent words. At each training step, the word embeddings given to the discriminator are sampled uniformly. Sampling them according to the word frequency did not have any noticeable impact on the results.
Orthogonality
In this work, the authors propose to use a simple update step to ensure that the matrix W stays close to an orthogonal matrix during training (Cisse et al. (2017)). Specifically, the following update rule on the matrix W is used:
\begin{align} W \leftarrow (1+\beta)W-\beta(WW^T)W \end{align}
where β = 0.01 is usually found to perform well. This method ensures that the matrix stays close to the manifold of orthogonal matrices after each update.
This update rule can be justified as follows. Consider the function \begin{align} g: \mathbb{R}^{d\times d} \to \mathbb{R}^{d \times d} \end{align} defined by \begin{align} g(W)= W^T W -I. \end{align}
The derivative of g at W is is the linear map \begin{align} Dg[W]: \mathbb{R}^{d \times d} \to \mathbb{R}^{d \times d} \end{align} defined by \begin{align} Dg[W](H)= H^T W + W^T H. \end{align}
The adjoint of this linear map is
\begin{align} D^\ast g[W](H)= WH^T +WH. \end{align}
Now consider the function f \begin{align} f: \mathbb{R}^{d \times d} \to \mathbb{R} \end{align}
defined by
\begin{align} f(W)=||g(W) ||_F^2=||W^TW -I ||_F^2. \end{align}
f has gradient: \begin{align} \nabla f (W) = 2D^\ast g[W] (g(W ) ) =2W(W^TW-I) +2W(W^TW-I)=4W W^TW-4W. \end{align} or \begin{align} \nabla f (W) = \nabla||W^TW-I||_F = \nabla\text{Tr}(W^TW-I)(W^TW-I)=4(\nabla(W^TW-I))(W^TW-I)=4W(W^TW-I)\text{ (check derivative of trace function)} \end{align}
Thus the update \begin{align} W \leftarrow (1+\beta)W-\beta(WW^T)W \end{align} amounts to a step in the direction opposite the gradient of f. That is, a step toward the set of orthogonal matrices.
Dictionary generation
The refinement step requires the generation of a new dictionary at each iteration. In order for the Procrustes solution to work well, it is best to apply it on correct word pairs. As a result, the CSLS method is used to select more accurate translation pairs in the dictionary. To further increase the quality of the dictionary, and ensure that W is learned from correct translation pairs, only mutual nearest neighbors were considered, i.e. pairs of words that are mutually nearest neighbors of each other according to CSLS. This significantly decreases the size of the generated dictionary, but improves its accuracy, as well as the overall performance.
Validation criterion for unsupervised model selection
This paper consider the 10k most frequent source words, and use CSLS to generate a translation for each of them, then compute the average cosine similarity between these deemed translations, and use this average as a validation metric. The choice of using the 10 thousand most frequent source words is requires more justification since we would expect those to be the best trained words and may not accurately represent the entire data set. Perhaps a k-fold cross validation approach should be used instead. Figure 2 below shows the correlation between the evaluation score and this unsupervised criterion (without stabilization by learning rate shrinkage)
Performance Analysis
Experiments
To illustrate the effectiveness of the methodology, the author demonstrated the unsupervised approach on several benchmarks, and compared it with state-of-the-art supervised methods to see if unsupervised model could do better job in terms of learning. The author firstly presented the cross-lingual evaluation tasks that are consider to evaluate the quality of our cross-lingual word embeddings. Then, presented the baseline model. Lastly, by comparing the unsupervised approach to baseline and to previous methods, tried to conclude with complementary analysis on the alignment of several sets of English embeddings trained with different methods and corpora.
Results
The results on word translation retrieval using the bilingual dictionaries are presented in Table 1, and a comparison to previous work in shown in Table 2 where the unsupervised model significantly outperforms previous approaches. The results on the sentence translation retrieval task are presented in Table 3, and the cross-lingual word similarity task in Table 4. Finally, the results on word-by-word translation for English-Esperanto are presented in Table 5. The bilingual dictionary used here does not account for words with multiple meanings.

Conclusion
It is clear that one major downfall of this method when it actually comes to translation is the restriction that the two languages must have similar intrinsic structures to allow for the embeddings to align. However, given this assumption, this paper shows for the first time that one can align word embedding spaces without any cross-lingual supervision, i.e., solely based on unaligned datasets of each language, while reaching or outperforming the quality of previous supervised approaches in several cases. Using adversarial training, the model is able to initialize a linear mapping between a source and a target space, which is also used to produce a synthetic parallel dictionary. It is then possible to apply the same techniques proposed for supervised techniques, namely a Procrustean optimization.
Open source code
The source code for the paper is provided at the following Github link: https://github.com/facebookresearch/MUSE. The repository provides the source code as written in PyTorch by the authors of this paper.
Source
Dinu, Georgiana; Lazaridou, Angeliki; Baroni, Marco | Improving zero-shot learning by mitigating the hubness problem | arXiv:1412.6568
Lample, Guillaume; Denoyer, Ludovic; Ranzato, Marc'Aurelio | Unsupervised Machine Translation Using Monolingual Corpora Only | arXiv: 1701.04087
Smith, Samuel L; Turban, David HP; Hamblin, Steven; Hammerla, Nils Y | Offline bilingual word vectors, orthogonal transformations and the inverted softmax | arXiv:1702.03859
Lample, G. (n.d.). Facebookresearch/MUSE. Retrieved March 25, 2018, from https://github.com/facebookresearch/MUSE
Tomas Mikolov, Kai Chen, Greg Corrado, Jeffrey Dean | Efficient Estimation of Word Representations in Vector Space, 2013 | arXiv:1301.3781
Xing, C., Wang, D., Liu, C., & Lin, Y. (2015). Normalized Word Embedding and Orthogonal Transform for Bilingual Word Translation. HLT-NAACL.