When can Multi-Site Datasets be Pooled for Regression? Hypothesis Tests, l2-consistency and Neuroscience Applications: Summary: Difference between revisions
| (7 intermediate revisions by 6 users not shown) | |||
| Line 10: | Line 10: | ||
constraints on the number of experiments and/or number | constraints on the number of experiments and/or number | ||
of participants within a trial, leading to small datasets. Similar datasets from multiple sites can be pooled to potentially | of participants within a trial, leading to small datasets. Similar datasets from multiple sites can be pooled to potentially | ||
improve statistical power and address the above issue. | improve statistical power and address the above issue. In reality, when analysis based a study/experiment, there comes about interesting follow-up questions during the course of the study; the purpose of the paper explore the ideology that when pooling the follow-up questions along with the original data set facilitate as necessities to deduce a viable prediction. | ||
====Regression Problems==== | ====Regression Problems==== | ||
Ridge and Lasso regression are powerful techniques generally used for creating parsimonious models in the presence of a ‘large’ number of features. Here ‘large’ can typically mean either of two things[2]: | Ridge and Lasso regression are powerful techniques generally used for creating parsimonious models in the presence of a ‘large’ number of features. Here ‘large’ can typically mean either of two things[2]: | ||
| Line 18: | Line 18: | ||
Ridge Regression is a technique for analyzing multiple regression data that suffer from multicollinearity [9]. When multicollinearity occurs, least squares estimates are unbiased, but their variances are large so they may be far from the true value. By adding a degree of bias to the regression estimates, ridge regression reduces the standard errors. It is hoped that the net effect will be to give estimates that are more reliable. | Ridge Regression is a technique for analyzing multiple regression data that suffer from multicollinearity [9]. When multicollinearity occurs, least squares estimates are unbiased, but their variances are large so they may be far from the true value. By adding a degree of bias to the regression estimates, ridge regression reduces the standard errors. It is hoped that the net effect will be to give estimates that are more reliable. | ||
Ridge regression is commonly used in | Ridge regression is commonly used in machine learning. When fitting a model, unnecessary inputs or inputs with co-linearity might bring disastrously huge coefficients (with a large variance). | ||
Ridge regression performs L2 regularization, i.e. it adds a factor of sum of squared coefficients in the optimization objective. Thus, ridge regression optimizes the following: | Ridge regression performs L2 regularization, i.e. it adds a factor of sum of squared coefficients in the optimization objective. Thus, ridge regression optimizes the following: | ||
*''Objective = RSS + λ * (sum of square of coefficients)'' | *''Objective = RSS + λ * (sum of square of coefficients)'' | ||
| Line 31: | Line 31: | ||
#λ < α < ∞: coefficients between 0 and that of simple linear regression | #λ < α < ∞: coefficients between 0 and that of simple linear regression | ||
A feature of Lasso regression is its job as a selection operator, i.e. it usually shrinks a part of coefficients to zero, while keeping the values of other coefficients. Thus it can be used in opting unnecessary coefficients out of the model. | A feature of Lasso regression is its job as a selection operator, i.e. it usually shrinks a part of coefficients to zero, while keeping the values of other coefficients. Thus it can be used in opting unnecessary coefficients out of the model. | ||
To describe this, let us rewrite the Lasso regression $\min_\beta ||y-X\beta||^2+\lambda||\beta||_1$ and ridge regression $\min_\beta ||y-X\beta||^2+\lambda||\beta||_2$ to its dual form | |||
\[ | |||
\text{Ridge Regression} \quad \min_\beta ||y-X\beta||^2, \quad \text{subject to } || \beta ||_2 \leq t | |||
\] | |||
\[ | |||
\text{Lasso Regression} \quad \min_\beta ||y-X\beta||^2, \quad \text{subject to } || \beta ||_1 \leq t | |||
\] | |||
Then the graph from Chapter 3 of Hastie et al. (2009) demonstrates how the Lasso regression shrinks a part of coefficients to zero. The advantage of LASSO over ridge regression is that it not only shrinks the coefficients, but performs automatic feature selection. | |||
[[File:lasso.jpg|thumb|alt=Alt text|]] | |||
Another type of regression model that is worth mentioning here is what we call Elastic Net Regression. This type of regression model is utilizing both L1 and L2 regularization, namely combining the regularization techniques used in lasso regression and ridge regression together in the objective function. This type of regression could also be of possible interest to be applied in the context of this paper. Its objective function is shown below, where we can see both the sum of absolute value of coefficients and the sum of square of coefficients are included: | Another type of regression model that is worth mentioning here is what we call Elastic Net Regression. This type of regression model is utilizing both L1 and L2 regularization, namely combining the regularization techniques used in lasso regression and ridge regression together in the objective function. This type of regression could also be of possible interest to be applied in the context of this paper. Its objective function is shown below, where we can see both the sum of absolute value of coefficients and the sum of square of coefficients are included: | ||
| Line 70: | Line 81: | ||
<math>n_i </math>: sample size of site i <br/> | <math>n_i </math>: sample size of site i <br/> | ||
<math>\hat{β}_i </math>: regression estimate from a specific site i. <br/> | <math>\hat{β}_i </math>: regression estimate from a specific site i. <br/> | ||
<math> | <math>\Delta β^T </math>: length ''kp'' vector<br/> | ||
<math>G \in\mathbb{R}^{(k-1)p | <math>\hat{\Sigma}_i </math>: the sample covariance matrix of the predictors from site i.<br/> | ||
<math>G \in\mathbb{R}^{(k-1)p \times (k-1)p} </math>: the covariance matrix of <math>\Delta\hat{β} </math>, with <math>G_{ii}=\left(n_1\hat{\Sigma}_1 \right)^{-1} + \left(n_i\tau_i^2\hat{\Sigma}_i \right)^{-1} </math> and <math>G_{ij}=\left(n_1\hat{\Sigma}_1 \right)^{-1} </math>, <math>i\neq j </math><br/> | |||
[[File:Equation_4567.png|thumb|alt=Alt text|]]Lemma 2.2 bounds the increase in bias and reduction in variance. Theorem 2.3 is the author's main test result.Although <math>\sigma_i</math> is typically | [[File:Equation_4567.png|thumb|alt=Alt text|]]Lemma 2.2 bounds the increase in bias and reduction in variance. Theorem 2.3 is the author's main test result.Although <math>\sigma_i</math> is typically | ||
| Line 148: | Line 160: | ||
#Show how pooling can be used ( in certain regimes of high dimensional and standard linear regression) even when the features are different across sites. For this the authors show the <math>\ell_2</math>-consistency rate which supports the use of spare-multi-task Lasso when sparsity patterns are not identical | #Show how pooling can be used ( in certain regimes of high dimensional and standard linear regression) even when the features are different across sites. For this the authors show the <math>\ell_2</math>-consistency rate which supports the use of spare-multi-task Lasso when sparsity patterns are not identical | ||
#Experimental results showing consistent acceptance power for early Alzheimer’s detection (AD) in humans, where data are pooled from different sites. | #Experimental results showing consistent acceptance power for early Alzheimer’s detection (AD) in humans, where data are pooled from different sites. | ||
==Critique== | |||
The main premise underlying pooling multiple datasets from a variety of sites is that the small, local sites can borrow statistical strength from the larger pooled, multisite data. Bayesian hierarchical models provide one standard tool that allow borrowing of statistical strength from a gestalt to an instance. While the current paper is very much in the frequentist spirit, there should be some justification as to why (or even whether) the pooling technique explicated in the paper may be a good alternative. Indeed, it is not even exactly clear whether the asymptotic properties enjoyed by the pooling method represent any substantial gain relative to classical methods from either Bayesian or frequentist statistics. Deciding whether to use the pooling method in practice will be difficult unless a careful comparative study is undertaken on, first, a theoretical level to quantify the extent to which better stability and asymptotic properties are obtained and second, a practical level with benchmark bio-medical datasets to see whether the theoretical guarantees obtain in real situations. | |||
==References== | ==References== | ||
Latest revision as of 20:45, 28 November 2017
This page is a summary for this ICML 2017 paper[1].
Introduction
Some Basic Concepts and Issues
While the challenges posed by large-scale datasets are compelling, one is often faced with a fairly distinct set of technical issues for studies in biological and health sciences. For instance, a sizable portion of scientific research is carried out by small or medium sized groups supported by modest budgets. Hence, there are financial constraints on the number of experiments and/or number of participants within a trial, leading to small datasets. Similar datasets from multiple sites can be pooled to potentially improve statistical power and address the above issue. In reality, when analysis based a study/experiment, there comes about interesting follow-up questions during the course of the study; the purpose of the paper explore the ideology that when pooling the follow-up questions along with the original data set facilitate as necessities to deduce a viable prediction.
Regression Problems
Ridge and Lasso regression are powerful techniques generally used for creating parsimonious models in the presence of a ‘large’ number of features. Here ‘large’ can typically mean either of two things[2]:
- Large enough to enhance the tendency of a model to overfit (as low as 10 variables might cause overfitting)
- Large enough to cause computational challenges. With modern systems, this situation might arise in case of millions or billions of features
Ridge Regression and Overfitting:
Ridge Regression is a technique for analyzing multiple regression data that suffer from multicollinearity [9]. When multicollinearity occurs, least squares estimates are unbiased, but their variances are large so they may be far from the true value. By adding a degree of bias to the regression estimates, ridge regression reduces the standard errors. It is hoped that the net effect will be to give estimates that are more reliable.
Ridge regression is commonly used in machine learning. When fitting a model, unnecessary inputs or inputs with co-linearity might bring disastrously huge coefficients (with a large variance). Ridge regression performs L2 regularization, i.e. it adds a factor of sum of squared coefficients in the optimization objective. Thus, ridge regression optimizes the following:
- Objective = RSS + λ * (sum of square of coefficients)
Note that performing ridge regression is equivalent to minimizing RSS ( Residual Sum of Squares) under the constraint that sum of squared coefficients is less than some function of λ, say s(λ). Ridge regression usually utilizes the method of cross-validation where we train the model on the training set using different values of λ and optimizing the above objective function. Then each of those model (each trained with different λ's) are tested on the validation set to evaluate their performance.
Lasso Regression and Model Selection:
LASSO stands for Least Absolute Shrinkage and Selection Operator. Lasso regression performs L1 regularization, i.e. it adds a factor of sum of absolute value of coefficients in the optimization objective. Thus, lasso regression optimizes the following.
- Objective = RSS + λ * (sum of absolute value of coefficients)
- λ = 0: Same coefficients as simple linear regression
- λ = ∞: All coefficients zero (same logic as before)
- λ < α < ∞: coefficients between 0 and that of simple linear regression
A feature of Lasso regression is its job as a selection operator, i.e. it usually shrinks a part of coefficients to zero, while keeping the values of other coefficients. Thus it can be used in opting unnecessary coefficients out of the model.
To describe this, let us rewrite the Lasso regression $\min_\beta ||y-X\beta||^2+\lambda||\beta||_1$ and ridge regression $\min_\beta ||y-X\beta||^2+\lambda||\beta||_2$ to its dual form \[ \text{Ridge Regression} \quad \min_\beta ||y-X\beta||^2, \quad \text{subject to } || \beta ||_2 \leq t \]
\[ \text{Lasso Regression} \quad \min_\beta ||y-X\beta||^2, \quad \text{subject to } || \beta ||_1 \leq t \] Then the graph from Chapter 3 of Hastie et al. (2009) demonstrates how the Lasso regression shrinks a part of coefficients to zero. The advantage of LASSO over ridge regression is that it not only shrinks the coefficients, but performs automatic feature selection.
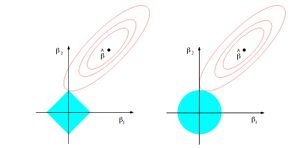
Another type of regression model that is worth mentioning here is what we call Elastic Net Regression. This type of regression model is utilizing both L1 and L2 regularization, namely combining the regularization techniques used in lasso regression and ridge regression together in the objective function. This type of regression could also be of possible interest to be applied in the context of this paper. Its objective function is shown below, where we can see both the sum of absolute value of coefficients and the sum of square of coefficients are included: [math]\displaystyle{ \hat{\beta} = argmin ||y – X \beta||^2 – λ_2 ||\beta||^2 – λ_1||\beta|| }[/math] w.r.t. [math]\displaystyle{ \beta }[/math]
Bias-Variance Trade-Off
The bias is error from erroneous assumptions in the learning algorithm. High bias can cause an algorithm to miss the relevant relations between features and target outputs (underfitting). The variance is error from sensitivity to small fluctuations in the training set. High variance can cause an algorithm to model the random noise in the training data, rather than the intended outputs (overfitting)[3]. Mean square error (MSE) is defined by (variance + squared bias). A thing to mention is the following theorem:
- For ridge regression, there exists a certain λ such that the MSE of coefficients calculated by ridge regression is smaller than that calculated by direct regression.
Related Work
Meta-analysis approaches
Meta analysis is a statistical analysis which combines the results of several studies. There are several methods for non-imaging Meta analysis: p-value combining, fixed effects model, random effects model, and Meta regression. When datasets at different sites cannot be shared or pooled, various strategies exist that cumulate the general findings from analyses on different datasets. However, minor violations of assumptions can lead to misleading scientific conclusions (Greco et al., 2013), and substantial personal judgment (and expertise) is needed to conduct them.
Domain adaptation/shift
The idea of addressing “shift” within datasets has been rigorously studied within statistical machine learning. However, these focuses on the algorithm itself and do not address the issue of whether pooling the datasets, after applying the calculated adaptation (i.e., transformation), is beneficial. The goal in this work is to assess whether multiple datasets can be pooled — either before or usually after applying the best domain adaptation methods — for improving our estimation of the relevant coefficients within linear regression. A hypothesis test is proposed to directly address this question.
Simultaneous High dimensional Inference
Simultaneous high dimensional inference models are an active research topic in statistics. Multi sample- splitting takes half of the data set for feature selection and the remaining portion of the data set for calculating p values. The authors use contributions in this area to extend their results to a higher dimensional setting.
The Hypothesis Test
The hypothesis test to evaluate statistical power improvements (e.g., mean squared error) when running a regression model on a pooled dataset is discussed below.β corresponds to the coefficient vector (i.e., predictor weights), then the regression model is
- [math]\displaystyle{ min_{β} \frac{1}{n}\left \Vert y-Xβ \right \|_2^2 }[/math] ........ (1)
Where $X ∈ R^{n×p}$ and $y ∈ R^{n×1}$ denote the feature matrix of predictors and the response vector respectively. If k denotes the number of sites, a domain adaptation scheme needs to be applied to account for the distributional shifts between the k different predictors [math]\displaystyle{ \lbrace X_i \rbrace_{i=1}^{k} }[/math], and then run a regression model. If the underlying “concept” (i.e., predictors and responses relationship) can be assumed to be the same across the different sites, then it is reasonable to impose the same β for all sites. For example, the influence of CSF protein measurements on cognitive scores of an individual may be invariant to demographics. if the distributional mismatch correction is imperfect, we may define ∆ βi = βi − β∗ where i ∈ {1,...,k} as the residual difference between the site-specific coefficients and the true shared coefficient vector (in the ideal case, we have ∆ βi = 0)[1]. Therefore we derive the Multi-Site Regression equation ( Eq 2) where [math]\displaystyle{ \tau_i }[/math] is the weighting parameter for each site
- [math]\displaystyle{ min_{β} \displaystyle \sum_{i=1}^k {\tau_i^2\left \Vert y_i-X_iβ \right \|_2^2} }[/math] ......... (2)
where for each site i we have $y_i = X_iβ_i +\epsilon_i$ and $\epsilon_i ∼ N (0, σ^2_i) $
Since the underlying relationship between predictors and responses is the same across the different datasets ( from which its pooled), estimates of [math]\displaystyle{ \beta_i }[/math] across all k sites are restricted to be the same. Without this constraint , (3) is equivalent to fitting a regression separately on each site. To explore whether this constraint improves estimation, the Mean Square Error (MSE) needs to be examined[1]. Hence, using site 1 as the reference, and setting [math]\displaystyle{ \tau_1 }[/math] = 1 in (2) and considering [math]\displaystyle{ \beta*=\beta_1 }[/math],
- [math]\displaystyle{ min_{β} \frac{1}{n}\left \Vert y_1-X_1β \right \|_2^2 + \displaystyle \sum_{i=2}^k {\tau_i^2\left \Vert y_i-X_iβ \right \|_2^2} }[/math] .........(3)
To evaluate whether MSE is reduced, we first need to quantify the change in the bias and variance of (3) compared to (1).
Case 1: Sharing all [math]\displaystyle{ \beta }[/math]s
[math]\displaystyle{ n_i }[/math]: sample size of site i
[math]\displaystyle{ \hat{β}_i }[/math]: regression estimate from a specific site i.
[math]\displaystyle{ \Delta β^T }[/math]: length kp vector
[math]\displaystyle{ \hat{\Sigma}_i }[/math]: the sample covariance matrix of the predictors from site i.
[math]\displaystyle{ G \in\mathbb{R}^{(k-1)p \times (k-1)p} }[/math]: the covariance matrix of [math]\displaystyle{ \Delta\hat{β} }[/math], with [math]\displaystyle{ G_{ii}=\left(n_1\hat{\Sigma}_1 \right)^{-1} + \left(n_i\tau_i^2\hat{\Sigma}_i \right)^{-1} }[/math] and [math]\displaystyle{ G_{ij}=\left(n_1\hat{\Sigma}_1 \right)^{-1} }[/math], [math]\displaystyle{ i\neq j }[/math]

Lemma 2.2 bounds the increase in bias and reduction in variance. Theorem 2.3 is the author's main test result.Although [math]\displaystyle{ \sigma_i }[/math] is typically
unknown, it can be easily replaced using its site specific estimation. Theorem 2.3 implies that we can conduct a non-central [math]\displaystyle{ \chi^2 }[/math] distribution test based on the statistic.
Theorem 2.3 implies that the sites, in fact, do not even need to share the full dataset to assess whether pooling will be useful. Instead, the test only requires very high-level statistical information such as [math]\displaystyle{ \hat{\beta}_i,\hat{\Sigma}_i,\sigma_i }[/math] and [math]\displaystyle{ n_i }[/math] for all participating sites – which can be transferred without computational overhead.
One can find R code for the hypothesis test for Case 1 in https://github.com/hzhoustat/ICML2017 as provided by the authors. In particular the Hypotest_allparam.R script provides the hypothesis test whereas Simultest_allparam.R provides some simulation examples that illustrate the application of the test under various different settings.
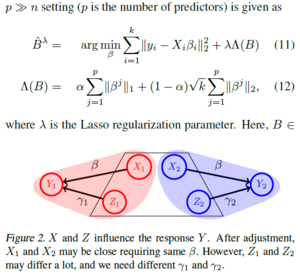
Case 2: Sharing a subset of [math]\displaystyle{ \beta }[/math]s
For example, socio-economic status may (or may not) have a significant association with a health outcome (response) depending on the country of the study (e.g., insurance coverage policies). Unlike Case 1, [math]\displaystyle{ \beta }[/math] cannot be considered to be the same across all sites. The model in (3) will now include another design matrix of predictors [math]\displaystyle{ Z\in R^{n*q} }[/math]and corresponding coefficients [math]\displaystyle{ \gamma_i }[/math] for each site i,
[math]\displaystyle{ min_{β,\gamma} \sum_{i=1}^{k}\tau_i^2\left \Vert y_i-X_iβ-Z_i\gamma_i \right \|_2^2 }[/math] ... (9)
where
[math]\displaystyle{ y_i=X_i \beta^* + X_i \Delta \beta_i + Z_i \gamma_i^* + \epsilon_i, \tau_1=1 }[/math] ... (10)
While evaluating whether the MSE of [math]\displaystyle{ \beta }[/math] reduces, the MSE change in [math]\displaystyle{ \gamma }[/math] is ignored because they correspond to site-specific variables. If [math]\displaystyle{ \hat{\beta} }[/math]is close to the “true” [math]\displaystyle{ \beta^* }[/math], it will
also enable a better estimation of site-specific variables[1]
One can find R code for the hypothesis test for Case 2 in https://github.com/hzhoustat/ICML2017 as provided by the authors. In particular the Hypotest_subparam.R script provides the hypothesis test whereas Simultest_subparam.R provides some simulation examples that illustrate the application of the test under various different settings.
Sparse Multi-Site Lasso and High Dimensional Pooling
Pooling multi-site data in the high-dimensional setting where the number of predictors p is much larger than number of subjects n studied ( p>>n) leads to a high sparsity condition where many variables have their coefficients with limits tending to 0. Lasso Variable Selection helps in selecting the right coefficients for representing the relationship between the predictors and subjects
[math]\displaystyle{ \ell_2 }[/math]-consistency
In the background of asymptotic analysis and approximations, the Lasso estimator is not variable selection consistent if the "Irrepresentable Condition" fails[7]. The Irrepresentable Condition: Lasso selects the true model consistently if and (almost) only if the predictors that are not in the true model are “irrepresentable” (in a sense to be clarified) by predictors that are in the true model. Which means, even if the exact sparsity pattern might not be recovered, the estimator can still be a good approximation to the truth. This also suggests that, for Lasso, estimation consistency might be easier to achieve than variable selection consistency.In classical regression, [math]\displaystyle{ \ell_2 }[/math] consistency properties are well known. Imposing the same [math]\displaystyle{ \beta }[/math] across sites works in (3) because we understand its consistency. In contrast, in the case where p>>n, one cannot enforce a shared coefficient vector for all sites before the active set of predictors within each site are selected — directly imposing the same leads to a loss of [math]\displaystyle{ \ell_2 }[/math]-consistency, making follow-up analysis problematic. Therefore, once a suitable model for high-dimensional multi-site regression is chosen, the first requirement is to characterize its consistency.
Sparse Multi-Site Lasso Regression
The sparse multi-site Lasso variant is chosen because multi-task Lasso underperforms when the sparsity pattern of predictors is not identical across sites[4].The hyperparameter [math]\displaystyle{ \alpha\in [0, 1] }[/math] balances both penalties between L1 regularization and the Group Lasso penalty on a group of features. The difference is that SMS Lasso generalizes the Lasso to the multi-task setting by replacing the L1-norm regularization with the sum of sup-norm regularization[8].
- Larger [math]\displaystyle{ \alpha }[/math] weighs the L1 penalty more
- Smaller [math]\displaystyle{ \alpha }[/math] puts more weight on the grouping.
Note that α = 0.97 discovers more always-active features, while preserving the ratio of correctly discovered active features to all the discovered ones. (MSE vs Sample Size plots(c))
Similar to a Lasso-based regularization parameter, [math]\displaystyle{ \lambda }[/math] here will produce a solution path (to select coefficients) for a given [math]\displaystyle{ \alpha }[/math][1].
Setting the hyperparameter [math]\displaystyle{ \alpha }[/math] using Simultaneous Inference
Step 1: They apply simultaneous inference (like multi sample-splitting or de-biased Lasso) using all features at each of the k sites with FWER control. This step yields “site-active” features for each site, and therefore, gives the set of always-active features and the sparsity patterns
Step 2: Then, each site runs a Lasso and chooses a λi based on cross-validation. Then they set λmulti-site to be the minimum among the best λs from each site. Using λmulti-site , we can vary to fit various sparse multi-site Lasso models – each run will select some number of always-active features. Then plot α versus the number of always-active features.
Step 3: Finally, based on the sparsity patterns from the site-active set, they estimate whether the sparsity patterns across sites are similar or different (i.e., share few active features). Then, based on the plot from step (2), if the sparsity patterns from the site-active sets are different (similar)
across sites, then the smallest (largest) value of that selects the minimum (maximum) number of always-active features is chosen
Experiments
There are 2 distinct experiments described:
- Performing simulations to evaluate the hypothesis test and sparse multi-site Lasso;
- Pooling 2 Alzheimer's Disease datasets and examining the improvements in statistical power. This experiment was also done with the view of evaluating whether pooling is beneficial for regression and whether it yields tangible benefits in investigating scientific hypotheses[1].
Power and Type I Error
- The first set of simulations evaluate Case 1 (Sharing all β): The simulations are repeated 100 times with 9 different sample sizes. As n increases, both MSEs decrease (two-site model and baseline single site model), and the test tends to reject pooling the multi-site data.
- The second set of simulations evaluates Case 2 variables (Sharing subset of β): For small n, MSE of two-site model is much smaller than baseline, and as sample size increases this difference reduces. The test accepts with high probability for small n,and as sample size increases it rejects with high power.
SMS Lasso L2 Consistency
In order to test the Sparse Multi-Site Model, the case where sparsity patterns are shared is considered separately from the case where they are not shared. Here, 4 sites with n = 150 samples each and p = 400 features were used.
- Few Sparsity Patterns Shared:6 shared features and 14 site-specific features (out of the 400) are set to be active in 4 sites. The chosen [math]\displaystyle{ \alpha }[/math]= 0:97 has the smallest error, across all [math]\displaystyle{ \lambda }[/math]s, thereby implying a better [math]\displaystyle{ \ell }[/math]2 consistency. [math]\displaystyle{ \alpha }[/math]= 0:97 discovers more always-active features, while preserving the ratio of correctly discovered active features to all the discovered ones.
- Most Sparsity Patterns Shared: 16 shared and 4 site-specific features to be active among all 400 features were set.The proposed choice of [math]\displaystyle{ \alpha }[/math] = 0.25 preserves the correctly discovered number of always-active features. The ratio of correctly discovered active features to all discovered features increases here.
Combining AD Datasets from Multiple Sites
Pooling is evaluated empirically in a neuroscience problem regarding the combination of 2 Alzheimer's Datasets from different sources: ADNI (Alzheimer’s Disease Neuroimage Initiative) and ADlocal ( Wisconsin ADRC). The sample sizes are 318 and 156 respectively. Cerebrospinal fluid (CSF) protein levels are the inputs, and the response is hippocampus volume. Using 81 age-matched samples from each dataset, first domain adaptation is performed (using a maximum mean discrepancy objective as a measure of distance between the two marginals), and then transform CSF proteins from ADlocal to match with ADNI. The main aim is to evaluate whether adding ADlocal data to ADNI will improve the regression performed on ADNI. This is done by training a regression model on the ‘transformed’ ADlocal and a subset of ADNI data, and then testing the resulting model on the remaining ADNI samples.
- The results show that pooling after transformation is at least as good as using ADNI data alone, thereby accepting the hypothesis test. The test rejection power increases with increase in n. The strategy rejects the pooling test if performed without domain adaptation[1].
Conclusion
The following are the contributions by the authors' research.
- The main result is a hypothesis test to evaluate whether pooling data across multiple sites for regression (before or after correcting for site-specific distributional shifts) can improve the estimation (mean squared error) of the relevant coefficients (while permitting an influence from a set of confounding variables).
- Show how pooling can be used ( in certain regimes of high dimensional and standard linear regression) even when the features are different across sites. For this the authors show the [math]\displaystyle{ \ell_2 }[/math]-consistency rate which supports the use of spare-multi-task Lasso when sparsity patterns are not identical
- Experimental results showing consistent acceptance power for early Alzheimer’s detection (AD) in humans, where data are pooled from different sites.
Critique
The main premise underlying pooling multiple datasets from a variety of sites is that the small, local sites can borrow statistical strength from the larger pooled, multisite data. Bayesian hierarchical models provide one standard tool that allow borrowing of statistical strength from a gestalt to an instance. While the current paper is very much in the frequentist spirit, there should be some justification as to why (or even whether) the pooling technique explicated in the paper may be a good alternative. Indeed, it is not even exactly clear whether the asymptotic properties enjoyed by the pooling method represent any substantial gain relative to classical methods from either Bayesian or frequentist statistics. Deciding whether to use the pooling method in practice will be difficult unless a careful comparative study is undertaken on, first, a theoretical level to quantify the extent to which better stability and asymptotic properties are obtained and second, a practical level with benchmark bio-medical datasets to see whether the theoretical guarantees obtain in real situations.
References
- Hao Henry Zhou, Yilin Zhang, Vamsi K. Ithapu, Sterling C. Johnson, Grace Wahba, Vikas Singh, When can Multi-Site Datasets be Pooled for Regression? Hypothesis Tests, [math]\displaystyle{ \ell_2 }[/math]-consistency and Neuroscience Applications, ICML 2017
- https://www.analyticsvidhya.com/blog/2016/01/complete-tutorial-ridge-lasso-regression-python/
- Understanding the Bias-Variance Tradeoff - Scott Fortmann Roe Link
- G Swirszcz, AC Lozano, Multi-level lasso for sparse multi-task regression, ICML 2012
- A Visual representation L1, L2 Regularization - https://www.youtube.com/watch?v=sO4ZirJh9ds
- Why does L1 induce sparse weights? https://www.youtube.com/watch?v=jEVh0uheCPk
- Meinshausen, Nicolai and Yu, Bin. Lasso-type recovery of sparse representations for high-dimensional data. The Annals of Statistics.
- Liu, Han, Palatucci, Mark, and Zhang, Jian. Blockwise coordinate descent procedures for the multi-task lasso, with applications to neural semantic basis discovery. In Proceedings of the 26th Annual International Conference on Machine Learning, pp. 649–656. ACM, 2009
- http://ncss.wpengine.netdna-cdn.com/wp-content/themes/ncss/pdf/Procedures/NCSS/Ridge_Regression.pdf