When Does Self-Supervision Improve Few-Shot Learning?
Presented by
Arash Moayyedi
Introduction
This paper seeks to solve the generalization issues in few-shot learning by applying self-supervised learning techniques on the base dataset. Few-shot learning refers to training a classifier on minimalist datasets, contrary to the normal practice of using massive data, in hope of successfully classifying previously unseen, but related classes. Additionally, self-supervised learning aims at teaching the agent the internal structures of the images by providing it with tasks such as predicting the degree of rotation in an image. This method helps with the mentioned generalization issue, where the agent cannot distinguish the difference between newly introduced objects.
Previous Work
This work leverages few-shot learning, where we aim to learn general representations, so that when facing novel classes, the agent can differentiate between them with training on just a few samples. Many few-shot learning methods currently exist, among which is this paper which focuses on Prototypical Networks or ProtoNets[1] for short. There is also a section of this paper that compares this model with model-agnostic meta-learner (MAML)[2].
The other machine learning technique that this paper is based on is self-supervised learning. In this technique we find a use for unlabelled data, while labelling and maintaining massive data is expensive. The image itself already contains structural information that can be utilized. There exist many SSL tasks, such as removing a part of the data in order for the agent to reconstruct the lost part. Other methods include tasks prediction rotations, relative patch location, etc.
The work in this paper is also related to multi-task learning. In multi-task learning training proceeds on multiple tasks concurrently to improve each other. Training on multiple tasks is known to decline the performance on individual tasks[3] and this seems to work only for very specific combinations and architectures. This paper shows that the combination of self-supervised tasks and few-shot learning are mutually beneficial to each other and this has significant practical implications since self-supervised tasks do not require any annotations.
Method
The authors of this paper suggest a framework, as seen in Fig. 1, that combines few-shot learning with self-supervised learning. The labeled training data consists of a set of base classes in pairs of images and labels, and its domain is denoted by [math]\displaystyle{ \mathcal{D}_s }[/math]. Similarly, the domain of the images used for the self-supervised tasks is shown by [math]\displaystyle{ \mathcal{D}_{ss} }[/math]. This paper also analyzes the effects of having [math]\displaystyle{ \mathcal{D}_s = \mathcal{D}_{ss} }[/math] versus [math]\displaystyle{ \mathcal{D}_s \neq \mathcal{D}_{ss} }[/math] on the accuracy of the final few-shot learning task.
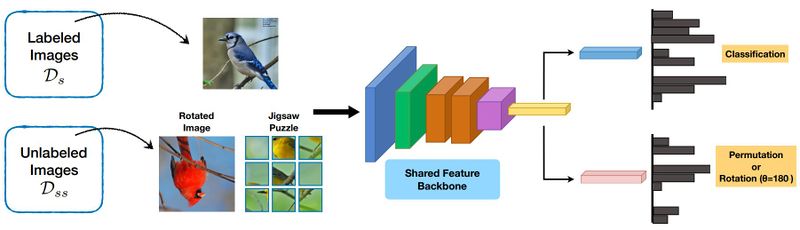
The input is connected to a feed-forward convolutional network [math]\displaystyle{ f(x) }[/math] and it is the shared backbone between the classifier [math]\displaystyle{ g }[/math] and the self-supervised target predictor [math]\displaystyle{ h }[/math]. The classification loss [math]\displaystyle{ \mathcal{L}_s }[/math] and the task prediction loss [math]\displaystyle{ \mathcal{L}_{ss} }[/math] are written as:
[math]\displaystyle{ \mathcal{L}_s := \sum_{(x_i,y_i)\in \mathcal{D}_s} \ell(g \circ f(x_i), y_i) + \mathcal{R}(f,g), }[/math]
[math]\displaystyle{ \mathcal{L}_{ss} := \sum_{x_i\in \mathcal{D}_{ss}} \ell(h \circ f(\hat{x_i}), \hat{y_i}). }[/math]
It is common to use cross-entropy loss for the loss function, [math]\displaystyle{ \ell }[/math], and [math]\displaystyle{ \ell_2 }[/math] norm for the regularization, [math]\displaystyle{ \mathcal{R} }[/math], in the above equations. Also, two common tasks for self-supervised losses as shown in Fig. 1 are the so-called jigsaw task and the rotation task. The jigsaw puzzle breaks the image into 3x3 regions, rearranges them and the training is done on the permutation of the indices. The rotated image task rotates the image with an angle [math]\displaystyle{ \theta \in \{0^{\circ}, 90^{\circ}, 180^{\circ}, 270^{\circ}\} }[/math] and the training is done on [math]\displaystyle{ \theta }[/math].
The final loss is [math]\displaystyle{ \mathcal{L} := \mathcal{L}_s + \mathcal{L}_{ss} }[/math], and thus the self-supervised losses act as a data-dependent regularizer for representation learning. The gradient updates are therefore performed based on this combined loss. It should be noted that in case [math]\displaystyle{ \mathcal{D}_s \neq \mathcal{D}_{ss} }[/math], a forward pass is done on a batch per each dataset, and the two losses are combined.
Experiments
The authors of this paper have experimented on the following datasets: Caltech-UCSD birds, Stanford cars, FGVC aircraft, Stanford dogs, Oxford flowers, mini-ImageNet, and tiered-Imagenet. Each dataset is divided into three disjoint sets: base set for training the parameters, val set for validation, and the novel set for testing with a few examples per each class. Data augmentation has been used with all these datasets to improve the results.
Two tasks have been used for the self-supervised learning part, rotation and the Jigsaw puzzle[4]. In the rotation task the image is rotated by an angle [math]\displaystyle{ \theta \in \{0^{\circ}, 90^{\circ}, 180^{\circ}, 270^{\circ}\} }[/math], which results in the input, and the target label is the index of the rotation in the list. In the Jigsaw puzzle task, the image is tiled into [math]\displaystyle{ 3\times3 }[/math] tiles and then these tiles are shuffled to produce the input image. The target is a number in range of 35 based on the hamming distance.
Results
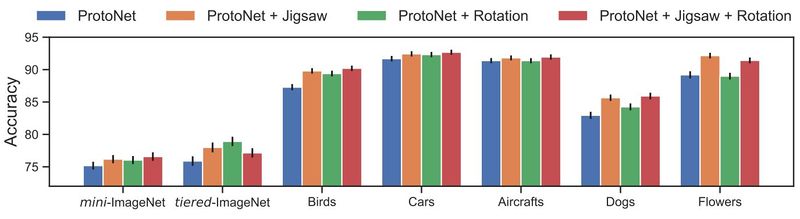
The results on 5-way 5-shot classification accuracy can be seen in Fig. 2. ProtoNet has been used as a baseline and is compared with the Jigsaw task, the rotation task, and both of them combined. The result is that the Jigsaw task always improves the result. However, the rotation task seems to not provide much improvement on the flowers and the aircraft datasets. The authors speculate that this might be because flowers are mostly symmetrical, making the task too hard, and that the planes are usually horizontal, making the task too simple.
In another attempt, it is also proven that the improvements self-supervised learning provides are much higher in more difficult few-shot learning problems. As it can be observed from Fig. 3, SSL is found to be more beneficial with greyscale or low-resolution images, which make the classification harder for natural and man-made objects, respectively.

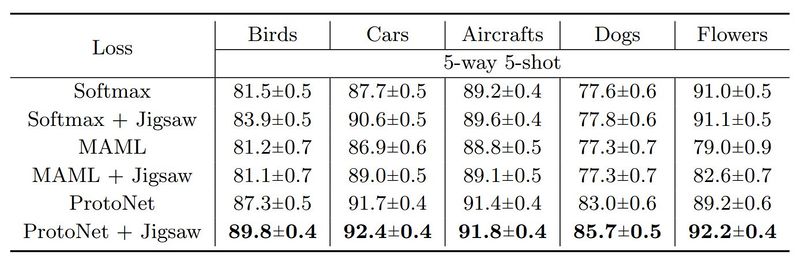
Self-supervision has also been combined with two other meta-learners in this work, MAML and a standard feature extractor trained with cross-entropy loss (softmax). Fig. 4 summarizes these results, and even though there is an accuracy gain in all scenarios (except for two), the ProtoNet + Jigsaw combination seems to work best.
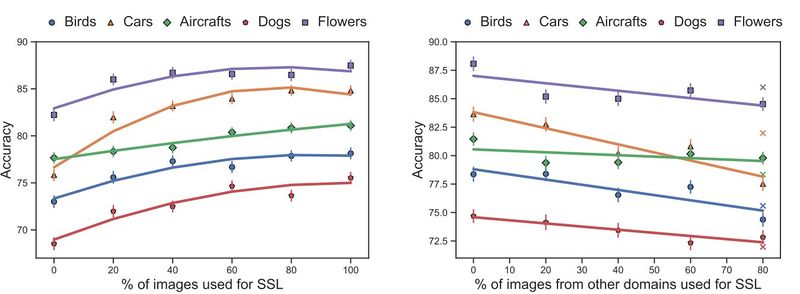
In Fig. 5 you can see the effects of size and domain of SSL on 5-way 5-shot classification accuracy. First, only 20 percent of the data is used for meta-learning. Fig. 5(a) shows the changes in the accuracy based on increasing the percentage of the images, from the whole dataset, used for SSL. It is observed that increasing the size of the SSL dataset domain has a positive effect, with diminishing ends. Fig. 5(b) shows the effects of shifting the domain of the SSL dataset, by changing a percentage of the images with pictures from other datasets. This has a negative result and moreover, training with SSL on the 20 percent of the images used for meta-learning is often better than increasing the size, but shifting the domain. This is shown as crosses on the chart.
The improvements obtained here generalize to other meta-learners as well. For instance, 5-way 5-shot accuracies across five fine-grained datasets for softmax, MAML, and ProtoNet improve when combined with the jigsaw puzzle task.
Results also show that Self-supervision alone is not enough. A ResNet18 trained with SSL alone achieved 32.9% (w/ jigsaw) and 33.7% (w/ rotation) 5-way 5-shot accuracy averaged across five fine-grained datasets. While this is better than a random initialization (29.5%), it is dramatically worse than one trained with a simple cross-entropy loss (85.5%) on the labels.
Conclusion
The authors of this paper provide us with a great insight on the effects of using SSL as a regulizer for few-shot learning methods. It is proven that SSL is beneficial in almost every case, however, these improvements are much higher in more difficult tasks. It also showed that the dataset used for SSL should not necessarily be large. Increasing the size of the mentioned dataset can possibly help, but only if the added images are from the same or a similar domain.
Critiques
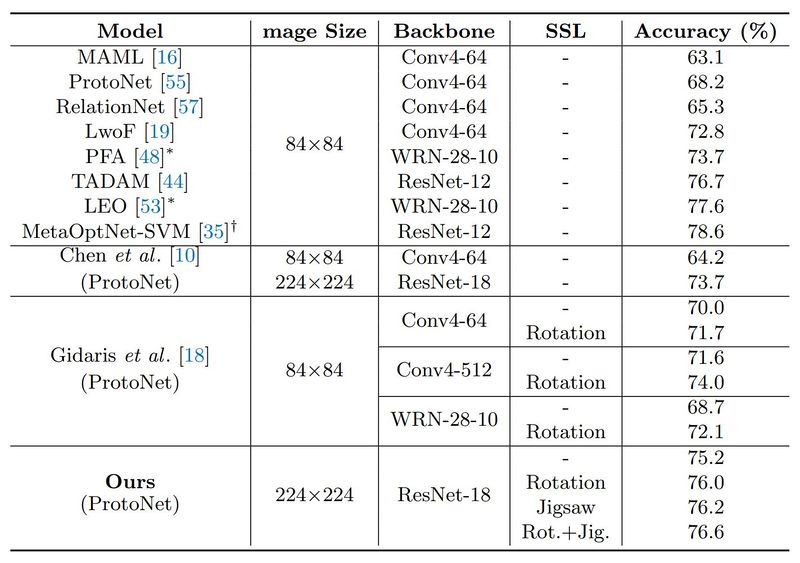
The authors of this paper could have analyzed other SSL tasks in addition to the Jigsaw puzzle and the rotation task, e.g. number of objects and removed patch prediction. Additionally, while analyzing the effects of the data used for SSL, they did not experiment with adding data from other domains, while fully utilizing the base dataset. Moreover, comparing their work with previous works (Fig. 6), we can see they have used mini-ImageNet with a picture size of [math]\displaystyle{ 244\times224 }[/math] in contrast to other methods that have used a [math]\displaystyle{ 84\times84 }[/math] image size. This gives them a huge advantage, however, we still notice that other methods with smaller images have achieved higher accuracy.
References
[1]: Snell, J., Swersky, K., Zemel, R.: Prototypical networks for few-shot learning. In: NeurIPS (2017)
[2]: Finn, C., Abbeel, P., Levine, S.: Model-agnostic meta-learning for fast adaptation of deep networks. In: ICML (2017)
[3]: Kokkinos, I.: Ubernet: Training a universal convolutional neural network for low-, mid-, and high-level vision using diverse datasets and limited memory. In: CVPR (2017)
[4]: Noroozi, M., Favaro, P.: Unsupervised learning of visual representations by solving jigsaw puzzles. In: ECCV (2016)